Impact of Spatial Rainfall Scenarios on River Basin Runoff Simulation a Nan River Basin Study Using the Rainfall-Runoff-Inundation Model
Abstract
:1. Introduction
2. Data Sets and Methods
2.1. Nan River Basin
2.2. Rainfall-Runoff-Inundation Model
2.3. Storm Events and Rainfall Observation Data
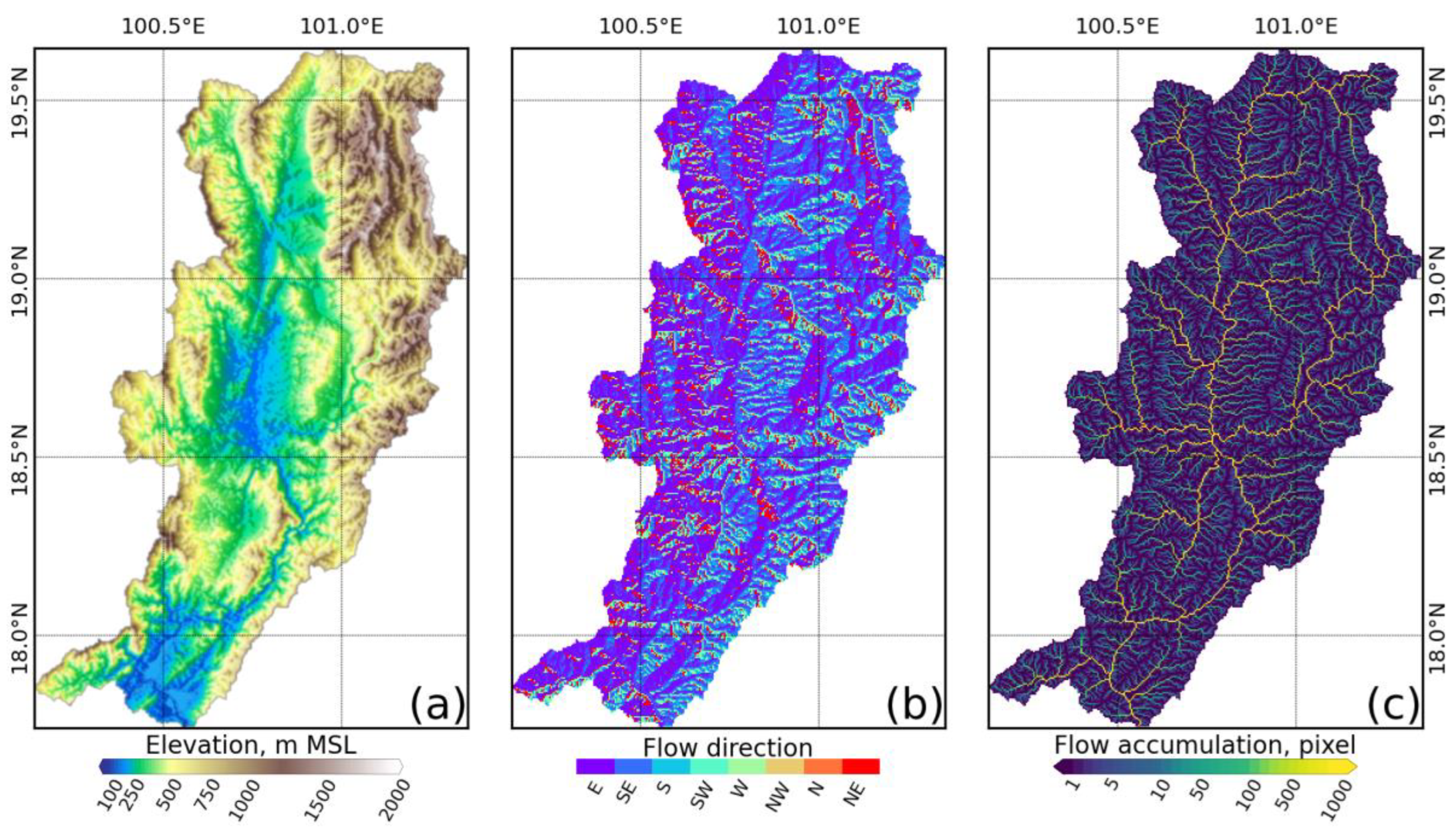
2.4. Topography Data
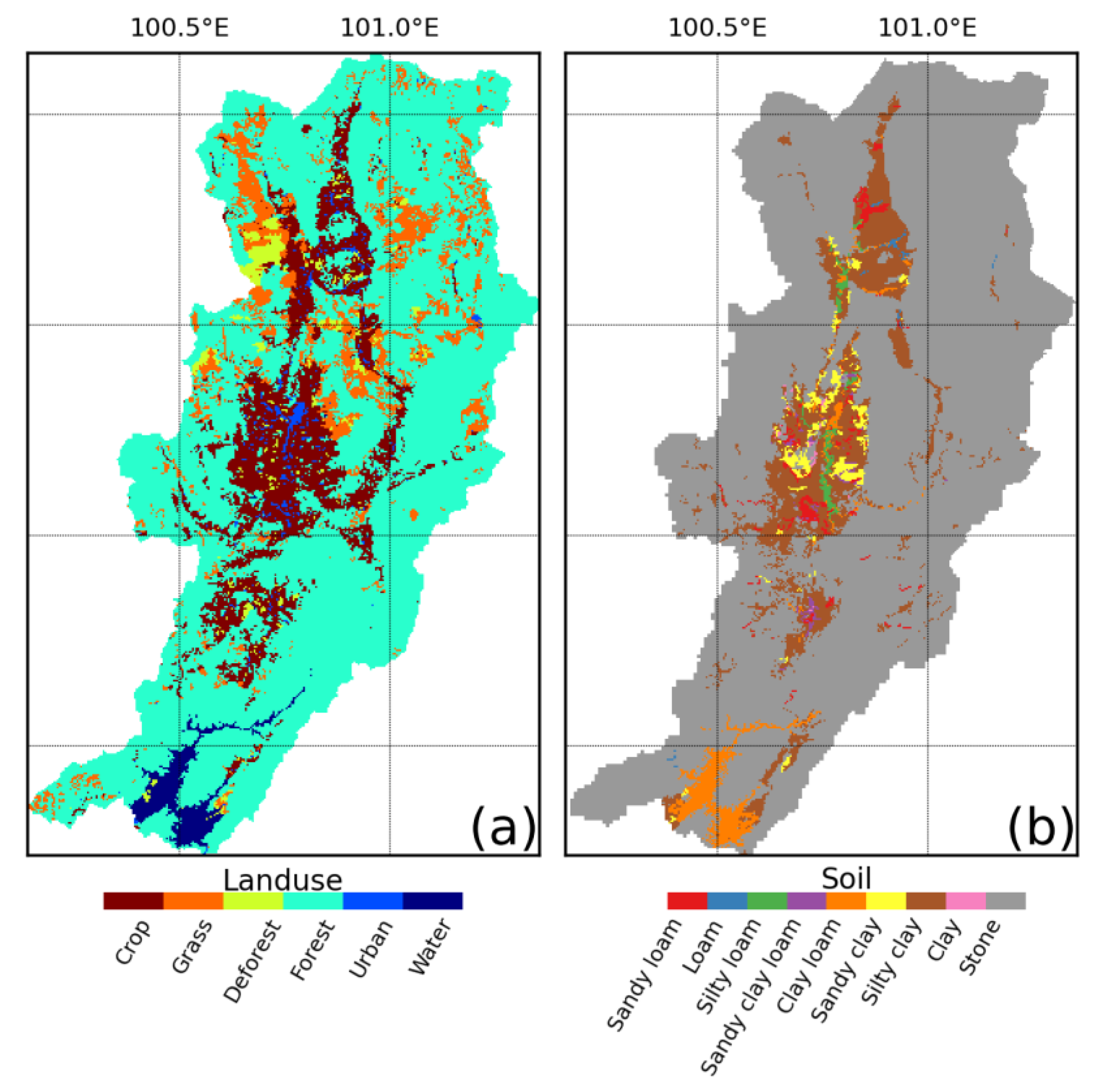
2.5. Landuse and Soil Types
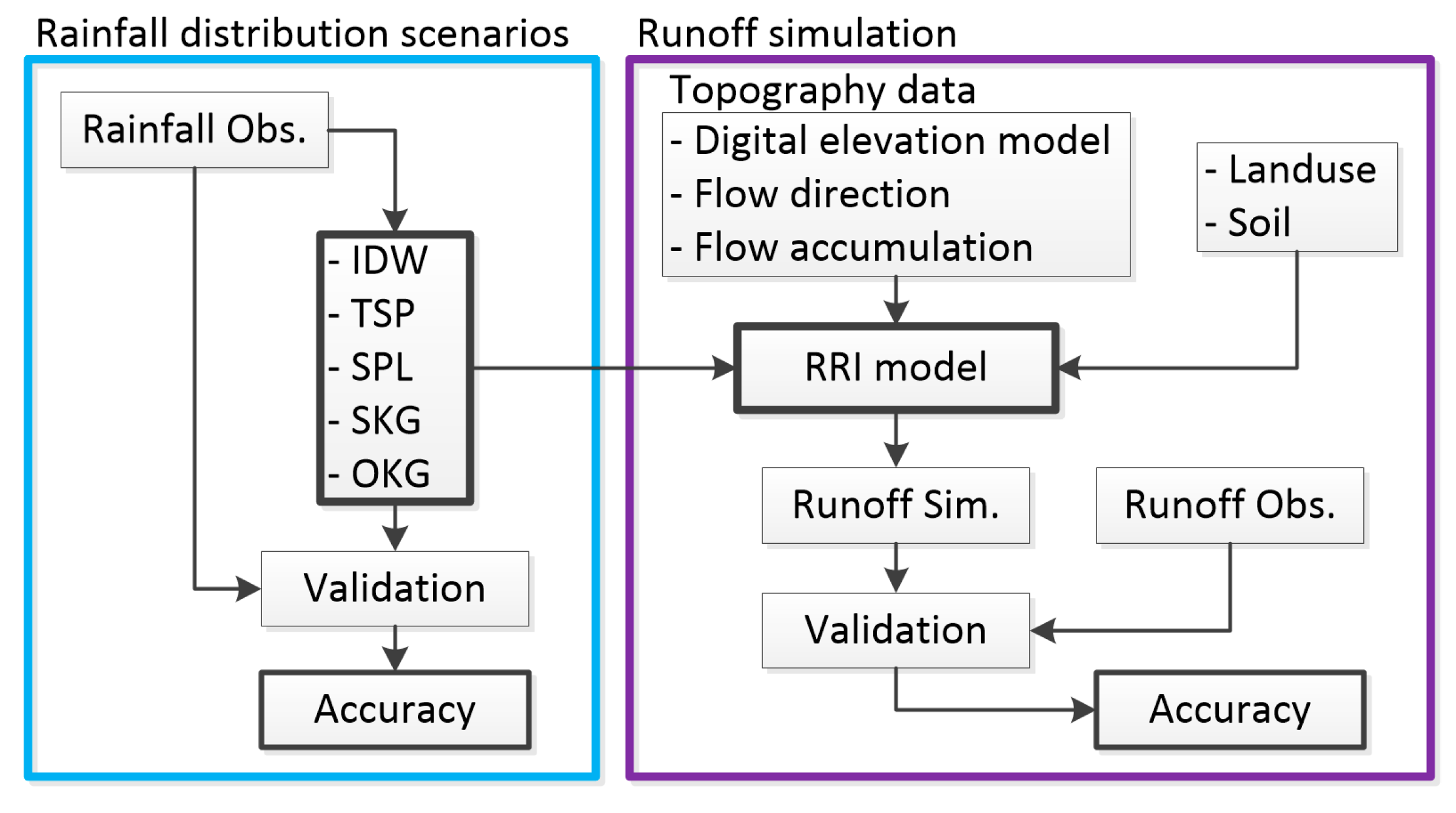
3. Methodology
3.1. Rainfall Spatial Scenario
3.1.1. Inverse Distance Weight (IDW)
3.1.2. Thiessen Polygon (TSP)
3.1.3. Surface Polynomial (SPL)
3.1.4. Simple Kriging (SKG)
3.1.5. Ordinary Kriging (OKG)
3.1.6. Semi-Variogram Model
3.2. Simulation Model Setup
3.3. Performance Statistics
4. Results and Discussion
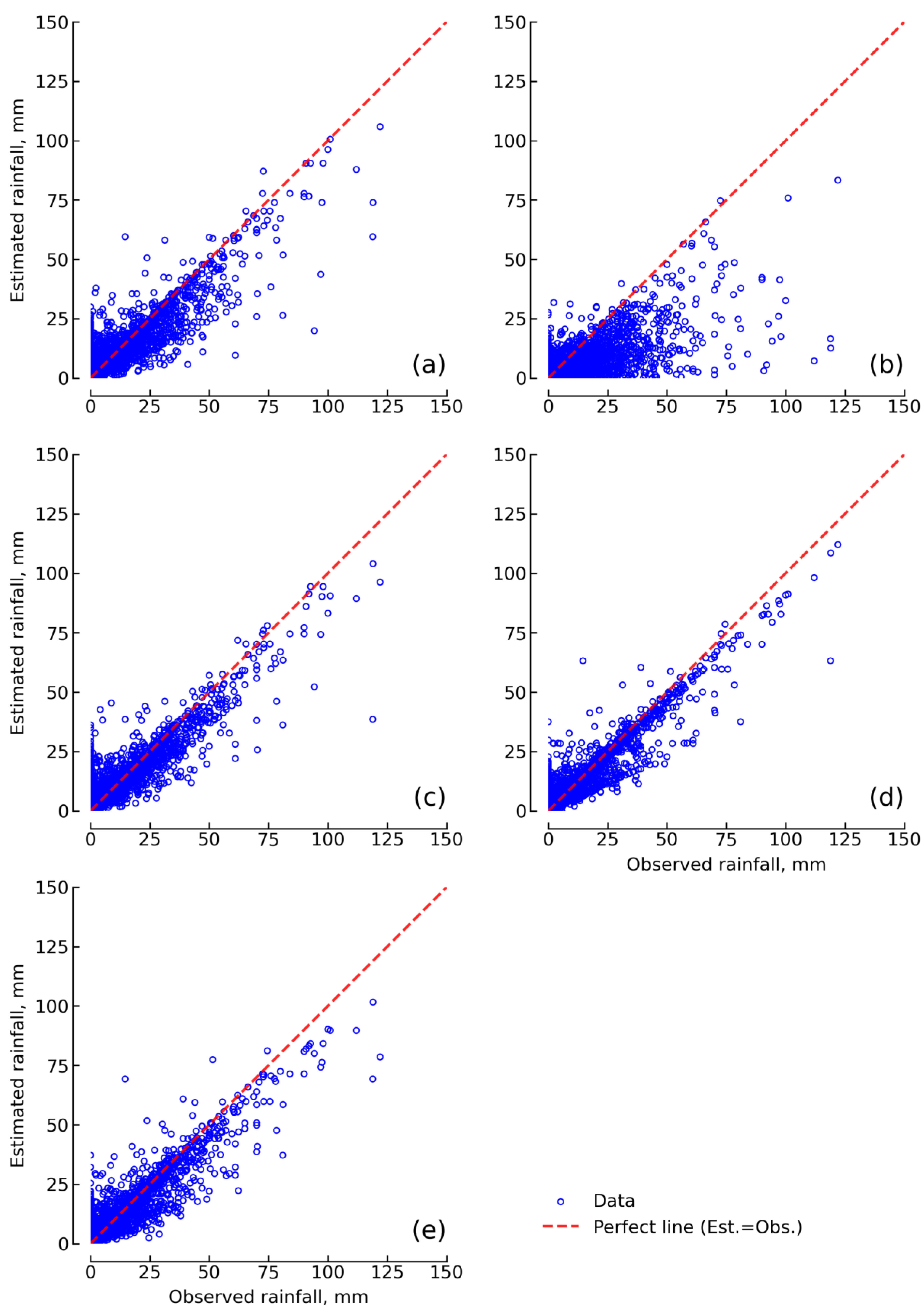
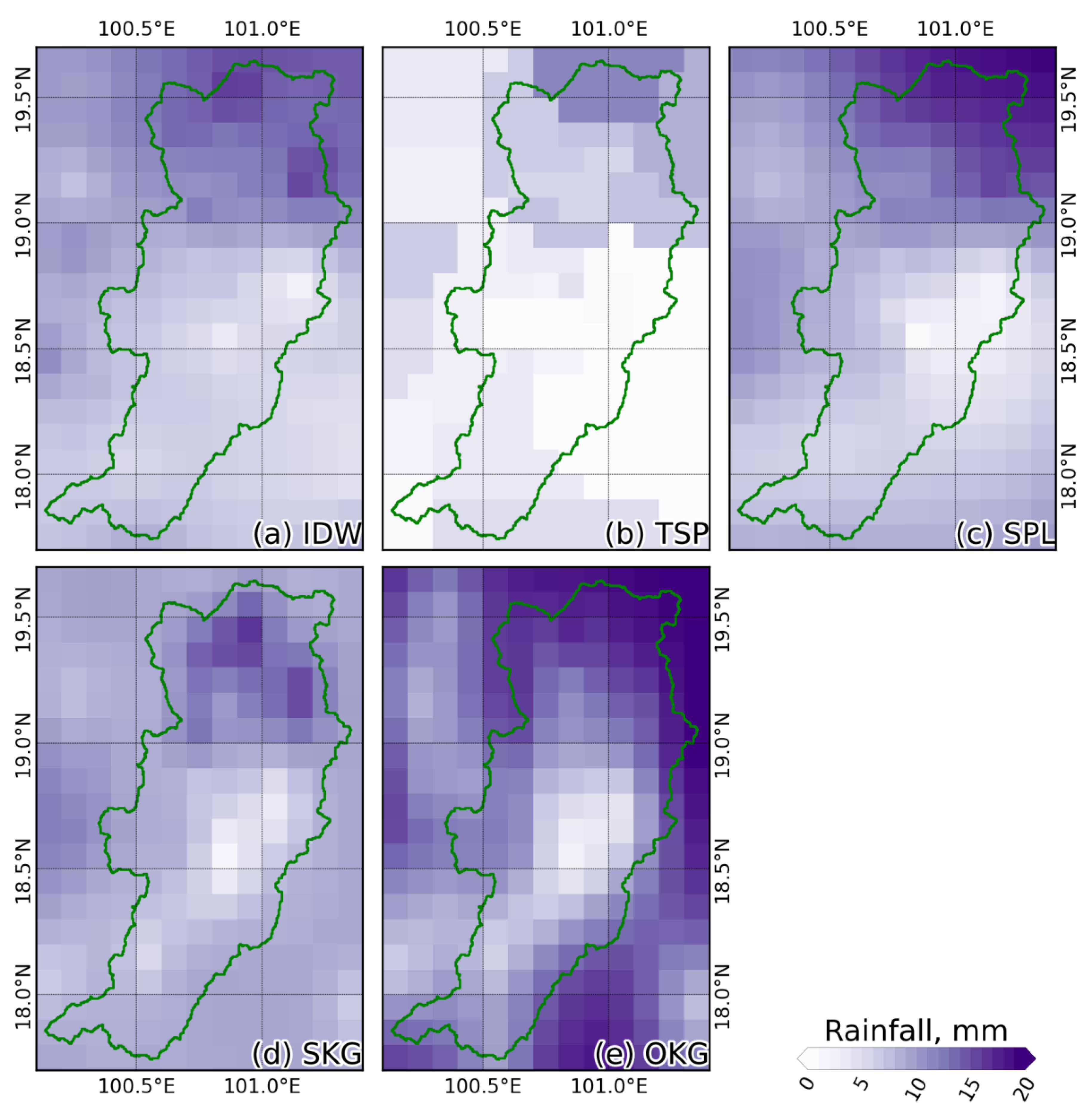
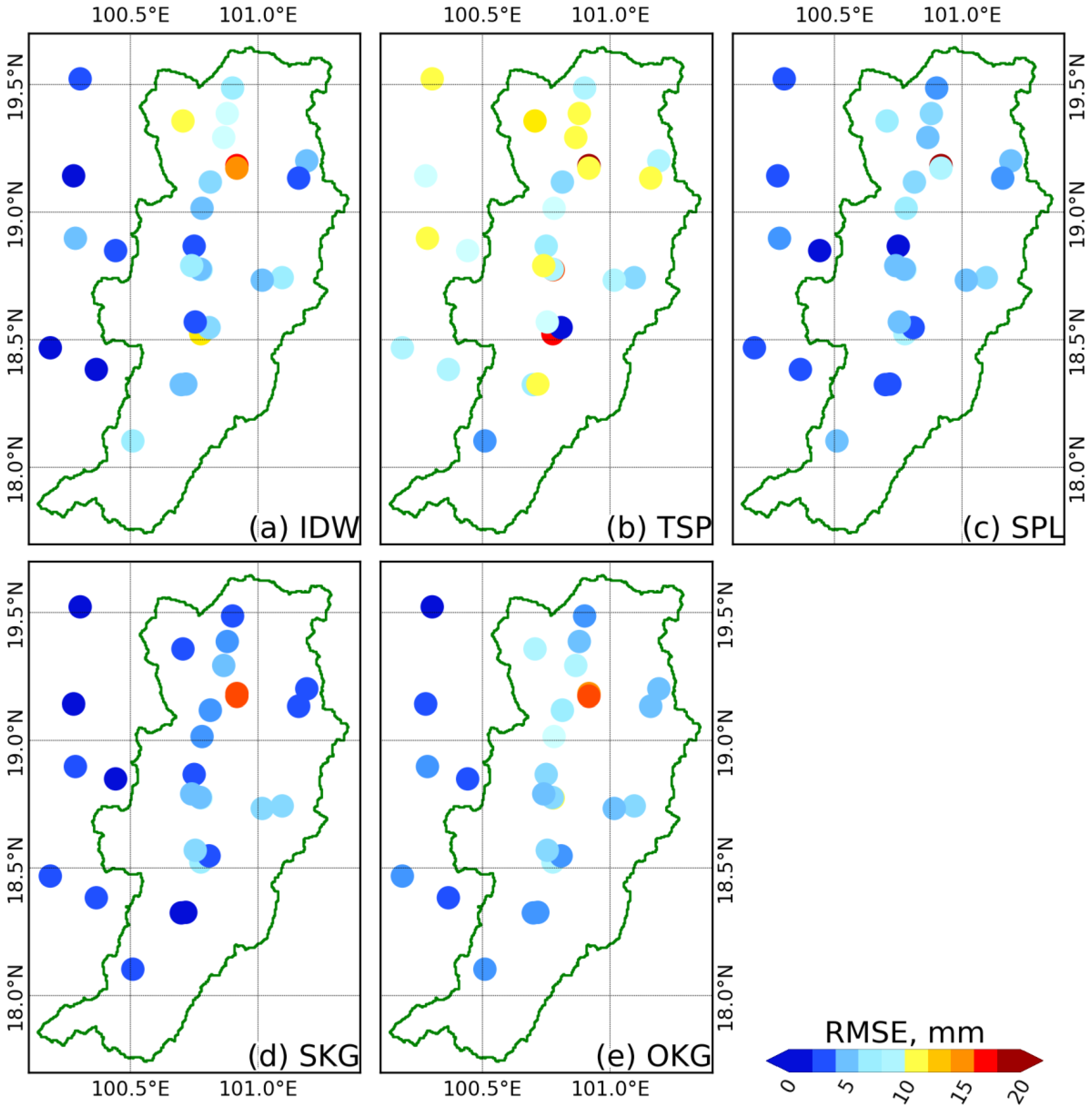
4.1. Rainfall Spatial Distribution Interpolation
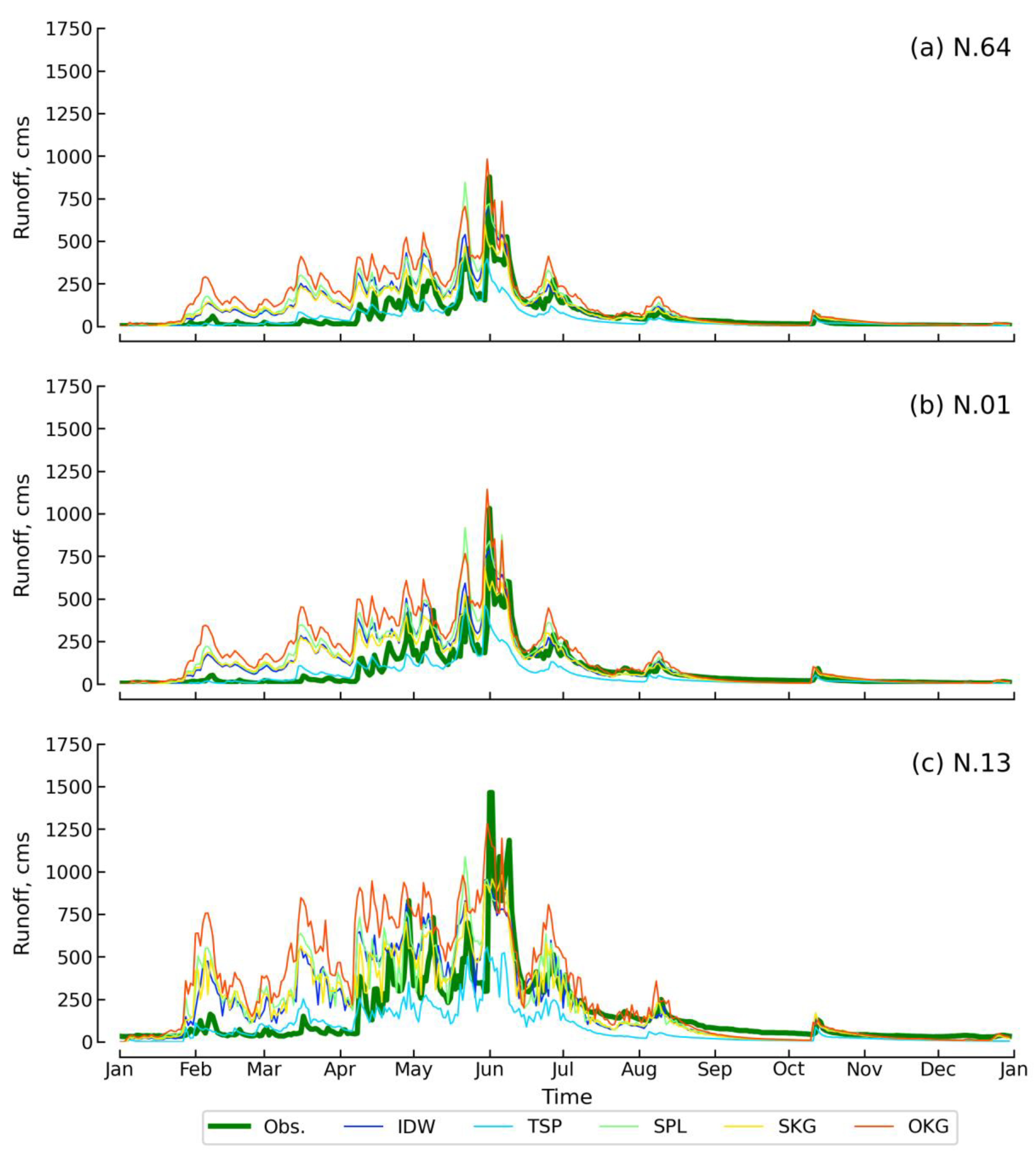
4.2. Runoff Data Resulted from Rainfall Spatial Distribution Interpolation
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Goodrich, D.C.; Faures, J.M.; Woolhiser, D.A.; Lane, L.J.; Sorooshain, S. Measurements and analysis of small-scale convective storm rainfall variability. J. Hydrol. 1995, 173, 283–308. [Google Scholar] [CrossRef]
- Schuurmans, J.M.; Bierkens, M.F.P. Effect of spatial distribution of daily rainfall on interior catchment reponse of a distributed hydrological model. Hydrol. Earth Syst. Sci. 2007, 11, 677–693. [Google Scholar] [CrossRef]
- Kim, C.; Kim, D.-H. Effects of Rainfall Spatial Distribution on the Relationship between Rainfall Spatiotemporal Resolution and Runoff Prediction Accuracy. Water 2020, 12, 846. [Google Scholar] [CrossRef]
- Wei, Z.; Sun, H.; Xu, H.; Wu, G.; Xie, W. The effects of rainfall regimes and rainfall characteristics on peak discharge in a small debris flow-prone catchment. J. Mt. Sci. 2019, 16, 1646–1660. [Google Scholar] [CrossRef]
- Yu, D.; Dian, L.; Hai, Y.; Randall, M.; Li, L.; Liu, J.; Zhang, J.; Zheng, X.; Wei, Y. Effect of rainfall characteristics on the sewer sediment, hydrograph, and pollutant discharge of combined sewer overflow. J. Environ. Manag. 2022, 303, 114268. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Xiong, L.; Li, H.; Liao, Z.; Yin, H.; Wu, J.; Jin, X.; Chen, H. Influences of rainfall variables and antecedent discharge on urban effluent concentrations and loads in wet weather. Water Sci. Technol. 2017, 75, 1584–1598. [Google Scholar] [CrossRef] [PubMed]
- Xiong, J.; Tang, C.; Gong, L.; Chen, M. Variability of rainfall time distributions and their impact on peak discharge in the Wenchuan County, China. Bull. Eng. Geol. Environ. 2021, 80, 7113–7129. [Google Scholar] [CrossRef]
- Tsintikidis, D.; Georgakakos, K.P.; Sperfslage, J.A.; Smith, D.E.; Carpenter, T.M. Precipitation uncertainty and rain gauge network design within Folsom Lake watershed. J. Hydrol. Eng. 2002, 7, 175–184. [Google Scholar] [CrossRef]
- Chintalapudi, S.; Sharif, H.O.; Yeggina, S.; Elhassan, A. Physically-based, hydrologic model results based on three precipitation products. J. Am. Water Resour. Assoc. 2012, 48, 1191–1203. [Google Scholar] [CrossRef]
- Arnaud, P.; Bouvier, C.; Cisner, L.; Dominguez, R. Influence of rainfall spatial variability on flood prediction. J. Hydrol. 2002, 260, 216–230. [Google Scholar] [CrossRef]
- Bell, V.A.; Moore, R.J. The sensitivity of catchment runoff models to rainfall data at different spatial scales. Hydrol. Earth Syst. Sci. 2000, 4, 653–667. [Google Scholar] [CrossRef]
- Hohmann, C.; Kirchengast, G.O.S.; Rieger, W.; Foelsche, U. Runoff sensitivity to spatial rainfall variability: A hydrological modeling study with dense rain gauge observations. Hydrol. Earth Syst. Sci. Discuss. 2020, 29, 1–28. [Google Scholar] [CrossRef]
- Trinugroho, M.W. Evaluating Influence of Number and Distribution Rainfall Stations on Rainfall-Runoff Simulation in Ping River, Thailand. J. Sumber Daya Air 2018, 14, 31–46. [Google Scholar] [CrossRef]
- Hohmann, C.; Kirchengast, G.O.S.; Rieger, W.; Foelsche, U. Small Catchment Runoff Sensitivity to Station Density and Spatial Interpolation: Hydrological Modeling of Heavy Rainfall Using a Dense Rain Gauge Network. Water 2021, 13, 1381. [Google Scholar] [CrossRef]
- Choi, Y.S.; Shin, M.-J.; Kim, K.T. Preliminary Study of Computational Time Steps in a Physically Based Distributed Rainfall–Runoff Model. Water 2018, 10, 1269. [Google Scholar] [CrossRef]
- Wang, Y.; Karimi, H.A. Impact of spatial distribution information of rainfall in runoff simulation using deep learning method. Hydrol. Earth Syst. Sci. 2022, 26, 2387–2403. [Google Scholar] [CrossRef]
- Sayama, T.; Ozawa, G.; Kawakami, T.; Nabesaka, S.; Fukami, K. Rainfall-runoff-inundation analysis of the 2010 Pakistan flood in the Kabul River basin. Hydrol. Sci. J. 2012, 57, 298–312. [Google Scholar] [CrossRef]
- Shakti, P.C.; Miyamoto, M.; Misumi, R.; Nakamura, Y.; Sriariyawat, A.; Visessri, S.; Kakinuma, D. Assessing Flood Risk of the Chao Phraya River Basin Based on Statistical Rainfall Analysis. J. Disaster Res. 2020, 15, 1025–1039. [Google Scholar] [CrossRef]
- Sriariyawat, A.; Pakoksung, K.; Sayama, T.; Tanaka, S.; Koontanakulvong, S. Approach to Estimate the Flood Damage in Sukhothai Province Using Flood Simulation. J. Disaster Res. 2013, 8, 406–414. [Google Scholar] [CrossRef]
- Arlis, A.P.; Farid, M.; Wahid, A.N.; Suryadi, Y.; Kuntoro, A.A. Prediction of Flooding Area in Batang Sinamar River Basin Based on Design Return Period Simulation by Using Rainfall Runoff Inundation Model. Environ. Sci. Proc. 2023, 25, 91. [Google Scholar] [CrossRef]
- Sihombing, Y.I.; Rizaldi, A.; Farid, M.; Januriyadi, N.F.; Moe, I.R. Jakarta’s 2020 New Year Flood Assessment with a Rainfall–Runoff–Inundation (RRI) Model. Environ. Sci. Proc. 2023, 25, 100. [Google Scholar] [CrossRef]
- Cahyaningtiyas, I.F.; Djoharin, M.; Grace, T.; Eugenie, A.; Avian, E.; Amaliyah, R.; Sapan, E.G.A.; Meliani, F.; Sulistyowati, R.; Priyadi, H.; et al. Preliminary Study on the Rainfall-Runoff Inundation and Its Economic Lost at Bekasi River Basin, West Jawa. In Proceedings of the 2022 IEEE Asia-Pacific Conference on Geoscience, Electronics and Remote Sensing Technology (AGERS), Surabaya, Indonesia, 21–22 December 2022; pp. 162–168. [Google Scholar] [CrossRef]
- Momoi, M.; Kotsuki, S.; Kikuchi, R.; Watanabe, S.; Yamada, M.; Abe, S. Emulating Rainfall–Runoff-Inundation Model Using Deep Neural Network with Dimensionality Reduction. Artif. Intell. Earth Syst. 2023, 2, e220036. [Google Scholar] [CrossRef]
- Shahid, H.; Toyoda, M.; Kato, S. Impact Assessment of Changing Landcover on Flood Risk in the Indus River Basin Using the Rainfall–Runoff–Inundation (RRI). Sustainability 2022, 14, 7021. [Google Scholar] [CrossRef]
- Chansaengkrachang, K.; Luadsong, A.; Aschariyaphotha, N. A Study of the Time Lags of the Indian Ocean Dipole and Rainfall Over Thailand by Using the Cross Wavelet Analysis. Arab. J. Sci. Eng. 2015, 40, 215–225. [Google Scholar] [CrossRef]
- Tantanee, S. Trends in Precipitation in Thailand from 1964 to 2012. Asia-Pac. J. Sci. Technol. 2016, 21, APST-21. [Google Scholar]
- Sangkharat, K.; Thornes, J.E.; Wachiradilok, P.; Pope, F.D. Determination of the impact of rainfall on road accidents in Thailand. Heliyon 2021, 7, e06061. [Google Scholar] [CrossRef] [PubMed]
- Pilahome, O.; Homchampa, C.; Kumharn, W. Trends of Climate Variables and Aerosol Optical Depth in Thailand. IOP Conf. Ser. Earth Environ. Sci. 2020, 489, 012029. [Google Scholar] [CrossRef]
- Pinidluek, P.; Konyai, S.; Sriboonlue, V. Regionalization of rainfall in northeastern Thailand. Int. J. Geomate 2020, 18, 135–141. [Google Scholar] [CrossRef]
- Schneider, T.; Bischoff, T.; Hang, G.H. Migrations and dynamics of the intertropical convergence zone. Nature 2014, 513, 45–53. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4. CGIAR-CSI SRTM 90 m Database 2008. Available online: http://srtm.csi.cgiar.org (accessed on 1 July 2012).
- Thenkabali, P.S.; Biradar, C.M.; Noojipady, P.; Dheeravath, V.; Li, Y.; Velpuri, M.; Gumma, M.; Gangalakunta, O.R.P.; Turral, H.; Cai, X.; et al. Global irrigated area map (GIAM), derived from remote sensing, for the end of the last millennium. Int. J. Remote Sens. 2009, 30, 3679–3733. [Google Scholar] [CrossRef]
- Land Development Department, Thailand. Soil Type. Available online: https://tswc.ldd.go.th/DownloadGIS/Index_Soil.html (accessed on 1 October 2023).
- Teegavarapu, R.; Chandramouli, V. Improved weighting methods, deterministic and stochastic data-driven models for estimation of missing precipitation records. J. Hydrol. 2005, 312, 191–206. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Lloyd, C.D. Assessing the effect of integrating elevation data into the estimation of monthly precipitation in Great Britain. J. Hydrol. 2005, 308, 128–150. [Google Scholar] [CrossRef]
- Nalder, I.A.; Wein, R.W. Spatial interpolation of climatic Normals: Test of a new method in the Canadian boreal forest. Agric. For. Meteorol. 1998, 92, 211–225. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degre, A. Different methods for spatial interpolation of rainfall data for operational hydrology and hydrological modeling at watershed scale: A review. Biotechnol. Agron. Soc. Environ. 2013, 17, 392–406. [Google Scholar]
- Tabios, G.Q.; Salas, J.D. A comparative analysis of techniques for spatial interpolation of precipitation. Water Resour. Bull. 1985, 21, 265–380. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; Wiley: New York, NY, USA, 1991; p. 900. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997; p. 483. [Google Scholar]
- Chiles, J.P.; Delfiner, P. Geostatistics: Modellimg Spatial Uncertainty; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists, Statistics in Practice Series; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2007; p. 315. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degré, A. Geostatistical interpolation of daily rainfall at catchment scale: The use of several variogram models in the Ourthe and Ambleve catchments, Belgium. Hydrol. Earth Syst. Sci. 2011, 15, 2259–2274. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology, 6th ed.; McGraw Hill International Editions: New York, NY, USA, 1988. [Google Scholar]
- Pakoksung, K.; Takagi, M. Effect of DEM source on Distributed hydrological model to results of runoff and inundation area. Model. Earth Syst. Environ. 2021, 7, 1891–1905. [Google Scholar] [CrossRef]
- Jenson, S.K.; Domingue, J.O. Extracting topographic structures from digital elevation data from geographic information system analysis. Photogramm. Eng. Remote Sens. 1988, 54, 1593–1600. [Google Scholar]
- Martz, L.W.; Jong, D.E. Catch: A Fortran program for measuring catchment area from digital elevation models. Comput. Geosci. 1988, 25, 835–844. [Google Scholar] [CrossRef]
- Pakoksung, K.; Takagi, M. Effect of satellite-based rainfall products on river basin responses of runoff simulation on flood event Model. Earth Syst. Environ. 2016, 2, 143. [Google Scholar] [CrossRef]
- Goovaerts, P. Using elevation to aid the geostatistics mapping of rainfall erosivity. Catena 1999, 34, 227–242. [Google Scholar] [CrossRef]
- Obled, C.; Wending, J.; Beven, K. The sensitivity of hydrological models to spatial rainfall pattern: An evaluateion using observaed data. J. Hydrol. 1994, 159, 305–333. [Google Scholar] [CrossRef]
- Máca, P.; Torfs, P. The influence of temporal rainfall distribution in the flood runoff modelling. Soil Water Res. 2009, 4, S102–S110. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Smith, J.A. Radar hydrology: Rainfall estimation. Adv. Water Resour. 2002, 25, 1387–1394. [Google Scholar] [CrossRef]
| Landuse Type | n’s Manning |
|---|---|
| Forest | 0.50 |
| Deforestation | 0.40 |
| Grasslands | 0.30 |
| Cropland | 0.35 |
| Urban and Build-up | 0.05 |
| Water bodies | 0.04 |
| Soil Type | Soil Depth, m | Saturated Hydraulic Conductivity (ka), cm/h | Beta, ka/kc | Green-Ampt Parameter | ||
|---|---|---|---|---|---|---|
| Ksv, cm/h | Porosity | Capillary Head, cm | ||||
| Clay | 1.0 | 0.462 | 0.06 | 0.475 | 31.63 | |
| Clay loam | 1.0 | 0.882 | 0.20 | 0.464 | 20.88 | |
| Loam | 1.0 | 2.500 | 1.32 | 0.463 | 8.89 | |
| Sandy clay | 2.0 | 0.781 | 0.12 | 0.430 | 23.90 | |
| Sandy clay loam | 1.5 | 2.272 | 0.30 | 0.398 | 21.85 | |
| Sandy loam | 1.5 | 12.443 | 2.18 | 0.453 | 11.01 | |
| Silty clay | 1.0 | 0.366 | 0.10 | 0.430 | 29.22 | |
| Silty loam | 1.0 | 2.591 | 0.68 | 0.501 | 16.68 | |
| Stone | 1.5 | - | - | - | - | |
| Rainfall Distribution Scenario | Rainfall Volume, MCM |
|---|---|
| OBS | 7900.01 |
| IDW | 7045.41 |
| TSP | 3012.01 |
| SPL | 7578.28 |
| SKG | 7787.04 |
| OKG | 10,653.01 |
| Distribution Scenario | Volume Bias, % | Peak Bias, % | RMSE, mm | Correlation | Mean Bias, mm | Nash-Sutcliffe |
|---|---|---|---|---|---|---|
| IDW | −1.84 | −18.35 | 7.66 | 0.85 | −0.24 | −0.053 |
| TSP | −59.47 | −60.23 | 11.22 | 0.80 | −5.51 | −0.073 |
| SPL | 0.38 | −23.66 | 7.11 | 0.88 | 0.05 | −0.047 |
| SKG | −0.18 | −20.12 | 5.08 | 0.92 | −0.02 | −0.049 |
| OKG | 4.39 | −12.94 | 6.86 | 0.90 | 0.46 | −0.048 |
| Distribution Scenario | Volume Bias, % | Peak Bias, % | RMSE, cms | Correlation | Mean Bias, cms | Nash-Sutcliffe |
|---|---|---|---|---|---|---|
| IDW | 16.88 | −29.20 | 184.12 | 0.755 | 64.19 | 0.437 |
| TSP | −40.59 | −59.46 | 275.05 | 0.691 | −168.02 | 0.427 |
| SPL | 33.25 | −16.73 | 239.53 | 0.704 | 135.89 | 0.223 |
| SKG | 6.80 | −35.80 | 164.48 | 0.803 | 27.99 | 0.499 |
| OKG | 43.64 | 1.92 | 275.37 | 0.702 | 185.38 | −0.557 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pakoksung, K. Impact of Spatial Rainfall Scenarios on River Basin Runoff Simulation a Nan River Basin Study Using the Rainfall-Runoff-Inundation Model. Eng 2024, 5, 51-69. https://doi.org/10.3390/eng5010004
Pakoksung K. Impact of Spatial Rainfall Scenarios on River Basin Runoff Simulation a Nan River Basin Study Using the Rainfall-Runoff-Inundation Model. Eng. 2024; 5(1):51-69. https://doi.org/10.3390/eng5010004
Chicago/Turabian StylePakoksung, Kwanchai. 2024. "Impact of Spatial Rainfall Scenarios on River Basin Runoff Simulation a Nan River Basin Study Using the Rainfall-Runoff-Inundation Model" Eng 5, no. 1: 51-69. https://doi.org/10.3390/eng5010004
APA StylePakoksung, K. (2024). Impact of Spatial Rainfall Scenarios on River Basin Runoff Simulation a Nan River Basin Study Using the Rainfall-Runoff-Inundation Model. Eng, 5(1), 51-69. https://doi.org/10.3390/eng5010004






