Remarks on Constitutive Modeling of Granular Materials
Abstract
:1. Introduction
2. Governing Equations
3. A Few Fundamental Concepts
“An assembly of discrete solid components dispersed in a fluid such that the constituents are substantially in contact with near neighbors. This definition excludes suspensions, fluidized beds, and materials embedded in a solid mixture.”
3.1. Dilatancy
“At one time the sand will be so firm and hard that you may walk with high heels without leaving a footprint; while at others, although the sand is not dry, one sinks in so as to make walking painful. Had you noticed, you would have found that the sand is firm as the tide falls and becomes soft again after it has been left dry for some hours. The tide leaves the sand, though apparently dry on the surface, with all its interstices perfectly full of water which is kept up to the surface of the sand by capillary attraction; at the same time the water is percolating through the sand from the sands above where the capillary action is not sufficient to hold the water. When the foot falls on this water-saturated sand, it tends to change its shape, but it cannot do this without enlarging the interstices—without drawing in more water. This is a work of time, so that the foot is gone again before the sand has yielded.”
“Taking a small indiarubber bottle with a glass neck full of shot and water, so that the water stands well into the neck. If instead of shot the bag were full of water or had anything of the nature of a sponge in it, when the bag was squeezed, the water would be forced up the neck. With the shot the opposite result is obtained; as I squeeze the bag, the water decidedly shrinks in the neck… When we squeeze a sponge between two planes, water is squeezed out; when we squeeze sand, shot, or granular material, water is drawn in.”
“During the shearing test on dense sand, the shearing stress reaches a peak value and if the deformation continued, the shearing stress drops to a smaller value, at which value it remains constant for all further deformations. During the drop in shearing stress, the sand continues to expand, finally reaching a critical value at which continuous deformation is possible at constant sharing stress.
When a loose sample of sand is subjected to shearing test under constant normal pressure, however, the shearing stress simply increases until it reaches the shearing strength and if the deformation is continued beyond this point the resistance remains unchanged. The volume of the sand in this state must correspond to the critical void ratio which is reached when performing a test on the same material in dense state therefore the curves representing the volume changes during shearing tests on material in the dense and the loose state must meet at the critical void ratio when stationary condition is established.”
3.2. Cohesionless and Cohesive Materials
“The angle to the horizontal assumed by the free surface of a heap at rest and obtained under stated conditions:
(i) The poured angle of repose is formed by pouring the bulk solid to form a heap below the pour point.
(ii) The drained angle of repose is formed by allowing a heap to emerge as superincumbent powder is allowed to drain away past the periphery of a horizontal flat platform previously buried in the powder.”
3.3. Yield Criterion
3.4. Void Ratio
- -
- For a given initial void ratio, the dilatancy decreases as the stress level increases.
- -
- For low confining pressure, the stress–strain curve of dense granular materials shows a peak. After the peak, the dilatant volume change becomes less pronounced.
- -
- Dense granular materials under high confining pressures and loose granular materials both show initially contractant volume change.
- -
- A critical state, characterized by the critical stress state and the critical void ratio, will be reached asymptotically with continued deformation. The void ratio at a critical state depends on the stress level; it decreases with an increasing stress level.
3.5. Hardening/Softening
3.6. Anisotropy
3.7. Cyclic Loading
3.8. Shear Banding
3.9. Rate Independence/Dependence
4. Constitutive Modeling of Granular Materials: The Frictional Flow Regime
- Physical and experimental models
- Numerical simulations
- Statistical mechanics approaches (e.g., extension of kinetic theory of gases)
- Standard continuum mechanics
- Ad-hoc approaches
- Explicit constitutive relations
- Implicit constitutive relations
- Ad hoc relations
4.1. Density (Volume Fraction) Gradient Theories
4.2. Non-Newtonian Fluid Models
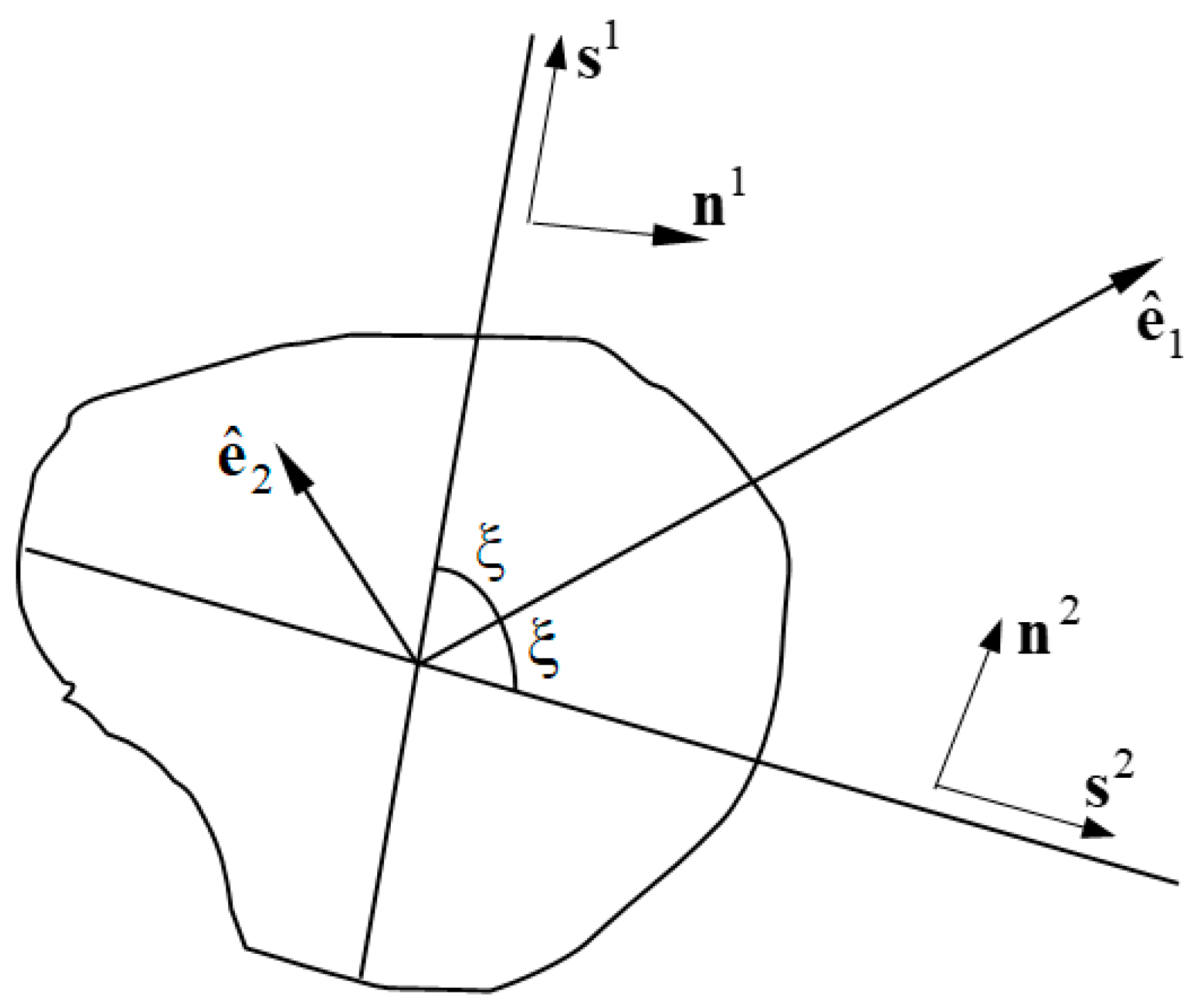
4.3. Micromechanical Approach
4.4. Hypoplastic Models
4.5. Double Shearing Model
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| the reference density of the material | |
| the current density | |
| the deformation gradient | |
| the divergence operator | |
| the velocity vector | |
| the gradient operator | |
| the body force vector | |
| or | the Cauchy stress tensor |
| and | the shear stress and the normal stress, respectively, acting on a plane at a point |
| the coefficient of cohesion | |
| the coefficient of static friction | |
| the internal angle of friction | |
| the normal direction | |
| the volume of solid particles | |
| the total volume of the voids | |
| the void ratio | |
| volume fraction | |
| the gradient operator | |
| the Laplacian operator | |
| the outer (dyadic) product of two vectors | |
| the symmetric part of the velocity gradient | |
| the viscosity | |
| the identity tensor | |
| P | pressure |
| the spin tensor | |
| the components of the velocity gradient associated with a typical class of contacts | |
| components of the overall velocity gradient. | |
| a parameter representing a measure of the contact area | |
| components of local stress associated with a class of contacts | |
| the unit branch vector | |
| a non-dimensional quantity related to the magnitude of the contact force | |
| the number of contacts per unit volume | |
| the branch vector | |
| the angle representing the inclination of the algebraically greater principal stress direction | |
| the angle of dilatancy | |
| the fabric tensor | |
| E | Young’s modulus |
| the Poisson ratio |
References
- Kolymbas, D.; Viggiani, G. (Eds.) Mechanics of Natural Solids; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Straughan, B.; Greve, R.; Ehrentraut, H.; Wang, Y. (Eds.) Continuum Mechanics and Applications in Geophysics and the Environment; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Jenike, A.W.; Johanson, J.R. Bins loads. J. Struct. Div. 1968, 94, 1011–1041. [Google Scholar] [CrossRef]
- Carson, J.; Craig, D. Silo design codes: Their limits and inconsistencies. Procedia Eng. 2015, 102, 647–656. [Google Scholar] [CrossRef]
- Turitzin, A.M. Dynamic pressure of granular material in deep bins. J. Struct. Div. 1963, 89, 49–73. [Google Scholar] [CrossRef]
- Bagnold, R.A. Experiments on a Gravity Free Dispersion of Large Solid Spheres in a Newtonian Fluid Under Shear. Proc. R. Soc. Lond. 1954, 225, 49–63. [Google Scholar]
- Bagnold, R.A. The Shearing and Dilatation of Dry Sand and the “Singing” Mechanism. Proc. R. Soc. A 1966, 295, 219–232. [Google Scholar]
- Reiner, M. A Mathematical Theory of Dilatancy. Am. J. Math. 1945, 67, 350–362. [Google Scholar] [CrossRef]
- McTigue, D.F. A Non-Linear Constitutive Model for Granular Materials: Applications to Gravity Flow. J. Appl. Mech. 1982, 49, 291–296. [Google Scholar] [CrossRef]
- Savage, S.B. Gravity Flow of Cohesionless Granular Materials in Chutes and Channels. J. Fluid Mech. 1979, 92, 53–96. [Google Scholar] [CrossRef]
- Goddard, J.D. Dissipative Materials as Models of Thixotropy and Plasticity. J. Non-Newton. Fluid Mech. 1984, 14, 141–160. [Google Scholar] [CrossRef]
- Astarita, T.; Ocone, R. Unsteady compressible flow of granular materials. Ind. Eng. Chem. Res. 1999, 38, 1177–1182. [Google Scholar] [CrossRef]
- Elaskar, S.A.; Godoy, L.A. Constitutive relations for compressible granular materials using non-Newtonian fluid mechanics. Int. J. Mech. Sci. 1998, 40, 1001–1018. [Google Scholar] [CrossRef]
- Tardos, G.I. A fluid mechanistic approach to slow, frictional flow of powders. Powder Tech. 1997, 92, 61–74. [Google Scholar] [CrossRef]
- Ivsic, T.; Galovic, A.; Kirin, D. Sand as a compressible fluid. Physica A 2000, 277, 47–61. [Google Scholar] [CrossRef]
- Gudehus, G. A comprehensive constitutive equation for granular materials. Soils Found. 1996, 36, 1–12. [Google Scholar] [CrossRef]
- Drucker, D.C.; Prager, W. Soil Mechanics and Plastic Analysis or Limit Design. Quart. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef]
- Maddalena, F.; Ferrari, M. Viscoelasticity of granular materials. Mech. Mater. 1995, 20, 241–250. [Google Scholar] [CrossRef]
- Wu, W.; Bauer, E.; Kolymbas, D. Hypoplastic constitutive model with critical state for granular materials. Mech. Mater. 1996, 23, 45–69. [Google Scholar] [CrossRef]
- Kanatani, K.I. A micropolar continuum theory for the flow of granular materials. Int. J. Eng. Sci. 1979, 17, 419–432. [Google Scholar] [CrossRef]
- Satake, M. Consideration on the stress-dilatancy equation through the work increment tensor. In Micromechanics of Granular Materials; Satake, M., Jenkins, J.T., Eds.; Elsevier: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Christoffersen, J.; Mehrabadi, M.M.; Nemat-Nasser, S. A micromechanical description of granular material behaviour. J. Appl. Mech. 1981, 48, 339–344. [Google Scholar] [CrossRef]
- Goodman, M.A.; Cowin, S.C. Two Problems in the Gravity Flow of Granular Materials. J. Fluid Mech. 1971, 45, 321–339. [Google Scholar] [CrossRef]
- Goodman, M.A.; Cowin, S.C. A Continuum Theory for Granular Materials. Arch. Ration. Mech. Anal. 1972, 44, 249–266. [Google Scholar] [CrossRef]
- Nunziato, J.W.; Passman, S.L.; Thomas, J.P., Jr. Gravitational Flows of Granular Materials with Incompressible Grains. J. Rheol. 1980, 24, 395–420. [Google Scholar] [CrossRef]
- Ahmadi, G. A generalized continuum theory for granular materials. Int. J. Non-Linear Mech. 1982, 17, 21–33. [Google Scholar] [CrossRef]
- Nedderman, R.M.; Tuzun, U.; Savage, S.B.; Houlsby, G.T. The flow of granular materials-I. Chem. Eng. Sci. 1982, 37, 1597–1609. [Google Scholar] [CrossRef]
- Savage, S.B. The Mechanics of Rapid Granular Flows. Adv. Appl. Mech. 1984, 24, 289–366. [Google Scholar]
- Campbell, C. Rapid granular flows. Annu. Rev. Fluid Mech. 1990, 22, 57–92. [Google Scholar] [CrossRef]
- Hutter, K.; Rajagopal, K.R. On the flows of granular materials. Contin. Mech. Thermodyn. 1994, 6, 81–139. [Google Scholar] [CrossRef]
- Jaeger, H.M.; Nagel, S.R.; Behringer, R.P. Granular solids, liquids, and gases. Rev. Mod. Phys. 1996, 68, 1259. [Google Scholar] [CrossRef]
- de Gennes, P.G. Reflections on the mechanics of granular matter. Physica A 1998, 261, 267–293. [Google Scholar] [CrossRef]
- Hermann, H.J.; Luding, S. Modeling granular media on the computer. Continuum Mech. Thermodyn. 1998, 10, 189–231. [Google Scholar] [CrossRef]
- Mehta, A. (Ed.) Granular Matter; Springer: New York, NY, USA, 1994. [Google Scholar]
- Fleck, N.A.; Cocks, A.C.F. (Eds.) IUTAM Symposium of Mechanics of Granular and Porous Materials; Kluwer Publishers: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Duran, J. Sands, Powders, and Grains; Springer: New York, NY, USA, 2000. [Google Scholar]
- Rao, K.K.; Nott, P.R. An Introduction to Granular Flow; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Batra, R.C. Elements of Continuum Mechanics; American Institute of Aeronautics and Astronautics (AIAA) Inc.: Reston, VA, USA, 2006. [Google Scholar]
- Liu, I.S. Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Muller, I. On the entropy inequality. Arch. Ration. Mech. Anal. 1967, 26, 118–141. [Google Scholar] [CrossRef]
- Ziegler, H. An Introduction to Thermomechanics, 7th ed.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Truesdell, C.; Noll, W. The Non-Linear Field Theories of Mechanics; Springer: New York, NY, USA, 1992. [Google Scholar]
- Antman, S.S. Nonlinear Problems of Elasticity; Springer: New York, NY, USA, 1995. [Google Scholar]
- Coussot, P. Rheometry of Pastes, Suspensions, and Granular Materials; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- McGlinchey, D. Characterisation of Bulk Solids; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Brown, R.L.; Richards, J.C. Principles of Powder Mechanic; Pergamon Press: London, UK, 1970. [Google Scholar]
- Hagen, G. Berlin Monatsber. Akad. Wiss. 1852, 35–42. [Google Scholar]
- Reynolds, O. On the Dilatancy of Media Composed of Rigid Particles in Contact with Experimental Illustrations. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1885, 20, 469–481. [Google Scholar] [CrossRef]
- Reynolds, O. Experiments Showing Dilatancy, a Property of Granular Material, Possibly Connected with Gravitation. Proc. R. Anthropol. Inst. Great Br. Irel. 1886, 11, 354–363. [Google Scholar]
- Jenkin, C.F. The pressure exerted by granular materials: An application of the principle of dilatancy. Proc. R. Soc. Lond. A 1931, 131, 53–89. [Google Scholar]
- Rowe, P.W. The stress-dilatancy relation far static equilibrium of an assembly of particles in contact. Proc. R. Soc. Lond. A 1962, 269, 500–527. [Google Scholar]
- Andrade, E.N.D.C.; Fox, J.W. The mechanism of dilatancy. Proc. Phys. Soc. 1949, 62, 483. [Google Scholar] [CrossRef]
- Bolton, M.D. The strength and dilatancy of sand. Geotechnique 1986, 36, 65–78. [Google Scholar] [CrossRef]
- Nixon, S.A.; Chandler, H.W. On the elasticity and plasticity of dilatant granular materials. J. Mech. Phys. Solids 1999, 47, 1397–1408. [Google Scholar] [CrossRef]
- Mehrabadi, M.M.; Nemat-Nasser, S. Stress, dilatancy and fabric in granular materials. Mech. Mater. 1983, 2, 155–161. [Google Scholar] [CrossRef]
- Goddard, J.D. Granular dilatancy and the plasticity of glassy lubricants. Ind. Eng. Chem. Res. 1999, 38, 820–822. [Google Scholar] [CrossRef]
- Massoudi, M.; Mehrabadi, M.M. A continuum model for granular materials: Considering dilatancy, and the Mohr-Coulomb criterion. Acta Mech. 2001, 152, 121–138. [Google Scholar] [CrossRef]
- Massoudi, M. A generalization of Reiner’s mathematical model for wet sand. Mech. Res. Commun. 2011, 38, 378–381. [Google Scholar] [CrossRef]
- Casagrande, A. Characteristics of cohesionless soils affecting the stability of slopes and earth fills. J. Boston Soc. Civ. Eng. 1936, 23, 13–32. [Google Scholar]
- Schofield, A.N.; Wroth, C.P. Critical States Soil Mechanics; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Feda, J. Mechanics of Particulate Materials: The Principles; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Anand, L.; Gu, C. Granular materials: Constitutive equations and strain localization. J. Mech. Phys. Solids 2000, 48, 1701–1733. [Google Scholar] [CrossRef]
- Zhu, H.; Mehrabadi, M.M.; Massoudi, M. The frictional flow of a dense granular material based on the dilatant double shearing model. Comput. Math. Appl. 2007, 53, 244–259. [Google Scholar] [CrossRef]
- Mandl, G.; Luque, R.F. Fully Developed Plastic Shear Flow of Granular Materials. Geotechnique 1970, 20, 277–307. [Google Scholar] [CrossRef]
- Taylor, D.W. Stability of earth slopes. J. Boston Soc. Civ. Eng. 1937, 24, 197–247. [Google Scholar]
- Terzaghi, K. Theoretical Soil Mechanics; Wiley and Sons, Inc.: New York, NY, USA, 1943. [Google Scholar]
- Wieghardt, K. Experiments in Granular Flow. Ann. Rev. Fluid Mech. 1975, 7, 89–114. [Google Scholar] [CrossRef]
- Wood, P.A. Fundamentals of Bulk Solids Flow; Report No. ICTIS/TR31; IEA Coal Research: London, UK, 1986. [Google Scholar]
- Nutting, P.G. The deformation of granular solids. J. Wash. Acad. Sci. 1929, 18, 123–126. [Google Scholar]
- Sokolovski, V.V. Statics of Granular Media; Pergamon: Oxford, UK, 1965. [Google Scholar]
- Nedderman, R.M. Statics and Kinematics of Granular Materials; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Nemat-Nasser, S. Plasticity: A Treatise on Finite Deformation of Heterogeneous Inelastic Materials; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Zhu, H. A Dilatant Double Shearing Model for Granular Materials Including the Effects of Fabric. Doctoral Dissertation, Tulane University, New Orleans, LA, USA, 2005. [Google Scholar]
- Bouvard, D.; Stutz, P. Experimental Study of Rheological Properties of a Sand Using a Special Triaxial Apparatus. Geotech. Test. J. 1986, 9, 10–18. [Google Scholar]
- Kolymbas, D.; Herle, I. Hypoplasticity: A Framework to Model Granular Materials. In Behaviour of Granular Materials; CISM Courses and Lectures No. 385; Springer: Berlin/Heidelberg, Germany, 1998; pp. 239–268. [Google Scholar]
- Nemat-Nasser, S.; Mehrabadi, M.M. Micromechanically based rate constitutive description for granular materials. In Mechanics of Engineering Materials; Desai, C.S., Gallagher, R.H., Eds.; John Wiley: Hoboken, NJ, USA, 1984; pp. 451–463. [Google Scholar]
- Nemat-Nasser, S. A micromechanically-based constitutive model for friction deformation of granular materials. J. Mech. Phys. Solids 2000, 48, 1541–1563. [Google Scholar] [CrossRef]
- Zhu, H.; Mehrabadi, M.M.; Massoudi, M. Incorporating the effects of fabric in the Dilatant Double Shearing Model for granular materials. Int. J. Plast. 2006, 22, 628–653. [Google Scholar] [CrossRef]
- Massoudi, M. An anisotropic constitutive relation for the stress tensor of a rod-like (fibrous-type) granular material. Math. Probl. Eng. 2005, 2005, 679–702. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Zhang, J. Constitutive relations for cohesionless frictional granular materials. Int. J. Plast. 2002, 18, 531–547. [Google Scholar] [CrossRef]
- Balendran, B.; Nemat-Nasser, S. Double sliding model for cyclic deformation of granular materials, including dilatancy effects. J. Mech. Phys. Solids 1993, 41, 573–612. [Google Scholar] [CrossRef]
- Zhu, H.; Mehrabadi, M.M.; Massoudi, M. Three-dimensional constitutive relations for granular materials based on the dilatant double shearing mechanism and the concept of fabric. Int. J. Plast. 2006, 22, 826–857. [Google Scholar] [CrossRef]
- Rudnicki, J.W.; Rice, J.R. Conditions for the Localization of deformation in pressure sensitivity dilatant materials. J. Mech. Phys. Solids 1975, 23, 371–394. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Mehrabadi, M.M.; Iwakuma, T. On Certain microscopic and macroscopic aspect of plastic flow of ductile materials. In Three Dimensional Constitutive Relations and Ductile Fracture; North Holland: Amsterdam, The Netherlands, 1981; pp. 157–172. [Google Scholar]
- Mehrabadi, M.M.; Cowin, S.C. On the double-sliding free-rotating model for the deformation of granular materials. J. Mech. Phys. Solids 1981, 29, 269–282. [Google Scholar] [CrossRef]
- Alshibli, K.; Sture, S. Shear Band Formation in Plane Strain Experiments of Sand. ASCE J. Geotech. Geoenviron. Eng. 2000, 126, 495–503. [Google Scholar] [CrossRef]
- Alshibli, K.; Batiste, S.; Sture, S. Strain Localization in Sand: Plane Strain versus Triaxial Compression. J. Geotech. Geoenviron. Eng. 2003, 129, 483–494. [Google Scholar] [CrossRef]
- Oda, M.; Kazama, H.; Konishi, J. Effects of induced anisotropy on the development of shear bands in granular materials. Mech. Mater. 1998, 28, 103–111. [Google Scholar] [CrossRef]
- Drescher, A.; Vardoulakis, I.; Han, C. A biaxial apparatus for testing soils. Geotech. Test. J. ASTM 1990, 13, 226–234. [Google Scholar]
- Wood, D.M. Soil Behavior and Critical State Soil Mechanics; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Kolymbas, D. Constitutive Modelling of Granular Materials; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Massoudi, M. Constitutive Modelling of Flowing Granular Materials: A Continuum Approach. In Granular Materials: Fundamentals and Applications; Antony, S.J., Hoyle, W., Ding, Y., Eds.; The Royal Society of Chemistry: Cambridge, UK, 2004; pp. 63–107. [Google Scholar]
- Massoudi, M. On the flow of granular materials with variable material properties. Int. J. Non-Linear Mech. 2001, 36, 25–37. [Google Scholar] [CrossRef]
- Massoudi, M.; Mehrabadi, M.M. Implicit Continuum Mechanics Approach to Heat Conduction in Granular Materials. Ind. Eng. Chem. Res. 2010, 49, 5215–5221. [Google Scholar] [CrossRef]
- Massoudi, M.; Mehrabadi, M.M. Implicit constitutive relations in thermoelasticity. Int. J. Non-Linear Mech. 2011, 46, 286–290. [Google Scholar] [CrossRef]
- Rajagopal, K.R. On implicit constitutive theories. Appl. Math. 2003, 48, 279–319. [Google Scholar] [CrossRef]
- Cowin, S.C. A theory for the flow of granular material. Powder Tech. 1974, 9, 61–69. [Google Scholar] [CrossRef]
- Cowin, S.C. Constitutive relations that imply a generalized Mohr-Coulomb criterion. Acta Mech. 1974, 20, 41–46. [Google Scholar] [CrossRef]
- Mehrabadi, M.M.; Cowin, S.C.; Massoudi, M. Conservation laws and constitutive relations for density-gradient-dependent viscous fluids. Contin. Mech. Thermodyn. 2005, 17, 183–200. [Google Scholar] [CrossRef]
- Wang, Y.; Hutter, K. Shearing flows in a Goodman-Cowin type granular material—Theory and numerical results. Part. Sci. Technol. 1999, 17, 97–124. [Google Scholar] [CrossRef]
- Fang, C.; Wang, Y.; Hutter, K. A variational principle for the revised Goodman–Cowin theory with internal length. Arch. Appl. Mech. 2006, 76, 119–131. [Google Scholar] [CrossRef]
- Massoudi, M. Heat transfer in complex fluids. In Two Phase Flow, Phase Change and Numerical Modeling; IntechOpen: Rijeka, Croatia, 2011. [Google Scholar]
- Reiner, M. Rheology. In Handbuch Der Physik; Flugge, S., Ed.; Springer: Berlin/Heidelberg, Germany, 1958. [Google Scholar]
- Truesdell, C. The mechanical foundations of elasticity and fluid dynamics. J. Ration. Mech. Anal. 1952, 1, 125–300. [Google Scholar] [CrossRef]
- Rivlin, R.S. The hydrodynamics of non-Newtonian fluids, I. Proc. R. Soc. Lond. 1948, 193, 260–281. [Google Scholar]
- Bingham, E.C. Fluidity and Plasticity; McGraw Hill: New York, NY, USA, 1922. [Google Scholar]
- Prager, W. Introduction to Mechanics of Continua; Dover Publications, Inc.: Mineola, NY, USA, 2004. [Google Scholar]
- Schaeffer, D.G. Instability in the evolution equations describing incompressible granular flow. J. Diff. Eq. 1987, 66, 19–50. [Google Scholar] [CrossRef]
- Oldroyd, J.G. A rational formulation of the equations of plastic flow for a Bingham solid. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1947; Volume 43, pp. 100–105. [Google Scholar]
- Lipscomb, G.G.; Denn, M.M. Flow of Bingham fluids in complex geometries. J. Non-Newton. Fluid Mech. 1984, 14, 337–346. [Google Scholar] [CrossRef]
- Mehrabadi, M.M.; Loret, B.; Nemat-Nasser, S. Incremental constitutive relations for granular materials based on micromechanics. Proc. R. Soc. Lond. A 1993, 441, 433–463. [Google Scholar]
- Chang, C.S.; Ma, L. Elastic material constants for isotropic granular solids with particle rotation. Int. J. Solids Struct. 1992, 29, 1001–1018. [Google Scholar] [CrossRef]
- Chang, C.S.; Chao, S.J.; Chang, Y. Estimates of elastic moduli for granular material with anisotropic random packing structure. Int. J. Solids Struct. 1995, 32, 1989–2008. [Google Scholar] [CrossRef]
- Cambou, B.; Dubujet, P.; Emeriault, F.; Sidoro, F. Homogenization for granular media. Eur. J. Mech. A Solids 1995, 14, 255–276. [Google Scholar]
- Calvetti, F. Limitations and perspectives of the micromechanical modelling of granular materials. In Mathematical and Computer Modelling; Elsevier: Amsterdam, The Netherlands, 2003; pp. 485–495. [Google Scholar]
- Truesdell, C. Hypo-elasticity. J. Ration. Mech. Anal. 1955, 4, 83–133, 1019–1020. [Google Scholar] [CrossRef]
- Truesdell, C. Remarks on hypo-elasticity. J. Res. Natl. Bur. Stand. B 1963, 67, 141–143. [Google Scholar] [CrossRef]
- Green, A.E. Hypo-elasticity and plasticity. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1956, 234, 46–59. [Google Scholar] [CrossRef]
- Green, A.E. Hypo-elasticity and plasticity. II. J. Ration. Mech. Anal. 1956, 5, 725–734. [Google Scholar] [CrossRef]
- Spencer, A.J.M. Theory of invaraints. In Continuum Physics; Eringen, A.C., Ed.; Academic Press: Cambridge, MA, USA, 1971; Volume I. [Google Scholar]
- Zheng, Q.-S. Theory of representations for tensor functions—A unified invariant approach to constitutive equations. Appl. Mech. Rev. 1994, 47, 545–587. [Google Scholar] [CrossRef]
- Kolymbas, D. An outline of hypoplasticity. Arch. Appl. Mech. 1991, 61, 143–151. [Google Scholar] [CrossRef]
- Kolymbas, D.; Wu, W. Introduction to hypoplasticity. In Proceedings of the Modern Approaches to Plasticity; Kolymbas, D., Ed.; Elsevier: Amsterdam, The Netherlands, 1993; pp. 213–223. [Google Scholar]
- Wu, W.; Bauer, E. A hypoplastic model for barotropy and pyknotropy of granular soils. In Proceedings of the Modern Approaches to Plasticity; Kolymbas, D., Ed.; Elsevier: Amsterdam, The Netherlands, 1993; pp. 225–245. [Google Scholar]
- Wu, W.; Bauer, E. A simple hypoplastic constitutive model for sand. Int. J. Numer. Anal. Meth. Geomech. 1994, 18, 833–862. [Google Scholar] [CrossRef]
- Bauer, E.; Wu, W. A hypoplastic constitutive model for cohesive powders. Powder Technol. 1995, 85, 1–9. [Google Scholar] [CrossRef]
- Bauer, E. Calibration of a comprehensive hypoplastic model for granular materials. Soils Found. 1996, 36, 13–26. [Google Scholar] [CrossRef]
- von Wolffersdorff, P.A. A hypoplastic relation for granular materials with a predefined limit state surface. Mech. Cohesive-Frict. Mater. 1996, 1, 251–271. [Google Scholar] [CrossRef]
- Hill, J.M. Similarity ‘hot-spot’ solutions for a hypoplastic granular material. Proc. R. Soc. Lond. A 2000, 456, 2653–2671. [Google Scholar] [CrossRef]
- Lubliner, J. Plasticity Theory; Dover Publications: New York, NY, USA, 2008. [Google Scholar]
- Khan, A.S.; Huang, S. Continuum Theory of Plasticity; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Gudehus, G. Granular materials as rate-independent simple materials: Constitutive relations. Powder Tech. 1969, 3, 344. [Google Scholar] [CrossRef]
- Mehrabadi, M.M.; Cowin, S.C. Initial planar deformation of dilatant granular materials. J. Mech. Phys. Solids 1978, 26, 269–284. [Google Scholar] [CrossRef]
- Hayes, M. On Pure Extension. Arch. Ration. Mech. Anal. 1968, 28, 155–164. [Google Scholar] [CrossRef]
- Spencer, A.J.M. A theory of the kinematics of ideal soils under plane strain conditions. J. Mech. Phys. Solids 1964, 12, 337–351. [Google Scholar] [CrossRef]
- Spencer, A.J.M. Deformation of ideal granular materials. In Mechanics of Solids; Pergamon Press: Oxford, UK; New York, NY, USA, 1982; pp. 607–652. [Google Scholar]
- Shield, R.T. On Coulomb’s law of failure in soils. J. Mech. Phys. Solids 1955, 4, 10–16. [Google Scholar] [CrossRef]
- Mandel, J. Sur les ligns de glissement et le calcul des deplacement dans la deformation plastique. Comptes Rendus L’académie Sci. 1947, 225, 1272–1273. (In French) [Google Scholar]
- de Josselin de Jong, G. Statistics and Kinematics of the Failure Zone of a Granular Material; Uitgeverij Waltman: Delft, The Netherlands, 1959. [Google Scholar]
- Mehrabadi, M.M.; Cowin, S.C. Prefailure and post-failure soil plasticity model. J. Eng. Mech. Div. 1980, 106, 991–1003. [Google Scholar] [CrossRef]
- Anand, L. Plane deformation of ideal granular materials. J. Mech. Phys. Solids 1983, 31, 105–122. [Google Scholar] [CrossRef]
- Cowin, S.C. The relationship between the elasticity tensor and the fabric tensor. Mech. Mater. 1985, 4, 137–147. [Google Scholar] [CrossRef]
- Massoudi, M. Boundary conditions in mixture theory and in CFD applications of higher order models. Comput. Math. Appl. 2007, 53, 156–167. [Google Scholar] [CrossRef]
- Massoudi, M.; Antaki, J.F. An Anisotropic Constitutive Equation for the Stress Tensor of Blood Based on Mixture Theory. Math. Probl. Eng. 2008, 2008, 579172. [Google Scholar] [CrossRef]
- Goudarzy, M.; König, D.; Santamarina, J.C.; Schanz, T. The influence of the anisotropic stress state on the intermediate strain properties of granular material. Géotechnique 2018, 68, 221–232. [Google Scholar] [CrossRef]
- Sitharam, T.G.; Vinod, J.S. Evaluation of shear modulus and damping ratio of granular materials using discrete element approach. Geotech. Geol. Eng. 2010, 28, 591–601. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massoudi, M. Remarks on Constitutive Modeling of Granular Materials. Eng 2023, 4, 2856-2878. https://doi.org/10.3390/eng4040161
Massoudi M. Remarks on Constitutive Modeling of Granular Materials. Eng. 2023; 4(4):2856-2878. https://doi.org/10.3390/eng4040161
Chicago/Turabian StyleMassoudi, Mehrdad. 2023. "Remarks on Constitutive Modeling of Granular Materials" Eng 4, no. 4: 2856-2878. https://doi.org/10.3390/eng4040161
APA StyleMassoudi, M. (2023). Remarks on Constitutive Modeling of Granular Materials. Eng, 4(4), 2856-2878. https://doi.org/10.3390/eng4040161






