A Numerical Study on the Response of a Very Large Floating Airport to Airplane Movement
Abstract
1. Introduction
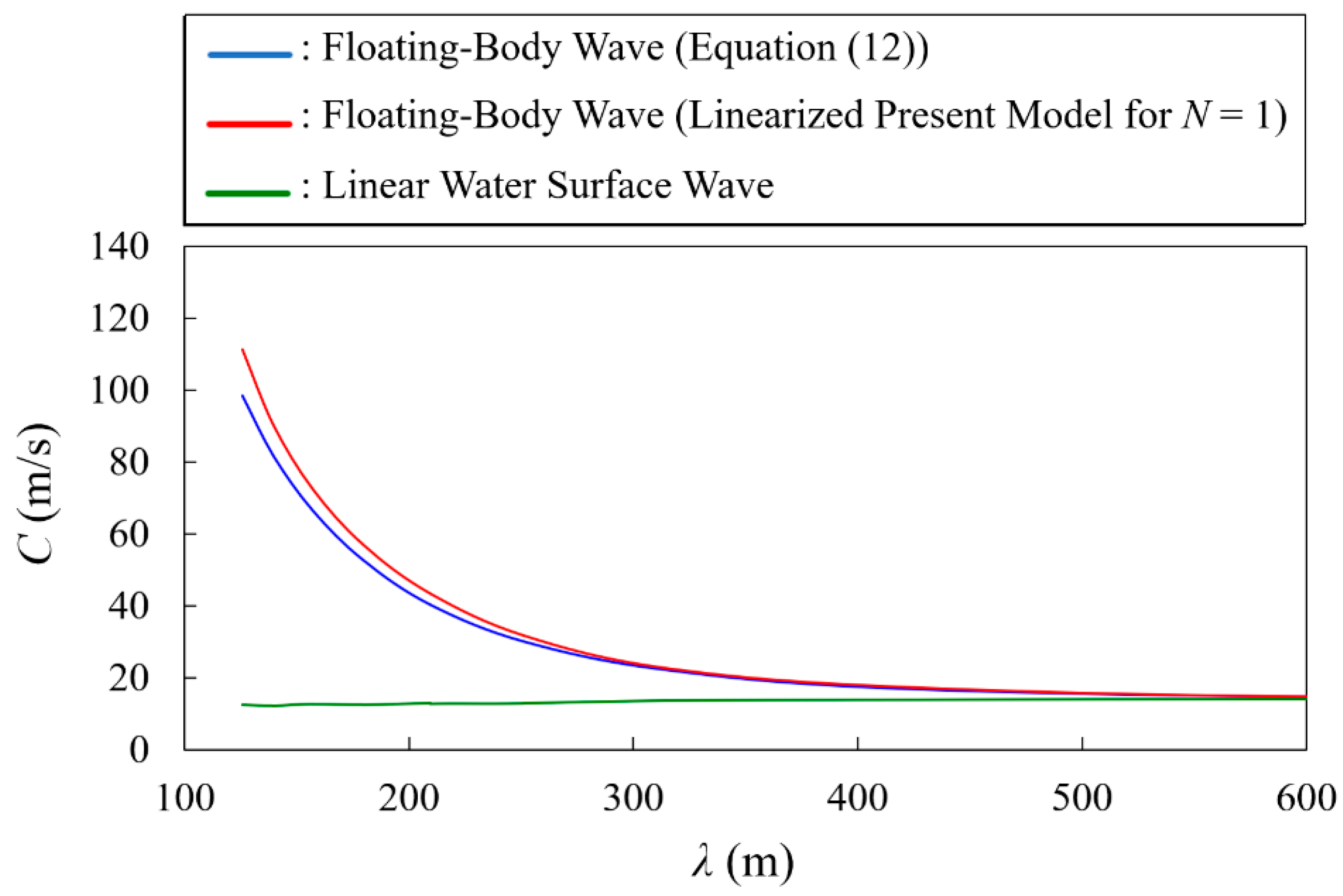
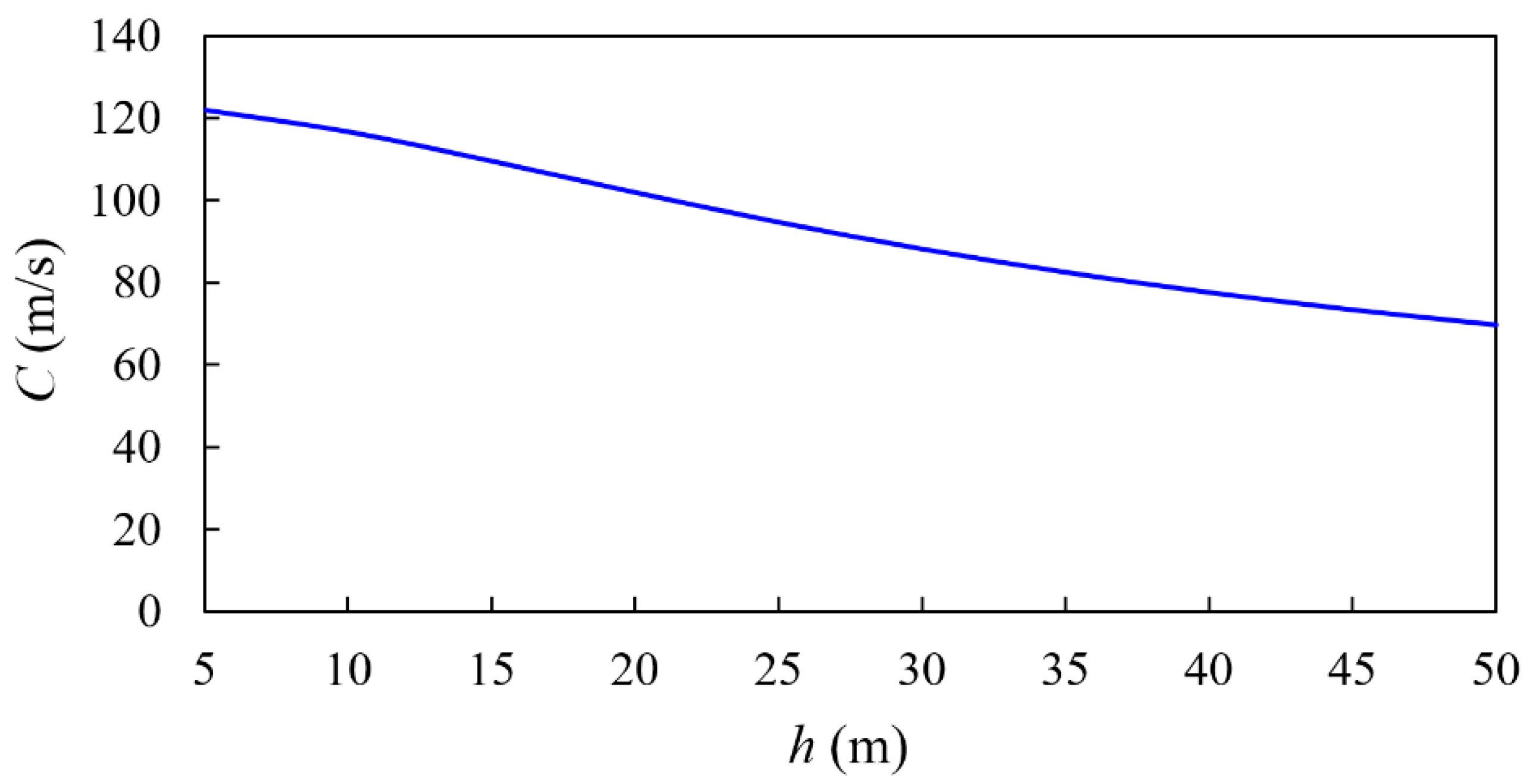
2. Numerical Calculation Method
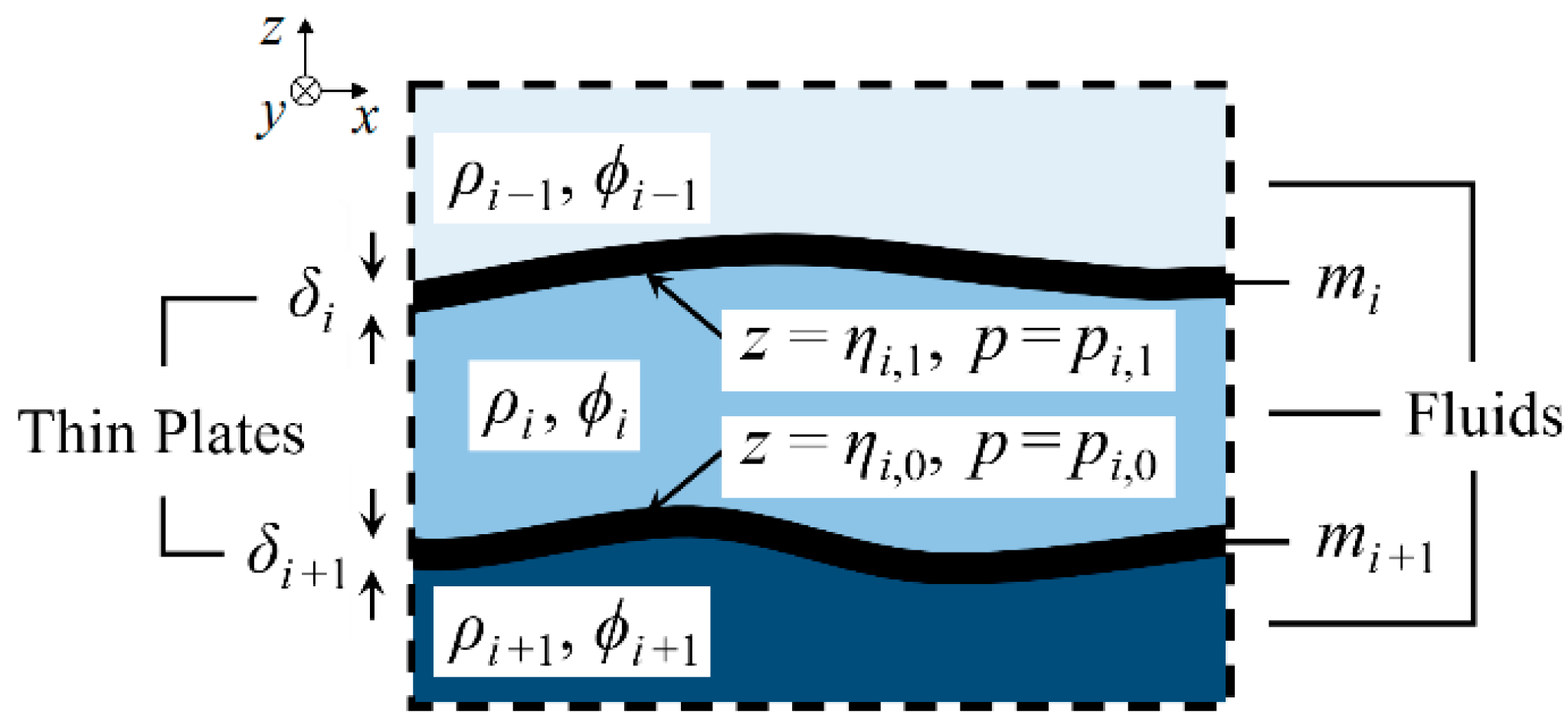
2.1. Governing Equations
2.2. Numerical Method
3. Calculation Conditions
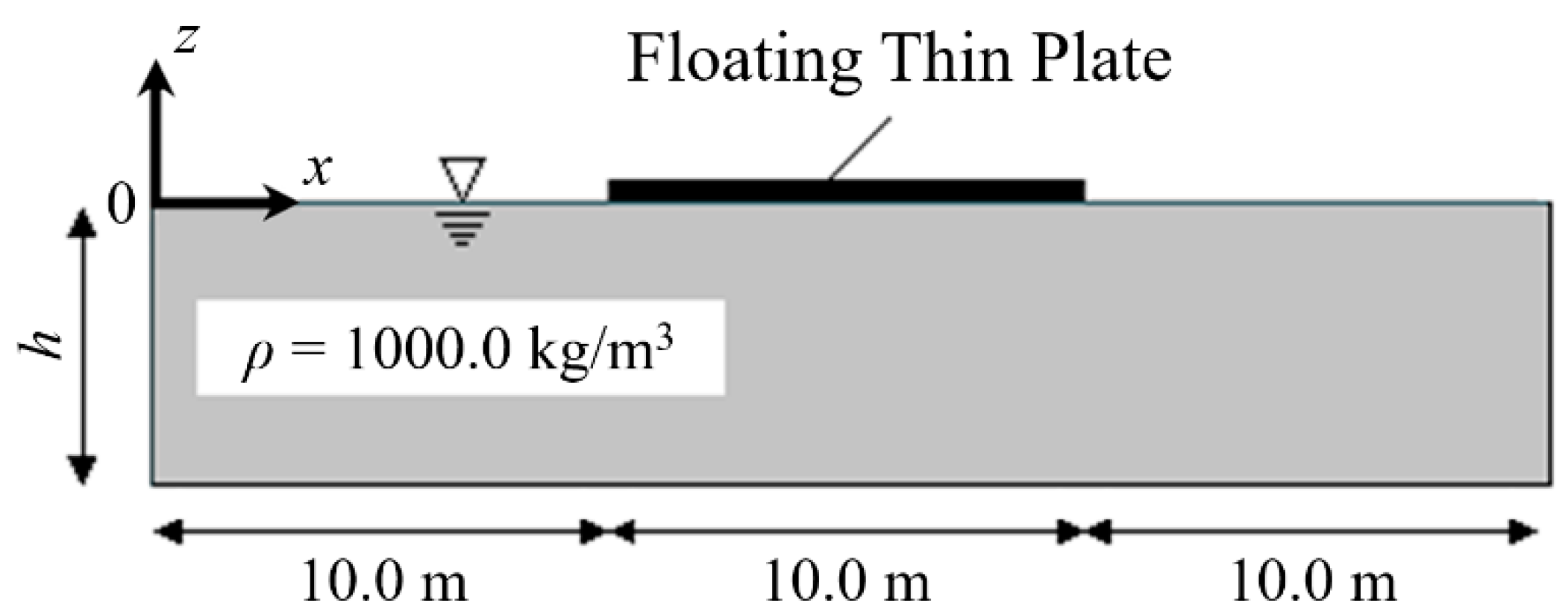
3.1. 1D Calculations
3.1.1. Common Conditions
3.1.2. Conditions for Touch-and-Go
3.1.3. Conditions for Landing
3.1.4. Conditions for Takeoff
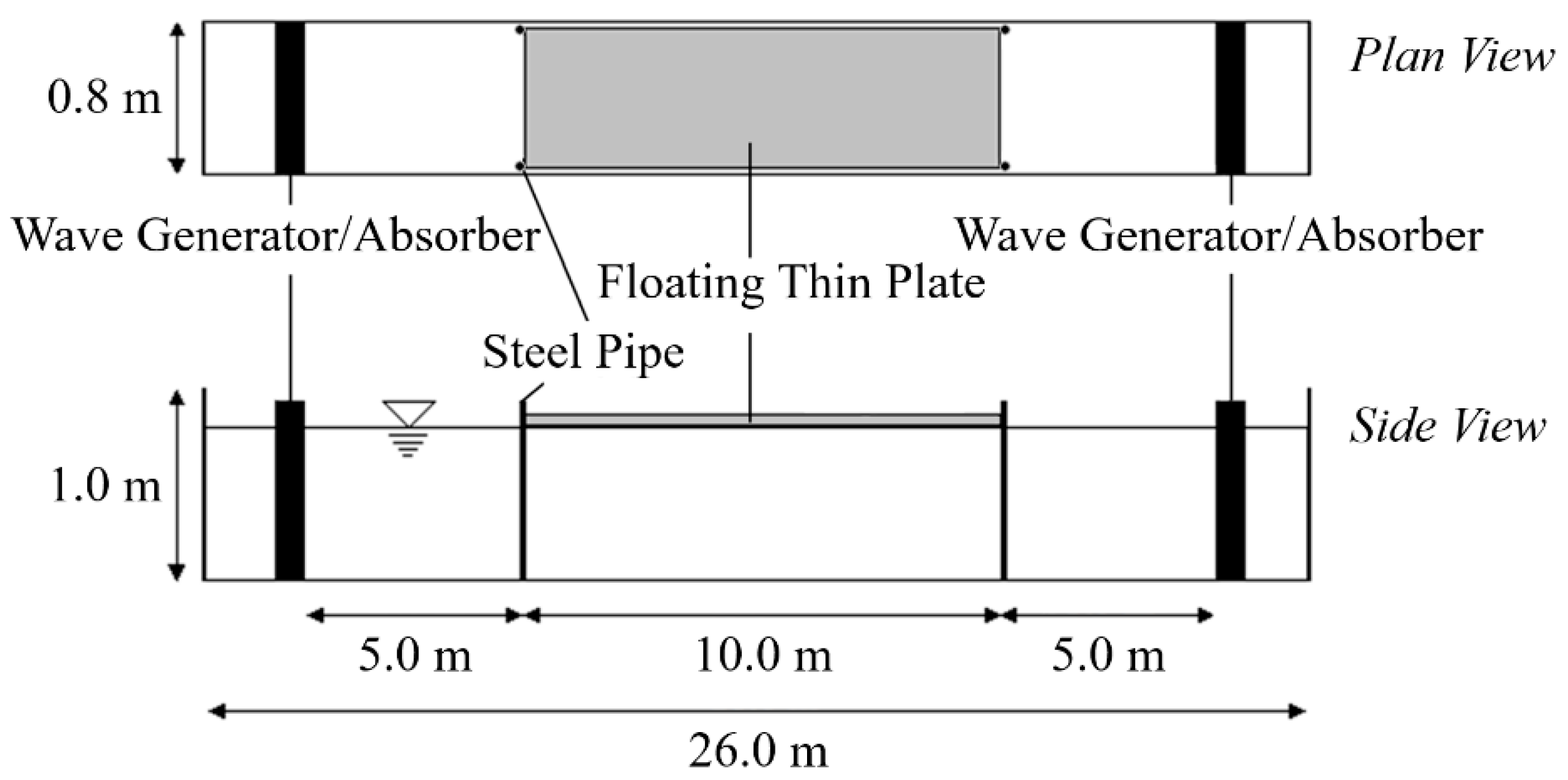
3.2. 2D Calculations
3.2.1. Common Conditions
3.2.2. Conditions for Landing
3.2.3. Conditions for Takeoff
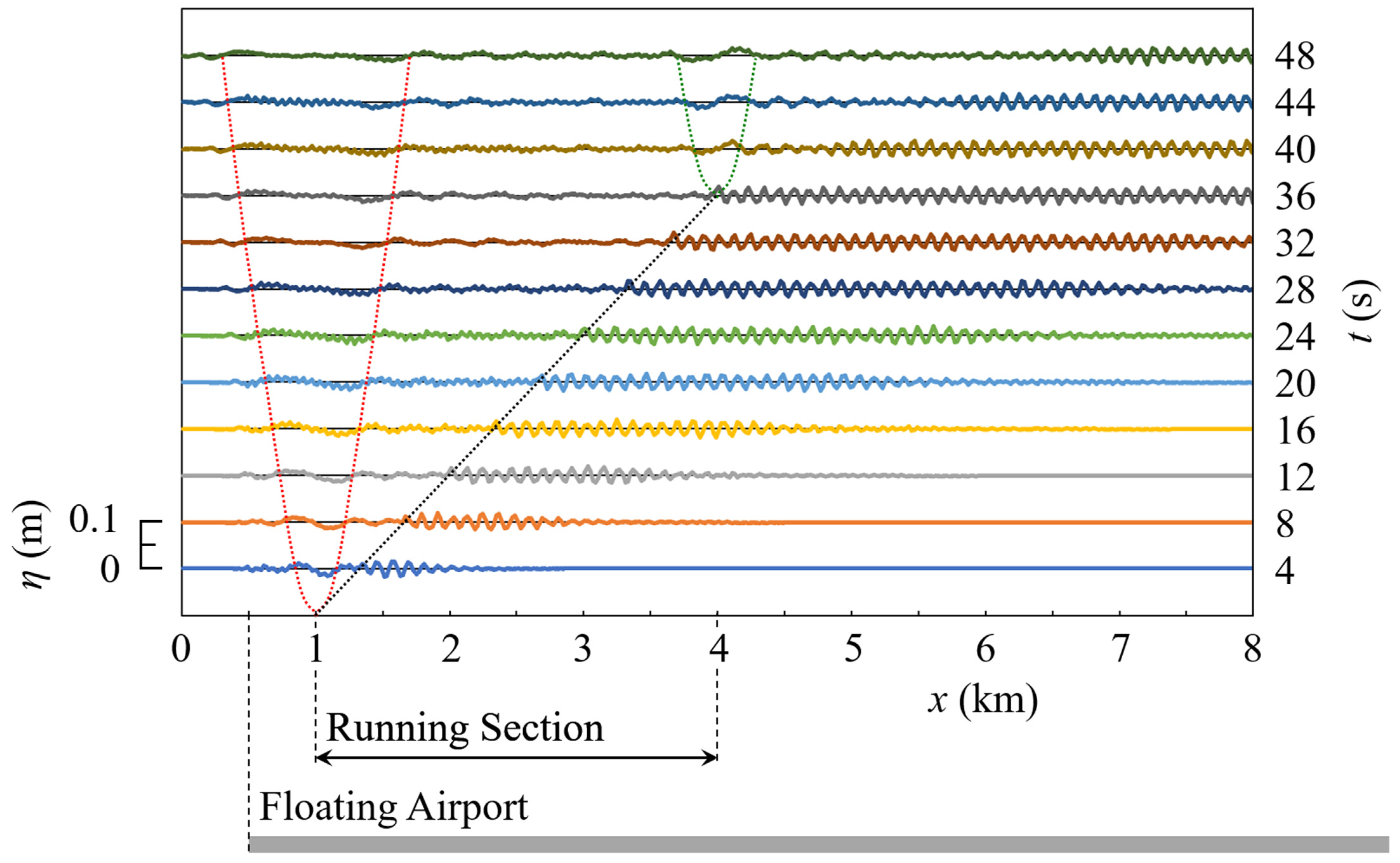
4. 1D Response of a Floating Airport to Airplane Movement
4.1. Touch-and-Go
4.2. Landing
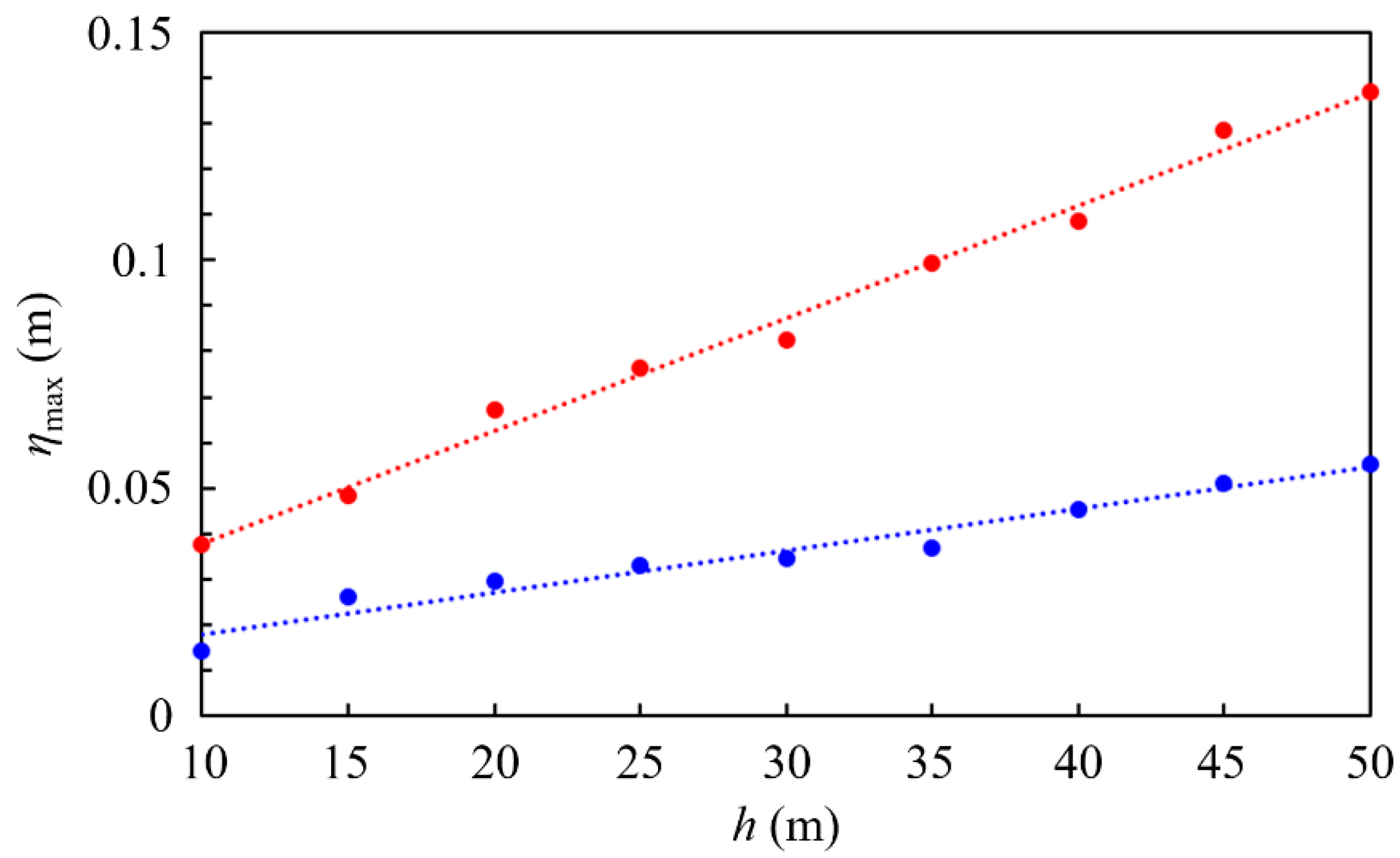
4.3. Takeoff
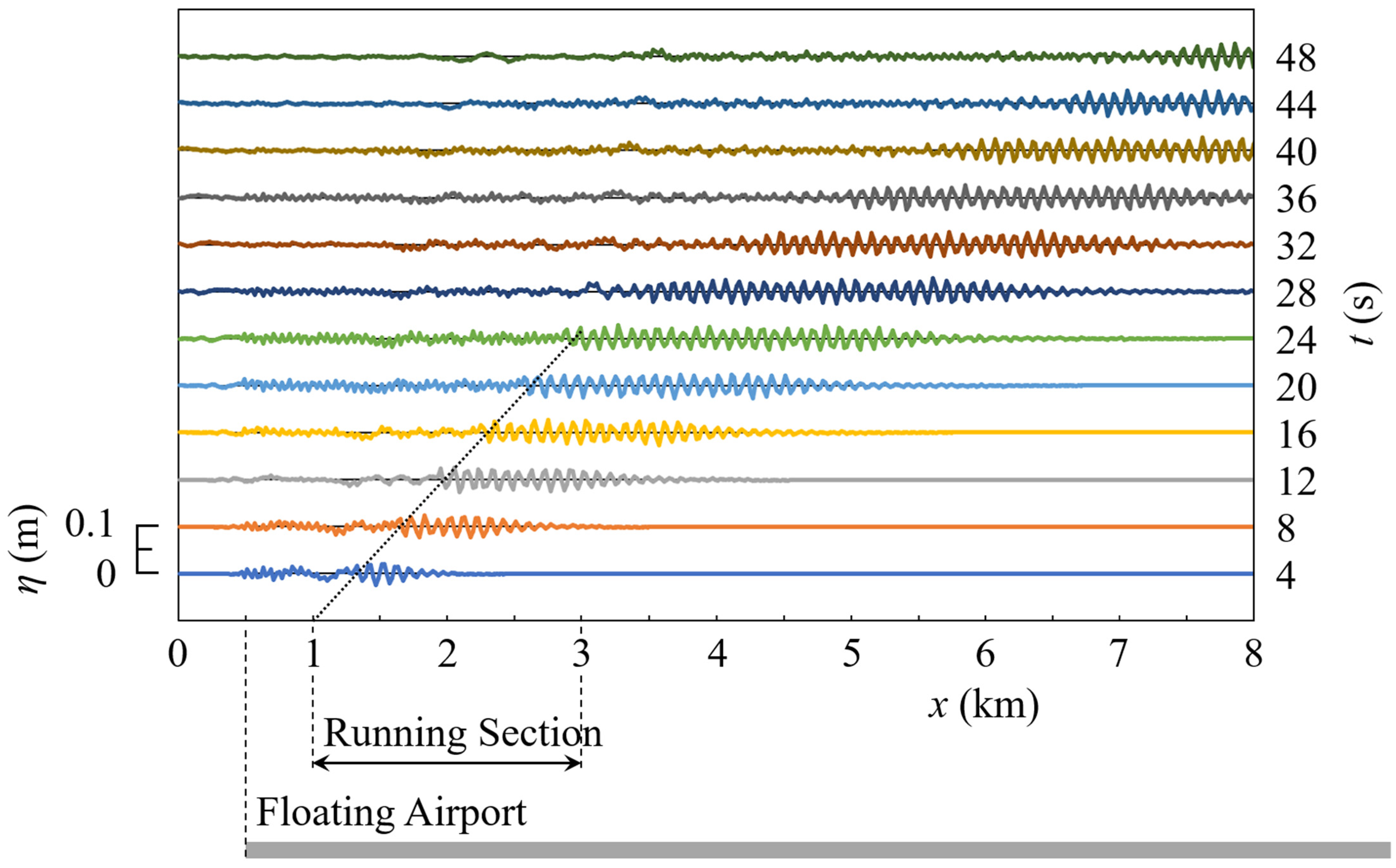
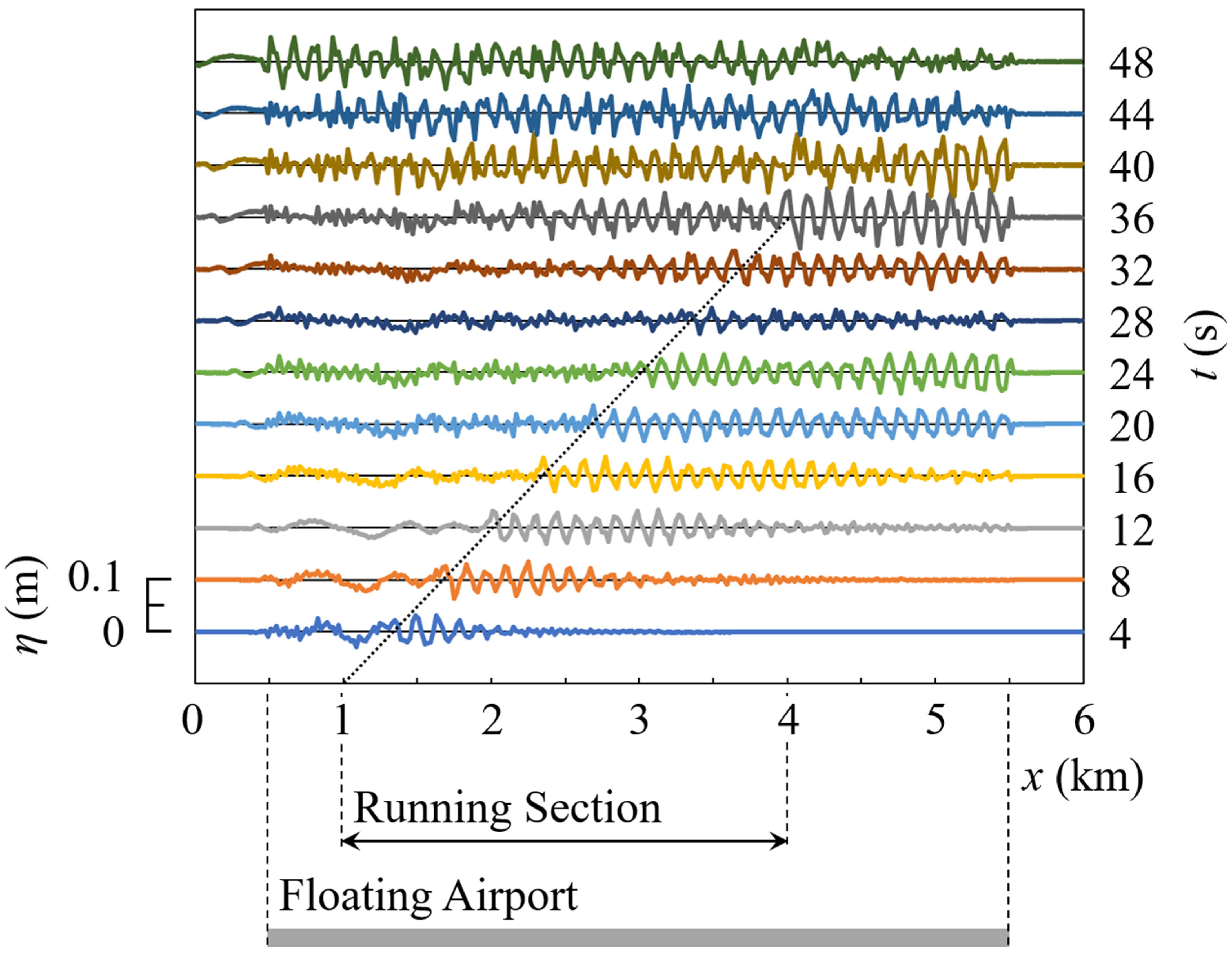
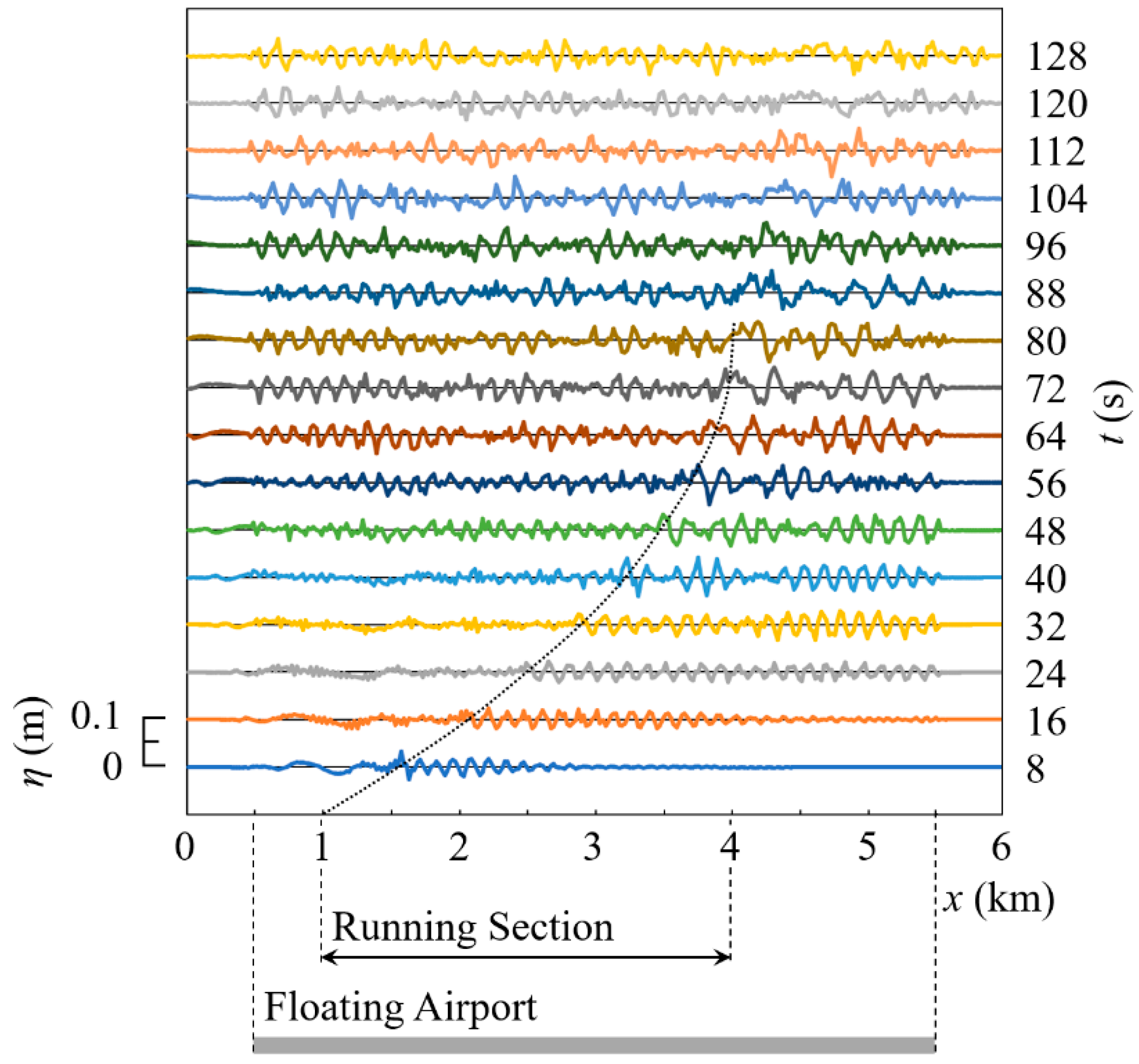
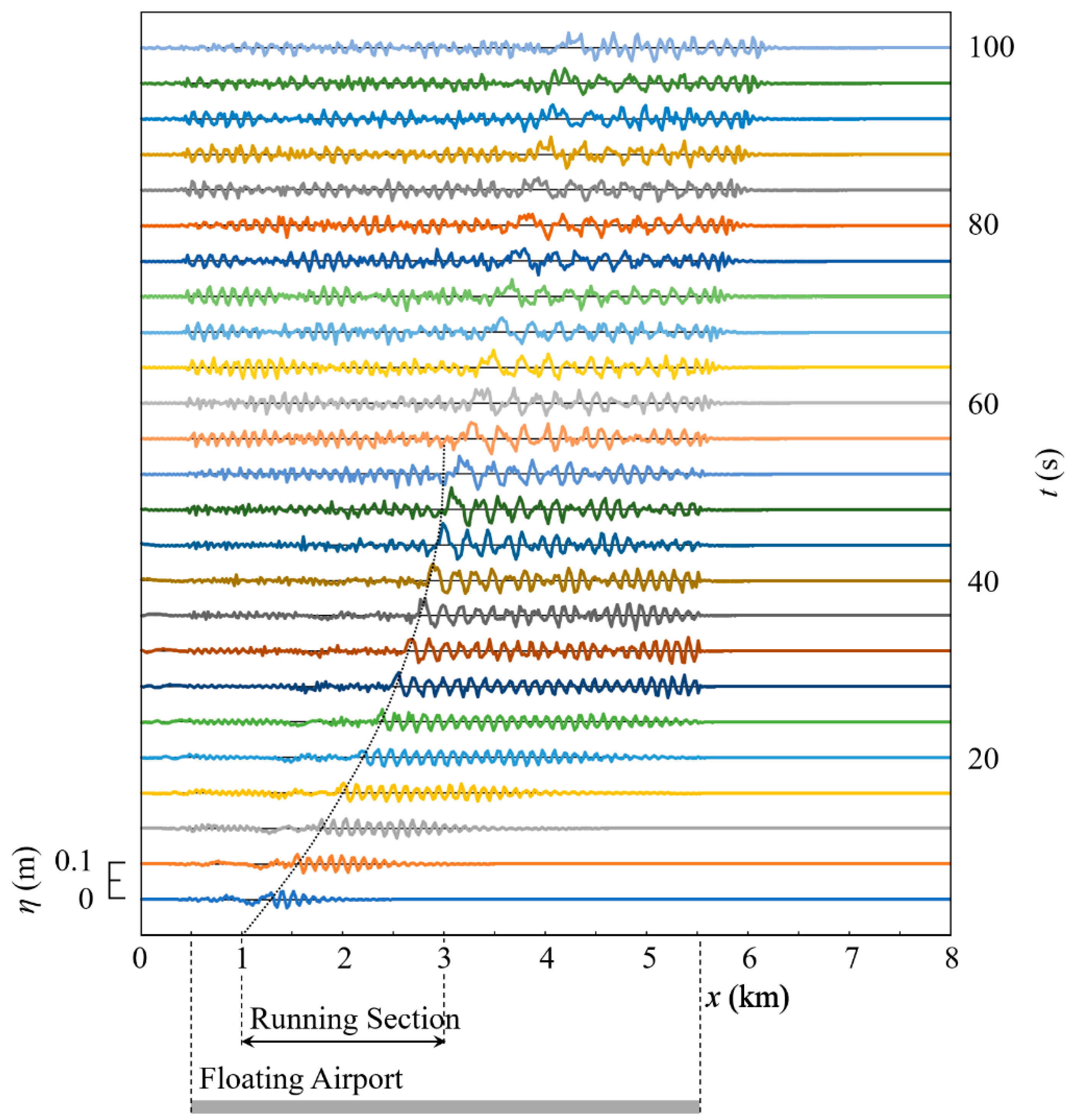
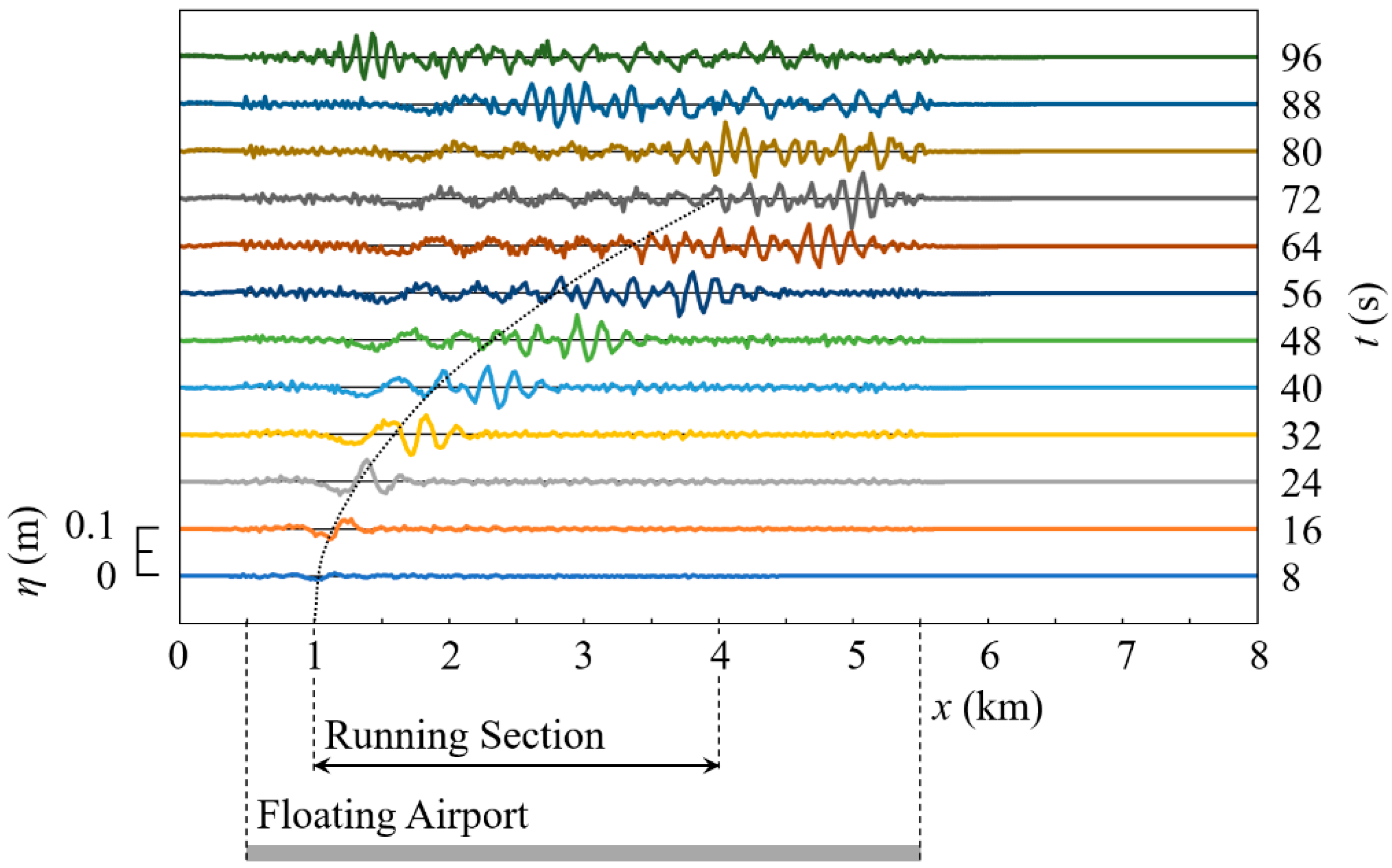
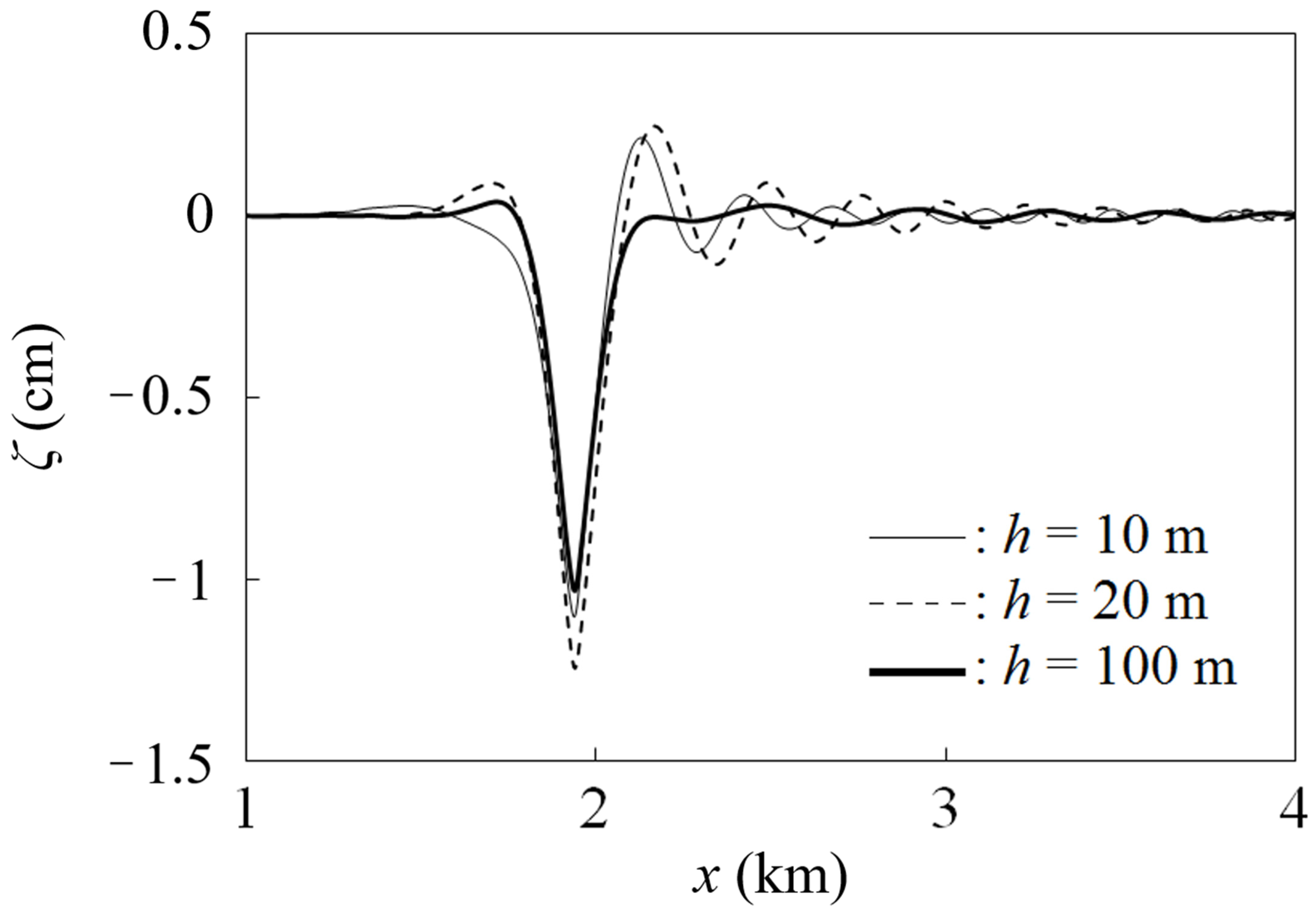
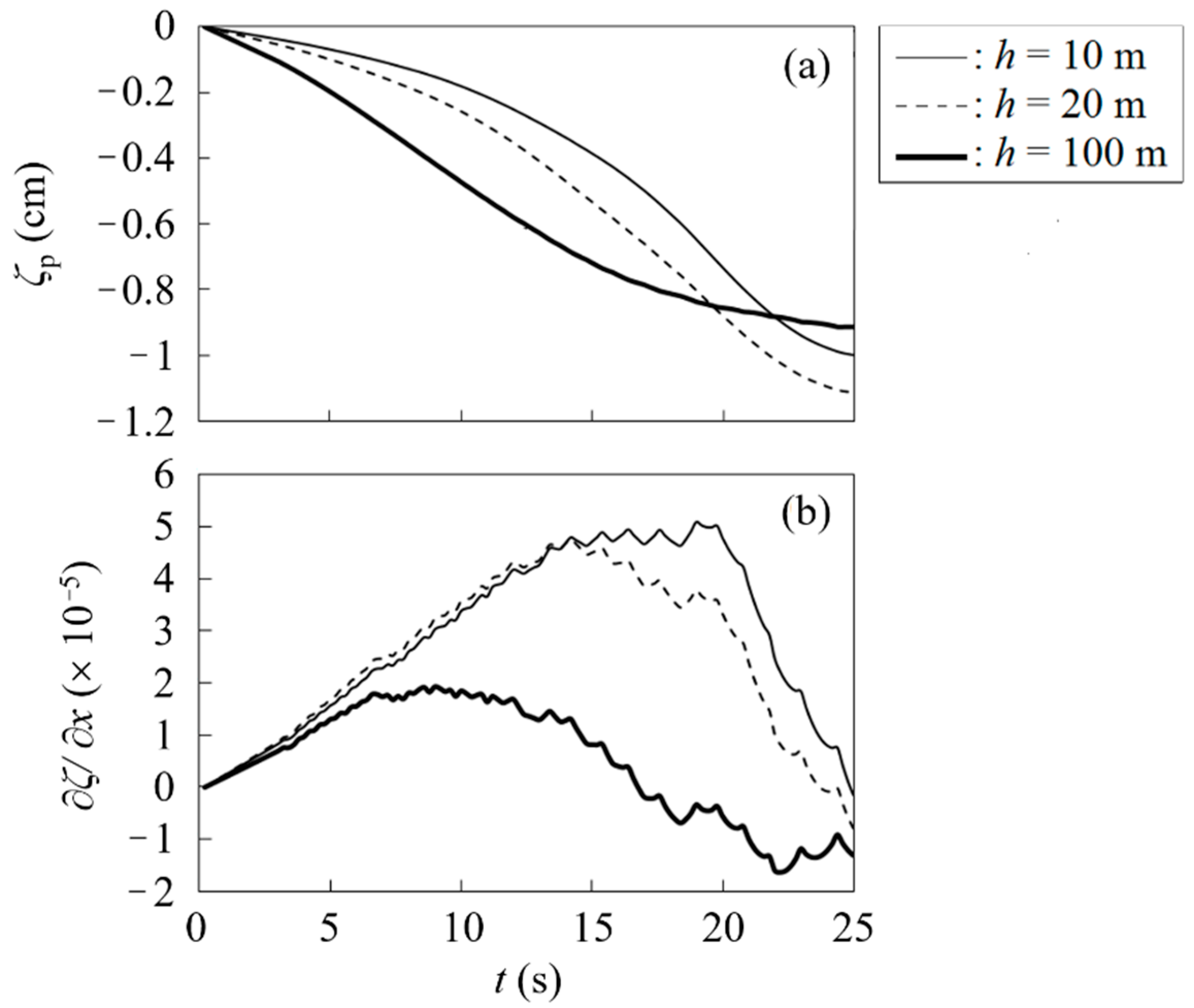
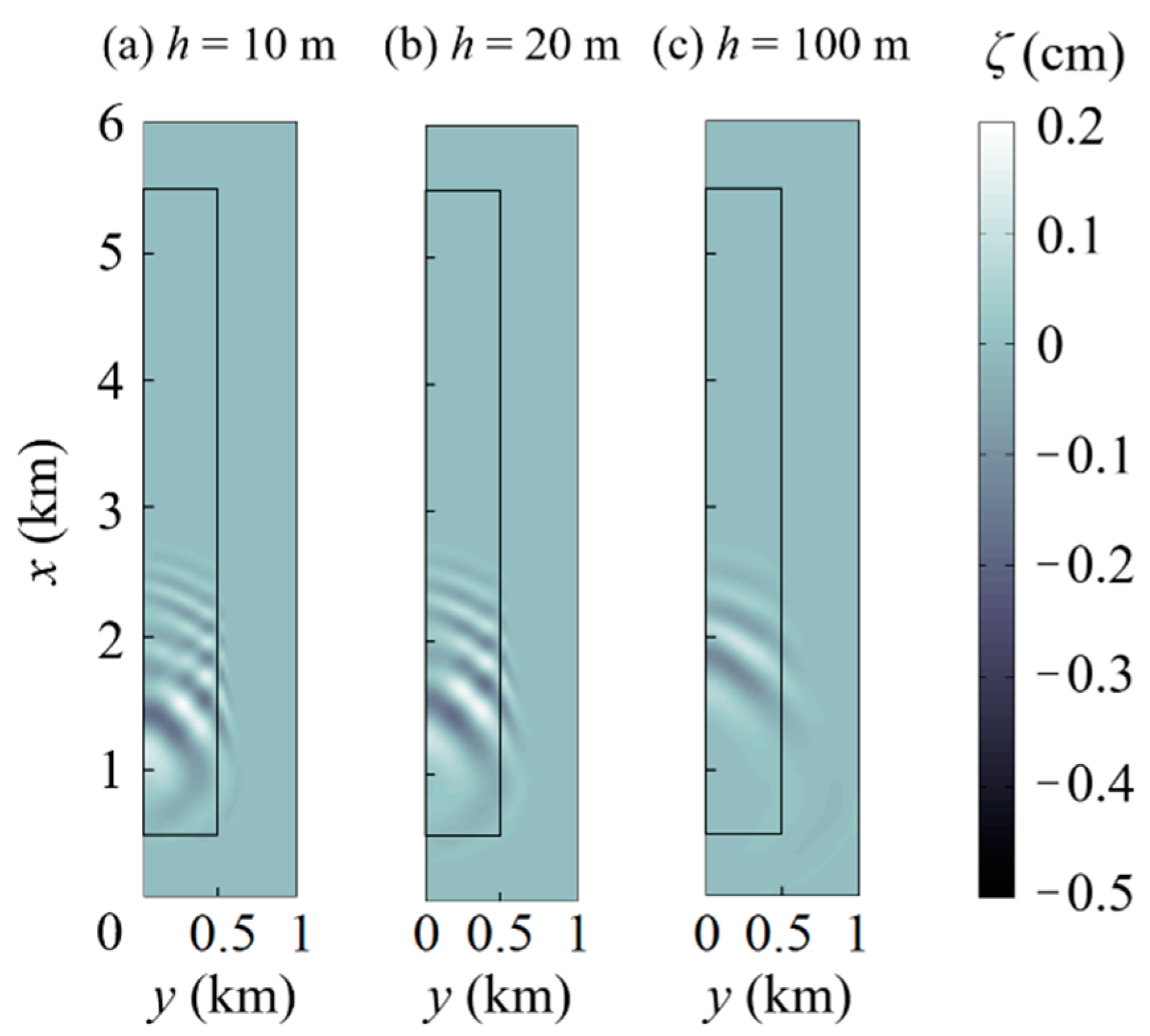
5. 2D Response of a Floating Airport to Airplane Movement
5.1. Landing
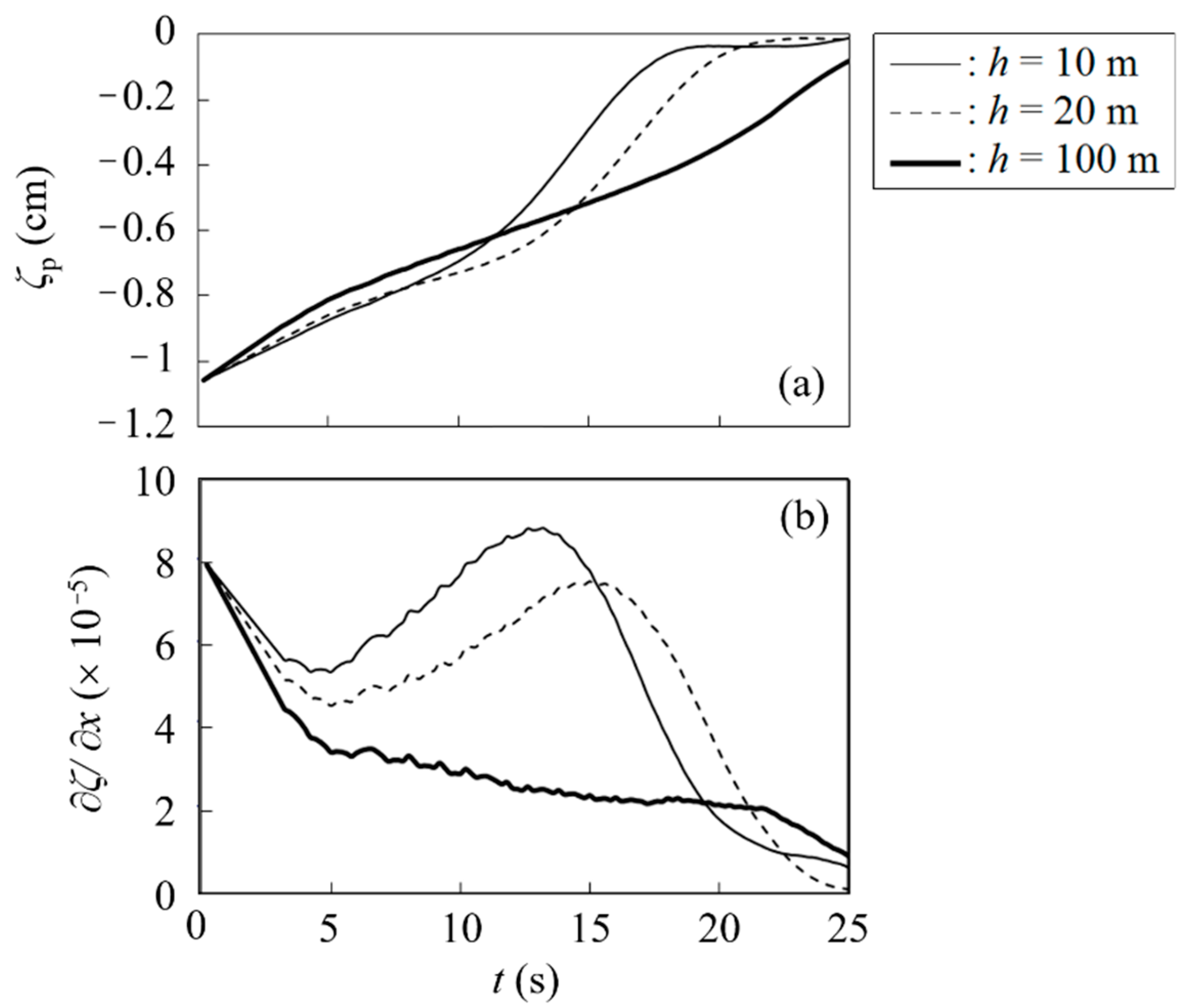
5.2. Takeoff
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Renzi, E.; Michele, S.; Zheng, S.; Jin, S.; Greaves, D. Niche applications and flexible devices for wave energy conversion: A review. Energies 2021, 14, 6537. [Google Scholar] [CrossRef]
- Michele, S.; Zheng, S.; Greaves, D. Wave energy extraction from a floating flexible circular plate. Ocean Eng. 2022, 245, 110275. [Google Scholar] [CrossRef]
- Kashiwagi, M. Research on hydroelastic responses of VLFS: Recent progress and future work. Int. J. Offshore Polar Eng. 2000, 10, 81–90. [Google Scholar]
- Watanabe, E.; Utsunomiya, T.; Wang, C.M. Hydroelastic analysis of pontoon-type VLFS: A literature survey. Eng. Struct. 2004, 26, 245–256. [Google Scholar] [CrossRef]
- Montiel, F.; Bonnefoy, F.; Ferrant, P.; Bennetts, L.; Squire, V.; Marsault, P. Hydroelastic response of floating elastic discs to regular waves. Part 1. Wave basin experiments. J. Fluid Mech. 2013, 723, 604–628. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, D.; Gao, Y.; Chen, L. A time domain discrete-module-beam-bending-based hydroelasticity method for the transient response of very large floating structures under unsteady external loads. Ocean Eng. 2018, 164, 332–349. [Google Scholar] [CrossRef]
- Ding, J.; Wu, Y.; Xie, Z.; Yang, W.; Wang, S.; Yu, J.; Yu, T. Overview: Research on hydroelastic responses of VLFS in complex environments. Mar. Struct. 2021, 78, 102978. [Google Scholar] [CrossRef]
- Michele, S.; Zheng, S.; Buriani, F.; Borthwick, A.G.L.; Greaves, D.M. Floating hydroelastic circular plate in regular and irregular waves. Eur. J. Mech. B Fluids 2023, 99, 148–162. [Google Scholar] [CrossRef]
- Li, W.; Ke, S.; Chen, J.; Zhu, T.; Ren, H. Hydrodynamic response and energy analysis in a very large floating structure supporting a marine airport under typhoon-driven waves. Ocean Eng. 2022, 266, 112987. [Google Scholar] [CrossRef]
- Squire, V.A.; Dugan, J.P.; Wadhams, P.; Rottier, P.J.; Liu, A.K. Of ocean waves and sea ice. Annu. Rev. Fluid Mech. 1995, 27, 115–168. [Google Scholar] [CrossRef]
- Meylan, M.H.; Squire, V.A. Response of a circular ice floe to ocean waves. J. Geophys. Res. Oceans 1996, 101, 8869–8884. [Google Scholar] [CrossRef]
- Sakai, S.; Hanai, K. Empirical formula of dispersion relation of waves in sea ice. In Proceedings of the Ice in the Environment: Proceedings of the 16th IAHR International Symposium on Ice, Dunedin, New Zealand, 2–6 December 2002; pp. 327–335. Available online: https://www.iahr.org/library/infor?pid=19937 (accessed on 10 February 2023).
- Meylan, M.H.; Bennetts, L.; Cavaliere, C.; Alberello, A.; Toffoli, A. Experimental and theoretical models of wave-induced flexure of a sea ice floe. Phys. Fluids 2015, 27, 041704. [Google Scholar] [CrossRef]
- Waseda, T.; Alberello, A.; Nose, T.; Toyota, T.; Kodaira, T.; Fujiwara, Y. Observation of anomalous spectral downshifting of waves in the Okhotsk Sea Marginal Ice Zone. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2022, 380, 256. [Google Scholar] [CrossRef] [PubMed]
- Părău, E.; Dias, F. Nonlinear effects in the response of a floating ice plate to a moving load. J. Fluid Mech. 2002, 460, 281–305. [Google Scholar] [CrossRef]
- Dinvay, E.; Kalisch, H.; Părău, E.I. Fully dispersive models for moving loads on ice sheets. J. Fluid Mech. 2019, 876, 122–149. [Google Scholar] [CrossRef]
- Ţugulan, C.; Trichtchenko, O.T.; Părău, E. Three-dimensional waves under ice computed with novel preconditioning methods. J. Comput. Phys. 2022, 459, 111129. [Google Scholar] [CrossRef]
- Takagi, K. Interaction between solitary wave and floating elastic plate. J. Waterw. Port Coastal Ocean Eng. 1997, 123, 57–62. [Google Scholar] [CrossRef]
- Sakai, S.; Liu, X.; Sasamoto, M.; Kagesa, T. Experimental and numerical study on the hydroelastic behavior of VLFS under tsunami. In Hydroelasticity in Marine Technology; Kashiwagi, M., Koterayama, W., Ohkusu, M., Eds.; Yomei Printing Cooperative Society: Fukuoka, Japan, 1998; pp. 385–392. ISBN 4-87780-001-8. [Google Scholar]
- Kakinuma, T.; Ochi, N. Tsunami-height reduction using a very large floating structure. In Mathematical Analysis of Continuum Mechanics and Industrial Applications III, CoMFoS 2018, Mathematics for Industry 34; Itou, H., Hirano, S., Kimura, M., Kovtunenko, V.A., Khludnev, A.M., Eds.; Springer: Singapore, 2020; pp. 193–202. [Google Scholar] [CrossRef]
- Xu, F.; Lu, D.Q. Wave scattering by a thin elastic plate floating on a two-layer fluid. Int. J. Eng. Sci. 2010, 48, 809–819. [Google Scholar] [CrossRef]
- Kakinuma, T.; Yamashita, K.; Nakayama, K. Surface and internal waves due to a moving load on a very large floating structure. J. Appl. Math. 2012, 2012, 830530. [Google Scholar] [CrossRef]
- Kim, J.W.; Webster, W.C. The drag on an airplane taking off from a floating runway. J. Mar. Sci. Technol. 1998, 3, 76–81. [Google Scholar] [CrossRef]
- Watanabe, E.; Utsunomiya, T.; Tanigaki, S. A transient response analysis of a very large floating structure by finite element method. Struct. Eng./Earthq. Eng. JSCE 1998, 15, 155s–163s. [Google Scholar] [CrossRef]
- Hermans, A.J. A boundary element method for the interaction of free-surface waves with a very large floating flexible platform. J. Fluids Struct. 2000, 14, 943–956. [Google Scholar] [CrossRef]
- Endo, H. The behavior of a VLFS and an airplane during takeoff/landing run in wave condition. Mar. Struct. 2000, 13, 477–491. [Google Scholar] [CrossRef]
- Kashiwagi, M. Transient responses of a VLFS during landing and take-off of an airplane. J. Mar. Sci. Technol. 2004, 9, 14–23. [Google Scholar] [CrossRef]
- Nguyen, X.V.; Luong, V.H.; Cao, T.N.T.; Lieu, X.Q.; Nguyen, T.B. Hydroelastic responses of floating composite plates under moving loads using a hybrid moving element-boundary element method. Adv. Struct. Eng. 2020, 23, 2759–2775. [Google Scholar] [CrossRef]
- Kakinuma, T. Nonlinear interaction of surface and internal waves with very large floating or submerged structures. In Fluid Structure Interaction II; Chakrabarti, S.K., Brebbia, C.A., Almorza, D., Gonzalez-Palma, R., Eds.; WIT Press: Billerica MA, USA, 2003; pp. 117–126. [Google Scholar]
- Luke, J.C. A variational principle for a fluid with a free surface. J. Fluid Mech. 1967, 27, 395–397. [Google Scholar] [CrossRef]
- Isobe, M. Time-dependent mild-slope equations for random waves. In Coastal Engineering 1994; Edge, B.L., Ed.; ASCE: Reston, VA, USA, 1995; pp. 285–299. [Google Scholar] [CrossRef]
- Iguchi, T. A Mathematical justification of the Isobe–Kakinuma model for water waves with and without bottom topography. J. Math. Fluid Mech. 2018, 20, 1985–2018. [Google Scholar] [CrossRef]
- Matsuno, Y. Hamiltonian formulation of the extended Green–Naghdi equations. Phys. D Nonlinear Phenom. 2015, 301–302, 1–7. [Google Scholar] [CrossRef]
- Nakayama, K.; Kakinuma, T. Internal waves in a two-layer system using fully nonlinear internal-wave equations. Int. J. Numer. Methods Fluids 2010, 62, 574–590. [Google Scholar] [CrossRef]
- Kakinuma, T. A numerical study on distant tsunami propagation considering the strong nonlinearity and strong dispersion of waves, or the plate elasticity and mantle fluidity of Earth. Fluids 2022, 7, 150. [Google Scholar] [CrossRef]
- Boeing Japan Homepage. Available online: https://www.boeing.jp (accessed on 10 February 2023).
- Andrianov, A.O.I. Hydroelastic Analysis of Very Large Floating Structures. Ph.D. Thesis, Electrical Engineering, Mathematics and Computer Science, TU Delft, Delft, The Netherlands, 2005. Available online: http://resolver.tudelft.nl/uuid:85cef785-c17c-41d7-9a58-6a183c468523 (accessed on 11 April 2023).
- Tsubogo, T. A basic investigation on deflection wave propagation and strength of very large floating structures (the 2nd report). J. Soc. Nav. Arch. Jpn. 1997, 1997, 381–390. [Google Scholar] [CrossRef]
- Kakinuma, T. Tsunamis generated and amplified by atmospheric pressure waves due to an eruption over seabed topography. Geosciences 2022, 12, 232. [Google Scholar] [CrossRef]
- Proudman, J. The effects on the sea of changes in atmospheric pressure. Geophys. J. Int. 1929, 2, 197–209. [Google Scholar] [CrossRef]
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley & Sons, Inc.: New York, NY, USA, 1974; pp. 511–532. [Google Scholar] [CrossRef]
- Wu, T. Generation of upstream advancing solitons by moving disturbances. J. Fluid Mech. 1987, 184, 75–99. [Google Scholar] [CrossRef]
- Lee, S.; Yates, G.; Wu, T. Experiments and analyses of upstream-advancing solitary waves generated by moving disturbances. J. Fluid Mech. 1989, 199, 569–593. [Google Scholar] [CrossRef]
- Kakinuma, T.; Akiyama, M. Numerical analysis of tsunami generation due to seabed deformation. In Coastal Engineering 2006; Smith, J.M., Ed.; World Scientific Publishing Co., Pte. Ltd.: Singapore, 2007; pp. 1490–1502. [Google Scholar] [CrossRef]
- Dalphin, J.; Barros, R. Optimal shape of an underwater moving bottom generating surface waves ruled by a forced Korteweg-de Vries equation. J. Optim. Theory Appl. 2018, 180, 574–607. [Google Scholar] [CrossRef]
- Michele, S.; Renzi, E.; Borthwick, A.; Whittaker, C.; Raby, A. Weakly nonlinear theory for dispersive waves generated by moving seabed deformation. J. Fluid Mech. 2022, 937, 94. [Google Scholar] [CrossRef]
- Hong, D.C.; Hong, S.Y.; Hong, S.W. Reduction of hydroelastic responses of a very-long floating structure by a floating oscillating-water-column breakwater system. Ocean Eng. 2006, 33, 610–634. [Google Scholar] [CrossRef]
- van Kessel, J.L.F.; Pinkster, J.A. The effect of aircushion division on the motions of large floating structures. In Proceedings of the ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering, San Diego, CA, USA, 10–15 June 2007; pp. 677–686. [Google Scholar] [CrossRef]
- Gao, R.P.; Wang, C.M.; Koh, C.G. Reducing hydroelastic response of pontoon-type very large floating structures using flexible connector and gill cells. Eng. Struct. 2013, 52, 372–383. [Google Scholar] [CrossRef]
- Ohmatsu, S. Numerical calculation method for the hydroelastic response of a pontoon-type very large floating structure close to a breakwater. J. Mar. Sci. Technol. 2000, 5, 147–160. [Google Scholar] [CrossRef]
- Regulation for Enforcement of the Civil Aeronautics Act. Order Minist. Land Infrastruct. Transp. Tour. 2008, 73, 79. Available online: https://www.japaneselawtranslation.go.jp/en/laws/view/4052 (accessed on 10 February 2023).
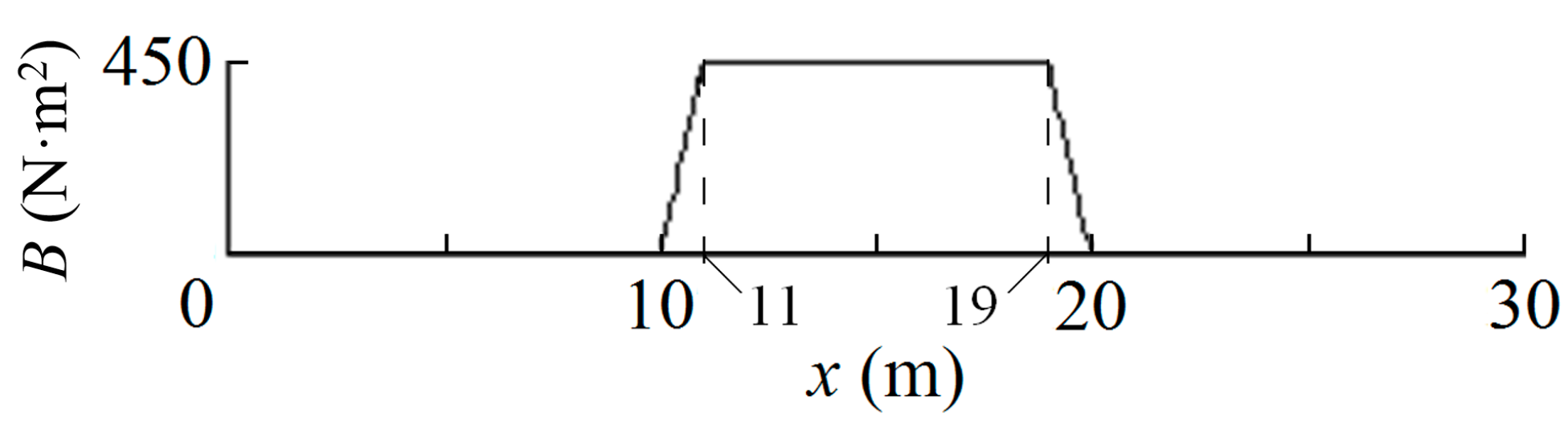














| Case * | Airplane | Airport | Water Depth | ||||
|---|---|---|---|---|---|---|---|
| Type (Mass) | Running Speed | Running Distance | Run Time | Length L | Flexural Rigidity B | h | |
| GA-L1 | B747-400 | 83 m/s | 3 km | 36.1 s | 15 km | 1 × 1011 N·m | 10 m |
| GA-L2 | (397,000 kgs) | 10 m to 50 m | |||||
| GA-S1 | 5 km | 10 m, 20 m | |||||
| GA-S2 | 1 × 1010 N·m | 10 m | |||||
| GB-L1 | B737-800 | 78 m/s | 2 km | 25.6 s | 15 km | 50 m | |
| GB-L2 | (79,000 kgs) | 10 m to 50 m | |||||
| GB-S1 | 5 km | 50 m | |||||
| Case * | Airplane | Airport | Water Depth | |||||
|---|---|---|---|---|---|---|---|---|
| Type (Mass) | Landing Speed ** | Running Deceleration | Running Distance | Run Time | Length L | Flexural Rigidity B | h | |
| LA-L | B747-400 | 72 m/s | 0.86 m/s2 | 3 km | 83.7 s | 15 km | 1 × 1011 N·m | 10 m |
| LA-S | (397,000 kgs) | 5 km | ||||||
| LB-L | B737-800 | 1.3 m/s2 | 2 km | 55.4 s | 15 km | 1 × 1010 N·m | 50 m | |
| LB-S | (79,000 kgs) | 5 km | ||||||
| Case * | Airplane | Airport | Water Depth | |||||
|---|---|---|---|---|---|---|---|---|
| Type (Mass) | Takeoff Speed ** | Running Acceleration | Running Distance | Run Time | Length L | Flexural Rigidity B | h | |
| TA-L | B747-400 | 83 m/s | 1.15 m/s2 | 3 km | 72.2 s | 15 km | 1 × 1011 N·m | 10 m |
| TA-S | (397,000 kgs) | 5 km | ||||||
| TA-S-B | 1 × 109 N·m to | 50 m | ||||||
| 1 × 1011 N·m | ||||||||
| TB-L | B737-800 | 78 m/s | 1.52 m/s2 | 2 km | 51.3 s | 15 km | 1 × 1010 N·m | |
| TB-S | (79,000 kgs) | 5 km | ||||||
| Case * | Airplane | Airport | Water Depth | |||||
|---|---|---|---|---|---|---|---|---|
| Type (Mass) | Landing/Takeoff Speed ** | Running Acceleration | Running Distance | Run Time | Length L | Flexural Rigidity B | h | |
| LC | B787 | 75 m/s | −3 m/s2 | 0.938 km | 25 s | 5 km | 1 × 1011 N·m2 | 10 m, 20 m, |
| TC | (228,400 kgs) | 3 m/s2 | or 100 m | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kakinuma, T.; Hisada, M. A Numerical Study on the Response of a Very Large Floating Airport to Airplane Movement. Eng 2023, 4, 1236-1264. https://doi.org/10.3390/eng4020073
Kakinuma T, Hisada M. A Numerical Study on the Response of a Very Large Floating Airport to Airplane Movement. Eng. 2023; 4(2):1236-1264. https://doi.org/10.3390/eng4020073
Chicago/Turabian StyleKakinuma, Taro, and Masaki Hisada. 2023. "A Numerical Study on the Response of a Very Large Floating Airport to Airplane Movement" Eng 4, no. 2: 1236-1264. https://doi.org/10.3390/eng4020073
APA StyleKakinuma, T., & Hisada, M. (2023). A Numerical Study on the Response of a Very Large Floating Airport to Airplane Movement. Eng, 4(2), 1236-1264. https://doi.org/10.3390/eng4020073







