Abstract
Auxetic structures (AXSs) are a novel class of materials with unique mechanical deformation behavior associated with negative Poisson ratio. The combination of AXS configurations with various types of materials has unveiled a wide field of applications, including military high-velocity protection against explosions and ballistic projectiles. However, the characteristic geometric re-entrant model of AXSs imposes limitations and difficulties when using conventional manufacturing methods to assemble the structure lattice. Additive manufacturing (AM) has recently been explored as a more efficient and cost-effective method to fabricate AXSs, regardless of the type of material. This review paper focuses on the development and applications of AM processed AXSs. The review highlights the significance and great potential for this class of materials that can be produced relatively fast and at a low cost. The advantages of AXS/AM are expected to extend to important industrial sectors, particularly for military ballistic armor, where the feasibility for products with improved properties is critical. The use of AM offers a viable solution to overcome the difficulties associated with the conventional manufacturing methods, and thus offers greater design flexibility, cost efficiency, and reduced material waste. This review paper aims to contribute to the understanding of the current state-of-the-art and future research prospects for the production and applications of AXS/AM.
1. Introduction
Owing to the continuous and pressing need for lighter and stronger structures for space systems, aircraft and military equipment, the development of a novel easy to fabricate and cost-effective sandwich panel composite stands as the most appropriated structural material. Indeed, the sandwich panel is one type belonging to the main class division of “Structural Composites” designed to be lightweight with high stiffness and strength [1], as well as remarkable energy absorption characteristics under the impact from blast or projectiles [2].
A sandwich panel is composed of two outer plates’ face sheets bonded by adhesive to an inner core as schematically illustrated in Figure 1. The outer plate in this figure must be made of materials strongly sufficient to resist the expected applied load in order to protect the inner core. According to Callister and Rethwisch [1], the core presents several functions: (i) provide support for the outer plates; (ii) hold them together with the adhesive contribution; (iii) have sufficient strength to withstand shear stresses; and (iv) be thick enough to resist buckling imposed by bending forces to the panel.
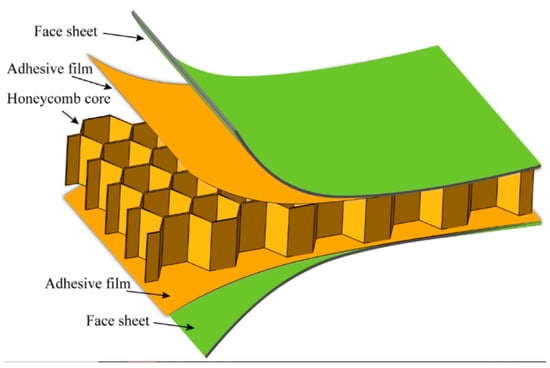
Figure 1.
Schematic of basic sandwich panel configuration. Reprinted with permission from [3]. Copyright 2012, MDPI AG.
The typical honeycomb structure for sandwich panels is fabricated with relatively thin foils arranged into interlocking cells exhibiting a proper configuration, which can display different geometrical patterns [4,5]. A characteristic hexagonal configuration exhibited in Figure 1 was the first proposed [6] and assisted as a basic model for other bio-inspired patterns [7,8], as depicted in Figure 2.
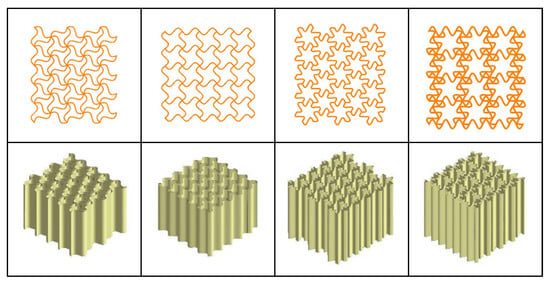
Figure 2.
Horse-shaped honeycombs with different cross sections. Adapted with permission from Ref. [7]. Copyright 2018, Elsevier.
It is important to emphasize that these honeycomb structures were also investigated for their energy absorption applications [9,10], which might be a fundamental aspect for the presently reviewed ballistic application. In particular, auxetic structures (AXSs) possessing honeycomb patterns are being investigated as sandwich panels’ cores for intrinsically higher energy absorption performance. As discussed in a prominent article, Yan et al. [11] indicated that this higher energy absorption of AXSs might be associated with both low-velocity [12,13,14,15] and high-velocity impact caused either by the blast shockwave from bomb explosions [16,17,18] or by ballistic projectiles [19,20]. This latter will be included in the present review regarding complementary aspects to the work of Yan et al. [11].
In spite of comparative improvement in the physical properties of sandwich panels with an AXS core, owing to their negative Poisson’s ratio (NPR), inherent fabrication difficulties and consequently higher costs were, until recently, a practical challenge for their common-scale engineering applications. The very recent remarkable review on anti-blast and impact performance of AXSs by Bohara et al. [21] discussed different manufacturing techniques and, in principle, recommended additive manufacturing (AM), also known as 3D printing, as it is currently the most used for small-scale pieces by enabling the construction of any kind of complex cellular structure such as those demonstrated in Figure 2. Furthermore, these authors indicate that future improvement in AM technology is necessary to produce large-scale AXSs for armor sandwich panels protecting personnel and vehicles from blast and impact projectiles.
Based on the aforementioned preliminary information, the objective of this article is to review the actual development and expected applications of 3D printing-processed AXSs intended for high-velocity impact protection as core sandwich panels. First, a deep discussion of relevant papers on AXSs, especially those not yet reviewed, is presented. Second, the current status of using the diversity of AM techniques for the fabrication of AXSs is critically discussed. Third, novel papers investigating the ballistic performance of 3D-printed AXSs are summarized. The following section discloses the existing and proposed ballistic and anti-blast applications for AXS. Final remarks on possible directions for large-scale production of AXSs, concerning specific interest as a material for ballistic armor, will provide the reader with an ongoing trajectory of a subject with indisputable future interest.
2. Properties of Auxetic Materiais
A novel class of materials, commonly known as “auxetics”, possess peculiar structures that give them distinctive deformation characteristics [22]. In fact, materials deform in different ways when forces act upon them. The vast majority behaves in a traditional manner, in which an object expands axially under tension stress while contracting in the transverse direction, as illustrated in Figure 3a. The inverse ratio of transverse strain to axial strain, indicating a measure of how a material deforms under load, is known as the Poisson’s ratio [23]. A material that stretches axially but contracts transversely in response to a tensile force, or enlarges transversely while axially contracting under compressive force has a positive Poisson’s coefficient. The material owning auxetic behavior expands in the axial direction in one or more orthogonal directions under tension, exhibiting a negative Poisson’s ratio (NPR), Figure 3b [24]. Under compressive forces, AXSs contract in both the axial and transverse directions, Figure 3d.
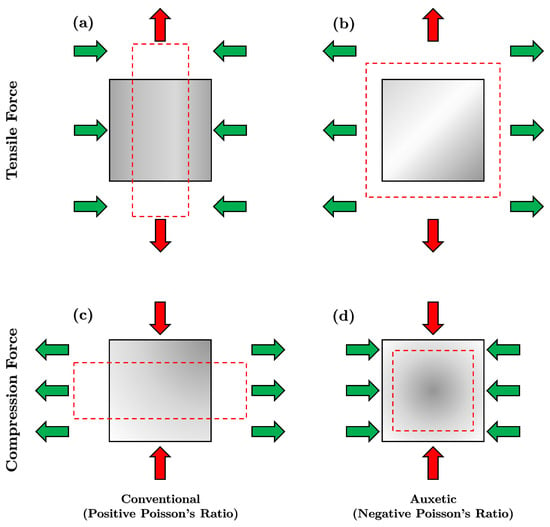
Figure 3.
Comparison of the mechanical behavior of conventional and auxetic materials under tensile and compressive forces: (a) Tensile forces acting on a conventional material; (b) Tensile forces acting on an auxetic material; (c) Compressive forces acting on a conventional material; (d) Compressive forces acting on an auxetic material.
In the late 1800s, some discoveries about AXSs were made; however, they were not significant at that time. In 1882, the existence of AXSs cellular structures in iron mineral pyrite was reported, verified by torsion and flexural tests [25,26]. In 1893, Voigt [27] documented the auxetic effect and negative Poisson’s coefficient in some materials. Until then, already known AXSs were limited to natural materials only, such as wood, and did not draw much attention to synthetic materials research. In 1987, almost a century later, Lakes [22] described for the first time an auxetic foam structure made of polyurethane (PU) that could be easily manufactured by compression and heating processes and that had an NPR equal to −0.6. Other works reported the existence of isolated materials possessing an NPR, such as bismuth, antimony and arsenic [28], cadmium [29], -cristobalite [30], as well as metals that crystallize in a cubic structure [31]. Some research has also demonstrated the existence of skin-like biological materials that exhibit auxetic behavior, such as cat skin [32], ox skin [33], and salamander skin [34], as well as human bones [35]. However, Lakes’ study [22] assisted as a basis for future research on AXSs acquired synthetically.
After this discovery, research on AXSs has been developed for several sectors. The range of applications for these materials is quite wide, for example: sports artifacts [36,37], auxetic foams [38,39,40] and military use [41,42,43], biomedicine [44,45,46,47], textiles [48,49,50], etc. Auxetic materials are found in basically all known material classes: metals [51,52,53], crystals [54,55,56], polymers [57,58,59], ceramics [60,61,62], and composites [63,64,65]. Table 1 presents a brief list based on the most recent known AXSs and their respective NPRs.

Table 1.
AXSs previously investigated and their Poisson ratios.
AXSs diverges from conventional materials (CMs), presenting a peculiar behavior associated with unique mechanical properties. When experimentally investigated, AXS materials display superior properties reported as uncommon, when compared to CMs. An unusual deformation pattern under compression and tension is found for AXSs bringing forth many desirable properties, such as superior shear resistance [78], indentation resistance [79,80], fracture toughness [81], synclastic behavior [22], variable permeability [82] and improved energy absorption performance [83,84,85]. These properties are listed in the following subsections.
2.1. Resistance to Indentation
The indentation resistance property occurs when a non-AXS is subjected to indentation, e.g., hardness testing. The load applied at the indentation location naturally compresses the material. To compensate for this localized pressure, it spreads perpendicular to the applied load, as shown in Figure 4a [86]. On the other hand, the AXSs behavior is different; when an indentation occurs on it, a local shrinkage is observed. Instead of spreading it perpendicularly, a flow occurs and accumulates under the indented region. Then, a denser area with higher indentation resistance is created below the indented zone, as depicted by Figure 4b [87]. As such, they have a higher resistance to indentation, when compared to CMs [79,88].
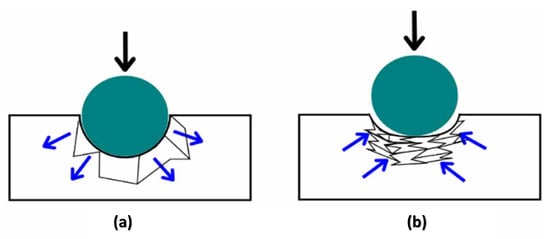
Figure 4.
Deformation behavior and indentation resistance of: (a) conventional material and (b) auxetic material. Reprinted with permission from Ref. [89]. Copyright 2021, IOP.
The increased indentation resistance can be explained by the theory of elasticity. The indentation resistance is associated with the hardness of the material () [90]. This property is correlated with the Poisson’s ratio () given by:
where E is the Young’s modulus, is the Poisson’s ratio of the base materials, and is the constant that assumes the value 1 or 2/3 in the case of uniform pressure distribution or Hertzian indentation, respectively.
Based on Equation (4), it can be seen that, for isotropic three-dimensional (3D) materials, when the Poisson’s ratio decreases to extreme values, for instance near −1, their hardness tends to infinity. Since the upper limit of Poisson’s ratio for 3D isotropic solids is 0.5, the observed values are substantially lower. By contrast, the upper limit of the Poisson’s ratio for two-dimensional (2D) isotropic systems is 1. Materials with such positive Poisson’s values can also have infinite hardness values [24,91,92].
2.2. Shear Resistance
As demonstrated for indentation resistance, AXSs are more resistant to shear forces than CMs [90]. The classical theory of elasticity for 3D isotropic solids shows that the elastic behavior of a body can be described by two out of four constants: the Young’s modulus (E), the shear modulus (G), the bulk modulus (K) and the Poisson’s ratio () [93]. In 3D solids, the relationship between these constants is given by the following equations [88]:
From these equations, it is inferred that the value of shear modulus increases as a function of the reduction in the Poisson’s ratio, resulting in a shear strength increase. The range of elastic modulus corresponding to instability and stability under different conditions is shown in the map of Figure 5. It indicates that the Poisson’s ratio of the isotropic solid should be ranging from −1 to 0.5. When it approaches −1, the shear modulus tends to infinity.
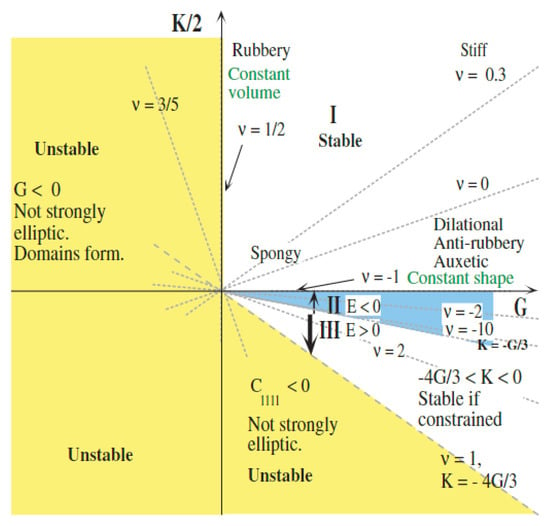
Figure 5.
Map showing the elastic material properties corresponding to different values of K-modulus and shear modulus G. Reprinted with permission from Ref. [94]. Copyright 2007, Wiley.
2.3. Fracture Resistance
AXSs display better fracture resistance than CMs [81]. AXSs also exhibit low crack propagation, requiring a greater amount of energy to expand than CMs [95]. Thus, auxetic materials present brittle fracture. Some works concerning the fracture toughness behavior of AXSs are worth reviewing. Maiti et al. [96] demonstrated that the stress intensity factor (K*IC) for conventional foams is proportional to the normalized density and can be described by:
where f is the fracture stress of the cell rib, l is the rib length, * is the foam density, and s is the density of the foam based material.
Some works reported increased fracture toughness of AXSs, while CMs did not disclose the same behavior. Yang et al. [97] have produced epoxy/Kevlar auxetic laminate composites and correlated the mechanical properties with plain Kevlar and polyurethane (PU) treated Kevlar fabrics. From the fracture initiation toughness (GIC) test, the authors observed that the auxetic fabrics disclose superior performance as compared to plain and PU treated kevlar fabrics, as illustrated in Figure 6. Some conditions of the auxetic epoxy/Kevlar composite disclosed a GIC value up to 225% higher than untreated woven Kevlar and up to 125% higher than PU-treated Kevlar.
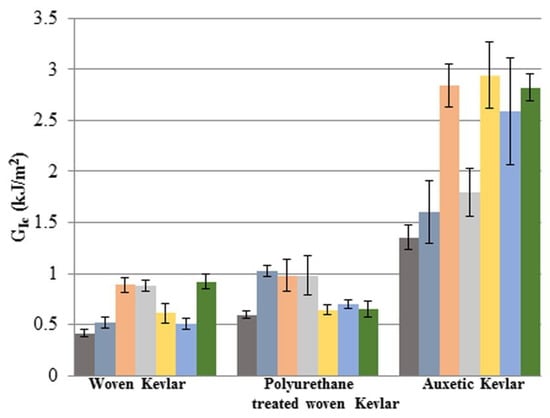
Figure 6.
Fracture initiation toughness (GIC) for all types of composites. Reprinted with permission from Ref. [97]. Copyright 2017, Elsevier.
2.4. Energy Absorption
AXSs manifest superior properties regarding energy absorption. Ultrasonic, acoustic and damping energy absorption are characteristics in which AXSs have an advantage over CMs. It is reported that auxetic foams can display better sound absorption ability than conventional foams at low frequencies [83]. Dynamic crushing properties were remarkable in the auxetic foam, while the conventional foam did not show significant resilience at a high constant stress rate [98].
Oh et al. [99] developed an auxetic foam made of PU and filled with wrinkled 2D graphene oxide (GO). The authors investigated the properties of acoustic energy absorption and damping absorption. Auxetic foam reinforced with GO was set side by side with another AXS without filling. Graphene-polyurethane oxide auxetic foam exhibited high sound absorption performance, with a range of 98.4% at 2 kHz due to the hierarchically porous structure. The improved mechanical compression stability is attributed to the superior energy absorption properties resulting from superb compressibility and internal auxeticity. This greatly increases the shock energy absorption time by 189% in the low-velocity impact test in contrast to the value of the pure PU foam. The blending of a 2D corrugated GO sheet and a flexible 3D AXS promoted greater acoustic and vibration absorption as a consequence of multiple energy dissipation mechanisms.
Najafi et al. [100] analyzed the mechanical performance and energy absorption in order to show differences and likenesses of three different AXSs produced in ABS by the 3D printing method: re-entrant, arrowhead and anti-tetra chiral, as depicted in Figure 7a–c. From the compression test results, the authors observed that the anti-tetra chiral structure presented a greater deformation (Figure 7d–f), when set against the arrowhead and re-entrant structures. Nevertheless, this structure also brought up a significantly higher specific energy absorption (SEA), illustrated in Figure 7g.
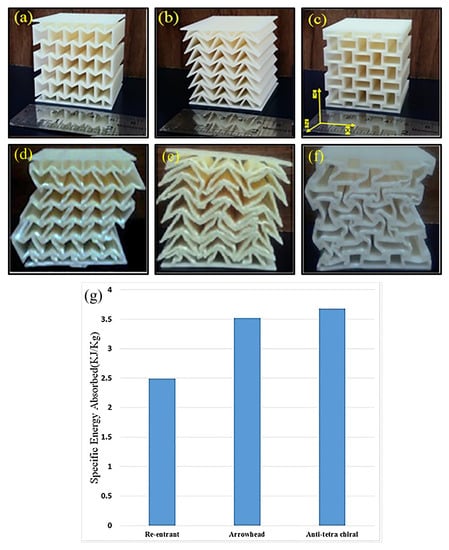
Figure 7.
Auxetic 3D printed ABS structures: (a) re-entrant; (b) arrowhead; (c) anti-tetrachiral; (d) re-entrant after compression test; (e) arrowhead after compression test; (f) anti-tetra chiral after compression test; and (g) specific energy absorption of the tested structures. Reprinted with permission from Ref. [100]. Copyright 2021, Elsevier.
2.5. Synclastic Behavior
Synclastic behavior is the ability of an AXS to suffer deformation into a dome shaped curvature when subjected to bending stresses [101]. Contrastingly, CMs uncover a stretching saddle-shaped on their surface when subjected to bending stresses, originating a shrinkage in their perpendicular direction. Therefore, it presents an anticlastic curvature, as shown in Figure 8a. On the other hand, the AXs, when bent, will present a dome shape because, throughout the application of stress, there is an expansion and contraction of the material both on the outside and inside, respectively [102]. Thus, the result of the expansion of the tensioned part and the shrinkage of the compressed part is the dome shape, shown in Figure 8b. This property is desired in materials for application in the biomedical and sports sectors, such as stents, prostheses, sports accessories, etc. [23,36,37,103,104,105,106].

Figure 8.
Curvature in bending: (a) anticlastic curvature of conventional, non-auxetic materials and (b) synclastic curvature of auxetic materials. Reprinted with permission from Ref. [37]. Copyright 2018, MDPI AG.
2.6. Variable Permeability
Currently, it is already known that AXSs own a porous microstructure and that its dimensions can vary under tensile or compressive stresses. Given this characteristic, a potential use that emerges from AXS porosity is the application in filters. Alderson et al. [107] detailed in their work that AXSs may offer superior performance in filter application at both the macro and nano-scale in view of their unique pore opening properties and characteristics. Variable permeability is paramount for medical applications such as smart stents, which are used to deliver pharmaceutical drugs into the human body [108,109]. In Figure 9, a schematic view of how variable permeability works is illustrated, in which a stress applied to the AXS develops the expansion of the pore structure, allowing a particle to go across it.
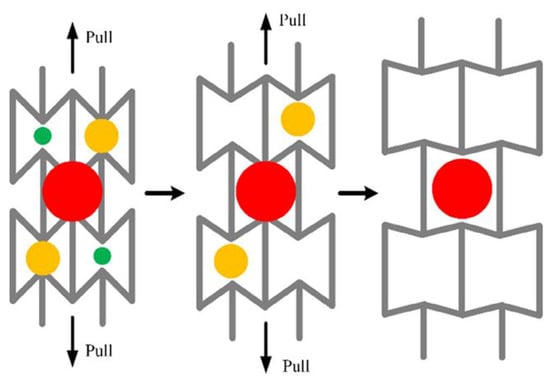
Figure 9.
Schematic of variable permeability in auxetic structures. Reprinted with permission from Ref. [110]. Copyright 2020, Wiley.
2.7. Shape Memory Auxetics
Another important property related to AXSs is shape memory. It occurs when a material subjected to deformation, whether plastic or elastic, has the ability to return to its original state after undergoing thermal excitation [111,112]. Currently, there are several studies reporting the shape memory effects in materials of different classes—for instance, NiTi alloy [113,114,115], PLA/TPU/Fe3O4 [116], SMEP/GNP [117], ZrO2/Y2O3 shape memory ceramic [118], among several others performing this singular characteristic. Studies demonstrate that it is possible to obtain auxetic foams that can be reverted to conventional foams several times without a loss of mechanical properties [119]. Therefore, shape memory is useful in situations that require variable auxetic and non-auxetic mechanical properties, being changed as a function for the temperature.
In Figure 10, a schematic of this effect in an AXS developed by Kamyab et al. [120] is illustrated for an acrylate shape memory polymer (SMP). In the schematic, it is possible to observe that, with the heating of the material, tensile stresses start to act, as a consequence. After this process, the SMP is cooled, and then its load is removed, inducing it to return to its first state. Finally, it is reheated in order to completely return to its original state.
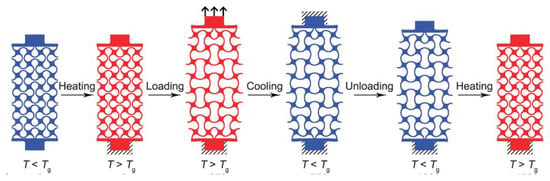
Figure 10.
Schematic illustrating the thermo-mechanical loading cycle under tensile mode for shape memory polymer (SMP). Reprinted with permission from Ref. [120]. Copyright 2022, ProQuest.
2.8. AXSs for Ballistic Protection
In Section 2, the properties of auxetic panels were described, which are made possible by the complex structures that compose them. In Section 3, these structures will be presented in more detail. The development of auxetic panels with these structures allows for the absorption of impact energy, which can be applied in various areas, such as protection of military vehicles against explosions and ballistic panels. According to Bohara et al. [21], energy absorption occurs in AXSs due to the deformation of the cell wall and the subsequent formation of plastic hinges in the wall. The inherent porosity of AXSs also contributes to greater energy absorption. The authors cite studies that show the use of AXSs in blast armor, vehicle bumpers, impact shields, and protective helmets.
An interesting example is the study by Yan et al. [11], who evaluated AXS honeycomb sandwich panels impacted by projectiles, made with carbon fiber-reinforced polymer. Figure 11 schematically illustrates the penetration of the bullet into the AXS. The authors observed that, as the bullet perforates the front steel plate, the honeycomb cells in its path are directly cut, resulting in brittle failure and delamination. The external steel plate had little effect on reducing the bullet’s velocity but contributed to reducing the crushing area. On the other hand, the internal core of the honeycomb played an important role in reducing the penetration velocity and, consequently, the impact energy.
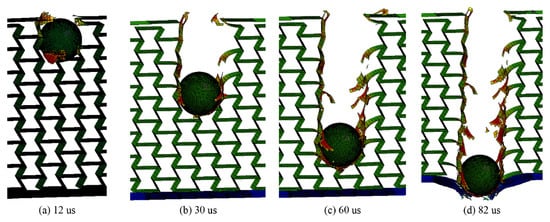
Figure 11.
The perforation process of bullet penetration into AXS honeycomb sandwich plate. Reprinted with permission from Ref. [11]. Copyright 2022, Elsevier.
3. Auxetic Structures
The term auxetic is used for both structures and materials. The AXS plays a key role in this material expansion and mechanical behavior. Therefore, several structural models have been investigated, and their auxetic behaviors have been discussed. For this topic, the main models of auxetic-related structures will be described.
3.1. Re-Entrant Structures
The re-entrant pattern is one of the most well-known structures used for developing AXSs. It was originally proposed in 1982 by Gibson et al. [121], where, from the deformation of a hexagonal honeycomb structure, it was possible to obtain 2D re-entrant structures, as schematically shown in Figure 12. When a load is applied, the diagonal ribs are stretched, moving the structure and giving rise to the auxetic effect.
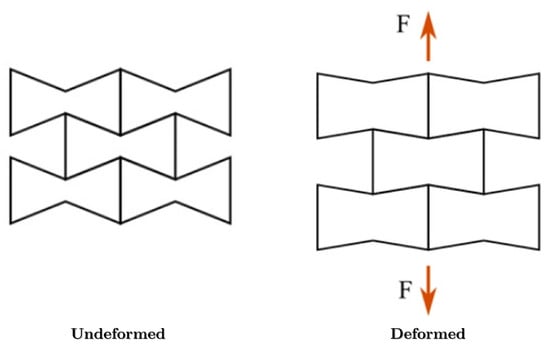
Figure 12.
Auxetic behavior of the re-entrant structures. Reprinted with permission from Ref. [122]. Copyright 2022, Wiley.
As a result of the development of this structure, advances in the development of AXSs have been significant. From the original re-entrant structure, others have been proposed, as illustrated in Figure 13. Similar to the re-entrant structure, the arrowhead and star models (Figure 13b,c) have the auxetic behavior coming from the re-entrant parts, as highlighted by the blue color in the figure. Using rhombus-shaped lines, the hexagonal re-entrant and grid-like models were established (Figure 13d,e). In Figure 13f, a sinusoidal structure is illustrated, in which one can observe the elongation occurring and, for this reason, the auxetic effect arises. In addition, links on the sinusoidal curves can be modified following the articulated linear ligaments.
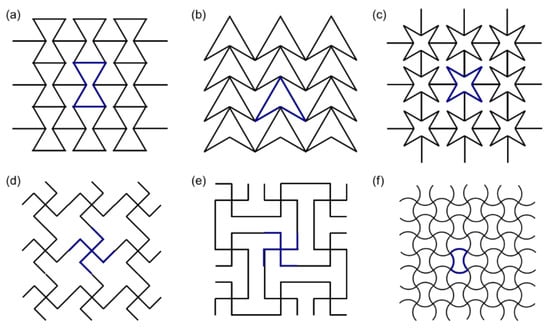
Figure 13.
Re-entrant structures. (a) re-entrant honeycomb; (b) double arrowhead; (c) star honeycomb; (d) structurally hexagonal re-entrant honeycomb; (e) lozenge grids; (f) sinusoidal ligaments. Reprinted with permission from Ref. [104]. Copyright 2021, MDPI.
3.2. Rotating Unit Structures
Another type of AXSs is related to rotating unit structures. In this model, different uniform geometric shapes such as rigid/semi-rigid squares, triangles, rectangles and tetrahedra are configured at their vertices [123,124,125]. The auxetic behavior of this structure occurs through the rotation of these shapes when stretched in a certain direction. This model was firstly proposed by Grima et al. [126], when they verified the occurrence of AXS in an inorganic material. The concept of rotating squares with rigid units was shown to be independent of the initial geometry and the direction of loading applied to the material, keeping the NPR near −1 [127]. Several studies have been conducted in order to better understand the deformational characteristics of this AXS.
The square rotating unit, Figure 14a, is the simplest 2D structure among a variety of 2D unit structures available to be manufactured. It is possible to acquire rectangle or parallelogram units by scaling and tilting square structures, as presented in Figure 14b [128,129]. It is also possible to acquire a rotating unit with two or more different types. Typical examples of these heterogeneous rotating units are the trans-rectangular, Figure 14c, and the two-square structures, Figure 14d. In addition, for rotating frames possessing a square section, there are 2D rotating frames with triangular units, owning three hinge points. They were manufactured similarly to the square type, but their structure is simpler, and might be developed based on simple geometrical units such as triangles, as shown in Figure 14e–g. The rotating structure that has a hexagonal unit, Figure 14h, can be used in two ways: (i) the hexagon attached to a square or triangular unit or (ii) triangular unit. However, it cannot be used individually to manufacture a rotating structure, without square or rectangular units. A hexagonal is employed with other types of units to create a heterogeneous rotating 2D structure.
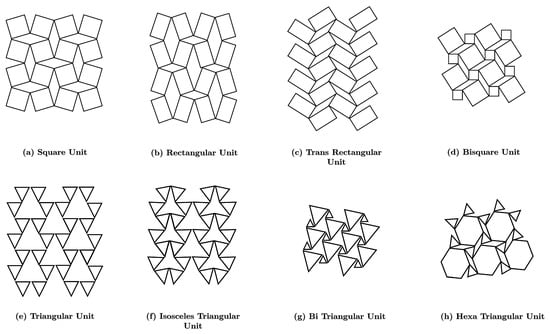
Figure 14.
AXSs Rotating units: (a) square; (b) rectangular; (c) trans-rectangular; (d) bisquare; (e) triangular; (f) isosceles triangular; (g) bi-triangular; and (h) hexa-triangular.
3.3. Chiral Structures
Chiral structures are manufactured by straight ligament connections (ribs) joined to central nodes that can be circles or other geometric shapes. The auxetic behavior regarding this structure is achieved by wrapping or unwrapping the ligaments around the nodes when a load is applied.
The unit circles present in chiral structures are uniformly aligned in tri-, tetra-, or hexahedral arrangements, where the ribs wrap around the circles and connect them to others. When a load is applied to a chiral structure, it is transferred to the circular units via chiral ribs, and the transmitted load is deflected from the center of the circle, producing a rotational torque. Thus, it rotates in a particular direction pulling and pushing adjacent units amongst ribs connected in a different direction of the load [130]. Two-dimensional chiral structures are composed of circular units and ribs, and are limited to five different basic types: tetrachiral, anti-tetrachiral, trichiral, anti-trichiral, and hexachiral, as illustrated in Figure 15 [131].
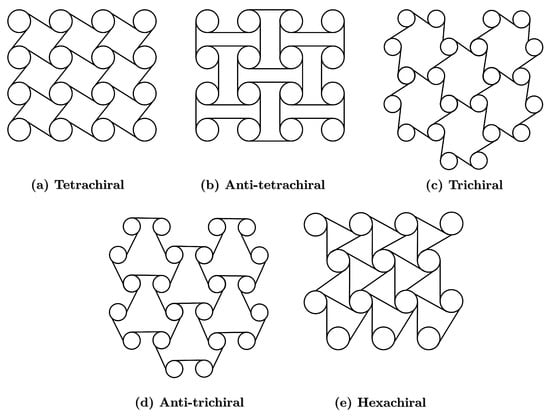
Figure 15.
Chiral AXSs: (a) tetrachiral; (b) anti-tetrachiral; (c) trichiral; (d) anti-trichiral; and (e) hexachiral structures.
Chiral structures are produced from narrow designs, which have similar auxetic characteristics to re-entrant structures. Even though the high porosity of chiral structures allows them to be lighter than re-entrant models, this reduction in weight ultimately obstructs the durability and stability. Moreover, even if the chiral structure exhibits NPR, it becomes vulnerable to local buckling if compressive loads between circular units are transmitted through thin ribs. Furthermore, due to the geometric arrangement, they have limited structural variation and narrow design space, unlike the re-entrant and rotating structures.
3.4. Nodule and Fibril Structures
Nodule and fibril structures consist of a rigid unit connected among fibrils. These fibrils are responsible for the load transfer to the rigid structures. The working scheme is schematically illustrated in Figure 16; without a load acting upon them, they are twisted around the rigid unit. When a tensile force is applied to the fibril structure, they tend to align and push it in a perpendicular direction, inducing an auxetic behavior. Initially, Alderson and Evans [132] developed a model for a polymer featuring auxetic micropores. These AXSs can be subdivided into classes based on how the rigid units and fibrils are connected: (i) network type; with (ii) circular or (iii) square nodules; and (iv) bundle type [133].
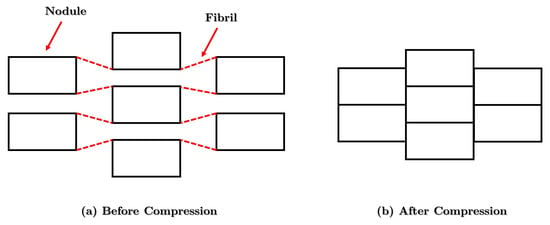
Figure 16.
Typical shape of fibril–nodule structures: (a) before compression; (b) after compression.
The fibril–nodule model was developed early in studies concerning AXSs, to be employed in polymeric materials. An example of an auxetic polymer is the liquid crystalline, where its behavior can be defined by the fibril–nodule mechanism. This material has a crystalline fibril–nodule structure when it has no load acting upon the material. However, when a stress is applied, it presents an amorphous AXS due to the decrystallization with its stretching [134]. Given this concept, the auxeticity of the fibril–nodule structures only occurs for a tensile condition, disappearing under the action of compressive loads.
3.5. Interlocking Structure
The auxetic interlocking structure was first proposed by Ravirala et al. [135], and its associated micromechanical model is schematically illustrated in Figure 17. The structure without a stress state is all connected and interlocked, Figure 17a. At the moment, a load is applied, it expands, exhibiting auxetic behavior, Figure 17b. The conventional hexagonal geometry shown in this model (0 < < 90) displays an auxetic behavior regarding its structure, while the reentrant hexagons (90 < < 180) disclose a positive Poisson’s coefficient.
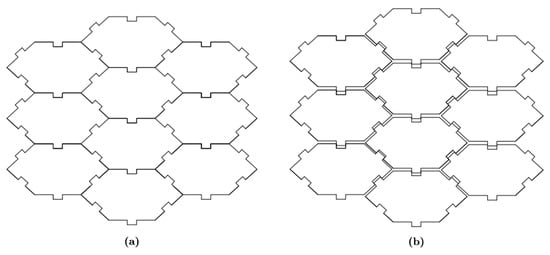
Figure 17.
Interlocking hexagon structure: (a) fully densified; (b) partially expanded.
3.6. Keyed Brick Structure
The keyed brick structure is designed to withstand the horizontal components of the forces generated throughout an earthquake, while allowing a motion that assists with differential thermal movements between the graphite core and the steel supporting the edges [86]. The free movement of the core was also designed to sustain the expansion and shrinkage of the graphite bricks when radiation exposure occurs. Furthermore, the structure needs to have high shear deformation resistance in the horizontal plane and low resistance to volume changes. As such, it expands in all radial directions when subjected to a tensile load in the horizontal plane and keeps the square mesh over deformation. In this way, this type of model becomes auxetic, obtaining = ± 1 in the horizontal plane [86]. They are arranged in columns of 10 ± 12 bricks, making the entire core possible to be approximated to a continuous anisotropic solid material. The scheme of the keyed brick structure is illustrated in Figure 18.
Figure 18.
Schematic of a keyed brick structure.
3.7. Other Geometries
In addition to the most well-known AXSs that were presented in the previous items, there are several other cellular structures that present auxetic characteristics. These structures end up forming new classifications, and it is often not possible to classify them according to the models already known.
Bohara et al. [85] developed three new AXSs for application in military vehicles protection by absorbing blast energy. They were named: (i) hourglass structure (HGS); (ii) braced cross-petal structure (BCPS); and (iii) cross-petal structure (CPS). The finite element method (FEM) was employed to analyze these novel ASXs using a variety of parameters such as stress–strain behavior, Poisson’s ratio, energy absorption capacity and others. From the simulations, the authors found that, for demands requiring high energy absorption, these three AXSs have shown superior performance contrasting the traditional ones. Figure 19 depicts a comparison of the specific energy absorbed (SEA) for all AXSs analyzed.
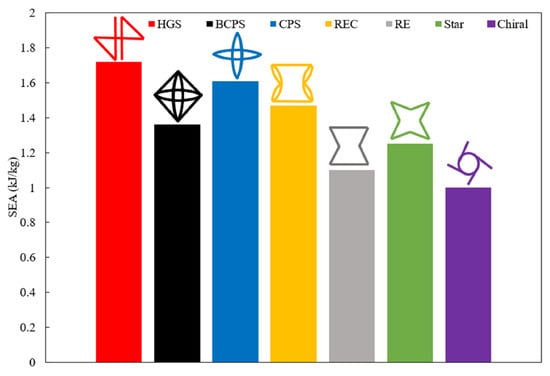
Figure 19.
SEA values for different AXSs. Reprinted with permission from Ref. [85]. Copyright 2021, Elsevier.
Moreover, another approach for acquiring novel structures is the union of two AXSs. Etemadi et al. [136] developed hybrid structures attaching re-entrants and arrowhead structures (RAH), Figure 20a, as well as star and arrowhead structures (SAH), Figure 20b. The authors produced the samples by the 3D fused deposition method using a standard polylatic acid (PLA) resin for the manufacture. FEM analyses were performed, as well as tensile and compression tests, in order to evaluate their mechanical properties. From the analyses, it was found that the hybrid models have shown higher E and than re-entrant and arrowhead ones. RAH and SAH achieved E and values of 66.21 and 86.24 GPa, and −1.34 and −0.98, respectively. On the other hand, the re-entrant and arrowhead conventional structures presented the following values: E = 22.86 and 34.67 GPa and = −1.24 and −1.00, respectively.
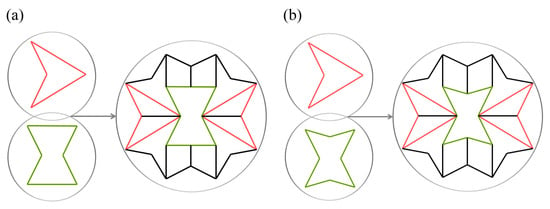
Figure 20.
Hybrid structures: (a) re-entrant arrowhead (RAH); (b) star arrowhead (SAH). The re-entrant, star, and arrowhead structures are illustrated in colors for better understanding. Reprinted with permission from Ref. [136]. Copyright 2023, Elsevier.
3.8. Brief Summary
In this section, it is worth noticing the impressive number of distinct models of auxetic structures that have been investigated so far, from reentrant [121,136] to cross-petals [85] for absorbing blast energy. It predicts a vast field of opportunity for the development of novel auxetic structures.
4. Manufacturing Techniques of Auxetic Structures
The special properties obtained through the development of AXSs are associated with their origin in the manufacturing of a complex 3D structure. Additionally, small details such as the reentrance dimensions of a unit cell are crucial to this auxetic behavior. However, these details also make it difficult to fabricate these materials using conventional techniques. To overcome this challenge, additive manufacturing (AM) techniques are employed in the fabrication of these structures. AM provides a quick and precise solution in the manufacturing of AXSs sandwich panels that present complex geometries at their core. However, conventional techniques are also used, albeit less commonly, in the fabrication of AXSs [137]. Currently, there are several manufacturing techniques available for the production of AXSs, including both conventional and AM/3D printing techniques such as:
- Self-Propagating Photopolymer Waveguide (SPPW);
- Microstereolitography (SLA);
- Direct Laser Writing (DLW);
- Self-Assembly
- Selective Laser Melting (SLM).
4.1. Self-Propagating Photopolymer Waveguides (SPPW)
The self-propagating photopolymer waveguides (SPPW) technique assembles a 3D polymeric structure in a cellular microscale arrangement, interconnected periodically [138]. It consists of an ultraviolet (UV) light beam enlightening a 2D mask, which has an aperture inside a photomonomer container, as demonstrated in Figure 21 [139]. The SPPW is based on the incident light self-trapping effect upon the polymer, being induced by a change in the refraction index among the liquid monomers and the rigid polymeric material. Owing to this event, the SPPW is able to create high aspect ratio beams having a continuous cross-section, being perfect for the 3D topologies construction based on beams. Furthermore, it is possible to control the topologies by an aperture pattern on the mask and orientation of the incident UV light. While the unit cell dimension and the smaller size details, regarding the topologies, rely on the aperture diameter and mask space. The material thickness is controlled mostly by the maximum waveguide length propagation. Moreover, a multilayer strategy could be applied in order to acquire structures displaying a higher thickness [140].
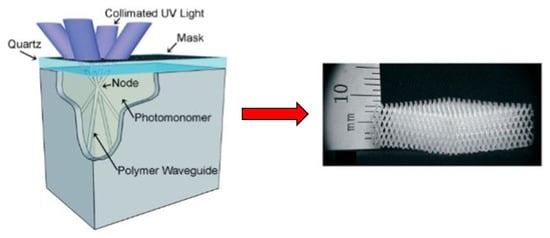
Figure 21.
Operational scheme of the self-propagating polymer waveguide (SPPW) technique. Reprinted with permission from Ref. [138]. Copyright 2007, Wiley.
However, in contrast to other AM techniques, the SPPW is limited regarding the topologies randomness, since it is just possible to manufacture variations of beam-based topologies. The extended UV light exposure requested to achieve the maximum waveguide length often enlarges the original diameter, developing thicker materials [138]. On the other hand, the great advantage of it is the high manufacture speed, being able to produce microscale AXS in a few minutes in addition to a great scalability capacity, yielding manufacture rates superior to 1 m2/min [141]. The aforementioned characteristics make it an attractive method for large-scale fabrication.
4.2. Microstereolithography (SLA)
Microstereolithography (SLA) is an AM technique classified according to the ISO/ASTM 52900:2021 standard [142] as belonging to the Vat Photopolymerization (VPP) category. SLA uses a UV light beam to cure the resin, resulting in the rapid assembly of structures. The operational mechanism of the SLA technique is based on the local polymerization of a photosensitive resin, as shown in Figure 22. Each layer is obtained by moving the UV light beam over a surface, which is guided on the x- and y-axes by galvanometric mirrors. The solidified object is then immersed in a resin reservoir, and a new layer is reflected onto the already polymerized layer, allowing the manufacture of the next layer [137,143,144].
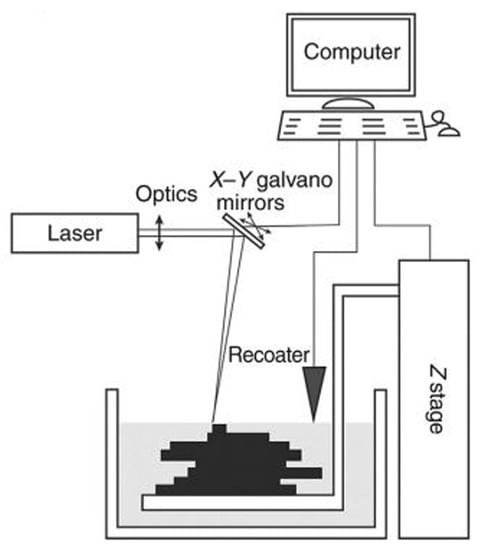
Figure 22.
Schematic of microstereolithography technique. Reprinted with permission from Ref. [145]. Copyright 2020, Elsevier.
Furthermore, the AM techniques yielded a strong influence on the production of industrial parts because they significantly reduced the processing time, entailing a manufacturing economy regarding objects with complex geometry. The SLA was one of the first to be developed, and due to its velocity, is, hitherto, the most applied in industry. The manufacturing costs for the SLA pieces are affordable, and the surface finishing is appropriate, without a requirement for further operations. The typical resolution range for SLA is 150 mm for the three space directions. However, some parameters, such as: resolution, precision, and surface roughness may change since they are based on over layering. In particular, the vertical resolution (over the construction axis) is associated with the overlapped layer thickness, whereas the lateral resolution (on the plane) is determined by the light beam dimension used to design each layer shape on the resin surface.
In comparison to others’ AM, the paramount SLA advantage is the production of 3D microscale objects holding complex structures and supporting a high velocity fabrication. On account of these compelling characteristics, SLA is assigned to several fields such as: biomedicine, tissue engineering, micro-optic devices, bioinspired materials, micro-electromechanical, among other systems [146,147,148,149].
The SLA is relevant regarding the development of AXSs since it can produce with ease auxetic cores for sandwich panels, and therefore apply them on a large scale. Alomarah et al. [150] manufactured re-entrant AXSs and re-entrant chiral auxetic (RCA) composed of a photopolymer composed by polypropylene (PP) by SLA. In a more recent work, Varas et al. [151] also used PP to produce different types of AXSs and evaluate the properties of each structure.
4.3. Direct Laser Writing (DLW)
Direct laser writing (DLW) is a well-known AM method for the fabrication of complex structures on a nanoscale up to 100 nm [152]. In this method, a beam laser is focused through an objective lens in order to cure photopolymers by means of a single or multi-photon absorption [153,154]. The DLW by single-photon absorption is limited to the manufacture of 2D structures because its absorption occurs inside a whole area of photopolymers exposed to light. The multi-photon absorption, also known as two-photon polymerization, takes place in a small voxel on the focal point of the laser beam, where the light intensity is remarkably high [155]; thus, arbitrary 3D structures possessing details excessively smaller could be fabricated by the voxel [156,157]. As a consequence, this process is an attractive tool for applications in several fields, such as micro-optics, supercapacitors, microfluidics, biomedical implants and tissue engineering [158,159,160,161,162,163,164]. In Figure 23, the schematic diagram of how the DLW works is illustrated.
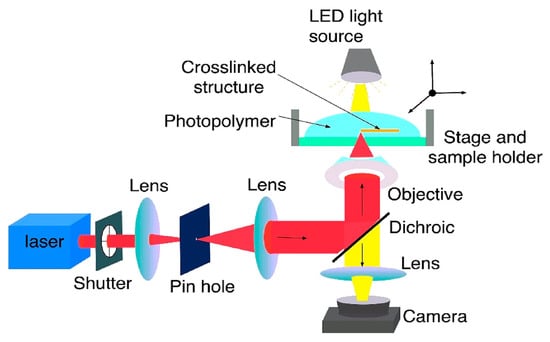
Figure 23.
Setup of the direct laser writing system. Reprinted with permission from Ref. [153]. Copyright 2020, ACS.
The principle of the DLW is based on a laser beam that is pulsed at a wavelength close to infrared ( = 780 nm). This laser is focused on a photoresist material, transparent to the wavelength, through a high aperture objective lens. The photoresist contains photoinitiators for the absorption of two-photons. Due to the focus through the objective lens, the photons are absorbed within the focal volume. Thus, initiators cause a chemical reaction when excited, which enables the formation of chemical bonds, for example, by polymerization or bond breaking. During sample manufacturing, moving the focal spot in different directions enables the fabrication of complex 3D structures at high fabrication speeds [165].
The DLW is able to manufacture materials without the necessity of supporting matrices or a layer by layer process, as the SPPW, owing to the capacity to precisely induce the polymerization within a particular spatial position of a photoresist thick-film [166]. Despite the aforementioned benefits, the DLW is not widely applied for mass production in all industries because it is much less scalable than other methods. Additionally, the costs of acquiring and conserving DLW systems are very high because accessories such as optical systems and femtosecond lasers are expensive and difficult to obtain. Thus, the process becomes unfeasible for large-scale fabrication of AXSs. Another factor that makes this technique inaccessible in the production of AXSs is the choice of photoresist materials. Because the transparency to the infrared beam is necessary for the processing to occur, and the selection of materials is limited to transparent polymers, other materials such as metallic and ceramic particles are not attainable in the process because they inhibit the penetration of the laser.
4.4. Self-Assembly
The Self-Assembly technique is characterized by the mechanism of polymeric phase separation, which can be in the form of emulsion or colloidal suspension. Although previously not considered an AM technique, due to its technological unfeasibility for such classification, since 2018, research involving this manufacturing method has been growing exponentially, allowing the technique to gain technological maturity to be classified as an AM technique [167]. This is due to its ability to rapidly produce complex structures in a distributed manner, making it a method of great importance during the COVID-19 pandemic between 2020 and 2022 [168,169,170]. The interactions between the components in the fabrication present van der Waals bonds, hydrogen bonding, electrostatic attraction, as well as hydrophobic and hydrophilic interactions. These interactions can create a self-assembly system owing to a thermodynamic condition of non-equilibrium, establishing a stable state within well arranged hydrophobic structures [171,172,173]. It is possible to develop materials with organized nanostructures from the separation of the microphases present in the material. Self-assembly is very competitive when compared to other AM techniques owing to the ability to produce parts with customizable morphology and functionalities [137].
In order to manufacture materials on a large scale, a block copolymer (BCP) phase separation technique was developed. BCPs are divided by the management of chemical properties and molecular weight of each polymer. The self-assembly by BCP separation occurs by the thermodynamic incompatibility of the copolymer phases, where a separation of microphases with a variety of nanoscale morphologies is generated, such as: lamellas, spheres, cylinders and others [174,175,176]. In Figure 24, a schematic of the separation and arrangement of the BCPs microphases is illustrated.
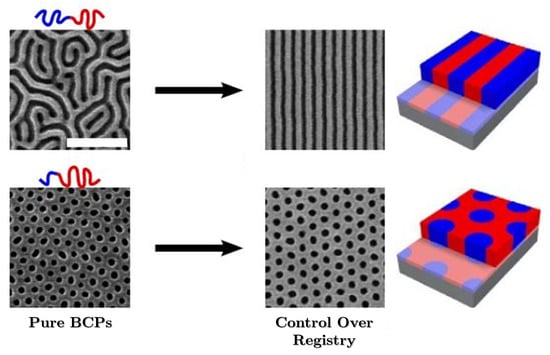
Figure 24.
Schematic of self-assembly. The AM method uses a substrate template to give long-range order to lamellar and cylindrical self-assembled block copolymer films. Reprinted with permission from Ref. [177]. Copyright 2016, Nature.
Manufacturing nanostructured materials by self-assembly is not limited only to polymers. Metallic and ceramic structures can also be processed by this technique; for instance, it has already been developed nanostructures of gold [178], CeO2/MnOx@C [179] CoPC/CNTs [180], Fe3O4/rGO [181] among others for several applications.
In comparison to other AM, self-assembly yields a unique low-cost opportunity, highly scalable and a fast manufacture for 3D structures possessing micro and nanoscale. However, this process’s ability for the fabrication of several morphologies, such as octet or cubic plate lattices, is still very limited. In addition, up to now, it is difficult to manage a self-assembled final topology [173]. As a consequence, defects are acquired in large-scale fabrications, and further investigations are required to solve these problems.
4.5. Selective Laser Melting (SLM)
The selective laser (SLM) is another method for the construction of 3D metallic structures. It uses computational support and a high energy laser in order to bond the metallic particles [182]. SLM makes viable the manufacture of metallic components layer by layer following a 3D-computer aided design (CAD) model. Thus, this enables an almost unlimited fabrication of complex geometries without the necessity for pre-production costs or specific tools [183]. The SLM mechanism is demonstrated in Figure 25, and occurs according to the following steps: (i) the 3D-CAD model is decomposed in layers and sent to a selective fusion laser equipment; (ii) a powder material is laid upon the substrate, creating a thin layer; (iii) each piece of geometry information is transferred by the laser beam to the powder bed where the regions having the solid materials are scanned under an inert atmosphere; thus, another layer can be manufactured; (iv) after a layer is constructed upon the substrate, the equipment bases connected to a plunger go down, so a new layer is inserted above the first one. Therefore, the manufacturing steps are repeated layer by layer until the sample is constructed [184,185]. The printed samples can reach a density value close to 100% because metallic powders are used, disclosing suitable mechanical properties combined with a rigorous management of the material composition [186].
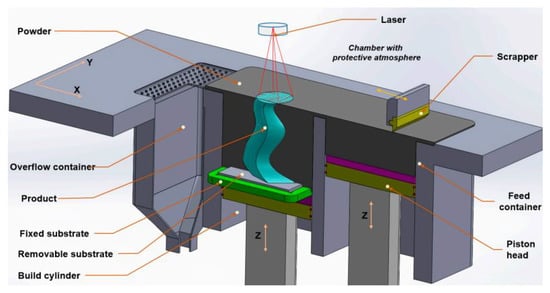
Figure 25.
Schematic of selective laser melting 3D printing method. Reprinted with permission from Ref. [187]. Copyright 2017, Elsevier.
The AXSs production by SLM allows the acquisition of materials with superior mechanical properties compared to the auxetic ones composed of polymers. A great majority of AM techniques process polymer structures. Although they present acceptable properties, they still exhibit limited characteristics, in comparison to metals in terms of a greater thermal and mechanical resistance. Singh et al. [188] processed re-entrant AXSs by SLM. They adjusted parameters and mechanical tests and were able to attain a Poisson’s Ratio of −3.1. Gao et al. [189] brought on auxetic contacted cube (ACC) structures by SLM using an AlSi10Mg alloy. The authors observed a superior density to 99% for the specimens; in addition, they displayed NPR and a good deformation distribution for all the samples.
4.6. Other Techniques
In addition to the previously mentioned techniques, there are several others for the production of AXSs. Each method has its own process particularities, making it viable to construct complex structures fast and with ease. As mentioned in the text, AXSs can be produced by both conventional techniques and more advanced techniques, such as AM techniques. Among all the available techniques, it is worth mentioning: extrusion [190,191,192], fused deposition modeling (FDM) [193,194,195], inkjet printing [196,197], selective electron beam melting (SEBM) [198,199,200,201], selective laser sintering (SLS) [202,203,204,205], aerosol jet printing [206,207,208], chemical vapor deposition (CVD) [209,210,211], and others. Classifying these techniques is a complex task because the research areas for the AM and AXSs present an accelerated expansion. However, certain methods may show similar features but manufacture distinct materials classes. Therefore, it is not possible to classify them in order to expand a range of applications and materials.
4.7. Brief Summary
In this section, the relevance of combining AXS and AM was emphasized. Indeed, the numerous proposed AXS, despite their complex shapes, certainly have a proper technique for cost-effective fabrication of armor protection against high-velocity projectile and blast protection.
5. Applications
The sandwich panels having a core assembled by AXSs present remarkable properties, allowing them to be applied in a variety of distinctive applications, such as biomedical, textiles, sports and military. The AM techniques enable fast processing for materials holding complex structures, while they display great precision and replicability. For this reason, these materials become attractive for large-scale demands. Table 2 presents the main sector and applications for auxetic materials manufactured by AM methods.

Table 2.
Summary of the main applications for auxetic materials [87,212].
Among the specified applications in Table 2, the area showing promising potential is in the military field. The AXSs are outstanding because they have the capacity to absorb high-velocity impacts, i.e., shock waves and blasts, commonly applied to bullet vests and ballistic helmets [213,214,215]. Moreover, auxetic materials enable the production of more lightweight and greater uniform shock wave energy absorption; thus, soldiers acquire higher mobility on the battlefield [36,216]. An example is a shoe based on an auxetic material, capable of reducing the body weight impact upon the ground, preventing injuries and providing more comfort [217].
High-speed military applications encompass ballistic protection, in which armor must absorb the energy of projectiles traveling at speeds above 300 m/s and prevent the dispensed projectile and/or shock wave from causing injury to the combatant. These speeds are classified in different ways according to the NIJ 0101.06 standard [218]. From these speeds, it is possible to classify light armor and heavy armor. Soft armor is classified in the lower and medium levels in the NIJ standard, IIA, II, and IIIA, in which protection requirements are against low-energy projectiles, such as the bullets shot from handguns [219,220]. The higher levels must include hard armor inserts in what is called “in conjunction design”. Those plates are destined for high-risk military applications, since they are subjected to higher energy projectiles, such as the bullets from AK-47s. Table 3 indicates the relationship of impact velocities of different projectile types to armor levels according to NIJ 0101.06 [218].

Table 3.
Test requirements from NIJ 0101.06 standard [218].
Considering the application of AXSs in anti-blast and high-velocity (impact and ballistic), Table 4 shows a summary of the most recent research investigating the behavior of auxetic materials for military demands.

Table 4.
Summary of recent papers discussing the auxetic sandwich panels for anti-blast and ballistic applications.
A relevant observation regarding the works previously mentioned in Table 4 is that most of them present a re-entrant structure. From the economic perspective, it is simpler to be designed, consumes less material for its manufacture, and less processing time is required. However, other models are being investigated for ballistic and anti-blast applications, such as the double-arrow [221], re-entrant circular [222] and hybrid structures [223,224].
Liu et al. [221] have developed sandwich panels consisting of double-arrow AXS, aiming to ballistic demands. The researchers fabricated the sandwich structure by the prepreg method, using carbon fiber reinforced polymer (CFRP) as the material for the panels. The auxetic core was also made of CFRP and manufactured by the computer numerical control (CNC) method, attached to the panels employing an epoxy resin and hot pressing process. Subsequently, the auxetic cores were filled with PU foam. The residual velocity tests were performed with a projectile’s incident velocity ranging from 75 to 178 m/s. The experiments were carried out by correlating the auxetic sandwich panel filled with PU and another specimen without the foam. From the ballistic test results, the authors discovered that, when the incident velocity was up to 105 m/s, the residual velocity for both panels conditions was the same. However, it was observed that the auxetic panel filled with PU foam presented a decrease in the residual velocity when there was an increase in the incident velocity. Thus, it shows a higher energy absorption throughout the ballistic impact.
Jiang et al. [222] published a study regarding the development of an auxetic sandwich panel for anti-blast protection that may be used in automobiles, ships, buildings and others. The novel material was based on a re-entrant structure. The authors modified it and produced the re-entrant circular (REC) model. It consists of a circular reinforcement attached to each side of the cellular wall. The panels were manufactured using 800 HSS steel, and the auxetic core was fabricated with AA6061 aluminum alloy. Explosion tests were performed, allowing the investigation concerning the absorption power of this AXS. From the acquired numerical results, the researchers verified a higher energy absorption capacity for the REC structure in comparison to the conventional ones because a reduction in the maximum displacement of 28% was observed for the FEM simulations and the experimental tests. In addition, the absorbed impact energy increased by approximately 2%. Therefore, the REC model presents a relevant potential for applications requiring structures resistant against explosions.
The work by Lan et al. [223] proposes the development of AXSs for ballistic applications based on a sandwich panel having its core built from a chiral hybrid structure. The sandwich panel core was fabricated by the selective laser melting (SLM) technique. and AlSi10Mg aluminum alloy powder was used. The panels were built using a 5052 aluminum alloy, while the auxetic re-entrant cores were filled with a PU foam. The ballistic performance was based on the comparison of a model without the foam and the other one filled with it. The ballistic test was performed with a projectile created from aluminum foam, with an incident velocity between 206 and 296 m/s, and a mass ranging from 302 to 364 g. The impact moment was recorded by a high-velocity camera, illustrated in Figure 26. The ballistic tests results have shown that the sandwich panel filled with PU presented severe delamination on the foam after the impact. However, it prevented greater delamination for the panels. On the other hand, the panel without a filling has shown severe delamination on its surface. The indentation region for both specimens exhibited bending, although the specimen filled with PU disclosed less bending due to the energy absorption.
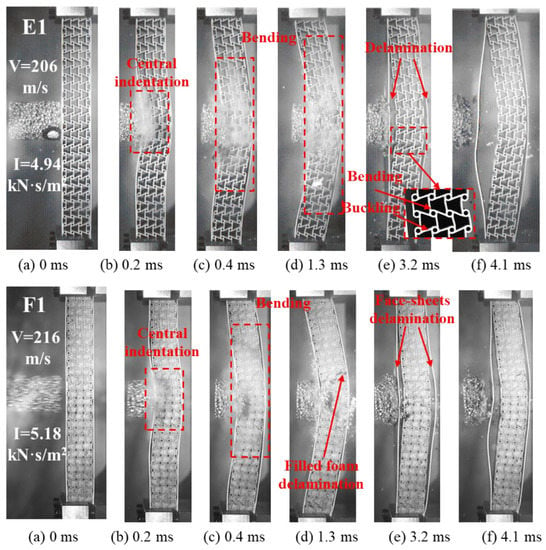
Figure 26.
Dynamic response recorded by high-speed camera of auxetic sandwich panels under impact: (E1) Panel without PU foam filling; (F1) Panel filled with PU foam. Reprinted with permission from Ref. [223]. Copyright 2023, Elsevier.
Haq et al. [224] proposed a comparison of the auxetic sandwich panels’ dynamic behavior against an explosion. The researchers performed FEM simulations, adopting hexagonal cores based on conventional honeycomb and auxetic star structures composed of AA2024 aluminum alloy, while the panels were made of a material known as “Armor Steel”. The explosion simulations were performed using trinitrotoluene (TNT), in concentrations of 1.5, 3 and 5 kg, and dropped over the sandwich panels on heights of 100, 300 and 500 mm. The FEM explosion simulations’ results have shown that the auxetic cellular structures absorbed 28% more energy than the conventional honeycomb model. The auxetic cores applied on sandwich panels have demonstrated effectiveness in absorbing a huge amount of energy displaying a relatively smaller deformation for the back panel. The cellular wall structure provides an increase in the energy absorption capacity by the uniform dissipation of impact energy. For the load of 1.5 kg, the findings revealed that delamination did not occur on the structure; on the other hand, for loads of 3 and 5 kg, the simulation identified a delamination.
Yan et al. [225] manufactured sandwich panels with an auxetic core focusing on anti-blast systems applications. The sandwich panel was fabricated from Q345 steel sheets, and the core based on a re-entrant structure was made of AlSi10Mg aluminum and constructed by the SLM method. An epoxy resin was applied to attach the core and the panels. The blasting test was performed using 500 g of TNT, placing it 10, 15 and 25 cm above the panel, as demonstrated in Figure 27a. A correlation was carried out with a structure manufactured by the same method. However, the core was a honeycomb non-auxetic model. The blasting test revealed that the auxetic core panel presented less deformation, as depicted in Figure 27b, attaining a maximum value of 19.58 mm, while the hexagonal core panel disclosed 26.29 mm after the explosion. This difference is associated with the amount of absorbed energy, where the AXS material displayed a higher absorption without fracturing. Figure 27c illustrates the panel after the explosion. It is possible to notice the damaged core, in which a re-entrant structure was completely disfigured near the explosion location, but the panel was not fractured. Moreover, the hexagonal core panel exhibited in Figure 27d presented a higher deformation since it absorbed less energy. In addition, the hexagonal core was fractured and bent out of shape while the explosion occurred, and delamination on the front panel has also been detected. These results unveil that the AXS is capable of absorbing greater amounts of energy, and, for this reason, it is suitable for anti-blast system applications.
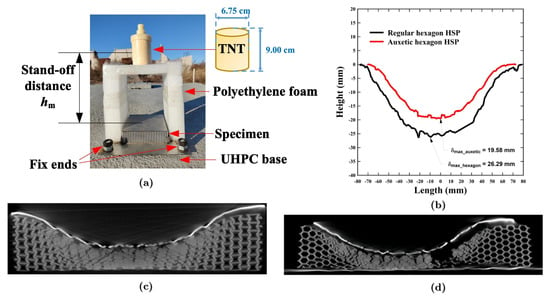
Figure 27.
(a) Blasting test setup; (b) comparison of the core deformation; (c) damage mode of auxetic sandwich; (d) damage mode of honeycomb sandwich. Reprinted with permission from Ref. [225]. Copyright 2023, Elsevier.
Critchley et al. [226] investigated the cellular wall angulation effect upon the explosion resistance for re-entrants’ AXSs. The samples were manufactured by the fused deposition modeling (FDM) method using a thermoplastic polyurethane (TPU). Five specimens were processed, with a range of cellular wall angulation and, as a result, the following structures were developed: 60° and 75° re-entrant, 90° square, and 105° and 120° hexagonal. Blasting tests were performed in a shocking tube, which simulates a controlled explosion on a lower scale and records the internal explosion reactions. The test findings have shown that the AXS cellular wall angulation is of utmost importance for the blast mitigation, where the 75° (re-entrant) angulation disclosed a mitigation of 23%, whereas the 60° model displayed a value of 12%. The hexagonal structures yielded a blast amplification effect, where the 105° and 120° angulation have shown values of 60% and 277%, respectively.
Usta et al. [15] portrayed the high velocity impact behavior for curved sandwich panels. They were fabricated from CFRP sheets, and the distinct cores were based on no-auxetic PU foams manufactured by CNC, with auxetic PLA presenting a re-entrant structure produced by FDM. High velocity impact tests were performed on a single stage air gas machine that simulates a gun. A spherical steel projectile was used with a radius and velocity of 5 mm and 100 m/s, respectively. The impact test results exposed an increase in the energy absorption as the curvate diminished for the panels and re-entrant cores. The sandwich panels having PU foams disclosed a superior impact resistance as a consequence of their synergistic interaction with the CFRP sheets. The failure mechanisms for the AXS and the PU foam are characterized by a fracture on the superior sheets, where the fibers rupture and matrix cracks have an influence. The foam cores are exposed to shear and crush deformation, while the auxetic core presents bends and cellular wall ruptures. Nevertheless, AXSs portrayed superior SEA values in comparison to the PU foam structures, suggesting that AXSs may have a relevant role in ballistic resistance. Meanwhile, other variables must be investigated in order to improve these metamaterials’ resistance.
Wu et al. [64] investigated the AXSs impact resistance developed with Kevlar foils based on the Kirigami sheets, whilst the specimens were cut and rearranged on a 3D hexagonal and re-entrant design. Among the hollow spaces of the structure, shear stiffening gel (SSG) was introduced. The tests revealed that the AXS disclosed higher flexibility and resistance than the hexagonal model. The re-entrant model joined with the SSG filing developed and increased up to 76% in comparison to the hexagonal model also filled with the same material. This result is a consequence of the mechanical behavior provided by an NPR, but also the thickening behavior supplied by the SSG. This research does not make a ballistic application approach. However, the employment of SSG as a filling for AXS might provide great findings on absorption energy and ballistic resistance investigations [61,228]. Furthermore, the SSG is able to enhance its hardness when a shear load is increased because of its thickening that raises the mechanical resistance [229,230]. The same phenomenon is found for the shear thickening fluid (STF), which is extensively used on fabrics for ballistic demands [231,232,233].
Brief Summary
A brief summary of this section is intended to reveal that, among the several sectors in Table 2, from aerospace to textile, AXS for military, high-velocity impact protection is included. However, only a few investigations [225,226] have used 3D-printed AXS, which is another open opportunity for future research works.
6. Conclusions
An impressive range of types and models of auxetic structures (AXSs), from the initially proposed re-entrant pattern to the novel cross-petal AXS structure for military applications requiring absorbing blast energy, are presently being investigated and industrially developed.
The numerous proposed AXS structures, independent of their complex shapes, can now be more cost-effectively fabricated by several techniques, either by traditional techniques or by AM, also known as 3D printing. In addition to being cheaper, 3D-printed AXS structures have the advantage of fast and easy fabrication.
Looking ahead, there is significant potential for the continued growth and development of 3D-printed AXS structures for use in high-velocity impact applications. As such, we can expect to see continued research and product development in this area in the coming years.
7. Final Remarks
Sandwich panels, particularly those with honeycomb structure inner core, have received considerable attention in the past few decades with an exponential growth in research works. Applications of these honeycomb panels extend to diversified industrial sectors, including military owing to their higher energy absorption. In particular, AXSs honeycomb patterns fabricated by AM have recently been the subject of relevant investigation on their ballistic characteristics, as in the remarkable work of Yan et al. [11] and a prominent review paper on anti-blast performance by Bohara et al. [21].
In the present review, the main points of published AXS/3D-printed articles discussing high-velocity impact were critically discussed. All of these reviewed articles emphatically indicated the superior resistance of AXS/3D-printed sandwich panels to shockwave blast and ballistic impact. One condition, however, is still uncertain in the opinion of Bohara et al. [21]. Under very high impact loads, the blast shockwave propagates much faster than the stress wave. As a result, the AXSs might not have time to deform with an NPR. The authors also recommended further research on improvements in 3D printing technology to produce large-scale AXSs to be applied in armors for high-velocity impact protection. The combination of AM and discrete assembly methods is suggested as a solution for today’s size limitation of 3D printers, in order to improve, optimize and fabricate AXS-based ballistic armor. As for the specific case of honeycomb AXS, constructed by SLM/AM, Yan et al. [11] concluded that carbon fiber reinforced polymer, as an outer sheet, is a potential reinforcement for associated sandwich panels with excellent ballistic performance.
Although the commercial use of AXS/AM-based high-velocity impact protective armor is still in its infancy [21], all presently reviewed works strongly support indisputable future military interest.
Author Contributions
Conceptualization, R.F.P.J. and L.F.C.N.; methodology, R.F.P.J., S.N.M. and L.F.C.N.; validation, S.N.M. and L.F.C.N.; formal analysis, R.F.P.J., P.H.P.M.d.S. and L.d.M.N.; investigation, R.F.P.J., P.H.P.M.d.S. and L.d.M.N.; resources, S.N.M.; data curation, P.H.P.M.d.S. and S.N.M.; writing—original draft preparation, R.F.P.J., P.H.P.M.d.S., S.N.M. and L.d.M.N.; writing—review and editing, P.H.P.M.d.S., R.F.P.J. and L.d.M.N.; visualization, L.F.C.N. and S.N.M.; supervision, L.F.C.N. and S.N.M.; project administration, S.N.M.; funding acquisition, S.N.M. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financed in part by the Brazilian Agency CAPES (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior), Protocol #001.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Poisson’s Ratio | |
| Wavelength | |
| ABS | Acrylonitrile Butadiene Styrene |
| ACC | Auxetic Contacted Cube |
| Ag | Silver |
| AM | Additive Manufacturing |
| Au | Gold |
| AXS | Auxetic Structures |
| BCP | Block Copolymers |
| BCPS | Braced Cross-Petal Structure |
| CFRP | Carbon Fiber Reinforced Polymer |
| CM | Conventional Material |
| CNC | Computer Numeric Control |
| Cu | Copper |
| CPS | Cross-Petal Structure |
| CVD | Chemical Vapor Deposition |
| DLW | Direct Laser Writing |
| E | Young’s Modulus |
| FDM | Fused Deposition Modeling |
| FEM | Finite Elements Method |
| Fe3O4 | Magnetite |
| G | Shear Modulus |
| GIC | Fracture Initiation Toughness |
| GNP | Graphene Nanoplatelets |
| GPa | Gigapascal |
| H | Hardness |
| HGS | Hourglass Structure |
| K | Bulk Modulus |
| KIC* | Fracture Toughness |
| LDPE | Low Density Polyethylene |
| LRP | Laser Rapid Prototyping |
| MPP | Multi-Photon Polymerization |
| NIJ | National Institute of Justice |
| NiTi | Nickel Titanium |
| NPR | Negative Poisson’s Ratio |
| PDA | Polydiacetylene |
| PLA | Polylactic Acid |
| PP | Polypropylene |
| PU | Polyurethane |
| RAH | Re-entrant Arrowhead Structure |
| RCA | Re-entrant Chiral Auxetic |
| REC | Re-entrant Circular |
| SAH | Star Arrowhead Structure |
| SEA | Specific Energy Absorbed |
| SEBM | Selective ELectron Beam Melting |
| SLA | Microstereolithography |
| SLM | Selective Melting Laser |
| SLS | Selective Laser Sintering |
| SMEP | Shape Memory Epoxy Polymer |
| SMP | Shape Memory Polymers |
| SPPW | Self-propagationg Photopolymer Waveguides |
| SSG | Shear Stiffening Gel |
| STF | Shear Thickening Fluid |
| TNT | Trinitrotoluene |
| TPU | Thermoplastic Polyurethane |
| UV | Ultraviolet |
| VPP | Vat Photopolymerization |
| ZrO2 | Zirconium Oxide |
References
- Callister, W.D., Jr.; Rethwisch, D.G. Fundamentals of Materials Science and Engineering: An Integrated Approach; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Li, X.; Zhang, P.; Wang, Z.; Wu, G.; Zhao, L. Dynamic behavior of aluminum honeycomb sandwich panels under air blast: Experiment and numerical analysis. Compos. Struct. 2014, 108, 1001–1008. [Google Scholar] [CrossRef]
- Han, X.; Cai, H.; Sun, J.; Wei, Z.; Huang, Y.; Wang, A. Numerical Studies on Failure Mechanisms of All-Composite Sandwich Structure with Honeycomb Core under Compression and Impact Loading Conditions. Polymers 2022, 14, 4047. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Yang, X.; Li, P.; Huang, G.; Feng, S.; Shen, C.; Han, B.; Zhang, X.; Jin, F.; Xu, F.; et al. Bioinspired engineering of honeycomb structure—Using nature to inspire human innovation. Prog. Mater. Sci. 2015, 74, 332–400. [Google Scholar] [CrossRef]
- Wahl, L.; Maas, S.; Waldmann, D.; Zürbes, A.; Frères, P. Shear stresses in honeycomb sandwich plates: Analytical solution, finite element method and experimental verification. J. Sandw. Struct. Mater. 2012, 14, 449–468. [Google Scholar] [CrossRef]
- Bitzer, T. Honeycomb Technology: Materials, Design, Manufacturing, Applications and Testing; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Yang, X.; Sun, Y.; Yang, J.; Pan, Q. Out-of-plane crashworthiness analysis of bio-inspired aluminum honeycomb patterned with horseshoe mesostructure. Thin-Walled Struct. 2018, 125, 1–11. [Google Scholar] [CrossRef]
- He, Q.; Feng, J.; Chen, Y.; Zhou, H. Mechanical properties of spider-web hierarchical honeycombs subjected to out-of-plane impact loading. J. Sandw. Struct. Mater. 2020, 22, 771–796. [Google Scholar] [CrossRef]
- Ha, N.S.; Lu, G. A review of recent research on bio-inspired structures and materials for energy absorption applications. Compos. Part B Eng. 2020, 181, 107496. [Google Scholar] [CrossRef]
- Haq, A.U.; Reddy, N.S.K. A brief review on various high energy absorbing materials. Mater. Today Proc. 2021, 38, 3198–3204. [Google Scholar] [CrossRef]
- Yan, J.; Liu, Y.; Yan, Z.; Bai, F.; Shi, Z.; Si, P.; Huang, F. Ballistic characteristics of 3D-printed auxetic honeycomb sandwich panel using CFRP face sheet. Int. J. Impact Eng. 2022, 164, 104186. [Google Scholar] [CrossRef]
- Yang, C.; Vora, H.D.; Chang, Y. Behavior of auxetic structures under compression and impact forces. Smart Mater. Struct. 2018, 27, 025012. [Google Scholar] [CrossRef]
- Hou, S.; Li, T.; Jia, Z.; Wang, L. Mechanical properties of sandwich composites with 3d-printed auxetic and non-auxetic lattice cores under low velocity impact. Mater. Des. 2018, 160, 1305–1321. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Z.; Xiao, D.; Wu, W.; Fang, D. The Dynamic response of shallow sandwich arch with auxetic metallic honeycomb core under localized impulsive loading. Int. J. Impact Eng. 2020, 137, 103442. [Google Scholar] [CrossRef]
- Usta, F.; Türkmen, H.S.; Scarpa, F. Low-velocity impact resistance of composite sandwich panels with various types of auxetic and non-auxetic core structures. Thin-Walled Struct. 2021, 163, 107738. [Google Scholar] [CrossRef]
- Jin, X.; Wang, Z.; Ning, J.; Xiao, G.; Liu, E.; Shu, X. Dynamic response of sandwich structures with graded auxetic honeycomb cores under blast loading. Compos. Part B Eng. 2016, 106, 206–217. [Google Scholar] [CrossRef]
- Qi, C.; Remennikov, A.; Pei, L.Z.; Yang, S.; Yu, Z.H.; Ngo, T.D. Impact and close-in blast response of auxetic honeycomb-cored sandwich panels: Experimental tests and numerical simulations. Compos. Struct. 2017, 180, 161–178. [Google Scholar] [CrossRef]
- Imbalzano, G.; Linforth, S.; Ngo, T.D.; Lee, P.V.S.; Tran, P. Blast resistance of auxetic and honeycomb sandwich panels: Comparisons and parametric designs. Compos. Struct. 2018, 183, 242–261. [Google Scholar] [CrossRef]
- Qi, C.; Yang, S.; Wang, D.; Yang, L.J. Ballistic resistance of honeycomb sandwich panels under in-plane high-velocity impact. Sci. World J. 2013, 2013, 892781. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Y.; Wang, C.; Zhou, G.; Karamoozian, A.; Zhao, W. On the out-of-plane ballistic performances of hexagonal, reentrant, square, triangular and circular honeycomb panels. Int. J. Mech. Sci. 2020, 173, 105402. [Google Scholar] [CrossRef]
- Bohara, R.P.; Linforth, S.; Nguyen, T.; Ghazlan, A.; Ngo, T. Anti-blast and-impact performances of auxetic structures: A review of structures, materials, methods, and fabrications. Eng. Struct. 2023, 276, 115377. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Mardling, P.; Alderson, A.; Jordan-Mahy, N.; Le Maitre, C.L. The use of auxetic materials in tissue engineering. Biomater. Sci. 2020, 8, 2074–2083. [Google Scholar] [CrossRef] [PubMed]
- Critchley, R.; Corni, I.; Wharton, J.A.; Walsh, F.C.; Wood, R.J.; Stokes, K.R. A review of the manufacture, mechanical properties and potential applications of auxetic foams. Phys. Status Solidi 2013, 250, 1963–1982. [Google Scholar] [CrossRef]
- Love, A. A Treatise on the Mathematical Theory of Elasticity; Cambridge University Press: Cambridge, UK, 1892. [Google Scholar]
- Greenhill, A. A treatise on the mathematical theory of elasticity. Nature 1893, 47, 529–530. [Google Scholar] [CrossRef]
- Voigt, W. Bestimmung der Elasticitätsconstanten für das chlorsaure Natron. Ann. Phys. 1893, 285, 719–723. [Google Scholar] [CrossRef]
- Gunton, D.; Saunders, G. The Young’s modulus and Poisson’s ratio of arsenic, antimony and bismuth. J. Mater. Sci. 1972, 7, 1061–1068. [Google Scholar] [CrossRef]
- Li, Y. The anisotropic behavior of Poisson’s ratio, Young’s modulus, and shear modulus in hexagonal materials. Phys. Status Solidi 1976, 38, 171–175. [Google Scholar] [CrossRef]
- Yeganeh-Haeri, A.; Weidner, D.J.; Parise, J.B. Elasticity of α-cristobalite: A silicon dioxide with a negative Poisson’s ratio. Science 1992, 257, 650–652. [Google Scholar] [CrossRef]
- Baughman, R.H.; Shacklette, J.M.; Zakhidov, A.A.; Stafström, S. Negative Poisson’s ratios as a common feature of cubic metals. Nature 1998, 392, 362–365. [Google Scholar] [CrossRef]
- Veronda, D.; Westmann, R. Mechanical characterization of skin—Finite deformations. J. Biomech. 1970, 3, 111–124. [Google Scholar] [CrossRef]
- Lees, C.; Vincent, J.F.; Hillerton, J.E. Poisson’s ratio in skin. Bio-Med. Mater. Eng. 1991, 1, 19–23. [Google Scholar] [CrossRef]
- Frolich, L.; LaBarbera, M.; Stevens, W. Poisson’s ratio of a crossed fibre sheath: The skin of aquatic salamanders. J. Zool. 1994, 232, 231–252. [Google Scholar] [CrossRef]
- Williams, J.; Lewis, J. Properties and an anisotropic model of cancellous bone from the proximal tibial epiphysis. J. Biomech. Eng. 1982, 104, 50–56. [Google Scholar] [CrossRef]
- Sanami, M.; Ravirala, N.; Alderson, K.; Alderson, A. Auxetic materials for sports applications. Procedia Eng. 2014, 72, 453–458. [Google Scholar] [CrossRef]
- Duncan, O.; Shepherd, T.; Moroney, C.; Foster, L.; Venkatraman, P.D.; Winwood, K.; Allen, T.; Alderson, A. Review of auxetic materials for sports applications: Expanding options in comfort and protection. Appl. Sci. 2018, 8, 941. [Google Scholar] [CrossRef]
- Du, L.; Luo, S.; Xu, Y. Understanding nonlinear behaviors of auxetic foams using X-ray tomography and pore structure analysis. Mech. Mater. 2022, 165, 104196. [Google Scholar] [CrossRef]
- Zhang, Q.; Scarpa, F.; Barton, D.; Zhu, Y.; Lang, Z.Q.; Zhang, D.; Peng, H.X. Impact properties of uniaxially thermoformed auxetic foams. Int. J. Impact Eng. 2022, 163, 104176. [Google Scholar] [CrossRef]
- Nazari, Z.; Ahmadi, H.; Liaghat, G.; Vahid, S. Investigation on the compressive properties of auxetic foams under different loading rates. Polym. Eng. Sci. 2022, 62, 1720–1730. [Google Scholar] [CrossRef]
- Shah, I.A.; Khan, R.; Koloor, S.S.R.; Petru, M.; Badshah, S.; Ahmad, S.; Amjad, M. Finite Element Analysis of the Ballistic Impact on Auxetic Sandwich Composite Human Body Armor. Materials 2022, 15, 2064. [Google Scholar] [CrossRef]
- Hassanin, H.; Abena, A.; Elsayed, M.A.; Essa, K. 4D printing of NiTi auxetic structure with improved ballistic performance. Micromachines 2020, 11, 745. [Google Scholar] [CrossRef]
- Imbalzano, G.; Tran, P.; Ngo, T.D.; Lee, P.V. Three-dimensional modelling of auxetic sandwich panels for localised impact resistance. J. Sandw. Struct. Mater. 2017, 19, 291–316. [Google Scholar] [CrossRef]
- Scarpa, F. Auxetic materials for bioprostheses [In the Spotlight]. IEEE Signal Process. Mag. 2008, 25. [Google Scholar] [CrossRef]
- Kolken, H.M.; Janbaz, S.; Leeflang, S.M.; Lietaert, K.; Weinans, H.H.; Zadpoor, A.A. Rationally designed meta-implants: A combination of auxetic and conventional meta-biomaterials. Mater. Horizons 2018, 5, 28–35. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Mechanical performance of additively manufactured meta-biomaterials. Acta Biomater. 2019, 85, 41–59. [Google Scholar] [CrossRef] [PubMed]
- Dusfour, G.; LeFloc’h, S.; Cañadas, P.; Ambard, D. Heterogeneous mechanical hyperelastic behavior in the porcine annulus fibrosus explained by fiber orientation: An experimental and numerical approach. J. Mech. Behav. Biomed. Mater. 2020, 104, 103672. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Yu, W.R. Development of a textile structure for multi-directional auxetic deformation. Mater. Des. 2022, 223, 111237. [Google Scholar] [CrossRef]
- Shah, A.A.; Shahid, M.; Siddiqui, N.A.; Nawab, Y.; Iqbal, M. Effect of Geometric Arrangement on Mechanical Properties of 2D Woven Auxetic Fabrics. Textiles 2022, 2, 606–623. [Google Scholar] [CrossRef]
- Yuping, C.; Liu, Y.; Hong, H. Deformation behavior of auxetic laminated fabrics with rotating square geometry. Text. Res. J. 2022, 92, 4652–4665. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y. Assessment of negative Poisson’s ratio effect on thermal post-buckling of FG-GRMMC laminated cylindrical panels. Adv. Nano Res. 2021, 10, 423–435. [Google Scholar]
- Kolken, H.; De Jonge, C.; Van der Sloten, T.; Garcia, A.F.; Pouran, B.; Willemsen, K.; Weinans, H.; Zadpoor, A. Additively manufactured space-filling meta-implants. Acta Biomater. 2021, 125, 345–357. [Google Scholar] [CrossRef]
- Muslov, S. Characteristics of elastic anisotropy of Ti-Ni crystals with shape memory and their relation to extreme values of the Poisson’s ratio. Lett. Mater. 2021, 11, 28–32. [Google Scholar] [CrossRef]
- Guo, L.; Zhao, S.; Guo, Y.; Yang, J.; Kitipornchai, S. Bandgaps in functionally graded phononic crystals containing graphene origami-enabled metamaterials. Int. J. Mech. Sci. 2023, 240, 107956. [Google Scholar] [CrossRef]
- Liao, M.E.; Li, C.; Shah, N.; Hsiao, Y.H.; Bauchy, M.; Sant, G.; Goorsky, M.S. Experimental evidence of auxeticity in ion implanted single crystal calcite. Sci. Rep. 2022, 12, 6071. [Google Scholar] [CrossRef]
- Jiang, Z.; Xu, N. Emergent Physics on the Route from Crystals to Amorphous Solids. Chin. J. Chem. 2022, 40, 1091–1098. [Google Scholar] [CrossRef]
- Amaya-Amaya, V.; de Icaza-Herrera, M.; Martínez-Hernández, A.L.; Martínez-Barrera, G.; Velasco-Santos, C. Experimental approximation of the sound absorption coefficient (∝) for 3D printed reentrant auxetic structures of poly lactic acid reinforced with chicken keratin materials. Mater. Lett. 2021, 283, 128757. [Google Scholar] [CrossRef]
- Magesh, M.; Jawahar, P. Examination of shape memory polymer-auxetic landing gears on landing approach for quadcopter. Mater. Today Proc. 2021, 47, 471–479. [Google Scholar] [CrossRef]
- Verma, P.; He, C.; Griffin, A.C. Implications for Auxetic Response in Liquid Crystalline Polymers: X-Ray Scattering and Space-Filling Molecular Modeling. Phys. Status Solidi 2020, 257, 2000261. [Google Scholar] [CrossRef]
- Zhang, J.; Dong, B.; Zhang, W. Dynamic Crushing of Gradient Auxetic Honeycombs. J. Vib. Eng. Technol. 2021, 9, 421–431. [Google Scholar] [CrossRef]
- Tang, H.; Jiang, X.; Li, L.; Ling, L.; Hu, Y. Electromechanical properties of ultra-low porous auxetic piezocomposite: From the perspective of Poisson’s ratio. J. Am. Ceram. Soc. 2021, 104, 2628–2645. [Google Scholar] [CrossRef]
- Lantada, A.D.; de Blas Romero, A.; Schwentenwein, M.; Jellinek, C.; Homa, J. Lithography-based ceramic manufacture (LCM) of auxetic structures: Present capabilities and challenges. Smart Mater. Struct. 2016, 25, 054015. [Google Scholar] [CrossRef]
- Zhang, X.G.; Jiang, W.; Zhang, Y.; Luo, C.; Zhang, X.Y.; Han, D.; Hao, J.; Teng, X.C.; Xie, Y.M.; Ren, X. Energy absorption properties of composite tubes with hexagonal and re-entrant honeycomb fillers. Constr. Build. Mater. 2022, 356, 129298. [Google Scholar] [CrossRef]
- Wu, L.; Zhao, F.; Lu, Z.; Lin, J.H.; Jiang, Q. Impact energy absorption composites with shear stiffening gel-filled negative poisson’s ratio skeleton by Kirigami method. Compos. Struct. 2022, 298, 116009. [Google Scholar] [CrossRef]
- Li, Z.Y.; Wang, X.T.; Ma, L.; Wu, L.Z. Study on the mechanical properties of CFRP composite auxetic structures consist of corrugated sheets and tubes. Compos. Struct. 2022, 292, 115655. [Google Scholar] [CrossRef]
- Jiang, F.; Yang, S.; Zhang, Y.; Qi, C.; Chen, S. Fabrication and crushing response of graded re-entrant circular auxetic honeycomb. Int. J. Mech. Sci. 2023, 242, 107999. [Google Scholar] [CrossRef]
- Reyes, G.; Ajdary, R.; Kankuri, E.; Kaschuk, J.J.; Kosonen, H.; Rojas, O.J. Cellulose gelation in NaOH (aq) by CO2 absorption: Effects of holding time and concentration on biomaterial development. Carbohydr. Polym. 2023, 302, 120355. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Goh, K.L.; Lee, H.P.; Yin, C.; Zhang, K.; Zhong, J. Experimental study and finite element analysis on energy absorption of carbon fiber reinforced composite auxetic structures filled with aluminum foam. Compos. Struct. 2023, 303, 116319. [Google Scholar] [CrossRef]
- Chen, X.Y.; Hamdi, O.; Rodrigue, D. Conversion of low density polyethylene foams into auxetic metamaterials. Polym. Adv. Technol. 2022, 34, 228–237. [Google Scholar] [CrossRef]
- Xue, B.Z.; Li, J.W.; Huang, R.; Yang, Y.Z.; Gong, H.S.; Zhang, Q.M.; Kong, L.H.; Li, D. A Study of Negative Poisson’s Ratio of 3D Printed Auxetic Structures. Mech. Solids 2022, 57, 1–10. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Y.; Jiang, D.; Chen, Y.; Xie, Y.M.; Jia, L.J. In-plane impact behavior of 3D-printed auxetic stainless honeycombs. Eng. Struct. 2022, 266, 114656. [Google Scholar] [CrossRef]
- Fan, Y.; Shen, H.S. Non-symmetric stiffness of origami-graphene metamaterial plates. Compos. Struct. 2022, 297, 115974. [Google Scholar] [CrossRef]
- Köllner, D.; Simon, S.; Niedermeyer, S.; Spath, I.; Wolf, E.; Kakimoto, K.i.; Fey, T. Relation between Structure, Mechanical and Piezoelectric Properties in Cellular Ceramic Auxetic and Honeycomb Structures. Adv. Eng. Mater. 2022, 25, 2201387. [Google Scholar] [CrossRef]
- Fan, G.Z.; Ren, X.; Wang, S.L.; Luo, C.; Xie, Y.M. A novel cement-based auxetic foam composite: Experimental study. Case Stud. Constr. Mater. 2022, 17, e01159. [Google Scholar] [CrossRef]
- Yolcu, D.A.; Baba, B.O. Measurement of Poisson’s ratio of the auxetic structure. Measurement 2022, 204, 112040. [Google Scholar] [CrossRef]
- Li, P.; Xu, Y.; Liang, C.; Zeng, X.C. MgXN2 (X = Hf/Zr) Monolayers: Auxetic Semiconductor with Highly Anisotropic Optical/Mechanical Properties and Carrier Mobility. J. Phys. Chem. Lett. 2022, 13, 10534–10542. [Google Scholar] [CrossRef]
- Fan, D.; Li, N.; Li, M.; Wang, S.; Li, S.; Tang, T. Polyurethane/polydopamine/graphene auxetic composite foam with high-efficient and tunable electromagnetic interference shielding performance. Chem. Eng. J. 2022, 427, 131635. [Google Scholar] [CrossRef]
- Choi, J.; Lakes, R. Nonlinear properties of metallic cellular materials with a negative Poisson’s ratio. J. Mater. Sci. 1992, 27, 5375–5381. [Google Scholar] [CrossRef]
- Argatov, I.I.; Guinovart-Díaz, R.; Sabina, F.J. On local indentation and impact compliance of isotropic auxetic materials from the continuum mechanics viewpoint. Int. J. Eng. Sci. 2012, 54, 42–57. [Google Scholar] [CrossRef]
- Coenen, V.; Alderson, K. Mechanisms of failure in the static indentation resistance of auxetic carbon fibre laminates. Phys. Status Solidi 2011, 248, 66–72. [Google Scholar] [CrossRef]
- Choi, J.; Lakes, R. Fracture toughness of re-entrant foam materials with a negative Poisson’s ratio: Experiment and analysis. Int. J. Fract. 1996, 80, 73–83. [Google Scholar] [CrossRef]
- Alderson, A.; Rasburn, J.; Ameer-Beg, S.; Mullarkey, P.G.; Perrie, W.; Evans, K.E. An auxetic filter: A tuneable filter displaying enhanced size selectivity or defouling properties. Ind. Eng. Chem. Res. 2000, 39, 654–665. [Google Scholar] [CrossRef]
- Francisco, M.B.; Pereira, J.L.J.; Oliver, G.A.; Roque da Silva, L.R.; Cunha, S.S., Jr.; Gomes, G.F. A review on the energy absorption response and structural applications of auxetic structures. Mech. Adv. Mater. Struct. 2022, 29, 5823–5842. [Google Scholar] [CrossRef]
- Gao, Q.; Liao, W.H. Energy absorption of thin walled tube filled with gradient auxetic structures-theory and simulation. Int. J. Mech. Sci. 2021, 201, 106475. [Google Scholar] [CrossRef]
- Bohara, R.P.; Linforth, S.; Nguyen, T.; Ghazlan, A.; Ngo, T. Novel lightweight high-energy absorbing auxetic structures guided by topology optimisation. Int. J. Mech. Sci. 2021, 211, 106793. [Google Scholar] [CrossRef]
- Evans, K.E.; Alderson, A. Auxetic materials: Functional materials and structures from lateral thinking! Adv. Mater. 2000, 12, 617–628. [Google Scholar] [CrossRef]
- Prawoto, Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio. Comput. Mater. Sci. 2012, 58, 140–153. [Google Scholar] [CrossRef]
- Carneiro, V.H.; Meireles, J.; Puga, H. Auxetic materials—A review. Mater. Sci. Poland 2013, 31, 561–571. [Google Scholar] [CrossRef]
- Wallbanks, M.; Khan, M.F.; Bodaghi, M.; Triantaphyllou, A.; Serjouei, A. On the design workflow of auxetic metamaterials for structural applications. Smart Mater. Struct. 2021, 31, 023002. [Google Scholar] [CrossRef]
- Liu, Q. Literature Review: Materials with Negative Poisson’s Ratios and Potential Applications to Aerospace and Defence; Defence Science and Technology Organisation: Victoria, Australia, 2006. [Google Scholar]
- Tretiakov, K.V.; Wojciechowski, K.W. Elasticity of two-dimensional crystals of polydisperse hard disks near close packing: Surprising behavior of the Poisson’s ratio. J. Chem. Phys. 2012, 136, 204506. [Google Scholar] [CrossRef]
- Narojczyk, J.; Alderson, A.; Imre, A.; Scarpa, F.; Wojciechowski, K. Negative Poisson’s ratio behavior in the planar model of asymmetric trimers at zero temperature. J. Non-Cryst. Solids 2008, 354, 4242–4248. [Google Scholar] [CrossRef]
- Yang, W.; Li, Z.M.; Shi, W.; Xie, B.H.; Yang, M.B. Review on auxetic materials. J. Mater. Sci. 2004, 39, 3269–3279. [Google Scholar] [CrossRef]
- Xinchun, S.; Lakes, R.S. Stability of elastic material with negative stiffness and negative Poisson’s ratio. Phys. Status Solidi 2007, 244, 1008–1026. [Google Scholar] [CrossRef]
- Donoghue, J.; Alderson, K.; Evans, K. The fracture toughness of composite laminates with a negative Poisson’s ratio. Phys. Status Solidi 2009, 246, 2011–2017. [Google Scholar] [CrossRef]
- Maiti, S.; Ashby, M.; Gibson, L. Fracture toughness of brittle cellular solids. Scr. Metall. 1984, 18, 213–217. [Google Scholar] [CrossRef]
- Yang, S.; Chalivendra, V.B.; Kim, Y.K. Fracture and impact characterization of novel auxetic Kevlar®/Epoxy laminated composites. Compos. Struct. 2017, 168, 120–129. [Google Scholar] [CrossRef]
- Scarpa, F.; Yates, J.; Ciffo, L.; Patsias, S. Dynamic crushing of auxetic open-cell polyurethane foam. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2002, 216, 1153–1156. [Google Scholar] [CrossRef]
- Oh, J.H.; Kim, J.S.; Oh, I.K. Auxetic graphene oxide-porous foam for acoustic wave and shock energy dissipation. Compos. Part B Eng. 2020, 186, 107817. [Google Scholar] [CrossRef]
- Najafi, M.; Ahmadi, H.; Liaghat, G. Experimental investigation on energy absorption of auxetic structures. Mater. Today Proc. 2021, 34, 350–355. [Google Scholar] [CrossRef]
- Grima, J. Modelling Auxetic Materials. In Proceedings of the 2009 Computational Nanotechnology Intensive Programme (CoNan 2009, EU Life-Long Learning Programme), Gdansk, Poland, 2–14 August 2009. [Google Scholar]
- Chen, Y.; Scarpa, F.; Farrow, I.R.; Liu, Y.; Leng, J. Composite flexible skin with large negative Poisson’s ratio range: Numerical and experimental analysis. Smart Mater. Struct. 2013, 22, 045005. [Google Scholar] [CrossRef]
- Veerabagu, U.; Palza, H.; Quero, F. Auxetic polymer-based mechanical metamaterials for biomedical applications. ACS Biomater. Sci. Eng. 2022, 8, 2798–2824. [Google Scholar] [CrossRef]
- Kim, Y.; Son, K.H.; Lee, J.W. Auxetic structures for tissue engineering scaffolds and biomedical devices. Materials 2021, 14, 6821. [Google Scholar] [CrossRef]
- Xue, H.; Luo, Z.; Brown, T.; Beier, S. Design of self-expanding auxetic stents using topology optimization. Front. Bioeng. Biotechnol. 2020, 8, 736. [Google Scholar] [CrossRef]
- Asadi, A.; Hedayat, D.; Ghofrani, S.; Abouei Mehrizi, A.; Shadalooyi, G.; Kadkhodapour, J.; Pourkamali Anaraki, A. Modification of hexachiral unit cell to enhance auxetic stent performance. Mech. Adv. Mater. Struct. 2022, 1–15. [Google Scholar] [CrossRef]
- Alderson, A.; Rasburn, J.; Evans, K.; Grima, J. Auxetic polymeric filters display enhanced de-fouling and pressure compensation properties. Membr. Technol. 2001, 2001, 6–8. [Google Scholar] [CrossRef]
- Dolla, W.J.S.; Fricke, B.A.; Becker, B.R. Structural and drug diffusion models of conventional and auxetic drug-eluting stents. J. Med. Devices. 2007, 1, 47–55. [Google Scholar] [CrossRef]
- Shirdel, M.; Ghofrani, S.; Mehrizi, A.A. Effect of increasing porosity as drug reservoirs for local drug delivery in an auxetic stent. In Proceedings of the 2021 28th National and 6th International Iranian Conference on Biomedical Engineering (ICBME), Tehran, Iran, 25–26 November 2021; pp. 65–69. [Google Scholar]
- Wang, Z.; Luan, C.; Liao, G.; Liu, J.; Yao, X.; Fu, J. Progress in auxetic mechanical metamaterials: Structures, characteristics, manufacturing methods, and applications. Adv. Eng. Mater. 2020, 22, 2000312. [Google Scholar]
- Otsuka, K.; Wayman, C.M. Shape Memory Materials; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Huang, W.; Ding, Z.; Wang, C.; Wei, J.; Zhao, Y.; Purnawali, H. Shape memory materials. Mater. Today 2010, 13, 54–61. [Google Scholar] [CrossRef]
- Le Sénéchal, N.V.; Teixeira, R.; Rodrigues, P.F.; Ribeiro, S.B.; dos Santos Paula, A. The influence of aging treatment on the microstructural and mechanical behavior by ultra-micro hardness tester in Ni-rich NiTi alloy. Cadernos UniFOA 2021, 16, 3810. [Google Scholar] [CrossRef]
- Freitas Rodrigues, P.; Teixeira, R.S.; Le Sénéchal, N.V.; Braz Fernandes, F.M.; Paula, A.S. The Influence of the Soaking Temperature Rotary Forging and Solution Heat Treatment on the Structural and Mechanical Behavior in Ni-Rich NiTi Alloy. Materials 2021, 15, 63. [Google Scholar] [CrossRef]
- Song, D.; Yu, C.; Zhang, C.; Kang, G. Superelasticity degradation of NiTi shape memory alloy in wide ranges of temperature and loading level: Experimental observation and micromechanical constitutive model. Int. J. Plast. 2023, 161, 103487. [Google Scholar] [CrossRef]
- Liu, H.; Wang, F.; Wu, W.; Dong, X.; Sang, L. 4D printing of mechanically robust PLA/TPU/Fe3O4 magneto-responsive shape memory polymers for smart structures. Compos. Part B Eng. 2023, 248, 110382. [Google Scholar] [CrossRef]
- Idowu, A.; Thomas, T.; Boesl, B.; Agarwal, A. Cryo-Assisted Extrusion Three-Dimensional Printing of Shape Memory Polymer–Graphene Composites. J. Manuf. Sci. Eng. 2023, 145, 041003. [Google Scholar]
- Lotfolahpour, A.; Huber, W.; Zaeem, M.A. A phase-field model for interactive evolution of phase transformation and cracking in superelastic shape memory ceramics. Comput. Mater. Sci. 2023, 216, 111844. [Google Scholar] [CrossRef]
- Bianchi, M.; Scarpa, F.; Smith, C.; Whittell, G.R. Physical and thermal effects on the shape memory behaviour of auxetic open cell foams. J. Mater. Sci. 2010, 45, 341–347. [Google Scholar] [CrossRef]
- Kamyab, A.; Ghasemi-Ghalebahman, A.; Fereidoon, A.; Khonakdar, H.A. Investigation into the shape memory behavior of peanut-pattern auxetic structures. Express Polym. Lett. 2022, 16, 679–693. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.; Robertson, C. The mechanics of two-dimensional cellular materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 1982, 382, 25–42. [Google Scholar]
- Bronder, S.; Herter, F.; Röhrig, A.; Bähre, D.; Jung, A. Design Study for Multifunctional 3D Re-entrant Auxetics. Adv. Eng. Mater. 2022, 24, 2100816. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic Behavior from Rotating Squares; Kluwer Academic Publishers: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating triangles. J. Mater. Sci. 2006, 41, 3193–3196. [Google Scholar] [CrossRef]
- Alderson, A.; Evans, K.E. Molecular origin of auxetic behavior in tetrahedral framework silicates. Phys. Rev. Lett. 2002, 89, 225503. [Google Scholar] [CrossRef]
- Grima, J.N.; Alderson, A.; Evans, K. Auxetic behaviour from rotating rigid units. Phys. Status Solidi 2005, 242, 561–575. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H. Auxetic materials and their potential applications in textiles. Text. Res. J. 2014, 84, 1600–1611. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Alderson, A.; Evans, K.E. On the auxetic properties of ‘rotating rectangles’ with different connectivity. J. Phys. Soc. Jpn. 2005, 74, 2866–2867. [Google Scholar] [CrossRef]
- Grima, J.N.; Farrugia, P.S.; Gatt, R.; Attard, D. On the auxetic properties of rotating rhombi and parallelograms: A preliminary investigation. Phys. Status Solidi 2008, 245, 521–529. [Google Scholar] [CrossRef]
- Prall, D.; Lakes, R. Properties of a chiral honeycomb with a Poisson’s ratio of—1. Int. J. Mech. Sci. 1997, 39, 305–314. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Farrugia, P.S. On the properties of auxetic meta-tetrachiral structures. Phys. Status Solidi 2008, 245, 511–520. [Google Scholar] [CrossRef]
- Alderson, A.; Evans, K. Microstructural modelling of auxetic microporous polymers. J. Mater. Sci. 1995, 30, 3319–3332. [Google Scholar] [CrossRef]
- Cho, H.; Seo, D.; Kim, D.N. Mechanics of Auxetic Materials. In Handbook of Mechanics of Materials; Schmauder, S., Chen, C.S., Chawla, K.K., Chawla, N., Chen, W., Kagawa, Y., Eds.; Springer: Singapore, 2019; pp. 733–757. [Google Scholar] [CrossRef]
- He, C.; Liu, P.; Griffin, A.C. Toward negative Poisson ratio polymers through molecular design. Macromolecules 1998, 31, 3145–3147. [Google Scholar] [CrossRef]
- Ravirala, N.; Alderson, A.; Alderson, K. Interlocking hexagons model for auxetic behaviour. J. Mater. Sci. 2007, 42, 7433–7445. [Google Scholar] [CrossRef]
- Etemadi, E.; Gholikord, M.; Zeeshan, M.; Hu, H. Improved mechanical characteristics of new auxetic structures based on stretch-dominated-mechanism deformation under compressive and tensile loadings. Thin-Walled Struct. 2023, 184, 110491. [Google Scholar] [CrossRef]
- Lu, C.; Hsieh, M.; Huang, Z.; Zhang, C.; Lin, Y.; Shen, Q.; Chen, F.; Zhang, L. Architectural Design and Additive Manufacturing of Mechanical Metamaterials: A Review. Engineering 2022, 17, 44–63. [Google Scholar] [CrossRef]
- Jacobsen, A.J.; Barvosa-Carter, W.; Nutt, S. Micro-scale truss structures formed from self-propagating photopolymer waveguides. Adv. Mater. 2007, 19, 3892–3896. [Google Scholar] [CrossRef]
- Erdeniz, D.; Schaedler, T.A.; Dunand, D.C. Deposition-based synthesis of nickel-based superalloy microlattices. Scr. Mater. 2017, 138, 28–31. [Google Scholar] [CrossRef]
- Bauer, J.; Meza, L.R.; Schaedler, T.A.; Schwaiger, R.; Zheng, X.; Valdevit, L. Nanolattices: An emerging class of mechanical metamaterials. Adv. Mater. 2017, 29, 1701850. [Google Scholar] [CrossRef]
- Jacobsen, A.; Kolodziejska, J.; Doty, R.; Fink, K.; Zhou, C.; Roper, C.; Carter, W. Interconnected self-propagating photopolymer waveguides: An alternative to stereolithography for rapid formation of lattice-based open-cellular materials. In Proceedings of the 2010 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 9–11 August 2010. [Google Scholar]
- ISO/ASTM 52900; Additive Manufacturing—General Principles—Fundamentals and Vocabulary. International Organization for Standardization: Geneva, Switzeland, 2021.
- Gibson, I.; Rosen, D.W.; Stucker, B.; Khorasani, M.; Rosen, D.; Stucker, B.; Khorasani, M. Additive Manufacturing Technologies; Springer: Berlin/Heidelberg, Germany, 2021; Volume 17. [Google Scholar]
- Choi, J.W.; MacDonald, E.; Wicker, R. Multi-material microstereolithography. Int. J. Adv. Manuf. Technol. 2010, 49, 543–551. [Google Scholar] [CrossRef]
- Bertsch, A.; Renaud, P. Microstereolithography. In Three-Dimensional Microfabrication Using Two-Photon Polymerization; Elsevier: Amsterdam, The Netherlands, 2020; pp. 25–56. [Google Scholar]
- Sun, Q.; Fang, F.; Wang, W.; Yin, J.; Liu, Q.; Hao, L.; Peng, Y. Stereolithography 3D printing of transparent resin lens for high-power phosphor-coated WLEDs packaging. J. Manuf. Process. 2023, 85, 756–763. [Google Scholar] [CrossRef]
- Kim, K.; Yeatts, A.; Dean, D.; Fisher, J.P. Stereolithographic bone scaffold design parameters: Osteogenic differentiation and signal expression. Tissue Eng. Part B Rev. 2010, 16, 523–539. [Google Scholar] [CrossRef]
- Mondschein, R.J.; Kanitkar, A.; Williams, C.B.; Verbridge, S.S.; Long, T.E. Polymer structure-property requirements for stereolithographic 3D printing of soft tissue engineering scaffolds. Biomaterials 2017, 140, 170–188. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, G.; Yu, Z.; Shao, G.; Li, L. Manufacturing of mesoscale non-assembly mechanism with water-soluble support in projection stereolithography process. J. Manuf. Process. 2023, 85, 658–665. [Google Scholar] [CrossRef]
- Alomarah, A.; Ruan, D.; Masood, S.; Sbarski, I.; Faisal, B. An investigation of in-plane tensile properties of re-entrant chiral auxetic structure. Int. J. Adv. Manuf. Technol. 2018, 96, 2013–2029. [Google Scholar] [CrossRef]
- Varas, D.; Pernas-Sánchez, J.; Fjeldberg, N.; Martín-Montal, J. Experimental analysis at different loading rates of 3D printed polymeric auxetic structure based on cylindrical elements. Polym. Test. 2023, 119, 107930. [Google Scholar] [CrossRef]
- Von Freymann, G.; Ledermann, A.; Thiel, M.; Staude, I.; Essig, S.; Busch, K.; Wegener, M. Three-dimensional nanostructures for photonics. Adv. Funct. Mater. 2010, 20, 1038–1052. [Google Scholar] [CrossRef]
- Kunwar, P.; Soman, P. Direct laser writing of fluorescent silver nanoclusters: A review of methods and applications. ACS Appl. Nano Mater. 2020, 3, 7325–7342. [Google Scholar] [CrossRef]
- Wang, R.; Wei, J.; Fan, Y. Chalcogenide phase-change thin films used as grayscale photolithography materials. Opt. Express 2014, 22, 4973–4984. [Google Scholar] [CrossRef]
- Fischer, J.; Wegener, M. Three-dimensional direct laser writing inspired by stimulated-emission-depletion microscopy. Opt. Mater. Express 2011, 1, 614–624. [Google Scholar] [CrossRef]
- Fanyaeu, I.; Mizeikis, V. Realisation of 3D metamaterial perfect absorber structures by direct laser writing. In Proceedings of the Advanced Fabrication Technologies for Micro/Nano Optics and Photonics X, San Francisco, CA, USA, 29 January–1 February 2017; Volume 10115, pp. 177–185. [Google Scholar]
- Debnath, S.; Zhang, X.; Guney, D.; Soukoulis, C. Two-dimensionally isotropic optical metamaterial feasible for stimulated emission depletion microscopy inspired direct laser writing. In Proceedings of the 2013 7th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics, Bordeaux, France, 16–21 September 2013; pp. 427–429. [Google Scholar]
- Melissinaki, V.; Gill, A.; Ortega, I.; Vamvakaki, M.; Ranella, A.; Haycock, J.; Fotakis, C.; Farsari, M.; Claeyssens, F. Direct laser writing of 3D scaffolds for neural tissue engineering applications. Biofabrication 2011, 3, 045005. [Google Scholar] [CrossRef] [PubMed]
- Selimis, A.; Mironov, V.; Farsari, M. Direct laser writing: Principles and materials for scaffold 3D printing. Microelectron. Eng. 2015, 132, 83–89. [Google Scholar] [CrossRef]
- Srikanth, S.; Dudala, S.; Raut, S.; Dubey, S.K.; Ishii, I.; Javed, A.; Goel, S. Optimization and characterization of direct UV laser writing system for microscale applications. J. Micromech. Microeng. 2020, 30, 095003. [Google Scholar] [CrossRef]
- Somers, N.; Jean, F.; Lasgorceix, M.; Preux, N.; Delmotte, C.; Boilet, L.; Petit, F.; Leriche, A. Fabrication of doped β-tricalcium phosphate bioceramics by Direct Ink Writing for bone repair applications. J. Eur. Ceram. Soc. 2023, 43, 629–638. [Google Scholar] [CrossRef]
- Samartzis, N.; Bhorkar, K.; Athanasiou, M.; Sygellou, L.; Dracopoulos, V.; Ioannides, T.; Yannopoulos, S.N. Direct laser-assisted fabrication of turbostratic graphene electrodes: Comparing symmetric and zinc-ion hybrid supercapacitors. Carbon 2023, 201, 941–951. [Google Scholar] [CrossRef]
- Zhan, T.; Gao, S.; Xu, B. Microfluidic cloth-based analytical devices through simple correction pen direct-writing. Sensors Actuators B Chem. 2023, 375, 132947. [Google Scholar] [CrossRef]
- Schmid, M.; Thiele, S.; Herkommer, A.; Giessen, H. Adjustment-free two-sided 3D direct laser writing for aligned micro-optics on both substrate sides. Opt. Lett. 2023, 48, 131–134. [Google Scholar] [CrossRef]
- Waller, E.H.; von Freymann, G. From photoinduced electron transfer to 3D metal microstructures via direct laser writing. Nanophotonics 2018, 7, 1259–1277. [Google Scholar] [CrossRef]
- Mao, M.; He, J.; Li, X.; Zhang, B.; Lei, Q.; Liu, Y.; Li, D. The emerging frontiers and applications of high-resolution 3D printing. Micromachines 2017, 8, 113. [Google Scholar] [CrossRef]
- Sola, A.; Trinchi, A.; Hill, A.J. Self-assembly meets additive manufacturing: Bridging the gap between nanoscale arrangement of matter and macroscale fabrication. Smart Mater. Manuf. 2023, 1, 100013. [Google Scholar] [CrossRef]
- Tareq, M.S.; Rahman, T.; Hossain, M.; Dorrington, P. Additive manufacturing and the COVID-19 challenges: An in-depth study. J. Manuf. Syst. 2021, 60, 787–798. [Google Scholar] [CrossRef]
- Choong, Y.Y.C.; Tan, H.W.; Patel, D.C.; Choong, W.T.N.; Chen, C.H.; Low, H.Y.; Tan, M.J.; Patel, C.D.; Chua, C.K. The global rise of 3D printing during the COVID-19 pandemic. Nat. Rev. Mater. 2020, 5, 637–639. [Google Scholar] [CrossRef]
- Colorado, H.A.; Mendoza, D.E.; Lin, H.T.; Gutierrez-Velasquez, E. Additive manufacturing against the Covid-19 pandemic: A technological model for the adaptability and networking. J. Mater. Res. Technol. 2022, 16, 1150–1164. [Google Scholar] [CrossRef]
- Soukoulis, C.M.; Wegener, M. Optical metamaterials—More bulky and less lossy. Science 2010, 330, 1633–1634. [Google Scholar] [CrossRef]
- Whitesides, G.M.; Grzybowski, B. Self-assembly at all scales. Science 2002, 295, 2418–2421. [Google Scholar] [CrossRef]
- Li, L.; Sun, R.; Zheng, R. Tunable morphology and functionality of multicomponent self-assembly: A review. Mater. Des. 2021, 197, 109209. [Google Scholar] [CrossRef]
- Kriksin, Y.A.; Neratova, I.V.; Khalatur, P.G.; Khokhlov, A.R. Pattern multiplication by template-guided self-assembly of cylinder-forming copolymers: Field-theoretic and particle-based simulations. Chem. Phys. Lett. 2010, 492, 103–108. [Google Scholar] [CrossRef]
- Li, L.; Wang, Q. Spontaneous self-assembly of silver nanoparticles into lamellar structured silver nanoleaves. Acs Nano 2013, 7, 3053–3060. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.H.; Wu, S.J.; Ho, C.C.; Su, W.F. Rational design of versatile self-assembly morphology of rod–coil block copolymer. Macromolecules 2013, 46, 2725–2732. [Google Scholar] [CrossRef]
- Stein, A.; Wright, G.; Yager, K.G.; Doerk, G.S.; Black, C.T. Selective directed self-assembly of coexisting morphologies using block copolymer blends. Nat. Commun. 2016, 7, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, Y.; Cardone, G.; Restrepo, D.; Zavattieri, P.D.; Baker, T.S.; Tezcan, F.A. Self-assembly of coherently dynamic, auxetic, two-dimensional protein crystals. Nature 2016, 533, 369–373. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Qin, M.; Wang, C.; Yan, T.; Zhen, Y.; Sun, X.; Wang, J.; Fu, F. CeO2/MnOx@ C hollow cathode derived from self-assembly of Ce-Mn-MOFs for high-performance aqueous zinc-ion batteries. J. Colloid Interface Sci. 2023, 629, 733–743. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, J.; Yu, J.; Wang, Z. Metal organic framework-derived hierarchical 0D/1D CoPC/CNTs architecture interlaminated in 2D MXene layers for superior absorption of electromagnetic waves. Synth. Met. 2023, 292, 117215. [Google Scholar] [CrossRef]
- Liu, C.; Liu, S.; Feng, X.; Zhu, K.; Lin, G.; Bai, Z.; Wang, L.; Liu, X. Phthalocyanine-mediated interfacial self-assembly of magnetic graphene nanocomposites toward low-frequency electromagnetic wave absorption. Chem. Eng. J. 2023, 452, 139483. [Google Scholar] [CrossRef]
- Waqar, S.; Guo, K.; Sun, J. FEM analysis of thermal and residual stress profile in selective laser melting of 316L stainless steel. J. Manuf. Process. 2021, 66, 81–100. [Google Scholar] [CrossRef]
- Bremen, S.; Meiners, W.; Diatlov, A. Selective laser melting: A manufacturing technology for the future? Laser Techn. J. 2012, 9, 33–38. [Google Scholar] [CrossRef]
- Korkmaz, M.E.; Gupta, M.K.; Robak, G.; Moj, K.; Krolczyk, G.M.; Kuntoğlu, M. Development of lattice structure with selective laser melting process: A state of the art on properties, future trends and challenges. J. Manuf. Process. 2022, 81, 1040–1063. [Google Scholar] [CrossRef]
- Tan, J.H.; Wong, W.L.E.; Dalgarno, K.W. An overview of powder granulometry on feedstock and part performance in the selective laser melting process. Addit. Manuf. 2017, 18, 228–255. [Google Scholar] [CrossRef]
- Vieira de Oliveira, R.; Pereira de Lima, Y.; Hoisler Sallet, E.; Abílio Corrêa Gonçalves, D.; Vieira Le Sénèchal, N.; Alves Oliveira Melo, E.; Teixeira, R.; Freitas Rodrigues, P.; Inforçatti Neto, P.; Vicente Lopes da Silva, J.; et al. Production of Cylindrical Specimens Based on the Ni-Ti System by Selective Laser Melting from Elementary Powders. J. Mater. Eng. Perform. 2021, 30, 5477–5490. [Google Scholar] [CrossRef]
- Park, H.S.; Nguyen, D.S. Study on flaking behavior in selective laser melting process. Procedia CIRP 2017, 63, 569–572. [Google Scholar] [CrossRef]
- Singh, D.; Tobin, D.; Dowling, L.; Trimble, D. Optimization of Cobalt Chrome 3D re-entrant Auxetics fabricated using Selective Laser Melting. Eng. Struct. 2023, 278, 115542. [Google Scholar] [CrossRef]
- Gao, M.; He, D.; Guo, X.; Wu, H.; Tan, Z.; Wu, X.; Shao, W.; Wang, G. Design, preparation and characterization of a 3D hierarchical auxetic lattice structure produced by selective laser melting. In Proceedings of the Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 44, pp. 1219–1231. [Google Scholar]
- Alderson, K.; Nazaré, S.; Alderson, A. Large-scale extrusion of auxetic polypropylene fibre. Phys. Status Solidi 2016, 253, 1279–1287. [Google Scholar] [CrossRef]
- Vyavahare, S.; Teraiya, S.; Kumar, S. Auxetic structures fabricated by material extrusion: An experimental investigation of gradient parameters. Rapid Prototyp. J. 2021, 27, 1041–1058. [Google Scholar] [CrossRef]
- Chikkanna, N.; Logakannan, K.P.; Krishnapillai, S.; Ramachandran, V. Quasi-static compression performance of material extrusion enabled re-entrant diamond auxetic metamaterial: Fabrication, tuning the geometrical parameters and fibre reinforcements. Thin-Walled Struct. 2022, 179, 109550. [Google Scholar] [CrossRef]
- Khadem-Reza, L.; Etemadi, E.; Abbaslou, M.; Hu, H. Design of novel 3D auxetic structures based on S-shaped unit-cells. Smart Mater. Struct. 2022, 31, 075024. [Google Scholar] [CrossRef]
- Li, B.; Liang, W.; Zhang, L.; Ren, F.; Xuan, F. TPU/CNTs flexible strain sensor with auxetic structure via a novel hybrid manufacturing process of fused deposition modeling 3D printing and ultrasonic cavitation-enabled treatment. Sens. Actuators A Phys. 2022, 340, 113526. [Google Scholar] [CrossRef]
- Shin, E.J.; Park, Y.; Jung, Y.S.; Choi, H.Y.; Lee, S. Fabrication and characteristics of flexible thermoplastic polyurethane filament for fused deposition modeling three-dimensional printing. Polym. Eng. Sci. 2022, 62, 2947–2957. [Google Scholar] [CrossRef]
- Walther, M.; Ortner, A.; Meier, H.; Löffelmann, U.; Smith, P.J.; Korvink, J.G. Terahertz metamaterials fabricated by inkjet printing. Appl. Phys. Lett. 2009, 95, 251107. [Google Scholar] [CrossRef]
- Kashiwagi, K.; Xie, L.; Li, X.; Kageyama, T.; Miura, M.; Miyashita, H.; Kono, J.; Lee, S.S. Inkjet-printed silver-nanoparticle THz metamaterial. In Proceedings of the 2016 41st International Conference on Infrared, Millimeter, and Terahertz waves (IRMMW-THz), Copenhagen, Denmark, 25–30 September 2016; pp. 1–2. [Google Scholar]
- Schwerdtfeger, J.; Schury, F.; Stingl, M.; Wein, F.; Singer, R.; Körner, C. Mechanical characterisation of a periodic auxetic structure produced by SEBM. Phys. Status Solidi 2012, 249, 1347–1352. [Google Scholar] [CrossRef]
- Schwerdtfeger, J.; Heinl, P.; Singer, R.; Körner, C. Auxetic cellular structures through selective electron-beam melting. Phys. Status Solidi 2010, 247, 269–272. [Google Scholar] [CrossRef]
- Schwerdtfeger, J.; Wein, F.; Leugering, G.; Singer, R.; Körner, C.; Stingl, M.; Schury, F. Design of auxetic structures via mathematical optimization. Adv. Mater. 2011, 23, 2650–2654. [Google Scholar] [CrossRef] [PubMed]
- Mitschke, H.; Schwerdtfeger, J.; Schury, F.; Stingl, M.; Körner, C.; Singer, R.F.; Robins, V.; Mecke, K.; Schröder-Turk, G.E. Finding auxetic frameworks in periodic tessellations. Adv. Mater. 2011, 23, 2669–2674. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, X.G.; Han, D.; Li, W.; Xu, L.F.; Zhang, Y.; Jiang, W.; Bao, S.; Teng, X.C.; Lai, T.; et al. The out-of-plane compressive behavior of auxetic chiral lattice with circular nodes. Thin-Walled Struct. 2023, 182, 110152. [Google Scholar] [CrossRef]
- Jiang, Y.; Shi, K.; Zhou, L.; He, M.; Zhu, C.; Wang, J.; Li, J.; Li, Y.; Liu, L.; Sun, D.; et al. 3D-printed auxetic-structured intervertebral disc implant for potential treatment of lumbar herniated disc. Bioact. Mater. 2023, 20, 528–538. [Google Scholar] [CrossRef]
- Li, Q.; Wu, L.; Hu, L.; Miao, X.; Liu, X.; Zou, T. A sinusoidal beam lattice structure with negative Poisson’s ratio property. Aerosp. Sci. Technol. 2023, 133, 108103. [Google Scholar] [CrossRef]
- Zhang, M.; Zhao, C.; Li, G.; Luo, K. Mechanical properties of the composite lattice structure with variable density and multi-configuration. Compos. Struct. 2023, 304, 116405. [Google Scholar] [CrossRef]
- Gamba, L.; Johnson, Z.T.; Atterberg, J.; Diaz-Arauzo, S.; Downing, J.R.; Claussen, J.C.; Hersam, M.C.; Secor, E.B. Systematic Design of a Graphene Ink Formulation for Aerosol Jet Printing. ACS Appl. Mater. Interfaces 2023, 15, 3325–3335. [Google Scholar] [CrossRef]
- Konstantinou, X.; Lan, X.; Nguyen, K.; Escorcia, A.; Sandhu, R.; Tice, J.; Spain, W.; Albrecht, J.D.; Papapolymerou, J. Fully Aerosol Jet-Printed Passive Components for 140–220-GHz Operation. IEEE Microw. Wirel. Technol. Lett. 2023, 1–4. [Google Scholar] [CrossRef]
- Ratnayake, D.; Curry, A.; Qu, C.; Wei, D.; Gerber, E.; Walsh, K. Optimizing the Conductivity of a New Nano-particle Silver Ink for Aerosol Jet Printing and Demonstrating its use as a Strain Gauge. IEEE J. Flex. Electron. 2023, 1. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Wang, H. Two-dimensional auxetic GeSe2 material with ferroelasticity and flexoelectricity. J. Phys. Chem. C 2021, 125, 19666–19672. [Google Scholar] [CrossRef]
- Coluci, V.R.; Hall, L.J.; Kozlov, M.E.; Zhang, M.; Dantas, S.O.; Galvao, D.S.; Baughman, R.H. Modeling the auxetic transition for carbon nanotube sheets. Phys. Rev. B 2008, 78, 115408. [Google Scholar] [CrossRef]
- Yuan, J.H.; Xue, K.H.; Wang, J.F.; Miao, X.S. Gallium thiophosphate: An emerging bidirectional auxetic two-dimensional crystal with wide direct band gap. J. Phys. Chem. Lett. 2019, 10, 4455–4462. [Google Scholar] [CrossRef]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 023001. [Google Scholar] [CrossRef]
- Ahmed, H.I.; Umair, M.; Nawab, Y.; Hamdani, S.T.A. Development of 3D auxetic structures using para-aramid and ultra-high molecular weight polyethylene yarns. J. Text. Inst. 2021, 112, 1417–1427. [Google Scholar] [CrossRef]
- Steffens, F.; Rana, S.; Fangueiro, R. Development of novel auxetic textile structures using high performance fibres. Mater. Des. 2016, 106, 81–89. [Google Scholar] [CrossRef]
- Khoshgoftar, M.; Abbaszadeh, H. Experimental and finite element analysis of the effect of geometrical parameters on the mechanical behavior of auxetic cellular structure under static load. J. Strain Anal. Eng. Des. 2021, 56, 131–138. [Google Scholar] [CrossRef]
- Janus-Michalska, M.; Jasińska, D.; Smardzewski, J. Comparison of contact stress distribution for foam seat and seat of auxetic spring skeleton. Int. J. Appl. Mech. Eng. 2013, 18, 55–72. [Google Scholar] [CrossRef]
- Dehaghani, M.R.; Nourani, A.; Arjmand, N. Effects of auxetic shoe on lumbar spine kinematics and kinetics during gait and drop vertical jump by a combined in vivo and modeling investigation. Sci. Rep. 2022, 12, 18326. [Google Scholar] [CrossRef]
- NIJ 0101.06; Ballistic Resistance of Body Armor. National Institute of Justice: Washington, DC, USA, 2008.
- Nayak, R.; Crouch, I.; Kanesalingam, S.; Ding, J.; Tan, P.; Lee, B.; Miao, M.; Ganga, D.; Wang, L. Body armor for stab and spike protection, Part 1: Scientific literature review. Text. Res. J. 2018, 88, 812–832. [Google Scholar] [CrossRef]
- Mawkhlieng, U.; Majumdar, A.; Laha, A. A review of fibrous materials for soft body armour applications. RSC Adv. 2020, 10, 1066–1086. [Google Scholar] [CrossRef]
- Liu, J.; Yang, W.; Liu, J.; Liu, J.; Huang, W. Ballistic impact analyses of foam-filled double-arrow auxetic structure. Thin-Walled Struct. 2023, 182, 110173. [Google Scholar] [CrossRef]
- Jiang, F.; Yang, S.; Qi, C.; Liu, H.T.; Remennikov, A.; Pei, L.Z. Blast response and multi-objective optimization of graded re-entrant circular auxetic cored sandwich panels. Compos. Struct. 2023, 305, 116494. [Google Scholar] [CrossRef]
- Lan, X.; Huang, G.; Bian, X.; Liu, Y. Impact resistance of foam-filled hybrid-chiral honeycomb beam under localized impulse loading. Int. J. Impact Eng. 2023, 173, 104477. [Google Scholar] [CrossRef]
- Ul Haq, A.; Gunashekar, G.; Narala, S.K.R. The Dynamic Response of AuxHex and Star-Reentrant Honeycomb Cored Sandwich Panels Subject to Blast Loading. Arab. J. Sci. Eng. 2023, 1–17. [Google Scholar] [CrossRef]
- Yan, Z.; Liu, Y.; Yan, J.; Wang, B.; Bai, F.; Shi, Z.; Huang, F. Anti-blast performance of 3D-printed sandwich panels with auxetic hexagonal and regular hexagonal honeycomb cores. Eng. Struct. 2022, 272, 114996. [Google Scholar] [CrossRef]
- Critchley, R.; Hazael, R.; Bhatti, K.; Wood, D.; Peare, A.; Johnson, S.; Temple, T. Blast mitigation using polymeric 3D printed auxetic re-entrant honeycomb structures: A preliminary study. Int. J. Prot. Struct. 2021, 13, 469–486. [Google Scholar] [CrossRef]
- Usta, F.; Türkmen, H.S.; Scarpa, F. High-velocity impact resistance of doubly curved sandwich panels with re-entrant honeycomb and foam core. Int. J. Impact Eng. 2022, 165, 104230. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Y.; Cao, S.; Xuan, S.; Jiang, W.; Gong, X. Conductive shear thickening gel/Kevlar wearable fabrics: A flexible body armor with mechano-electric coupling ballistic performance. Compos. Sci. Technol. 2019, 182, 107782. [Google Scholar] [CrossRef]
- Zhang, Q.; Qin, Z.; Yan, R.; Wei, S.; Zhang, W.; Lu, S.; Jia, L. Processing technology and ballistic-resistant mechanism of shear thickening fluid/high-performance fiber-reinforced composites: A review. Compos. Struct. 2021, 266, 113806. [Google Scholar] [CrossRef]
- Zhao, C.; Gong, X.; Wang, S.; Jiang, W.; Xuan, S. Shear stiffening gels for intelligent anti-impact applications. Cell Rep. Phys. Sci. 2020, 1, 100266. [Google Scholar] [CrossRef]
- Ribeiro, M.P.; da Silveira, P.H.P.M.; de Oliveira Braga, F.; Monteiro, S.N. Fabric Impregnation with Shear Thickening Fluid for Ballistic Armor Polymer Composites: An Updated Overview. Polymers 2022, 14, 4357. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Zhou, J.; Wu, J.; Liu, S.; Sang, M.; Liu, B.; Pan, Y.; Gong, X. Multi-functional STF-based yarn for human protection and wearable systems. Chem. Eng. J. 2023, 453, 139869. [Google Scholar] [CrossRef]
- Sheikhi, M.R.; Gürgen, S. Deceleration behavior of multi-layer cork composites intercalated with a non-Newtonian material. Arch. Civ. Mech. Eng. 2023, 23, 1–11. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).