On Long-Range Characteristic Length Scales of Shell Structures
Abstract
1. Introduction
2. Preliminaries
2.1. Navier’s Equations of Elasticity
2.2. Surface Definitions
Profile Functions and Parametrisation
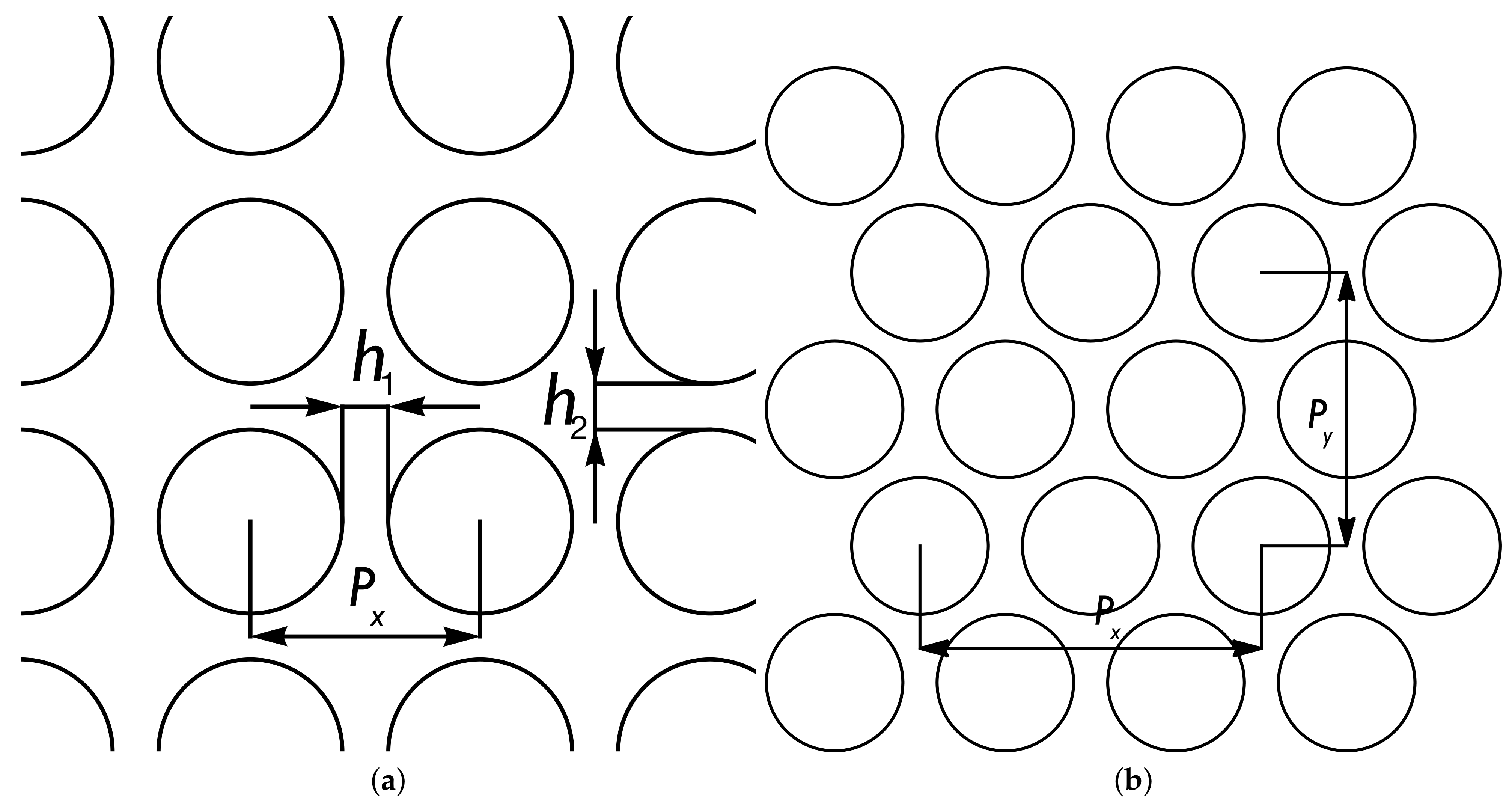
2.3. Perforations
2.4. Finite Element Method
Implementations
3. Shell Models
- 1
- Parabolic (Zero Gaussian curvature shells). .
- 2
- Elliptic (Positive Gaussian curvature shells). .
- 3
- Hyperbolic (Negative Gaussian curvature shells). .
Dimensionally Reduced Elasticity Equations: Naghdi Model
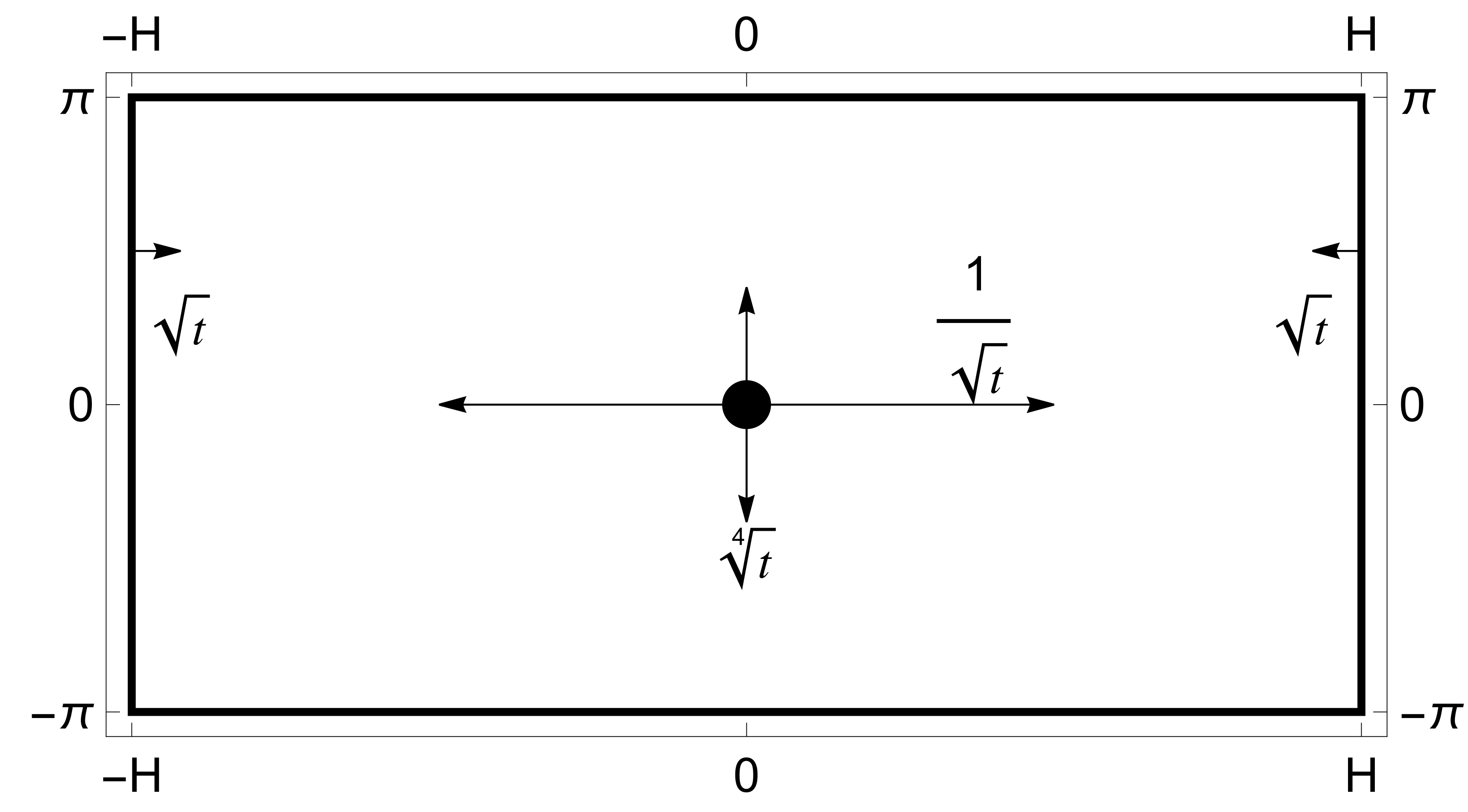
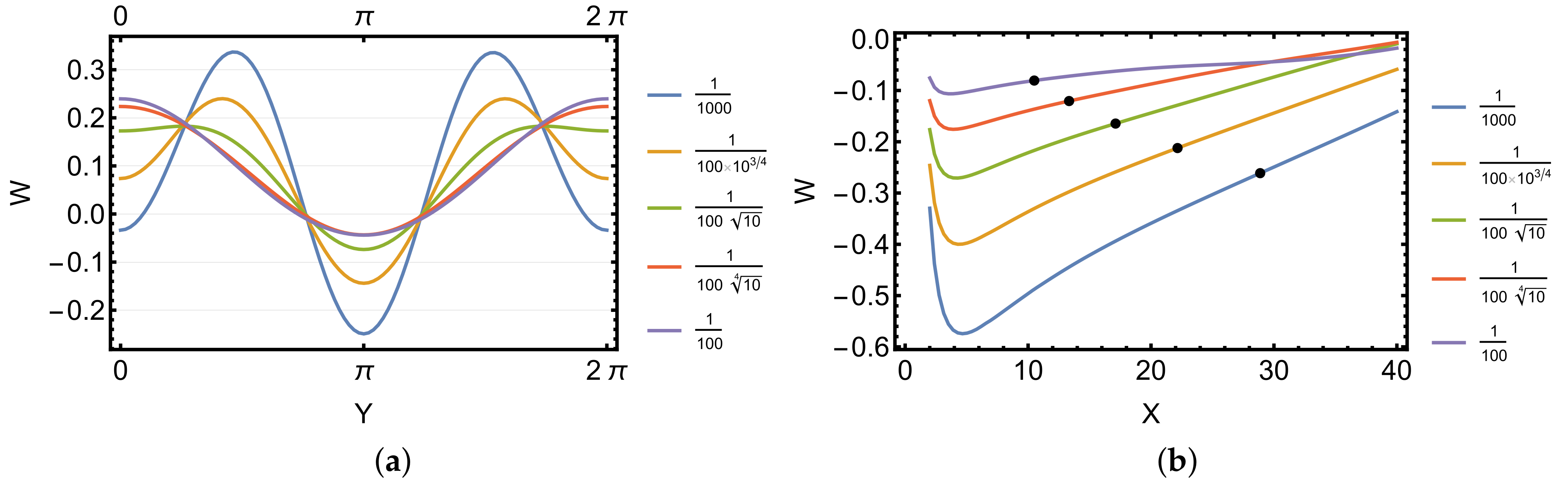
4. Boundary and Internal Layers
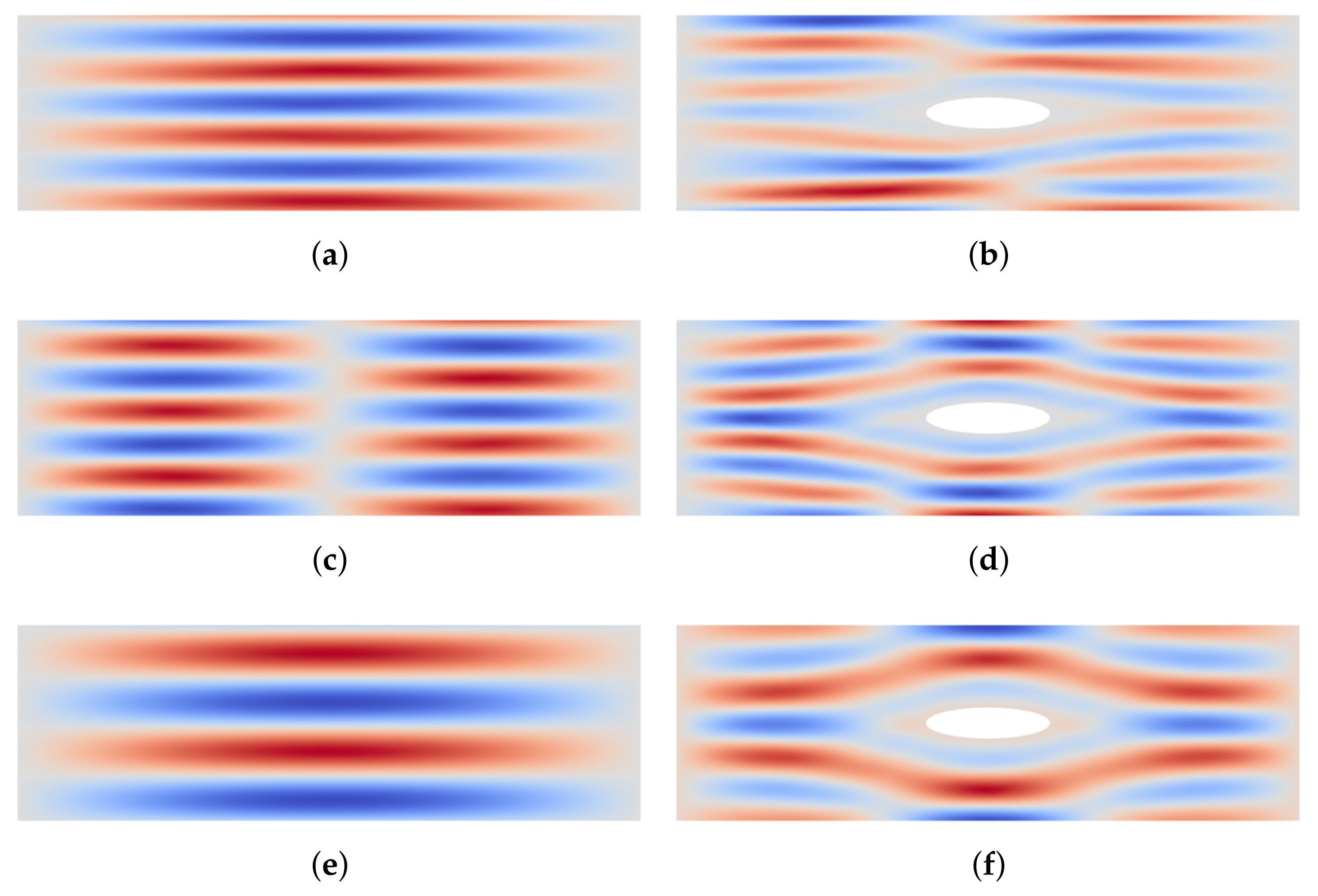
5. Numerical Simulations
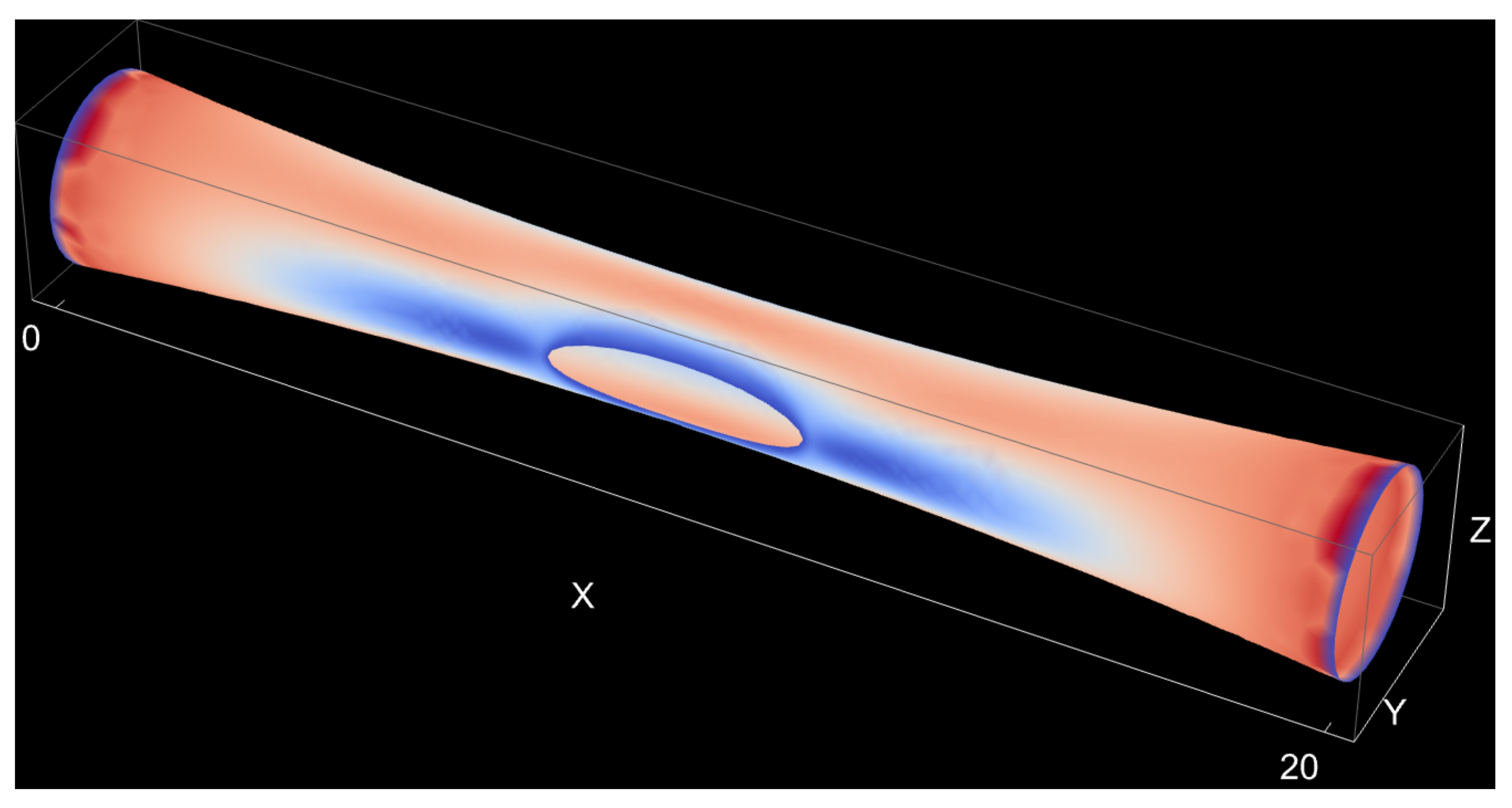
5.1. Wind Turbine: Manhole
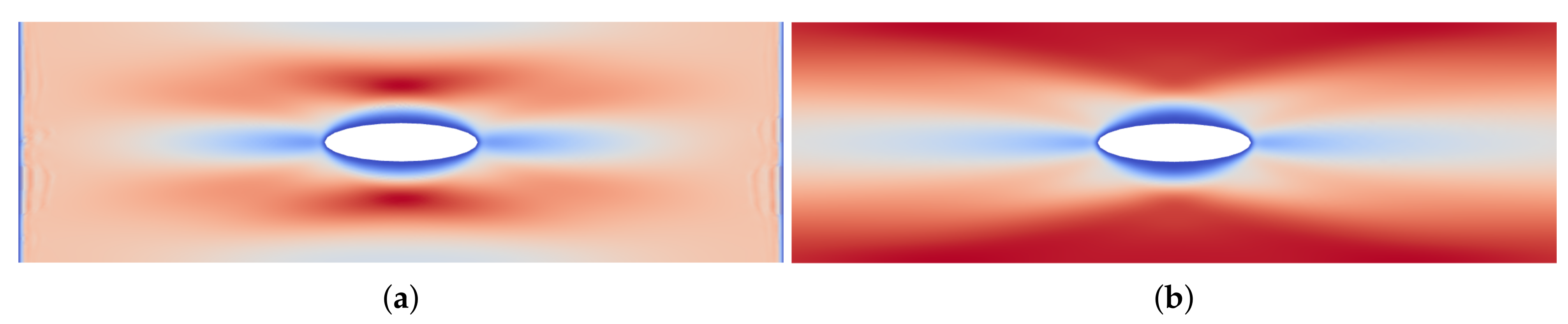
5.2. Slit Shells: Torsion Effect
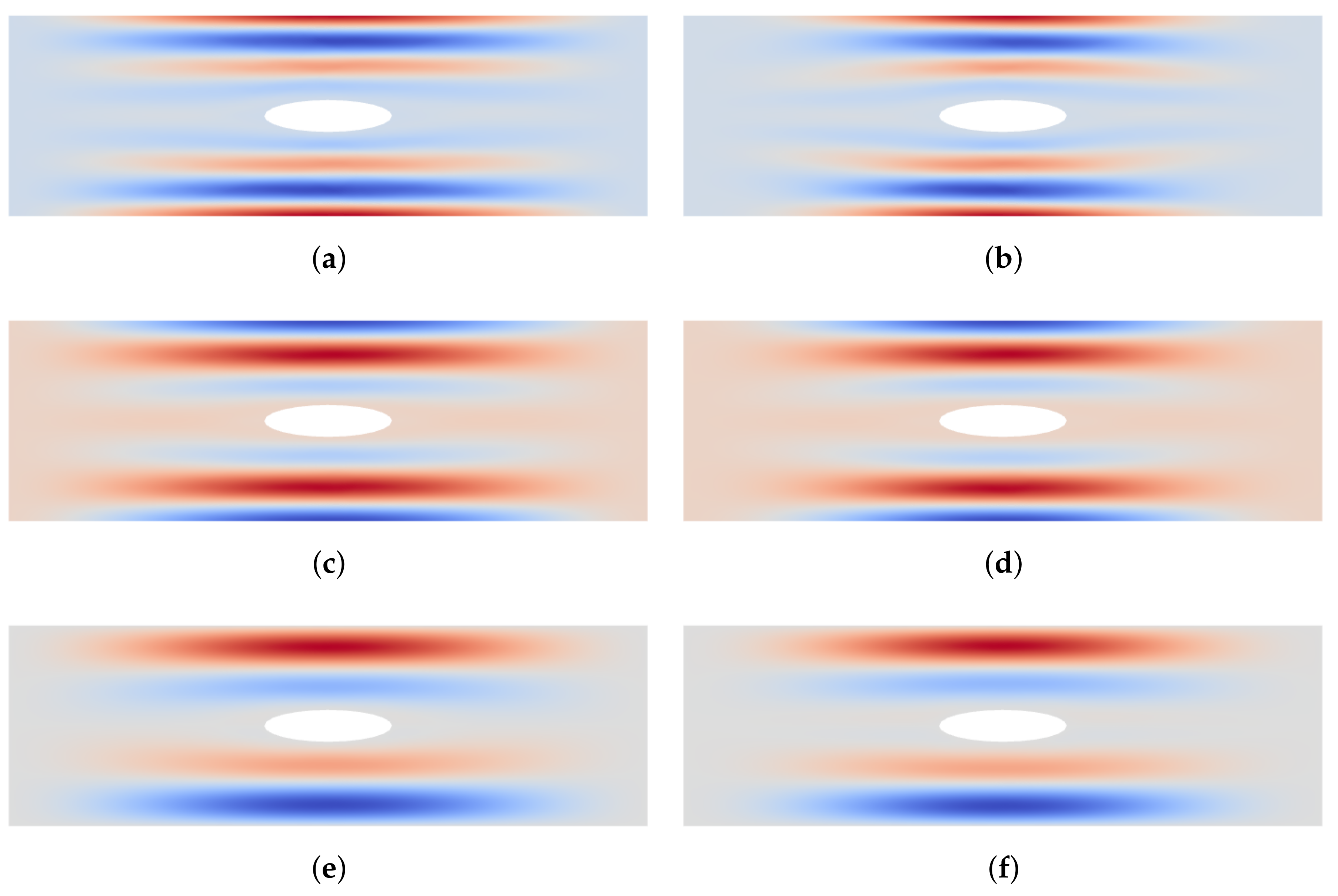
5.3. Curvature Effect
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Mathematical Shell Model
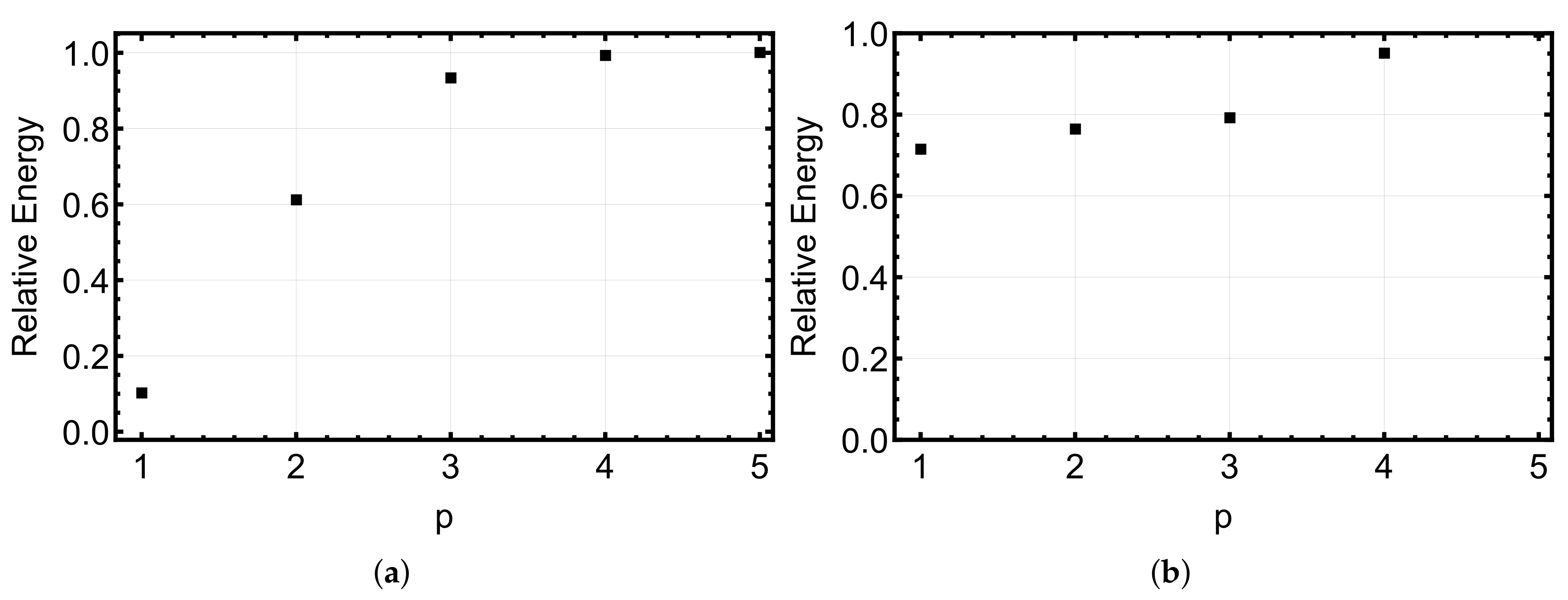
Appendix B. On Buckling Modes

References
- Chapelle, D.; Bathe, K.J. The Finite Element Analysis of Shells; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Pitkäranta, J.; Leino, Y.; Ovaskainen, O.; Piila, J. Shell Deformation states and the Finite Element Method: A Benchmark Study of Cylindrical Shells. Comput. Methods Appl. Mech. Eng. 1995, 128, 81–121. [Google Scholar] [CrossRef]
- Pitkäranta, J.; Matache, A.M.; Schwab, C. Fourier mode analysis of layers in shallow shell deformations. Comput. Methods Appl. Mech. Eng. 2001, 190, 2943–2975. [Google Scholar] [CrossRef]
- Hakula, H.; Havu, V.; Beirao de Veiga, L. Long-Range Boundary Layers in Shells of Revolution. In Proceedings of the 5th International Conference on Computation of Shell and Spatial Structures, Salzburg, Austria, 1–4 June 2005. [Google Scholar]
- Hakula, H. Hp-boundary layer mesh sequences with applications to shell problems. Comput. Math. Appl. 2014, 67, 899–917. [Google Scholar] [CrossRef]
- Sanchez-Palencia, E.; Millet, O.; Béchet, F. Singular Problems in Shell Theory; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Pietraszkiewicz, W.; Konopińska, V. Junctions in shell structures: A review. Thin Walled Struct. 2015, 95, 310–334. [Google Scholar] [CrossRef]
- Malliotakis, G.; Alevras, P.; Baniotopoulos, C. Recent Advances in Vibration Control Methods for Wind Turbine Towers. Energies 2021, 14, 7536. [Google Scholar] [CrossRef]
- Szabo, B.A.; Muntges, D.E. Procedures for the Verification and Validation of Working Models for Structural Shells. J. Appl. Mech. 2005, 72, 907–915. [Google Scholar] [CrossRef]
- Szabo, B.; Babuska, I. Finite Element Analysis; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Niemi, A.H. Numerical buckling analysis of circular cylindrical shells. In Proceedings of the MAFELAP 2019, Uxbridge, UK, 18–21 June 2019. [Google Scholar]
- Bartels, S.; Bonito, A.; Muliana, A.H.; Nochetto, R.H. Modeling and simulation of thermally actuated bilayer plates. J. Comput. Phys. 2018, 354, 512–528. [Google Scholar] [CrossRef]
- McMillen, T.; Goriely, A. Tendril Perversion in Intrinsically Curved Rods. J. Nonlinear Sci. 2002, 12, 241–281. [Google Scholar] [CrossRef]
- Giani, S.; Hakula, H. On effective material parameters of thin perforated shells under static loading. Comput. Methods Appl. Mech. Eng. 2020, 367, 113094. [Google Scholar] [CrossRef]
- Slaughter, W.S. The Linearized Theory of Elasticity; Birkhäuser: Basel, Switzerland, 2002. [Google Scholar]
- Malinen, M. On the classical shell model underlying bilinear degenerated shell finite elements: General shell geometry. Int. J. Numer. Methods Eng. 2002, 55, 629–652. [Google Scholar] [CrossRef]
- Forskitt, M.; Moon, J.R.; Brook, P.A. Elastic properties of plates perforated by elliptical holes. Appl. Math. Model. 1991, 15, 182–190. [Google Scholar] [CrossRef]
- Burgemeister, K.; Hansen, C. Calculating Resonance Frequencies of Perforated Panels. J. Sound Vib. 1996, 196, 387–399. [Google Scholar] [CrossRef]
- Jhung, M.J.; Yu, S.O. Study on modal characteristics of perforated shell using effective Young’s modulus. Nucl. Eng. Des. 2011, 241, 2026–2033. [Google Scholar] [CrossRef]
- Pitkäranta, J. The problem of membrane locking in finite element analysis of cylindrical shells. Numer. Math. 1992, 61, 523–542. [Google Scholar] [CrossRef]
- Hakula, H.; Leino, Y.; Pitkäranta, J. Scale resolution, locking, and high-order finite element modelling of shells. Comput. Methods Appl. Mech. Engrg. 1996, 133, 157–182. [Google Scholar] [CrossRef]
- Hakula, H.; Tuominen, T. Mathematica implementation of the high order finite element method applied to eigenproblems. Computing 2013, 95, 277–301. [Google Scholar] [CrossRef]
- Do Carmo, M. Differential Geometry of Curves and Surfaces; Prentice Hall: Hoboken, NJ, USA, 1976. [Google Scholar]
- Schwab, C. p- and hp-Finite Element Methods; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Artioli, E.; da Veiga, L.B.; Hakula, H.; Lovadina, C. On the asymptotic behaviour of shells of revolution in free vibration. Comput. Mech. 2009, 44, 45–60. [Google Scholar] [CrossRef]


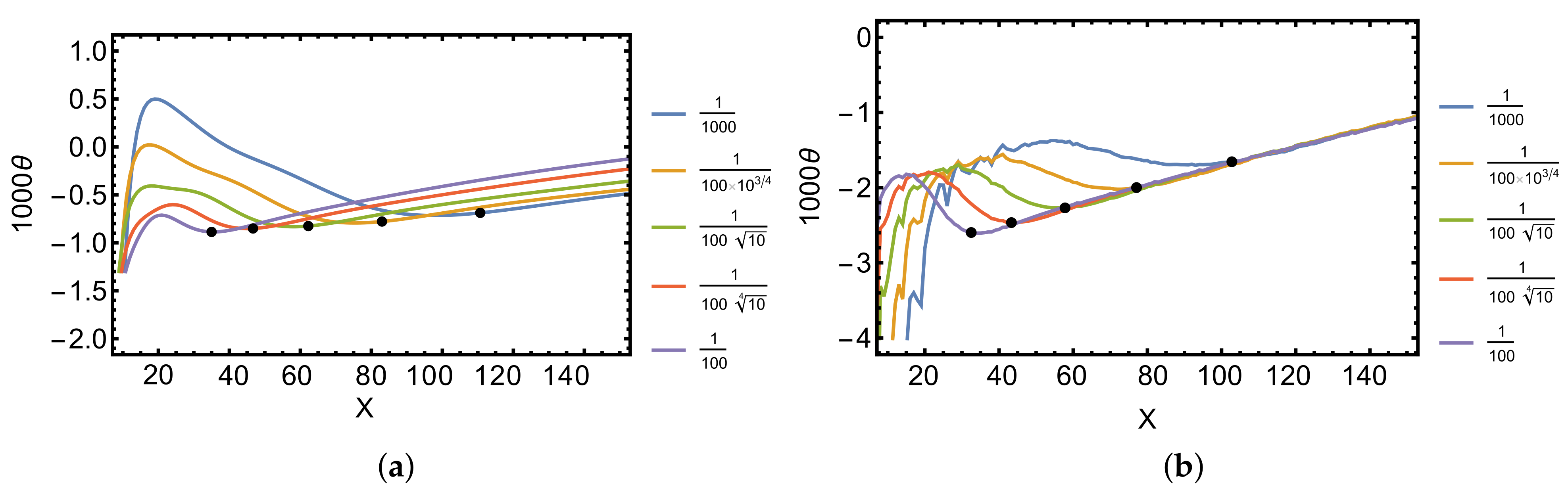


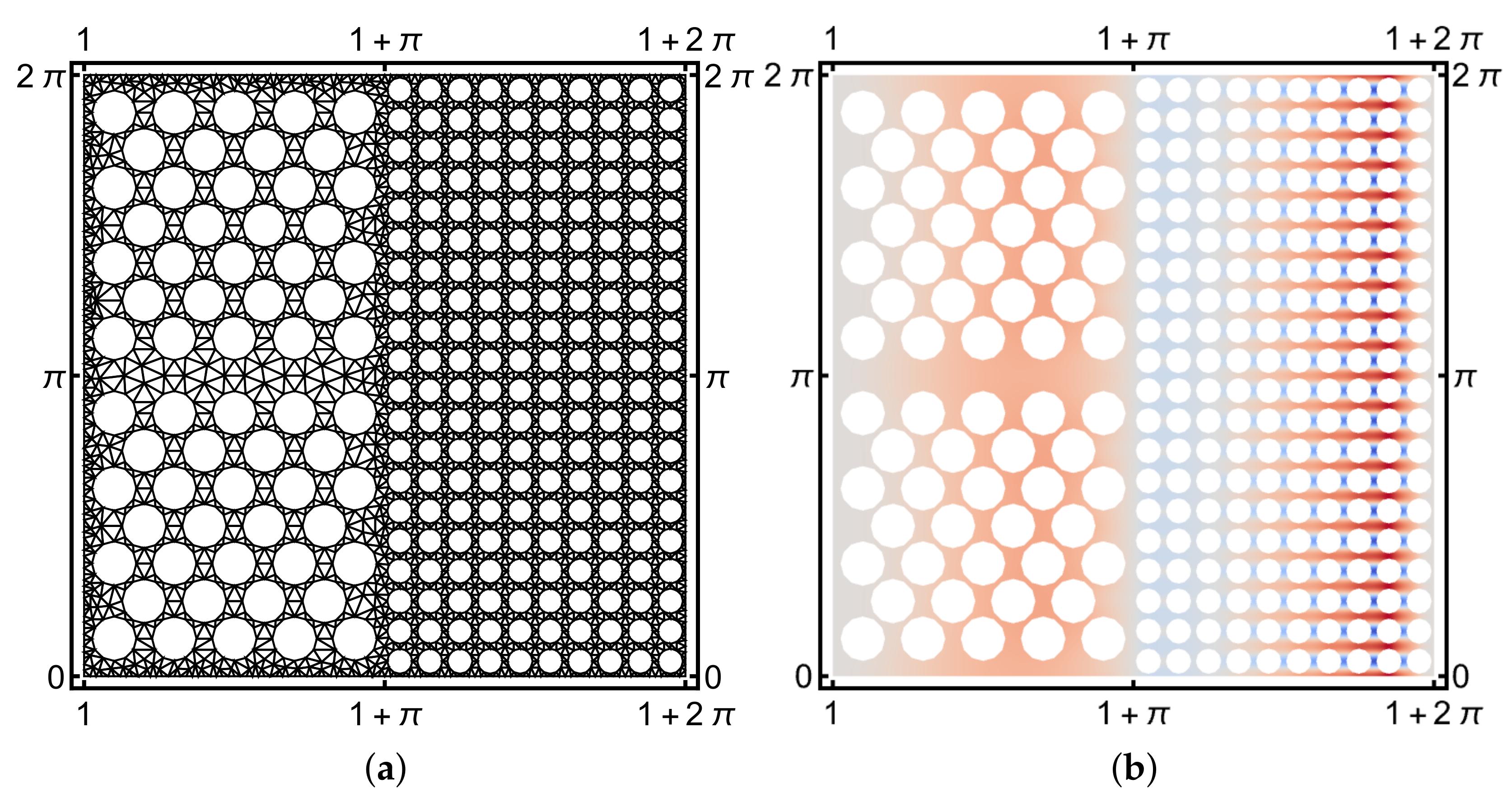
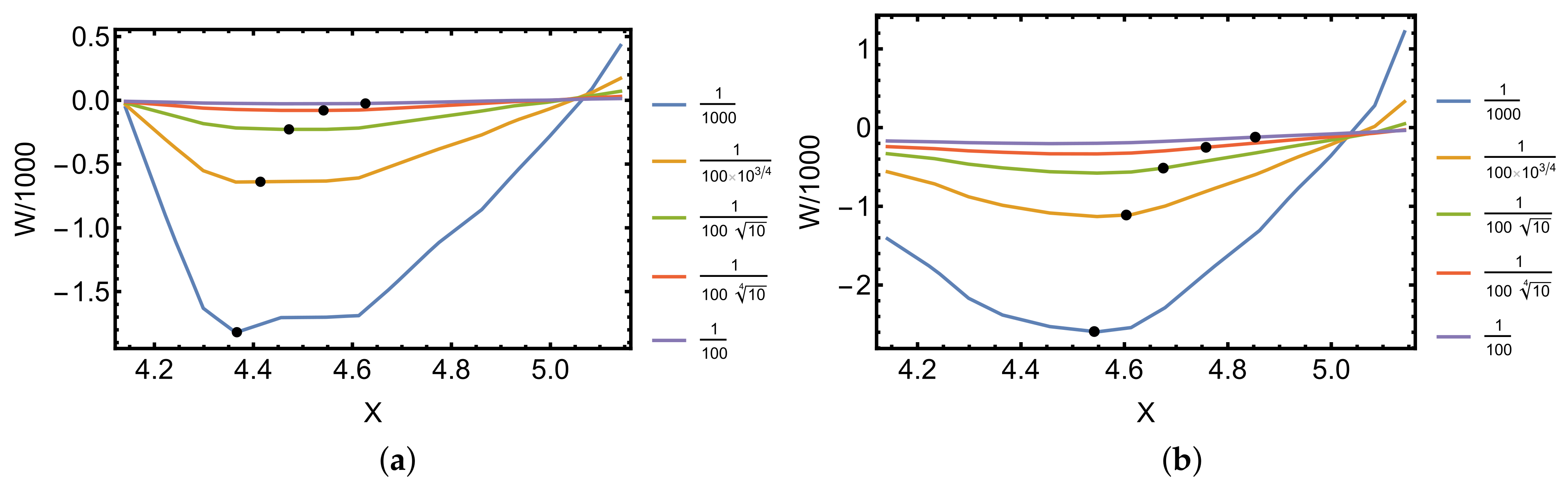
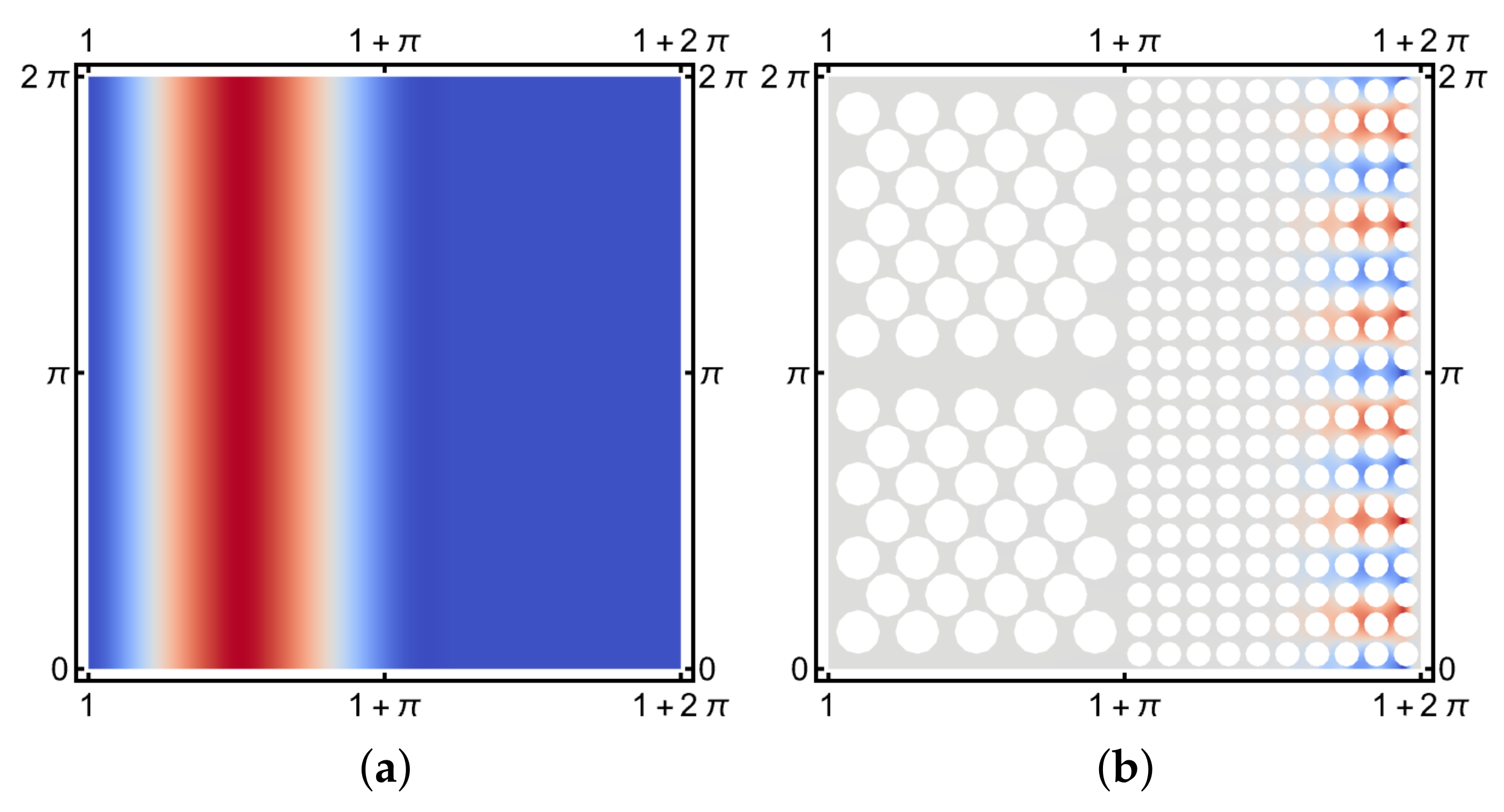
| Case | Geometry | Perforation | H | p | N |
|---|---|---|---|---|---|
| Wind Turbine: Manhole | Parabolic | 60 | 8 | 197,440 | |
| Parabolic | 1000 | 6 | 2,127,240 | ||
| Hyperbolic | 1000 | 6 | 2,127,240 | ||
| Slit Shell: Torsion Effect | Parabolic | 100 | 5 | 1,907,980 | |
| Parabolic | Triangular | 100 | 5 | 2,841,675 | |
| Hyperbolic | 100 | 5 | 1,907,980 | ||
| Parabolic | 1000 | 5 | 1,907,980 | ||
| Parabolic | Regular | 1000 | 5 | 7,126,755 | |
| Hyperbolic | 1000 | 5 | 1,907,980 | ||
| Curvature Effect | Mixed | Multipanel | 6 | 490,145 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hakula, H. On Long-Range Characteristic Length Scales of Shell Structures. Eng 2023, 4, 884-902. https://doi.org/10.3390/eng4010053
Hakula H. On Long-Range Characteristic Length Scales of Shell Structures. Eng. 2023; 4(1):884-902. https://doi.org/10.3390/eng4010053
Chicago/Turabian StyleHakula, Harri. 2023. "On Long-Range Characteristic Length Scales of Shell Structures" Eng 4, no. 1: 884-902. https://doi.org/10.3390/eng4010053
APA StyleHakula, H. (2023). On Long-Range Characteristic Length Scales of Shell Structures. Eng, 4(1), 884-902. https://doi.org/10.3390/eng4010053






