Abstract
A technique alternative to the direct numerical simulation of turbulent combustion of gas mixtures is proposed. It is based on the solution of the three-dimensional transport equations for species concentrations and the energy conservation equation in the “synthetic” field of constant-pressure homogeneous, isotropic and statistically stationary (forced) turbulence using the detailed reaction mechanism. The synthetic turbulence with given spatial and temporal correlation functions is generated using the Monte Carlo method, assuming that the components of the vector of fluctuation velocity obey the normal Gaussian distribution. The technique is applied to the problem of turbulent combustion of fuel-lean and stoichiometric mixtures of hydrogen and methane with air at a turbulence intensity up to 10 m/s. The calculated turbulent flame propagation velocities agree satisfactorily with the values measured in the fan-stirred bomb. The predicted volume fractions of active reaction centers H, O, and OH in a turbulent flame are shown to be less than in a laminar flame up to an order of magnitude, which also agrees with the experiment. In general, calculations indicate that the “wrinkled flame” model is applicable to fuel-lean and stoichiometric mixtures of hydrogen and methane with air at turbulence intensities up to 10 m/s
1. Introduction
The nonempirical theoretical description of turbulent flames based on direct numerical simulation (DNS) was probably first proposed in [1] for incompressible, isotropic, and homogeneous turbulence, and implemented in [2] to the incompressible homogeneous reacting turbulent flow with irreversible, second-order, isothermal chemical reaction of two initially unmixed gases. Further steps in the development of the DNS concept with respect to turbulent combustion can be found elsewhere (see, e.g., [3,4,5,6,7,8] and recent reviews [9,10,11]). As of today, DNS includes all important features of a three-dimensional (3D) turbulent reacting flow with a complete spectrum of velocity fluctuations, a set of relevant chemical species with their individual molecular transport and thermochemical properties, as well as with adequate boundary conditions. The flow equations are integrated numerically on computational grids resolving turbulent eddies of the Kolmogorov scale, using high-order approximation schemes. In many relevant publications, the initial energy spectrum of turbulent velocity fluctuations is approximated by Gaussian or quasi-normal probability distributions. Despite the presence of kinetic energy transfer (cascade) from large to small spatial scales of turbulence leading to the non-Gaussian nature of the turbulent velocity field, the deviations from the Gaussian distribution for isotropic turbulence are shown to be insignificant [12].
In reference [13], using the example with a two-dimensional (2D) turbulent flame propagation in a mixture of hydrogen with air, a simplified nonempirical approach alternative to DNS was proposed. Instead of the numerical solution of all governing equations for turbulent flame propagation in a reacting gas, only the transport equations for species concentrations and the energy conservation equation in the “synthetic” field of constant-pressure homogeneous, isotropic, and statistically stationary (forced) turbulence were solved. The synthetic turbulence with given spatial and temporal correlation functions was generated using the Monte Carlo method assuming that the components of the fluctuation velocity vector satisfied the normal Gaussian distribution both initially and during the entire process of turbulent flame propagation. The latter implied that there was a continuous generation of turbulence in the flow, for example, with the help of fans in fan-stirred bombs [14,15] or upstream turbulence-generating grids [16]. It was also assumed that flame propagation did not affect the characteristics of turbulence in the pre-flame zone. Despite the existence of several other available approaches to produce homogeneous and isotropic synthetic turbulence [17,18], the approach of [13] appeared fruitful for homogeneous, isotropic, and statistically stationary (forced) turbulence and was further developed in [19,20]. Contrary to [13], where hydrogen combustion was modeled using an overall single-stage chemical reaction, in [19,20] a multistage detailed reaction mechanism (DRM) of hydrogen oxidation with the participation of active radicals was used. In [19], only a combustible mixture of a specific composition was considered, whereas in [20], the technique of [19] was modified to study the propagation of a 2D flame in hydrogen–air mixtures of different compositions at different initial pressures. Both in [19] and [20], a satisfactory agreement between experimental data [14] and the calculation results was reported. However, to compare the results of 2D calculations with the realistic 3D experiment, it was required to scale the calculated value of the root-mean-square (RMS) velocity fluctuation [19,20].
The objective of this work is to advance from modeling turbulent combustion in a 2D approximation [19,20] to a physically adequate 3D problem, which will allow direct comparison of calculations and experiments without scaling the RMS velocity fluctuation. The availability of such a 3D-validated approach for nonempirical calculation of the turbulent burning velocity in premixed gases is very attractive for multiple engineering applications, such as piston and gas turbine engines, as well as various industrial burners. For example, such an approach could be used for creating extensive look-up tables of turbulent burning velocities for different fuels at different thermodynamic and turbulence conditions for the flame tracking—particle (FTP) method [21]. The look-up tables for the turbulent burning velocity could replace the multiple empirical correlations (see, e.g., [22,23,24,25] used in engineering calculations. Thus, we propose and validate a nonempirical technique alternative to the standard DNS of turbulent flame propagation in reacting gas mixtures, which is a distinctive and novel feature of the present work.
2. Materials and Methods
2.1. Mathematical Statement of the Problem
In a general form, the problem statement was formulated in [20], but we repeat it partially herein. The equations governing turbulent flame propagation are the Navier–Stokes equations supplemented by the continuity equations for chemical species, and the energy conservation equation [26]:
where is time; is the velocity vector; is the density; is the pressure; is the tensor of pressure force; is the gravity vector acting on the th substance; , , and are mass fraction, vector of diffusion velocity, enthalpy, and rate of chemical depletion/production of the th species; is the number of species in the reacting gas; is the internal energy; is the vector of molecular heat flux; is the standard enthalpy of formation of the th species; is the molecular mass of the th species; is the universal gas constant; is the specific heat of the th species at constant pressure; is the temperature; and index 0 denotes the initial conditions.
The system (1) is further supplemented with the DRM of fuel oxidation, thermochemical data of each substance (, ) and relations for , , , and , as well as the boundary and initial conditions. The solution of the problem provides the structure of the turbulent flame in a reacting gas and the stationary turbulent burning velocity .
The solution of the problem is simplified by adopting the following assumptions:
- (i)
- the flow domain is simple; turbulence is homogeneous, isotropic, and statistically stationary (forced);
- (ii)
- the effect of gravity is negligible, and the pressure is constant (). These assumptions greatly simplify the problem as the solution of the momentum equation is not required;
- (iii)
- radiative heat transfer is negligible, and heat flux is due to solely the molecular thermal conductivity;
- (iv)
- thermal diffusivity is negligible;
- (v)
- Fick’s law with a binary diffusion coefficient is applicable to the diffusion fluxes.
These assumptions together with the considerations described in [13,19,20] allow the reduction of Equation (1) to the form:
where is the specific heat capacity at constant volume; is the coefficient of molecular thermal conductivity; is the vector of velocity fluctuation in the fresh mixture; and is the diffusion coefficient of the th species. Thus, as in [13,19,20], instead of solving a complex system (1) numerically, it is proposed to solve a simplified system (2). Contrary to system (1), system (2) consists only of the transport equations for scalars—energy and mass fractions of species—on the preset field of turbulence with certain RMS velocity fluctuations and with given integral temporal and spatial scales. In the 3D coordinate system , Equation (2) together with the ideal-gas equations of state will take the following expanded form:
The system of Equation (3) includes equations for variables ( species mass fractions , density , and temperature ). To close the system, the following relations are used:
where , , , and are the coefficients and index denotes nitrogen. The rates of chemical reactions are determined using the relationship [26]:
where is the pre-exponential factor of the th reaction; and are the stoichiometric coefficients; is the temperature exponent; is the activation energy; is the mole fraction of the th species; is the total number of chemical reactions.
Equation (3) includes the parameters of homogeneous, isotropic, and statistically stationary (forced) turbulence: three components of the fluctuation velocity vector . Synthetic turbulence is generated using the approach suggested in [13,19,20]. In this approach, the components of the fluctuation velocity vector and are obtained by the Monte Carlo method, assuming that they obey the normal Gaussian distribution, , and the turbulence structure is characterized by exponentially decaying spatial, and temporal‚ , correlation functions. From now on, for the sake of simplicity, we omit zeros in the components of the fluctuation velocity vector and denote the -component of the vector and its RMS as and , respectively. The distribution function of is given by the relationship
where is the RMS deviation of velocity fluctuations. This relationship is also applied to - and -components of the fluctuation velocity vector, and , and and , respectively. The spatial and temporal correlation functions are taken in the form:
where is the distance in physical space; is the turbulence scale in the , , and directions, respectively; is the Lagrange time scale. In accordance with the assumption (), the scales and are taken constant in time and space. The RMS length of the fluctuation velocity vector (turbulence intensity) is determined as
It is worth emphasizing that the specification of turbulence intensity and spatial turbulence scale is equivalent to the specification of the turbulent energy dissipation and the Kolmogorov scale , where . Increasing the turbulence intensity leads to a decrease in the integral scales and (e.g., [27]). This effect must be taken into account when modeling synthetic turbulence. Unfortunately, in the literature, there are no generalized dependences such as
However, such dependences can be obtained by comparing the calculated and measured velocities of turbulent flame in a given reacting mixture and extended to other mixtures of the same combustible gas and, possibly, to mixtures of other combustible gases. The initial and boundary conditions for Equation (3) are considered below for a simple geometry.
2.2. Numerical Method
The flow geometry is simply a rectangular box whose bottom and top faces are flat squares. Initially, at , the computational domain contains two layers which are separated by a surface parallel to the box bottom and located at some distance from it. The near-bottom layer is composed of combustion products, whereas the top layer is composed of fresh reactive mixture. The bottom and top faces of the box are situated far enough away from the separating surface to ensure that the pressure in the system remains constant throughout the calculation. The lateral faces of the box are impermeable walls with flow slip. The flame propagates from bottom to top. Figure 1 shows an example of the 3D flame surface deformed (wrinkled) by velocity fluctuations.
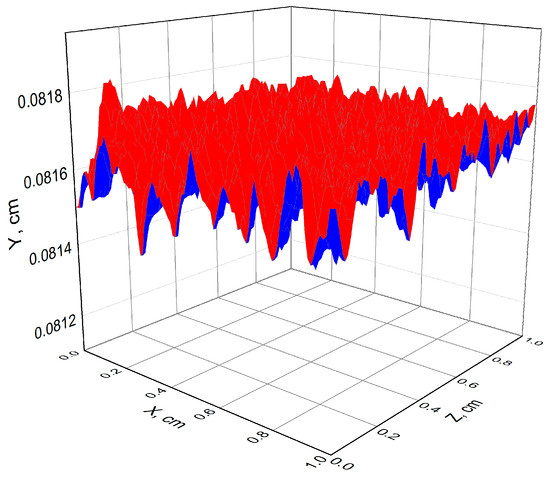
Figure 1.
The calculated instantaneous surface of the propagating flame in a mixture of hydrogen with air with 9.09%vol. H2 at NPT conditions ( = 293 K, = 0.1 MPa); = 242 cm/s, = 1 cm, = 0.01 s; red and blue colors correspond to the upper and lower surfaces of the flame, respectively.
Figure 2 shows the plane section of the flow in the chosen coordinate system for a certain value of . The dashed line shows the flame position at . At , the cut of the true flame surface in the plane is shown by a solid curve, and the instantaneous flame position is conditionally represented by another dashed line parallel to the box bottom. Above this line, there is only a fresh mixture, whereas below this line there is only the reaction products. Note that this line is a conditional flame front as the flame itself possesses the finite-thickness reaction zone. To determine the flame propagation velocity, it is assumed that the fresh mixture conditionally occupies a space with a temperature , whereas the reaction products conditionally occupy a space with a temperature . The value of is taken as the arithmetic mean between and (the thermodynamic equilibrium combustion temperature):
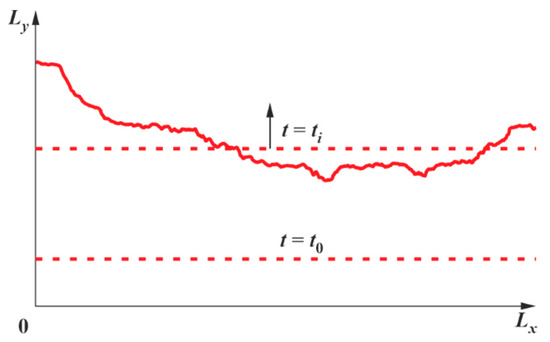
Figure 2.
Plane section of the computational domain.
The problem of flame propagation in the field of synthetic turbulence was solved numerically using the method of alternating directions [28]. Equation (3) was discretized on a uniform computational mesh using an implicit difference scheme constructed based on the method of additive decomposition [29]. This scheme is first-order accurate in time and space and is absolutely stable. The nonlinear source terms were linearized on the upper time layer. The computational domain had a size of 1 cm × 0.5 cm × 1 cm in the x–y–z directions. Computational cells had a size of 0.01 cm × 0.01 cm × 0.01 cm or 0.005 cm × 0.005 cm × 0.005 cm. The number of computational cells was either 500,000 or 4,000,000 respectively. Grid sensitivity tests showed that doubling of the number of cells along all three directions while maintaining the dimensions of the computational domain virtually did not affect the value of the turbulent flame propagation velocity. The time step was variable and depended on the number of iterations, but was less than 1 μs. The convergence criterion was .
The fluctuating velocity fields , , and for given turbulence characteristics , , and were modeled using the procedure described in detail in [20] for the 2D statement of the problem. Extending this procedure from 2D to 3D problem formulation is straightforward. It is worth noting that this procedure does not require the specification of the turbulence spectrum: it appears implicitly in the correlation functions.
The initial conditions used in the calculations are:
The boundary conditions used in the calculations are:
3. Results and Discussion
3.1. Results of Calculations for Hydrogen-Air Mixtures and Discussion
Consider, as in [20], flame propagation in hydrogen–air mixtures. For this purpose, a block of reactions of hydrogen oxidation from the DRM of combustion of normal hydrocarbons [30] is used. The values of coefficients , , , and for all species are taken from [31]. The coefficients and are calculated according to [32].
To compare the calculated and measured turbulent burning velocities for the mixtures of different compositions depending on the turbulence intensity , the experimental data of [14] are used. The maximum time for calculating the flame was 1 ms, i.e., it was less than the integral time scale . Therefore, the solutions can be treated as individual realizations of the flame front position. Both large- and small-scale spatial inhomogeneities are observed on the flame front surface (see Figure 1). Flame surface elements with linear dimensions both larger and smaller than the flame thickness can be identified. Large-scale turbulence affects the flame shape leading to the increase in its surface area. Small-scale turbulence affects (increases) the rate of mass and energy transfer processes inside the flame.
Figure 3 is an example of the calculated time history of the distance traveled by the flame for the mixture of hydrogen with air with 17.36%vol. H2 at = 675 cm/s, = 1 cm, and = 10 ms. The calculated flame velocity is seen to be almost constant in time despite a relatively short calculation time (). From the position of the flame front, one can readily determine the apparent velocity of flame propagation . Taking into account the thermal expansion of the reaction products, the turbulent burning velocity can be determined from the relationship:
where and are the mole numbers in the initial mixture and in the reaction products, respectively.
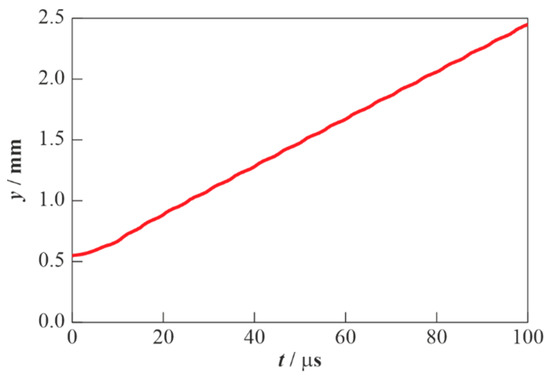
Figure 3.
Predicted time history of the distance traveled by the flame in the 17.36%vol. H2–air mixture at NPT conditions ( = 293 K, = 0.1 MPa), = 675 cm/s, = 1 cm, and = 10 ms.
Figure 4 compares the measured and predicted dependences of the turbulent burning velocities for the various hydrogen—air mixtures on the turbulence intensity (as in [14]). Note that the calculations were carried out both for > 0 and for = 0, i.e., for the laminar flame. As seen from Figure 4, the results are in satisfactory qualitative agreement. In these calculations, no dependences such as that of Equation (5) were used, i.e., it was assumed that the integral scales and did not change with turbulence intensity.
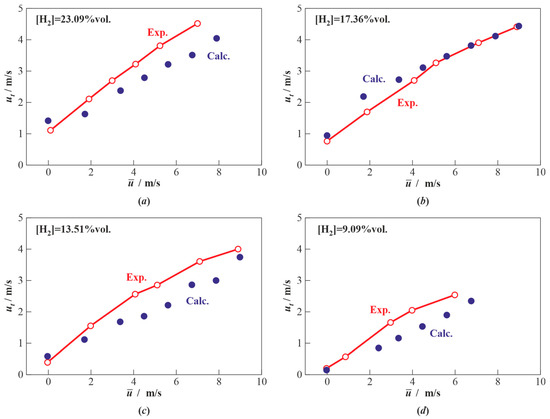
Figure 4.
Calculated (Calc.) and measured [14] (Exp.) turbulent burning velocities vs. turbulence intensity for hydrogen–air mixtures with different hydrogen content [H2]: (a) 23.09%vol., (b) 17.36%vol., (c) 13.51%vol., and (d) 9.09%vol.; = 293 K, = 0.1 MPa, = 1 cm, and = 10 ms.
Figure 5 compares the predicted temperature profiles in turbulent and laminar flames in the same mixture. The profile of temperature in the turbulent flame is plotted for a small patch of flame with the local normal vector directed along the -axis, and the distribution of temperature is taken along the normal to the flame. From these profiles, one can estimate the thickness of the flame and compare it with the spatial scales of turbulence. As compared to the laminar flame, the profile of temperature in the turbulent flame and its width are seen to be flatter and wider due to the effect of small-scale mass and energy transfer processes.
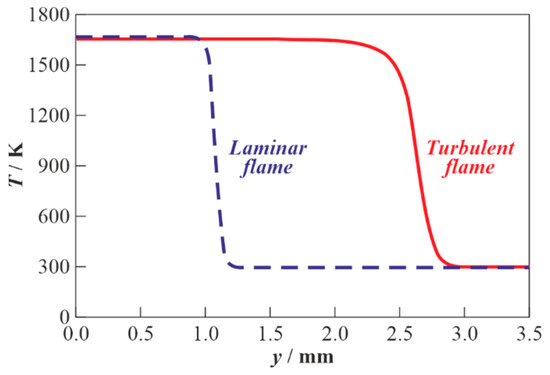
Figure 5.
Calculated profiles of temperature in turbulent and laminar flames propagating in the 17.36%vol. H2–air mixture at = 293 K, = 0.1 MPa. For the turbulent flame, = 675 cm/s, = 1 cm, and = 10 ms.
Figure 6 is an example of predicted profiles of temperature and some selected species concentrations in the turbulent flame propagating in the mixture of hydrogen with air with 17.36%vol. H2 at = 675 cm/s, = 1 cm, and = 10 ms (similar to that shown in Figure 3 and Figure 5). Despite the apparent similarity in the structures of the turbulent and laminar flames, there exist some differences. Thus, the molar fractions of active species, such as H, O, and OH, in the turbulent flame turn out to be smaller than in the laminar counterpart. This is demonstrated by the calculated dependences of the maximum molar fractions of OH in the reaction zone on the turbulence intensity for fuel-lean hydrogen–air mixtures with different hydrogen content (Figure 7). The drop in the concentration of active species is a result of increasing turbulence intensity, i.e., a result of the acceleration of mass and energy transfer processes. Such a conclusion was also made in [33] based on some indirect data.
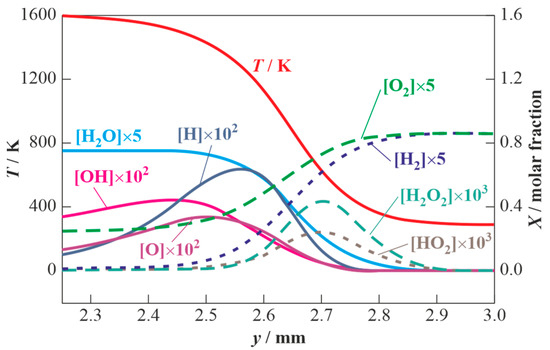
Figure 6.
Calculated profiles of temperature and some selected species in the turbulent flame propagating through the 17.36%vol. H2–air mixture at = 293 K, = 0.1 MPa, = 675 cm/s, = 1 cm, and = 10 ms.
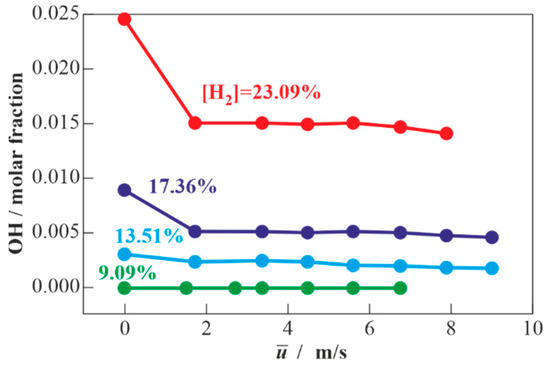
Figure 7.
Calculated dependences of the maximum hydroxyl concentration in turbulent flames on turbulence intensity for fuel-lean mixtures of hydrogen with air with different hydrogen content at = 293 K, = 0.1 MPa, = 1 cm, and = 10 ms.
3.2. Results of Calculations for Methane-Air Mixtures and Discussion
Consider now flame propagation in methane–air mixtures. A reduced block of methane oxidation reactions with 22 species and 150 forward and reverse reactions from the DRM of combustion of normal hydrocarbons [30] is used. The values of coefficients , , , , and for all species were taken from [31]. The coefficients and were obtained using the data in [32]. In contrast to the calculations for hydrogen mixtures, the calculations for methane–air mixtures additionally take into account the dependence (5) of the spatial scale on turbulence intensity . In the first approximation, the function in (5) is represented as a piecewise linear function:
The values of coefficients and for NPT conditions ( = 0.1 MPa and = 293 K) are presented in Table 1. Equation (6) was derived from the condition of the best fit between the measured and calculated values of the turbulent burning velocity in methane–air mixtures of different composition. The data in Table 1 can be approximated by the function:

Table 1.
Coefficients and for NPT conditions.
Figure 8 compares the measured and predicted dependences of the turbulent burning velocities for methane–air mixtures of different compositions on turbulence intensity . The mixture composition is given in terms of the fuel-to-air equivalence ratio . In contrast to hydrogen–air mixtures (see Figure 4), the turbulent flame in methane–air mixtures tends to decay with increasing turbulence intensity: the curves flatten and even pass through the maximum. Such a behavior of the curves is associated with the dependences (6) or (7). Interestingly, the application of Equations (6) or (7) to the calculation of turbulent flame propagation in hydrogen mixtures does not lead to any noticeable changes in the results shown in Figure 4, Figure 5, Figure 6 and Figure 7. The latter is caused by very narrow reaction zones in hydrogen–air flames, so that at the chosen turbulence intensities, small-scale mass and energy exchange processes do not lead to flame extinction yet. Flame extinction in less reactive methane–air mixtures is caused by a noticeable deceleration of chemical reactions by small-scale turbulence. Under these conditions, mass and energy exchange processes significantly reduce the concentrations of active reaction centers. In methane–air mixtures, the flame thickness is noticeably wider (Figure 9) than in hydrogen–air mixtures (see Figure 6), and the rate of the chemical process is lower. Therefore, when simulating turbulent combustion of hydrogen–air mixtures, such deceleration of chemical reactions was virtually not observed within the studied range of turbulence intensities.
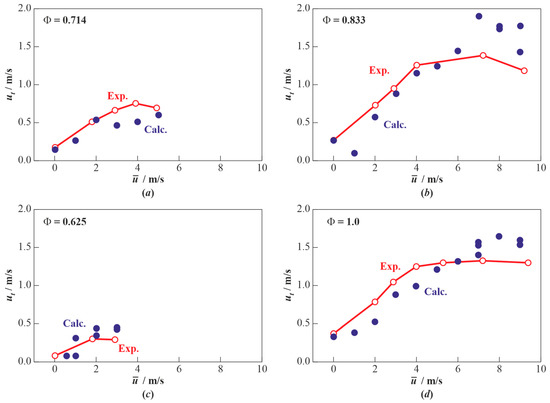
Figure 8.
Calculated (Calc.) and measured (Exp.) [14] turbulent burning velocities vs. turbulence intensity for methane–air mixtures with different : (a) 0.714, (b) 0.833, (c) 0.625, and (d) 1.0; = 293 K and = 0.1 MPa.
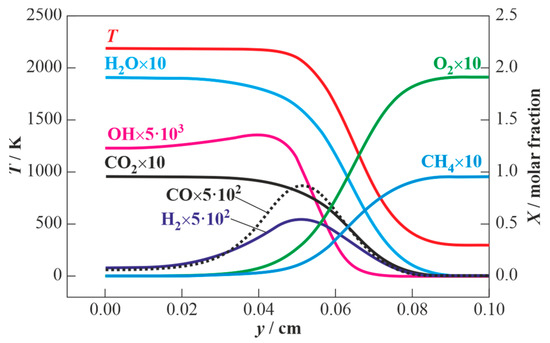
Figure 9.
Calculated profiles of temperature and some selected species in the turbulent flame propagating through the stoichiometric CH4–air mixture () at = 293 K, = 0.1 MPa, and = 400 cm/s.
Using the calculated temperature profiles, one can estimate the flame thickness and compare it with the spatial scale of turbulence. Similar to hydrogen–air mixtures, the profile of temperature in the turbulent flame is flatter and wider than in the laminar flame due to the effect of small-scale mass and energy transfer processes. This can be clearly seen from Figure 9 which demonstrates an example of predicted profiles of temperature and molar fractions of some selected species in the stoichiometric turbulent methane–air flame. Despite the similar appearances of the structures of the turbulent and laminar flame, there exist some differences. Thus, the molar fractions of active species in the turbulent flame turn out to be smaller than in the laminar counterpart. This is demonstrated by Figure 10, which shows the calculated dependence of the maximum hydroxyl molar fraction in the stoichiometric methane–air flame as a function of turbulence intensity . The drop in the concentration of OH is a consequence of increasing turbulence intensity, i.e., a result of the acceleration of mass and energy transfer processes. Such a conclusion was also made in [33] based on some indirect experimental data.
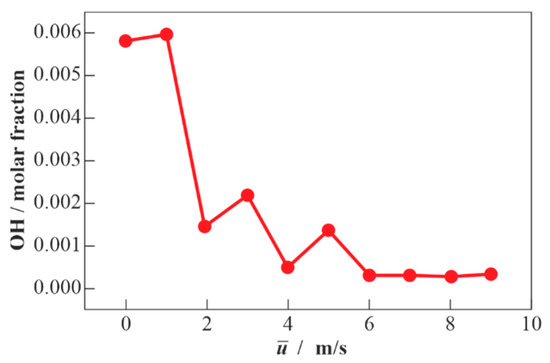
Figure 10.
The calculated maximum hydroxyl concentration in the stoichiometric methane–air turbulent flame vs. turbulence intensity at NPT conditions ( = 293 K, = 0.1 MPa).
4. Conclusions
A new approach for 3D DNS of turbulent combustion of homogeneous reacting mixtures in conditions of homogeneous, isotropic, and statistically stationary (forced) turbulence is demonstrated. The approach applies the detailed reaction mechanism of combustion of a reactive mixture. The approach is demonstrated on the calculation of turbulent flame propagation in fuel-lean and stoichiometric mixtures of hydrogen and methane with air. Calculation results are shown to agree satisfactorily with available experimental data: both in calculations and experiments, the turbulent burning velocity increases with turbulence intensity. For methane–air mixtures at a high turbulence intensity, there is a tendency for flame extinction. Calculations indicate that the “wrinkled flame” model is applicable to fuel-lean and stoichiometric hydrogen–air and methane–air mixtures at turbulence intensities up to 10 m/s. The concentrations of active species, such as H, O, and OH, in the turbulent flame are shown to be smaller than in the laminar counterpart, which also agrees with measurements. One observation is worth noting, since it is instructive for understanding the turbulent flame structure; the flame surface was always simply connected both for hydrogen and methane flames. The calculations did not reveal “pockets” of unburned mixture surrounded by combustion products, as was the case in DNS calculations [6]. Apparently, one of the possible reasons for this difference lies in the differences between the methods of simulating the turbulence field. Another reason could be the insufficiently long simulation of the process of turbulent flame propagation in the present study. This issue will be further investigated.
One of the problems of the proposed approach is the lack of a physically substantiated unambiguous mathematical relationship between the turbulence spectrum and the RMS velocity fluctuation. Having such a relationship, it would be possible to compare such a turbulence spectrum with the spectrum of synthetic turbulence used in this study.
Author Contributions
Conceptualization, V.Y.B. and S.M.F.; methodology, V.Y.B. and A.A.B.; software, A.A.B. and F.S.F.; validation, A.A.B. and F.S.F.; investigation, V.Y.B., A.A.B. and F.S.F.; resources, S.M.F.; data curation, A.A.B. and F.S.F.; writing—original draft preparation, V.Y.B. and S.M.F.; writing—review and editing, V.Y.B. and S.M.F.; supervision, S.M.F.; project administration, S.M.F.; funding acquisition, S.M.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a subsidy given to Semenov Federal Research Center for Chemical Physics of the Russian Academy of Sciences to implement the state assignments with registration numbers 122040500073-4 and 122040500068-0.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be available on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Orszag, S.A. Analytical theories of turbulence. J. Fluid Mech. 1970, 41, 363–386. [Google Scholar] [CrossRef]
- Leonard, A.D.; Hill, J.C. Direct numerical simulation of turbulent flows with chemical reaction. J. Sci. Comput. 1988, 3, 25–43. [Google Scholar] [CrossRef]
- Bell, J.B.; Day, M.S.; Grcar, J.F. Numerical simulation of premixed turbulent methane combustion. Proc. Combust. Inst. 2002, 29, 1987–1993. [Google Scholar] [CrossRef]
- Echekki, T.; Chen, J.H. Direct numerical simulation of autoignition in nonhomogeneous hydrogen–air mixtures. Combust. Flame 2003, 134, 169–191. [Google Scholar] [CrossRef]
- Bell, J.B.; Cheng, R.K.; Day, M.S.; Shepherd, I.G. Numerical simulation of Lewis number effects on lean premixed turbulent flames. Proc. Combust. Inst. 2006, 31, 1309–1317. [Google Scholar] [CrossRef]
- Aspden, A.J.; Day, M.S.; Bell, J.B. Three-dimensional direct numerical simulation of turbulent lean premixed methane combustion with detailed kinetics. Combust. Flame 2016, 166, 266–283. [Google Scholar] [CrossRef]
- Lamioni, R.; Lapenna, P.E.; Berger, L.; Kleinheinz, K.; Attili, A.; Pitsch, H.; Creta, F. Pressure-induced hydrodynamic instability in premixed methane-air slot flames. Combust. Sci. Techn. 2020, 192, 1998–2009. [Google Scholar] [CrossRef]
- Lapenna, P.E.; Lamioni, R.; Creta, F. Subgrid modeling of intrinsic instabilities in premixed flame propagation. Proc. Combust. Inst. 2021, 38, 2001–2011. [Google Scholar] [CrossRef]
- Trisjono, P.; Pitsch, H. Systematic analysis strategies for the development of combustion models from DNS: A review. Flow Turbul. Combust 2015, 95, 231–259. [Google Scholar] [CrossRef]
- Driscoll, J.F.; Chen, J.H.; Skiba, A.W.; Carter, C.D.; Hawkes, E.R.; Wang, H. Premixed flames subjected to extreme turbulence: Some questions and recent answers. Prog. Energy Combust. Sci. 2020, 76, 100802. [Google Scholar] [CrossRef]
- Domingo, P.; Vervisch, L. Recent developments in DNS of turbulent combustion. Proc. Combust. Inst. 2022, in press. [Google Scholar] [CrossRef]
- Da Silva, C.B.; Malico, I.; Coelho, P.J. Radiation statistics in homogeneous isotropic turbulence. New J. Phys. 2009, 11, 093001. [Google Scholar] [CrossRef]
- Basevich, V.Y.; Volodin, V.P.; Kogarko, S.M.; Peregudov, N.I. Calculations of turbulent flame in two-dimensional approximation. Khim. Fiz. 1982, 1, 1130–1137. [Google Scholar]
- Karpov, V.P.; Severin, E.S. Effects of molecular transport coefficients on the rate of turbulent combustion. Combust. Explos. Shock Waves 1980, 16, 41–46. [Google Scholar] [CrossRef]
- Bradley, D.; Lawes, M.; Mansour, M.S. Correlation of turbulent burning velocities of ethanol–air, measured in a fan-stirred bomb up to 1.2 MPa. Combust. Flame 2011, 158, 123–138. [Google Scholar] [CrossRef]
- Kobayashi, H. Experimental study of high-pressure turbulent premixed flames. Exp. Therm. Fluid Sci. 2002, 26, 375–387. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Diffusion by a random velocity field. Phys. Fluids 1970, 13, 22–31. [Google Scholar] [CrossRef]
- Heinz, S. A review of hybrid RANS-LES methods for turbulent flows: Concepts and applications. Prog. Aerosp. Sci. 2020, 114, 100597. [Google Scholar] [CrossRef]
- Basevich, V.Y.; Belyaev, A.A.; Frolov, S.M.; Basara, B. Direct numerical simulation of turbulent combustion of gases in two-dimensional approximation. Combust. Explos. 2017, 10, 4–10. [Google Scholar]
- Basevich, V.Y.; Belyaev, A.A.; Frolov, S.M.; Frolov, F.S. Direct numerical simulation of turbulent combustion of hydrogen–air mixtures of various compositions in a two-dimensional approximation. Russ. J. Phys. Chem. B 2019, 13, 75–85. [Google Scholar] [CrossRef]
- Frolov, S.M.; Ivanov, V.S.; Basara, B.; Suffa, M. Numerical simulation of flame propagation and localized preflame autoignition in enclosures. J. Loss Prev. Process Ind. 2013, 26, 302–309. [Google Scholar] [CrossRef]
- Zimont, V.L. Theory of turbulent combustion of a homogeneous fuel mixture at high Reynolds numbers. Combust. Explos. Shock Waves 1979, 15, 305–311. [Google Scholar] [CrossRef]
- Guelder, Ö.L. Turbulent premixed flame propagation models for different combustion engines. Proc. Comb. Inst. 1990, 23, 743–750. [Google Scholar] [CrossRef]
- Bradley, D. How fast can we burn? Proc. Combust. Inst. 1992, 24, 247–253. [Google Scholar] [CrossRef]
- Peters, N. The turbulent burning velocity for large scale and small-scale turbulence. J. Fluid Mech. 1999, 384, 107–132. [Google Scholar] [CrossRef]
- Williams, F.A. The Combustion Theory; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Loitsyanskii, L.G. Mechanics of Liquids and Gases; Drofa Publs: Moscow, Russia, 2003. [Google Scholar]
- Godunov, S.K.; Ryaben’kiy, V.S. Finite-Difference Schemes; Nauka: Moscow, Russia, 1977. [Google Scholar]
- Douglas, J.; Rachford, H.H. On the numerical solution of heat conduction problems in two and three space variables. Trans. Amer. Math. Soc. 1956, 82, 421–439. [Google Scholar] [CrossRef]
- Basevich, V.Y.; Belyaev, A.A.; Posvyanskii, V.S.; Frolov, S.M. Mechanisms of the oxidation and combustion of normal paraffin hydrocarbons: Transition from C1–C10 to C11–C16. Russ. J. Phys. Chem. B 2013, 7, 161–169. [Google Scholar] [CrossRef]
- Burcat, A. Ideal Gas Thermodynamic Data in Polynomial Form for Combustion and Air Pollution Use. Lab. Chem. Kinetics. Available online: http://garfield.chem.elte.hu/Burcat/burcat.html (accessed on 15 January 2023).
- Reid, C.; Prausnitz, J.; Sherwood, T. The Properties of Gases and Liquids, 3rd ed.; McGraw Hill: London, UK, 1977. [Google Scholar]
- Basevich, V.Y.; Kogarko, S.M. Hydrocarbon formation in turbulent combustion of a methane–air mixture. Combust. Explos. Shock Waves 1985, 21, 514–518. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).