Refinement of the Heuristic Solution for the Problem of TE-Polarized Electromagnetic Wave Diffraction on a Half-Plane with Two-Sided Impedance Boundary Conditions

Abstract

A technique for obtaining refined heuristic solutions for problems with electromagnetic wave diffraction by scatterers with non-ideal boundary conditions is proposed. Based on the method of fundamental components for the problem of TE-polarized wave diffraction on a “semitransparent” half-plane with two-sided impedance boundary conditions, an improved heuristic solution for the scattered field is obtained by replacing the primary heuristic formula. A quantitative and qualitative assessment of the accuracy of the heuristic relationship is carried out as well as a physical interpretation of the rigorous solution based upon them. A classification of heuristic solutions is proposed according to the purpose of their application in practical problems.

1. Introduction

The construction of heuristic formulas for various diffraction problems is a topical task. The problem is that for many diffraction problems, obtaining rigorous analytical solutions is a long and laborious task, the ultimate success of which is not guaranteed.

Unlike rigorous analytical formulas, heuristic formulas are based not on the mathematical formulation of the problem, but on knowledge of the physical features of the diffraction process. Heuristic formulas are needed to increase the performance of solvers designed to study the resource-intensive problems of diffraction, the physical interpretation of numerical solutions, the refinement of numerical solutions that differ from experimental data as a result of the inaccurate formulation of the problem, etc. Traditional heuristic methods such as the method of edge waves (MEW) and the geometric theory of diffraction (GTD) are widely known [1,2,3].

All heuristic formulas are verified at the stage of creation for all values of their input parameters. By verification, we mean a comparison with a reliable solution, usually a numerical one. In the process of verification, the limits of the application of heuristic formulas and their accuracy are established. Later on, heuristic formulas are employed without verification.

Traditional heuristic methods are based on field behavior postulates and have inherent methodological errors [4,5] that can lead to a lack of accuracy.

Recently, the method of fundamental components (MFC) has been developed [4,5]. Along with verification, in contrast to the traditional heuristic methods of GTD and MEW, MFC involves an adjustment procedure (correction of primary heuristic formulas based on the results of verification). The adjustment procedure minimizes the inherent methodological error and allows the provision of a predetermined accuracy needed for solving a given practical problem in the entire range of parameters.

MFC consists of three stages:

• Obtaining a verification solution.
• Construction of primary heuristic formulas.
• Construction of tuning formulas.

With the possibility of performing two stages (1) and (2) (see above), the MFC approach is suitable for any type of boundary conditions and allows one to obtain heuristic formulas that can be used in solvers instead of numerical solutions.

The physical meaning of the technique used in MFC is that we single out the factors that have the greatest influence on the solution (singularities and the coefficient of reflection from an unbounded surface R), and introduce them into the primary heuristic formulas. Then, during the adjustment process, we obtain additional expressions that affect the accuracy and add them to the final heuristic formulas. Additional expressions may have a physical meaning and describe the features of the scatterer that are not taken into account in the primary heuristic formulas, or can simply be a mathematical correction that increases the accuracy of the solution. As a result, we obtain a refined heuristic analytical solution that can be used in the solver of a practical problem instead of a numerical one.

If, as in GTD and MEW, unaccounted physical factors are determined in advance, formalized, and limited to this, then the resulting expressions, as a rule, contain an inherent methodological error leading to inaccurate solutions and may need further clarification if this is required by the interests of a practical problem.

Heuristic formulas for a half-plane with nonideal boundary conditions can be built based on a combination of well-known GTD and MEW solutions for a perfectly conducting half-plane with reflection and transmission coefficients for an unbounded surface. The use of heuristic formulas instead of numerical solutions is a topical line of research. Performance improvement is especially effective in multiple calculations. Works [6,7,8,9,10] are based on the use of ready-made numerical–analytical solutions; refinement can be obtained by reducing the solution to a form that satisfies the reciprocity principle. However, the calculations made by the final heuristic formulas still differ from the verification solution.

The purpose of this work is to improve the technique for working with numerical solutions of reference problems, in particular, to find a way of improving accuracy, and not to obtain a specific engineering formula for specific boundary conditions and a specific practical problem. This article refines the solution at the edges of the range of angles by switching to another primary heuristic formula.

The statement of the problem in this work is to find heuristic expressions for diffraction on semitransparent objects that could be used in solvers instead of a numerical solution to increase performance. Such a problem is relevant when a numerical solution requires significant computer resources. The technique for obtaining a heuristic solution can be applied to translucent objects with different properties. In this work, in order to demonstrate the effectiveness of the applied technique, a half-plane with two-sided impedance boundary conditions is chosen as a semitransparent object [11,12,13]. To solve the problem of diffraction on a semitransparent half-plane, S.E. Bankov [14,15] created a numerical solution based on the formulation of the diffraction problem, formulated independently of the earlier works of T.B.A. Senior [16].

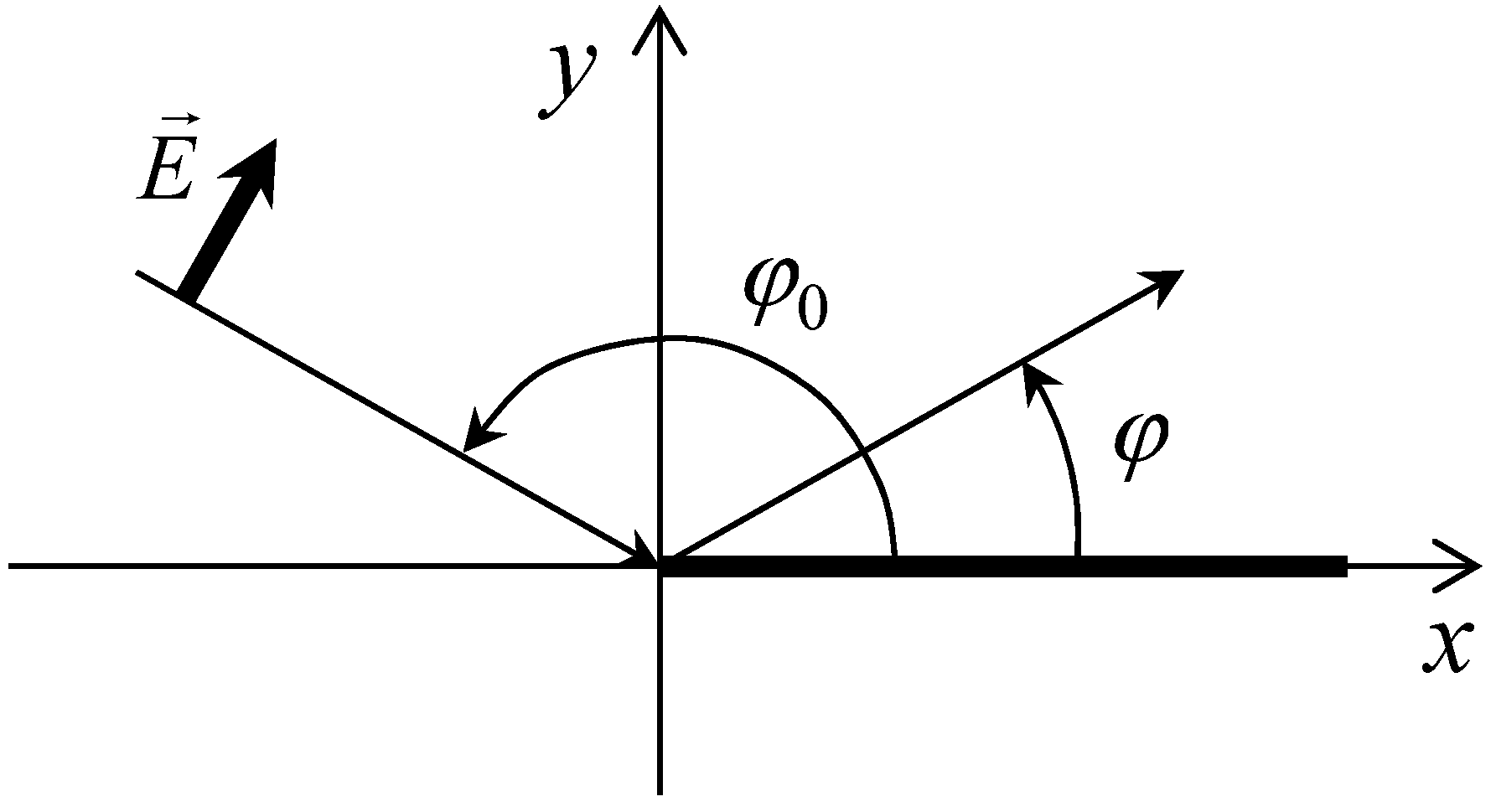
2. Boundary Conditions for the TE Polarization

Two-sided impedance boundary conditions for the case of TE-polarized electromagnetic wave diffraction on a half-plane (sometimes such a half-plane is called “semitransparent”) have the form [14,15,17]:

$$\left\{\begin{array}{l}Z\left(H_{z+}-H_{z-}\right)=E_x\\ E_{x+}=E_{x-}=E_x\hspace{0.33em}\mathrm{w}hen\hspace{0.33em}y=0\end{array}\right.,$$

(1)

where impedance Z = iX, X is a variable parameter on which the reflection coefficient depends, and i is an imaginary unit. Here, the signs “+” and “−” correspond to the regions y > 0 and y < 0, respectively (see Figure 1).

Figure 1 shows the geometry of a two-dimensional diffraction problem for the normal incidence of a TE-polarized electromagnetic wave on the edge of a semitransparent half-plane.

Two-sided impedance boundary conditions have existed in diffraction theory for quite a long time [11,12,13,17]. They should not be confused with the Schukin–Leontovich impedance boundary conditions at the interface between two media. Two-sided impedance boundary conditions are written for a half-plane that has no physical thickness but is characterized by impedance—a proportionality coefficient between the amplitudes of electric and magnetic fields, which is included in the mathematical expressions for these boundary conditions.

Real physical objects for which two-sided impedance boundary conditions can be applied include metal gratings and thin films, including those made of resistive material. Such structures are used to obtain antennas with desired characteristics [17,18].

3. Numerical Solution and Analytical Formulas

A rigorous approach [14] based on the Wiener–Hopf method (WHM) [19,20] makes it possible to find a verification solution (“WHM solution”):

$$gr\left(X,\varphi ,{\varphi }_0\right).$$

(2)

Introducing the parameters (X, φ, φ₀) into the calculation program for the WHM, we obtain the values of the solution gr(X, φ, φ₀) (2), which we will further use to verify the heuristic solutions. In the first stage, the verification solution (2) does not have a compact analytical form, and our task is to find an analytical heuristic formula that could be employed instead of (2) in practical problems.

If the boundary conditions (1) are satisfied on the unbounded half-plane, then the reflection and transmission coefficients R and T can be found:

$$R\left(X,{\varphi }_0\right)=\frac{W_0}{W_0+2i{\left[\sin \left({\varphi }_0\right)\right]}^{-1}X}, W_0=120\pi ,$$

(3)

$$T\left(X,{\varphi }_0\right)=1-R\left(X,{\varphi }_0\right).$$

(4)

4. Primary Heuristic Formulas

Primary heuristic formulas for describing the solution of the diffraction problem for a TE-polarized field on a “semitransparent” half-plane with two-sided impedance boundary conditions (1) have the form [5,15,21,22,23]:

$$gf\left(R,T,\varphi ,{\varphi }_0\right)=\frac{1}{2}\left(\frac{1-T}{-\cos \frac{\varphi -{\varphi }_0}{2}}+\frac{R}{-\cos \frac{\varphi +{\varphi }_0}{2}}\right),$$

(5)

$$g{f}^0\left(R,T,\varphi ,{\varphi }_0\right)=\frac{1}{2}\left[\left(1-T\right)\frac{\sin \frac{\varphi -{\varphi }_0}{2}}{-\cos \frac{\varphi -{\varphi }_0}{2}}+R\frac{\sin \frac{\varphi +{\varphi }_0}{2}}{-\cos \frac{\varphi +{\varphi }_0}{2}}\right].$$

(6)

Here, R and T are the reflection and transmission coefficients for a flat unbounded surface (3) and (4). A similar form of heuristic solutions was used in [6,7,8,9,10,15,21,22,23,24,25].

Primary heuristic formulas (5) and (6) are combinations of reflection and transmission coefficients for a flat unbounded surface R and T and singular diffraction coefficients for a perfectly conducting half-plane [1,4,5,22]. Primary heuristic formulas describing solutions to diffraction problems on a semitransparent and nontransparent half-plane for a TH-polarized field are given in [5,21,26]. It should be noted that the primary heuristic formulas for a semitransparent or nontransparent half-plane are significantly different. The adjustment functions and the physical interpretation of the results differ in the same way. Primary heuristic formulas can be obtained both from a rigorous solution of the two-dimensional problem of diffraction using a perfectly conducting half-plane and from the solution of the same problem in the approximation of physical optics. Let us call them, respectively, the generalized diffraction coefficient (GDC) (5) and the generalized diffraction coefficient in the approximation of physical optics (PODC) (6) [4,5,15,21,22,23]. The ODC approximation has been known in diffraction theory for a long time [24,25]. However, its accuracy for a specific statement of the problem can be established only in the process of verification.

The verification solution gr(X, φ, φ₀) (2) is constructed in such a way that it can be compared with the singular diffraction coefficients GDC (5) and PODC (6). From relationships (3) and (4) it follows that at the point X = 0: R = 1, T = 0, and the relationship gf(R, T, φ, φ₀) = gr(X, φ, φ₀) holds for all angles φ, φ₀. Therefore, the WHM solution coincides with the corresponding solution (5), which in this case gives a rigorous solution to the problem.

For the implementation of the MFC algorithm, it is not critical whether we have analytical expressions for R and T. If necessary, they can be taken in the form of numerical solutions, especially when the edge profile and the reflecting surface have a complex structure and there are no analytical solutions. The important thing is that we apply a unified approach to all tasks in which we use R and T.

5. Obtaining Heuristic Formulas Employing the Adjustment Process

The study of the WHM solution gr(X, φ, φ₀) (2) at 0 < X < ∞ (see, for example, [15,21,22,23]) showed that for small values of the “transparency” parameter X, the WHM solution (2) behaves like the GDC (5), and for large values of X, the WHM solution (2) behaves like the PODC (6). Taking into account the influence of the parameter X on the solution, we can introduce a new concept of “adjustment function” cxg(X, φ) and approximately describe it employing the phenomenological formula:

$$cxg\left(X,\varphi \right)={\left[\sin \left(\frac{\varphi }{2}\right)\right]}^{x\left(X\right)}, x\left(X\right)=1-\exp \left(-\frac{X}{W_0}\right).$$

(7)

Here, x(X) is a function of the parameter X (not to be confused with the x coordinate axis). As X→0 we have x(X)→0 and cxg(X, φ)→1. As X→∞, we have: x(X)→1 and cxg(X, φ)→sin(φ/2).

Employing (5) and (7), we can construct a heuristic formula gh(R, T, φ, φ₀):

$$gh\left(R,T,\varphi ,{\varphi }_0\right)=gf\left(R,T,\varphi ,{\varphi }_0\right)\frac{cxg\left(X,\varphi \right)}{cxg\left(X,{\varphi }_s\right)}.$$

(8)

The formula for gh(R, T, φ, φ₀) (8), which describes the behavior of the WHM solution better than each of the individual diffraction coefficients GDC (5) or PODC (6), is the desired heuristic approximation of the MFC and can be used in practical applications instead of the WHM solution gr(X, φ, φ₀) (2). Formula (7) can be included in the list of fundamental components along with (5), (6), (3), (4), etc. [5]. It should be noted that the form of the fundamental component (7), if necessary, can be changed according to the accuracy required to solve a specific practical problem.

The physical meaning of Formula (8) is that the function gh(R, T, φ, φ₀) changes when g→g⁰ as the parameter X increases.

The results of the calculation employing the WHM solution gr(X, φ, φ₀) (2) and heuristic formulas (8), (5), and (6) are shown in Figure 2.

Figure 2. The scattering diagrams (SD) modules for X = 300, x(X) = 0.549, and φ₀ = 90 are plotted along the vertical axis. Circles—GDC (5), triangles—PODC (6), solid gray line—WHM solution gr(X,φ,φ₀) (2), and squares—heuristic solution gh(R, T, φ, φ₀) (8).

Figure 2. The scattering diagrams (SD) modules for X = 300, x(X) = 0.549, and φ₀ = 90 are plotted along the vertical axis. Circles—GDC (5), triangles—PODC (6), solid gray line—WHM solution gr(X,φ,φ₀) (2), and squares—heuristic solution gh(R, T, φ, φ₀) (8).

In Figure 2, the modules of the scattering diagrams of the WHM solution gr(X, φ, φ₀) (2), the heuristic solution gh(R, T, φ, φ₀) (8), the GDC (5), and the PODC (6) are plotted along the vertical axis. The WHM solution moves between the GDC and the PODC, and the heuristic solution moves along with the WHM solution.

6. Qualitative Evaluation of Accuracy

Let us compare the scattering diagram of the WHM solution gr(X, φ, φ₀) for the case of the incidence of a TE-polarized electromagnetic wave on a semitransparent half-plane at 0 < X < ∞ with the expressions (3) and (4) substituted into approximate solutions for GDC (5) and PODC (6). Let us introduce a qualitative criterion for estimating the accuracy of approximate solutions in the form of modules for the ratios of amplitudes in the WHM solution (2) and heuristic approximations GDC (5), PODC (6), and MFC (8), respectively:

$$ag\left(R,T,\varphi ,{\varphi }_0\right)=\left|\frac{gr\left(X,\varphi ,{\varphi }_0\right)}{gf\left(R,T,\varphi ,{\varphi }_0\right)}\right|,$$

(9)

$$a{g}^0\left(R,T,\varphi ,{\varphi }_0\right)=\left|\frac{gr\left(X,\varphi ,{\varphi }_0\right)}{g{f}^0\left(R,T,\varphi ,{\varphi }_0\right)}\right|,$$

(10)

$$ah\left(R,T,\varphi ,{\varphi }_0\right)=\left|\frac{gr\left(X,\varphi ,{\varphi }_0\right)}{gh\left(R,T,\varphi ,{\varphi }_0\right)}\right|.$$

(11)

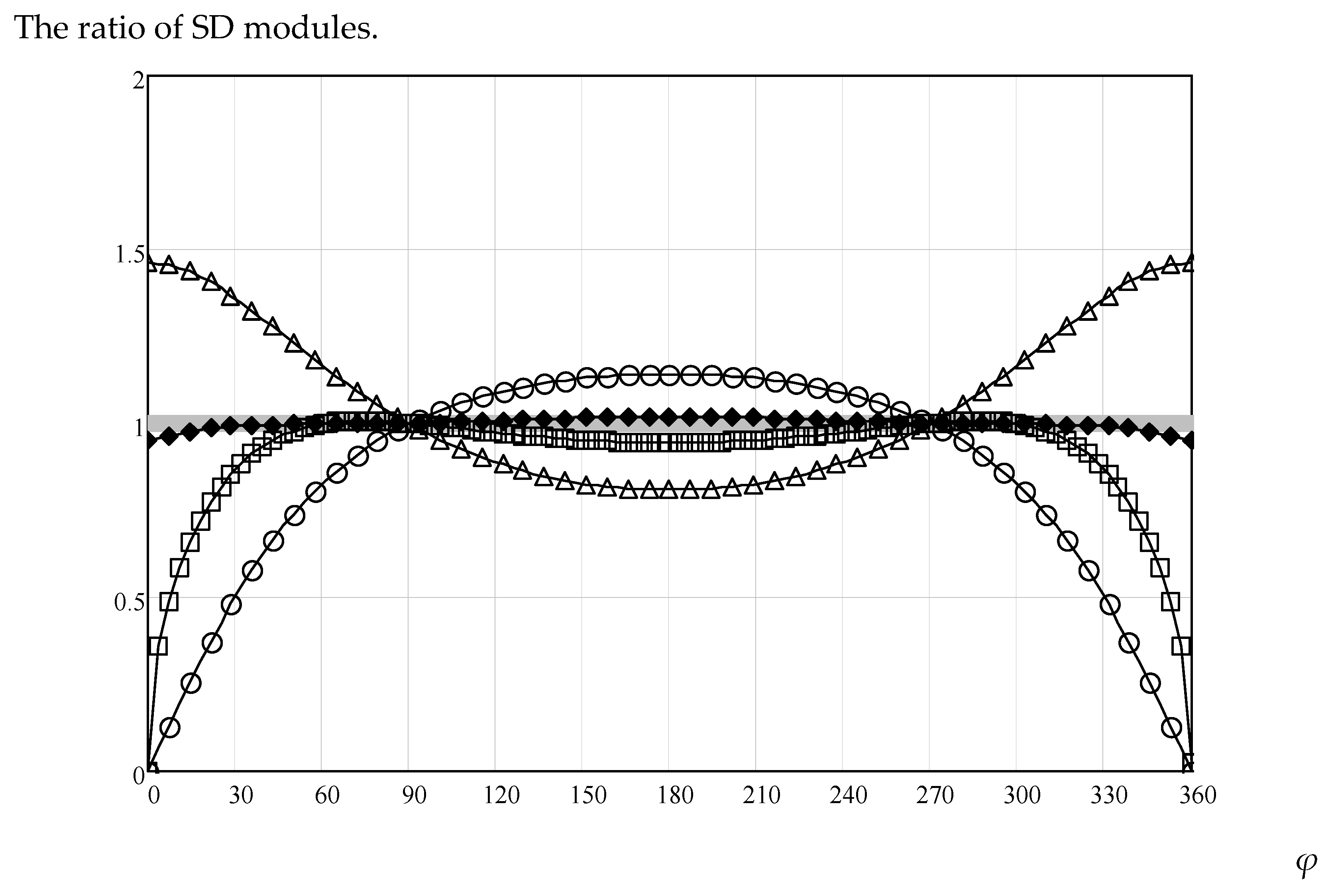
In the case of the best coincidence of one of the solutions with the WHM solution gr(X, φ, φ₀) (2), the corresponding function (9)–(11) is located closer than the others with respect to the straight line on which the modulus of the amplitude ratio is equal to one.

The results of the heuristic formula calculations (9)–(11) are shown in Figure 3.

Figure 3 shows amplitude ratio modules for ag(R, T, φ, φ₀) (9), ag⁰(R, T, φ, φ₀) (10), and ah(R, T, φ, φ₀) (11).

Figure 3. The ratios of the scattering diagram modules. The ratios of the scattering diagram (SD) modules for X = 300, x(X) = 0.549, and φ₀ = 90 are plotted vertically. Circles—ag(R, T, φ, φ₀) (9), triangles—ag⁰(R, T, φ, φ₀) (10), squares—ah(R, T, φ, φ₀) (11), and diamonds—ah⁰(R, T, φ, φ₀) (14).

Figure 3. The ratios of the scattering diagram modules. The ratios of the scattering diagram (SD) modules for X = 300, x(X) = 0.549, and φ₀ = 90 are plotted vertically. Circles—ag(R, T, φ, φ₀) (9), triangles—ag⁰(R, T, φ, φ₀) (10), squares—ah(R, T, φ, φ₀) (11), and diamonds—ah⁰(R, T, φ, φ₀) (14).

7. Adjustment Function for PODC

Formulas (1)–(11) were given in [15]. As a disadvantage of the MFC formula (8), one can note a reduced accuracy at the edges of the zone of observed angle change (Figure 3).

When analyzing Figure 3, the idea arises that, based on PODC, the heuristic formula can be tuned more accurately at the edges. The ratio ag(R, T, φ, φ₀) (9) has a drop to zero at the edges of the angular range, while the ratio ag⁰(R, T, φ, φ₀) (10) does not have such a drop. This can make it possible to more accurately select the parameters of the heuristic formula.

Let us build a new heuristic solution no longer based on the GDC (5), but on the basis of the PODC (6). To do this, we find a new “adjustment function” cxg⁰(X, φ). As necessary, we employ the technique of constructing engineering formulas employing phenomenological digital coefficients.

As the initial formula for constructing the “adjustment function” cxg⁰(X, φ), we take the expression $\cos \left\{\varphi /p\left[x\left(X\right)\right]\right\}$. Next, we subject this expression to a series of transformations, choosing the size of the curve in height, the vertical and horizontal offsets, and the form of the dependence p[x(X)], which changes the periodicity of the original function with respect to the angle φ.

In addition, it is necessary to maintain the equality 1 for the “adjustment function” at the singularity points φ_s of expressions (5) and (6) (the angles φ_s = π ± φ₀ correspond to the directions “straight ahead” and “mirror reflection”, see Figure 1), since at these points, the values of GDC and PODC are the same—they give the correct value for the scattered field, and no correction is required. The set of selected parameters should provide the best match between the heuristic formula and the WHM solution (2). As a result, we obtain a phenomenological heuristic function cxg⁰(X, φ), which gives the best match for the vast majority of x(X) values and other parameters:

$$g{h}^0\left(R,T,\varphi ,{\varphi }_0\right)=g{f}^0\left(R,T,\varphi ,{\varphi }_0\right)\frac{cx{g}^0\left(X,{\varphi }_s\right)}{cx{g}^0\left(X,\varphi \right)},$$

(12)

where

$$\begin{gathered} \frac{cx{g}^0\left(X,{\varphi }_s\right)}{cx{g}^0\left(X,\varphi \right)}=\frac{\cos \left(\frac{{\varphi }_s}{p\left[x\left(X\right)\right]}\right)-12+12p\left[0.85-x\left(X\right)\right]}{\cos \left(\frac{\varphi }{p\left[x\left(X\right)\right]}\right)-12+12p\left[0.85-x\left(X\right)\right]}, \\ p\left[x\left(X\right)\right]=0.52+\frac{2}{1+\sqrt{10x\left(X\right)}}. \end{gathered}$$

(13)

The amplitude ratio modulus (see item 5) for formula (12):

$$a{h}^0\left(R,T,\varphi ,{\varphi }_0\right)=\left|\frac{gr\left(\varphi ,{\varphi }_0\right)}{g{h}^0\left(R,T,\varphi ,{\varphi }_0\right)}\right|.$$

(14)

The results of the calculation from Formula (14) are also shown in Figure 3. It can be seen from the graphs that the heuristic solution ah⁰(R, T, φ, φ₀) (14) gives the best accuracy with respect to the WHM solution since it is located closer than others relative to the unit line.

8. Classification of Heuristic Solutions

The MFC diffraction coefficient (8) can be considered a physically clear simplified form and used for the physical interpretation of the verification solution. For example, in this work, employing a relatively simple expression for the “adjustment function” (8), one can approximately trace the nature of the transformation of the singular diffraction coefficient GDC (5) into the PODC (6) as the parameter X changes from 0 to ∞.

The problem of physical interpretation can also arise when, as a result of a simplified formulation of the problem, a mathematically rigorous solution diverges from the experimental results.

There are practical tasks in which, for example, it is required to increase the performance of a resource-intensive solver. Then accuracy is more important than physical clarity, and one can rely more on phenomenological engineering approaches, complicate heuristic expressions, and apply adjustment formulas such as (13).

9. Quantification of Accuracy

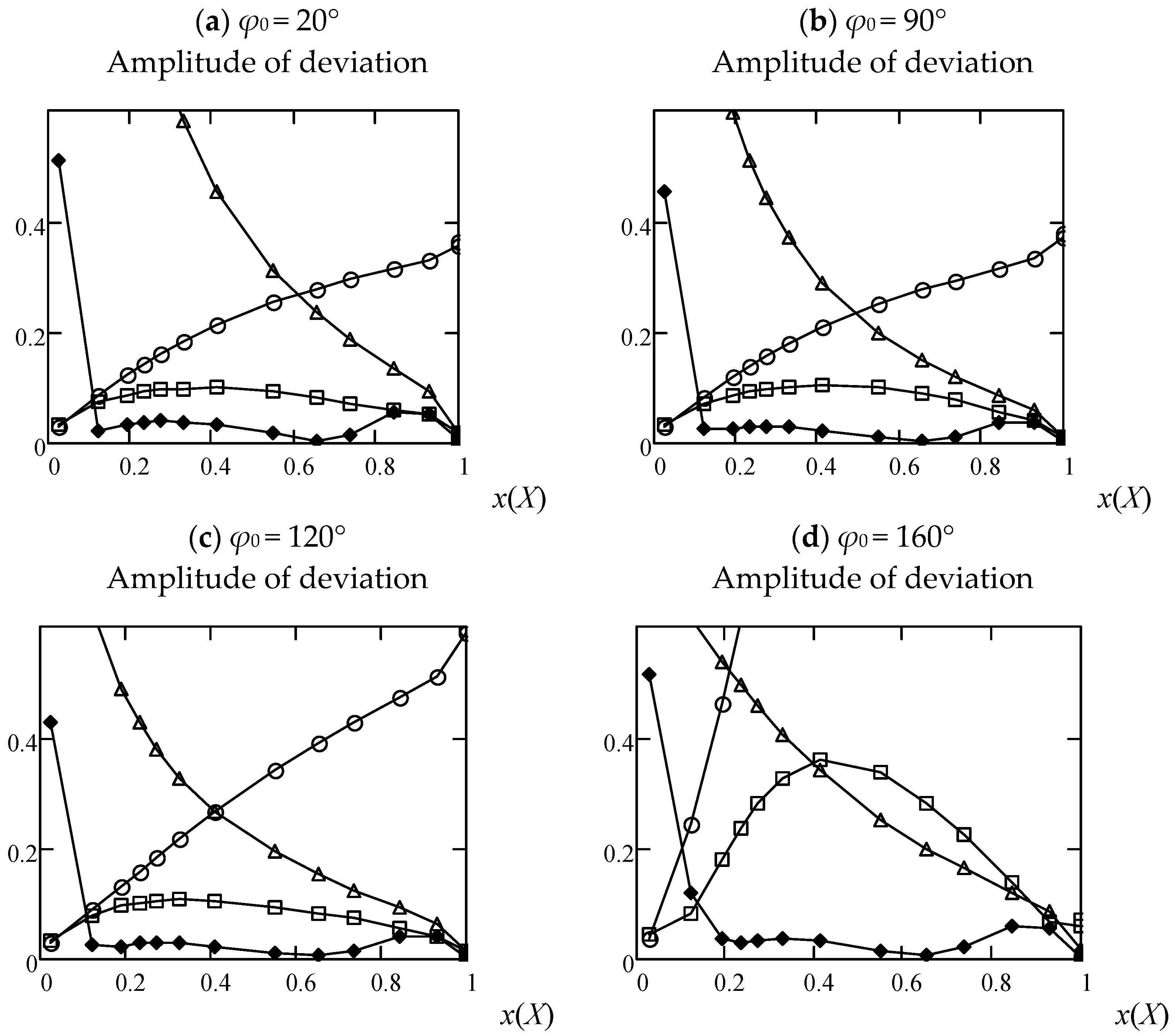
A graphical comparison of amplitude ratios (Figure 3) is a qualitative way to evaluate accuracy. We introduce a quantitative criterion for estimating accuracy in the form of an integral over the area of change in the observation angle φ. The integrand will be the average deviation from the unity of the absolute values of the ratios of the amplitudes of the WHM solution (2) and qualitative evaluation criteria according to the GDC (9), PODC (10), MFC (11), and (14), respectively:

$$Dg\left(R,T,\varphi ,{\varphi }_0\right)=\frac{1}{2\pi }{\displaystyle \underset{\varphi =0}{\overset{2\pi }{\int }}\left|ag\left(R,T,\varphi ,{\varphi }_0\right)-1\right|d\varphi },$$

(15)

$$D{g}^0\left(R,T,\varphi ,{\varphi }_0\right)=\frac{1}{2\pi }{\displaystyle \underset{\varphi =0}{\overset{2\pi }{\int }}\left|a{g}^0\left(R,T,\varphi ,{\varphi }_0\right)-1\right|d\varphi },$$

(16)

$$Dh\left(R,T,\varphi ,{\varphi }_0\right)=\frac{1}{2\pi }{\displaystyle \underset{\varphi =0}{\overset{2\pi }{\int }}\left|ah\left(R,T,\varphi ,{\varphi }_0\right)-1\right|d\varphi },$$

(17)

$$D{h}^0\left(R,T,\varphi ,{\varphi }_0\right)=\frac{1}{2\pi }{\displaystyle \underset{\varphi =0}{\overset{2\pi }{\int }}\left|a{h}^0\left(R,T,\varphi ,{\varphi }_0\right)-1\right|d\varphi }.$$

(18)

The smaller the value of any of these integrals, the greater the accuracy of the corresponding approximation. Graphs of the values of the integrals for the MFC, GDC, and PODC approximations depending on the value of x(X) are shown in Figure 4.

It follows from the graphs of the average deviation that the best agreement with the WHM solution is given by the approximations MFC and (14). For small values of X (in this case x(X)~0), the GDC approximation is also close to the WHM solution, and for large values of X (with x(X)~1), the PODC approximation is closer to the WHM solution. When incident from the side of the end, when scattering occurs at small “grazing” angles to the half-plane, the accuracy of the coincidence of the MFC approximation with the WHM solution deteriorates. It follows that this case needs to be considered more carefully. It is possible that in the case of a three-dimensional structure of finite size, the MFC approximations (8) and (12) will work equally well in all directions; however, this assumption needs to be checked separately.

10. Reasons for Decreasing the Accuracy of the Solution Based on Physical Optics for Some Values of x(X)

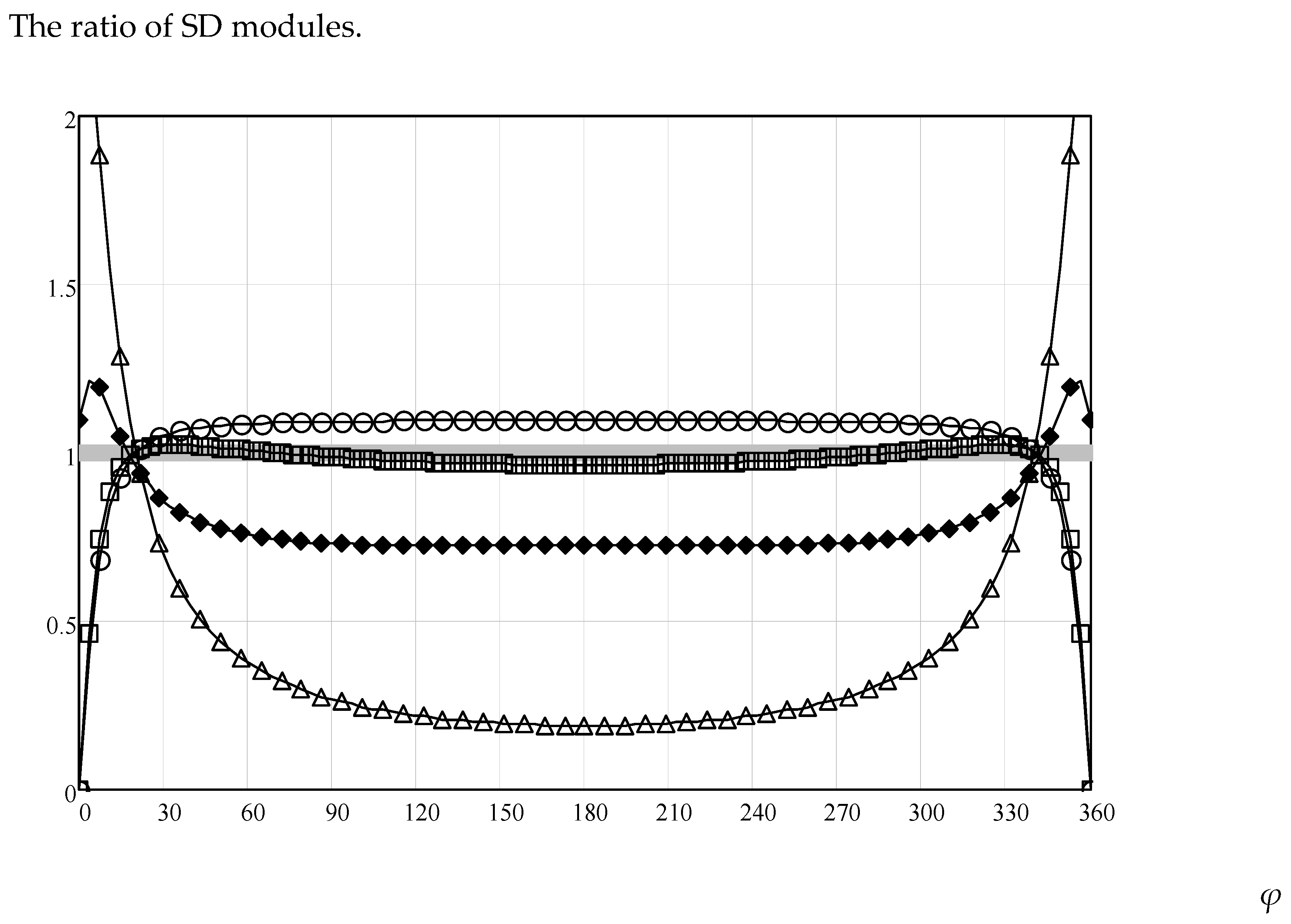
Let us try to understand the reasons for the decrease in the accuracy of solution (12) for small x(X) (see Figure 4). Figure 5 shows the ratios of the modules of scattering diagrams (SD) for X = 30, x(X) = 0.076, and φ₀ = 160°, corresponding to the situation when approximation (12) has a large error Dh⁰(R, T, φ, φ₀) (18) (see Figure 4).

Figure 5. The ratios of the scattering diagram modules. The ratios of the scattering diagram (SD) modules for X = 30, x(X) = 0.076, and φ₀ = 160º are plotted along the vertical axis. Circles—GDC (9), triangles—PODC (10), squares—ah(R, T, φ, φ₀) (11), and diamonds—ah⁰(R, T, φ, φ₀) (14).

Figure 5. The ratios of the scattering diagram modules. The ratios of the scattering diagram (SD) modules for X = 30, x(X) = 0.076, and φ₀ = 160º are plotted along the vertical axis. Circles—GDC (9), triangles—PODC (10), squares—ah(R, T, φ, φ₀) (11), and diamonds—ah⁰(R, T, φ, φ₀) (14).

Observing the behavior of the graph of the function ah⁰(R, T, φ, φ₀) (14) shown in Figure 5, it can be seen that its deviation from the unit line is caused by the imposition of the equality condition 1 at the singularity points. Therefore, to improve the accuracy, it is necessary to either complicate the expression corresponding to the formulas gh⁰(R, T, φ, φ₀) (12) and cxg⁰(X, φ) (13) or simply use another function for small x(X), for example, the MFC expression corresponding to the formulas gh(R, T, φ, φ₀) (8) and cxg(X, φ) (7).

11. Discussion of the Results

The purpose of this paper is not to study certain types of boundary conditions, but to develop a specific heuristic approach for the method of fundamental components [4,5]. This article demonstrates the possibility of increasing the accuracy of the heuristic solution by replacing the primary heuristic formula with another one that has a useful property (nonzero values at the ends of the angle range). Therefore, only one polarization is considered and there is no detailed comparison with other analytical approaches; this does not matter for the heuristic technique. On the other hand, a quantitative comparison with the results of calculations employing other heuristic approaches is given. The result of this paper is a heuristic solution of increased accuracy.

When constructing a heuristic formula employing the MFC, it is important to correctly choose the main points of the solution: (A) the primary heuristic formula; (B) the type of correction function (e.g., additive or multiplicative); and (C) the location of the phenomenological adjustment factors, etc. All of these steps should be performed based on solutions to the simplest problems, experience, and physical intuition.

In the process of constructing heuristic formulas, one can act in two ways. The first way is to first determine the unaccounted-for physical features, and then write an addition to the primary formula. An example of such an approach is an MEW containing an additive, namely, Ufimtsev’s edge currents. The second way is to first find the discrepancy between the primary heuristic formula and the verification solution, and then determine the physical meaning of this discrepancy. An example of such an approach is the MFC containing a factor—an adjustment function. The determination of the physical meaning of the discrepancy with the verification solution may require some time and additional research; this is a common situation for such science as physics.

Strict analytical solutions are not required to build heuristic formulas for MFC, which is a certain advantage that gives MFC flexibility and versatility compared to other approaches. Unlike well-known heuristic approaches (for example, GTD and MEW, which use analytical solutions), this method allows one to obtain heuristic formulas as a result of verification and adjustment procedures based on numerical solutions. In fairness, it should be noted that there are hybrid methods (which also do not require strict analytical formulas) that combine the MEW and numerical approaches. Hybrid methods, just like numerical ones, require an application package.

The traditional heuristic approaches GTD and MEW are based on “postulates” that require a priori assumptions and a certain sequence of actions to obtain a heuristic solution. A priori assumptions, such as “the field on a curved edge is the same as on a straight edge”, on one hand, make it easier to obtain a solution, but on the other hand, create a laid-down methodological error.

Unlike traditional heuristic methods, the MFC approach is not based on postulates but in comparison with a verification solution. Depending on the task, the heuristic formulas of the MFC can be different. More complex and accurate heuristic formulas are better suited for use in solvers instead of a numerical reference problem calculator. Simpler and more physically clear heuristic formulas are better suited for the physical interpretation of the numerical calculation results. If the numerical verification solution differs from the experimental data (for example, due to inaccuracies in the mathematical formulation of the problem), it is possible to adjust the heuristic formulas according to the experimental results.

First, the researcher must make a “strategic” decision about which type of heuristic formula is best suited for a given practical problem. Then, one can proceed to “tactical” actions: choose the most physically clear primary heuristic formula for the “adjustment function”, carry out an adjustment procedure employing an engineering formula with phenomenological coefficients (as in this work), or interpolate with splines, or construct a solution based on the primary formula, which satisfies the principle of reciprocity. A specific formula can be developed manually, as well as employing standard programs such as Wolfram Mathematica.

Primary heuristic formulas have a clear physical meaning. If you choose them correctly, as well as the type of adjustment formula, then an adjustment will be easy. Previously, the GDC approximation was chosen as the primary heuristic formula. In this article, approximation PODC is chosen and an adjustment function containing adjustment coefficients is added to it. These coefficients were found phenomenologically, employing a numerical procedure to ensure the minimum discrepancy between the verification solution and the heuristic function. As a result, the accuracy of the heuristic solution increased significantly, which was shown by quantitative evaluation.

As already mentioned, heuristic solutions are obtained based on physical considerations, which may be different. Therefore, for the same statement of the problem, several different heuristic solutions can be constructed. Usually, by saying “exact heuristic solution”, one of the following options is meant:

• This heuristic solution is more accurate than other known heuristic solutions;
• This heuristic solution has an accuracy that meets the requirements of the practical problem to which it is applied.

In some cases when employing the MFC, it is possible to obtain a very accurate heuristic analytical solution [27], but this does not detract from the results of this work since the described technique can be applied to a wider class of problems.

As is known, heuristic approaches are highly efficient and widely used. In particular, the issue of replacing numerical solutions with heuristic ones in solving practical problems is topical. Heuristic solutions for wedge diffraction with impedance boundary conditions [28] were obtained in [6,7,8,9]. The Malyuzhinets function is calculated for a rather long time, so obtaining heuristic solutions significantly speeds up the calculation. An exact match with the verification solution was not obtained, but the agreement with the experimental results was satisfactory [9].

Impedance boundary conditions [28] are formulated at the interface between two media. When solving the problem of diffraction on bodies with such boundary conditions, the penetration of a wave into a conducting medium is neglected and is limited to taking into account reflection; for diffraction by a scatterer with impedance boundary conditions T = 0, 0 < |R| < 1 [6,7,8,9].

Two-sided impedance boundary conditions on the half-plane lead to the fact that the field can pass through, 0 < |T| < 1. When T = 0 from (4), it follows that R = 1. Thus, the boundary conditions in this article are different from the impedance boundary conditions.

12. Conclusions

This article presents a technique for improving the accuracy of the solution by replacing the primary heuristic formula with another that does not have features at the boundaries of the range of angles. For the “adjustment function,” a formula containing phenomenological numerical coefficients is obtained. The technique has been tested on a certain types of boundary conditions and for the corresponding verification solution, but there is every reason to believe that it will work in other cases as well.

A quantitative comparison for the accuracy of MFC solutions showed that the accuracy of formula (12) obtained employing engineering methods, as expected, turned out to be higher than the accuracy of formulas (5), (6), and (8). It can be additionally increased, if necessary, for the purposes of a specific practical task. In some areas with a significant deviation of the “improved” curves, one can switch to the old solutions.