A Model Predictive Control-Based Decision-Making Strategy for Residential Microgrids
Abstract
:1. Introduction
2. Problem Statement
- The number of dwellings and their electricity and heat profiles for the prediction horizon
- Electricity and gas tariff prices, prices for selling excess electricity
- Allocation and capacity of DER technologies
- Storage capacities
- Initial values for all state variables
- The electricity and heat generation profiles for each individual dwelling within the network
- The heat transferred between dwellings through the pipeline network
- The electricity transferred between the dwellings and between the dwelling and the grid
2.1. Mathematical Model
2.1.1. Objective Function
2.1.2. Supply–Demand Relationships
2.1.3. Grid Interaction Constraints
2.1.4. CHP Unit
2.1.5. Back-Up Boiler
2.1.6. Heat Storage Tank
2.1.7. Electricity Storage
2.2. Illustrative Example
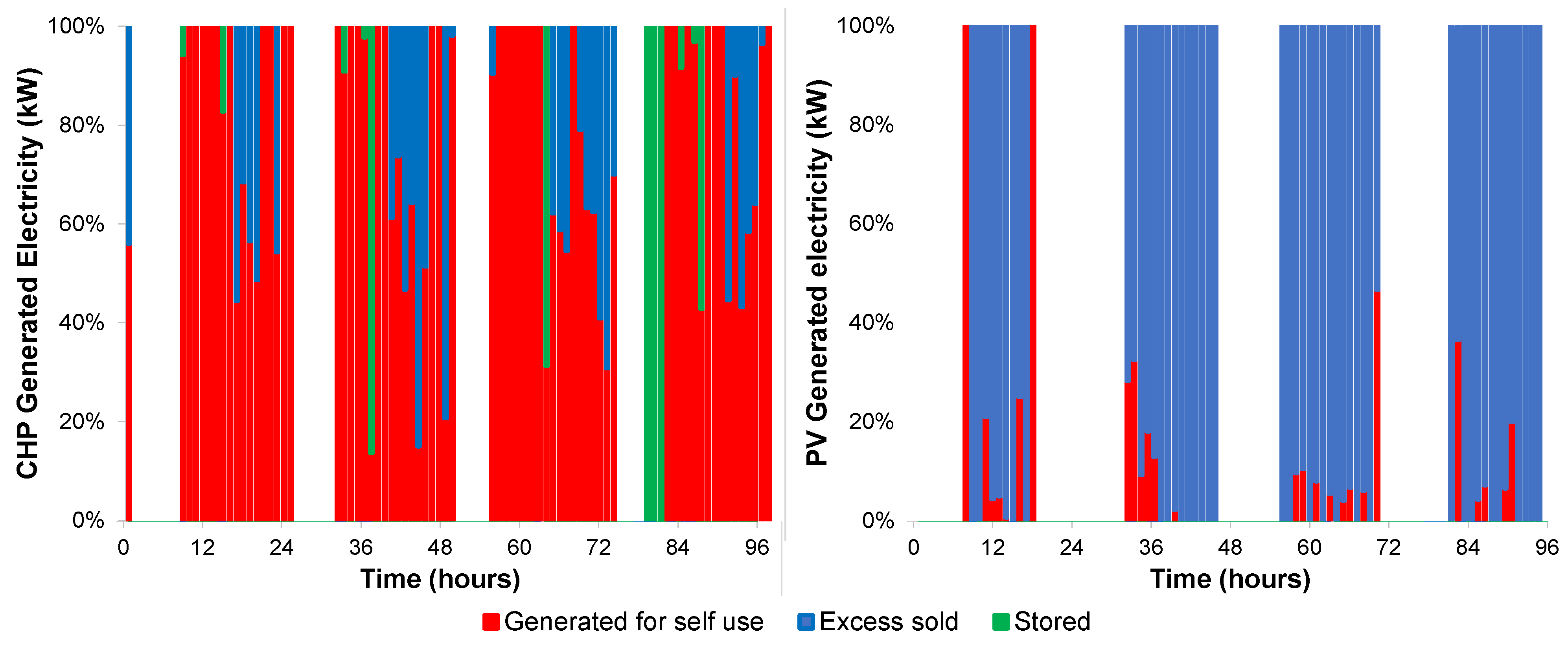
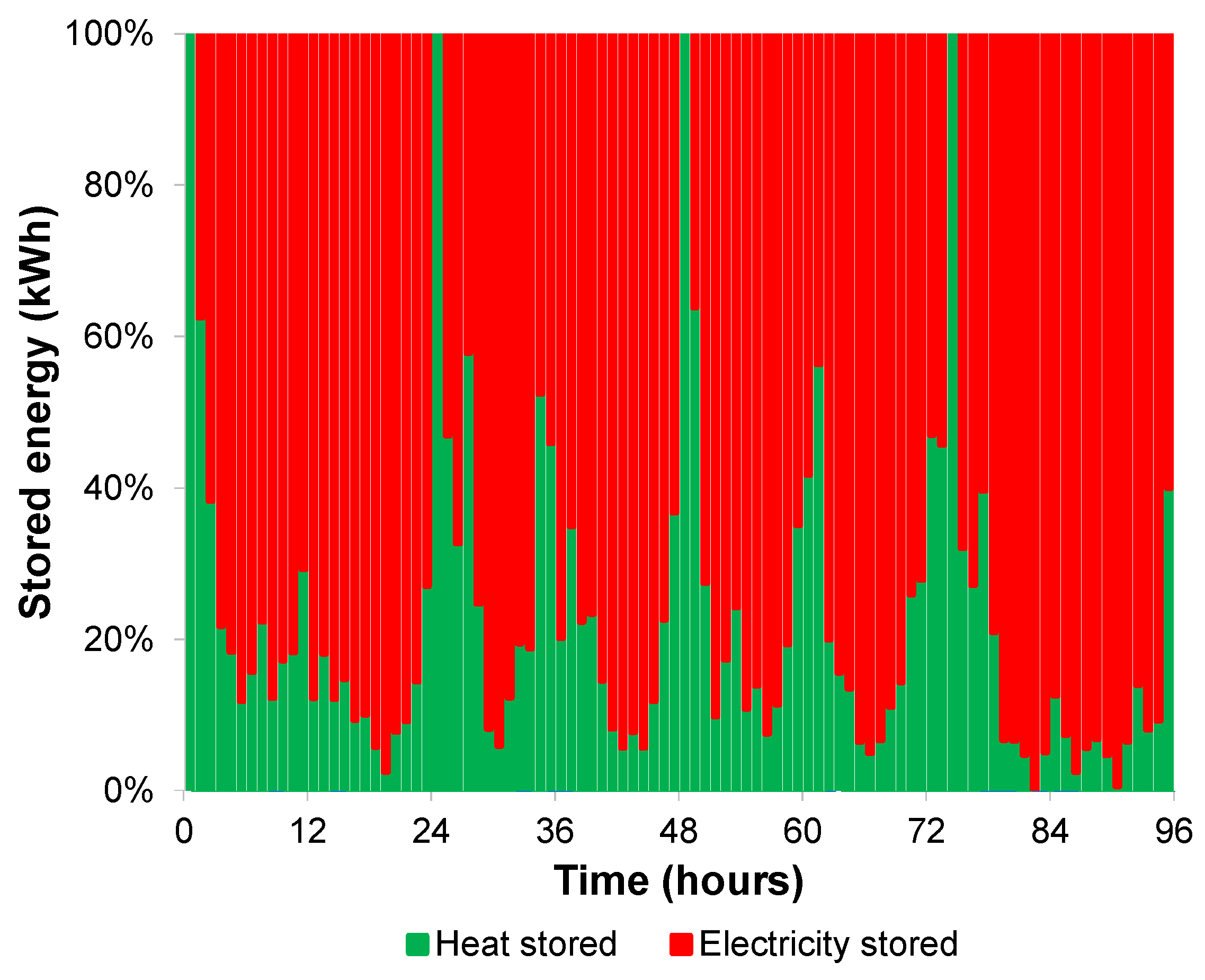
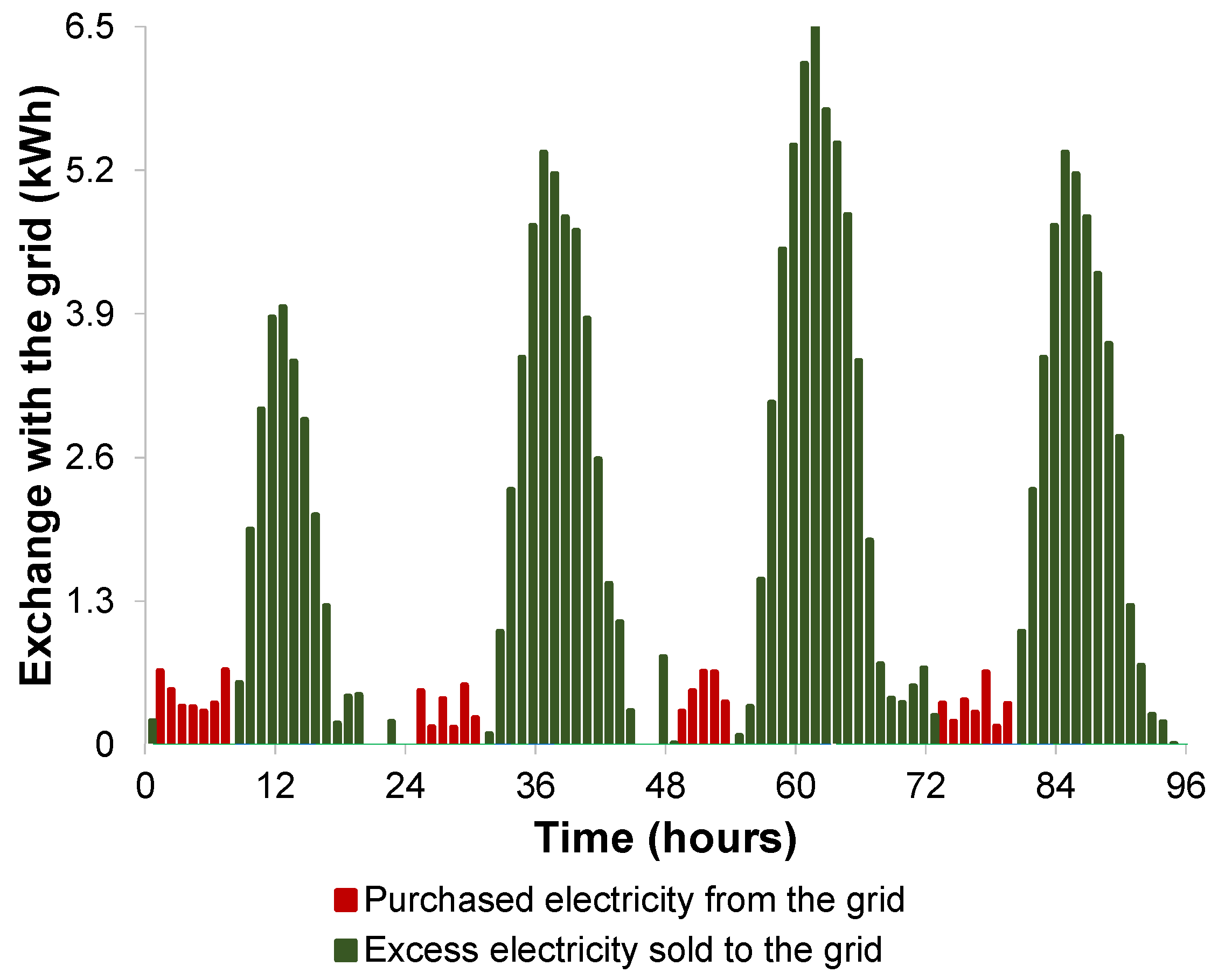
3. Results and Discussion
- (a)
- An integrated microgrid with no central electricity storage
- (b)
- An integrated microgrid case with central electricity storage.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Specification of Cost Terms
| PV investment cost (EUR) | |
| Boiler investment cost (EUR) | |
| CHP investment cost (EUR) | |
| Operational and maintenance cost of PV (EUR/year) | |
| Operational and maintenance cost of boiler (EUR/year) | |
| Operational and maintenance cost of CHP (EUR/year) | |
| Total cost for purchased electricity (EUR/year) | |
| Total environmental cost (EUR/year) | |
| Income from selling electricity to the grid (EUR/year) |
Appendix B. Input Data
| Natural gas price (EUR/kWh) | 0.054 | |
| Interest rate | 0.075 | |
| Carbon intensity of electricity (kg CO2/kWh electricity) | 0.781 | |
| Carbon tax of CO2 (EUR/kg CO2) | 0.017 | |
| Carbon intensity of natural gas (kg CO2/kWh natural gas) | 0.184 | |
| Regulated tariff for electricity purchases (EUR/kWh) | 0.11 | |
| Capital cost of PV (EUR/kW) | 4140 | |
| Capital cost of boiler (EUR/kW) | 100 | |
| Project lifetime (years) | 20 | |
| Electrical efficiency of the PV unit | 0.12 | |
| Thermal efficiency of the boiler | 0.80 | |
| Price of selling excess electricity from PV unit (EUR/kWh) | 0.55 | |
| Price of selling excess electricity from CHP unit (EUR/kWh) | 0.0875 | |
| Capital cost of the heat storage tank (EUR/kW) | 25 | |
| Heat loss coefficient of the heat storage tank (kWh lost/hour) | 0 | |
| Operational and maintenance cost of the heat storage tank (EUR/kWh) | 0.001 | |
| Capital cost of the electricity storage tank (EUR/kW) | 415 | |
| Operational and maintenance cost of the electricity storage tank (EUR/kWh) | 0.01 | |
| Charge loss of the lead-acid battery | 0.10 | |
| Discharge loss of the lead-acid battery | 0.15 |
Appendix C. Binary Variables
| 1 if dwelling may sell excess electricity to the grid at period ; 0 if it may buy from the grid | |
| 1 if the CHP unit in dwelling is in operation during period ; 0 otherwise | |
| 1 if the CHP unit in dwelling shuts down in period ; 0 otherwise | |
| 1 if the CHP unit in dwelling starts up in period ; 0 otherwise | |
| 1 if the CHP unit in dwelling is in operation by still in start-up mode during period ; 0 otherwise |
References
- Qi, W.; Liu, J.; Christofides, P.D. Distributed supervisory predictive control of distributed wind and solar energy systems. IEEE Trans. Control Syst. Technol. 2013, 21, 504–512. [Google Scholar] [CrossRef]
- Eltigani, D.; Masri, S. Challenges of integrating renewable energy sources to smart grids: A review. Renew. Sustain. Energy Rev. 2015, 52, 770–780. [Google Scholar] [CrossRef]
- Kakran, S.; Chanana, S. Smart operations of smart grids integrated with distributed generation: A review. Renew. Sustain. Energy Rev. 2018, 81, 524–535. [Google Scholar] [CrossRef]
- Farmanbar, M.; Parham, K.; Arild, Ø.; Rong, C. A widespread review of smart grids towards smart cities. Energies 2019, 12, 4484. [Google Scholar] [CrossRef] [Green Version]
- Dileep, G. A survey on smart grid technologies and applications. Renew. Energy 2020, 146, 2589–2625. [Google Scholar] [CrossRef]
- Akorede, M.F.; Hizam, H.; Pouresmaeil, E. Distributed energy Resources and benefits to the environment. Renew. Sustain. Energy Rev. 2010, 14, 724–734. [Google Scholar] [CrossRef]
- Allan, G.; Eromenko, I.; Gilmartin, M.; Kochar, I.; McGregor, P. The economics of distributed energy generation: A literature review. Renew. Sustain. Energy Rev. 2015, 42, 543–556. [Google Scholar] [CrossRef] [Green Version]
- Obi, M.; Slay, T.; Bass, R. Distributed energy resource aggregation using customer owned-equipment: A review of literature and standards. Energy Rep. 2020, 6, 2358–2369. [Google Scholar] [CrossRef]
- Asrari, A.; Ansari, M.; Khazaei, J.; Fajri, P.; Amini, M.H.; Ramos, B. The impacts of a decision making framework on distribution network reconfiguration. IEEE Trans. Sustain. Energy 2021, 12, 634–645. [Google Scholar] [CrossRef]
- Rangu, S.K.; Lolla, P.R.; Dhenuvakonda, K.R.; Singh, A.R. Recent trends in power management strategies for optimal operation of distributed energy resources in microgrids: A comprehensive review. Int. J. Energy Res. 2020, 44, 9889–9911. [Google Scholar] [CrossRef]
- Li, S.; Pan, Y.; Xu, P.; Zhang, N. A decentralized peer-to-peer control scheme for heating and cooling trading in distributed energy systems. J. Clean. Prod. 2021, 285, 124817. [Google Scholar] [CrossRef]
- Tooryan, F.; HassanzadehFard, H.; Collins, E.R.; Jin, S.; Ramezani, B. Smart integration of renewable energy resources, electrical, and thermal energy storage in microgrid applications. Energy 2020, 212, 118716. [Google Scholar] [CrossRef]
- Rezkallah, M.; Chandra, A.; Ibrahim, H.; Feger, Z.; Aissa, M. Control systems for hybrid energy systems. In Hybrid Renewable Energy Systems and Microgrids; Academic Press: Cambridge, MA, USA, 2021; pp. 373–397. [Google Scholar] [CrossRef]
- Khan, M.W.; Wang, J.; Xiong, L. Optimal energy scheduling strategy for multi-energy generation grid using multi-agent systems. Int. J. Electr. Power Energy Syst. 2021, 124, 106400. [Google Scholar] [CrossRef]
- Wolsink, M. Distributed energy systems as common goods: Socio-political acceptance of renewables in intelligent microgrids. Renew. Sustain. Energy Rev. 2020, 127, 109841. [Google Scholar] [CrossRef]
- Rahman, H.A.; Majid, M.S.; Jordehi, A.R.; Gan, C.K.; Hassan, M.Y.; Fadhl, S.O. Operation and control strategies of integrated distributed energy resources: A review. Renew. Sustain. Energy Rev. 2015, 51, 1412–1420. [Google Scholar] [CrossRef]
- Hou, J.; Wang, J.; Zhou, Y.; Lu, X. Distributed energy systems: Multi-objective optimization and evaluation under different operational strategies. J. Clean. Prod. 2021, 280, 124050. [Google Scholar] [CrossRef]
- Muhanji, S.; Muzhikyan, A.; Farid, A.M. Long-term challenges for future electricity markets with distributed energy resources. In Smart Grid Control; Stoustroup, J., Annaswamy, A., Chakrabortty, A., Qu, Z., Eds.; Power Electronics and Power Systems; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Zhang, Y.; Wang, J.; Li, Z. Uncertainty modeling of distributed energy resources: Techniques and challenges. Curr. Sustain./Renew. Energy Rep. 2019, 6, 42–51. [Google Scholar] [CrossRef]
- Söderman, J.; Pettersson, F. Structural and operational optimisation of distributed energy systems. Appl. Therm. Eng. 2006, 26, 1400–1408. [Google Scholar] [CrossRef]
- Weber, C.; Shah, N. Optimisation based design of a district energy system for an eco-town in the United Kingdom. Energy 2011, 36, 1292–1308. [Google Scholar] [CrossRef]
- Mechleri, E.D.; Sarimveis, H.; Markatos, N.C.; Papageourgiou, L.G. Optimal design and operation of distributed energy systems: Application to Greek residential sector. Renew. Energy 2013, 51, 331–342. [Google Scholar] [CrossRef]
- Morvaj, B.; Evins, R.; Carmeliet, J. Optimization framework for distributed energy systems with integrated electrical grid constraints. Appl. Energy 2016, 171, 296–313. [Google Scholar] [CrossRef]
- Karmellos, M.; Mavrotas, G. Multi-objective optimization and comparison framework for the design of distributed energy systems. Energy Convers. Manag. 2019, 180, 473–495. [Google Scholar] [CrossRef]
- Yan, Y.; Yan, J.; Song, M.; Zhou, X.; Zhang, H.; Liang, Y. Design and optimal sitting of regional heat-gas-renewable energy system based on building clusters. Energy Convers. Manag. 2020, 217, 112963. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy 2018, 222, 1033–1055. [Google Scholar] [CrossRef]
- Choudhury, S. A comprehensive review on issues, investigations, control and protection trends, technical challenges and future directions for microgrid technology. Int. Trans. Electr. Energy Syst. 2020, 30, e12446. [Google Scholar] [CrossRef]
- Tomin, N.; Shakirov, V.; Kozlov, A.; Sidorov, D.; Kurbatsky, V.; Rehtanz, C.; Lora, E.E.S. Design and optimal energy management of community microgrids with flexible renewable energy sources. Renew. Energy 2022, 183, 903–921. [Google Scholar] [CrossRef]
- Morstyn, T.; Hredzak, B.; Agelidis, V.G. Control Strategies for microgrids with distributed energy storage systems: An overview. IEEE Trans. Smart Grid 2018, 9, 3652–3666. [Google Scholar] [CrossRef] [Green Version]
- Nikam, V.; Kalkhambkar, V. A review on control strategies for microgrids with distributed energy resources, energy storage systems, and electric vehicles. Int. Trans. Electr. Energy Syst. 2020, 31, e12607. [Google Scholar] [CrossRef]
- Grosspietch, D.; Saenger, M.; Girod, B. Matching decentralized energy production and local consumption: A review of renewable energy systems with conversion and storage technologies. WIREs Energy Environ. 2019, 8, e336. [Google Scholar] [CrossRef]
- Abazari, A.; Monsef, H.; Wu, B. Coordination strategies of distributed energy resources including FESS, DEG, FC, WTG in load frequency control (LFC) scheme of isolated micro-grid. Int. J. Electr. Power Energy Syst. 2019, 109, 535–547. [Google Scholar] [CrossRef]
- Quadri, I.A.; Bhowmick, S.; Joshi, D. A comprehensive technique for optimal allocation of distributed energy resources in radial distribution systems. Appl. Energy 2018, 211, 1245–1260. [Google Scholar] [CrossRef]
- Houwing, M.; Negenborn, R.P.; De Schutter, B. Demand response with micro-CHP systems. Proc. IEEE 2010, 99, 200–213. [Google Scholar] [CrossRef] [Green Version]
- Halvgaard, R.; Vandenberghe, L.; Poulsen, N.K.; Madsen, H.; Jørgensen, J.B. Distributed model predictive control for smart energy systems. IEEE Trans. Smart Grid 2016, 7, 1675–1682. [Google Scholar] [CrossRef]
- Sultan, Y.A.; Kaddah, S.S.; Elhosseini, M.A. Enhancing the performance of smart grid using model predictive control. Mansoura Eng. J. 2017, 42, 1–9. [Google Scholar] [CrossRef]
- Harder, N.; Qussous, R.; Weidlich, A. The cost of providing operational flexibility from distributed energy resources. Appl. Energy 2020, 279, 115784. [Google Scholar] [CrossRef]
- Sarimveis, H.; Patrinos, P.; Tarantilis, C.D.; Kiranoudis, C.T. Dynamic modelling and control of supply chain systems: A review. Comput. Oper. Res. 2008, 35, 3530–3561. [Google Scholar] [CrossRef]
- Garcia-Tirado, J.; Corbett, J.P.; Boiroux, D.; Jørgensen, J.B.; Breton, M.D. Closed-loop control with announced exercise for adults with type 1 diabetes using the ensemble model predictive control. J. Process Control 2019, 80, 202–210. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Ierapetritou, M. Rolling horizon based planning and scheduling integration with production capacity consideration. Chem. Eng. Sci. 2010, 65, 5887–5900. [Google Scholar] [CrossRef]
- Wang, X.; Palazoglu, A.; El-Farra, N.H. Operational optimization and demand response of hybrid renewable energy systems. Appl. Energy 2015, 143, 324–335. [Google Scholar] [CrossRef]
- Mechleri, E.D.; Papageorgiou, L.G.; Markatos, N.C.; Sarimveis, H. A model predictive control framework for residential microgrids. Comput. Aided Chem. Eng. 2012, 30, 327–331. [Google Scholar] [CrossRef]
- Balaras, C.A.; Dascalacki, E.G.; Droutsa, K.G.; Kontoyiannidis, S. Empirical assessment of calculated and actual heating energy use in Hellenic residential buildings. Appl. Energy 2016, 164, 115–132. [Google Scholar] [CrossRef]
- Brooke, A.; Kendrick, D.; Meeraus, A.; Raman, R. GAMS—A User’s Guide; GAMS Development Corporation: Washington, DC, USA, 2008. [Google Scholar]
- Sidnell, T.; Dorneanu, B.; Mechleri, E.; Vassiliadis, V.S.; Arellano-Garcia, H. Effects of dynamic pricing on the design and operation of distributed energy resource networks. Processes 2021, 9, 1306. [Google Scholar] [CrossRef]
- Gabrielli, P.; Gazzani, M.; Martelly, E.; Mazzotti, M. Optimal design of multi-energy systems with seasonal storage. Appl. Energy 2018, 219, 408–424. [Google Scholar] [CrossRef]
- Mitterutzner, B.; Sanz, W.; Nord, L.O. A part-load analysis and control strategies for the Graz Cycle. Int. J. Greenh. Gas Control 2022, 113, 103521. [Google Scholar] [CrossRef]
- Karamov, D.N.; Sidorov, D.N.; Muftahov, I.R.; Zhukov, A.V.; Liu, F. Optimization of isolated power systems with renewables and storage batteries based on nonlinear Volterra models for the specially protected natural area of Lake Baikal. J. Phys. Conf. Ser. 2020, 1847, 012037. [Google Scholar] [CrossRef]
- Teichgraeber, H.; Lindenmeyer, C.P.; Baumgärtner, N.; Kotzur, L.; Stolten, D.; Robinius, M.; Bardow, A.; Brandt, A.R. Extreme events in time series aggregation: A case study for optimal residential supply systems. Appl. Energy 2020, 275, 115223. [Google Scholar] [CrossRef]
- Zatti, M.; Gabba, M.; Freschini, M.; Rossi, M.; Gambarotta, A.; Morini, M.; Martelly, E. k-MILP: A novel clustering approach to select typical and extreme days for multi-energy systems design optimization. Energy 2019, 181, 1051–1063. [Google Scholar] [CrossRef]
- Sidnell, T.; Clarke, F.; Dorneanu, B.; Mechleri, E.; Arellano-Garcia, H. Optimal design and operation of distributed energy resources systems for residential neghbourhoods. Smart Energy 2021, 4, 100049. [Google Scholar] [CrossRef]
- Clarke, F.; Dorneanu, B.; Mechleri, E.; Arellano-Garcia, H. Optimal design of heating and cooling pipeline networks for residential distributed energy systems. Energy 2021, 235, 121430. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, H. Exploring blockchain for the coordination of distributed energy resources. In Proceedings of the 2021 55th Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 24–26 March 2021; pp. 1–6. [Google Scholar] [CrossRef]



| Solar Irradiance (kW) | p1 | p2 | p3 | p4 | p5 | p6 |
|---|---|---|---|---|---|---|
| Winter | 0.006 | 0.230 | 0.481 | 0.333 | 0.006 | 0 |
| Summer | 0.013 | 0.270 | 0.515 | 0.574 | 0.143 | 0.002 |
| Mid-season | 0.037 | 0.333 | 0.536 | 0.421 | 0.123 | 0 |
| Heat Load (kW) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i1 | p1 | p2 | p3 | p4 | p5 | p6 | i6 | p1 | p2 | p3 | p4 | p5 | p6 |
| s1 | 23.02 | 4.61 | 2.21 | 7.66 | 22.14 | 28.08 | s1 | 16.58 | 13.84 | 4.42 | 5.47 | 25.83 | 46.80 |
| s2 | 0 | 0 | 0 | 0 | 0 | 0 | s2 | 0 | 0 | 0 | 0 | 0 | 0 |
| s3 | 31.10 | 1.72 | 6.55 | 1.49 | 8.15 | 28.11 | s3 | 2.49 | 1.72 | 8.85 | 3.58 | 24.44 | 20.08 |
| i2 | p1 | p2 | p3 | p4 | p5 | p6 | i7 | p1 | p2 | p3 | p4 | p5 | p6 |
| s1 | 36.83 | 22.83 | 2.21 | 2.95 | 2.95 | 23.40 | s1 | 46.04 | 22.14 | 4.42 | 4.81 | 23.61 | 4.68 |
| s2 | 0 | 0 | 0 | 0 | 0 | 0 | s2 | 0 | 0 | 0 | 0 | 0 | 0 |
| s3 | 12.44 | 3.78 | 0.82 | 0.50 | 26.07 | 10.84 | s3 | 26.12 | 10.32 | 0.98 | 4.48 | 14.66 | 6.42 |
| i3 | p1 | p2 | p3 | p4 | p5 | p6 | i8 | p1 | p2 | p3 | p4 | p5 | p6 |
| s1 | 33.15 | 16.60 | 1.21 | 12.03 | 26.57 | 15.44 | s1 | 41.44 | 18.68 | 1.10 | 10.83 | 29.52 | 33.70 |
| s2 | 0 | 0 | 0 | 0 | 0 | 0 | s2 | 0 | 0 | 0 | 0 | 0 | 0 |
| s3 | 27.99 | 6.19 | 4.42 | 3.13 | 2.99 | 24.09 | s3 | 30.78 | 1.89 | 5.24 | 1.19 | 2.44 | 35.34 |
| i4 | p1 | p2 | p3 | p4 | p5 | p6 | i9 | p1 | p2 | p3 | p4 | p5 | p6 |
| s1 | 35.45 | 11.53 | 5.30 | 6.01 | 5.90 | 41.19 | s1 | 18.42 | 16.14 | 1.32 | 7.66 | 30.99 | 14.98 |
| s2 | 0 | 0 | 0 | 0 | 0 | 0 | s2 | 0 | 0 | 0 | 0 | 0 | 0 |
| s3 | 33.58 | 15.48 | 7.37 | 5.37 | 5.43 | 44.17 | s3 | 24.88 | 12.39 | 9.01 | 4.38 | 12.22 | 8.83 |
| i5 | p1 | p2 | p3 | p4 | p5 | p6 | i10 | p1 | p2 | p3 | p4 | p5 | p6 |
| s1 | 25.32 | 13.84 | 6.62 | 10.50 | 17.71 | 3.74 | s1 | 32.23 | 2.77 | 8.94 | 0.87 | 44.28 | 20.59 |
| s2 | 0 | 0 | 0 | 0 | 0 | 0 | s2 | 0 | 0 | 0 | 0 | 0 | 0 |
| s3 | 2.49 | 20.64 | 4.50 | 2.24 | 24.44 | 14.46 | s3 | 29.85 | 13.25 | 5.24 | 1.00 | 5.97 | 30.92 |
| Electricity Load (kW) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i1 | p1 | p2 | p3 | p4 | p5 | p6 | i6 | p1 | p2 | p3 | p4 | p5 | p6 |
| s1 | 3.10 | 0.44 | 0.56 | 1.08 | 7.79 | 3.52 | s1 | 0.50 | 3.97 | 1.35 | 5.83 | 0.86 | 1.16 |
| s2 | 2.58 | 2.29 | 1.17 | 2.95 | 2.23 | 0.72 | s2 | 0.64 | 3.67 | 4.68 | 1.59 | 6.68 | 2.60 |
| s3 | 3.16 | 0.45 | 1.15 | 5.09 | 3.80 | 2.14 | s3 | 1.26 | 4.46 | 1.55 | 1.81 | 0.84 | 1.96 |
| i2 | p1 | p2 | p3 | p4 | p5 | p6 | i7 | p1 | p2 | p3 | p4 | p5 | p6 |
| s1 | 2.79 | 2.65 | 3.15 | 4.16 | 5.61 | 1.27 | s1 | 0.25 | 2.65 | 4.33 | 3.40 | 0.70 | 2.46 |
| s2 | 2.26 | 0.73 | 0.59 | 5.19 | 2.00 | 2.89 | s2 | 1.06 | 2.94 | 2.63 | 2.60 | 5.94 | 0.97 |
| s3 | 1.42 | 2.25 | 4.13 | 0.62 | 7.30 | 0.64 | s3 | 1.77 | 4.05 | 4.13 | 1.86 | 2.43 | 2.56 |
| i3 | p1 | p2 | p3 | p4 | p5 | p6 | i8 | p1 | p2 | p3 | p4 | p5 | p6 |
| s1 | 1.55 | 4.77 | 4.50 | 4.38 | 2.80 | 2.32 | s1 | 2.79 | 2.21 | 1.52 | 3.24 | 2.34 | 1.05 |
| s2 | 0.58 | 3.30 | 0.59 | 1.42 | 5.94 | 4.33 | s2 | 1.81 | 0.46 | 4.21 | 1.42 | 2.67 | 1.59 |
| s3 | 3.13 | 1.22 | 4.59 | 5.42 | 0.91 | 2.49 | s3 | 1.52 | 0.90 | 2.75 | 4.07 | 8.37 | 1.18 |
| i4 | p1 | p2 | p3 | p4 | p5 | p6 | i9 | p1 | p2 | p3 | p4 | p5 | p6 |
| s1 | 1.49 | 0.44 | 5.06 | 1.30 | 7.48 | 2.95 | s1 | 3.41 | 1.94 | 1.69 | 2.16 | 4.21 | 2.22 |
| s2 | 2.84 | 3.86 | 5.15 | 0.71 | 4.45 | 0.40 | s2 | 1.16 | 2.89 | 2.11 | 1.95 | 2.00 | 1.95 |
| s3 | 1.71 | 3.78 | 1.26 | 6.10 | 3.35 | 1.18 | s3 | 0.25 | 3.60 | 1.89 | 3.56 | 3.65 | 0.43 |
| i5 | p1 | p2 | p3 | p4 | p5 | p6 | i10 | p1 | p2 | p3 | p4 | p5 | p6 |
| s1 | 1.74 | 1.06 | 6.19 | 1.46 | 3.43 | 3.80 | s1 | 1.49 | 3.53 | 3.15 | 1.30 | 8.57 | 3.16 |
| s2 | 0.32 | 3.86 | 7.02 | 1.06 | 6.53 | 3.61 | s2 | 2.13 | 0.37 | 6.44 | 5.66 | 2.97 | 2.89 |
| s3 | 1.04 | 2.43 | 3.44 | 0.51 | 6.85 | 1.71 | s3 | 2.43 | 3.47 | 5.68 | 0.45 | 7.30 | 3.92 |
| Technology | Type | Company | Electrical Power (kW) | Electrical Efficiency | Heat to Electricity Ratio HER | Capital Cost (EUR) | |
|---|---|---|---|---|---|---|---|
| 1. | Fuel Cell (SOFC) | Galileo | Hexis | 1.0 | 35 | 2.00 | 35,000 |
| 2. | Stirling Engine | Whispergen | Powergen | 1.0 | 12 | 6.60 | 14,000 |
| 3. | Stirling Engine | Solo | 9.5 | 24 | 3.00 | 25,000 | |
| 4. | ICE | Vaillant | 1.0 | 26 | 2.50 | 23,000 | |
| 5. | ICE | Ecogen | BaxiDachs | 5.3 | 32 | 1.96 | 15,000 |
| 6. | ICE | Ecopower | Vaillant | 4.7 | 25 | 2.60 | 11,750 |
| 7. | ICE | ECPower | 15.2 | 27 | 1.97 | 26,425 |
| Technology | Capital Cost (EUR/kW) | Operational and Maintenance Cost (EUR/kWh) | Efficiency | Heat Loss Coefficient (kWh/h) | Charge Loss Coefficient | Discharge Loss Coefficient |
|---|---|---|---|---|---|---|
| PV unit | 4140 | - | 0.12 | - | - | - |
| Boiler | 100 | Cost of fuel | 0.80 | - | - | - |
| Thermal energy storage | 25 | 0.001 | - | 0 | - | - |
| Electricity storage | 415 | 0.01 | - | - | 0.10 | 0.15 |
| Building | Heat Storage Tank (kWh) | CHP (kWe) | PV (kWe) | Boiler (kWth) |
|---|---|---|---|---|
| i1 | 2.5 | 1 | 10 | 2 |
| i2 | 2.5 | 1 | 10 | 2 |
| i3 | 2.5 | 1 | 10 | 2 |
| i4 | 2.5 | 1 | 10 | 2 |
| i5 | 2.5 | 1 | 10 | 2 |
| i6 | 2.5 | 1 | 10 | 2 |
| i7 | 2.5 | 1 | 10 | 2 |
| i8 | 2.5 | 1 | 10 | 2 |
| i9 | 2.5 | 1 | 10 | 2 |
| i10 | 2.5 | 1 | 10 | 2 |
| Baseline | Microgrid (No Electricity Storage) | Integrated Microgrid (with Electricity Storage) | |
|---|---|---|---|
| Total Cost (EUR) | 1430.20 | −631.21 | −712.87 |
| Operational Cost CHP (EUR) | 233.75 | 110.63 | 93.14 |
| Operational Cost of Boiler (EUR) | 1043.54 | 0.87 | 0.88 |
| Environmental Cost (EUR) | 84.47 | 7.00 | 7.62 |
| Cost of Purchased Electricity (EUR) | 86.83 | 10.58 | 8.93 |
| Income from Selling Electricity to the Grid (EUR) | 20.13 | 760.30 | 823.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mechleri, E.; Dorneanu, B.; Arellano-Garcia, H. A Model Predictive Control-Based Decision-Making Strategy for Residential Microgrids. Eng 2022, 3, 100-115. https://doi.org/10.3390/eng3010009
Mechleri E, Dorneanu B, Arellano-Garcia H. A Model Predictive Control-Based Decision-Making Strategy for Residential Microgrids. Eng. 2022; 3(1):100-115. https://doi.org/10.3390/eng3010009
Chicago/Turabian StyleMechleri, Evgenia, Bogdan Dorneanu, and Harvey Arellano-Garcia. 2022. "A Model Predictive Control-Based Decision-Making Strategy for Residential Microgrids" Eng 3, no. 1: 100-115. https://doi.org/10.3390/eng3010009
APA StyleMechleri, E., Dorneanu, B., & Arellano-Garcia, H. (2022). A Model Predictive Control-Based Decision-Making Strategy for Residential Microgrids. Eng, 3(1), 100-115. https://doi.org/10.3390/eng3010009







