Abstract
When the concentration of a gas exceeds the equilibrium concentration in a liquid, the gas–liquid system is referred as a supersaturated system. The supersaturation can be achieved by either changing the pressure and/or temperature of the system. The gas from a supersaturated liquid escapes either through bubble nucleation that usually occurs on solid surface and/or gas diffusion through the gas–liquid interface. The bubble nucleation requires a minimum threshold supersaturation. A waiting time is required to observe whether the applied supersaturation is sufficient to initiate bubble nucleation. When the supersaturation is not sufficient to cause bubble nucleation, some or all of the supersaturated gas may diffuse out from the liquid through the gas–liquid interface before further reducing the pressure in order to increase the supersaturation. In this article, using Fick’s second law of diffusion and Henry’s law, an analytical method is proposed to estimate the level of supersaturations generated in three gas–liquid systems at different step-down pressures. Characteristic times of the gas–liquid systems were estimated to validate whether the waiting times used in this study are in accordance with the semi-infinite diffusion model used to estimate the supersaturations generated.
1. Introduction
A gas–liquid system is referred to as supersaturated when the concentration of the solute phase (gas) exceeds the equilibrium concentration in the solvent phase (liquid). A supersaturated solution can be achieved by changing either the temperature and/or pressure of the system [1,2]. Thermodynamically, the degree of supersaturation can be described by chemical potential (), which represents the deviation from equilibrium at a given temperature and pressure for a component i.
For a component in a mixture, the chemical potential in an isothermal–isobaric ensemble is given by:
where is the free energy of the system , is the number of moles of the component, is the temperature, is the pressure, refers to the number of remaining components, and is the molar fraction of the component in the mixture [3]. For a supersaturated system, the change in chemical potential of the component ( w.r.t. temperature and pressure is >0.
Dissolution and exsolution of CO2 in and from water/brine are relevant in CO2 sequestration. Depending on whether the CO2 exsolution proceeds with or without bubble nucleation, the pressure response and relative permeability characteristics of the fluids in the porous media would be influenced [4]. Bubble nucleation and growth are important in sparkling beverages that are weakly supersaturated with CO2 [5]. During limnic eruptions, which are natural calamities, high concentrations of gas slowly built up in the water column of a lake suddenly erupt after a trigger mechanism leads to local supersaturation [6]. For example, disproportionate accumulations of magmatic CO2 in the bottom layers of Lakes Monoun and Nyos in Cameroon and their eruptions in 1984 and 1986, respectively, caused a sudden release of huge quantities of CO2 into the atmosphere causing the loss of thousands of lives. In addition, Lake Kivu located in the Democratic Republic of the Congo is known to have about 2 and 10 trillion cubic feet of high concentrations of CH4 and CO2 gas, respectively, in its deep water [7,8,9]. The presence of high concentrations of such gases in the lake and the high population density in the nearby area pose a similar risk. The CH4-water system is also relevant to nucleation of methane gas hydrates [10]. Nitrogen removal from wastewater streams is necessary to limit eutrophication and algal blooms [11].
When the pressure of a gas-saturated liquid is reduced at a constant temperature, the liquid becomes supersaturated with the gas and it may lead to bubble nucleation [12]. In our study on the influence of wettability on pressure-driven bubble nucleation of sparingly soluble gases CH4 and N2 in water, we observed that when a supersaturation is created with a higher (500 mbar) step-down pressure, the liberation of dissolved gas occurred through bubble nucleation on a hydrophobic solid surface. However, with a smaller (100 mbar) step-down pressure, the dissolved gas separation occurred only via diffusion of gas molecules from the liquid to the free gas through the gas–liquid interface, as there is not enough supersaturation to cause bubble nucleation even when the pressure is reduced to atmospheric pressure. In the case where bubble nucleation occurs with the available supersaturation, a certain waiting time is required for the gas bubbles to nucleate and grow in order to be observed using a microscope or naked eye, before applying further step-down pressure for generating higher supersaturation. Therefore, in order to know whether a given supersaturation is sufficient for bubble nucleation or not, it is important to estimate the supersaturation level at different step-down pressures [2]. In this study, we present a simple analytical method developed based on Fick’s second law of diffusion and Henry’s law to estimate the supersaturations generated in three gas–liquid systems (CO2-water, CH4-water, and N2-water) with two step-down pressures (100 and 500 mbar). The three gas–liquid systems were chosen based on their importance in many natural and industrial applications. Moreover, we also had conducted experimental investigations to study the influence of wettability and step-down pressure on bubble nucleation of these gases in water [2,13].
Gas liberation from its dissolved state (in the liquid) to free gas state requires supersaturation. In our previous experimental study, we observed that bubble nucleation did not occur in a CO2-supersaturated water in a hydrophilic container, even when the pressure was reduced in one step from the saturation pressure (6000 mbar) to atmospheric pressure (0 mbar) [13]; whereas in the case of hydrophobic container, the incipiation pressure for bubble nucleation and hence, the required supersaturation was observed to be influenced by the surface wettability of the container for all the three gases (CO2, CH4, and N2) and the step-down pressure for the sparingly soluble gases (CH4 and N2). A certain waiting time is required at each pressure reduction step to ensure either enough time is given for the bubbles to nucleate and grow, or to conclude that the supersaturation is not sufficient to initiate the bubble nucleation. However, during the waiting time, some (or all) of the supersaturated gas may diffuse out before initiating the next step-down pressure. Therefore, it is important to know the actual supersaturation (which is the difference in the gas saturations at the initial and current pressures minus the gas diffused out until that point of time) in the system as a function of time during the waiting time in order to quantify the actual supersaturation required to initiate the bubble nucleation. Therefore, in this study, we investigated the influence of step-down pressure, and the waiting time between the pressure reduction steps on supersaturation.
2. Methodology
2.1. Derivation of Supersaturation Equation
The Fick’s second law of diffusion given below describes the one-dimensional diffusion equation for binary mixtures of species A and B under transient condition [14,15]:
where is the diffusion coefficient of species A (gas) in species B (liquid), is the solute concentration, is the time, and is the position.
The derivation to solve Equation (1) is briefly demonstrated below; however, the detailed derivation of the differential equation can be found out in the supplementary section provided with this paper.
defined by the following dimensionless characteristic equation:
From the Gaussian integral [16], we have
The following error function and the boundary conditions were used to solve Fick’s second law of diffusion [14]:
The initial and boundary conditions for the gas–liquid system shown in Figure 1 are given below:
where is the saturated gas concentration in mol/L (after complete saturation), is the gas concentration after any time , is the gas concentration at the gas–liquid interface at equilibrium (with the current gas pressure) in mol/L. As mentioned earlier, ; therefore, it is required to redefine x and y in Figure 1. In Figure 1, x is an independent variable and it is a position in the liquid column, which is taken as 5 mm (total height of the liquid column) for estimating in Tables S2–S7 in the Supplementary Material. y is a dependent variable that varies with position in the liquid column, and the waiting time after each pressure reduction step.
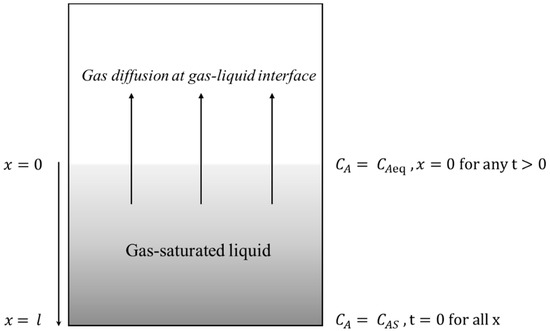
Figure 1.
Schematic of bubble nucleation system used to study gas diffusion and saturation in a liquid.
Solving the differential equation mentioned in Equation (1) and applying the boundary conditions, we get the following:
Equation (11) is the solution to the problem for time-dependent diffusion assuming a semi-infinite system.
For a given , , and , assuming as , Equation (11) reduces to:
The gas concentration in water at any given time can be determined using the following equation:
The equilibrium concentration of gas can be calculated by using Henry’s law for low-pressure systems, which is given by:
where is the Henry’s constant in mol/L/Pa and is the partial pressure of the gas [17].
The saturation time for carbon dioxide, methane and nitrogen gases in water can be estimated using the one-dimensional bounded diffusion equation, given below [14].
where τ is the dimensionless time, is the diffusion coefficient in mm2/s, is the diffusion time in seconds, and 𝑙 is the height of the water column in mm.
For this study, is taken as 4 to achieve 99.99% gas saturation, and the height of the water column 𝑙 is 5 mm. The saturation times required to achieve 99.99% saturation of carbon dioxide, methane, and nitrogen gases in water at the initial pressure, and constant in the diffusion equation, are given in Table S1, in the Supplementary Material provided with this paper.
2.2. Validation of Waiting Time after Each Pressure Reduction Step with ‘Characteristic Time’
Since semi-infinite diffusion solution is used to estimate the supersaturations in this study, therefore, it is important to validate whether the waiting time, i.e., 15 min, after each pressure reduction step satisfies the semi-infinite diffusion model. The characteristic diffusion time for a gas to diffuse on a liquid column of height and diffusion co-efficient is given by [18]:
3. Results and Discussion
The saturation times for CO2-water, CH4-water, and N2-water systems are 62,500 s (17.4 h), 56,497 s (15.7 h), and 52,910 s (14.7 h), respectively (ref.: Table S1). The details of characteristic time for all the three gases used in this study are given in Table 1.

Table 1.
Characteristic time and calculations for carbon dioxide, methane, and nitrogen gases.
Since the time allowed after each pressure reduction step (15 min) is much less than the characteristic time, a semi-infinite diffusion model is applicable for this study. For 15 min waiting time, the supersaturation generated, remaining CO2 concentration, and amount of CO2 diffused out from water after each pressure reduction step, for 500 mbar and 100 mbar step-down pressures, are given in Tables S2 and S3, respectively. The corresponding calculations for two sparingly soluble gases, methane and nitrogen, are given in Tables S4–S7, respectively, in the Supplementary Material provided with this paper.
Effect of Waiting Time on Supersaturation after Each Pressure Reduction Step
To study the effect of waiting time on supersaturation in CO2-water, CH4-water, and N2-water systems, the supersaturations were estimated at four different waiting times (15, 30, 45, and 60 min) for 100 and 500 mbar step-down pressures. Figure 2a–c represent the effect of waiting time on supersaturation in CO2-water, CH4-water, and N2-water systems, respectively. From the figures, it can be observed that as the waiting time increases, at a given pressure, the supersaturation decreases as the consequence of the decrease in the actual concentration of gas in the liquid phase for both the step-down pressures. In addition, from the figures, it can be observed that the supersaturations generated in the CO2-water system are an order of magnitude higher compared to those of CH4-water and N2-water systems. This is due to fact that the Henry’s law constants for CO2 (3.36 × 10−7 mol/L/Pa) are approximately 25- and 56-times higher than CH4 (1.36 × 10−8 mol/L/Pa) and N2 (6.02 × 10−9 mol/L/Pa) gases, respectively. Hence, the dissolved gas concentration of CO2 in water is much higher compared to the sparingly soluble gases CH4 and N2 in the pressure range considered in this work. The supersaturation calculations for both 100 and 500 mbar step-down pressures for the aforementioned gas–liquid systems are tabulated in Tables S8–S13 (100 mbar), in the Supplementary Material provided with this paper. It is important to note that the mathematical model presented in this study is not applicable at the onset nucleation pressure for bubble nucleation or any pressure below that.
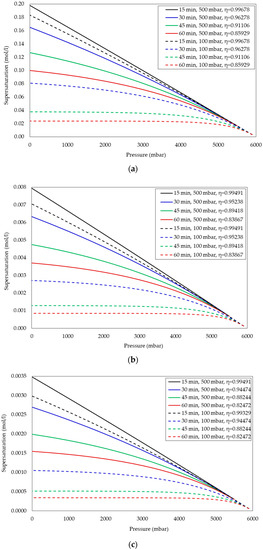
Figure 2.
Effect of waiting time on supersaturation in the (a) CO2-water system; (b) CH4-water system; (c) N2-water system.
4. Conclusions
In this study, an analytical method to estimate the supersaturations generated with two different step-down pressures from an initial saturation pressure is presented. The proposed method estimates supersaturation by integrating Fick’s second law of diffusion and Henry’s law. The semi-infinite diffusion model was used to estimate the supersaturations generated in gas–liquid systems. Since a certain waiting time is required to observe bubble nucleation after creating a supersaturation, the waiting times used in this study were validated with the characteristic times. In addition, we analyzed the effect of waiting time on supersaturation and found that, at a given pressure, as the waiting increases, the supersaturation decreases due to the decrease in the actual concentration of gas in the liquid. The supersaturation is higher with the higher step-down pressure. The dissolved gas concentration of CO2 in water is much higher compared to CH4 and N2, in the pressure range of this work; therefore, the supersaturations generated in the CO2-water system are correspondingly higher compared to CH4-water and N2-water systems.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/eng3010010/s1, Table S1: Saturation time calculations for carbon dioxide, methane, and nitrogen gases in water, Table S2: Supersaturation and diffusion calculations for carbon dioxide with 500 mbar (50,000 Pa) step-down pressure, Table S3: Supersaturation and diffusion calculations for carbon dioxide with 100 mbar (10,000 Pa) step-down pressure, Table S4: Supersaturation and diffusion calculations for methane gas with 500 mbar (50,000 Pa) step-down pressure, Table S5: Supersaturation and diffusion calculations for methane with 100 mbar (10,000 Pa) step-down pressure, Table S6: Supersaturation and diffusion calculations for nitrogen with 500 mbar (50,000 Pa) step-down pressure, Table S7: Supersaturation and diffusion calculations for nitrogen with 100 mbar (10,000 Pa) step-down pressure, Table S8: CO2 supersaturations generated in water with 500 mbar (50,000 Pa) step-down pressure and different waiting times (saturation pressure: 6000 mbar or 600,000 Pa), Table S9: CO2 supersaturations generated in water with 100 mbar (10,000 Pa) step-down pressure and different waiting times (saturation pressure: 6000 mbar or 600,000 Pa), Table S10: CH4 supersaturations generated in water with 500 mbar (50,000 Pa) step-down pressure and different waiting times (saturation pressure: 6000 mbar or 600,000 Pa), Table S11: CH4 supersaturations generated in water with 100 mbar (10,000 Pa) step-down pressure and different waiting times (saturation pressure: 6000 mbar or 600,000 Pa), Table S12: N2 supersaturations generated in water with 500 mbar (50,000 Pa) step-down pressure and different waiting times (saturation pressure: 6000 mbar or 600,000 Pa), Table S13: N2 supersaturations generated in water with 100 mbar (10,000 Pa) step-down pressure and different waiting times (saturation pressure: 6000 mbar or 600,000 Pa).
Author Contributions
Conceptualization, P.K.B. and S.P.; methodology, S.P.; validation, S.P. and P.K.B.; formal analysis, S.P. and P.K.B.; investigation, S.P.; resources, P.K.B.; data curation, S.P.; writing—original draft preparation, S.P.; writing—review and editing, P.K.B.; visualization, P.K.B.; supervision, P.K.B.; project administration, P.K.B.; funding acquisition, P.K.B. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge American Chemical Society Petroleum Research Fund (PRF# 58560-DNI5) for the financial support for this research project.
Institutional Review Board Statement
Not relevant.
Informed Consent Statement
Not applicable.
Data Availability Statement
In this research, there was no data availability statement.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bikkina, P.K.; Pradhan, S. A potential solution for boiling crisis. In Proceedings of the 18th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH 18), Portland, Oregon, OR, USA, 18–23 August 2019; American Nuclear Society: Portland, OR, USA, 2019; pp. 1383–1396. [Google Scholar]
- Pradhan, S.; Qader, R.J.; Sedai, B.R.; Bikkina, P.K. Influence of wettability on pressure-driven bubble nucleation: A potential method for dissolved gas separation. Sep. Purif. Technol. 2019, 217, 31–39. [Google Scholar] [CrossRef]
- Baillon, F.; Espitalier, F.; Cogne, C.; Peczalski, R.; Louisnard, O. Crystallization and Freezing Processes Assisted by power Ultrasound, in Power Ultrasonics; Elsevier: Amsterdam, The Netherlands, 2015; pp. 845–874. [Google Scholar]
- Zuo, L.; Krevor, S.; Falta, R.W.; Benson, S.M. An experimental study of CO2 exsolution and relative permeability measurements during CO2 saturated water depressurization. Transp. Porous Media 2012, 91, 459–478. [Google Scholar] [CrossRef]
- Liger-Belair, G.; Parmentier, M.; Jeandet, P. Modeling the kinetics of bubble nucleation in champagne and carbonated beverages. J. Phys. Chem. B 2006, 110, 21145–21151. [Google Scholar] [CrossRef] [PubMed]
- Schmid, M.; Lorke, A.; Wuest, A.; Halbwachs, M.; Tanyileke, G. Development and sensitivity analysis of a model for assessing stratification and safety of lake nyos during artificial degassing. Ocean Dyn. 2003, 53, 288–301. [Google Scholar] [CrossRef][Green Version]
- Kusakabe, M. Lakes nyos and monoun gas disasters (Cameroon)—Limnic eruptions caused by excessive accumulation of magmatic CO2 in crater lakes. Geochem. Monogr. Ser. 2017, 1, 1–50. [Google Scholar] [CrossRef]
- Vaselli, O.; Tedesco, D.; Cuoco, E.; Tassi, F. Are limnic eruptions in the CO2–CH4-rich gas reservoir of lake kivu (Democratic Republic of the Congo and Rwanda) possible? Insights from physico-chemical and isotopic data. In Volcanic Lakes; Springer: New York, NY, USA, 2015; pp. 489–505. [Google Scholar]
- Jones, N. How dangerous is Africa’s explosive lake kivu? Nature 2021, 597, 466–469. [Google Scholar] [CrossRef] [PubMed]
- Hawtin, R.W.; Quigley, D.; Rodger, P.M. Gas hydrate nucleation and cage formation at a water/methane interface. Phys. Chem. Chem. Phys. 2008, 10, 4853–4864. [Google Scholar] [CrossRef] [PubMed]
- Sharp, R.; Khunjar, W.; Daly, D.; Perez-Terrero, J.; Chandran, K.; Niemiec, A.; Pace, G. Nitrogen removal from water resource recovery facilities using partial nitrification, denitratation-anaerobic ammonia oxidation (PANDA). Sci. Total Environ. 2020, 724, 138283. [Google Scholar] [CrossRef] [PubMed]
- Bergeron, V.; Walstra, P. Foams, in Fundamentals of Interface and Colloid Science; Elsevier: Amsterdam, The Netherlands, 2005; pp. 7.1–7.38. [Google Scholar]
- Pradhan, S. Influence of Wettability on Dissolved Gas Separation, Nucleate Boiling, and Enhanced Oil Recovery, in School of Chemical Engineering. Ph.D. Dissertation, Oklahoma State University, Stillwater, OK, USA, 2021. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena 2002; JohnWiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1979. [Google Scholar]
- Conrad, K. The Gaussian Integral; University of Connecticut: Storrs, CT, USA, 2016; pp. 1–2. [Google Scholar]
- Smith, J.M. Introduction to Chemical Engineering Thermodynamics; ACS Publications: Washington, DC, USA, 1950. [Google Scholar]
- Berthier, J.; Silberzan, P. Microfluidics for Biotechnology; Artech House: Norwood, MA, USA, 2010. [Google Scholar]
- Himmelblau, D. Diffusion of dissolved gases in liquids. Chem. Rev. 1964, 64, 527–550. [Google Scholar] [CrossRef]
- Witherspoon, P.; Saraf, D. Diffusion of methane, ethane, propane, and n-butane in water from 25 to 43. J. Phys. Chem. 1965, 69, 3752–3755. [Google Scholar] [CrossRef]
- Ferrell, R.T.; Himmelblau, D.M. Diffusion coefficients of nitrogen and oxygen in water. J. Chem. Eng. Data 1967, 12, 111–115. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).