Wave Dispersion in Multilayered Reinforced Nonlocal Plates under Nonlinearly Varying Initial Stress
Abstract
:1. Introduction
2. Prestressed Small-Scale Plates with SMA Nanoscale Wires
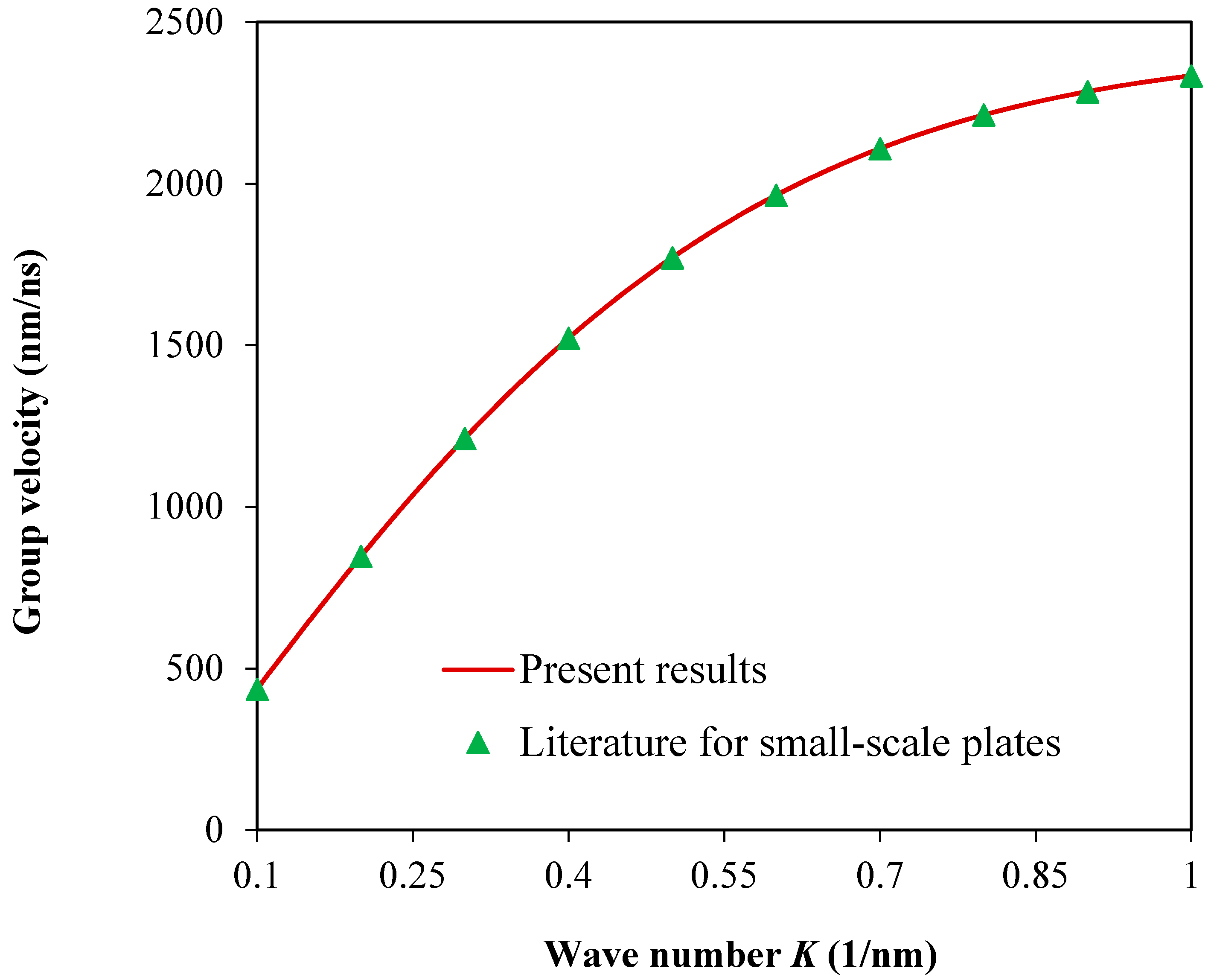
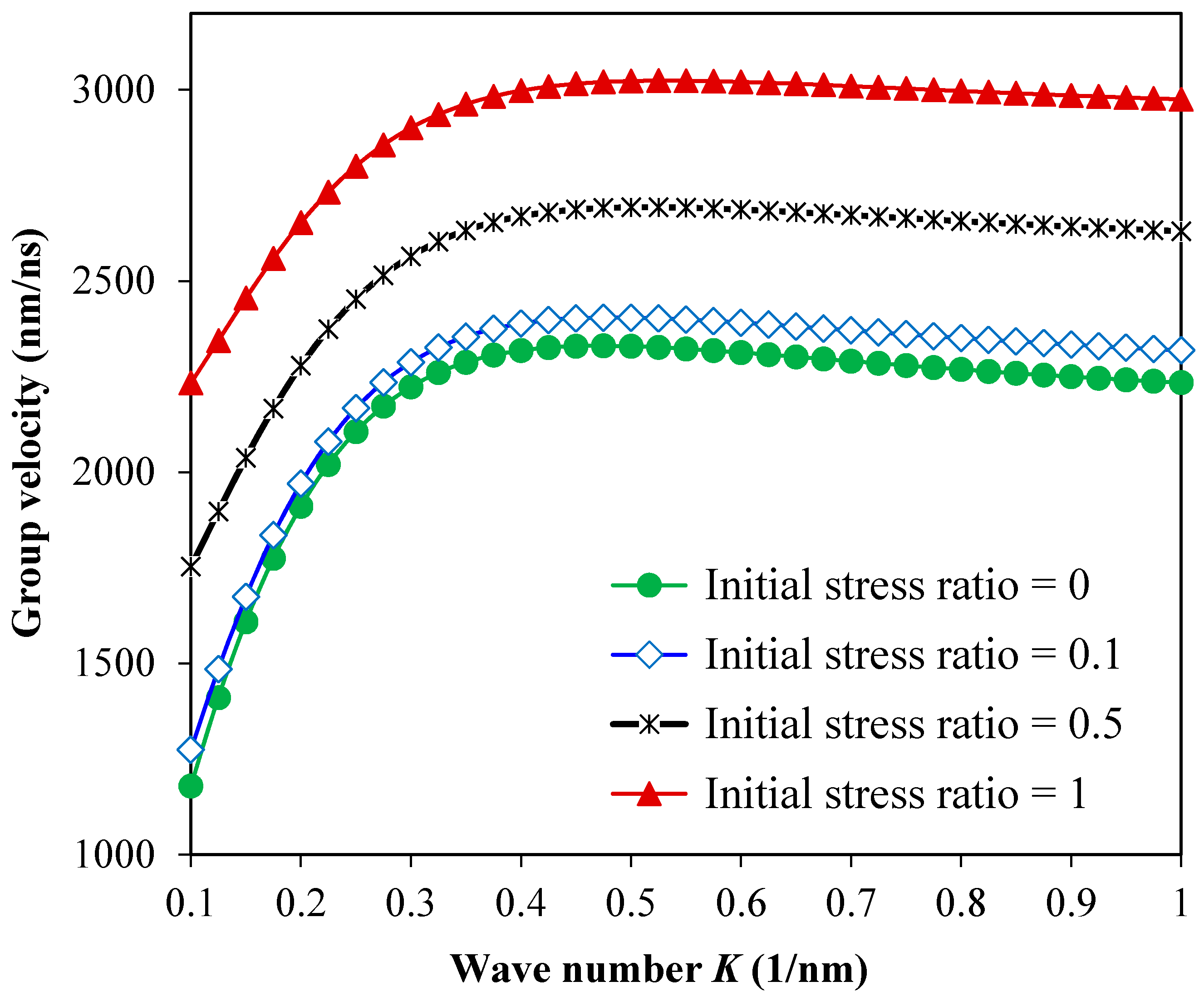
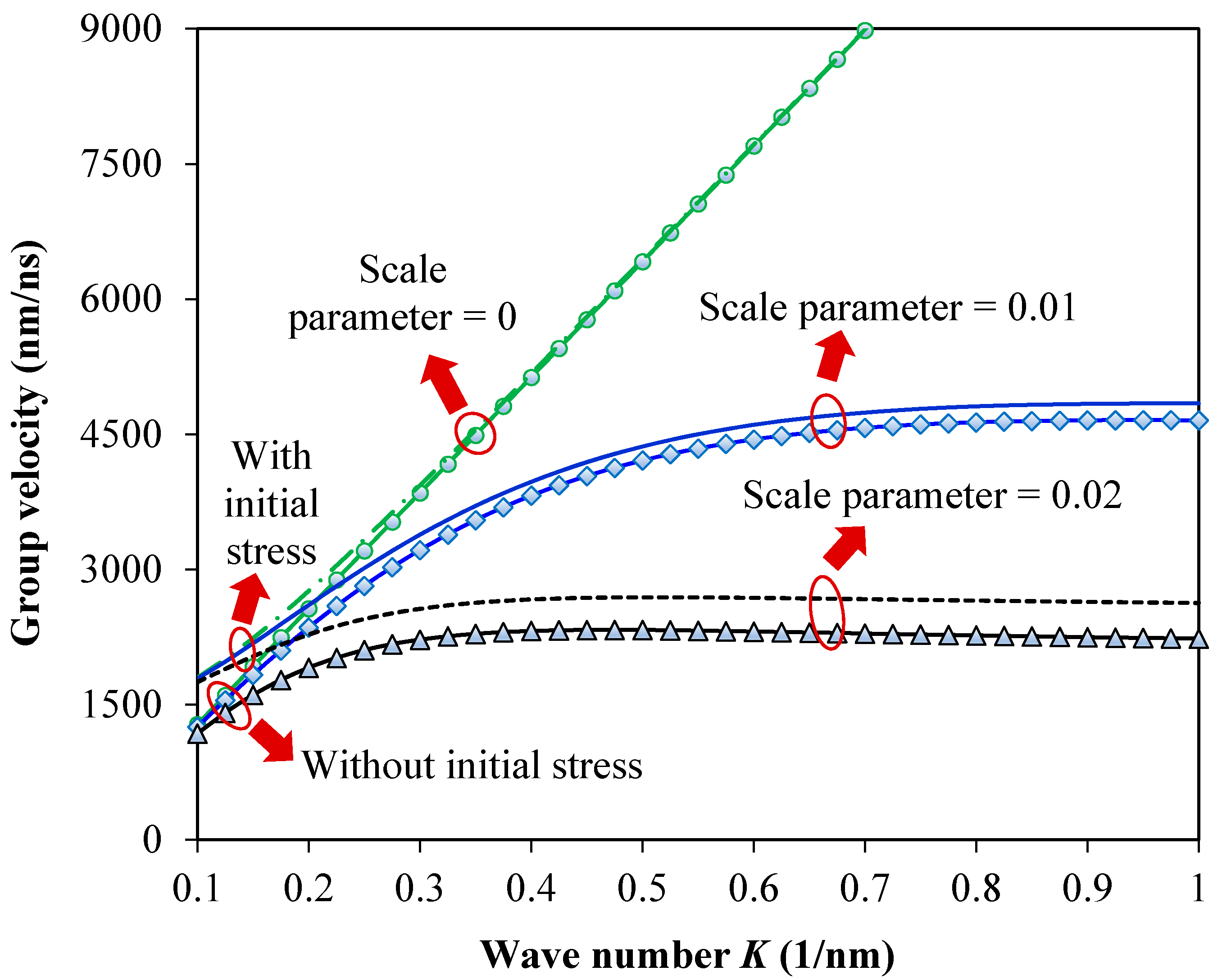
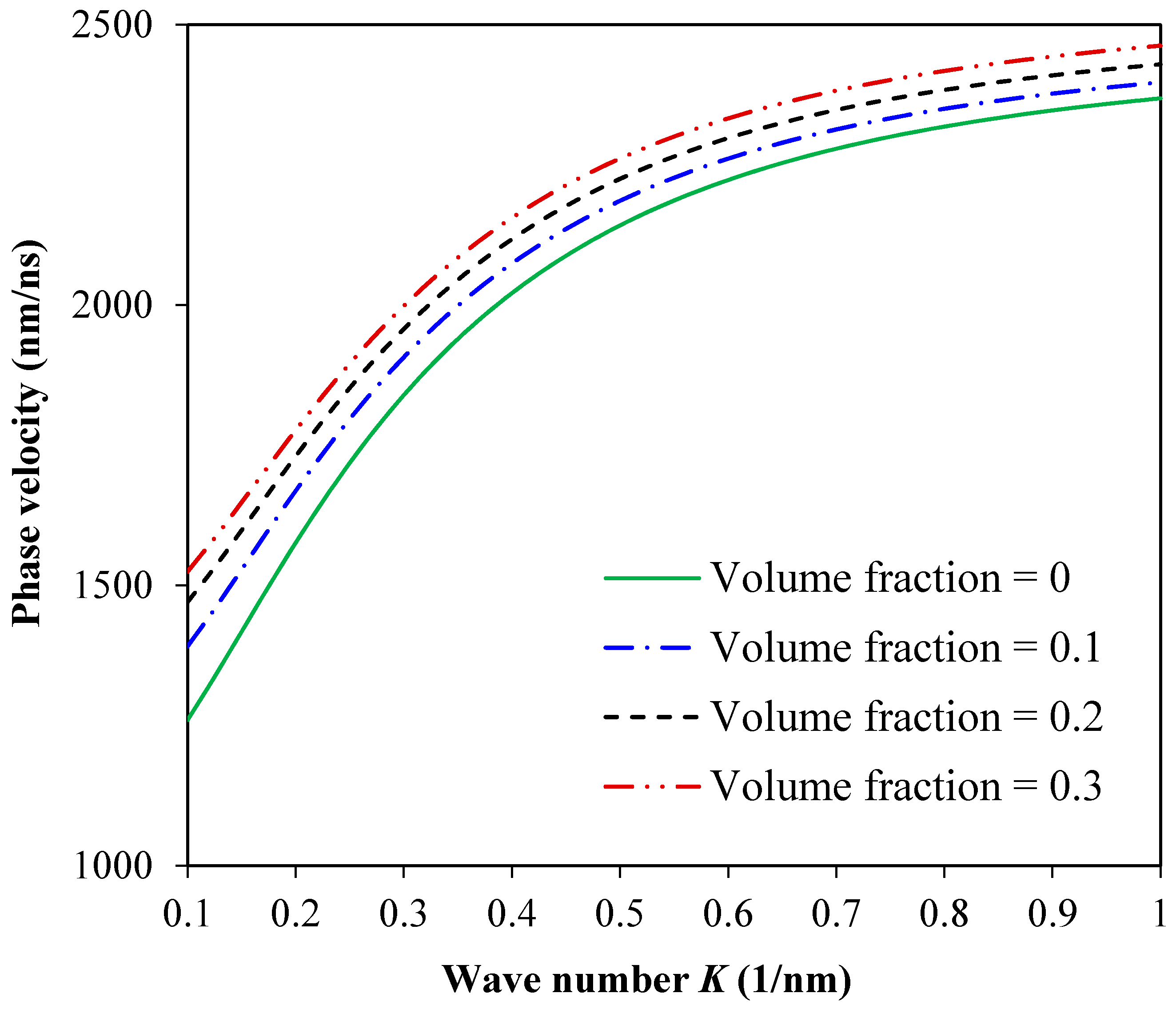
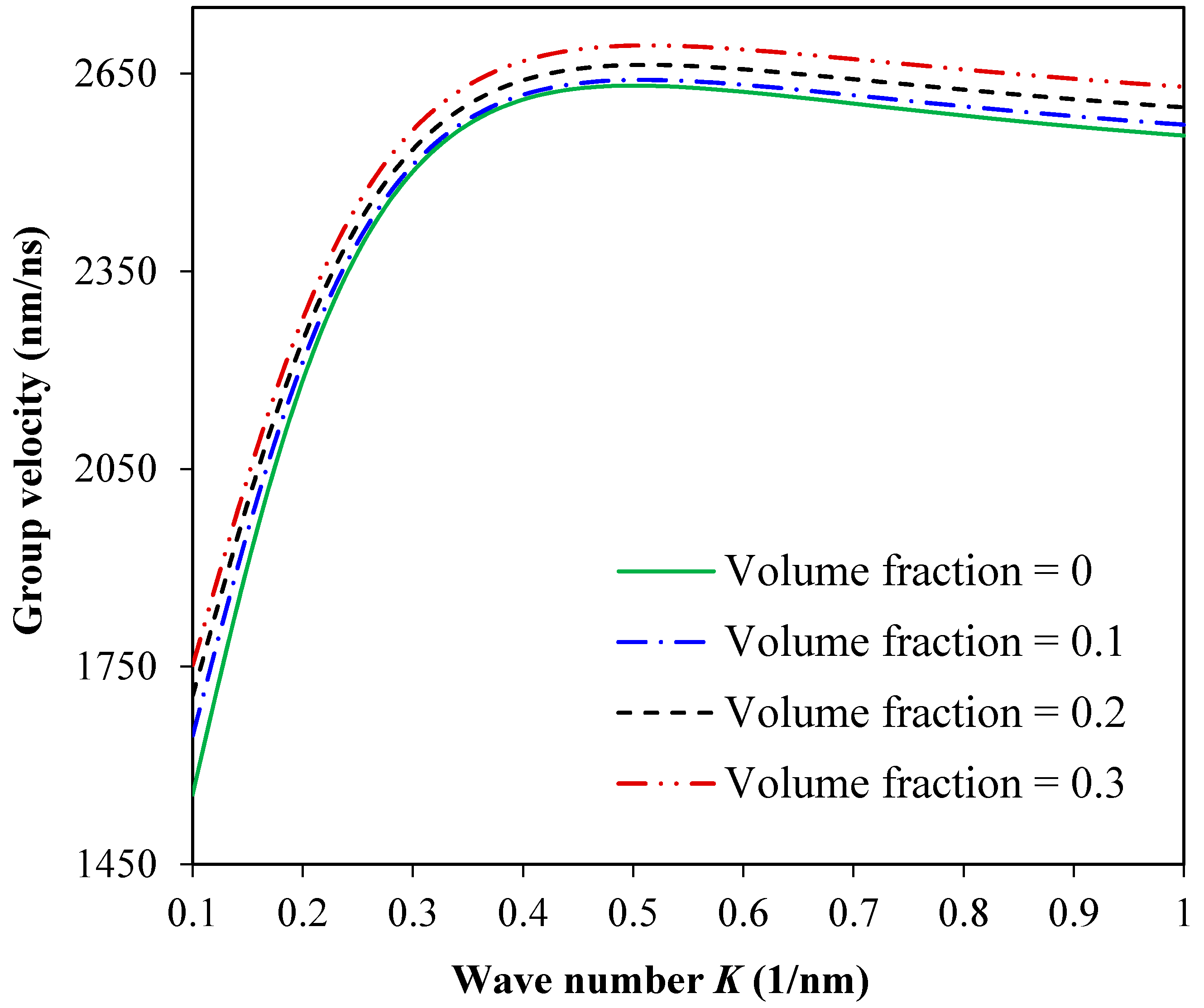
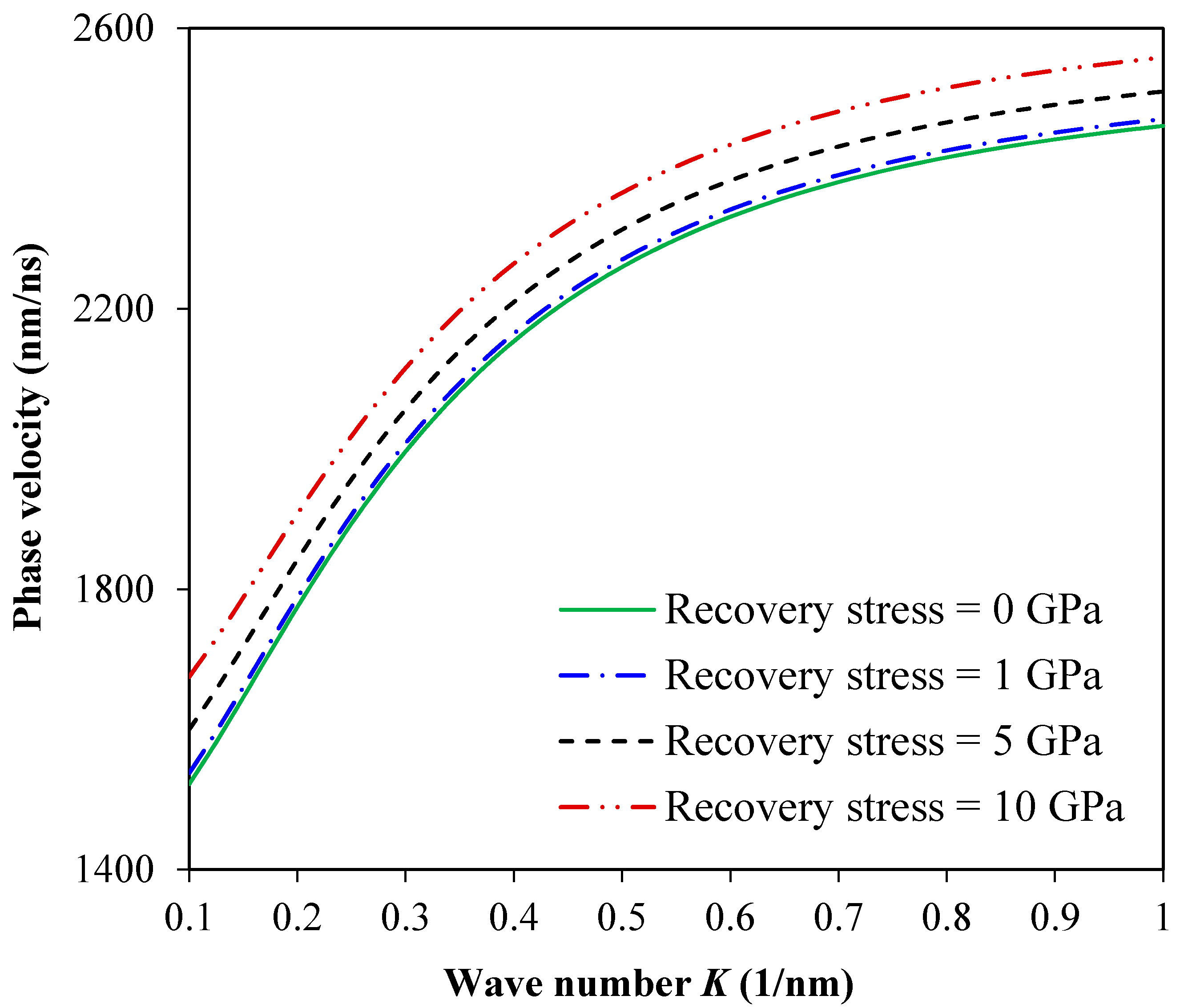
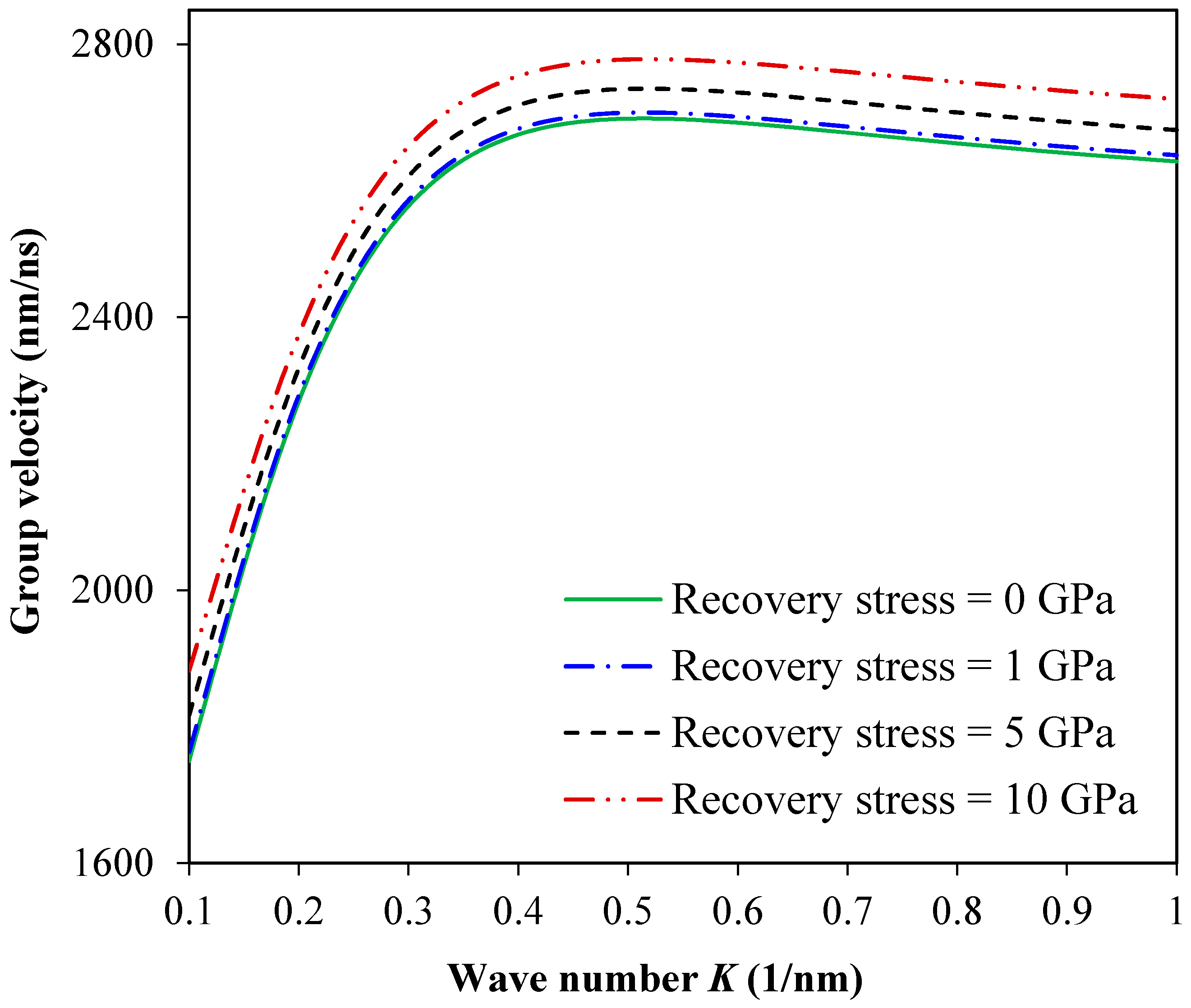
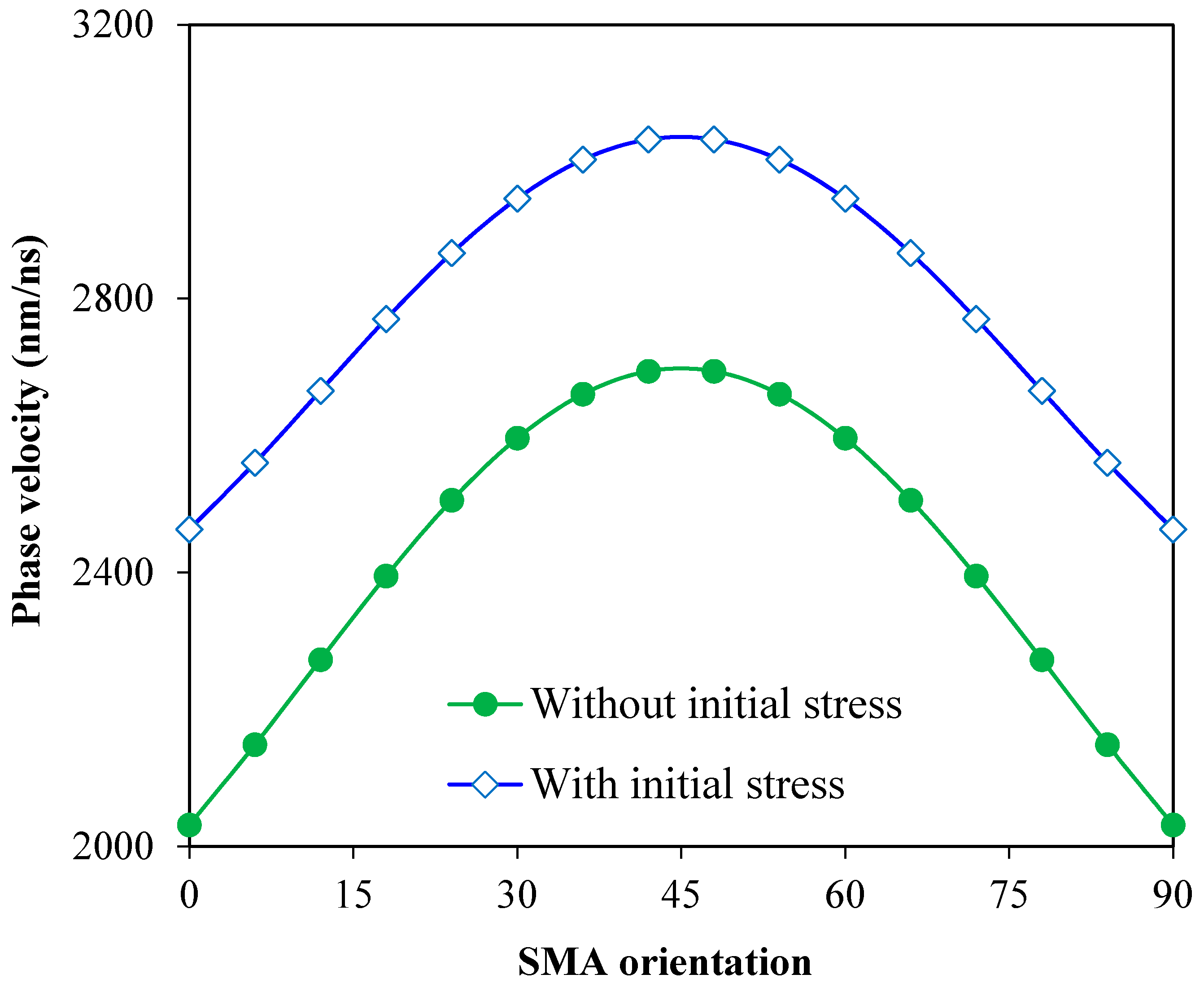
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rohani Rad, E.; Vahabi, H.; Formela, K.; Saeb, M.R.; Thomas, S. Injectable poloxamer/graphene oxide hydrogels with well-controlled mechanical and rheological properties. Polym. Adv. Technol. 2019, 30, 2250–2260. [Google Scholar] [CrossRef]
- Vahabi, H.; Rad, E.R.; Parpaite, T.; Langlois, V.; Saeb, M.R. Biodegradable polyester thin films and coatings in the line of fire: The time of polyhydroxyalkanoate (PHA)? Prog. Org. Coat. 2019, 133, 85–89. [Google Scholar] [CrossRef]
- Rad, E.R.; Vahabi, H.; de Anda, A.R.; Saeb, M.R.; Thomas, S. Bio-epoxy resins with inherent flame retardancy. Prog. Org. Coat. 2019, 135, 608–612. [Google Scholar] [CrossRef]
- Rohani Rad, E.; Farajpour, M.R. Dynamics analysis of microparticles in inertial microfluidics for biomedical applications. J. Comput. Appl. Mech. 2019, 50, 157–164. [Google Scholar]
- Goodarzi, M.; Mohammadi, M.; Farajpour, A.; Khooran, M. Investigation of the effect of pre-stressed on vibration frequency of rectangular nanoplate based on a visco-Pasternak foundation. J. Solid Mech. 2014, 6, 98–121. [Google Scholar]
- Mohammadi, M.; Farajpour, A.; Goodarzi, M.; Dinari, F. Thermo-mechanical vibration analysis of annular and circular graphene sheet embedded in an elastic medium. Lat. Am. J. Solids Struct. 2014, 11, 659–682. [Google Scholar] [CrossRef] [Green Version]
- Farajpour, M.R.; Shahidi, A.R.; Farajpour, A. Frequency behavior of ultrasmall sensors using vibrating SMA nanowire-reinforced sheets under a non-uniform biaxial preload. Mater. Res. Express 2019, 6, 065047. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Farajpour, A. Axisymmetric free and forced vibrations of initially stressed circular nanoplates embedded in an elastic medium. Acta Mech. 2012, 223, 2311–2330. [Google Scholar] [CrossRef]
- Ebrahiminejad, S.; Marzbanrad, J.; Boreiry, M.; Shaghaghi, G.R. On the electro-thermo-mechanical vibration characteristics of elastically restrained functionally graded nanobeams using differential transformation method. Appl. Phys. A 2018, 124, 800. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Dabbagh, A. Effect of humid-thermal environment on wave dispersion characteristics of single-layered graphene sheets. Appl. Phys. A 2018, 124, 301. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Vibration and bending analyses of magneto–electro–thermo-elastic sandwich microplates resting on viscoelastic foundation. Appl. Phys. A 2017, 123, 550. [Google Scholar] [CrossRef]
- Xiao, W.; Li, L.; Wang, M. Propagation of in-plane wave in viscoelastic monolayer graphene via nonlocal strain gradient theory. Appl. Phys. A 2017, 123, 388. [Google Scholar] [CrossRef]
- Jandaghian, A.; Rahmani, O. Buckling analysis of multi-layered graphene sheets based on a continuum mechanics model. Appl. Phys. A 2017, 123, 324. [Google Scholar] [CrossRef]
- Ghadiri, M.; Hajbarati, H.; Safi, M. Vibration analysis of single-walled carbon peapods based on nonlocal Timoshenko beam theory. Appl. Phys. A 2017, 123, 260. [Google Scholar] [CrossRef]
- Ansari, R.; Torabi, J. Numerical study on the free vibration of carbon nanocones resting on elastic foundation using nonlocal shell model. Appl. Phys. A 2016, 122, 1073. [Google Scholar] [CrossRef]
- Kiani, K. Vibrations of fluid-conveying inclined single-walled carbon nanotubes acted upon by a longitudinal magnetic field. Appl. Phys. A 2016, 122, 1038. [Google Scholar] [CrossRef]
- Farajpour, M.; Shahidi, A.; Farajpour, A. Elastic waves in fluid-conveying carbon nanotubes under magneto-hygro-mechanical loads via a two-phase local/nonlocal mixture model. Mater. Res. Express 2019, 6, 0850a8. [Google Scholar] [CrossRef]
- Hadi, A.; Nejad, M.Z.; Hosseini, M. Vibrations of three-dimensionally graded nanobeams. Int. J. Eng. Sci. 2018, 128, 12–23. [Google Scholar] [CrossRef]
- Nejad, M.Z.; Hadi, A. Non-local analysis of free vibration of bi-directional functionally graded Euler–Bernoulli nano-beams. Int. J. Eng. Sci. 2016, 105, 1–11. [Google Scholar] [CrossRef]
- Aydogdu, M. Longitudinal wave propagation in multiwalled carbon nanotubes. Compos. Struct. 2014, 107, 578–584. [Google Scholar] [CrossRef]
- Aydogdu, M. A nonlocal rod model for axial vibration of double-walled carbon nanotubes including axial van der Waals force effects. J. Vib. Control 2015, 21, 3132–3154. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Setoodeh, A.; Beni, A.A. Small scale effect on the thermal buckling of orthotropic arbitrary straight-sided quadrilateral nanoplates embedded in an elastic medium. Compos. Struct. 2011, 93, 2083–2089. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Shojaee, M. Surface and nonlocal effects on the nonlinear free vibration of non-uniform nanobeams. Compos. Part B Eng. 2013, 52, 84–92. [Google Scholar] [CrossRef]
- Rohani Rad, E.; Farajpour, M.R. Influence of taxol and CNTs on the stability analysis of protein microtubules. J. Comput. Appl. Mech. 2019, 50, 140–147. [Google Scholar]
- Wang, X.; Cai, H. Effects of initial stress on non-coaxial resonance of multi-wall carbon nanotubes. Acta Mater. 2006, 54, 2067–2074. [Google Scholar] [CrossRef]
- Song, J.; Shen, J.; Li, X. Effects of initial axial stress on waves propagating in carbon nanotubes using a generalized nonlocal model. Comput. Mater. Sci. 2010, 49, 518–523. [Google Scholar] [CrossRef]
- Heireche, H.; Tounsi, A.; Benzair, A.; Mechab, I. Sound wave propagation in single-walled carbon nanotubes with initial axial stress. J. Appl. Phys. 2008, 104, 014301. [Google Scholar] [CrossRef]
- Güven, U. Transverse vibrations of single-walled carbon nanotubes with initial stress under magnetic field. Compos. Struct. 2014, 114, 92–98. [Google Scholar] [CrossRef]
- Selim, M.; Abe, S.; Harigaya, K. Effects of initial compression stress on wave propagation in carbon nanotubes. Eur. Phys. J. B 2009, 69, 523–528. [Google Scholar] [CrossRef] [Green Version]
- Shen, Z.-B.; Tang, G.-J.; Zhang, L.; Li, X.-F. Vibration of double-walled carbon nanotube based nanomechanical sensor with initial axial stress. Comput. Mater. Sci. 2012, 58, 51–58. [Google Scholar] [CrossRef]
- Asemi, S.; Farajpour, A.; Asemi, H.; Mohammadi, M. Influence of initial stress on the vibration of double-piezoelectric-nanoplate systems with various boundary conditions using DQM. Phys. E Low-Dimens. Syst. Nanostruct. 2014, 63, 169–179. [Google Scholar] [CrossRef]
- Wang, Y.-Z.; Li, F.-M.; Kishimoto, K. Scale effects on flexural wave propagation in nanoplate embedded in elastic matrix with initial stress. Appl. Phys. A 2010, 99, 907–911. [Google Scholar] [CrossRef]
- Murmu, T.; Pradhan, S. Vibration analysis of nanoplates under uniaxial prestressed conditions via nonlocal elasticity. J. Appl. Phys. 2009, 106, 104301. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Janghorban, M.; Li, L. Wave dispersion of mounted graphene with initial stress. Thin-Walled Struct. 2018, 122, 102–111. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Shafiei, N. Influence of initial shear stress on the vibration behavior of single-layered graphene sheets embedded in an elastic medium based on Reddy’s higher-order shear deformation plate theory. Mech. Adv. Mater. Struct. 2017, 24, 761–772. [Google Scholar] [CrossRef]
- Mohammadi, M.; Farajpour, A.; Goodarzi, M. Numerical study of the effect of shear in-plane load on the vibration analysis of graphene sheet embedded in an elastic medium. Comput. Mater. Sci. 2014, 82, 510–520. [Google Scholar] [CrossRef]
- Phung-Van, P.; Lieu, Q.X.; Nguyen-Xuan, H.; Wahab, M.A. Size-dependent isogeometric analysis of functionally graded carbon nanotube-reinforced composite nanoplates. Compos. Struct. 2017, 166, 120–135. [Google Scholar] [CrossRef]
- Kuang, Y.; Ou, J. Self-repairing performance of concrete beams strengthened using superelastic SMA wires in combination with adhesives released from hollow fibers. Smart Mater. Struct. 2008, 17, 025020. [Google Scholar] [CrossRef]
- Ho, M.; McMillan, A.B.; Simard, J.M.; Gullapalli, R.; Desai, J.P. Toward a meso-scale SMA-actuated MRI-compatible neurosurgical robot. IEEE Trans. Robot. 2012, 28, 213–222. [Google Scholar] [CrossRef]
- Kahn, H.; Huff, M.; Heuer, A. The TiNi shape-memory alloy and its applications for MEMS. J. Micromech. Microeng. 1998, 8, 213. [Google Scholar] [CrossRef]
- Park, J.-S.; Kim, J.-H.; Moon, S.-H. Vibration of thermally post-buckled composite plates embedded with shape memory alloy fibers. Compos. Struct. 2004, 63, 179–188. [Google Scholar] [CrossRef]
- Brinson, L.C. One-dimensional constitutive behavior of shape memory alloys: Thermomechanical derivation with non-constant material functions and redefined martensite internal variable. J. Intell. Mater. Syst. Struct. 1993, 4, 229–242. [Google Scholar] [CrossRef]
- Farajpour, M.; Shahidi, A.; Farajpour, A. Influence of shear preload on wave propagation in small-scale plates with nanofibers. Struct. Eng. Mech. 2019, 70, 407–420. [Google Scholar]
- Malekzadeh, P.; Shojaee, M. Free vibration of nanoplates based on a nonlocal two-variable refined plate theory. Compos. Struct. 2013, 95, 443–452. [Google Scholar] [CrossRef]
- Asemi, S.R.; Farajpour, A.; Borghei, M.; Hassani, A.H. Thermal effects on the stability of circular graphene sheets via nonlocal continuum mechanics. Lat. Am. J. Solids Struct. 2014, 11, 704–724. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R.; Dabbagh, A. A nonlocal strain gradient theory for wave propagation analysis in temperature-dependent inhomogeneous nanoplates. Int. J. Eng. Sci. 2016, 107, 169–182. [Google Scholar] [CrossRef]
- Allen, D.; Sayers, C. The measurement of residual stress in textured steel using an ultrasonic velocity combinations technique. Ultrasonics 1984, 22, 179–188. [Google Scholar] [CrossRef]
- Vangi, D. Stress evaluation by pulse-echo ultrasonic longitudinal wave. Exp. Mech. 2001, 41, 277–281. [Google Scholar] [CrossRef]
- Wang, Y.-Z.; Li, F.-M.; Kishimoto, K. Flexural wave propagation in double-layered nanoplates with small scale effects. J. Appl. Phys. 2010, 108, 064519. [Google Scholar] [CrossRef]
- Farajpour, M.; Shahidi, A.; Farajpour, A. A nonlocal continuum model for the biaxial buckling analysis of composite nanoplates with shape memory alloy nanowires. Mater. Res. Express 2018, 5, 035026. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farajpour, M.R.; Shahidi, A.R.; Farajpour, A. Wave Dispersion in Multilayered Reinforced Nonlocal Plates under Nonlinearly Varying Initial Stress. Eng 2020, 1, 31-47. https://doi.org/10.3390/eng1010003
Farajpour MR, Shahidi AR, Farajpour A. Wave Dispersion in Multilayered Reinforced Nonlocal Plates under Nonlinearly Varying Initial Stress. Eng. 2020; 1(1):31-47. https://doi.org/10.3390/eng1010003
Chicago/Turabian StyleFarajpour, Mohammad Reza, Ali Reza Shahidi, and Ali Farajpour. 2020. "Wave Dispersion in Multilayered Reinforced Nonlocal Plates under Nonlinearly Varying Initial Stress" Eng 1, no. 1: 31-47. https://doi.org/10.3390/eng1010003
APA StyleFarajpour, M. R., Shahidi, A. R., & Farajpour, A. (2020). Wave Dispersion in Multilayered Reinforced Nonlocal Plates under Nonlinearly Varying Initial Stress. Eng, 1(1), 31-47. https://doi.org/10.3390/eng1010003



