Recursive Time Series Prediction Modeling of Long-Term Trends in Surface Settlement During Railway Tunnel Construction
Abstract
1. Introduction
- Peck’s formula does not apply to shallow-buried tunnels [24], and it is more sensitive to geological conditions, making parameter determination difficult and greatly affecting prediction accuracy in areas with complex and variable geological conditions.
- Numerical simulation methods mainly study the settlement trough of the tunnel section surface settlement and cannot predict the long-term trend of surface settlement.
- Machine learning multi-input predictions based on static geological conditions, construction parameters, and other data all fail to capture the dynamic changes in the construction process. Additionally, the currently used machine learning algorithms have deficiencies. For example, BP neural networks are slow, require a large amount of data for training, and are prone to overfitting [27]. SVR only applies to small data samples, and selecting kernel functions is challenging [28]. The LSTM model is prone to overfitting and contains multiple parameters, which results in a long training time.
- The current time series surface settlement prediction mostly focuses on data fitting and fails to provide accurate predictions, specifically in predicting future long-term surface settlement trends based on previously recorded surface settlement data.
2. Methods
2.1. Surface Settlement Data Pre-Processing
2.1.1. Cubic Hermite Interpolation
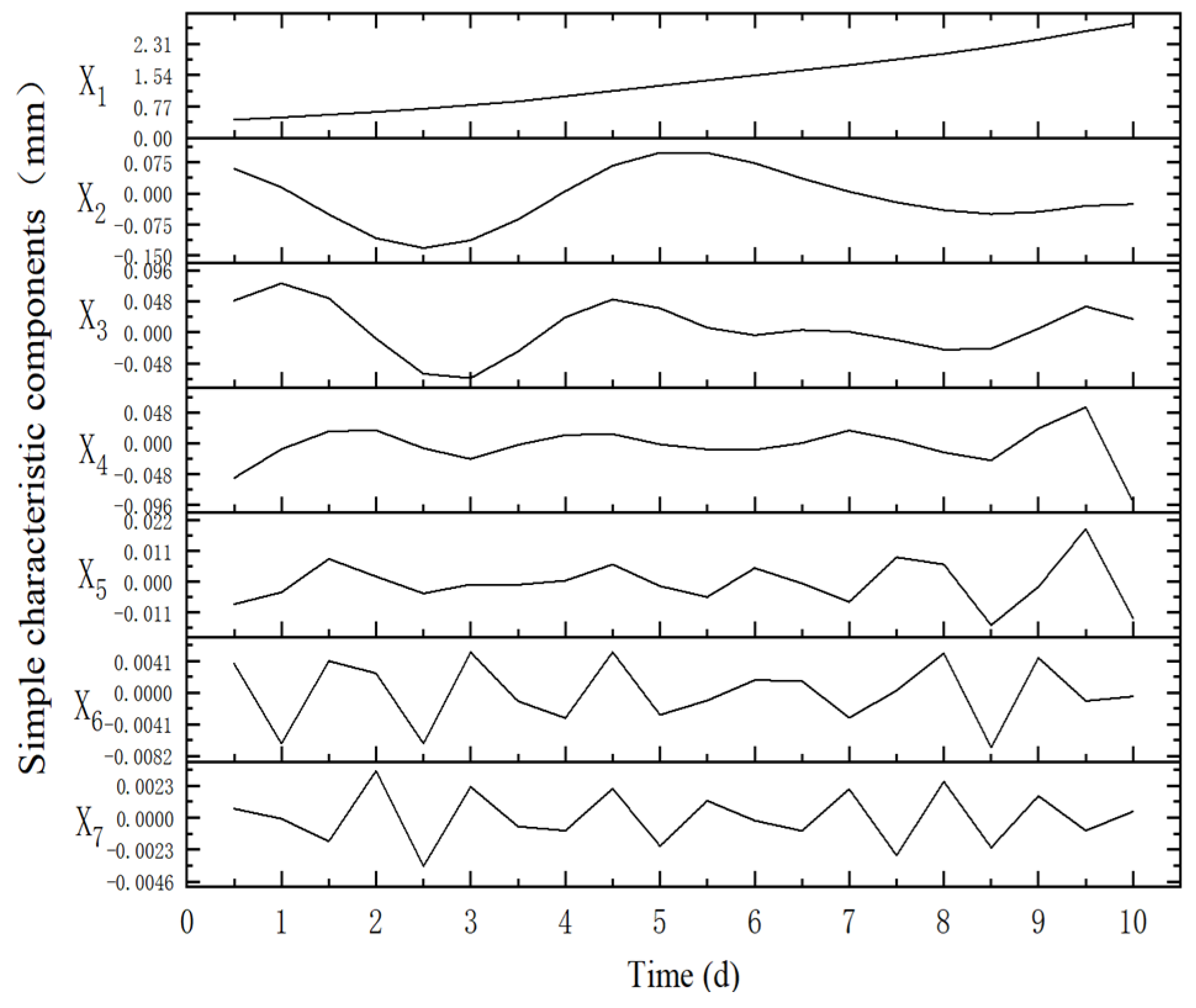
2.1.2. SSA
2.1.3. Sliding Window Method
2.2. KELM
2.3. ISCSO
2.3.1. SCSO Principle
2.3.2. SCSO
3. Surface Settlement Prediction Model Based on SSA-ISCSO-KELM
3.1. Indicators for Evaluating Projected Results
3.2. Overview of Predictive Models
4. Simulation Experiments and Analysis
4.1. Performance Analysis of the ISCSO Algorithm
4.1.1. Test Function Selection
4.1.2. Algorithm Parameterization
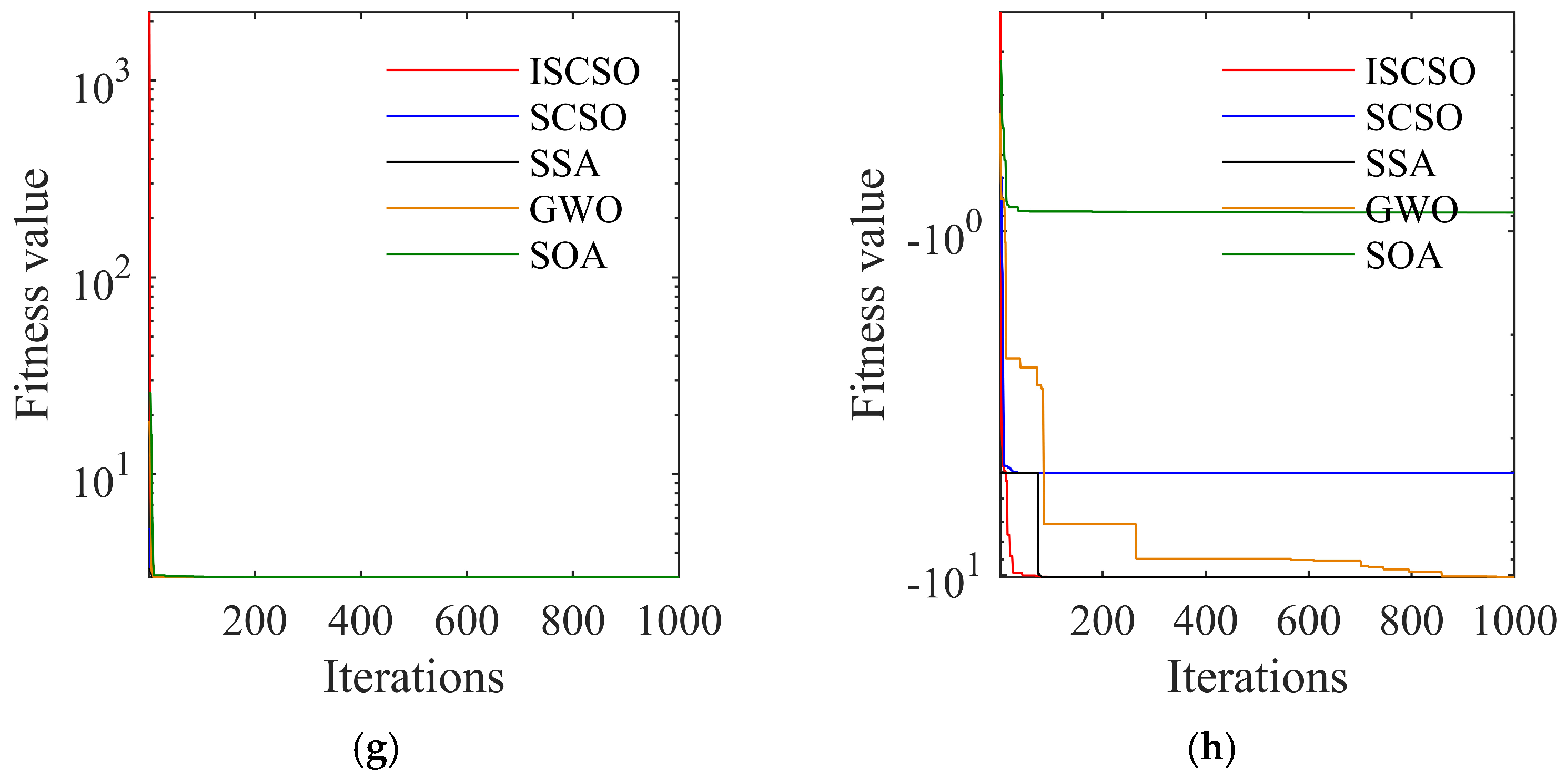
4.1.3. Comparative Analysis of Algorithm Performance
4.2. Performance Analysis of SSA-ISCSO-KELM Prediction Models
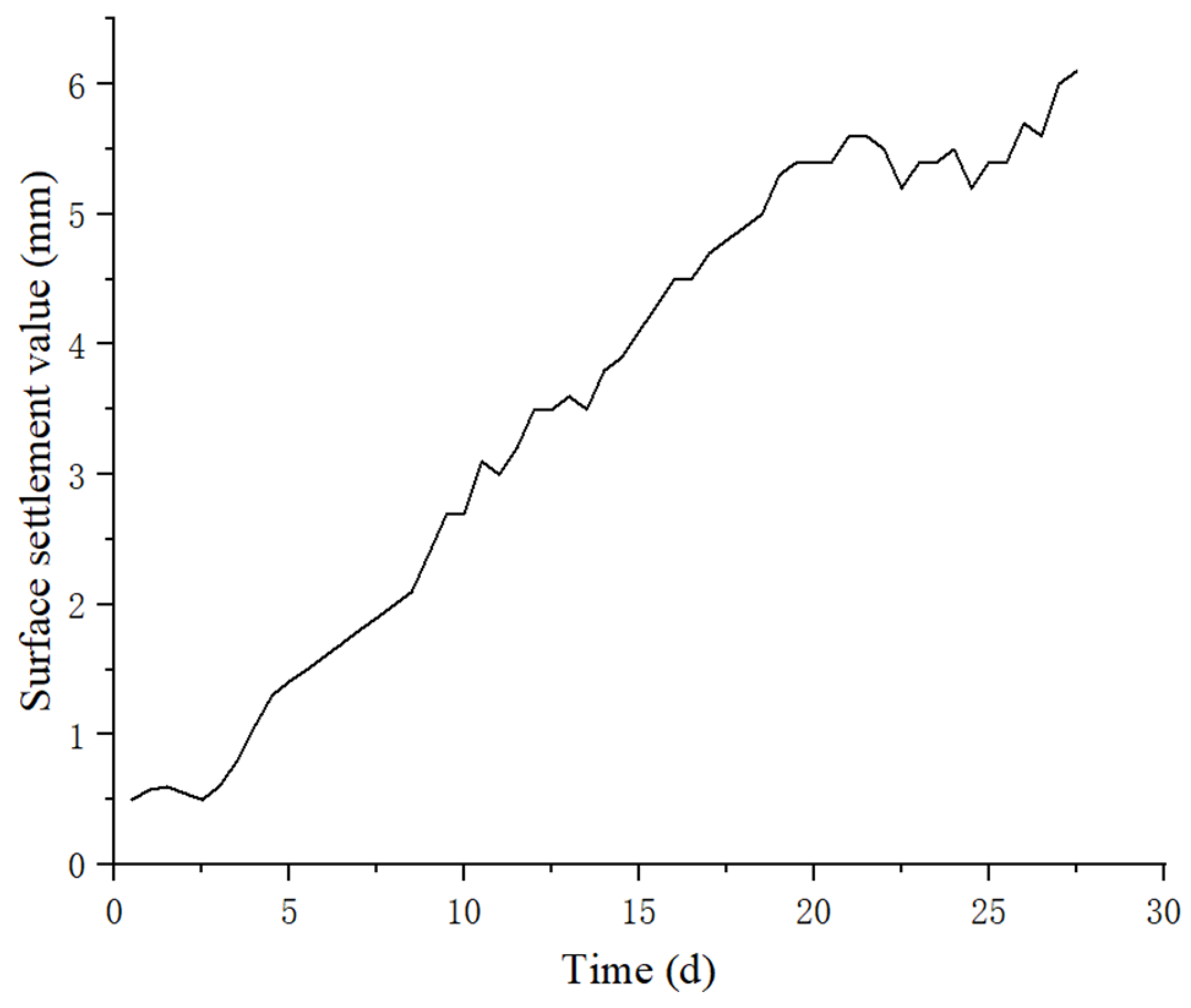
4.2.1. Data Acquisition
4.2.2. Surface Settlement Data Preprocessing
4.2.3. Model Training Predictions
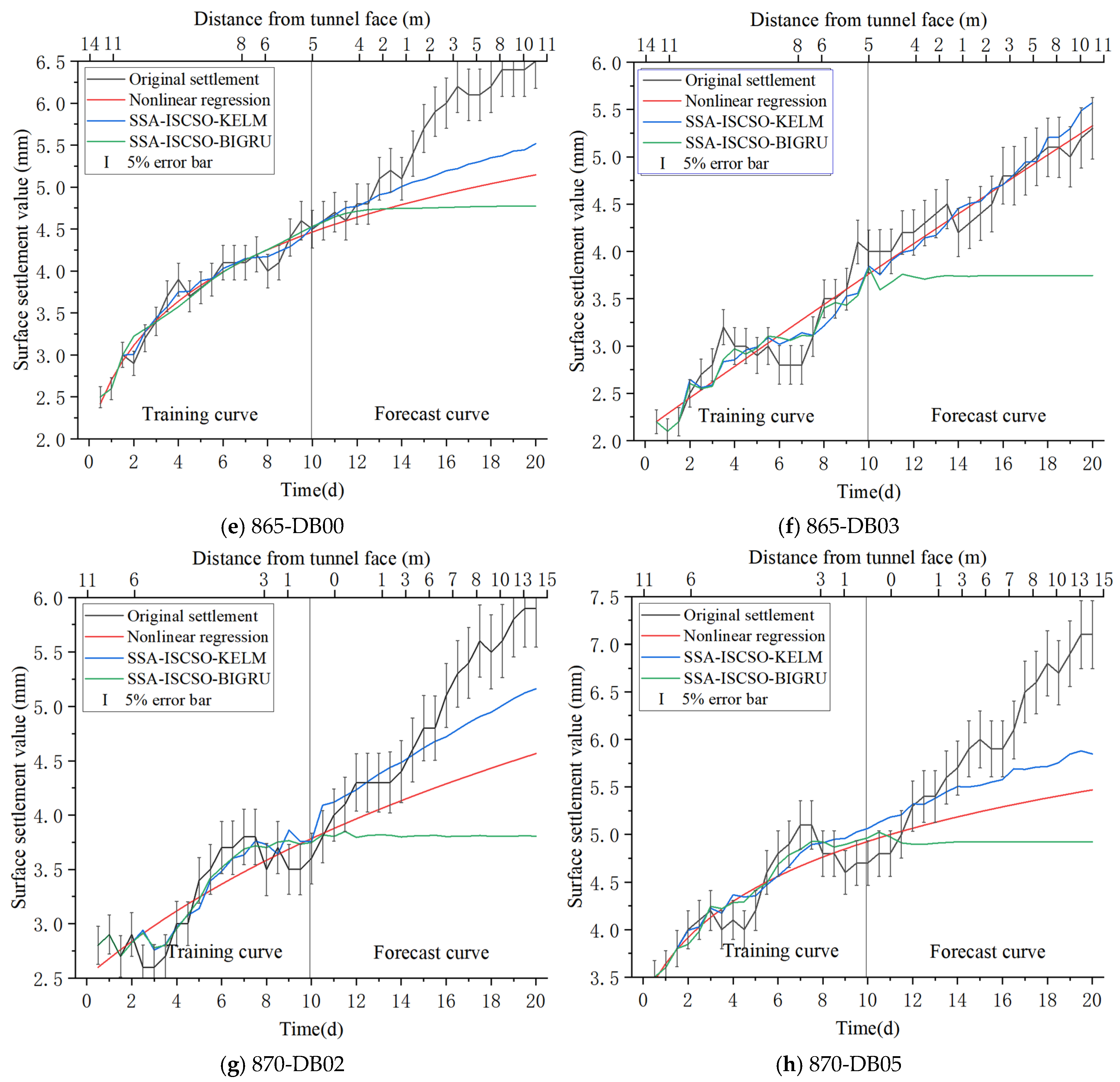
4.2.4. Analysis and Comparison of Forecast Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, F.; Wu, Z.; Wang, X.; He, Y. Safety risk assessment of railway tunnel construction by drilling and blasting method in complex and dangerous areas. J. Railw. Sci. Eng. 2023, 20, 1891–1901. [Google Scholar]
- Wang, Z.; Wong, R.C.K.; Li, S.; Qiao, L. Finite element analysis of long-term surface settlement above a shallow tunnel in soft ground. Tunn. Undergr. Space Technol. 2012, 30, 85–92. [Google Scholar]
- Zhang, F.; Xu, W.; Wang, M.; Luo, L. Risk assessment and trend research of railway tunnel construction safety. J. Saf. Environ. 2024, 24, 2473–2482. [Google Scholar]
- Saeed, H.; Uygar, E. Equation for Maximum Ground Surface Settlement due to Bored Tunnelling in Cohesive and Cohesionless Soils Obtained by Numerical Simulations. Arab. J. Sci. Eng. 2022, 47, 5139–5165. [Google Scholar] [CrossRef]
- Litwiniszyn, J. The Theories and Model Research of Movements of Ground. Available online: https://www.researchgate.net/publication/285379913_The_theories_and_model_research_of_movements_of_ground (accessed on 1 December 2024).
- Swoboda, G.; Abu-Krisha, A. Three-dimensional numerical modelling for TBM tunnelling in consolidated clay. Tunn. Undergr. Space Technol. 1999, 14, 327–333. [Google Scholar] [CrossRef]
- Sagaseta, C. Analysis of undraind soil deformation due to ground loss. Géotechnique 1987, 37, 301–320. [Google Scholar] [CrossRef]
- Peck, R.B. Deep Excavation and tunnelling in soft ground. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 25–29 August 1969; Volume 4, pp. 225–290. [Google Scholar]
- Khademian, A.; Abdollahipour, H.; Bagherpour, R.; Faramarzi, L. Model uncertainty of various settlement estimation methods in shallow tunnels excavation; case study: Qom subway tunnel. J. Afr. Earth Sci. 2017, 134, 658–664. [Google Scholar] [CrossRef]
- Ma, Z.; Xie, X.; Jia, H.; Zhao, J.; He, S.; Wang, X. Prediction and Application of Surface Settlement of Shallow Buried Tunnels Taking into Account Strata Slip Cracks. Processes 2023, 11, 1575. [Google Scholar] [CrossRef]
- Xu, Q.; Zhu, Y.; Lei, S.; Liu, Y.; Zhao, W.; Fang, Z.; Wang, C.; Xu, S. Improved stochastic medium theoretical model for predicting deformation of existing tunnels and strata caused by excavation of new undercrossing tunnels. Chin. J. Geotech. Eng. 2023, 45, 301–309. [Google Scholar]
- Shang, X.; Miao, S.; Wang, H.; Yang, P.; Xia, D. A prediction model for surface settlement during the construction of variable cross-section tunnels under existing structures based on stochastic medium theory. Tunn. Undergr. Space Technol. 2024, 155, 106177. [Google Scholar] [CrossRef]
- Thai, D.N.; Kien, D.V.; Vi, P.V.; Quang, N.V. Prediction of Surface Settlement Due to Twin Tunnel Construction in Soft Ground of Hanoi Metro Line 03. Int. J. GEOMATE 2022, 22, 66–72. [Google Scholar]
- Singh, D.K.; Aromal, V.; Mandal, A. Prediction of surface settlements in subway tunnels by regression analysis. Int. J. Geotech. Eng. 2020, 14, 836–842. [Google Scholar] [CrossRef]
- Maroof, A.; Mohammadzadeh, S.D.; Karballaeezadeh, N.; Bajgiran, K.S.; Mosavi, A.; Felde, I. Investigation of Empirical and Analytical Methods Accuracy for Surface Settlement Prediction in Train Tunnel Excavation Projects. Acta Polytech. Hung. 2024, 21, 167–186. [Google Scholar] [CrossRef]
- Ercelebi, S.G.; Copur, H.; Ocak, I. Surface settlement predictions for Istanbul Metro tunnels excavated by EPB-TBM. Environ. Earth Sci. 2010, 62, 357–365. [Google Scholar] [CrossRef]
- Fattah, M.Y.; Shlash, K.T.; Salim, N.M. Prediction of settlement trough induced by tunneling in cohesive ground. Acta Geotech. 2012, 8, 167–179. [Google Scholar] [CrossRef]
- Hu, D.; Hu, Y.; Yi, S.; Liang, X.; Li, Y.; Yang, X. Prediction method of surface settlement of rectangular pipe jacking tunnel based on improved PSO-BP neural network. Sci. Rep. 2023, 13, 1–15. [Google Scholar] [CrossRef]
- Ambrožič, T.; Turk, G. Prediction of subsidence due to underground mining by artificial neural networks. Comput. Geosci. 2003, 29, 627–637. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D.; Donta, P.K.; Amgoth, T. Land subsidence prediction using recurrent neural networks. Stoch. Environ. Res. Risk Assess. 2021, 36, 373–388. [Google Scholar] [CrossRef]
- Bai, X.; Rong, M.; Wen, Z.; Zhang, N. Prediction of Surface Settlement in Construction Stage of Earth Pressure Balance Shield Tunnel Based on Differential Evolution Algorithm-Support Vector Regression Machine. Tunn. Constr. 2021, 41, 336–345. [Google Scholar]
- Wang, S.H.; Zhu, B.Q. Time series prediction for ground settlement in portal section of mountain tunnels. Chin. J. Geotech. Eng. 2021, 43, 813–821. [Google Scholar]
- Yin, Q.; Zhou, Y.; Rao, J.A. Deep learning-based method for predicting surface settlement induced by shield tunnel construction. J. Cent. South Univ. (Sci. Technol.) 2024, 55, 607–617. [Google Scholar]
- Han, X.; Li, N.; Standing, J.R. An adaptability study of Gaussian equation applied to predicting ground settlements induced by tunneling in China. Rock Soil Mech. 2007, 1, 23–28. [Google Scholar]
- Franza, A.; Marshall, A.M. Empirical and semi-analytical methods for evaluating tunnelling-induced ground movements in sands. Tunn. Undergr. Space Technol. 2019, 88, 47–62. [Google Scholar] [CrossRef]
- Song, Z.; Tian, X.; Zhang, Y. A New Modified Peck Formula for Predicting the Surface Settlement Based on Stochastic Medium Theory. Adv. Civ. Eng. 2019, 7328190. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Y.; Guo, J.; Chen, J. An Optimized Adaptive BP Neural Network Based on Improved Lion Swarm Optimization Algorithm and Its Applications. Arab. J. Sci. Eng. 2023, 49, 3417–3434. [Google Scholar] [CrossRef]
- Jin, C.; Jin, S.-W. Software reliability prediction model based on support vector regression with improved estimation of distribution algorithms. Appl. Soft Comput. 2014, 15, 113–120. [Google Scholar] [CrossRef]
- QCR 9218-2024; Technical Specification for Monitoring and Measurement of Railway Tunnels. China State Railway Group Co., Ltd.: Beijing, China, 2024.
- Golyandina, N.; Korobeynikov, A. Basic Singular Spectrum Analysis and forecasting with R. Comput. Stat. Data Anal. 2014, 71, 934–954. [Google Scholar] [CrossRef]
- Yang, X.; Ren, Z.; Zhou, G.; Yi, J.; He, Y. CNN-BiLSTM Short-term Air Conditioning Load Prediction Model Based on Singular Spectrum Analysis. Chin. J. 2024, 52, 64–73. [Google Scholar]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.M.; Ding, X.J.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2012, 42, 513–529. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2022, 39, 2627–2651. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.S. Improved Whale Optimization Algorithm Based on Nonlinear Adaptive Weight and Golden Sine Operator. IEEE Access 2020, 8, 77013–77048. [Google Scholar] [CrossRef]

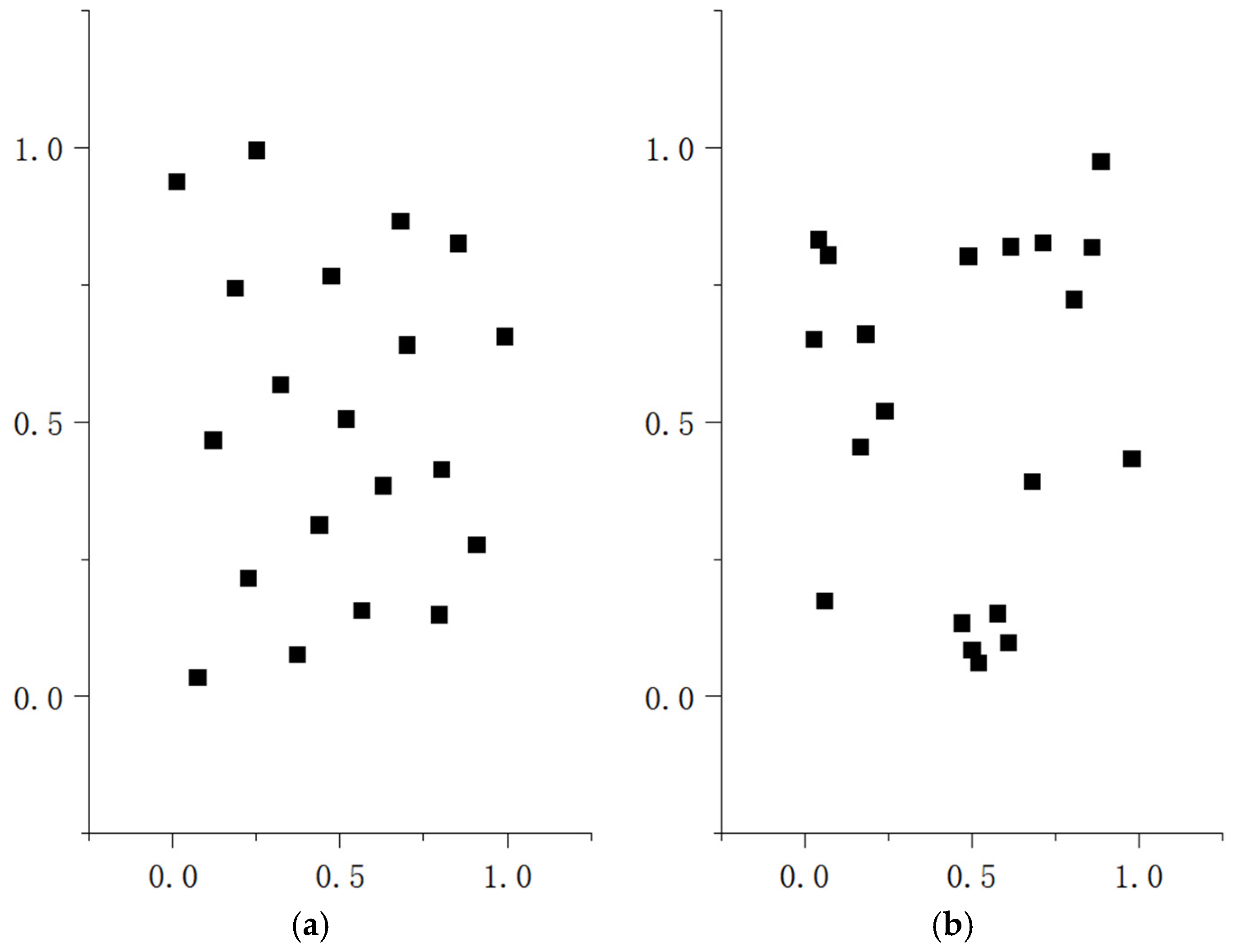


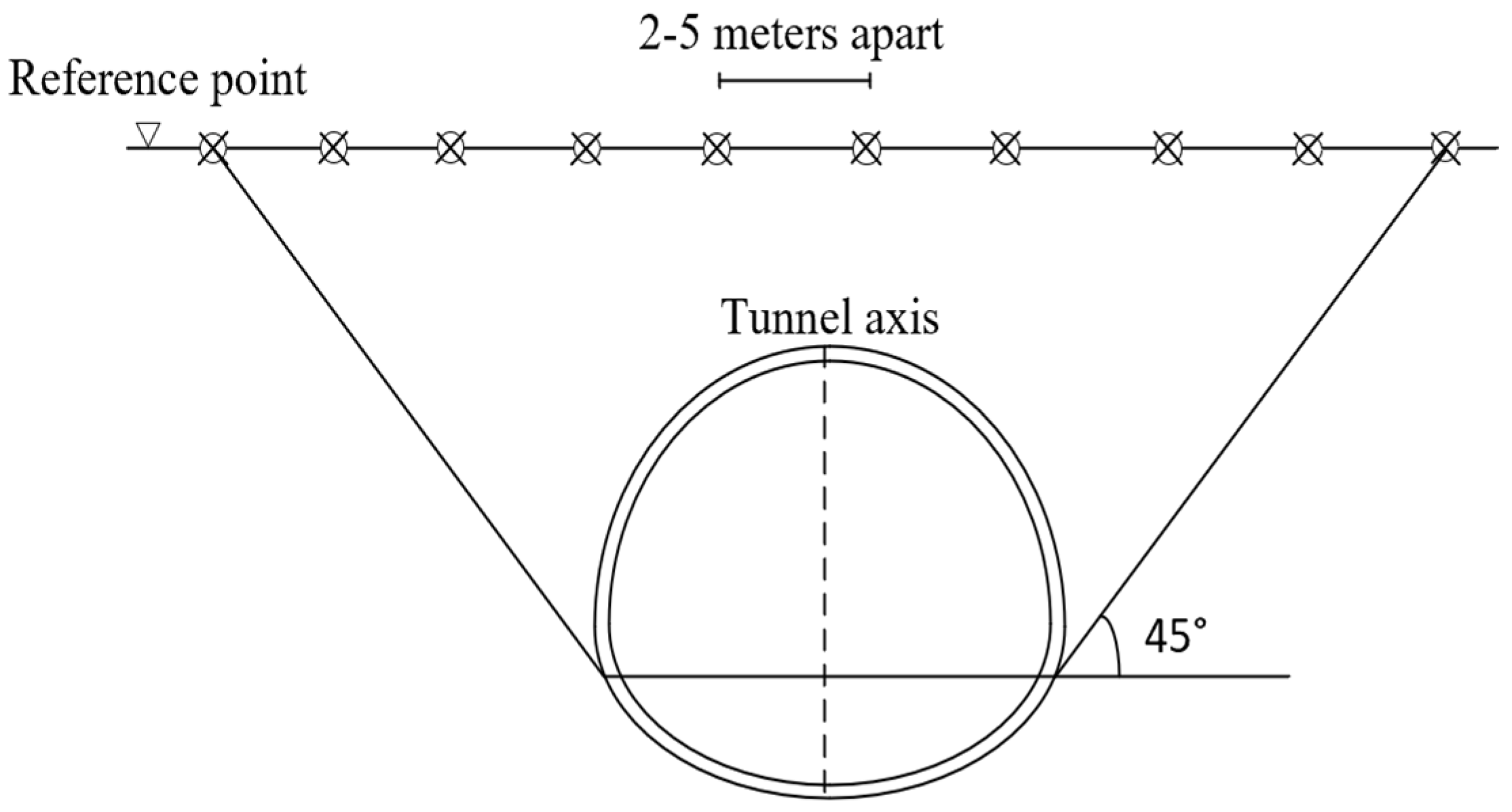


| Distance of Monitoring Section from Excavation Surface(m) | Monitoring Frequency |
|---|---|
| (0–1) B | Two times/d |
| (1–2) B | One time/d |
| (2–5) B | Two times/two to three d |
| >5 B | One time/seven d |
| Function Name | Function Formula | Dimension | Test Range | Optimal Solution |
|---|---|---|---|---|
| Sphere | 30 | [−100, 100] | 0 | |
| Schwefel’s Problem 2.22 | 30 | [−100, 100] | 0 | |
| Schwefel’s Problem 2.21 | 30 | [−100, 100] | 0 | |
| Quartic | 30 | [−1.28, 1.28] | 0 | |
| Ackley’s | 30 | [−32, 32] | 0 | |
| Kowalik’s | 4 | [−5, 5] | 0.003075 | |
| Goldstein-Price | × | 2 | [−2, 2] | 3 |
| Shekel’s | 4 | [0, 10] | −10 |
| Optimization Algorithm | Parameterization |
|---|---|
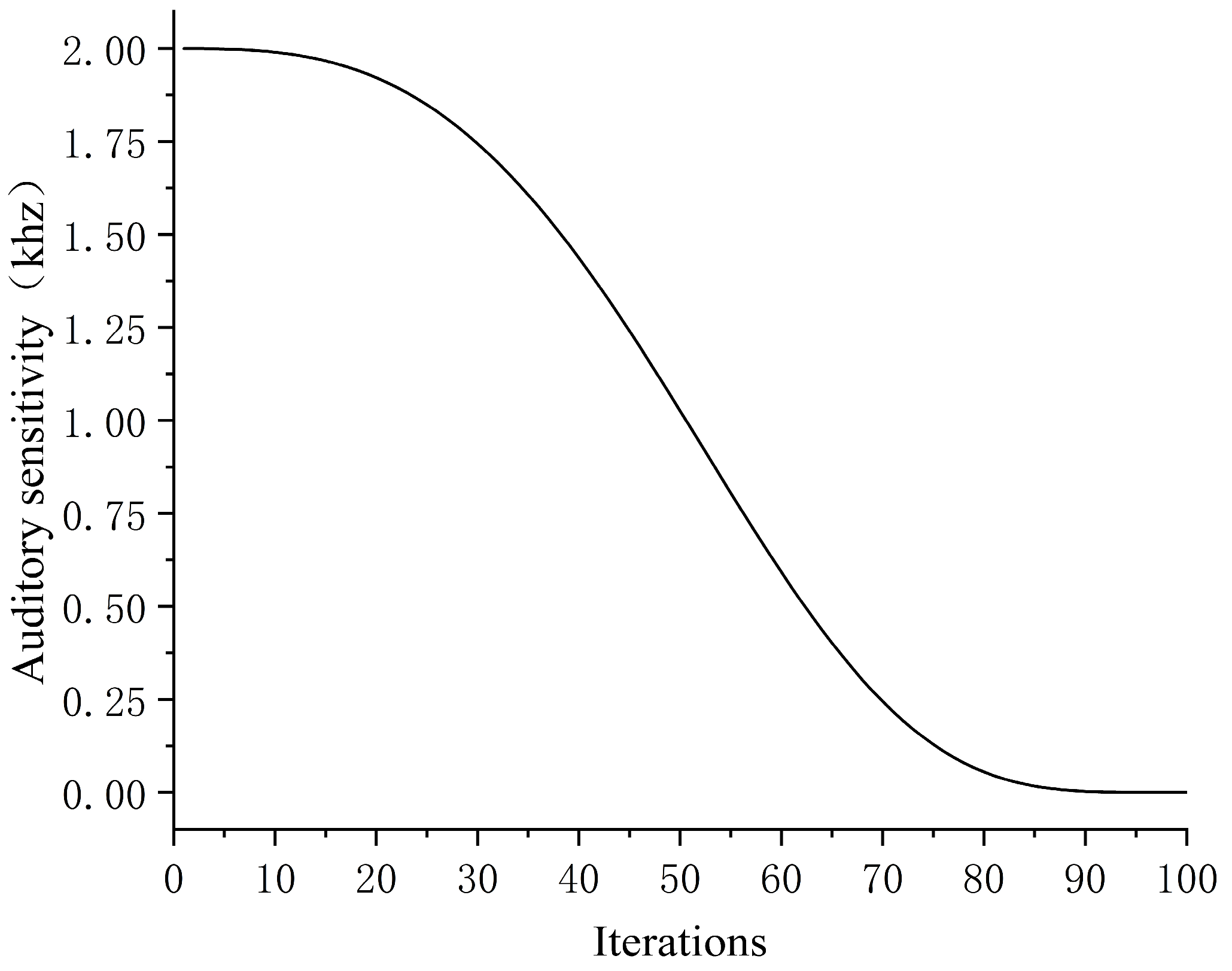
| ISCSO | adaptive nonlinear decrease from 2 to 0 |
| SCSO | adaptive nonlinear decrease from 2 to 0 |
| SSA | ST = 0.8, PD = 0.2, SD = 0.2 |
| GWO | a adaptive linear decrease from 2 to 0 |
| SOA | fc adaptive linear decrease from 2 to 0 |
| Fn | ISCSO | SCSO | SSA | GWO | SOA | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Average Value | Standard Deviation | Average Value | Standard Deviation | Average Value | Standard Deviation | Average Value | Standard Deviation | Average Value | Standard Deviation | |
| F1 | 1.83 × 10−264 | 0 | 6.90 × 10−237 | 0 | 2.85 × 10−105 | 1.98 × 10−104 | 3.83 × 10−70 | 8.93 × 10−70 | 1.13 × 10−15 | 4.03 × 10−15 |
| F2 | 1.93 × 10−135 | 1.14 × 10−134 | 2.12 × 10−123 | 8.92 × 10−123 | 2.34 × 10−89 | 1.64 × 10−88 | 6.90 × 10−40 | 5.71 × 10−40 | 3.45 × 10−14 | 1.19 × 10−13 |
| F3 | 2.01 × 10−119 | 1.38 × 10−118 | 2.33 × 10−102 | 1.48 × 10−101 | 1.58 × 10−44 | 1.06 × 10−43 | 1.52 × 10−17 | 2.94 × 10−17 | 0.0089404 | 0.0122475 |
| F4 | 3.86 × 10−5 | 0.0001051 | 4.56 × 10−05 | 5.28 × 10−5 | 0.0001310 | 0.0001272 | 0.0004439 | 0.0002373 | 0.0211484 | 0.0115433 |
| F5 | 8.88 × 10−16 | 0 | 8.88 × 10−16 | 0 | 8.88 × 10−16 | 0 | 1.35 × 10−14 | 2.58 × 10−15 | 1.46 × 10−9 | 1.96 × 10−9 |
| F6 | 0.0003074 | 6.469 × 10−10 | 0.0004723 | 0.0003517 | 0.0003101 | 5.24 × 10−6 | 0.0032068 | 0.0069275 | 0.0010744 | 0.0003040 |
| F7 | 3.0000009 | 1.13 × 10−06 | 3.0000011 | 1.739 × 10−6 | 4.08 | 5.2908978 | 3.0000031 | 3.12 × 10−6 | 3.0000007 | 1.64 × 10−6 |
| F8 | −10.15319 | 5.80 × 10−12 | −5.909652 | 2.2726361 | −10.05124 | 0.713720 | −9.442788 | 1.759854 | −1.219453 | 0.803839 |
| Predictive Model | Population Size | Maximum Iterations | Parameterization | Search Boundary |
|---|---|---|---|---|
| SSA-ISCSO-KELM | 200 | 400 | Regularization coefficients, kernel parameters | [−1017, 1017] |
| SSA-ISCSO-BIGRU | 100 | 200 | Learning rate; Learning rate decline factor; Regularization factor; Number of hidden layers | [5 × 10−10, 1]; [5 × 10−10, 1]; [0, 100]; [1, 15] |
| Predictive Model | 855-DB04 | MAE | MSE | RMSE | MAPE | MBE |
|---|---|---|---|---|---|---|
| Nonlinear regression | Forecast 5d | 0.148 | 0.028 | 0.166 | 4.953% | 0.032 |
| SSA-ISCSO-KELM | 0.213 | 0.069 | 0.260 | 5.741% | −0.111 | |
| SSA-ISCSO-BIGRU | 1.010 | 1.373 | 1.146 | 30.461% | −0.862 | |
| Nonlinear regression | Forecast 10d | 0.286 | 0.132 | 0.363 | 8.077% | 0.224 |
| SSA-ISCSO-KELM | 0.221 | 0.075 | 0.265 | 5.722% | 0.026 | |
| SSA-ISCSO-BIGRU | 1.393 | 2.380 | 1.502 | 38.568% | −1.204 | |
| Predictive model | 855-DB08 | MAE | MSE | RMSE | MAPE | MBE |
| Nonlinear regression | Forecast 5 d | 0.530 | 0.331 | 0.575 | 16.561% | −0.530 |
| SSA-ISCSO-KELM | 0.205 | 0.059 | 0.231 | 6.632% | −0.162 | |
| SSA-ISCSO-BIGRU | 0.899 | 1.030 | 1.013 | 27.556% | −0.880 | |
| Nonlinear regression | Forecast 10d | 0.770 | 0.695 | 0.834 | 19.354% | −0.770 |
| SSA-ISCSO-KELM | 0.221 | 0.077 | 0.258 | 5.861% | −0.138 | |
| SSA-ISCSO-BIGRU | 1.624 | 3.388 | 1.839 | 39.482% | −1.610 | |
| Predictive model | 860-DB01 | MAE | MSE | RMSE | MAPE | MBE |
| Nonlinear regression | Forecast 5 d | 0.250 | 0.090 | 0.299 | 7.393% | −0.209 |
| SSA-ISCSO-KELM | 0.207 | 0.062 | 0.244 | 6.653% | −0.085 | |
| SSA-ISCSO-BIGRU | 0.270 | 0.103 | 0.312 | 8.783% | 0.382 | |
| Nonlinear regression | Forecast 10d | 0.347 | 0.147 | 0.384 | 9.184% | −0.326 |
| SSA-ISCSO-KELM | 0.226 | 0.073 | 0.259 | 6.343% | −0.152 | |
| SSA-ISCSO-BIGRU | 0.367 | 0.203 | 0.435 | 10.345% | 0.388 | |
| Nonlinear regression | Forecast 5d | 0.188 | 0.112 | 0.334 | 5.212% | −0.173 |
| SSA-ISCSO-KELM | 0.192 | 0.109 | 0.329 | 5.428% | −0.130 | |
| SSA-ISCSO-BIGRU | 0.434 | 0.362 | 0.601 | 12.803% | −0.393 | |
| Nonlinear regression | Forecast 10d | 0.882 | 1.369 | 1.170 | 18.113% | −0.875 |
| SSA-ISCSO-KELM | 0.872 | 1.381 | 1.173 | 17.955% | −0.832 | |
| SSA-ISCSO-BIGRU | 1.398 | 3.109 | 1.763 | 29.663% | −1.340 | |
| Predictive model | 865-DB00 | MAE | MSE | RMSE | MAPE | MBE |
| Nonlinear regression | Forecast 5d | 0.306 | 0.154 | 0.393 | 5.826% | −0.307 |
| SSA-ISCSO-KELM | 0.183 | 0.066 | 0.254 | 3.469% | −0.136 | |
| SSA-ISCSO-BIGRU | 0.311 | 0.184 | 0.427 | 5.877% | −0.291 | |
| Nonlinear regression | Forecast 10d | 0.751 | 0.800 | 0.894 | 12.513% | −0.751 |
| SSA-ISCSO-KELM | 0.548 | 0.460 | 0.674 | 9.064% | −0.516 | |
| SSA-ISCSO-BIGRU | 0.880 | 1.160 | 1.075 | 14.546% | −0.872 | |
| Predictive model | 865-DB03 | MAE | MSE | RMSE | MAPE | MBE |
| Nonlinear regression | Forecast 5d | 0.156 | 0.026 | 0.160 | 3.668% | −0.051 |
| SSA-ISCSO-KELM | 0.151 | 0.037 | 0.193 | 3.540% | −0.074 | |
| SSA-ISCSO-BIGRU | 0.298 | 0.103 | 0.315 | 6.954% | −0.534 | |
| Nonlinear regression | Forecast 10d | 0.111 | 0.016 | 0.128 | 2.509% | −0.020 |
| SSA-ISCSO-KELM | 0.197 | 0.057 | 0.235 | 4.212% | 0.020 | |
| SSA-ISCSO-BIGRU | 0.591 | 0.470 | 0.681 | 12.295% | −0.880 | |
| Predictive model | 870-DB02 | MAE | MSE | RMSE | MAPE | MBE |
| Nonlinear regression | Forecast 5d | 0.270 | 0.095 | 0.308 | 6.109% | −0.264 |
| SSA-ISCSO-KELM | 0.165 | 0.043 | 0.203 | 3.813% | 0.050 | |
| SSA-ISCSO-BIGRU | 0.446 | 0.262 | 0.511 | 10.064% | −0.477 | |
| Nonlinear regression | Forecast 10d | 0.674 | 0.658 | 0.811 | 12.779% | −0.671 |
| SSA-ISCSO-KELM | 0.410 | 0.296 | 0.516 | 7.787% | −0.258 | |
| SSA-ISCSO-BIGRU | 1.040 | 1.523 | 1.234 | 19.773% | −1.080 | |
| Predictive model | 870-DB05 | MAE | MSE | RMSE | MAPE | MBE |
| Nonlinear regression | Forecast 5d | 0.361 | 0.180 | 0.424 | 6.457% | −0.282 |
| SSA-ISCSO-KELM | 0.256 | 0.093 | 0.303 | 4.774% | −0.039 | |
| SSA-ISCSO-BIGRU | 0.542 | 0.415 | 0.643 | 9.638% | −0.460 | |
| Nonlinear regression | Forecast 10d | 0.775 | 0.865 | 0.930 | 12.142% | −0.736 |
| SSA-ISCSO-KELM | 0.552 | 0.484 | 0.687 | 8.703% | −0.437 | |
| SSA-ISCSO-BIGRU | 1.114 | 1.719 | 1.310 | 17.509% | −1.049 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Wei, Q.; Wu, Z.; Cao, J.; Jian, D.; Xiang, L. Recursive Time Series Prediction Modeling of Long-Term Trends in Surface Settlement During Railway Tunnel Construction. CivilEng 2025, 6, 19. https://doi.org/10.3390/civileng6020019
Zhang F, Wei Q, Wu Z, Cao J, Jian D, Xiang L. Recursive Time Series Prediction Modeling of Long-Term Trends in Surface Settlement During Railway Tunnel Construction. CivilEng. 2025; 6(2):19. https://doi.org/10.3390/civileng6020019
Chicago/Turabian StyleZhang, Feilian, Qicheng Wei, Zhe Wu, Jiawei Cao, Danlin Jian, and Lantian Xiang. 2025. "Recursive Time Series Prediction Modeling of Long-Term Trends in Surface Settlement During Railway Tunnel Construction" CivilEng 6, no. 2: 19. https://doi.org/10.3390/civileng6020019
APA StyleZhang, F., Wei, Q., Wu, Z., Cao, J., Jian, D., & Xiang, L. (2025). Recursive Time Series Prediction Modeling of Long-Term Trends in Surface Settlement During Railway Tunnel Construction. CivilEng, 6(2), 19. https://doi.org/10.3390/civileng6020019







