1. Introduction
Elastic elements undergoing stick–slip motion in the presence of friction can be found in many physics and engineering systems in a range of length scales from micrometers [
1] to kilometers [
2]. In the civil engineering field, for instance, various solutions proposed for protecting buildings from earthquakes, e.g., devices for controlling the amplitude of oscillations or isolating buildings from the ground [
3,
4,
5,
6,
7,
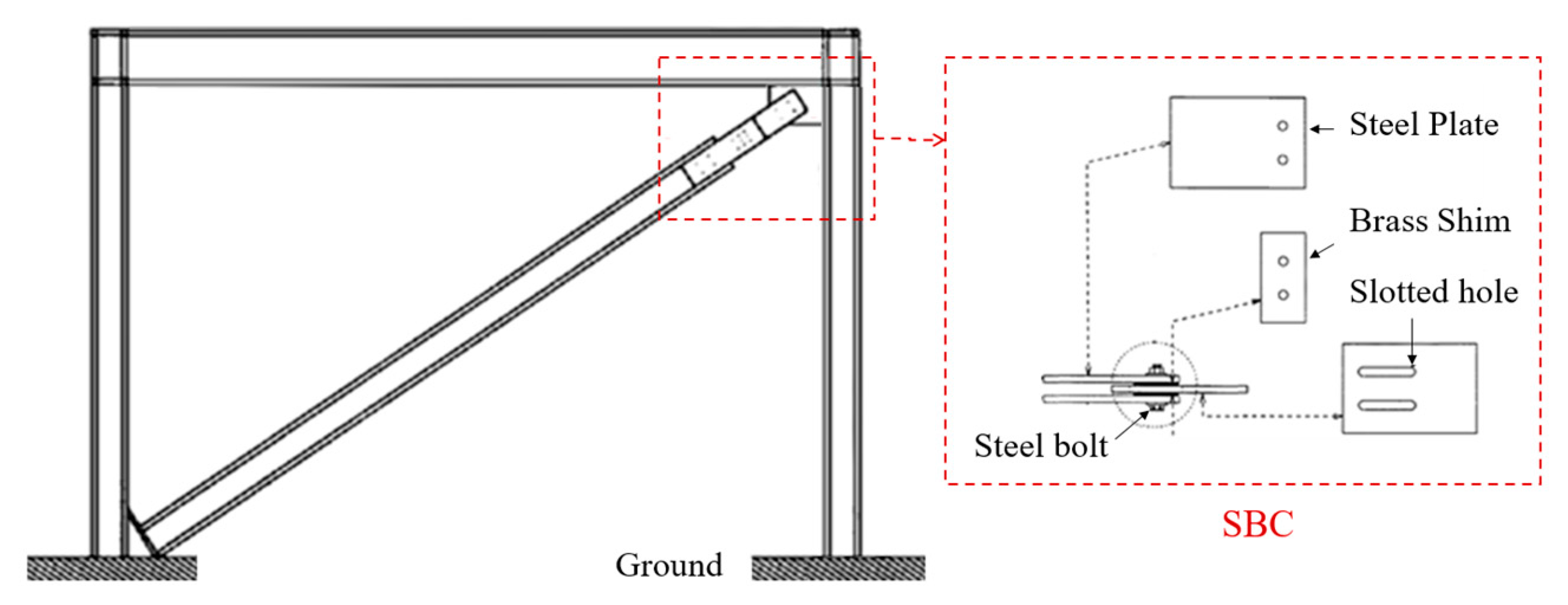
8], undergo stick–slip motions. Among the damping devices, a common solution exploits the friction force that develops between elements forced to slide with friction over each other, as in the slotted bolted connection (SBC) [
4] represented in
Figure 1. As for isolation systems, a typical solution is based on interposing sliding elements between the foundation and the base of the superstructure [
5,
6].
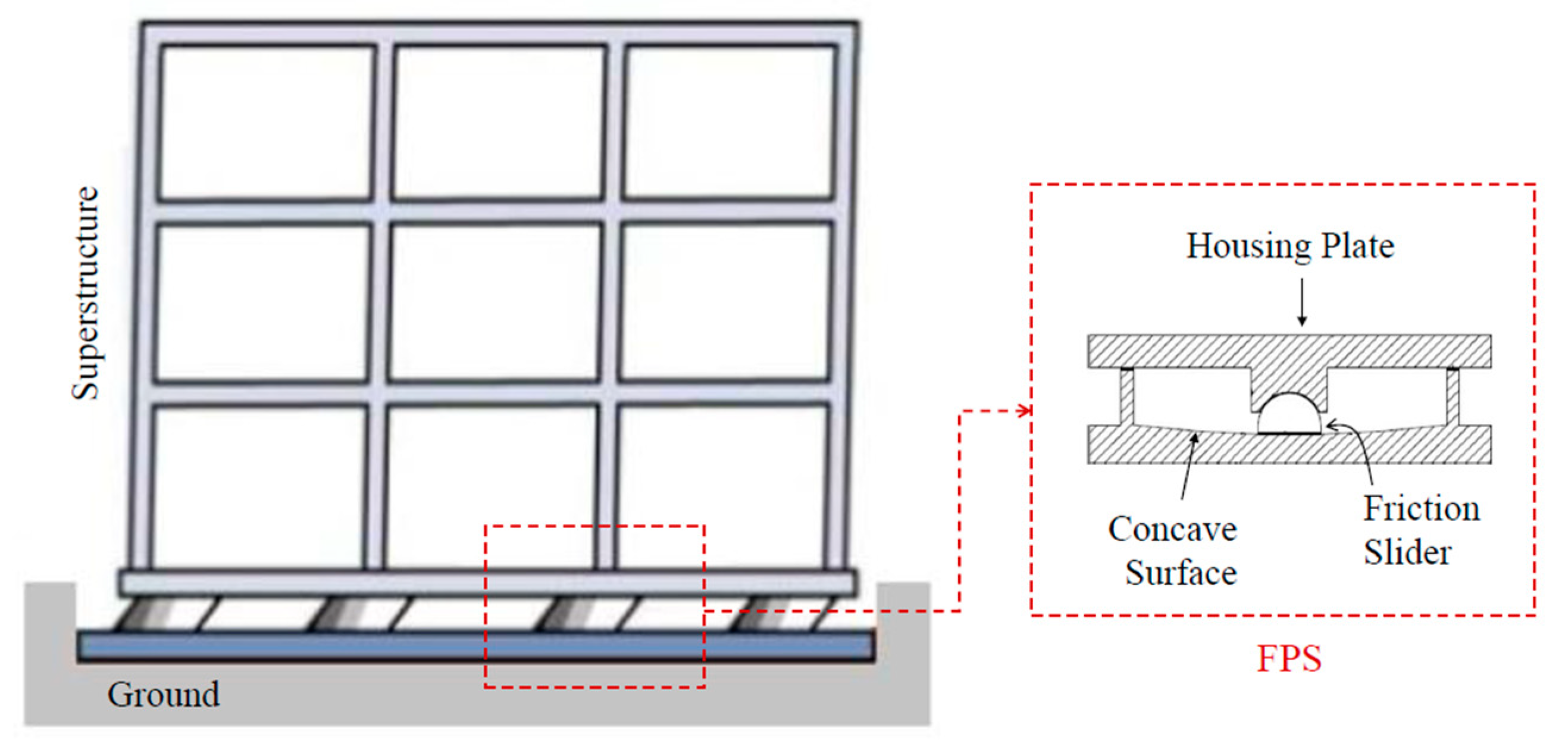
Figure 2 reports, by way of example, the case of a structure fitted with a friction pendulum system (FPS). The shear force transmitted to the superstructure via the isolation system is usually limited by keeping the coefficient of friction as low as practical to cope with strong winds and minor earthquakes without associated sliding, while sliding displacements due to significant seismic events are controlled by either high-tension springs, or laminated rubber bearings, or by the means of curved sliding surfaces, which provide the restoring force to return the structure to its equilibrium position [
9].
Seismic protection devices for buildings are a particular example of the systems containing components forced to slide with friction over other components. The systems of this sort can also be found in industrial engineering applications (e.g., wiper blades, brakes, or drill bits [
10]) and may exhibit complex dynamic behavior even when only a small number of degrees of freedom are involved.
In addition to examples from the civil and industrial engineering sectors, other examples of dynamic responses in which the stick–slip phenomenon may play an important role can be drawn from the physics of earthquakes. The Burridge–Knop, off fault model [
1] clearly highlights stick–slip dynamics during the fault movement that gives rise to seismic waves (
Figure 3). The instability of such motion can be triggered in simple models like this by assuming velocity-decreasing friction forces [
11,
12].
Over the years many studies have been conducted to better understand the dynamics of systems in which components are forced to slide with friction over other components, the ultimate objective being to identify the conditions that may disrupt their smooth, efficient functioning. The body of literature on the topic may be subdivided into two main categories. The first is represented by numerical methods, usually based on finite element models [
13]. The second (which includes the present work) is represented by analytical approaches [
7,
14], in which simplified models based on a small number of degrees of freedom are employed to describe the behavior of the system, whose equations of motion are solved analytically or semi-analytically with reduced computational effort.
The paradigmatic case of the single-degree-of-freedom system subjected to elastic and friction forces has been studied extensively over the last century. After Den Hartog’s study [
15], many researchers have addressed similar problems. Among the various contributions, some works addressing the forced oscillations of the mass–spring system are worth recalling. In 1984, Parnes [
16] and Marui and Kato [
17] studied a single-degree-of-freedom system subjected to ground motion or external forces and analyzed the influence of important parameters on the system dynamics. In 1986, Shaw [
18] discussed the stability of the long-term response of a damped system. Numerical analysis dealing with discontinuity between static and kinematic friction forces is illustrated by Leine [
19], and Hong and Liu [
20]. The chaotic response that friction can cause is outlined in the works of Popp and Stelter [
21], and is further investigated by Andreaus and Casini [
22], and Licskó and Csernák [
23]. More recent works addressed the evolution of the stick and slip phases in the system limit cycles as a function of the system parameters (see, e.g., the works of Csernák and Stépán [
24], and Butikov [
25]), or performed bifurcation analyses [
26].
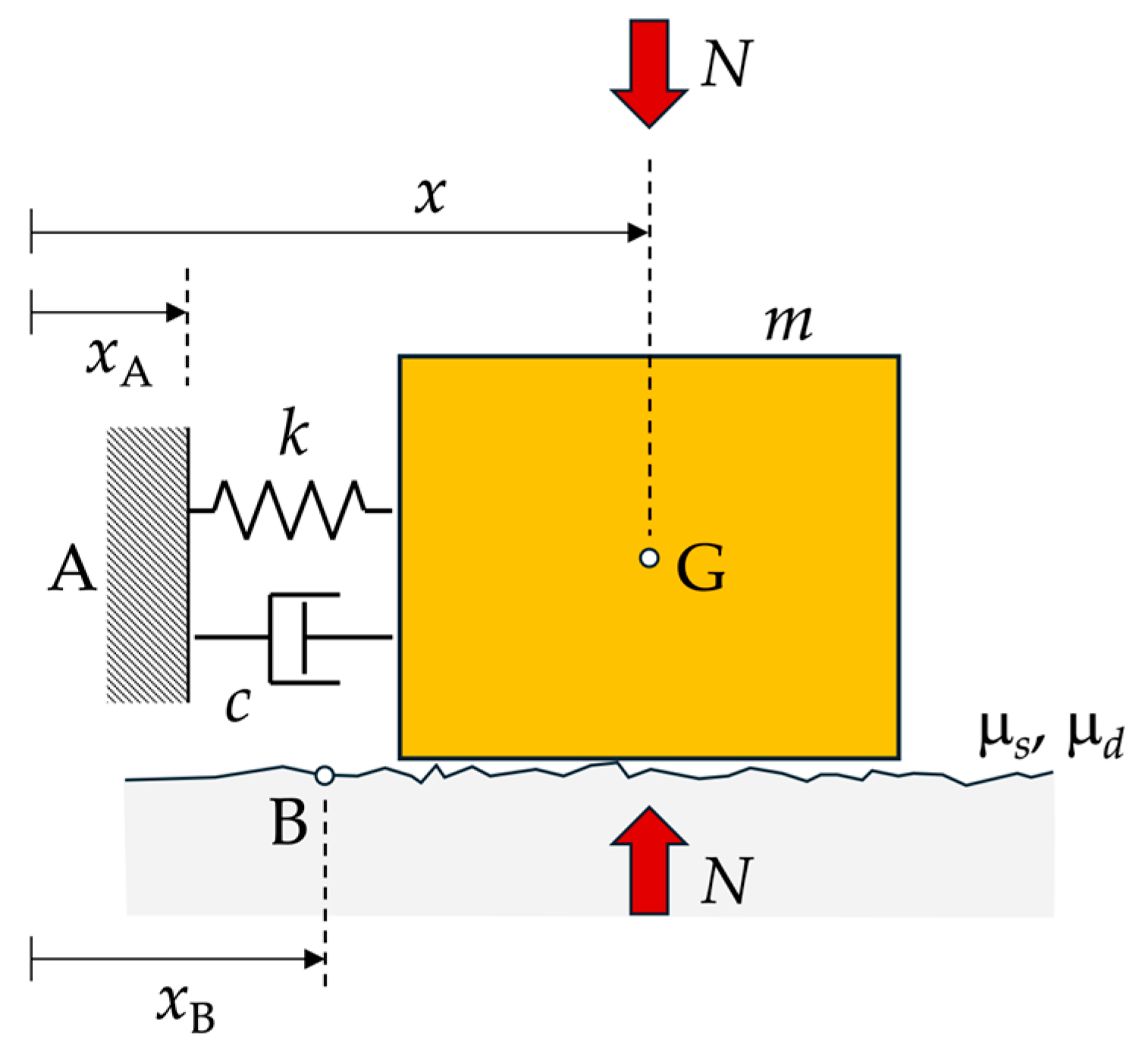
This paper presents a mathematical model that enables providing a simplified description of the dynamics of the systems like those mentioned in the foregoing. By virtue of its simplicity, the model may be used to study the dynamics of many physical systems undergoing a stick–slip motion in the presence of friction, such as structures fitted with seismic protection systems subjected to a ground motion or faults undergoing relative slip. We begin by considering the simple scheme depicted in
Figure 4, in which a rigid block (G) is connected elastically to a first rigid support (A) and is in frictional contact with a second rigid support (B). Preliminary results concerning this one degree-of-freedom model have been presented by the authors in [
11,
27,
28].
The analytical description of the system’s stick and slip phases is outlined in
Section 2 for Coulomb-like friction forces between the rigid block and moving support B. An event-driven solution scheme is adopted, consisting of identifying the transition times (if any) between the stick and slip phases and assembling the analytical expressions that hold in such phases. A description of the different types of long-term motions that such systems may undergo is provided in
Section 3. We investigate the role played by three dimensionless parameters: the ratio between the oscillation frequency of the moving support B and the natural frequency of the mass–spring system; the ratio between the kinematic and static friction forces; and finally, the ratio between the amplitude of oscillations of the moving support B and a reference length. Once such parameters are known, it is possible to foresee some features of the system’s long-term dynamic response. In this regard, reference maps are presented to provide indications of the main characteristics of the possible long-term dynamic responses of the system. Finally, in
Section 4, we illustrate numerical results that confirm the analytical findings of the present study.
2. The Mechanical Model
Finding the exact solution to non-linear dynamic problems like those mentioned in the foregoing is not a simple matter. For example, an actual building, fitted with various energy dissipation mechanisms and subjected to external actions such as those due to an earthquake may be considered as an elastic structure with an infinite number of degrees of freedom. Viscous–elastic and friction-based mechanisms are two relevant examples and make the dynamic problem non-linear and difficult to solve analytically.
In this work, we investigate some features of the non-linear dynamic response of a single-degree-of-freedom system that is connected elastically to a rigid support A and can slide with friction over a rigid support B, as represented in
Figure 3.
The system is formed by a rigid block of mass
m attached to a spring with elastic constant
k. The other end of the spring is connected to point A of a rigid support, whose position with respect to a suitable inertial reference frame is
xA(
t). The rigid block is free to slide with friction over a second rigid support, whose reference point B moves according to a prescribed law,
xB(
t). The friction force between this second rigid support and the rigid block is
Fa. The position of the block’s center of gravity (G) with respect to the inertial reference frame is
x(
t). The following equation of motion holds
The condition of null relative motion between the rigid block and rigid support moving with point B is expressed as .
In the following, we focus attention on the case in which
c = 0, point A is fixed with respect to the inertial reference frame, and point B moves with respect to it. Moreover, we set the origin of the inertial reference frame at a point O, between point A and point G, in such a way that the distance between O and A is the length of the unstrained spring. In such case, the equation of motion takes the form
where
x(
t) represents the position of the block’s center of gravity G with respect to O.
A simple harmonic motion is assumed for point B, such that , where and are the positive amplitude and angular frequency that define the motion of the point B. Note that B is at the origin O at time t = 0.
2.1. The Friction Law: A Modified Version of the Coulomb’s Formulation
When dealing with a specific application, the friction law depends heavily on the physical properties of the materials involved, as well as on the conditions of the contact surfaces, which can vary widely. Consequently, different laws have been proposed in the literature to describe the experimental evidence via state-dependent and rate-dependent approaches (Sampson [
29], Rabinowicz [
30], Pennestrì [
31]). Our aim is to investigate some features of the non-linear dynamic response of the elastic system described in the foregoing without focusing on a specific material or timescale. To this end, we assume a simple friction law which is a modified version of Coulomb’s formulation.
Let us denote by
and
the static and kinematic friction forces, respectively. In order to account in a simplified way for the short time the system needs to return to the sticking condition at the end of a sliding phase, we assume that a sticking phase following a sliding phase can only begin if the friction force does not exceed
at the first instant the relative velocity vanishes,
. In other terms, we assume following:
Hence, a sticking phase may begin only if a friction force no greater than
is required at the first instant the relative velocity vanishes, otherwise the sliding phase will continue, as also discussed in [
27,
28]. According to the rule introduced here, a sticking phase following a sliding phase may begin at any time
at which the relative velocity vanishes only if the following condition holds:
2.2. Event-Driven Solution of the Equation of Motion
In the following, we assume the observation of the block motion begins at an initial time . The block’s initial position and velocity are and , respectively. In the general case, the system’s motion may involve both sticking phases, during which the block follows the motion of the moving support B, and sliding phases, during which the block moves with respect to it. In each phase, the equation of motion may be formally written as (2), where is the non-smooth friction force (3–5).
Any sticking phase following a sliding phase will begin at a time
if both the block and the moving support have the same velocity and if the magnitude of the friction force required to start sticking at
does not exceed
. Depending on the values of the system parameters, the sticking phase may last indefinitely. In such a case, the modulus of the friction force
remains lower than
for
. Vice versa, any sliding phase following a sticking phase may begin at a time
if and only if the magnitude of the friction force on the block reaches the static value
and a friction force greater than
would be required to extend sticking to
. Under appropriate conditions, the sliding phase may also last indefinitely. In the next sections, both the sticking and sliding phases are discussed in detail. Here, as in [
27,
28], we only recall that during any sticking phase, the velocity of the rigid block coincides with that of the moving support B, while during any sliding phase, the explicit expression of the block’s motion is the following:
where constants
and
depend on the conditions holding at the beginning of the sliding phase and
.
2.3. End Time of Sticking Phases
Let us assume that the rigid block is going through a sticking phase, and let
C denote the block position at the beginning of this phase. Let us also introduce the dimensionless initial position
, with
. Simple calculations, omitted here for brevity, show that the end time
is a solution of one of the two following equations:
where
,
,
, and
, this latter denoting the dimensionless amplitude of the oscillations of the moving support B.
Equations (8) and (9) can be obtained by determining the time instant (if any) at which the dimensionless form of the sticking condition, i.e., , may no longer be satisfied.
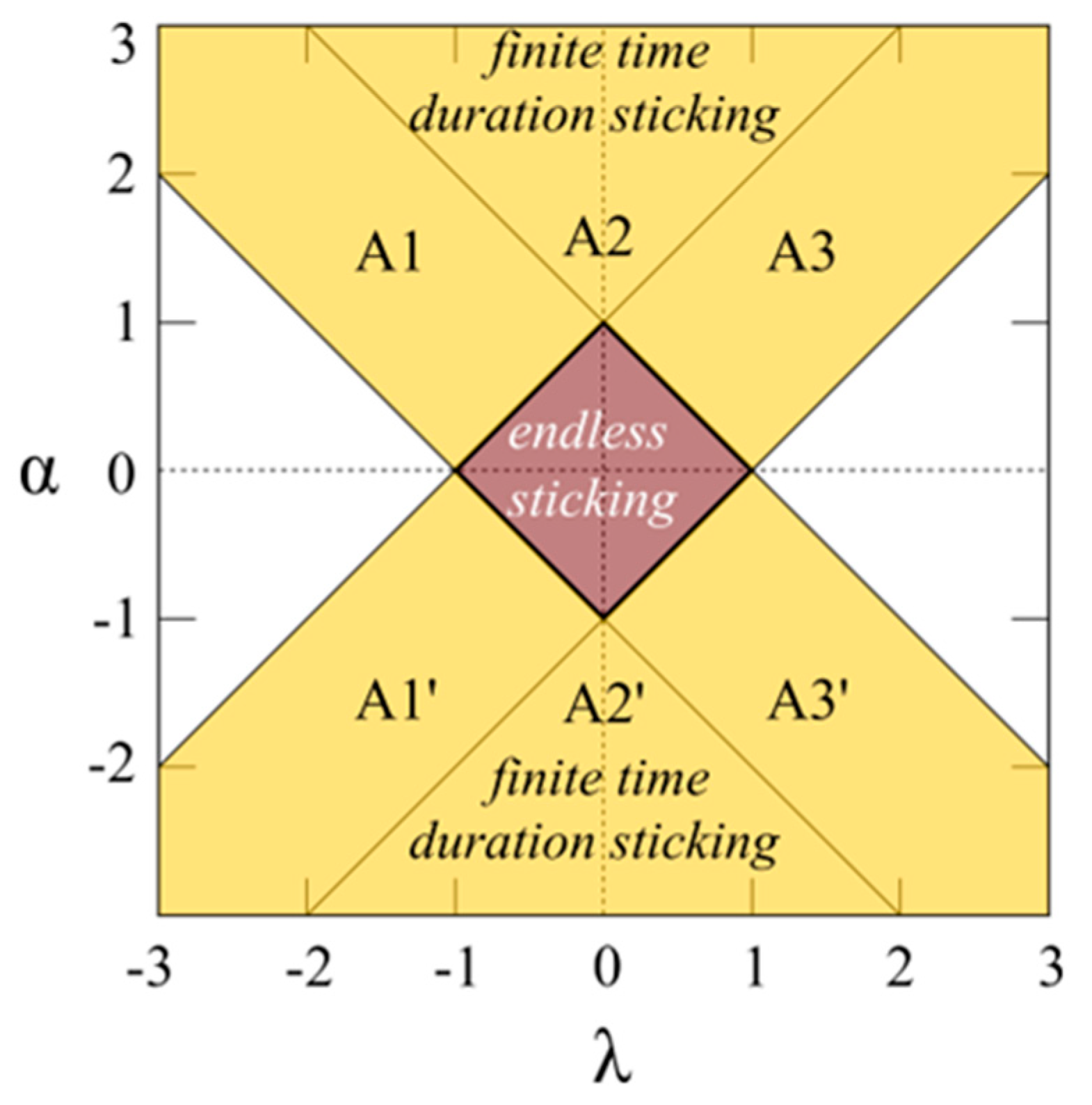
With reference to
Figure 5, the time instant
is determined according to Equation (8) in regions A1 and A1′, by Equation (9) in regions A3 and A3′, and is the lower of the two solutions to (8) and (9) in regions A2 and A2′.
As is apparent, the duration of any sticking phase can be inferred by checking the dimensionless initial position,
, of the rigid block and the dimensionless amplitude and frequency of the oscillations,
and
, of the moving support B. A sticking condition will last up to a certain time if the corresponding point (
,
) in
Figure 5 belongs to the yellow-shaded regions A1, A2, and A3 (or A1′, A2′, and A3′). On the contrary, sticking will last indefinitely if the point falls within the central diamond-shaped region. Lastly, the lateral unshaded regions are incompatible with sticking conditions.
2.4. End Time of Sliding Phases
Let us assume that the block is sliding. The necessary conditions for the sliding phase to stop at a certain time
require that the relative velocity between the block and the moving support B become zero and the additional condition (6) be fulfilled, which can be expressed by the following:
where
is the kinematic–static friction ratio.
Condition (10) ensures that the magnitude of the friction force on the block needed to start a sticking phase is not greater than . If condition (10) is not satisfied, then the friction force on the block remains greater than , a sticking phase cannot begin, and the block continues sliding with respect to the moving support.
3. Remarks on the System Limit Cycles
Limit cycles are periodic solutions to the equation of motion characterized by a net balance between the amount of energy dissipated by and supplied to the mass–spring system over each period. Different types of limit cycles may be observed for systems like those considered here [
17,
24,
25]. By following the evolution of the system, starting with different initial conditions and considering different values of its characteristic parameters,
a,
, and
, it can be observed that the system trajectories may tend towards periodic motion. Specifically, after an initial transient phase, the system may approach limit cycles during which the block keeps sliding indefinitely, other limit cycles where it keeps sticking indefinitely, and yet others where it passes from sliding to sticking in a periodic way. In this section, we consider these three types of motion.
3.1. Sticking Limit Cycles
Once a sticking phase has begun, the motion of the block is expressed as
, where C is a constant. The block will go on sticking if the friction force transmitted from the moving support does not exceed the maximum static value,
. Hence, endless sticking is possible if the following necessary condition is fulfilled
Moreover, it is straightforward to conclude that the stability of endless sticking will be assured if the following more stringent condition is fulfilled
where
is the kinematic–static friction ratio. In this regard, let it suffice to recall that if small perturbations start the block sliding, its oscillatory motion will be described by (7). Inequality (12) ensures that as soon as the relative velocity between the block and the moving support B returns to zero, the friction force needed to restore sticking will surely be lower than
, and sticking will take place again.
3.2. Sliding Limit Cycles
This section takes up a particular set of sliding limit cycles discussed in a preliminary investigation by the authors of [
27,
28]. More precisely, we consider a block that is undergoing periodic motion and assume the block slides over the moving support B without ever sticking to it. We consider a generic time interval
and, counting the time from the beginning of the period, we restrict our attention to periodic motions satisfying the following constraints:
accordingly rewriting the law of motion of the moving support as
where angle
accounts for the phase shift between the oscillations of the block and those of the moving support.
During each period two conditions are assumed: (i) first, the component of the friction force along the -axis has a prescribed sign (e.g., it is positive) over one-half of the period and the opposite sign over the other half of the period (this is referred to here as relative velocity sign condition); (ii) in addition, at the beginning of any half-period, when the relative velocity is zero, the sticking condition (10) must not be fulfilled.
In order for this kind of sliding motion to take place the phase angle
must satisfy the condition
in which the reciprocal of
cannot be an odd integer number. It is worth noting that critical values of
have previously been cited for other systems analogous to the one considered here (e.g., [
24,
25]).
Simple calculations enable concluding that the conditions imposed on the periodic sliding motion can be summarized through the single inequality
where
The stability of the periodic sliding motion considered here can be evaluated by considering the superposition of small perturbances,
, to the sliding motion. From Equation (2), we observe that
is the solution to the homogeneous equation
In other terms, small perturbances can cause the small oscillations of the system to appear around the periodic sliding motion, which may not be unconditionally stable.
3.3. The Influence of the System Parameters on Its Long-Term Response
The motion of systems like those considered in this study can be determined if the values of their characteristic parameters, such as a, , and , are known, together with the system’s initial conditions. Conversely, it appears reasonable to assume that given the values of such parameters, it should be possible to determine some features of the system’s long-term response. In other words, given a, , and , it should be possible to predict the evolution of the system and the existence of the limit cycles to which it may tend.
In this paper, we have demonstrated that conditions (11) and (17) enable making predictions about characteristic solutions, e.g., continuous sticking or continuous sliding, that may be observed. Therefore, if the system parameters
a,
, and
are assigned, it is possible to forecast some features of the system’s long-term response. For instance, if such parameters do not satisfy inequality (11), then the system cannot undergo continuous sticking and a sliding phase will ensue. Moreover, if condition (17) is not verified, the system cannot undergo the sliding motion defined in
Section 3.2. Instead, if the system verifies the conditions introduced in
Section 3.2 and its parameters are compliant with (17), then it may undergo the periodic sliding motion discussed in
Section 3.2.
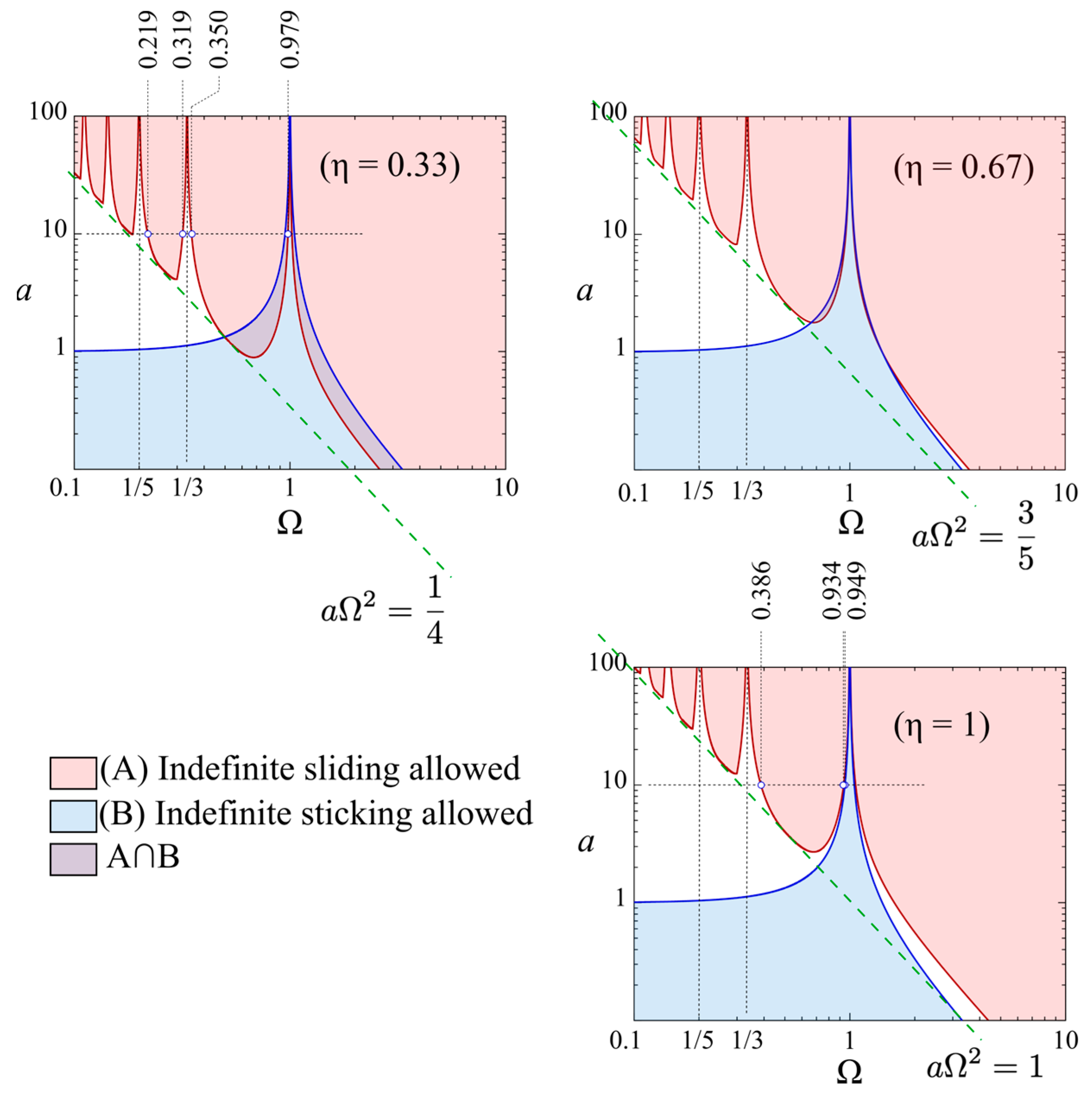
Figure 6 shows a partition of the
a-
plane in terms of long-term system responses, for three cases, namely,
= 1/3,
= 2/3,
= 1. The partition is based on conditions (11) and (17). Indefinite sliding motions are allowed in the pink regions. Indefinite sticking may take place in the blue regions. Regions not colored allow for stick–slip motions.
The dashed green line bounds from below, albeit approximately, the set of indefinite sliding motions for
in the logarithmic plots (
Figure 6). The analytical expression for this lower bound locus, for the three cases considered here (
= 1/3, 2/3, 1), is
where
is a coefficient depending on
, which for the three cases
= 1/3, 2/3, 1 can be approximated as
. It is worth observing that Equation (22) for
is similar to a condition found in Shaw [
18] for the forced sliding oscillations of a system analogous to the one studied here.
It should be cautioned that the present investigation is not conclusive. Further studies are needed which will be conducted in subsequent works to carry out an exhaustive or, at least, a wider examination of the possible limit cycles and the relevant existence conditions for systems such as those considered here. However, the results obtained, and the reference maps introduced within this work, already provide some important information.
3.4. Bifurcation Diagrams
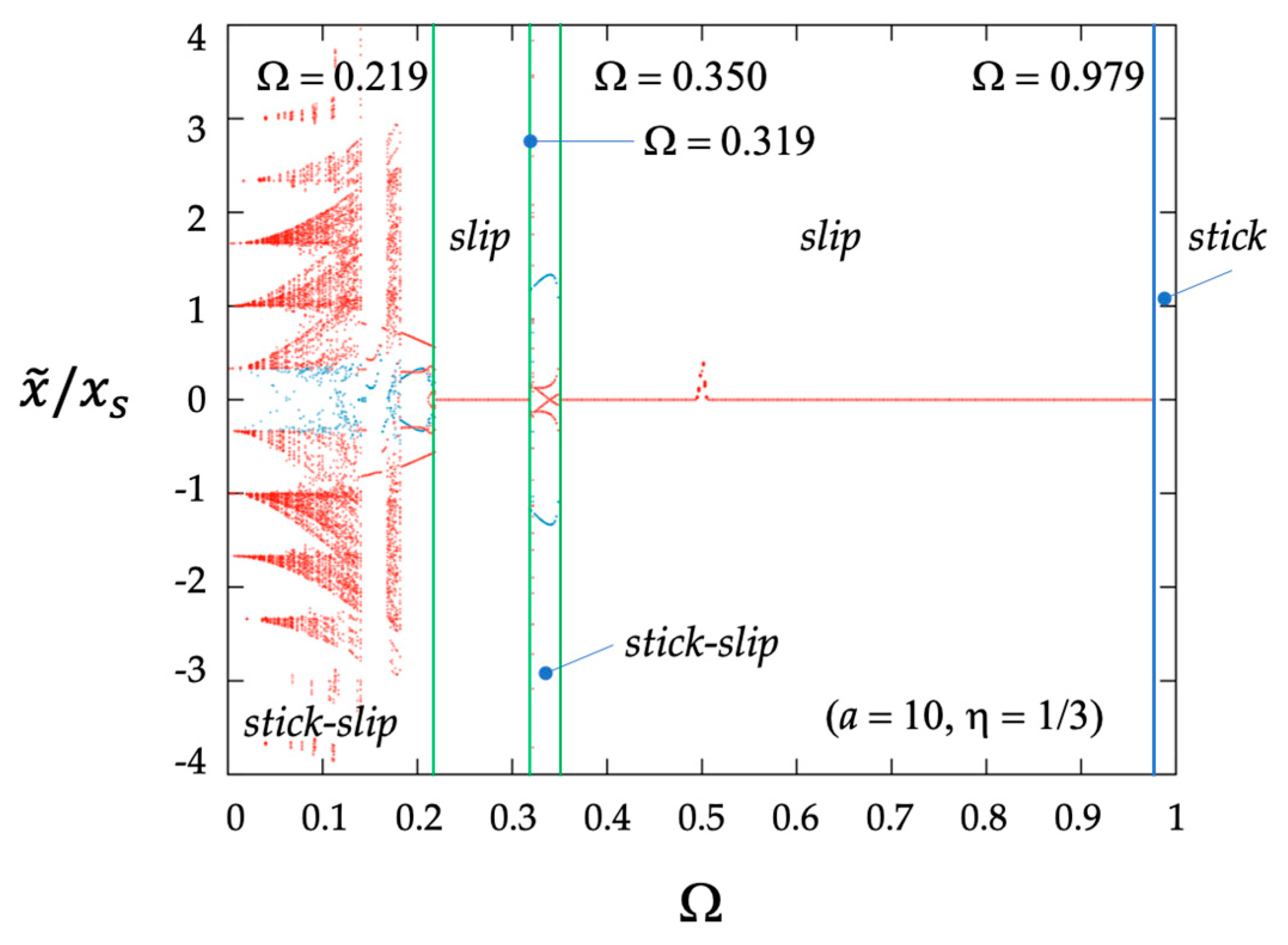
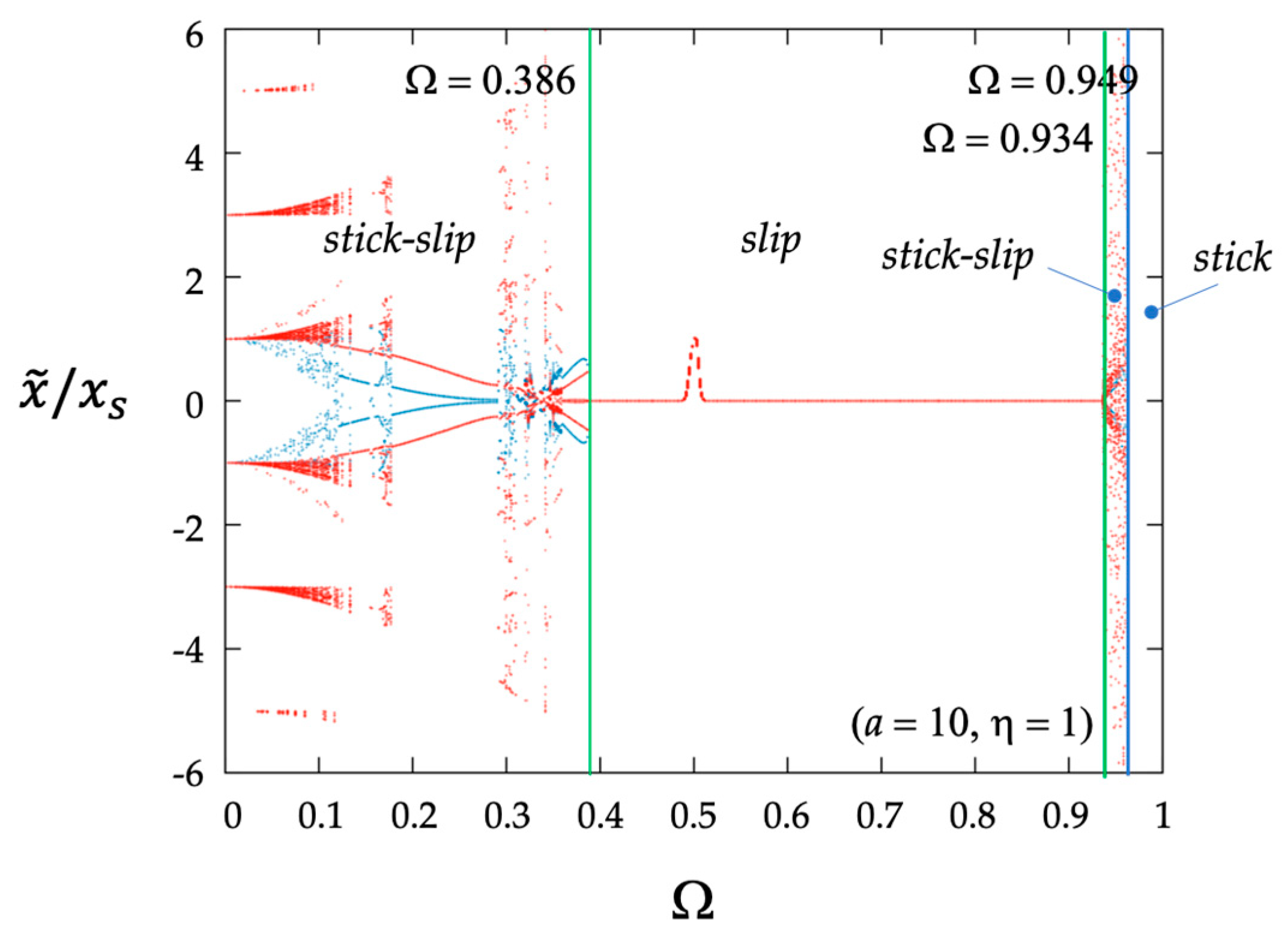
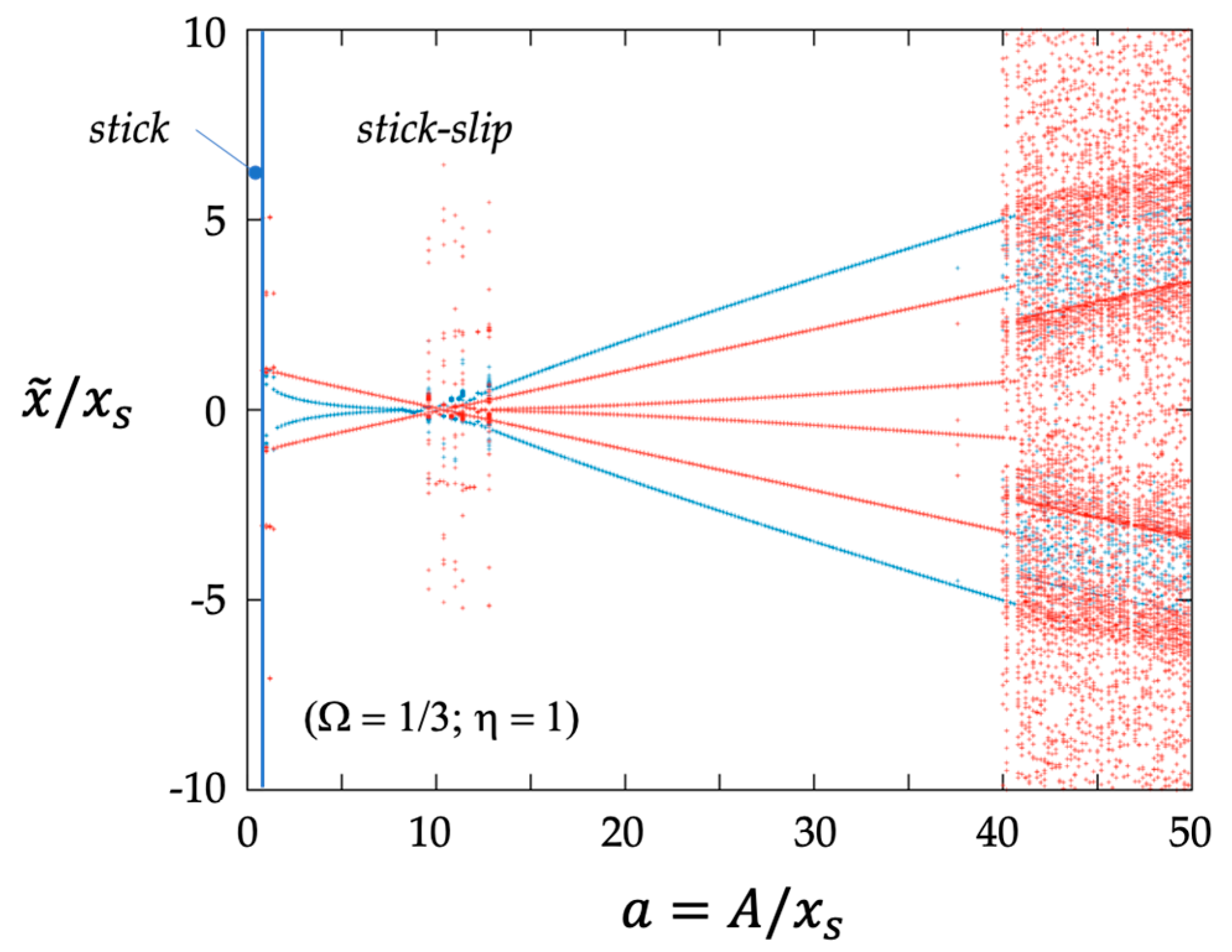
Figure 7,
Figure 8,
Figure 9 and
Figure 10 show bifurcation diagrams for the system at hand. The motion of the system is examined for the prescribed values of
a,
, and
. Homogeneous initial conditions are assumed, i.e.,
,
. The diagrams report the positions,
, at which the relative velocity between the block and the moving support B vanishes, divided by the characteristic length
. If a sticking phase starts, the corresponding points on the diagram are colored in blue, otherwise, if the block keeps on sliding, they are red.
Figure 7 and
Figure 8 focus on the systems having the same dimensionless amplitude as the imposed oscillation,
a = 10. The diagrams show the change in the system response produced by the variations in the parameter
(the ratio between the frequency of the moving support B and that of the mass–spring system). In the case of
= 1/3, a chaotic response is observed for
. The critical values for
separating smooth slip motions from irregular stick–slip responses are in close agreement with the predictions that can be made using the corresponding reference map in
Figure 6. When
= 1 the system highlights a smoother response. Once again, the critical values for
are in close agreement with the predictions based on the relevant reference map in
Figure 6. Chaos in stick–slip systems analogous to the system considered here is discussed in [
21,
23], amongst other works. As was expected, the lower values of
promote chaotic motion. Nevertheless, it is worth observing that for
= 1, irregular stick–slip motions are observed close to
= 1, where regions of indefinite sticking and indefinite sliding overlap.
The bifurcation diagrams shown in
Figure 9 and
Figure 10 highlight the effects produced by the parameter
a (dimensionless oscillation amplitude). In both cases, the frequency ratio
is set equal to 1/3. The stick–slip response predicted by using the reference maps in
Figure 6 for
a > 1 is confirmed. In addition, a transition from smooth to chaotic motion is observed when the dimensionless oscillation amplitude
a exceeds the threshold value which depends on
. In this regard, it is worth recalling that the chosen value for
(
= 1/3) is a critical value that separates the two regions where indefinite sliding is allowed. The distance between the two regions narrows for the increasing amplitude of oscillations (
Figure 6) and this could trigger a chaotic system response.
4. Numerical Examples
In this section, we report the results of the numerical simulations that confirm the analytical findings of the previous sections. Many simulations have been performed, starting with different initial conditions and for different values of the system parameters,
a,
, and
. By way of example, three paradigmatic cases are shown in
Figure 11,
Figure 12,
Figure 13,
Figure 14,
Figure 15 and
Figure 16.
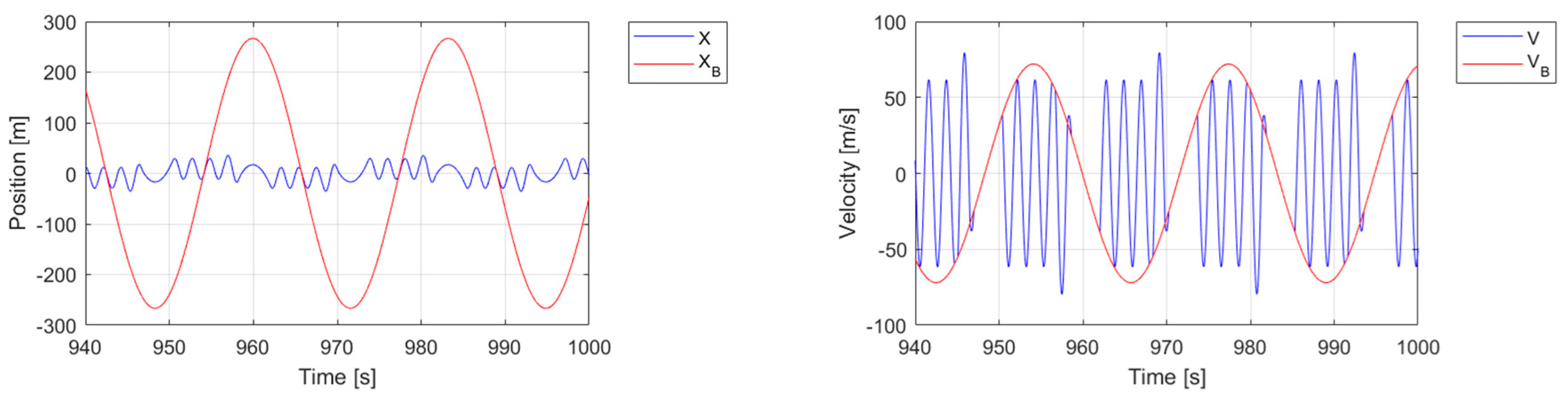
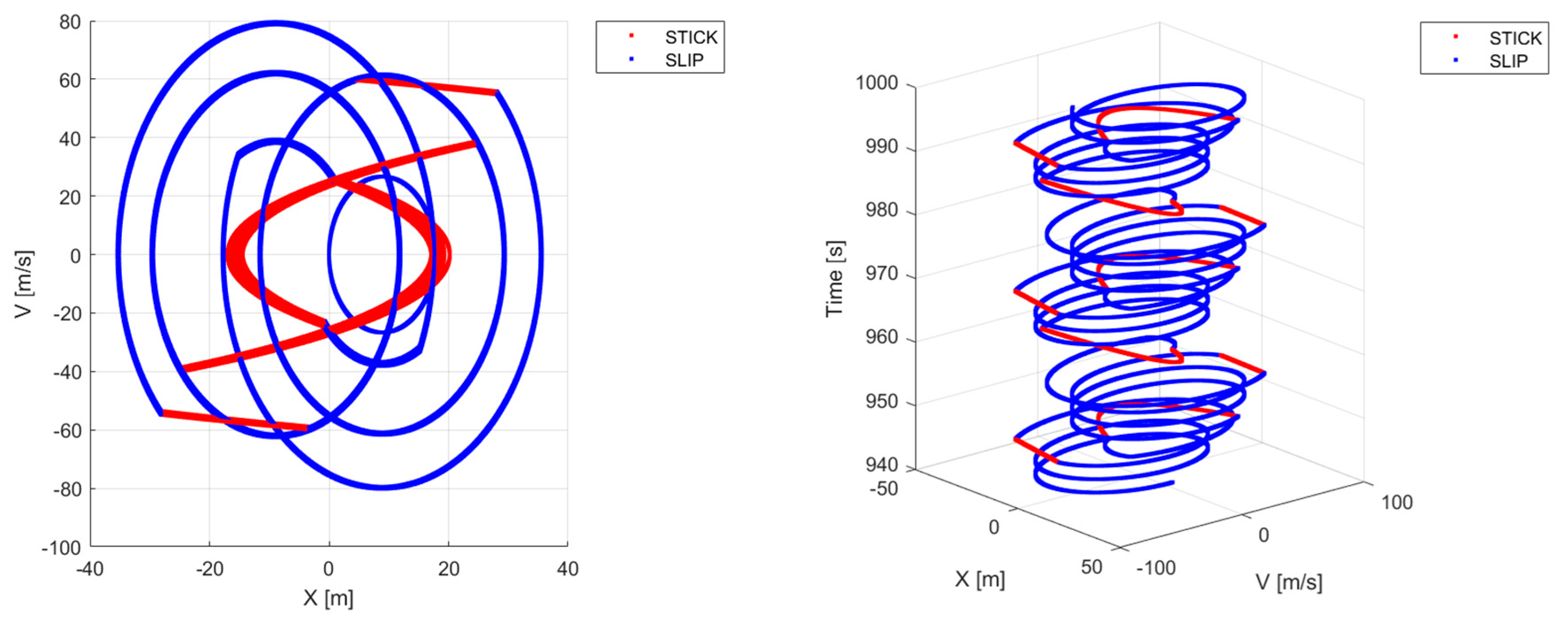
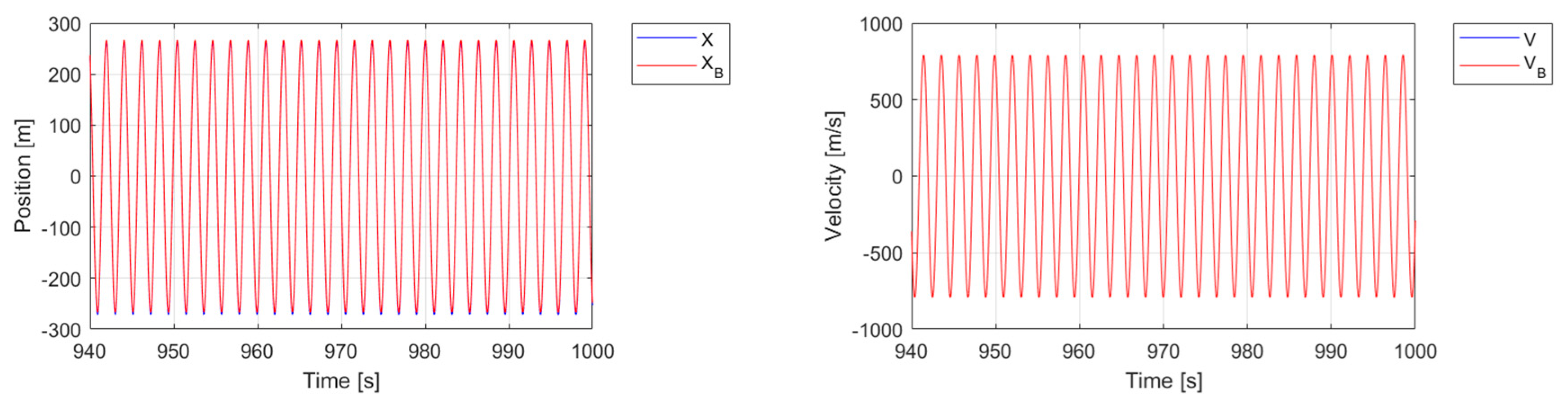
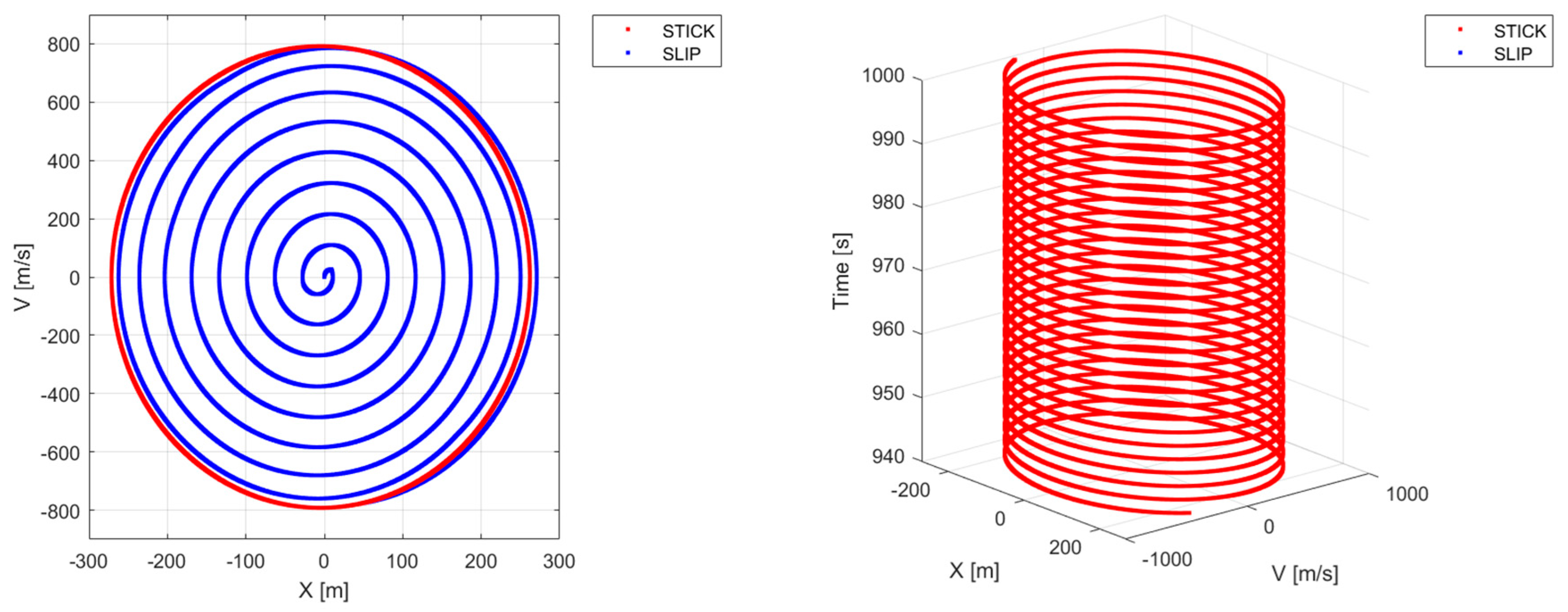
Figure 11 and
Figure 12 illustrate the steady state of a system whose parameters are
a = 10,
= 1/3, and
= 0.09. Specifically,
Figure 11 reports the last 60 s of the time history of the system position and velocity, while
Figure 12 shows the phase portrait of the system, i.e., its two-dimensional representation from the beginning (
t = 0) to the end (
t = 1000 s) of the simulation, along with a three-dimensional view of the last 60 s. As expected, the system’s steady state is characterized by sticking and sliding phases.
Figure 13 and
Figure 14 illustrate similar results for a system with parameters
a = 10,
= 1/3, and
= 0.6, whose steady state coincides with a sliding limit cycle. Finally,
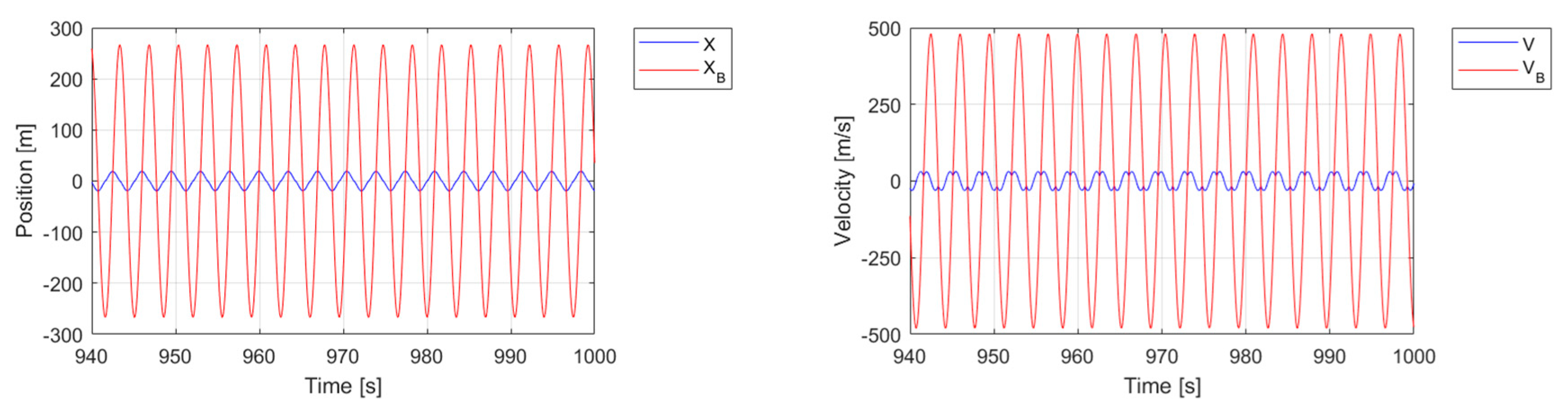
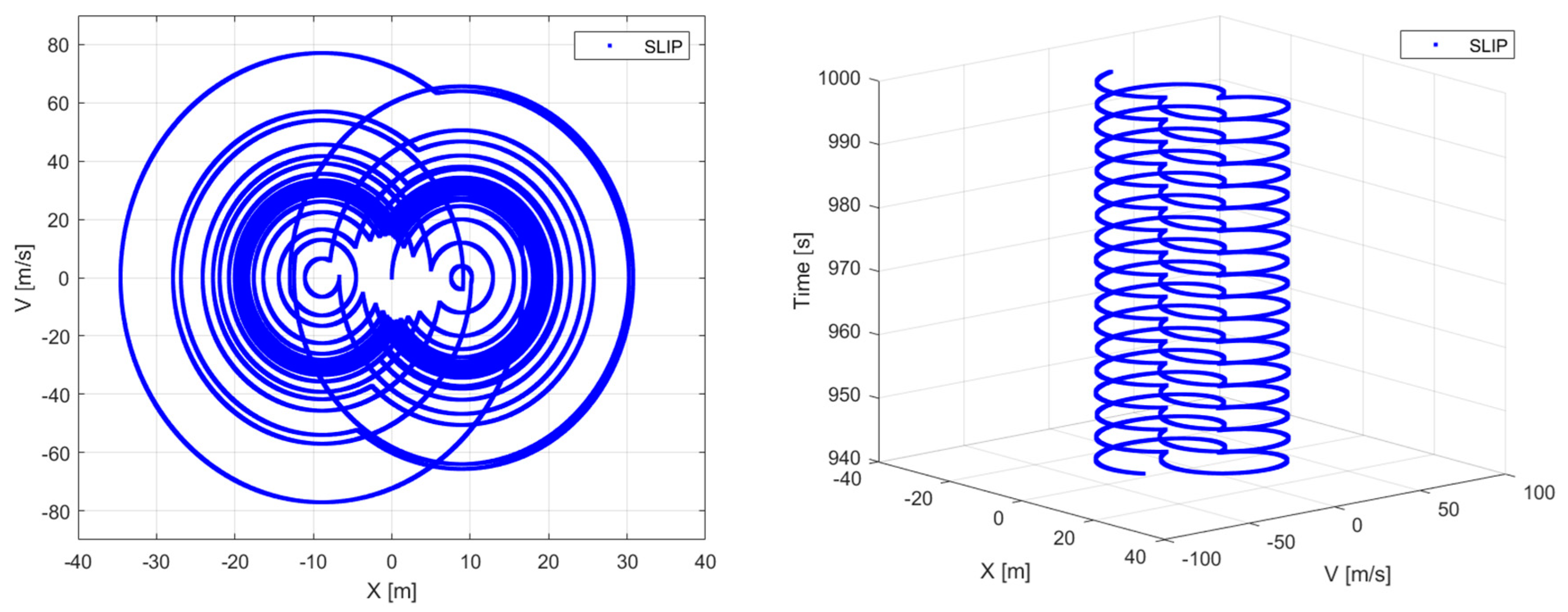
Figure 15 and
Figure 16 show the numerical results obtained for a system whose parameters are
a = 10,
= 1/3, and
= 0.99. In this case, the system’s steady state coincides with a sticking limit cycle.
To sum up, the motion of the systems examined numerically agrees fully with the predictions that can be made via the reference maps shown in
Figure 6. Specifically,
Figure 11 and
Figure 12 confirm the stick–slip long-term response for
= 0.09,
Figure 13 and
Figure 14 confirm the continuous sliding long-term response for
= 0.6, and
Figure 15 and
Figure 16 confirm the continuous sticking long-term response for
= 0.99.
5. Conclusions
This paper has addressed the dynamics of an elastic system that can slide with friction over a moving support. In particular, it has investigated the case of a rigid block connected elastically to a fixed support and with friction to another support which is moving according to a sinusoidal law. The contact between the block and the moving support is described by a modified version of Coulomb’s law to account for the short time needed to restore the sticking contact condition after a sliding phase. Although the system dynamics is highly non-linear due to the non-linear friction law, the system equation of motion can be solved analytically in each phase of sticking and sliding. The exact sequence of the sticking and sliding phases given the initial conditions can be predicted by the means of two simple criteria that allow for identifying the transition time (if any) between the two phases.
A simulation campaign has been carried out to verify the outcomes of the event-driven analytical approach presented in the paper and to highlight the effects of the main system parameters on its long-term dynamic response. The influence on the solution of three dimensionless parameters has been discussed. They are the ratio between the frequency of the oscillations of the moving support and the system’s natural frequency, the ratio between the kinetic and static friction forces, and finally, the ratio a between the maximum amplitude of the oscillations of the moving support and a reference length.
Some limit cycles corresponding to continuous sliding or continuous sticking have been analyzed. The conditions ensuring their existence have also been discussed. In this regard, we have introduced reference maps showing the partition of the a- plane for the given values of into regions corresponding to different expected or possible long-term system responses. According to the results obtained, it is possible to conclude that once the system parameters, a, , and , are known, some characteristics of the system’s long-term dynamic are foreseeable. The regions in the a- plane for which a continuous sticking motion or a particular periodic sliding motion can be excluded or may be possible have been determined. The numerical results have confirmed the analytical predictions.
The analysis of the non-linear dynamics of the elastic systems undergoing frictional stick–slip motions via reference maps and the event-driven analytical solution presented in the paper makes it possible to achieve a better understanding of some features of the long-term dynamic response of such systems. The outcomes obtained may also be useful for applications, such as those requiring the definition of design criteria to avoid undesired jerking motions between components of important safety systems (e.g., seismic protection systems), with the objective of optimizing their performance.
Future investigations will address the more general case in which forced oscillations are imposed on both the base and the elastic spring. The influence of a linear dashpot on the stick–slip dynamics of the considered system will also be investigated. Moreover, hysteretic models will be considered to study the evolution of the stick–slip phenomenon in more complex non-linear systems. In addition, future analytical studies will address the existence of limit cycles other than those considered in this work, as well as the conditions under which other limit cycles may become possible.