The Second Variation of the Potential Energy and the Theory of Elastic Stability

Abstract

We remember and comment on the research scenario of the theory of elastic stability that accompanied all the course of studies, carried out with enthusiasm and passion, of Prof. Marcello Pignataro, who we still miss and to whom our affectionate memory goes. Marcello was in continuous contact with Professor Koiter in Delft, to study, with a new approach, the many and still open problems of the nonlinear theory of elastic stability. In those times, the entire approach used in the study of the equilibrium stability of elastic structures was in question and its basis seemed to need to be reformulated. The central theme was the definition of the stability criterion of the second variation of the potential energy and how it being definite positive could effectively imply stability.

1. Introduction

We recall the traditional approach [1,2] used to formulate the common stability criterion of elastic structures.

An elastic structure T is at the equilibrium configuration C₀ under the loads λ that admit a potential function E (λ, u). The structure T is moved along the displacement u from C₀ to the near configuration C. Let ΔE be the corresponding variation of the potential energy E occurring between C and C₀:

ΔE = E (λ, 0 + u) – E (λ, 0) = E₁(λ, u) + E₂(λ, u) + _…

(1)

where the initial configuration C₀ has been assumed coincident with the configuration 0. The variations E₁(λ, u) and E₂(λ, u), of the first and the second order in u, are represented by the first and the second-order works made by all the forces acting on T during the change of configuration from C₀ to C. The equilibrium of all the forces at C₀ requires:

E₁(λ, u) = 0

(2)

so that (1) becomes:

ΔE = E₂(λ, u) _{+ …}

(3)

The stability condition of the equilibrium of T in C₀ is therefore expressed through the second variation $E_2(\lambda ,\mathit{u})$ of $E(\lambda ,\mathit{u})$ as:

$$E_2(\lambda ,\mathit{u})>0\hspace{1em}\forall \mathit{u}\ne 0\hspace{1em}\in V$$

(4)

where V is the set of all the admissible displacements u of T starting from C₀. Due to the proximity of C₀ to C, according to (3), the variation ΔE (λ, u) of E (λ, u) has been evaluated considering only the second-order terms in u. From this simplification derive the linear equations of the varied equilibrium and, consequently, the so-called linear theory of stability.

Condition (4), established without taking into account the dynamic implications inherent the concept of stability, originates from the simple static consideration that any stable elastic structure must oppose any additional displacement starting from its equilibrium configuration.

Many issues are tacitly admitted in formulating (1) and (4). First of all, it is assumed, with (1), that the smaller the displacement u of T from C₀ to C, the smaller is the variation ΔE of the potential energy E. In brief, it is admitted that the potential energy E (λ, u) is differentiable at C₀. But how can we evaluate the distance between configurations?

For systems with a finite number of degrees of freedom, these problems are overcome. All the norms are equivalent in Rⁿ and the differentiability condition for the potential energy, as a rule, is satisfied. The displacement u is defined by the n parameters q₁, q₂, .. q_n and at the equilibrium configuration:

$${\displaystyle \frac{𝜕E}{𝜕q_1}}=0, {\displaystyle \frac{𝜕E}{𝜕q_2}}=0.............{\displaystyle \frac{𝜕E}{𝜕q_n}}=0$$

(5)

If equilibrium is stable at C₀, the second variation, expressed by the quadratic form:

$$E_2(\lambda , \mathit{u})={\displaystyle \frac{{𝜕}^{2}E(\lambda )}{𝜕q_i𝜕q_j}}{q}_i{q}_j$$

(6)

is positive definite. Tacitly the (1) and (4) are extended to continuous elastic structures. This extension will be the subject of an in-depth analysis in the subsequent sections.

2. Explicit Evaluation of the Second Variation of Potential Energy

We now evaluate, according to the usual approach, the second variation E₂(λ, u) of the total potential energy which is at the basis of the linear theory of elastic stability.

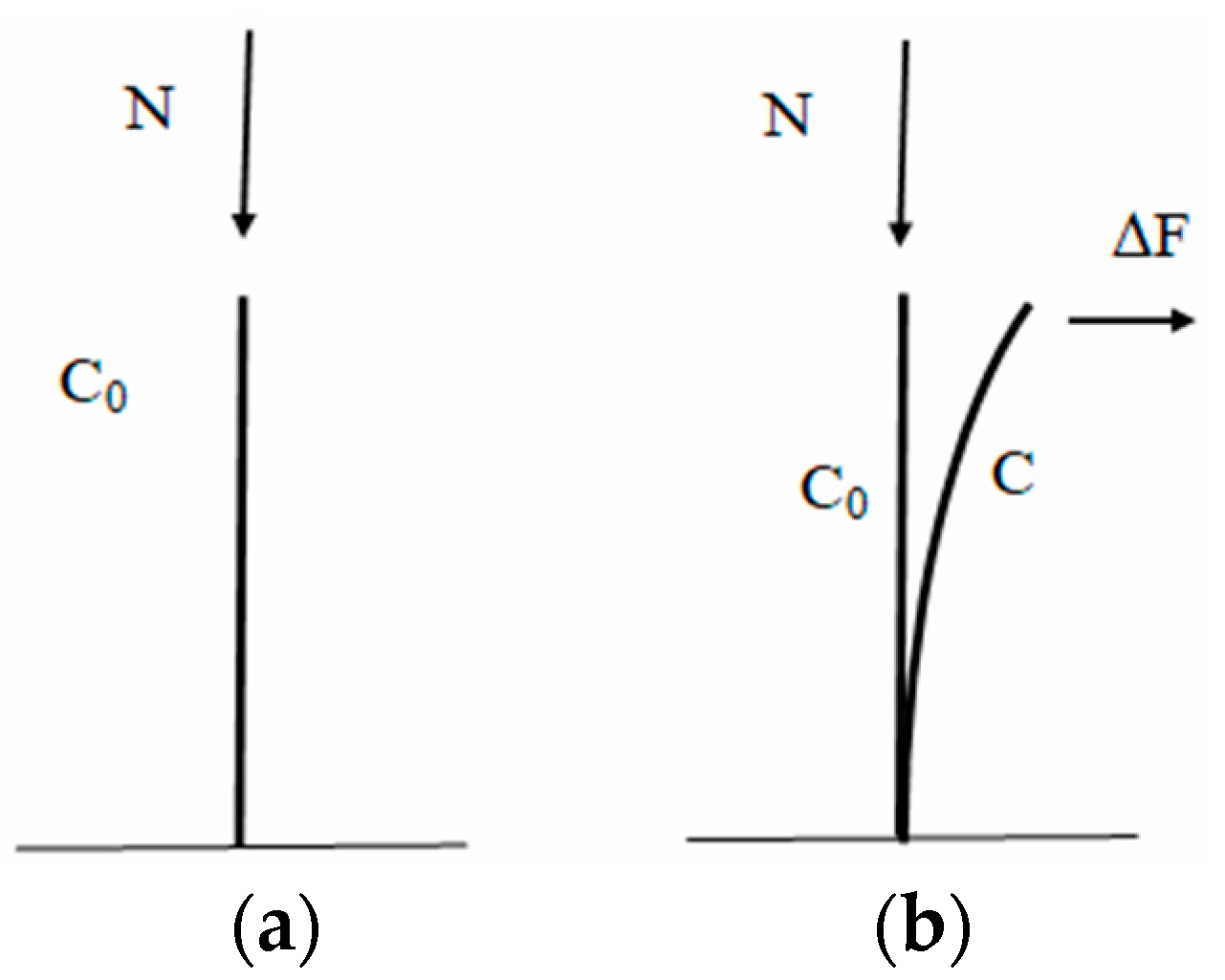
Figure 1a shows the example of the elastic strut loaded by the axial force N, in equilibrium at its initial rectilinear configuration C₀.

Figure 1b shows the structure, loaded also by the additional load ΔF, at the new equilibrium configuration C, near to C₀.

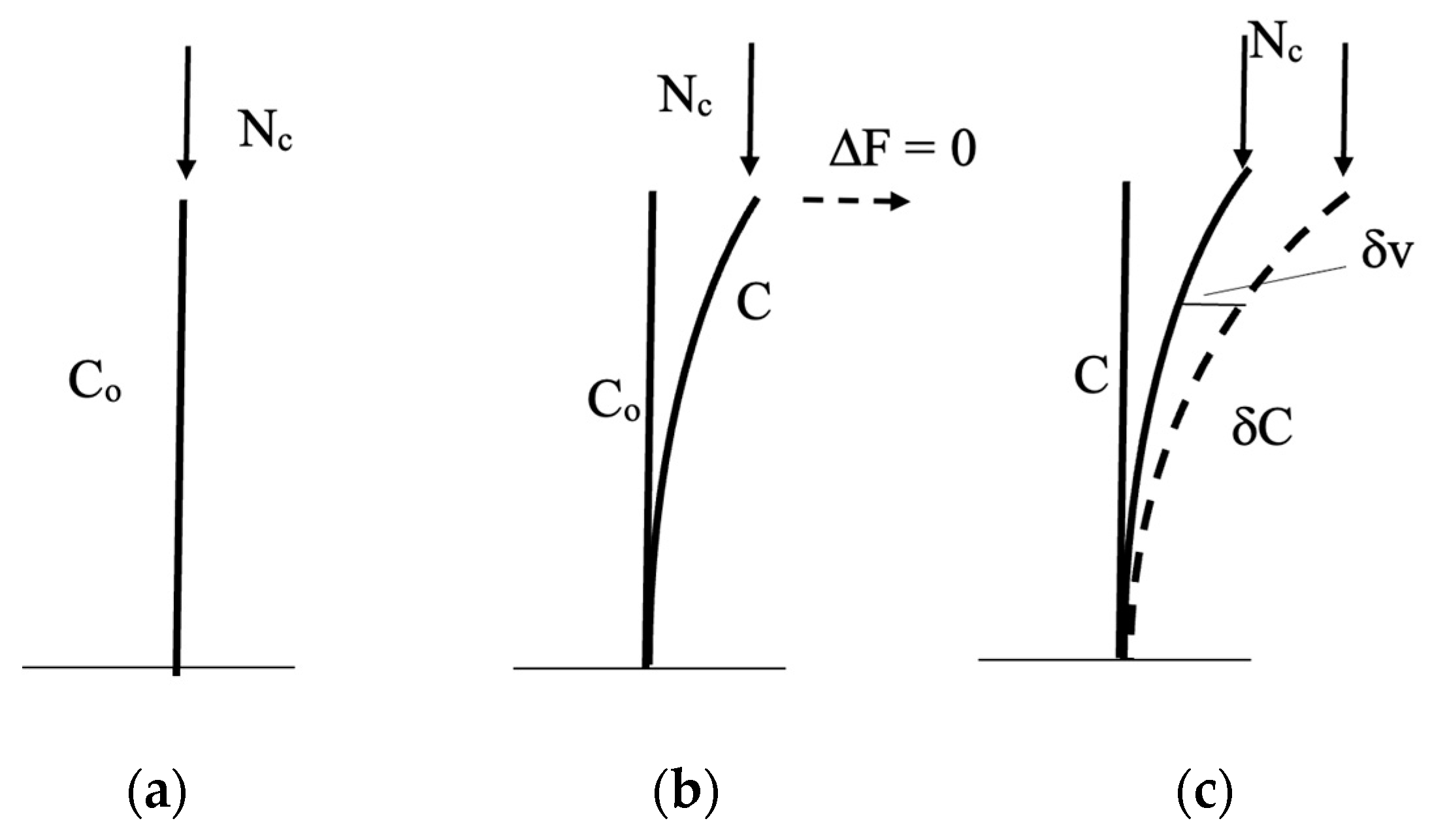
Let us formulate, through the virtual work principle, the equilibrium of T in C. We therefore assume that T undergoes a virtual additional deformation δv which moves it from C to the near configuration δC. The equilibrium condition of T at C is obtained equating the virtual works of the loads F and ΔF along δv to the corresponding virtual works of the internal stresses. These last are represented by the primary stresses S_ij, already present at C₀, and by the additional stresses s_ij, developing in the passage of T from C₀ to C.

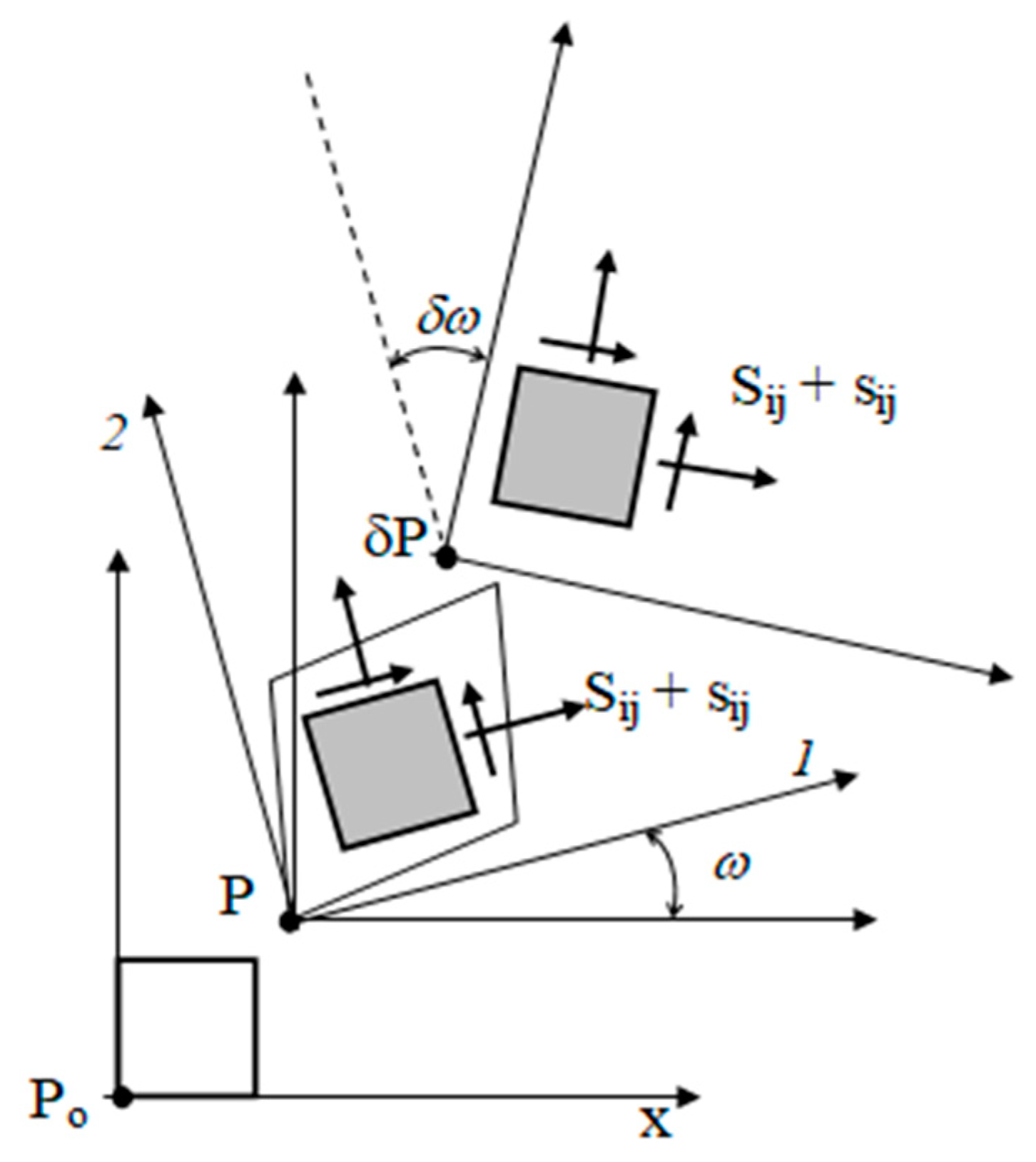
We can refer to a generic neighbourhood N_Po of a point P₀ in T: it translates, rotates, and deforms in the passage of T from C to δC (Figure 2). The primary stress components S_ij, integral with the fibres of T, move together with N_Po during the additional displacement δu. (Biot, [3]).

The stress increments s_ij, due to the deformation of N_Po in the passage of T from C₀ to C, and therefore acting on the deformed element N_Po, because of the great stiffness of the structural material of which T is composed, can be considered acting on the elements N_Po only rotated, but non-deformed, as well as the S_ij. Consequentially, in the evaluation of the virtual works of S_ij and s_ij, in the passage of T form C to δC, we have:

$$\mathsf{\delta }W*=\mathsf{\delta }W+\delta L_1^{*}+\mathsf{\delta }{L}_2^{*}$$

(7)

with:

$$\mathsf{\delta }W={\int }_{\Omega }{s}_{ij}(e_{ij})\delta e_{ij}d\Omega \hspace{1em}\mathsf{\delta }{L}_1^{*}={\int }_{\Omega }{S}_{ij}\delta e_{ij}d\Omega \hspace{1em}\mathsf{\delta }{L}_2^{*}={\int }_{\Omega }{S}_{ij}\delta {\epsilon }_{ij}^{(2)}d\Omega$$

(8)

and:

$$\delta e_{ij}=1/2(\delta u_{i,j}+\delta u_{j,i})\hspace{1em}\delta {\omega }_{ij}=1/2(\delta u_{i,j}-\delta u_{j,i})\hspace{1em}\delta {\epsilon }_{ij}^{(2)}=1/2(\delta {\omega }_{i\mu }\delta {\omega }_{j\mu })$$

(9)

respectively, the first-order strains and rotations components and $\delta {\epsilon }_{ij}^{(2)}$ the corresponding pure strains, of the second order in δv. (Biot, [3], Como [4]).

In the (8) the term δW represents the virtual variation of the elastic energy W stored in T due to the displacement of T from C to δC. Further, $\mathsf{\delta }{L}_1^{*}$ and $\delta L_2^{*}$ are the corresponding virtual works, of the first and second order, of the primary stresses S_ij. The application of the virtual work principle gives:

$$\delta W*=\delta L_E$$

(10)

The virtual work increment of the external loads δL_E, on the other hand, is:

δL_E = −δU + δL_ΔF

(11)

where δU is the corresponding increment of the potential of the external loads F:

δU = δU₁ + δU₂ +…

(12)

where δU₁, δU₂ are the first- and the second-order increments of the potential U of the loads F and δL_ΔF is the virtual work of the additional forces ΔF. Thus, by using (7), from (10) we attain:

$$\delta L_1^{*}+\delta L_2^{*}+\delta W+\delta U_1+\delta U_2=\delta L_{\Delta F}$$

(13)

The equilibrium at the initial configuration C₀ requires the cancellation of all first-order terms so that Equation (13), simplified, becomes:

$$\mathsf{\delta }{L}_2^{*}+\mathsf{\delta }W+\delta U_2=d{L}_{\mathsf{\Delta }F}$$

(14)

The first member of (14) represents the increment:

$$D_1{E}_2(\lambda ,\mathit{u}; \delta \mathit{u})=[{\displaystyle \frac{𝜕E_2(\lambda :\mathit{u}+\alpha \delta \mathit{u})}{𝜕\alpha }}{]}_{\alpha =0}=\delta L_2^{*}+\mathsf{\delta }W+\delta U_2$$

(15)

of the second variation of the potential energy:

$$E_2(\lambda ,\mathit{u}; \delta \mathit{u})=L_2^{*}+W+U_2$$

(16)

For instance, if T is an elastic beam, we have:

$$W={\displaystyle \frac{EI}{2}}{\int }_0^L(v^{″}{)}^{2}dz$$

(17)

The equilibrium of T at C can be expressed by means (13) and gives:

$$D_1{E}_2(\lambda ,\mathit{u}; \delta \mathit{u})=\delta L_{\mathsf{\Delta }F}$$

(18)

The equilibrium is called indifferent or balanced (Figure 3) at the critical configuration C_C, defined by the critical displacement u_c if, for any choice of the additional forces ΔF, the work of these forces is zero along any virtual displacement δu: i.e., if, with $\delta L_{\mathsf{\Delta }F}$ = 0:

$$D_1{E}_2\left({\lambda }_c,{\mathbf{u}}_c;\delta \mathbf{u}\right)=0$$

(19)

or, according to another terminology:

$$D_1{E}_2\left(\lambda ,\mathbf{u};\delta \mathbf{u}\right)=E_{11}\left(\lambda ;\mathbf{u},\delta \mathbf{u}\right)={\left[{\displaystyle \frac{𝜕E_2(\lambda :\mathbf{u}+\mathsf{\alpha }\delta \mathbf{u})}{𝜕\alpha }}\right]}_{\alpha =0}=0$$

(20)

Condition (20) is the variational condition that gives the critical load λ = λ_c and the critical displcement u = u_c. Further, from (20), taking δu = u_c, we attain:

E₁₁(λ_c, u_c; u_c) = 0

(21)

Taking into account that E₁₁(λ_c, u_c; δu) is the bilinear form in (v, δv) associated with the quadratic functional E₂(λ_c, v), we have:

E₁₁(λ_c, u_c; u_c) = 2 E₂(λ_c, u_c) = 0

(22)

At the critical state E₂((λ_c, u) becomes semi-definite positive and reaches its minimum, equal to zero, with λ = λ_c and along u = u_c according to the theorem of Dirichlet [1]. Considering, for instance, the functional (17), we have:

$$W\left(v^{″}+{\alpha u}^{″}\right)={\displaystyle \frac{EI}{2}}{\int }_0^l{(v^{″}+{\alpha u}^{″})}^{2}dz$$

(23)

and:

$$D_1\left[W(\mathbf{u},\mathbf{v})\right]=W_{11}\left(\mathbf{u},\mathbf{v}\right)={\left[{\displaystyle \frac{𝜕W\left(u^{″}+{\alpha v}^{″}\right)}{𝜕\alpha }}\right]}_{\alpha =0}=EI{\int }_0^l{u}^{″}{v}^{″}dz$$

(24)

so that, with v = u:

$$W_{11}\left(\mathbf{u},\mathbf{u}\right)=2W(\mathbf{u})$$

(25)

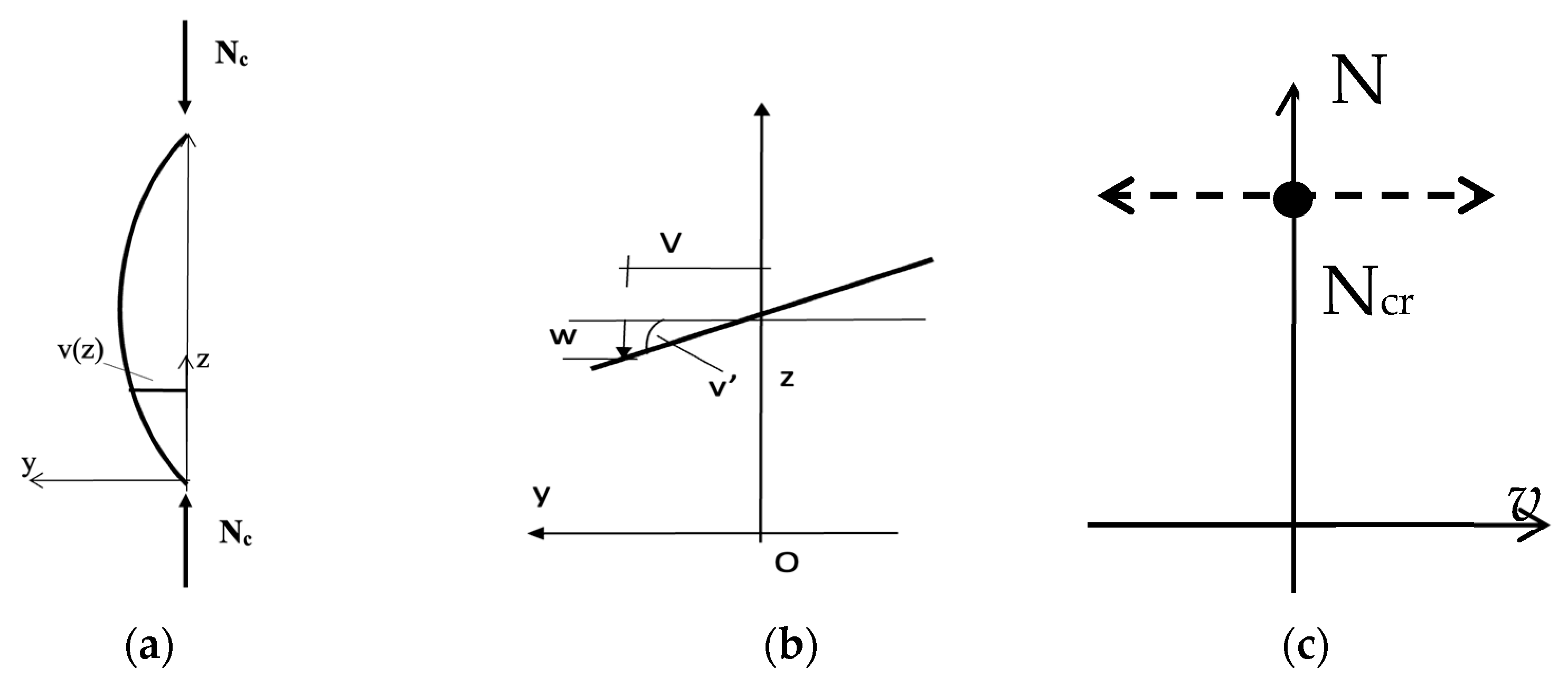
An example

The primary stress acting in the compressed beam of Figure 4 at its initial configuration C₀ is S_zz = −N/A. The beam moves from the rectilinear configuration C₀ to the side flexed configuration C according to the displacement field (Figure 4b):

$$u(x,y,z)= 0 \hspace{1em}u(x,y,z)= \mathrm{v}(z)\hspace{1em}w(x,y,z)=-{\mathrm{yv}}^{\prime }$$

(26)

Consequentially, the second-order strain component ${\epsilon }_{zz}^{(2)}$ and the corresponding second-order works are:

$${\epsilon }_{zz}^{(2)}={v\prime }^2/2\hspace{1em}{L}_2^{*}= -{\displaystyle \frac{N}{2}}{\int }_0^L{v\prime }^{2}dz\hspace{1em}W={\displaystyle \frac{E{I}_x}{2}}{\int }_0^L{v″}^{2}dz\hspace{1em}{U}_2= 0$$

(27)

where $U_2= 0$ because the displacements (26) are only of the first order in v. The second variation of the potential energy is therefore:

$$E_2({\lambda }_c,v;\delta v)={\displaystyle \frac{E{I}_x}{2}}{\int }_0^L{v″}^{2}dz -{\displaystyle \frac{N}{2}}{\int }_0^L{v\prime }^{2}dz$$

(28)

From the variational condition (20), we have:

$$\begin{gathered} {\delta }_1{E}_2\left({\lambda }_c,v;\delta v\right)=E{I}_x{\int }_0^{L}v″\delta v″dz-N_c{\int }_0^L{v}^{\prime }\delta v^{\prime }dz= \\ ={\int }_0^L(EI{{v_c}^I}^V+N_{c}v″)\delta v dz+{\left|EI{v}_c″\delta v\prime \right|}_0^L-{\left|(EI{v}_c″\prime +N_c{v}_c\prime )\delta v\right|}_0^L=0\forall \delta \mathrm{v} \end{gathered}$$

(29)

which gives the equations determining the critical load N_c and the critical configuration v_c:

$$EI{{v_c}^I}^V+N_{c}v″=0\hspace{1em}{\left|EI{v}_c″\delta v\prime \right|}_0^L-{\left|(EI{v}_c″\prime +N_c{v}_c\prime )\delta v\right|}_0^L=0\forall \delta \mathrm{v}$$

(30)

For instance, with the boundary conditions v = v”= 0 at z = 0 and z = L (Figure 4), the solution of (30) gives:

$$N_{cr}={\displaystyle \frac{EI}{4L^2}}{\pi }^2\hspace{1em}{v}_c(z)=B\mathit{sin}{\displaystyle \frac{\pi z}{2L}}$$

(31)

and:

$$B{\displaystyle \frac{{\pi }^2}{4L^2}}({\displaystyle \frac{EI{\pi }^2}{4L^2}}-N_c)=0 \hspace{1em}\Rightarrow \forall B\ne 0\Rightarrow N_c={\displaystyle \frac{EI{\pi }^2}{4L^2}}$$

(32)

Condition (20) is actually satisfied so that the beam reaches the neutral equilibrium state when the axial load N reaches the critical value N_cr (32). The axially compressed strut maintains its equilibrium also in the curved configuration $v_c=B\mathit{sin}\pi z/L$ for any value of the constant B. The symmetrical branching of Figure 4 takes place. At the critical state $L_{2 }^{*}$ and W balance each other and condition (22) is satisfied.

3. Equilibrium in the Neighborhood of the Critical State

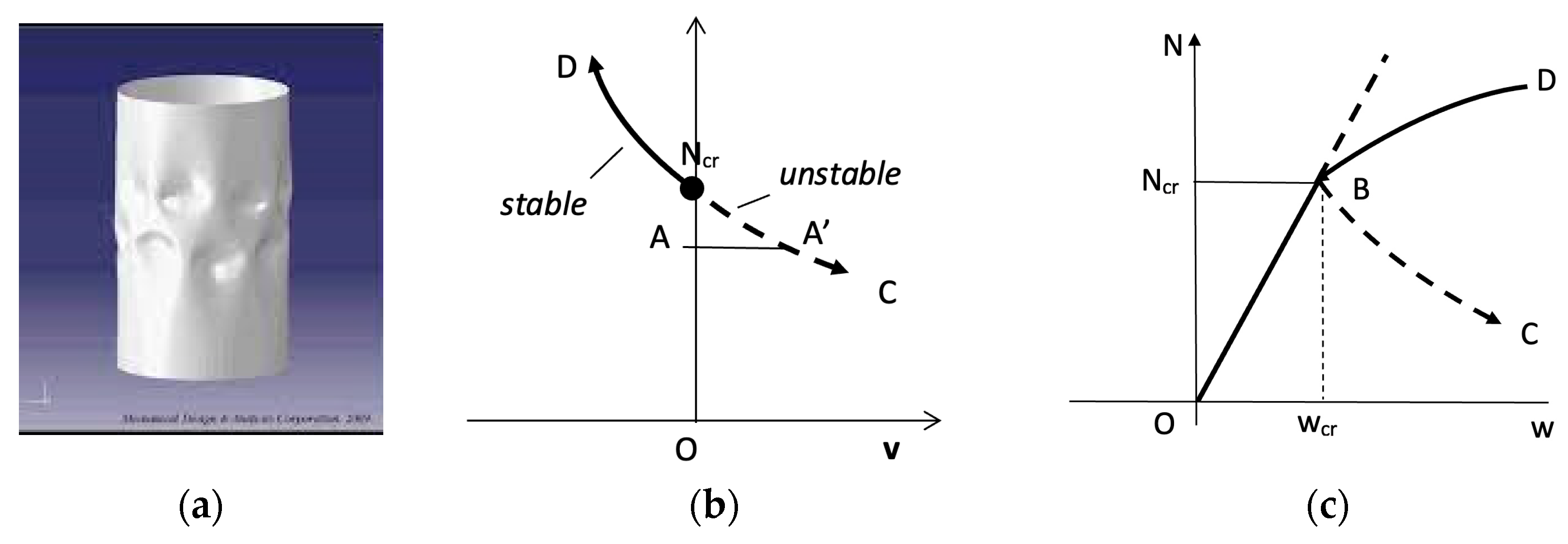
The asymmetrical behavior of the thin cylinder compressed in the critical state is very different compared to the tip-loaded beam (Figure 5) (Karman, Tsien [5], Wolmir [6], Budiansky [7]). How to explain it?

This result is a consequence of the fact that the potential energy increment ΔE (λ, v), with position (3), is approximately taken equal to the second variation E₂ (λ, v). Therefore, at the critical state, defined by (19), it necessarily follows that the structure moves under constant loads and the branching is symmetrical.

To control, at the critical state, the structure can move. In this way, it is necessary to take into account the variations of the potential energy higher than those of the second order and, according to Koiter [8,9], to consider:

E (λ, u) = E₂(λ, u) + E₃(λ, u) + E₄(λ, u)

(33)

where E₃(λ, u) and E₄(λ, u) are the third and the fourth order variations of E (λ, u) in u. At the critical state so it turns out that:

E (λ_c, u_c) = E₃(λ_c, u_c) + E₄(λ_c, u_c)

(34)

The third variation E₃(λ, u) changes sign by varying the sign of di u_c. The asymmetrical branching defined by:

$$E_3({\mathit{u}}_c) \ne 0$$

(35)

is therefore unstable. By means of (34), the necessary stability conditions at the symmetrical critical state are achieved:

E₃(λ_c, u_c) = 0 E₄(λ_c, u_c) > 0

(36)

together with the sufficient conditions of stability at the critical symmetrical critical state:

$$E_3({\mathit{u}}_c)=0,\hspace{1em}{E}_4({\mathit{u}}_{\mathit{c}})-E_2({\mathit{\phi }}_1)\ge 0$$

(37)

where ${\mathit{\phi }}_1$ is a suitable displacement function to be suitably determined. Conditions (35) and (37) were firstly given by da Koiter [8,9].

The case represented by (35) occurs in the model of Figure 5. Conditions (34)–(36) constitute important steps in the study of the nonlinear theory of elastic stability which became the dominant research topic in a large part of engineering schools.

The echo of the Koiter’s thesis crossed in the following decades the entire world of the Applied Mechanics. In this new context, the problem of the instability of the compressed thin cylinder dominated (Figure 5).

Equilibrium states in proximity to the critical state were studied following the approach of Sewell [10] and Thompson [11]. In this context, Pignataro, Rizzi, and Luongo [12] studied the problem, in general, through the analysis of simple models to illustrate the different behaviors found at the critical state. Grimaldi and Pignataro studied the post-buckling behaviour of thin walled open cross compressed section members [13]. The study of the post-critical behaviour of elastic structures was also given bt G. Romano [14].

A model of a simple structure that at the critical state behaves similarly to the thin compressed cylinder is shown in Figure 6a–c.

If the loaded node moves to the left (Figure 6a), the vertical strut bends and the inclined bar lengthens, transferring its traction to the inflected strut, increasing the compression force acting in it. This increase, which reduces the magnitude of the critical value of the axial load N applied at the head of the strut, involves the equilibrium states located on the descending left branch of Figure 6b, in which the horizontal displacement of the node appears on the horizontal axis.

Conversely, if the node moves to the right (Figure 6c), the compression, which is taken out in the inclined bar, unloads the compression force acting in the vertical beam and increases the load N required at the head to reach the critical state. The asymmetric response of the model is due to the occurrence of (35). At the critical state, an asymmetric branching takes place due to the different response of the system, whether it is moved to the left or to the right (Figure 6b).

This result is similar to what occurs on the compressed thin cylinder (Figure 7). Let us imagine the cylindrical wall made up of a set of vertical and annular bands: these last have different response according to whether they are forced to widen or to narrow.

The outside buckling of the vertical bands is contrasted by the horizontal rings. The opposite occurs with regards to the inside buckling: it produces circumferential compressions in the thin rings, which become easily unstable and uncapable of counteracting the inside deformation of the vertical bands. This is the reason why the buckling bubbles of the cylindrical wall are always directed inside (Figure 7a).

In the two diagrams of Figure 7, we see, on the dotted lines, the equilibrium states in the cylinder buckled at the inside. In the first diagram, the average lateral displacement v of the cylinder wall is represented on the horizontal axis, positive if towards the inside. In the second diagram is represented the axial shortening w of the compressed cylinder. Positive values of w correspond to states of unstable equilibrium with deformations that increase as the applied compression N decreases.

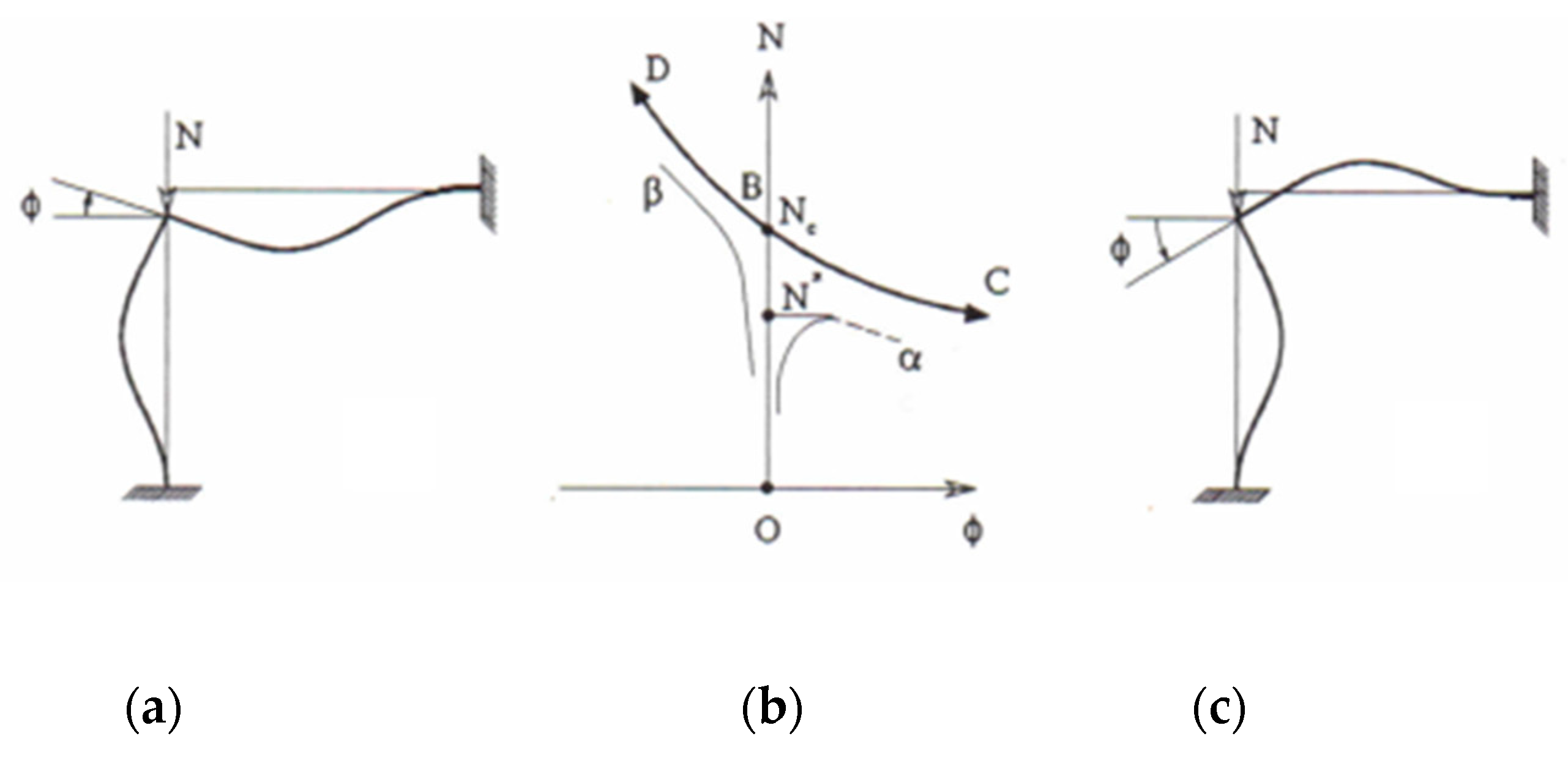
This situation is again analogous to what happens in the frame of Figure 8 in which the asymmetric branching is due to its different response according to the rotation of the node being clockwise or counterclockwise. The occurrence of a clockwise rotation of the node involves the inflection of the crosspiece towards the inside and therefore the insurgence of a shear action on the pillar directed upward. A reduction in the compression in the pillar thus takes place and a consequent increment of the critical vertical load N. Stable equilibrium states correspond to points on the ascending branch of Figure 7b. The opposite happens with regard to actions that involve the counter-clockwise rotation of the node (Figure 7c). (Hutchinson, Koiter [15]).

4. Criticisms on the Formulation of the Stability Criterion of the Second Differential

Despite the successes obtained in interpreting the behavior of many structures at the critical state, many underlying problems remain unaddressed and there are numerous criticisms in this regard. The observations essentially originate from the fact that, since the theory of stability has to examine the response of the elastic system moved from one configuration to another adjacent, the problem of how to define the distance between these configurations should emerge.

In line with Lyapunov (1892 [16]), who was the first to give a rigorous definition of stable equilibrium, we recall the important article by Knops and Wilkes [17] in the Handbuch of Physik, “Theory of Elastic Stability” (1973), which still constitutes a complete synthesis of all the problems present in the topic of instability. Among these, the basic problem was that of extending the energy criterion from elastic systems with a finite number of degrees of freedom to continuous ones, i.e., to systems with an infinite number of degrees of freedom.

Another remark originated from the fact that for an elastic structure, in stable equilibrium in C₀, if moved slightly from this configuration to another nearby C, the corresponding variation ΔE(u) of the potential energy must be correspondingly smaller, the smaller the displacement u between C₀ and C. A first clarification of the problem was provided by G. Romano [18]: in the case of structural models with a linear pre-buckling behaviour, it was possible to give a formulation of the energy criterion based on expansion of the energy functional in Taylor’s formula.

It is therefore necessary to define, on one side, the distance between C₀ and C—the norm in the configuration space—and, on the other, to verify whether the variation in potential energy becomes smaller as the distance between C₀ and C reduces. The problem of the differentiability of E(u) is therefore emerging.

For structural systems with a finite number of degrees of freedom in the displacement space, all the norms are equivalent to each other and therefore for them there is no problem of how to choose the norm.

For continuous systems, i.e., for systems with an infinite number of degrees of freedom, the norms are not equivalent to each other. For them, there is the preliminary problem of which the norm to choose in this configuration space. Therefore, the second variation of the potential energy, being defined as positive, cannot guarantee stability, without indicating with respect to which norm its differentiability occurs, leaving open a large number of problems to be solved.

We understand how the formulation of the energy stability criterion for continuous systems—which are the beam, the plate, the shell, etc.—had to be reformulated.

In this regard, I want to recall the thoughts expressed on the topic by Koiter and Hutchinson in an Applied Mechanics Review ([15] 1970):

The energy criterion of stability for elastic systems subject to conservative loading is almost universally adopted by workers in the field of structural stability. A positive definite second variation of the potential energy about a static equilibrium state is accepted as a sufficient condition for the stability of that state. Numerous attempts to undermine these two pillars of structural stability theory have been made, but confidence in them remains undiminished. With a proper shoring-up of certain aspects of these criteria, they will undoubtedly continue to serve as the foundation of elastic stability theory. An account of the present status of the fundamentals of stability theory is given in therein.

The problem of revising the basis of the energy methods in the theory of elastic stability was therefore posed (Koiter [19]) and determined a series of profound reflections and clarifications in subsequent times. (Koiter [20] To address this problem, it is necessary to revisit the formulation of the energy criterion for elastic systems with a finite number of degrees of freedom for which there could be no doubts about its validity.

5. Recalls of the Energy Methods to the Stability Analysis of Elastic Systems with a Finite Number of Degrees of Freedom

The energy method had its origins in the context of elastic systems with a finite number n of degrees of freedom. These are the n parameters q₁, q₂…, q_n, which indicate the Lagrangian coordinates, defined in the Rⁿ space of the vectors which describe the displacement of the structure from the initial equilibrium configuration C₀ to the generic configuration C. To the displacement v = 0 corresponds the configuration 0 = C₀.

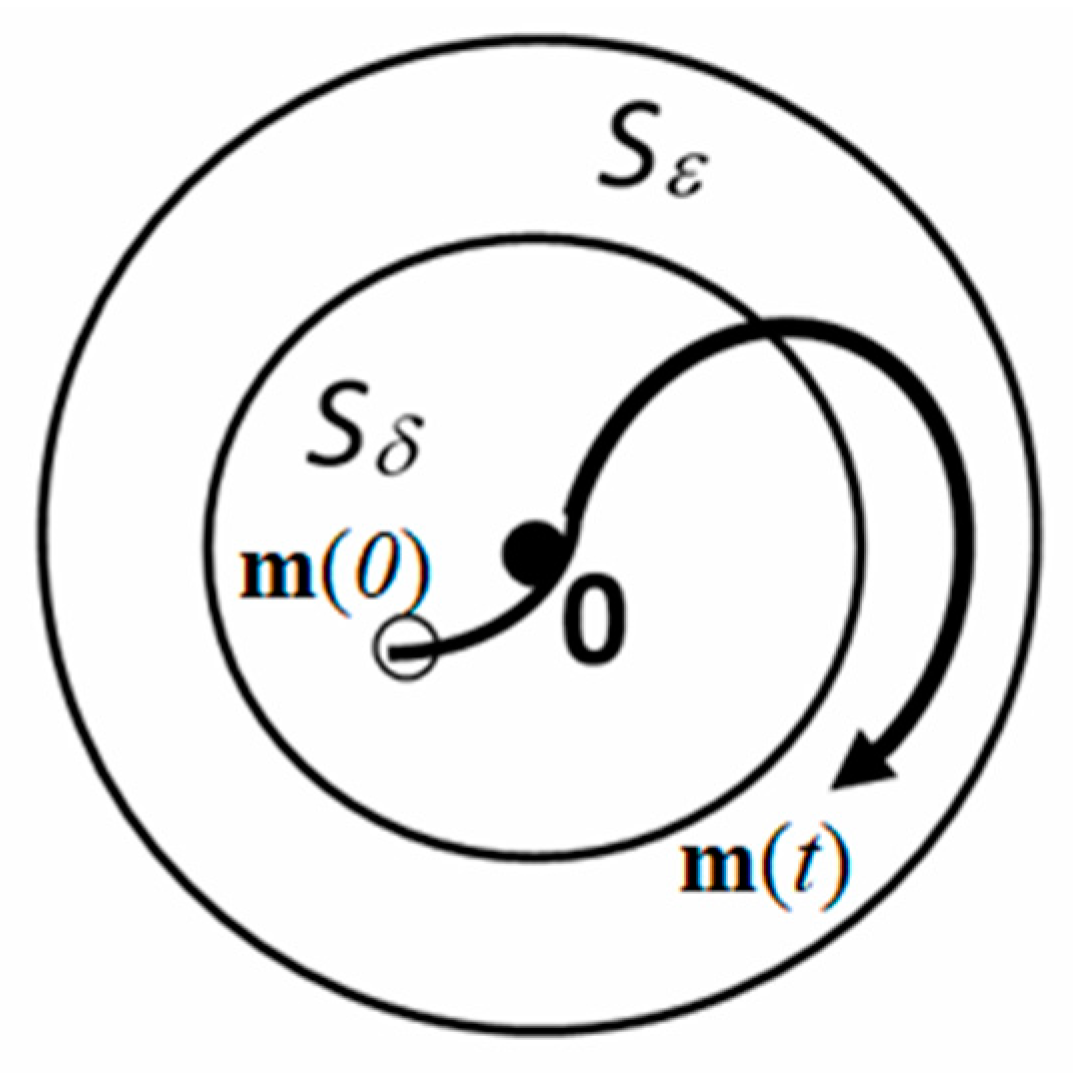
It is necessary to refer to the general definition of stability according to Lyapunov [16], which considers the response of the system to small perturbations of its equilibrium state: “the equilibrium configuration C₀ is stable if, given any spherical neighbourhood S_ε of C₀ of the space R²ⁿ of the motion states, it is possible to determine a corresponding spherical neighbourhood S_δ of C₀ such that any initial disturbance m(0) starting from the interior of S_δ, leads to a disturbed motion m(t) always contained in S_ε” (Figure 9).

Proceeding in this way, it is first necessary to define a state of motion of the structure, defined by the vector:

$$\mathit{m}(t)=[q_1(t),q_2(t),...q_n(t);{\dot{q}}_1(t),{\dot{q}}_2(t),...{\dot{q}}_n(t)]$$

(38)

in the R²ⁿ space, which is the direct sum of the Rⁿ space of the displacements with the Rⁿ space of the velocities. The distance between two states of motion m’ and m” is therefore:

$$d(\mathit{m}\prime ,\mathit{m}″)=[\sum (q_i^{\prime }-q_i^{″}{)}^2+\sum ({\dot{\cancel{q}}}_{\prime }^{\prime }-{\dot{q}}_i^{″}{)}^2{]}^{1/2}$$

(39)

In systems with a finite number of degrees of freedom, all the norms are equivalent to each other. The definition of stability therefore does not depend on the choice of the norm defining the distance between two states of motion of the system.

After this premise, we return to the energy method and examine it in the passage of the system T from the main equilibrium configuration C₀ to a nearby configuration C.

The change in the potential energy E(λ,u) of all internal and external forces acting on T, represented by the parameter λ, must be considered. The equilibrium configuration C₀ is a stationary point of E(λ, u) and conditions (5) hold.

The Lagrange–Dirichlet Theorem for the Elastic Systems with a Finite Number of Degrees of Freedom

The Lagrange–Dirichlet (1846 [21]) tells us that the equilibrium in 0 is stable if there is a neighborhood S_k of C₀, this last coinciding, for simplicity, with the configuration 0, in which:

$$E(\mathsf{\lambda }, \mathbf{u})>0, \mathrm{except} \mathrm{in} \mathbf{0}, \mathrm{where} E(\mathsf{\lambda }, \mathbf{0}) = 0$$

(40)

E (λ, u) is continuous throughout S_k

In short, the conditions:

$$\exists k>0: 0<\left|\mathit{u}-0\right|<k\Rightarrow E\mathit{u})>0$$

(41)

$$\underset{\left|\mathit{u}-\mathit{v}\right|\to 0}{lim}E(\mathit{v})=E(\mathit{u})>0\hspace{1em}\mathbf{u},\mathbf{v} \in S_k$$

(42)

are sufficient to guarantee the stability of T at C₀, that is (Figure 9)

$$\forall \epsilon >0 \exists \delta (\epsilon )>0: \forall \left|\mathit{m}(0)-0\right|<\delta \Rightarrow \left|\mathit{m}(t)-0\right|<\epsilon ,\forall t>0$$

(43)

It is useful to follow the steps of the proof of this theorem because they help to understand the problems connected to its extension to systems with an infinite number of degrees of freedom, i.e., to continuous systems.

Consider the total potential energy E_T(m) of the moving system, obtained by adding the potential energy $E(\lambda ,\mathit{u})$ of all forces involved with the kinetic energy $L_c(\dot{\mathbf{u}})$ of the masses of the system:

$$E_T(\mathit{m})=E(\lambda ,\mathit{u})+L_c(\dot{\mathit{u}})$$

(44)

with:

$$L_c(\dot{\mathit{u}})=\sum m_i{\dot{q}}_i^2$$

(45)

Firstly, it should be noted that, due to the nature of $L_c(\dot{\mathit{u}})$, also $E_T(\mathit{m})$ is continuous. Further, the origin 0 in the space R²ⁿ of the states m of the motion is a minimum of the total energy $E_T(\mathit{m})$, as well it happens for $E(\lambda ,\mathit{u})$ in Rⁿ and, as well as for E(u):

$$\underset{\left|\mathit{m}\right|\to 0}{lim}{E}_T(\mathit{m})=0$$

(46)

Accordingly, the closer the state of motion m of the system is to the initial configuration 0, the smaller the change of the total potential energy. Therefore, however you take a number θ, it will always be possible to choose a δ $>0$ such that:

$$\left|\mathit{m}-0\right|<\delta \Rightarrow E_T(\mathit{m})<\theta$$

(47)

Let us consider the spherical surface $𝜕S_{\epsilon }$ of radius ε $<k$ of the neighbourhood S_ε, included in S_k, i.e., the set of the states of motion m such that (Figure 9):

$$\left|\mathit{m}-0\right|=\epsilon <k$$

(48)

This set is closed and limited, that is, compact, in R²ⁿ. By the Weiestrass theorem Reddy [22], the continuous function $E_T(\mathit{m})$ has the minimum on $𝜕S_{\epsilon }$, i.e.,

$$\exists \stackrel{-}{\mathit{m}}\in 𝜕S_{\epsilon }: \underset{𝜕S_{\epsilon }}{\mathrm{INF}}{E}_T(\mathit{m})=\underset{𝜕S_{\epsilon }}{MIN}{E}_T(\mathit{m})=E_T(\stackrel{-}{\mathit{m}})$$

(49)

Now take a number $0<\stackrel{-}{\theta }<E_T(\stackrel{-}{\mathit{m}}).$ By virtue of (49), there will be a neighbourhood $S_{\delta (\stackrel{-}{\theta })}:$

$$\forall \mathit{m} \in S_{\delta (\stackrel{-}{\theta })}:E_T(\mathit{m})<\stackrel{-}{\theta }<E_T(\stackrel{-}{\mathit{m}}).$$

(50)

Here is now the crucial passage of the theorem which, from the consequences of the existence of the minimum of $E_T(\mathit{m})$, allows us to examine the properties of the motion m(t) of the system disturbed by m(0).

If the initial disturbance m(0) is included in $S_{\delta (\stackrel{-}{\theta })}$, i.e., m(0)$\in S_{\delta (\stackrel{-}{\theta })}$, it will be $E_T(\mathit{m}(0))<E_T(\stackrel{-}{\mathit{m}})$. But the total potential energy is constant during the motion and at any time t so that:

$$E_T(\mathit{m}(t))=E_T(\mathit{m}(0))$$

(51)

The point representative of the state of motion m(t) will never be able to reach the boundary $𝜕S_{\delta (\stackrel{-}{\theta })}$ of $S_{\delta (\stackrel{-}{\theta })}$ and will remain always inside $S_{\delta (\stackrel{-}{\theta })}$. Thus, we have (Figure 9):

$$\forall \stackrel{-}{\theta }>0 \exists \delta (\stackrel{-}{\theta })>0: \forall \mathit{m}(0)\in S_{\delta (\stackrel{-}{\theta })}<\delta \Rightarrow \left|\mathit{m}(t)-0\right|<\delta ,\forall t>0$$

(52)

The Lyapunov condition (43) is verified and the equilibrium of T at C₀ is stable.

6. The Problematic Extension of the Lagrange–Dirichlet Theorem to Continuous Systems

We can now better understand the difficulties encountered in extending the stability criteria of discrete systems to continuous ones. Many hypotheses or results of the Lagrange–Dirichlet theorem are, in fact, not verified in any way in systems with an infinite number of degrees of freedom. For example, condition (49) no longer holds. In a space of infinite dimension, the continuity of potential energy in a compact set does not guarantee the existence of the minimum. Despite $E_T(\mathit{m})>0$ on $𝜕S_{\epsilon }$, it can turn out $INF{E}_Y(\mathit{m})=0$. The perturbed system can therefore escape from the neighbourhood S_ε.

Further, if we apply the stability criterion involving the second differential E₂(u) of the potential energy, the simple occurrence of the condition E₂(u) $>0$ does not make sense. For systems with a finite number of degrees of freedom, the potential energy E₂(u) must be at least twice differentiable at 0 so that the condition E₂(u) $>0$ can imply stability. First of all, E₂(λ,u) must be continuous at 0. The problem of choosing the norm thus immediately emerges.

For example, we can verify that the continuity of E₂(u) at u = 0 does not exist for an elastic beam assuming for E₂(u) the simple expression:

$$W={\displaystyle \frac{EI}{2}}{\int }_0^L(v″{)}^{2}dz$$

(53)

In fact, at the rectilinear configuration of the beam, for instance, it must occur:$\forall z\in [0,\mathrm{L}]$:

$$\underset{\mathit{u}\to 0}{lim}{E}_2(\mathit{u})=0$$

(54)

assuming for instance, that $\mathit{u}\to 0$ according to the metric:

$$d\left(\mathbf{u},0\right)=\underset{\left[0,L\right]}{\max }\left|\mathbf{u}(z)\right|=0$$

(55)

If we take a displacements sequence [u_n] converging to the rectilinear configuration of the beam according to the chosen metric (55), i.e., such that:

$$\lim d\left({\mathbf{u}}_n,0\right)=\lim \underset{\left[0,L\right]}{\max }\left|{\mathbf{u}}_n\left(z\right)\right|=0$$

(56)

it must be:

$$\underset{un\to 0}{lim}{E}_2({\mathit{u}}_n)=0$$

(57)

Let us choose the sequence:

$${\mathit{u}}_n={\displaystyle \frac{1}{n}}\mathit{sin}{\displaystyle \frac{n\pi z}{L}}n\in N$$

(58)

converging to zero for any z in [0.L] in the sense of the metric (55). But, with (58):

$$E_2({\mathit{u}}_n)={\displaystyle \frac{EI}{4}}{\displaystyle \frac{n^2{\pi }^2}{L^2}}$$

(59)

it turns out that:

$$\underset{{\mathit{u}}_n\to 0}{lim}{E}_2({\mathit{u}}_n)=+\infty$$

(60)

Comparing (60) with (57) shows that E₂(u) is not continuous at u = 0 with the metric (55).

7. Extension of the Lagrange–Dirichlet Theorem to Elastic Continuous Systems: The Potential Well

As we will see later, it is possible to define a suitable space H(u) and choose a norm ||v||_H that allows us to validly express the stability condition, in particular the continuity and the differentiability of E (λ, u).

Nevertheless, this result is not still enough to extend the Lagrange–Dirichlet theorem to continuous systems. In a space of infinite dimension, the continuity of potential energy in a compact set—a condition required in the previous demonstration of the Lagrange–Dirichlet theorem—does not guarantee the existence of the minimum in it.

To overcome these difficulties, remaining in the H(u) space, it is necessary, (Coleman [23], Knops [24]), in place of the continuity of E(u) in C₀, to consider a more restrictive assumption, the existence in C₀ of the energy well for the potential E(u). In brief, it is necessary that the energy E(u) is bounded below by a positive and strictly increasing function of the distance $||\mathit{u}|{|}_{H(\mathit{u})}$ between C and C₀. According to this assumption it is possible to extend the Lagrange–Dirichlet theorem to continuous elastic systems.

In what follows, we trace the general lines of the proof of this statement.

Let us consider the space H of the displacement u of T the moves T from C₀ to another near configuration C. This space has norm ||u||_H, which will be defined later. The functional E(u) is null at the equilibrium configuration C₀, i.e., E (0) = 0.

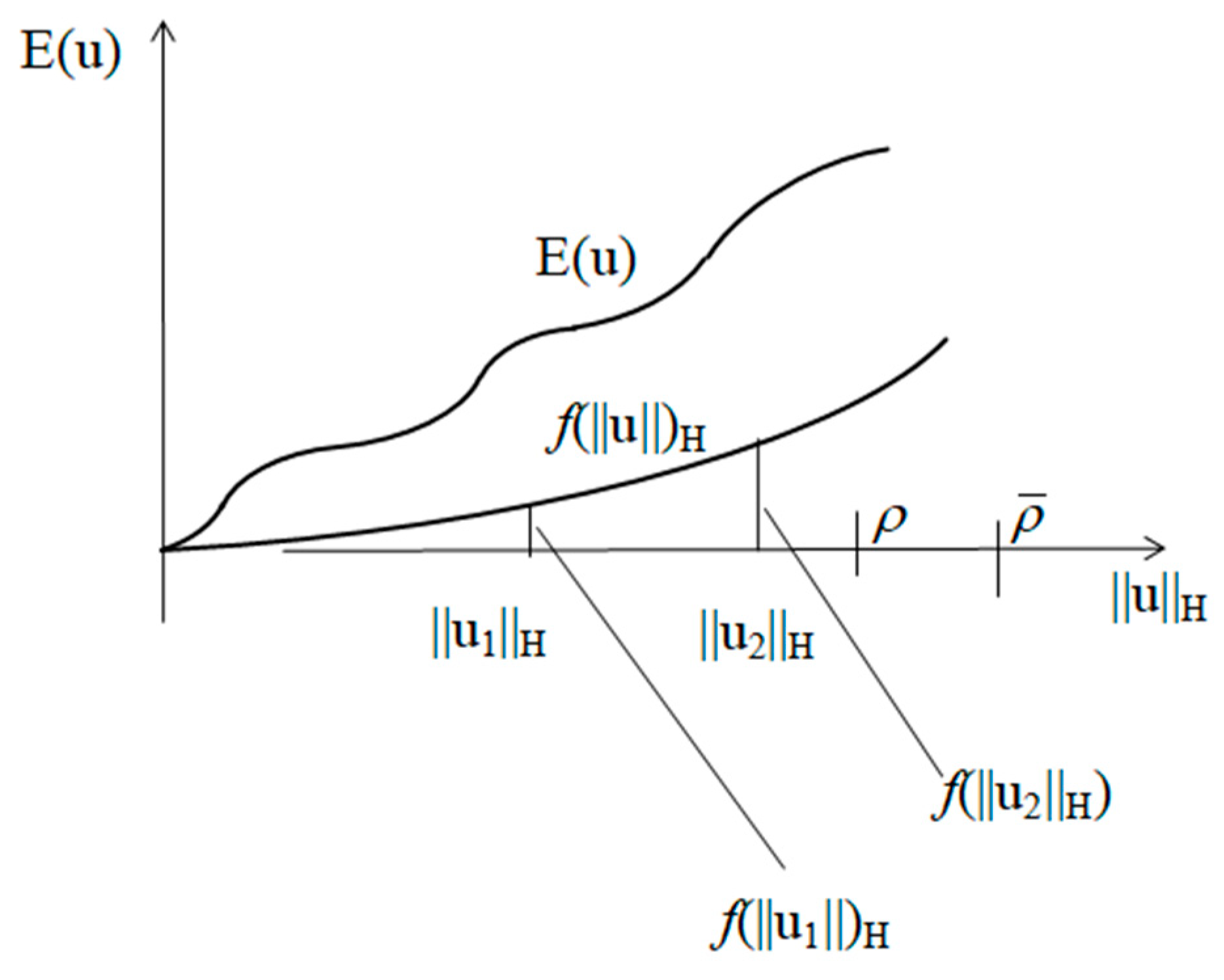
The assumptions of this important theorem are the following (Figure 10):

• The functional E(u) is continuous in C₀$\in \mathrm{H}$, i.e.,

  $$\underset{||\mathit{u}|{|}_H\to 0}{lim}E(||\mathit{u}|{|}_H)=0$$

  (61)
• In the spherical neighbourhoods $S_{\rho }$ of the origin 0: $S_{\rho }=\left[\mathit{u} \in \mathrm{H}: 0\le ||\mathbf{u}|{|}_H=\rho \le \stackrel{-}{\rho }\right],$ there is a function $f(|\left|\left|\mathit{u}\right|{|}_H\right)$, such that:

  $$f(|||\mathit{u}|{|}_H)>0\hspace{1em}\mathbf{u}\ne 0,$$

  $$\mathrm{f}||{\mathrm{u}}_2|{|}_{\mathrm{H}})>\mathrm{f}(||{\mathrm{u}}_1|{|}_{\mathrm{H}}) \mathrm{if} ||{\mathrm{u}}_2|{|}_{\mathrm{H}}>||{\mathrm{u}}_1|{|}_{\mathrm{H}}$$

  (62)

  $$E(\mathit{u})\ge f(||\mathit{u}|{|}_H)>0$$

A condition equivalent to (a) and (b) for the existence of a potential well for E(u) is the hypothesis that the infima of E(u) on the spherical surfaces $𝜕S_{\rho }, 0 <\rho <\stackrel{-}{\rho }$, with centres in C₀, are positive and monotonically increasing with the distance from C₀, i.e.,

$$\underset{𝜕S_{\rho 1}}{inf}E(\mathit{u})\ge f({\rho }_1)>0 : 0<{\rho }_1<{\rho }_2<\stackrel{-}{\rho } ; f({\rho }_1)<f({\rho }_2) \Rightarrow \underset{𝜕S_{\rho 1}}{inf}E(\mathit{u})<\underset{𝜕S_{\rho 2}}{inf}E(\mathit{u})$$

(63)

The main lines of the proof are now reported. Let us firstly define the potential energy of the system:

$$E_T(\mathit{m})=E(\mathit{u})+T(\dot{\mathbf{u}})$$

(64)

with:

$$T(\dot{\mathit{u}})={\int }_{\Omega }\rho \dot{\mathit{u}}\cdot \dot{\mathit{u}} d\Omega$$

(65)

the kinetic energy of the system. E_T(m) and $T(\dot{\mathit{u}})$ are defined in the space H_m of the motion states $\mathit{m}=\left[\begin{array}{cc}\mathit{u},& \dot{\mathit{u}}\end{array}\right]$, with norm:

$$||\mathit{m}|{|}^2=||\mathit{u}|{|}_H^2+T(\dot{\mathit{u}})$$

(66)

As a consequence of the assumption (2), for the peculiar form of $T(\dot{\mathit{u}})$ and of the norm ||m||, the total potential energy E_T(m) in H_m, as well as E(u) in H, has in H_m positive infima monotonically increasing with the distance from C₀, i.e., along the spherical surfaces $𝜕S_{\epsilon }$ of the origin 0 = C₀, so that:

$$\underset{|𝜕S_{\epsilon }}{inf}{E}_T(\mathit{m})>0\hspace{1em}\forall \epsilon : 0 <\epsilon <\stackrel{-}{\rho }\hspace{1em}𝜕S_{\epsilon }=\left[ \mathrm{m}\in H_m: || \mathrm{m} |{|}_{H_m}=\epsilon , \epsilon <\stackrel{-}{\rho }\right]$$

(67)

$$\underset{|𝜕S_{\epsilon 1}}{inf}{E}_T(\mathit{m})<\underset{|𝜕S_{\epsilon 2}}{inf}{E}_T(\mathit{m})\hspace{1em}{\epsilon }_1<{\epsilon }_2<\stackrel{-}{\rho }$$

(68)

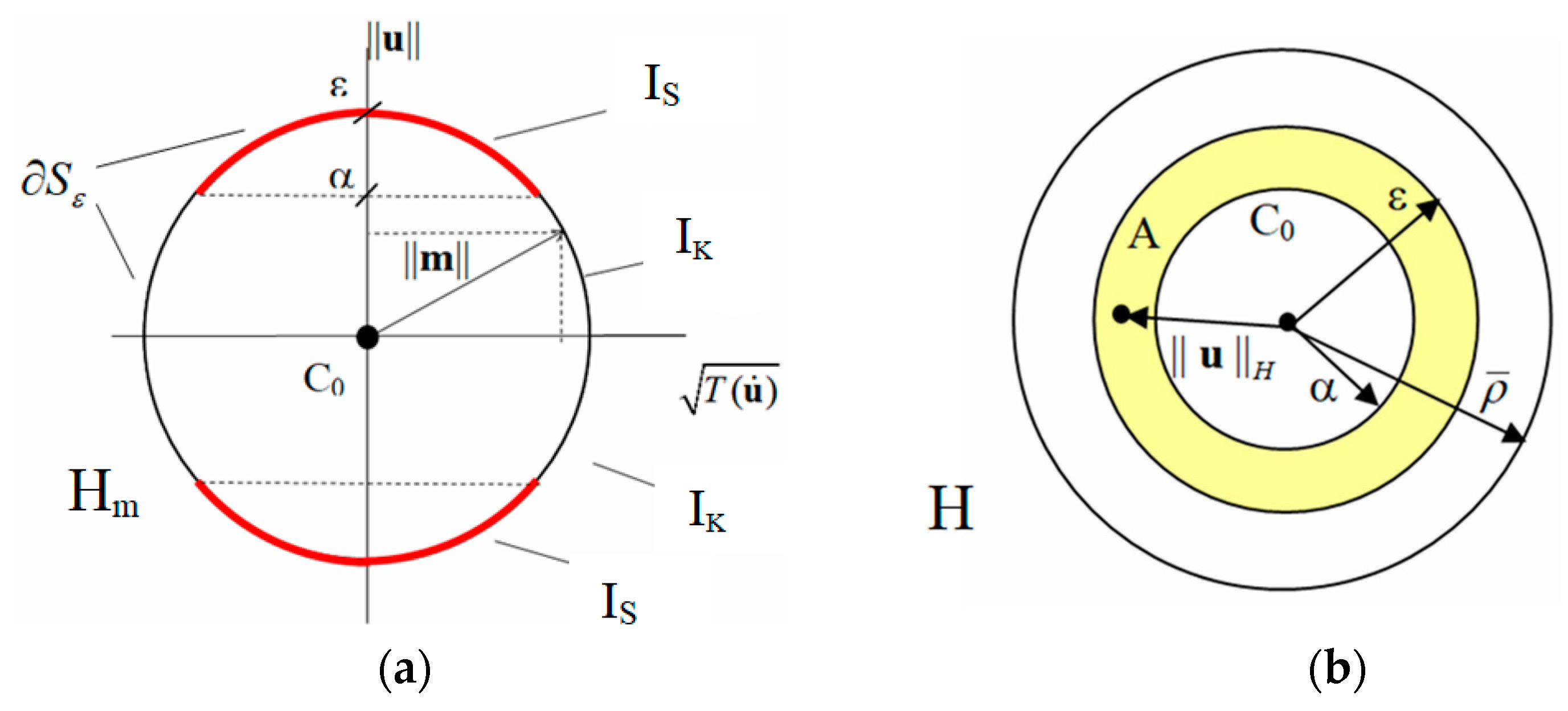
The spherical surface $𝜕S_{\epsilon }$ is subdivided into two regions, I_k and I_s, of which the first I_k has a dominant content of kinetic energy while the other I_s has a dominant content of strain energy (Figure 11a). But when $\mathit{m} \in I_s$ the component u in H of m belongs to the annular region A in H:$\mathrm{A}=\left\{\mathit{u}\in H:\alpha \le ||\mathit{u}|| \le \epsilon , \epsilon <\stackrel{-}{\rho }\right\}$ (Figure 11b). On the other hand, for $\mathit{u}\in A\supset S_{\rho }$, according the assumption (65):

$$E_T(\mathit{m})\ge E(\mathit{u})\ge f(||u||)\ge f(\alpha )>0$$

(69)

and E_T(m) is lower bounded in I_s.

It is also shown that, with the definition (64) and the norm (66), the continuity of E(u) in 0 = C₀ also implies the continuity of E_T(m) in 0 = C₀ and therefore, in analogy with (1) and (2), it results, with (66) and (69):

$$\underset{||\mathit{m}||\to 0}{lim}{E}_T(||\mathit{m}|{|}_H)=E_T(\mathbf{0})=0\hspace{1em}\underset{𝜕S_{\epsilon }}{inf}{E}_T(\mathit{m})>0 \forall \epsilon : 0<\epsilon <\stackrel{-}{\rho }$$

(70)

Let:

$$E_T^{*}(\epsilon )=\underset{|𝜕S_{\epsilon }}{inf}{E}_T(\mathit{m})>0$$

(71)

and take a number $\stackrel{-}{\theta }$:$0<\stackrel{-}{\theta }<E_T^{*}$. By virtue of (71), there will be a δ $>0,$ such that in the neighbourhood $S_{\delta (\stackrel{-}{\theta })}:$

$$\forall \mathit{m} \in S_{\delta (\stackrel{-}{\theta })}:E_T(\mathit{m})<\stackrel{-}{\theta }<E_T^{*}.$$

(72)

If the initial disturbance m(0) is included in $S_{\delta (\stackrel{-}{\theta })}$, i.e., m (0)$\in S_{\delta (\stackrel{-}{\theta })}$, it will be $E_T(\mathit{m}(0))<E_T^{*}$. Consequentially, if the disturbance m(x,t) starts with m(0,t) contained inside the spherical neighbourhood $S_{\delta (\stackrel{-}{\theta })}$, i.e., such that ||m(0,t)|| $<\delta$, it turns out E_T(m(0)) $<\theta <{\mathrm{E}}_T^{*}(\epsilon )$. But the potential total energy is constant during the motion so that, for every time t:

$$\forall t>0 E_{\mathrm{T}}(\mathbf{m}(t)) <\theta < E_T^{*}(\epsilon )$$

(73)

The representative point m(t) of the state of the motion in H_m will never reach the contour $𝜕S_{\epsilon }$ along which $E_T(\mathit{m})>E_T^{*}(\epsilon )$. The disturbed motion will be always contained inside S_ε. The equilibrium is thus Lyapunov stable in C₀ (Figure 9):

$$\forall \epsilon >0:\forall \theta : 0<\theta <{\mathrm{E}}_T^{*}(\epsilon ), \exists \delta >0: || \mathrm{m} ||<\delta \Rightarrow E_T(\mathit{m})<E_T^{*}(\epsilon )$$

(74)

8. The Choice of the “Energy” Norm Passing from Discrete to Continuous Systems

For systems with a finite number n of degrees of freedom all the norms are equivalent to each other. This, however, does not happen for continuous systems, such as, for example, the beam or the plate. Consequently, an equilibrium state that for example, for the axially loaded beam, is stable with respect to one norm, may not be stable with respect to another.

Unbounded amounts of energy can be imparted to the beam of Figure 12a by imposing very small disturbances, in the sense of the norm, e.g.,

$$‖\mathbf{u}‖=\underset{\left[a,b\right]}{\max }\left|\mathbf{u}\right|$$

(75)

On the contrary, in the case of a system with a finite number of degrees of freedom, such as the articulated system with a finite number of elastic hinges of Figure 12b, we recognize that limiting the amplitude of the displacements is limited also the elastic energy of the system. It is therefore preliminary, in formulating the stability criteria of continuous structures, to establish which norm should be chosen in the space of the displacement fields of the structural system. (Como, Grimaldi, [25]).

9. Stability of the Natural Configuration of T, Free from External Forces and Internal Stresses

The condition of instability in a structure subjected to the action of forces can be reached at a given point of the loading process acting on T. It is therefore recognized that, in the choice of the norm, it must be taken into account that the natural state of equilibrium in the structure, i.e., the state of the system with zero external loads and internal stresses, must be stable.

This condition is satisfied by assuming, as a measure of the distance between two configurations of the system, the “energy” norm, i.e., the norm that corresponds to the elastic energy stored in the deformed structure, evaluated using the traditional linear theory of elasticity. For instance, for the elastic beam, the energy product and the energy norm are:

$$[v_1,v_2]={\int }_0^{L}EI{v}_1^{″}{v}_2^{″}dz\hspace{1em}\hspace{1em}|||u||{|}^2={\displaystyle \frac{EI}{2}}{\int }_0^L(v″{)}^{2}dz$$

(76)

To choose the norm it is necessary to consider simultaneously the criterion of stability via the second differential of the energy E(u).

Let us firstly consider a generic norm $||\mathit{h}||$ in a Banach space of the configurations with the preliminary assumption of at least the second differentiability of the potential energy in it. The proof of this differentiability with respect to the chosen norm is now postponed. Assume therefore:

$$E(\mathit{u}+\mathit{h})-E(\mathit{u})=E_2(\mathit{u};\mathit{h})+o( ||\mathit{h}|{|}^2) \underset{||\mathit{h}|{|}^2\to 0}{lim}{\displaystyle \frac{o( ||\mathit{h}|{|}^2)}{||\mathit{h}|{|}^2}}=0$$

(77)

con $E_2(\mathit{u};\mathit{h})$ quadratic and continuous with respect to h, i.e., such that:

$$|E_2(\mathit{u};\mathit{h})|\le k||\mathit{h}|{|}^2$$

(78)

The second differential of the energy at the natural configuration coincides with the same energy norm:

[E₂(0,u)]_nat = ½|||u|||

(79)

so that:

$$|||\mathbf{u}|||2\le k||\mathbf{u}|{|}_H^2$$

(80)

i.e., the norm ||u||_H cannot be weaker than the energy norm $|||\mathbf{u}|||$. Further, the stability of the natural configuration requires:

$$\underset{𝜕S*\subset H}{INF}[E_2(0,\mathit{u}*){]}_{nat}=\omega >0 , \mathit{u}*={\displaystyle \frac{\mathit{u}}{||\mathit{u}|{|}_H^2}}\Rightarrow [E_2(0,\mathit{u}){]}_{nat}>\omega ||\mathit{u}|{|}_H^2$$

(81)

Therefore, with (80):

$$|||\mathbf{u}|||2>2\omega ||\mathit{u}|{|}_H^2$$

(82)

and the norm ||u||_H cannot be stronger than the energy norm. We conclude that ||u||_H must be equivalent to the energy norm |||u|||. Of course, it must be provided that E(u) is at least twice differentiable in C₀, in the energy space.

10. The Space Energy

In the functional analysis (Reddy [22]), the “energy” space is defined as the Sobolev space H^(m)(Ω), i.e., the space of all the functions that in Ω have weak derivatives D^ku$\in$L₂(Ω), k $\le$ m.

We recall that the weak derivative is a generalization of the concept of derivative of a function of a real variable to functions that are not necessarily differentiable, but only integrable, i.e., to functions that belong to the L¹ space. This definition is motivated by the technique of the integration by parts.

Let u(z) a function in L¹([a,b]): $v\in L^1([a,b])$ is the weak derivative of u if, for any $\phi \in C^{\infty }([a,b]) \mathrm{with} \phi (a)=\phi (b)=0,$ it results:

$${\int }_a^{b}u(t)\phi \prime (t)dt=-{\int }_a^{b}v(t)\phi (t)dt$$

(83)

This definition is generalized to n dimensional spaces whose norm is:

$$||u|{|}^{(m)}=({\int }_{\Omega }{\displaystyle \sum _{0\le |k|\le m}}(D^{k}u{)}^{2}dx{)}^{1/2}=({\int }_{\Omega }{\displaystyle \sum _{0\le |k|\le m}}(D^{k}u{)}^2{)}^{1/2}$$

(84)

where the sum is taken over all possible combination of indices such that $0\le |k|\le m$. Recalling the great immersion theorem of Sobolev, from the definition of H^(m)(Ω), with $m_2>m_1>0$, it results (Sobolev [26], 1953):

$$H^{(m_2)}(\Omega )\subset H^{(m_1)}(\Omega )\subset H^{(m_0)}(\Omega )=L_2(\Omega ),\hspace{1em}{m}_2>m_1>0$$

(85)

Further, the immersion of $H^{(m_2)}(\Omega )$ in $H^{\left(m_1\right)}\left(\Omega \right)$ is compact, i.e., each set limited in $H^{(m_2)}(\Omega )$ is compact in $H^{(m_1)}(\Omega )$.

For functions of a single variable, the existence of the derivative implies continuity. This does not occur for multivariable functions. However, a consequence of the Sobolev’s immersion theorems is the fact that, if $u\in H^{(m)}(\Omega )$, the function u has relevant regularity properties because $u\in C^{(s)}(\Omega )$ always that:

$$s<m-{\displaystyle \frac{r}{2}}, r=\mathit{dim}(\Omega )$$

(86)

The great Sobolev theorem therefore tell us that all the functions of the space $H^{(m)}(\Omega )$ are continuous in Ω with their derivatives until the order s defined by (86). The following Sobolev inequalities hold:

$${||u||}_{C^{(s)}(\Omega )}={\displaystyle \underset{\Omega }{\max |u|}}\le M{||u||}^{(m)}$$

(87)

where C^(s)(Ω) is the space of the functions s times continuously differentiable in Ω.

10.1. Continuity and Differentiability of the Energy Functional in H^(m) of Elastic Structures

10.1.1. The Elastic Beam

r$=\mathit{dim}([0,L])=1$ and the energy norm, according to (79) is:

$$|||u||{|}^2={\displaystyle \frac{EI}{2}}{\int }_0^L(u″{)}^{2}dz$$

(88)

so that $H^{(m)}=H^{(2)}$.

With the dimension r = 1 of the set Ω = [0, L], where the functions u are defined, as it must be:

$$s<m-r/2=2-1/2=3/2$$

(89)

it turns out:

$$C^{(s)}=C^{(1)}([0,L])$$

(90)

According to Sobolev theorem we have also:

$$\exists k_1>0:[{{\int }_0^L{v}^{2}dz]}^{1/2}=||v||\le k_1|||v|||,\exists k_2>0:[{{\int }_0^{L}v{\prime }^{2}dz]}^{1/2}=||v\prime ||\le k_2|||v|||,$$

(91)

$$\exists k_3>0:\underset{[9,L]}{max}|v(z)|\le k_3|||v|||,\exists k_4>0:\underset{[9,L]}{max}|v\prime (z)|=||v\prime ||\le k_4|||v|||,$$

(92)

Concluding, for the beam the functions v(z) of the space H ⁽²⁾ are continuous functions together their first derivatives. The energy convergence implies the convergence according to the uniform norm.

The proof of the strong differentiability, at least up to the fourth order in the energy space, of the energy functional E (λ, u) for the elastic beam is now reported in detail. It has been given by Como and Grimaldi [27].

$$E(v)={\displaystyle \frac{EI}{2}}{\int }_0^L{\displaystyle \frac{v{″}^2}{1-v{\prime }^2}}dz+N{\int }_0^L(\sqrt{1-v{\prime }^2}-1)dz$$

(93)

and:

$$D^{2}E(0;v,v)=2\left[{\displaystyle \frac{EI}{2}}{\int }_0^{L}v{″}^{2}dz-{\displaystyle \frac{N}{2}}{\int }_0^{L}v{\prime }^{2}dz\right]$$

(94)

According to the mean value Lagrange theorem:

$$\Delta E=E(0,v)-E(0)={\displaystyle \frac{1}{2}}{D}^{2}E(0,v)+{\displaystyle \frac{1}{2}}[D^{2}E(\alpha v,v)-D^{2}E(0,v)], 0 <\alpha < 1$$

(95)

On the other hand, from (94) and (92):

$$|D^{2}E(0;v)| \le (1+N{k}_2^2)|||v||{|}^2$$

(96)

The functional $D^{2}E(0;v)$ is quadratic and continuous in the function v. Further:

$$r_2(v)={\displaystyle \frac{1}{2}}[D^{2}E(\alpha v;v)-D^{2}E(0;v)]$$

(97)

and:

$$r_2(v)\le {\displaystyle \frac{|||v||{|}^2}{2}}\left[{\displaystyle \frac{2m^2(3-m^2)}{(1-m^2{)}^2}}+N{\displaystyle \frac{(1-m^2)[1-(1-m^2)]+m^2{k}_2^2.}{(1-m^2{)}^{3/2}}}\right]$$

(98)

with:

$$m=\underset{[a,b]}{max}|v(z)|$$

(99)

so that, taking into account (91):

$$\underset{[9,L]}{max}|v\prime (z)||=m\le k_4|||v|||,$$

(100)

we obtain

$$\underset{|||v|||\to 0}{lim}{\displaystyle \frac{r_2(v)}{|||v||{|}^2}}=0$$

(101)

and the functional E(v) is two times differentiable at v = 0. It is similarly proven the third and fourth differentiability of E(v) at v = 0 [27].

10.1.2. The Elastic Plate

The energy norm is:

$$|||\mathit{u}||{|}^2={\displaystyle \frac{1}{2}}D{\iint }_{\Omega }[({\displaystyle \frac{{𝜕}^{2}w}{𝜕x^2}}{)}^2+({\displaystyle \frac{{𝜕}^{2}w}{𝜕y^2}}{)}^2+2\nu {\displaystyle \frac{{𝜕}^{2}w}{𝜕x^2}}{\displaystyle \frac{{𝜕}^{2}w}{𝜕y^2}}]dxdy$$

(102)

and the space $H^{(m)}=H^{(2)}$, so that:

$$\mathit{u}\in H^{(m)}(\Omega )=H^{(2)}(\Omega ),\mathit{dim}(\Omega )=r=2\Rightarrow \mathit{u}\in C^{(s)}(\Omega )$$

(103)

With the dimension r = 2 of the domain Ω, from (87), we have:

$$s<m-r/2=2-2/2=1$$

(104)

and $C^{(s)}=C^{(0)}(\mathsf{\Omega })$.

The displacement functions w(x,y) are continuous. Further, as proven (Como and Grimaldi [25]), the corresponding energy functional E₂(w) is quadratic, continuous, and differentiable at w = 0. Similar results can be proven for the elastic shells.

10.1.3. Three-Dimensional Elasticity

The domain Ω has dimension r = 3 and the space $H^{\left(m\right)}\left(\Omega \right)=H^{\left(1\right)}\left(\Omega \right),$ with:

$$s<m-r/2=1-3/2<0$$

(105)

The displacement functions are not continuous and the corresponding energy functional is not differentiable at v = 0.

11. The Definitive Formulation of the Stability Criterion of the Second Differential of the Potential Energy in H⁽²⁾

We have shown that the potential energy E(u) of elastic systems T, composed by beams, plates, or shells, is at least two times Fréchet differentiable in H⁽²⁾ at the equilibrium configuration C₀. This result can finally permit to formulate, for them, the stability criterion involving the second differential of E(u).

An elastic structure T is at the equilibrium configuration C₀ under the loads λ that admit a potential function E(u). The structure T is moved along the displacement u from C₀ to the near configuration C. Let ΔE be the corresponding variation of the potential energy E occurring between C and C₀:

ΔE = E (0 + u) − E (0) = E(u) + E₂(u) _{+ …}

(106)

where E₂(u) is the second strong differential of E(u) at C₀, so that:

$$E\left(\mathbf{u}\right)=E_2\left(\mathbf{u}\right)+\mathrm{o}\left({\left|‖\mathbf{u}‖\right|}^2\right){ E}_2\left(\mathbf{u}\right)\le \mathrm{k}{\left|‖\mathbf{u}‖\right|}^2\hspace{1em}\hspace{1em}\underset{\left|‖u‖\right|\to 0}{\lim }{\displaystyle \frac{o\left({\left|‖\mathbf{u}‖\right|}^2\right)}{{\left|‖\mathbf{u}‖\right|}^2}}=0$$

(107)

The second differential E₂(u) is definite positive if:

$$\omega =\underset{𝜕S^{*}}{\inf }{E}_2\left({\mathbf{u}}^{\mathit{*}}\right)>0 {\mathbf{u}}^{\mathit{*}}\in 𝜕S^{*}:\left|‖\mathrm{u}‖\right|=1\}$$

(108)

The equilibrium is Lyapunov stable at C₀.

In fact, according to the Taylor theorem, taking into account of the equilibrium in C₀:

$$E\left(\mathbf{u}\right)\ge {\left|‖\mathbf{u}‖\right|}^2\left[\omega +{\displaystyle \frac{\mathrm{o}\left({\left|‖\mathbf{u}‖\right|}^2\right)}{{\left|‖\mathbf{u}‖\right|}^2}}\right]\ge {\left|‖\mathbf{u}‖\right|}^2\left[\omega -{\displaystyle \frac{\mathrm{o}\left({\left|‖\mathbf{u}‖\right|}^2\right)}{{\left|‖\mathbf{u}‖\right|}^2}}\right]$$

(109)

Taking into account the second condition (107), therefore, we have:

$$\forall \epsilon >0 \exists \rho >0:\mathbf{u}\in {\mathrm{H}}^{\left(2\right)}:0<\left|‖\mathbf{u}‖\right|<\rho =>E\left(\mathbf{u}\right)>(\omega -\epsilon ){\left|‖\mathbf{u}‖\right|}^2$$

(110)

and condition (63), required to ensure the existence of an energy well of the potential energy at C₀, is satisfied. Condition (110) therefore guarantees that the equilibrium of T in Co is stable in the energy space H⁽²⁾ [27].

12. Conclusions

The paper has followed the long wake of studies on elastic stability that occurred in the times in which Prof. Marcello Pignataro went to Delft to meet Prof. Koiter to study there the post-critical behaviour of thin elastic structures.

Recalling those times, the paper has travelled the long path crossing the various problems debated at those times, to consistently formulate the energy method to the study of the elastic stability of continuous elastic structures, as columns, beams, plates, and shells. The basic problem was the formulation of the second variation of the potential energy of all the forces, external and internal, acting on elastic structure.

The paper has firstly examined the traditional energy approach used in the stability analysis of elastic structures evaluating the second variation of the potential energy by means of the second-order works made by all the forces when the structure T moves, passing from the initial equilibrium configuration C₀ to another near configuration C.

Limits and criticisms on this approach were made pointing out the necessity to define the measure of distances between different configurations of the structure and, at the same time, the consequent variation of the energy potential energy functional. The approach used in stability analysis of elastic systems with a finite number of degrees of freedom cannot be directly applied to continuous systems.

It has been necessary to call into question the various results obtained involving the extension of the Lagrange–Dirichlet theorem to systems with infinite degrees of freedom, as elastic beams, plates, etc., and at the same time, the fundamental results given by Sobolev in the mathematical formulation of the energy spaces H^(m). The paper terminates with the definitive formulation of the criterion of the stability of elastic structures by means of the criterion of the second variation of the energy, making reference to the results of the research, including those of Como and Grimaldi, collected in [28]. The application of the energy potential stability in tri-dimensional elasticity remains, on the contrary, a still open problem.