Modeling Techniques, Seismic Performance, and the Application of Rocking Shallow Foundations: A Review

Abstract

The intriguing rocking behavior of foundations has attracted the attention of both researchers and professionals, owing to its beneficial characteristics such as energy absorption and self-adjusting capability. This paper offers a thorough examination of various modeling techniques, seismic performance evaluation methods, and the practical application of innovative rocking shallow foundations. While conventional fixed-base designs can absorb seismic energy, they often suffer from lasting damage due to residual deformation. In contrast, rocking foundation structures facilitate controlled rocking movements by loosening the connection between the structure and the foundation, thereby enhancing overall stability. Historical studies dating back to the 19th century demonstrate the effectiveness of rocking foundations in reducing seismic impact and ductility demands, leading to cost savings. Furthermore, this paper extends its focus to contemporary considerations, exploring modern modeling techniques, seismic performance assessments, and practical applications for rocking shallow foundations. By highlighting their role in improving structural resilience, this study investigates seismic hazard analysis, geological factors, and site-specific conditions influencing foundation behavior. It covers essential aspects such as dynamic responses and modeling methodologies, drawing insights from real-world case studies. Through a comprehensive review of both numerical and experimental investigations, the article provides a synthesis of current knowledge and identifies avenues for future research.

1. Introduction

The field of performance-based earthquake engineering emphasizes the importance of understanding the nonlinear behavior of shallow foundations in both bridges and buildings under significant seismic loads. In buildings, this approach is utilized to assess the seismic performance of high-rise buildings, residential complexes, and commercial structures, ensuring their resilience during significant seismic events [1]. Khalil et al. (2023) [1] conducted research to assess the seismic vulnerability of cylindrical ground-supported steel silos designed for storing solid materials. Similarly, in bridge engineering, the nonlinear behavior of shallow foundations is crucial for evaluating the seismic response of bridges and enhancing their durability and safety. Over decades, researchers and engineers have dedicated extensive efforts to model testing and analytical modeling to comprehend the nonlinearity and uplift associated with foundations, aiming to address the complexities of seismic responses [2]. Civil engineering structures face challenges in design due to varying shaking intensities during ground motions. Extensive research on seismic performance has significantly enhanced our understanding of structural behavior during earthquakes. This improved knowledge has enabled the development of resilient structures capable of better performance and increased safety during and after seismic events [3]. This enhanced knowledge has, in turn, facilitated the development of resilient structures that can perform better and ensure greater safety during and after earthquakes. According to Wang (2016) [4], seismic design evolution for civil engineering structures has seen advancements in high-performance structural materials like high-strength concrete and steel, as well as high-performance structural components such as steel-reinforced concrete columns, concrete-filled steel tubular columns, concealed steel shear walls, and steel plate shear walls. Progress has also been made in developing high-performance structural systems such as the tube-in-tube system and the frame-tube bundle structure system.

Rocking shallow foundations incorporate a rocking mechanism that allows controlled rotating around a hinge or curved interface, thereby improving seismic performance. This design feature helps to dissipate energy, leading to reduced structural damage, lower foundation stresses, and enhanced resilience during seismic events [5]. The benefits extend to cost-effectiveness, simplified design processes, and increased adaptability to dynamic loads. Current research on rocking shallow foundations highlights the importance of physical model testing, which involves subjecting models to real-world conditions for observation. Analytical modeling and simulation techniques are then employed and validated against experimental results. The validation process ensures the accuracy and reliability of the analytical models, allowing for the derivation of modeling recommendations that can be effectively applied in practical engineering scenarios. This iterative process of testing, validation, and application enhances the understanding of the performance of rocking shallow foundations and contributes to the development of reliable modeling practices in engineering applications. Allowing a shallow foundation to undergo rocking during a seismic event results in permanent settlement and rotation [6]. Typically, these outcomes prompt bridge engineers to adopt pile foundations as the standard practice for bridges and other structures. Despite this, there are scenarios where shallow-spread foundations may offer a cost-effective alternative [7]. This is especially applicable in situations where bridges can be supported on stable soil. With this solution, geotechnical hazards can be effectively mitigated, and the nonlinear load-displacement behavior of the soil presents an opportunity for energy dissipation at the interface between the soil and the structure [8]. This recognition is not new; for instance, Housner (1963) [9] proposed that allowing a structure, represented as a block, to rock could serve as an efficient method of energy dissipation. The referred author provided fundamental equations that describe the loss of kinetic energy per rocking motion as the system releases energy. Furthermore, Housner (1963) [9] identified a scale effect, explaining why small buildings are more susceptible to collapse in comparison to their taller counterparts. This insight reflects a longstanding awareness within the field regarding the potential benefits of rocking as a mechanism for energy dissipation. The industry is now recognizing the potential benefits of foundations that are allowed to rock [10,11]. Both experimental studies and simulations of such foundations have demonstrated superior re-centering capabilities compared to traditionally designed ductile columns [12,13]. Additionally, structures incorporating hinging and rocking systems, where hinge yielding and foundation rotation yielding are equal, exhibit identical load-displacement and moment-rotation pushover curves. This similarity in behavior suggests that the design approach for these systems could be similar as well [14].

Over the past few decades, a substantial amount of research has been conducted to investigate the behavior of rocking shallow foundations, including experimental testing and modeling approaches. Gajan and Kutter (2008) [14] conducted a study on the rocking behavior of shallow footings using numerical simulations within the OpenSees (version 3.6.0) computational platform. They compared the numerical results with results from centrifuge experiments, focusing on capacity, energy dissipation, and the settlement of shallow foundations. The findings revealed that the rocking of shallow footings enhances the seismic performance of structures. Key conclusions from the research include: (a) the rocking mechanism does not result in significant permanent settlements; (b) the self-centering nature of rocking foundations is associated with uplift and gap closure; and (c) incorporating rocking footings, either independently or together with structural base isolation and energy dissipation devices, enhances the overall structural performance under seismic loading conditions. Deng et al. (2011) [12] focused on enhancing the seismic performance of bridge piers by allowing rocking at the foundation level. The investigations conducted by Hakhamaneshi (2014) [15] and the collaborative research by Hakhamaneshi and Kutter (2016) [16] were focused on evaluating rocking foundations with different shapes and embedment depths. Their findings indicated that narrower rectangular and I-shaped footings exhibited larger settlements in the rocking foundation system. Liu et al. (2013) [17] and Liu (2014) [18] explored the performance of low-rise frames, highlighting the beneficial aspects of balancing foundation rocking and structural inelasticity. Supporting the idea of controlled sharing of ductility demand between the superstructure and the foundation, Pecker et al. (2014) [19] provided an overview of experimental activities for seismic evaluation of nonlinear foundations and theoretical advancements using foundation macro-element models in a displacement-based design framework. Figini and Paolucci (2017) [20] investigated the coupled nonlinear response of rocking foundations and structures, considering three base conditions: fixed, elastic, and nonlinear. They observed the positive impacts of the nonlinear foundation, observing its substantial contribution to the overall energy dissipation. Gajan and Kayser (2019) [21] focused on quantifying the effects of soil uncertainties on the performance of rocking foundations. Additionally, Soundararajan and Gajan (2020) [22], along with Gajan et al. (2021) [23], conducted an analysis and summary of results from nine experimental series. Their aim was to investigate the performance of rocking foundations and explore potential correlations between performance, capacity, and seismic demand parameters.

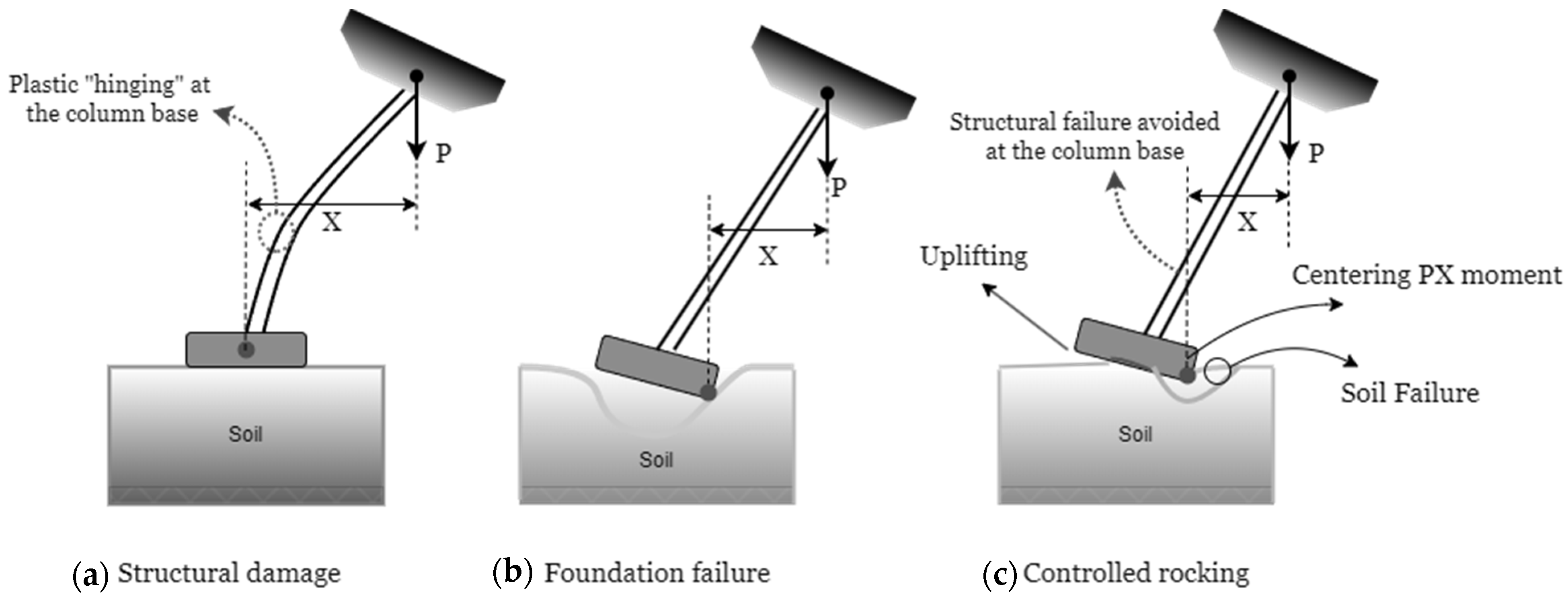
The conventional method for designing earthquake-resistant structures involves allowing controlled yielding in flexible structural elements to absorb seismic energy [24]. Simultaneously, it requires foundations to possess sufficient strength to establish a stable and immovable base, as illustrated in Figure 1 (adapted from [24]). In the case of tall or slender structures, especially those susceptible to rocking on an unstable foundation, there is a risk of substantial soil yielding [25]. Introducing base isolation, also referred to as rocking isolation, helps mitigate peak shear forces and bending moments in the structural elements. However, it is important to acknowledge that this strategy may result in a notable settlement or residual tilt [26]. This could potentially cause irreversible damage to the entire soil-structure interaction system, even if the strains in structural components can be fully recovered (see Figure 1). Anastasopoulos et al. (2013) [27] proposed a technique to enhance the resilience of a rocking isolation soil-structure interaction (SSI) system by introducing self-centering rocking shallow foundations. This involves designing foundations in a way that allows them to undergo rocking motions, promoting base uplifting while limiting the plastic soil region. By doing so, an SSI system can achieve effective self-centering through gravitational restoring forces, thereby minimizing residual foundation deformation, as shown in Figure 1. Consequently, the utilization of self-centering rocking shallow foundations holds significant potential for contributing to the resilience-oriented design of earthquake-resistant structures. The self-centering characteristics of a rocking shallow isolation system are widely acknowledged to be closely linked to the static factor of safety (F_sv) against foundation bearing-capacity failure under vertical loading [28]. In general, systems with light loads (i.e., F_sv ≥ 10 for sand and F_sv ≥ 5 for clay) exhibit notably superior self-centering abilities compared to heavily loaded systems [29]. Deng et al. (2011) [12] introduced the concept of a “recentering ratio” R_d to quantify the self-centering capability of rocking shallow foundations. This ratio is determined using residual rotations and the corresponding peak rotations observed on the foundation moment–rotation hysteresis loops. Additionally, Deng et al. (2011) [12] provided an empirical expression to estimate R_d as a function of F_sv, relying on experimental data obtained from sand. Sharma and Deng (2018) [28] carried out field snap-back experiments involving rocking footings on clay, discovering that footings on clay exhibited superior recentering capability compared to those on sand. This finding was recently corroborated by Gajan et al. (2021) [23], who conducted a comparative analysis of experimental results from a broader database. Additionally, it was noted that R_d varied with the amplitudes of cyclic rotation, with a dependence on the shape of the footing [16]. In instances of soft soil conditions, foundation enhancement may be necessary to improve the self-centering capability of rocking isolation systems [30].

Figure 2 shows the summary of this review, which encompasses literature on modeling techniques, seismic performance assessment, and the application of innovative rocking shallow foundations. It spans historical studies to present-day insights, highlighting the significant benefits of rocking foundations in reducing seismic impact and improving structural resilience. The aim of this review is to acknowledge the critical role of these foundations in mitigating seismic hazards and to consolidate existing knowledge while identifying avenues for further research. Its novelty lies in its comprehensive coverage of both numerical and experimental investigations, supplemented by real-world case studies. Organized to address fundamental aspects, from dynamic responses to site-specific conditions, this article serves as a valuable resource for advancing seismic-resistant foundation design for both researchers and practitioners.

2. Rocking Isolation Concept

The critical contact area ratio (A_ac) is defined as the ratio between the critical contact area (A_c) and the total footing area (A). The critical contact area (A_c) represents the minimum area necessary to sustain the vertical load when the soil’s ultimate bearing capacity (q_ult) is fully utilized.

$$A_{ac}=\frac{A_c}{A}$$

(1)

Once A_ac is defined, the rocking moment capacity (M_c) for a rectangular footing, as derived by previous researchers like Gajan and Kutter [14] and Deng et al. [12] using statics analysis, can be expressed as:

$$M_c=\frac{Q.L_f}{2}.\left(\frac{1-A_c}{A}\right)=\frac{Q.L_f}{2}.(1-A_{ac})$$

(2)

where Q represents the total vertical load acting on the soil-footing interface, including the superstructure, overburden soil, and footing weight; and L_f denotes the in-plane length of the footing. For a rectangular footing, the critical contact length (L_c) equals the in-plane footing length (L_f), which is equal to A_c divided by A, where A_c represents the critical contact area and A represents the entire footing area. Equation (2) indicates that M_c foot is directly proportional to both Q and L_f, with a coefficient of (1 − A_ac), which approaches 1 when A_ac is small. Other researchers, such as Meyerhof (1965) [31], Allotey and El Naggar (2003) [32], and Smith-Pardo et al. (2012) [33], have derived similar expressions to Equation (2) but with A_ac replaced by 1/FS_v, where FS_v represents the safety factor against vertical bearing capacity failure. The difference between A_ac and 1/FS_v is influenced by the shape factors and size of the critical contact area compared to those of the footing. Typically, A_ac is within a factor of two of 1/FS_v, and this difference can have around a 10% effect on the calculated moment capacity based on Equation (2) [12]. The dynamic settlement resulting from a rocking foundation can be computed using Equation (3), which was derived empirically from experimental data by Deng et al. [12]:

$$S_{dyn}=c_{sett}.L_f.Q_{cum}$$

(3)

Here, c_sett represents the dynamic settlement coefficient, while Q_cum denotes the cumulative footing rotation, which is essentially the accumulation of all rotations exceeding a certain threshold [12]. Equation (3) provides a dynamic settlement calculation that acts as an envelope, compressing more than 68% of the observed settlement data derived from dynamic and cyclic loading experiments on centrifuge models of rocking foundations. Assuming that the foundation experiences two rotations equal to the design amplitude during most seismic events (except for potentially large-magnitude, long-duration earthquakes), Equation (4) is utilized to establish a correlation between the design rotation and the dynamic settlement.

$$S_{dyn}=4. c_{sett}.L_f.d$$

(4)

where d is the maximum rotation in radians.

According to Turner (2023) [5], foundation rocking or rocking isolation mechanisms represent a novel approach in the performance-based seismic design of soil-foundation-structure systems. This concept arises from acknowledging the expected highly inelastic material response under significant seismic forces and the imperative avoidance of plastic hinging in the foundation. Traditional foundation designs address this challenge by incorporating factors of safety greater than 1 to ensure elastic behavior. However, this conservative approach results in expensive foundations and may not always guarantee safety, especially when faced with significant effective ground acceleration (Mergos and Kawashima 2005) [34]. Consequently, preventing plastic hinging in foundations becomes a challenging task if soil-foundation yielding does not occur. Controlled inelastic deformations in foundations are approved by FEMA 356 [35]. One of the six degrees of freedom that a thin structure foundation experiences under lateral stresses is rocking motion. With forces applied at the top of the structure and inertial forces concentrated there (including half the mass of the column), this behavior is viewed as being identical to that of an inverted pendulum. In a slender structure, rocking motion (as shown in Figure 3b) induces uplifting, sinking, and sliding at the edges of the footing alternately during each cycle [36]. This may or may not result in excessive rotation and settlement; however, it allows for energy dissipation and prevents plastic hinging, thereby preventing failure.

Despite these advantages, prevailing building codes prohibit the development of “plastic hinging” in the foundation. To meet this requirement, Bao et al. (2019) [37] suggested that factors of safety should be incorporated, aiming to prevent both uplifting and sinking at the footing edges (refer to Figure 1). However, this approach may result in high seismic demand. The approach to design that takes into account displacements is referred to as performance-based design, in opposition to the traditional force-centric strength-based design. Performance-based design allows for controlled deformations in the foundation, as specified by FEMA 356 [35], while ensuring they remain within acceptable limits. Considering this, and recognizing that slender structures exposed to intense seismic shaking encounter greater overturning moments than vertical loads, investigating rotational mode vibration becomes crucial. In Figure 3 (adapted from [38]), it is evident that in the case of rocking isolation, the soil-foundation undergoes plastic deformation, a stage referred to as the “recentering overturning moment”. This is in contrast with conventional design, where columns support loads and experience plastic deformation, a scenario termed the “destructive bending moment”.

Anastasopoulos et al. (2012) [39] conducted a study that brought to light several crucial findings, mainly observing that commonly employed seismic design approaches often yield excessively conservative foundation solutions. These foundations not only prove to be cost-inefficient but also pose implementation challenges. Particularly, they serve as channels for transmitting substantial accelerations to the superstructure. This, in turn, generates significant inertial forces that respond as substantial overturning moments (and shear forces) back onto the foundation, creating a negative feedback loop [40]. Conversely, foundations with significantly underestimated dimensions restrict the transmitted accelerations to levels corresponding with their modest ultimate moment capacity. This factor contributes to the creation of much safer superstructures. In earthquake engineering terms, the plastic hinging shifts from the columns to the foundation-soil system, preventing potentially hazardous structural damage [41]. Turner (2023) [5] conducted a study that revealed how, in the case of tall and slender structures primarily exhibiting rocking behavior in seismic response, inadequate design of footings tends to result in pronounced uplifting and activation of bearing capacity failure mechanisms. It is interesting to note that, at least for a restricted number of cycles in the majority of occurrences, the statically computed ultimate overturning moment capacity seems to hold up throughout cyclic loading without degrading. This emphasizes how such a method has inherent geotechnical reliability. Moreover, the static factor of safety (Fs) against vertical bearing-capacity failure is a crucial component in controlling the balance between the degree of uplifting and the level of yielding [42]. Additionally, the authors of [42] claimed that a designer has the choice to, for example, alter the subsurface to enhance Fs and encourage rising over soil inelasticity. Surprisingly, because of the shallow dynamic “pressure bulb” connected to a rocking base, such intervention can be quite small in vertical extenta design. The primary practical goal of classical geotechnical engineering is to avoid bearing capacity failure. However, seismic “loading” differs significantly; it involves imposed displacement rather than a uniform load. Sliding mechanisms occur beneath the footing only briefly and irregularly, potentially resulting in, at worst, increased settlement [3].

3. Modeling of Rocking Foundations

A foundation placed on a soil relatively exhibits six degrees of freedom in a rigid configuration, including translational movements (vertical, longitudinal, and lateral) and rotational motions (yawing, pitching, and rocking), as shown in Figure 4 (adapted from [43]). Conversely, a flexible foundation is characterized by an infinite number of degrees of freedom. Nonetheless, by putting certain restrictions in place, it is frequently possible to reduce a multi-degree of freedom (MDF) system to a single-degree of freedom (SDOF) system. This simplification helps to achieve practical and appropriate results [24].

In earthquake engineering, the use of single-degree of freedom oscillators (SDOFO) has been prevalent to simplify the analysis of intricate structural systems [44]. According to Srbulov (2008) [45], a SDOFO on a rigid base is described as one of the easiest ways of modeling the vibration of a structure. Structures commonly modeled using SDOFO include single-story building frames, bridges with hinged columns, and multi-story buildings responding to rigid base conditions. For these complex structures to be accurately represented as SDOFO, as outlined by Srbulov (2008) [45], several key assumptions must be met. Firstly, the structure should manifest only one vibration mode. Secondly, the influence of soil-foundation interaction is considered negligible and is excluded from the model. Additionally, the horizontal and vertical ground motions resulting from earthquakes are treated as independent factors. Lastly, the model assumes that only a lumped mass is capable of oscillating in a single mode. These assumptions are significant for the effective application of the SDOFO model to such structures.

As noted by Bhandari and Sengupta (2014) [46], the machine-foundation-system (MFS) uses idealizations and simplifications of physical systems to study their dynamic behavior under varying loads. One popular simplification is the application of the SDOF technique. They reported that dynamic loads affecting MFS encompass a range of factors, including: (a) unbalanced rotating and reciprocating components generating both transient and steady-state dynamic loads; (b) impact loads; (c) the surrounding vibration environment; (d) seismic forces; (e) wind-induced forces; (f) periodic and aperiodic forces; and moments arising from activities such as blasting, mining, drilling, piling operations, and sonic booms; and (g) moving loads. These considerations enable a comprehensive assessment of the MFS response to diverse dynamic loading scenarios. Gazetas and Stokoe (1992) [47] classified experimental studies on the dynamic response of foundations into three categories. Firstly, they considered measurements of the response of actual foundations subjected to dynamic loading, documented as case histories. Secondly, they investigated the small- and large-scale field experiments conducted under controlled conditions at selected sites, allowing for a closer examination of the dynamic behavior of foundations in outdoor environments. Lastly, the third category involves small and very small-scale laboratory experiments, typically performed on soil placed in a strongbox, where the footing undergoes either steady-state or transient vibrations. Together, these categories provide a comprehensive approach to investigating the dynamic response of foundations under various conditions. This specifically applies when the footing is subjected to transient vibrations. Figure 4 illustrates the schematic diagram, depicting the cyclic operation and the forces involved in the SDOFO model.

The variables in Figure 4 are defined as follows: “m” identifies the SDOFO’s equivalent mass; “H” indicates the equivalent SDOF model’s effective height; “B” indicates the square footing’s width; “θ” indicates the angle at which the foundation rotates; “P” indicates the actuator’s total weight; “F” indicates the lateral force; and “X” indicates the dynamic target’s centroid’s horizontal distance from the static target.

Resonance amplification, also known as the resonance effect, is a phenomenon in structural engineering that happens when the inherent vibration frequency of a structure coincides with the frequency of incoming seismic waves, especially when rocking motion is caused by seismic activity [48]. Higher seismic forces are applied to the structure as a result of this resonance, which causes a noticeable increase in the amplitude of the structure’s motion.

4. Numerical Studies and Computer Vision

Housner (1963) [9] initially explored the phenomenon of a rigid body undergoing rocking motions in response to lateral ground movements at the base. The discovery of structures being able to rock on their footing pad emerged following the survival of numerous slender structures during the 1960 Chile earthquake. The analysis of the rocking motion of these structures treated them as inverted pendulums, yielding a closed-form solution. The assumptions underlying the analyses were: (i) the rocking body and its base are treated as rigid; (ii) neglect of sliding and uplift; and (iii) a description of the energy dissipation resulting from rocking through an energy reduction factor. In Housner’s analysis from 1963 [9], the rocking block (Figure 5, adapted from [9]) was examined under free excitation. The study involved calculating the time and energy consumption of the rocking rigid body subjected to a constant, horizontal acceleration as well as under the influence of a single sine wave and overturning force during a horizontal earthquake excitation. The findings indicated that larger-sized superstructures result in a more stable rocking structure compared to smaller-sized ones, which was attributed to the scale effect. Moreover, the stability of tall, slender blocks under earthquake action was observed to be superior under constant horizontal force. Nevertheless, the uplift phenomenon cannot be disregarded. Consequently, to account for the impact of uplift on the rocking response, other researchers made substantial efforts.

Particle image velocimetry was used by Moradi et al. (2023) [49] to investigate the deformation mechanisms beneath shaking foundations. They found that during loading cycles, foundations with larger FS_v have less contact area with the earth, which causes visible rise on the unloaded side (heel side). In contrast, foundations with lower FS_v experience severe wedge deformation and settlement, as well as the establishment of a greater soil contact area. As a result, as shown in Figure 6, the footing experiences negligible uplift on the unloaded side of the foundation and settles into the earth (sinking mechanism).

Psycharis and Jennings (1983) [50] explored the dynamic behavior of a rocking, rigid block allowed to uplift. This investigation involved an elastic foundation with damping, considering two cases: the Winkler model, commonly employed in soil mechanics, and the simplified two-spring foundation model, where the structure is supported by two springs and dashpots symmetrically positioned under the base. The findings of this research indicated that uplift results in a more compliant vibrating system, and the apparent rocking period increases with the uplift magnitude. Beck and Skinner (1973) [51] initiated the first analytical investigation into a rocking pier incorporating energy-dissipating devices as a seismic-resistant structural system for bridges. This innovative approach reduces the strength and ductility requirements of the pier and minimizes the top displacement caused by rocking. The successful application of this system is exemplified in the design and construction of the South Rangitikei Railway Bridge in New Zealand, completed in 1981 [46]. Kawashima and Hosoiri (2003) [52] conducted a study on the inelastic rocking response of large, rigid foundations. Their findings revealed that rigid foundations do not undergo overturning, even when exposed to ground motions with acceleration peaks significantly exceeding those observed in conventional static analyses.

5. Analysis of the Key Parameters Affecting the Seismic Response of Rocking Shallow Foundations

The thorough analysis of key parameters influencing the seismic response of rocking shallow foundations includes a complex investigation carried out by Beck and Skinner (1973) [51]. The authors emphasize that a key aspect of this analysis involves understanding the underlying soil properties, such as stiffness, damping, and shear strength, which greatly influence the interaction between the foundation and the soil. Additionally, the geometry of the foundation, including its dimensions, shape, and the position of the rocking axis, is crucial in determining its capacity to rock and absorb seismic energy effectively. As a result, structural properties like material type, flexibility, and damping characteristics play significant roles in the absorption and redistribution of energy. 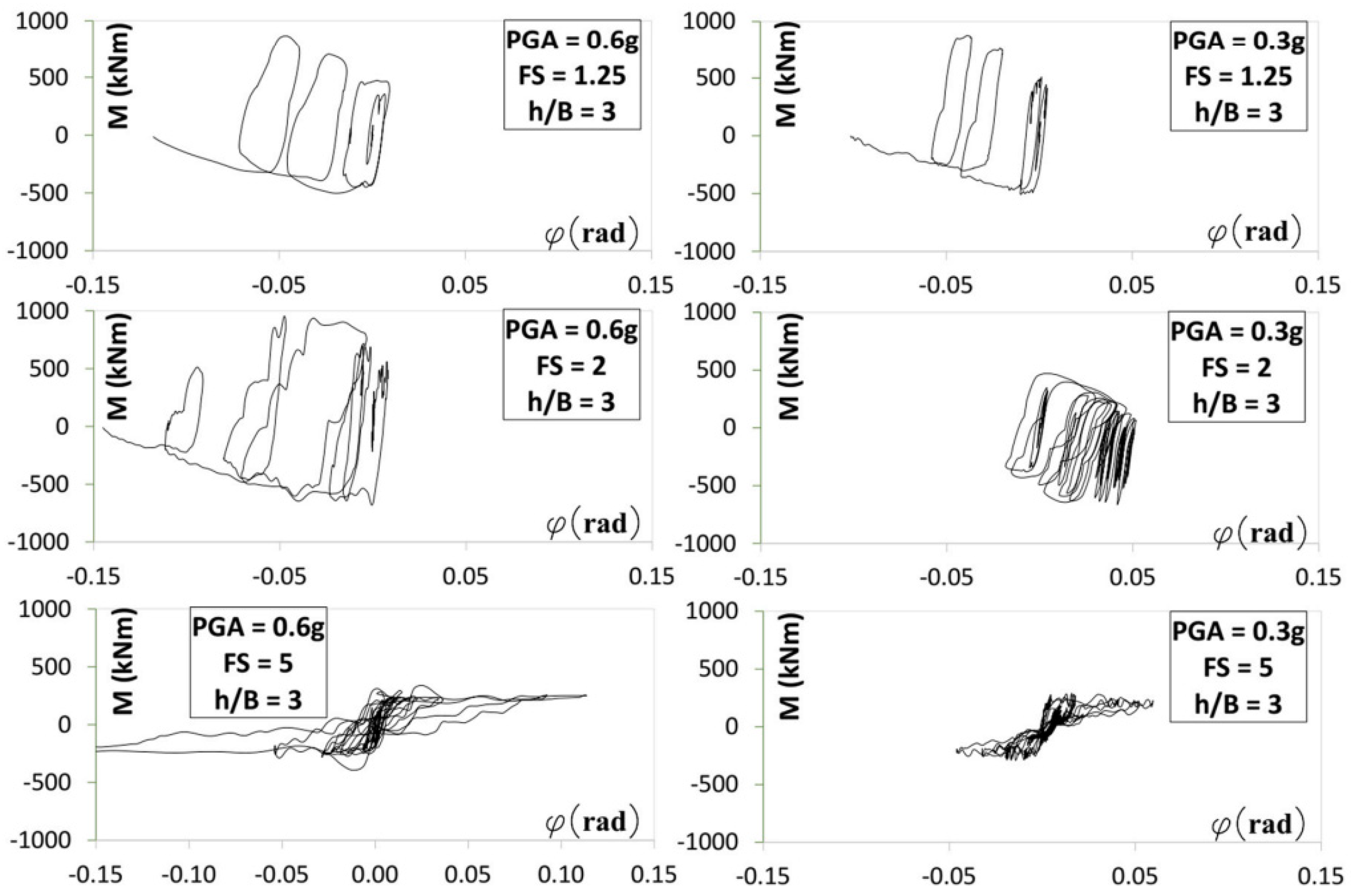Furthermore, the seismic input, characterized by ground motion parameters, introduces external forces that must be thoroughly comprehended for accurate predictions [44]. Khamesi and Hosseini [53] conducted a numerical investigation into the factors influencing the rocking response of shallow foundations in single degree of freedom (SDOF) structures. Their study focused on examining the impact of static safety factors related to soil bearing capacity failure, ground motion characteristics, and the depth at which the foundation is embedded on the overall behavior of the system. The results they obtained highlighted significant changes in the system’s response during seismic events due to variations in these parameters; refer to Figure 7, Figure 8 and Figure 9.

The dynamic rocking mechanism, considering hinge points, rotational resistance, and energy dissipation, is dominant [54,55]. Beyond linear assumptions, the analysis investigates nonlinear effects, including material yielding and soil-structure interaction. Dynamic soil-structure interaction further analyzes how the foundation rocking motion influences the surrounding soil. Using sophisticated numerical modeling methods, such as finite element analysis, enables a detailed simulation that integrates these intricate parameters, resulting in a more precise representation of the seismic response. Luitel and Guan (2021) [42] stated that the general approach not only enhances the understanding of rocking shallow foundations but also enables the optimization of design parameters, contributing to the development of more resilient structures in seismic-prone regions.

6. Case Studies and Applications

The successful outcomes of both numerical simulations and practical experiments assessing the viability of rocking foundations have prompted their integration into the design and retrofitting of numerous structures. Scholars such as Priestley et al. in 1978 [55] and 1996 [56], Pollino and Bruneau (2007) [57], and Astaneh-Asl (1996) [58] have supported the utilization of rocking foundations in the design and retrofitting of bridges. An illustrative example is the construction of the Rion Antirion Bridge in Greece [59], where the foundations of the structure, specifically the reinforced soil (clay-steel composite) and the pylon bases, are intentionally not rigidly connected. Figure 10 shows the main bridge concept and the construction of pylon bases. The construction of the pylon bases near Antirion was carried out in two phases. Initially, the footings were cast on a dry deck measuring 230 m in length and 100 m in width (refer to Figure 10b). Subsequently, the conical shafts were completed in a wet dock with adequate water depth. This design allows the pylon bases to experience uplift or slide in relation to the reinforced soil. The outcome is that the forces and overturning moments applied to the soil consistently remain within the bounding surface during analysis, confirming the highly favorable behavior of a fully suspended deck in isolation.

The retrofitting of various bridges, including iconic structures like the Golden Gate Bridge in San Francisco, California [60], the Carquinez Bridge in Vallejo, California [61] (Jones et al. 1997), and the Lions Gate Bridge in Vancouver, British Columbia [62], has incorporated the rocking foundation concept.

Wang et al. (2013) [54] conducted a study on the San Francisco Bay Area Rapid Transit (BART) system, which has served as a vital transportation link for the Bay Area since its inception in 1972, catering to over 360,000 passengers daily. They conducted seismic assessment and retrofitting for a total of 11 aerial stations as part of the program. These stations are situated along the “A-line”, “C-line”, and “R-line” of the BART system. Given the heightened earthquake risk in the San Francisco Bay Area and the critical role of the BART system in the region, significant public attention has been drawn to the BART earthquake safety program since its inception. The seismic retrofit design of BART’s elevated stations was executed in a cost-effective manner, with a focus on upgrading the stations to meet safety performance goals.

Noteworthy projects, like the seismic retrofit of the Golden Gate Bridge and the implementation of rocking shallow foundations in the Rion Antirion Bridge, highlight the effectiveness of innovative strategies in bolstering seismic resilience. These examples underscore the ongoing exploration and adoption of innovative solutions within the engineering community to enhance infrastructure resilience in the face of seismic challenges.

While rocking shallow foundations offer advantages in seismic resilience and energy dissipation, they come with several limitations that must be carefully considered. Construction costs can be higher due to the need for specialized engineering and materials, including features like bearings and articulation points [18]. Site suitability is critical, as unsuitable soil conditions or geological factors can hinder foundation performance [63]. Regular maintenance and inspection are necessary to ensure ongoing effectiveness, and the design complexity of these foundations may require specialized expertise. Kelly (2009) [64] stated that the applicability of rocking shallow foundations may be limited by factors such as structure height, load distribution, and local building codes. Concerns about uplift risk during seismic events, durability in harsh environments, and long-term performance also need to be addressed. To overcome these limitations, thorough site assessments, collaboration with experts, adherence to standards, and careful planning are essential to ensuring the successful implementation of rocking shallow foundations while mitigating potential risks.

It is also worth noting that rocking systems have been employed in various structures beyond bridge foundations, as exemplified before, including pallet racking structures, with promising results [65]. This broader application highlights the versatility and potential effectiveness of rocking mechanisms in mitigating seismic impacts across different types of structures.

7. Conclusions and Future Research Needs

Based on advanced numerical and experimental investigations, it is evident that rocking structures and foundations play a significant role in enhancing their seismic performance. The non-linear behavior of soil and its ability to dissipate energy through hysteresis form the basis of rocking foundations. These foundations outperform conventional fixed base alternatives by efficiently dissipating seismic energy, providing a cost-effective solution for base isolation. Notably, rocking foundations exhibit effectiveness in both shallow and deep pile foundations, contributing to the seismic resilience of buildings and bridges. An essential aspect of comprehending the rocking foundation phenomenon lies in understanding the dynamic interaction between soil and structure, emphasizing the significance of this study in advancing seismic engineering knowledge.

Further research is needed to understand and enhance the acceptance of rocking foundations as an alternative to traditional designs in engineering. Key areas for expansion include conducting regression analysis of nondimensional parameters, which can lead to more precise design equations. Exploring complex soil models and introducing sliding into the model are also crucial for better understanding the system’s behavior.

While research supports the benefits of rocking foundations for seismic energy dissipation, current design codes, particularly in the U.S., prohibit their use in bridge design due to concerns about permanent settlements and rotation. To promote the adoption of rocking foundations, there is a need for comprehensive design methods that address overall and local deformation, deformation limits, foundation rotation limits, and additional damping ratios.