Energy-Based Design of Buckling-Restrained Steel Braced Frames for Concurrent Occurrences of Earthquake and Wind
Abstract
1. Introduction
1.1. Studies on Dual Hazards on Structures
1.2. Buckling Restrained Braces
2. Research Objectives
- The steel frames are in an undamaged state when the dual hazards strike.
- The excitations caused by earthquakes and wind have the same duration and their maximum effects occur within this time span, i.e., the structure is experiencing its most severe loading condition during this time interval.
- The FEMA-recommended drift limits [11] for the performance-based seismic design (PBSD) of moment and braced steel frames are used in the present study to assess the adequacy of these frames when subject to dual wind–earthquake excitations. This is because in the proposed methodology, the dual hazard effect is represented by a time-varying excitation like that of an earthquake.
3. Dual Earthquake–Wind Hazard Power Spectrum
3.1. Earthquake Power Spectrum
3.2. Wind Power Spectrum
3.3. Proposed Dual Hazard Power Spectrum
4. Earthquake and Wind Data Characterizations
4.1. Earthquake Data
4.2. Wind Data
5. Dual Earthquake–Wind Hazard Excitations
6. Analysis Results for Moment Resisting Frame Responses to Dual Earthquake and Wind Hazards
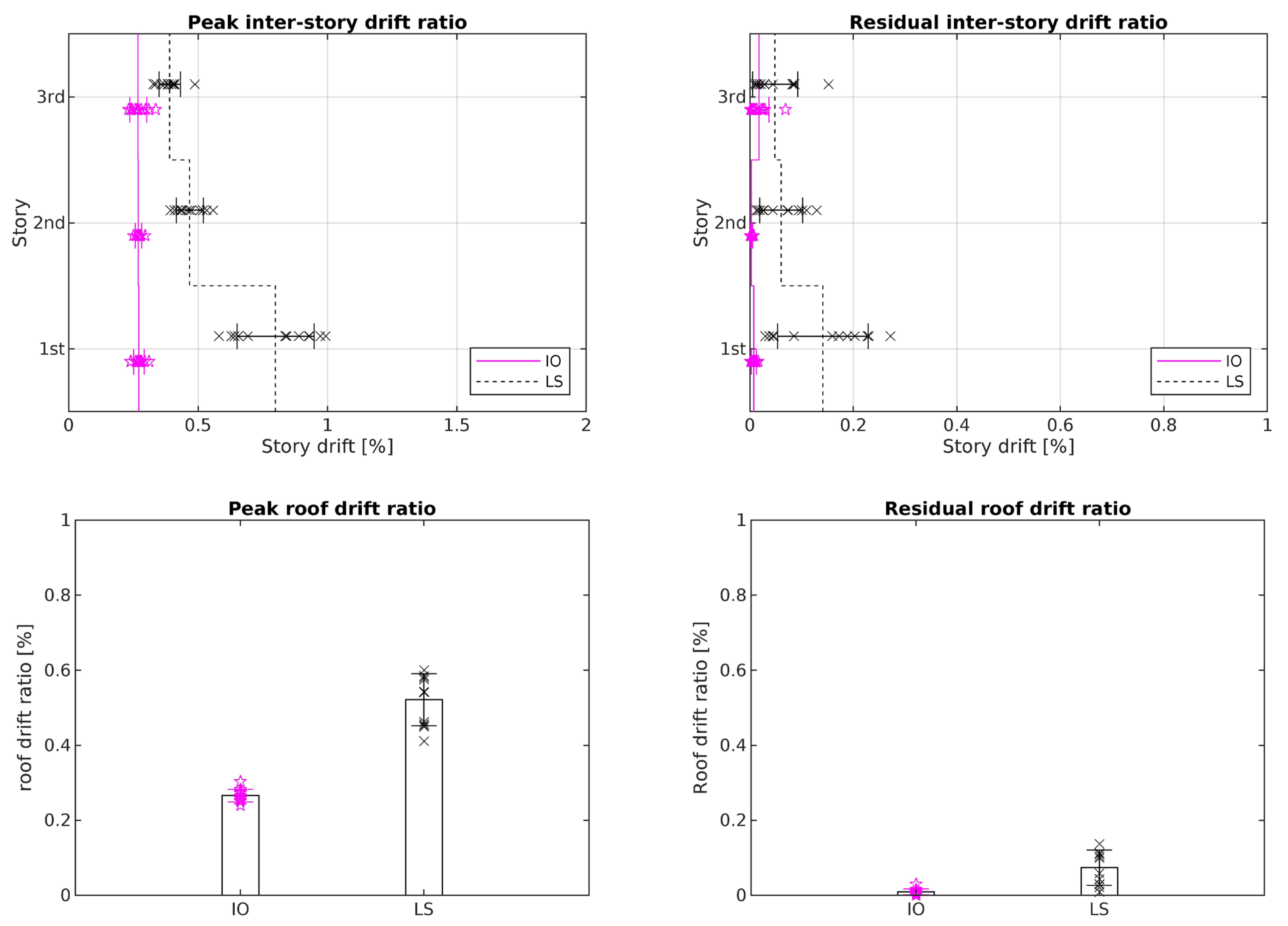
6.1. Three-Story Frame
- Los Angeles:
- Charleston:
6.2. Nine-Story Frame
- Los Angeles:
- Charleston:
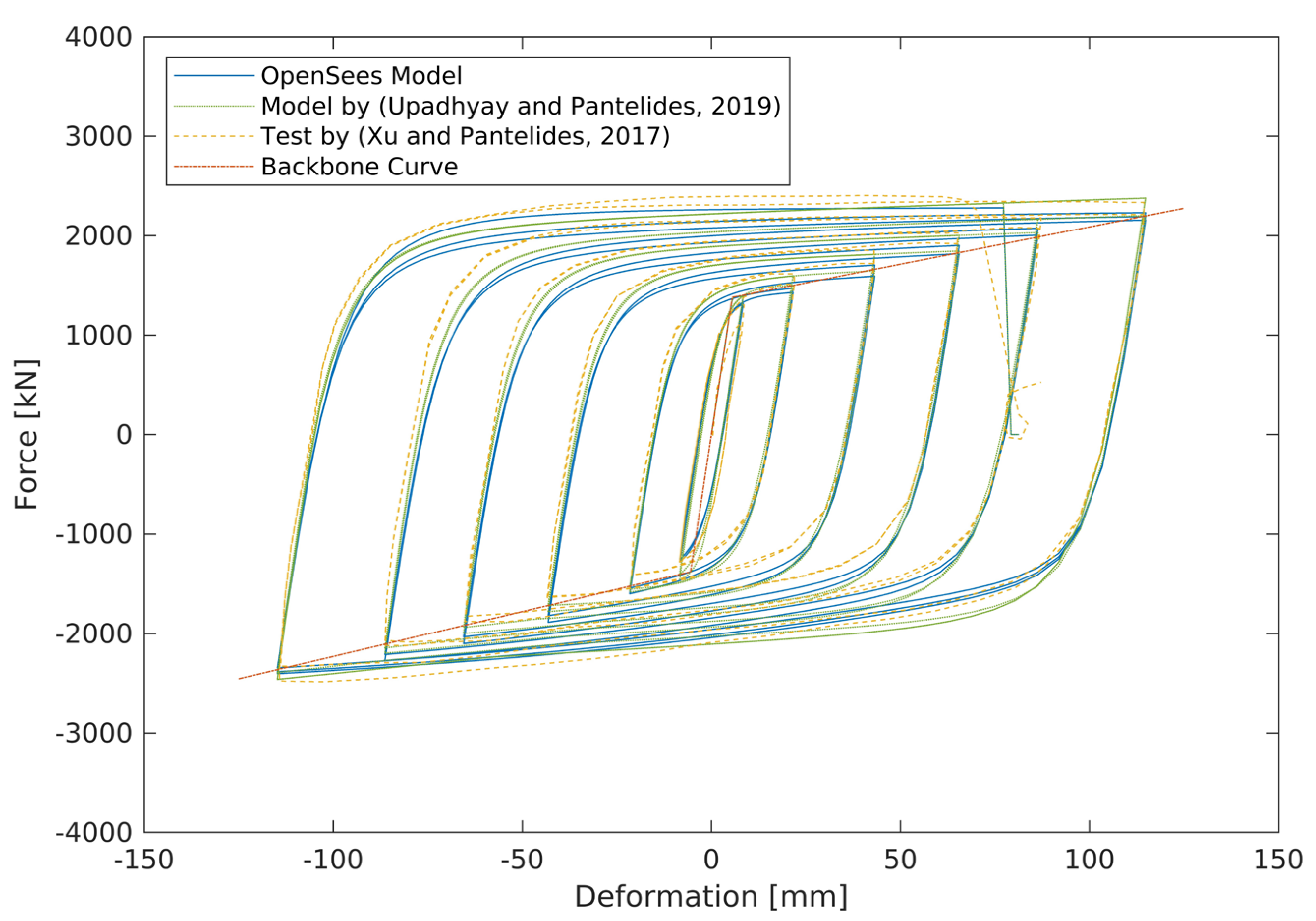
7. Modeling of Buckling-Restrained Braces
8. Energy-Based Design of Buckling-Restrained Braced Frames
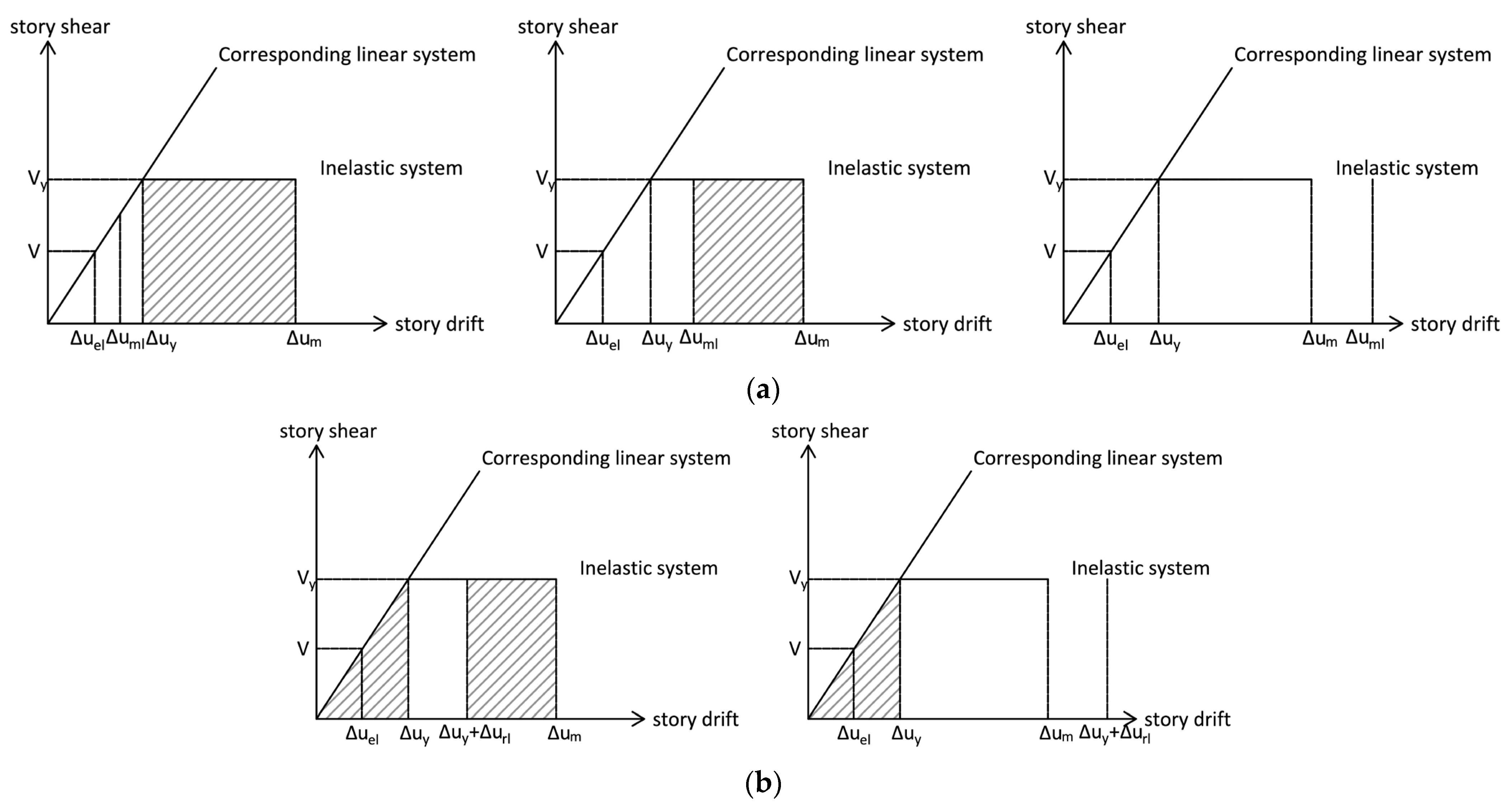
8.1. Energy Capacity of a BRB
8.2. Energy Demand from the Dual Hazards
8.3. Proposed Energy-Based Design Procedure for BRB
- Step 1: Construct elastic response spectra for the dual excitations.Pseudo (or spectral) acceleration response spectra (often expressed in m/s2 or in terms of acceleration due to gravity, g) are plots of pseudo accelerations Sa against system periods T (in seconds). These spectra can be constructed for the dual excitations using software such as Bispec, SeismoSoft, OpenSees, etc.
- Step 2: Run a modal analysis to obtain (or estimate) the fundamental period for the intermediate moment frame.
- Step 3: Calculate the base shear using the equation
- Step 4: Determine the equivalent lateral force (ELF) and story shear at story using the equation:
- Step 5: Perform a linear static analysis on the intermediate moment resisting frame subject to this ELF and determine its maximum inter-story displacement response . The maximum displacement response of the frame accounting for inelasticity can be estimated using the equation:
- Step 6: Use the energy equation to determine the required BRB cross-section area for each story. The required BRB yielding core area can be obtained by equating Equation (11) or Equation (14) with Equation (17) and solving for to give
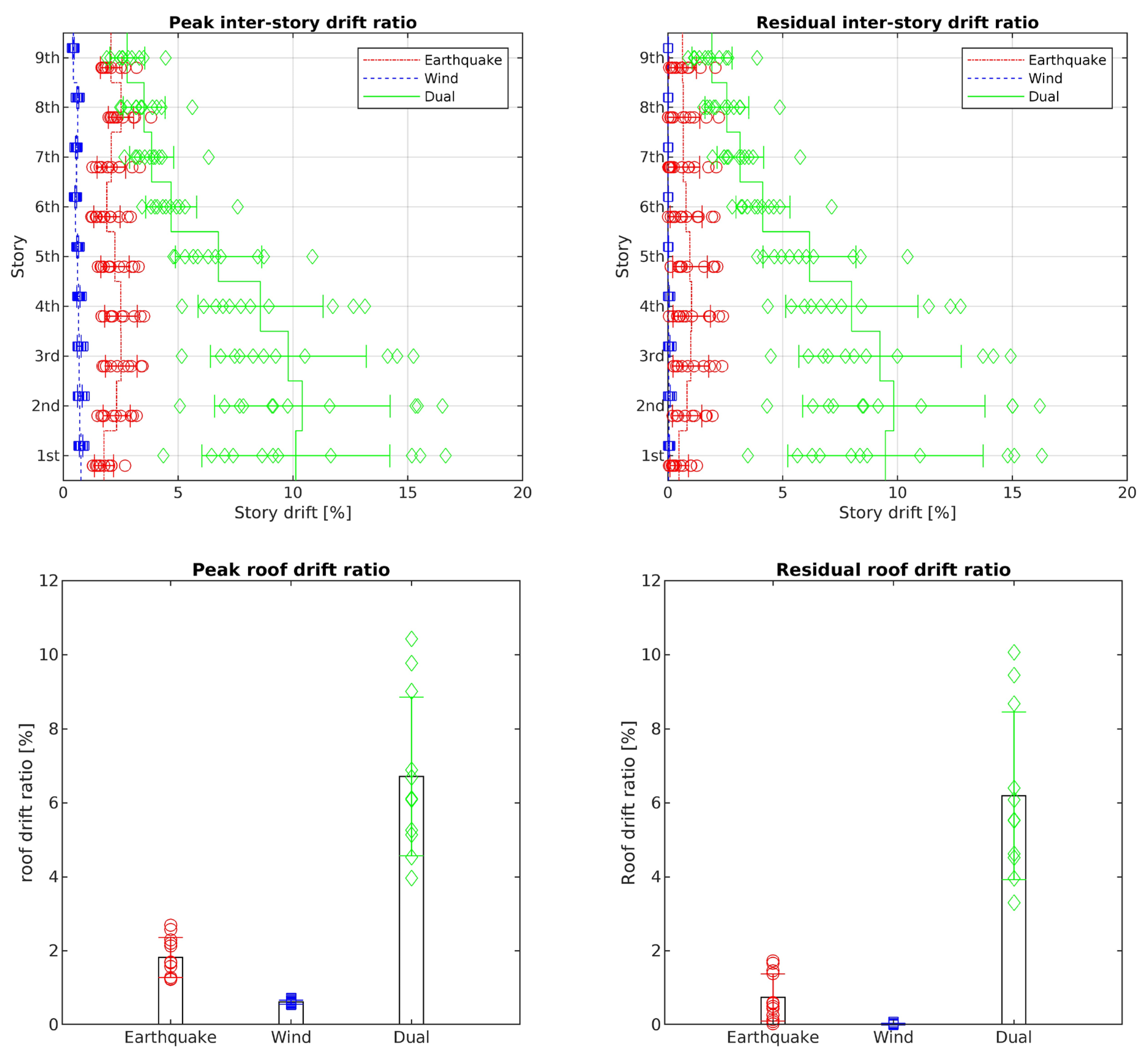
9. Analysis Results for Buckling-Restrained-Braced-Frame Responses to Dual Earthquake and Wind Hazards
9.1. Three-Story Frame
9.2. Nine-Story Frame
10. Results and Discussion
11. Summary and Conclusions
- When compared to results obtained for earthquake only or wind only excitation, the two steel frames used in the present study were shown to experience peak and residual inter-story and roof drift ratios that were noticeably higher under the dual earthquake–wind excitations.
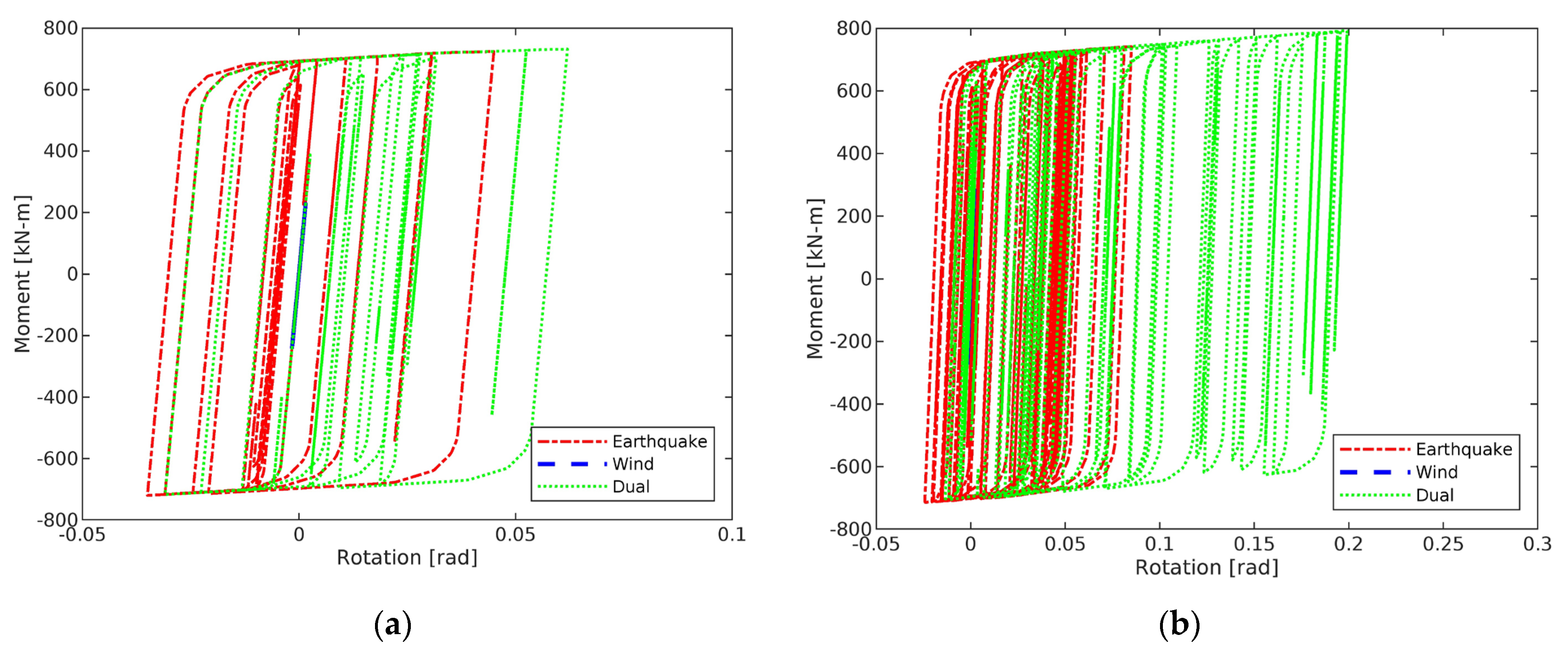
- From Table 6 and Table 7, it can be seen that dynamic responses due to the combined earthquake–wind dual excitations cannot be obtained just by adding the dynamic responses due to earthquake only and wind only excitations. This is because of the presence of inelasticity. Once the structure experiences yielding, inelastic deformations will increase rapidly with the applied forces (as illustrated in Figure 10 and Figure 12).
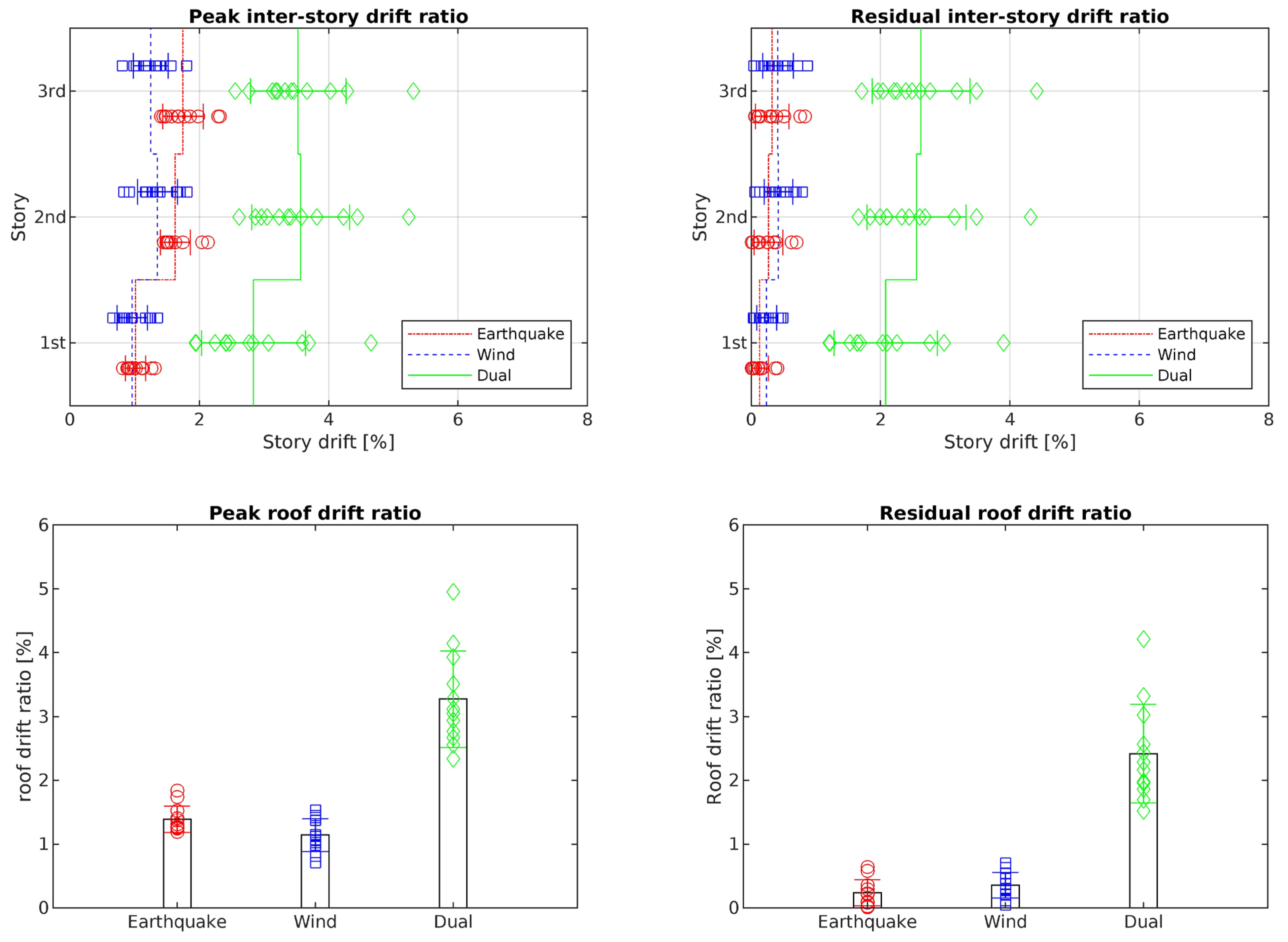
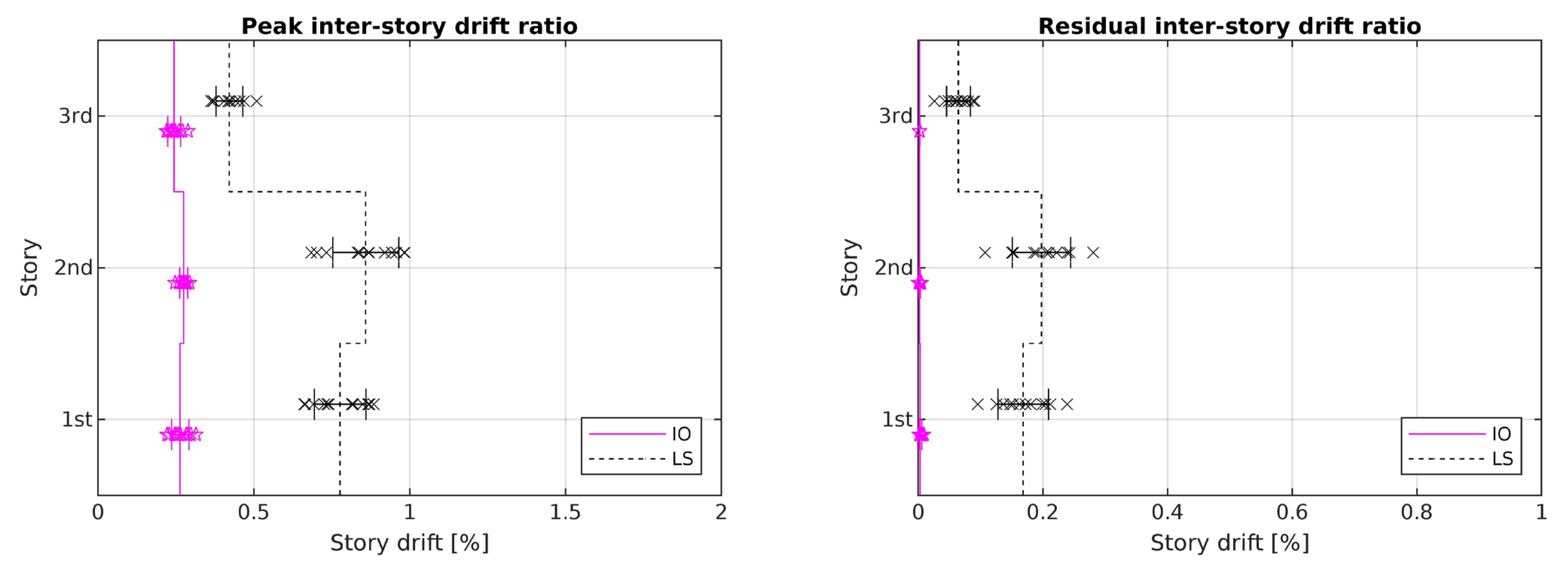
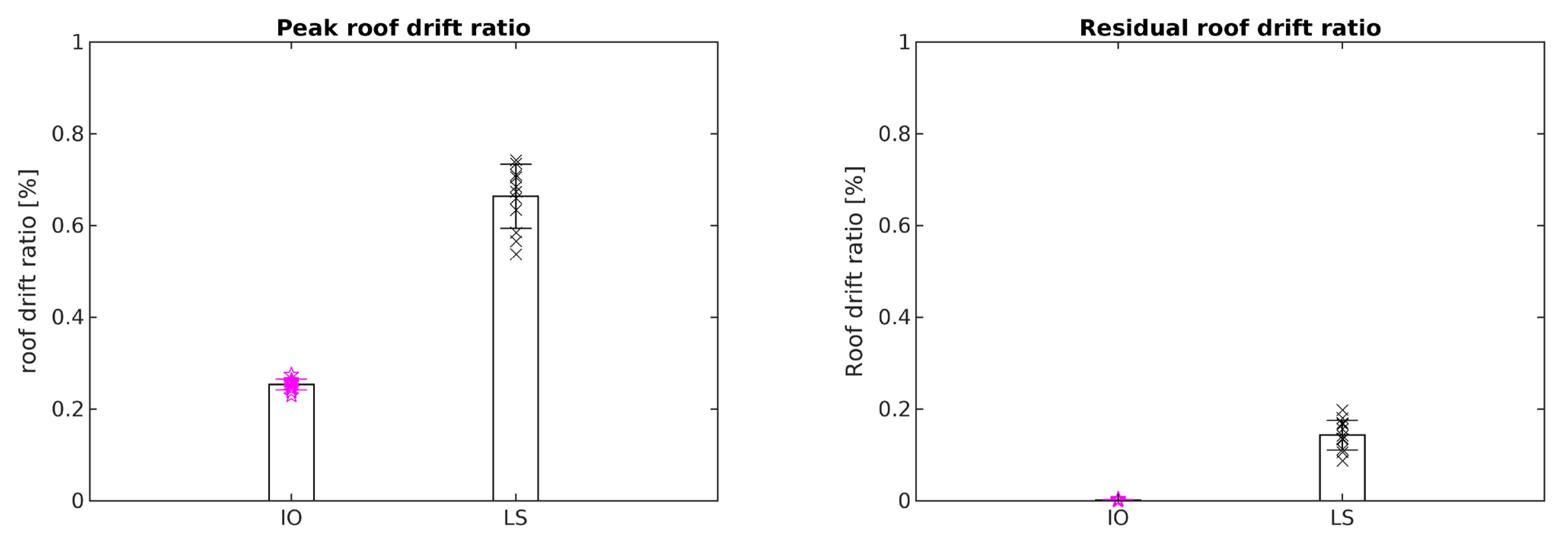
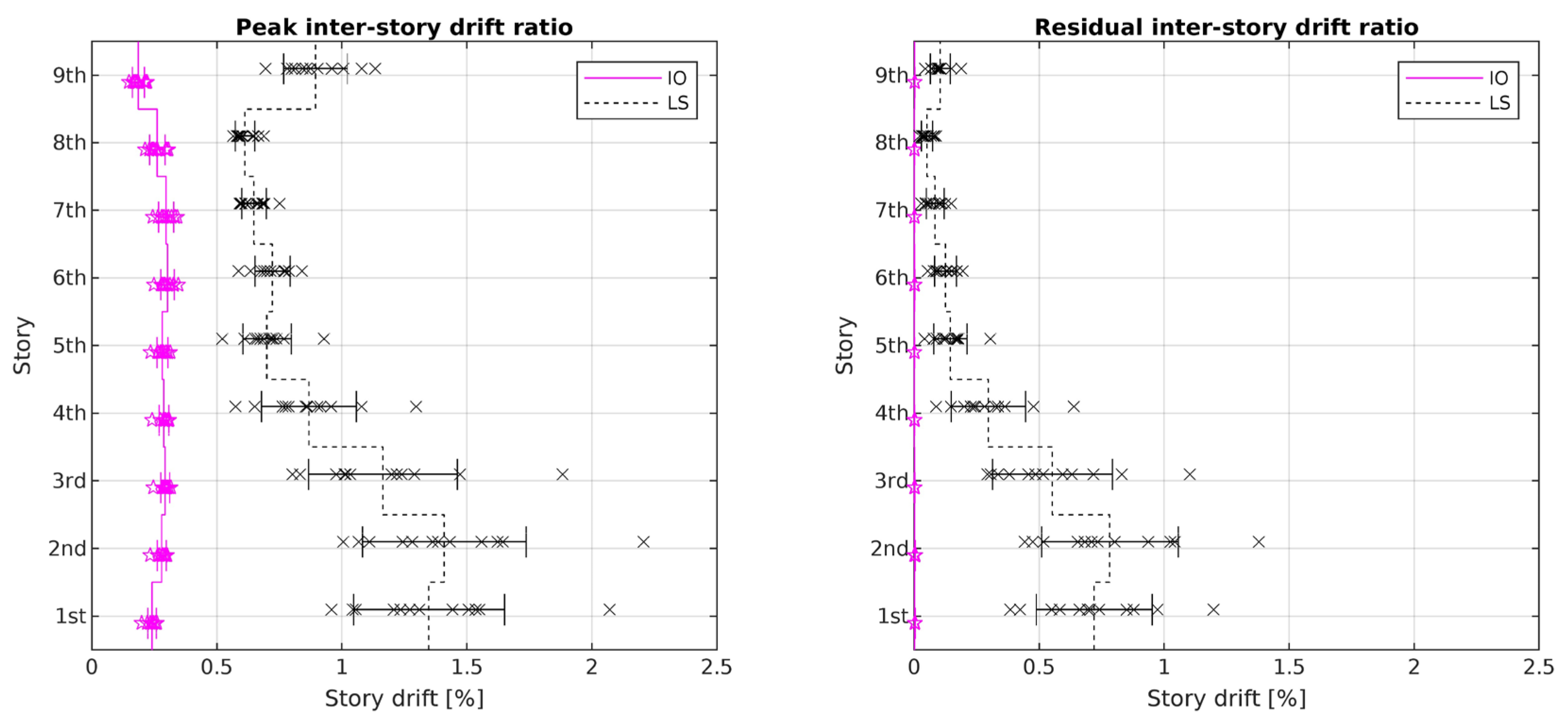
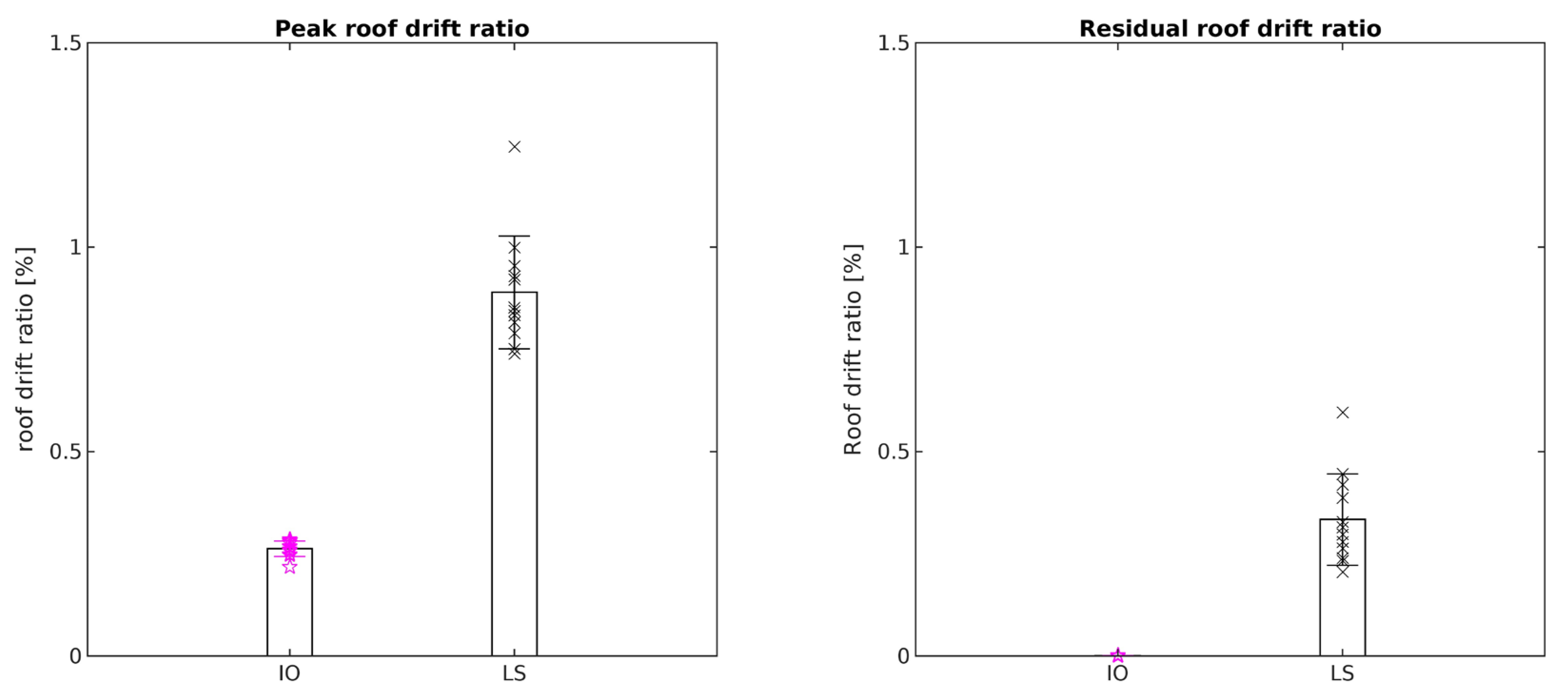
- By retrofitting these frames with BRBs using the proposed energy-based design methodology presented in Section 8, the drift ratios of these frames were drastically reduced, and they all fell below or came very close to the FEMA 356 drift limits.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Abbreviations
| ASCE | American Society of Civil Engineers |
| BRB | Buckling Restrained Brace |
| BRBF | Buckling-Restrained-Braced Frame |
| DBE | Design Based Earthquakes |
| EDP | Engineering Demand Parameters |
| ELF | Equivalent Lateral Force |
| FEMA | Federal Emergency Management Agency |
| FFT | Fast Fourier Transform |
| IBC | International Building Code |
| IFFT | Inverse Fast Fourier Transform |
| IO | Immediate Occupancy |
| LS | Life Safety |
| MCE | Maximum Considered Earthquakes |
| MRF | Moment Resisting Frame |
| PSD | Power Spectral Density |
| RSN | Record Sequence Number |
| SEI | Structural Engineering Institute |
| SRSS | Square Root of the Sum of Squares |
Appendix A
| RSN | Event | Year | Station Name | Magnitude | Vs30 (m/s) |
|---|---|---|---|---|---|
| 100 | “Hollister-03” | 1974 | “San Juan Bautista_ 24 Polk St” | 5.14 | 336 |
| 187 | “Imperial Valley-06” | 1979 | “Parachute Test Site” | 6.53 | 347 |
| 280 | “Trinidad” | 1980 | “Rio Dell Overpass-FF” | 7.2 | 312 |
| 292 | “Irpinia_ Italy-01” | 1980 | “Sturno (STN)” | 6.9 | 382 |
| 313 | “Corinth_ Greece” | 1981 | “Corinth” | 6.6 | 361 |
| 725 | “Superstition Hills-02” | 1987 | “Poe Road (temp)” | 6.54 | 317 |
| 832 | “Landers” | 1992 | “Amboy” | 7.28 | 383 |
| 1119 | “Kobe_ Japan” | 1995 | “Takarazuka” | 6.9 | 312 |
| 1762 | “Hector Mine” | 1999 | “Amboy” | 7.13 | 383 |
| 2093 | “Nenana Mountain_ Alaska” | 2002 | “TAPS Pump Station #09” | 6.7 | 383 |
| 5865 | “El Mayor-Cucapah_ Mexico” | 2010 | “Palm Springs Airport” | 7.2 | 312 |
| 6911 | “Darfield_ New Zealand” | 2010 | “HORC” | 7 | 326 |
| RSN | Event | Year | Station Name | Magnitude | Vs30 (m/s) |
|---|---|---|---|---|---|
| 26 | “Hollister-01” | 1961 | “Hollister City Hall” | 5.6 | 198.8 |
| 35 | “Northern Calif-06” | 1967 | “Hollister City Hall” | 5.2 | 198.8 |
| 163 | “Imperial Valley-06” | 1979 | “Calipatria Fire Station” | 6.53 | 206 |
| 314 | “Westmorland” | 1981 | “Brawley Airport” | 5.9 | 209 |
| 462 | “Morgan Hill” | 1984 | “Hollister City Hall” | 6.19 | 198.8 |
| 718 | “Superstition Hills-01” | 1987 | “Imperial Valley Wildlife” | 6.22 | 179.0 |
| 1931 | “Anza-02” | 2001 | “El Centro Array #10” | 4.92 | 203 |
| 1992 | “Gulf of California” | 2001 | “Calipatria Fire Station” | 5.7 | 206 |
| 4100 | “Parkfield-02_ CA” | 2004 | “Parkfield-Cholame 2WA” | 6 | 173.0 |
| 4462 | “L’Aquila_ Italy” | 2009 | “Avezzano” | 6.3 | 199.0 |
| 180 | “Imperial Valley-06” | 1979 | “El Centro Array #5” | 6.53 | 206 |
| 726 | “Superstition Hills-02” | 1987 | “Salton Sea Wildlife Refuge” | 6.54 | 191.1 |
| Story | ||||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 0.941 | 0.261 | 5101 | 5075 | 0.557 | 2121 | 416 | 616 |
| 2 | 0.952 | 0.264 | 4694 | 4724 | 0.312 | 1189 | 647 | 960 |
| 1 | 0.946 | 0.263 | 4694 | 4694 | 0.1305 | 497 | 505 | 750 |
| Story | ||||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 1.422 | 0.395 | 5101 | 5089 | 0.558 | 3205 | 857 | 337 |
| 2 | 1.435 | 0.398 | 4694 | 4723 | 0.312 | 1792 | 1331 | 523 |
| 1 | 1.426 | 0.396 | 4694 | 4694 | 0.1303 | 749 | 908 | 357 |
| Story | ||||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 0.435 | 0.1207 | 5101 | 4223 | 0.513 | 1017 | 96.7 | 143 |
| 2 | 0.523 | 0.1453 | 4694 | 4678 | 0.342 | 679 | 169.1 | 251 |
| 1 | 0.525 | 0.1458 | 4694 | 4694 | 0.1445 | 286 | 136.8 | 203 |
| Story | ||||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 0.625 | 0.1735 | 5101 | 4380 | 0.521 | 1452 | 127.5 | 50 |
| 2 | 0.732 | 0.2033 | 4694 | 4722 | 0.338 | 943 | 223 | 88 |
| 1 | 0.728 | 0.2021 | 4694 | 4694 | 0.1413 | 394 | 162.5 | 64 |
| Story | ||||||||
|---|---|---|---|---|---|---|---|---|
| 9 | 0.433 | 0.1202 | 5248 | 5247 | 0.273 | 1482 | 222 | 330 |
| 8 | 0.456 | 0.1265 | 4856 | 5108 | 0.215 | 1168 | 502 | 744 |
| 7 | 0.453 | 0.1257 | 4856 | 5077 | 0.1681 | 914 | 621 | 921 |
| 6 | 0.450 | 0.1249 | 4856 | 5043 | 0.1271 | 691 | 631 | 936 |
| 5 | 0.446 | 0.1240 | 4856 | 5007 | 0.0916 | 498 | 763 | 1131 |
| 4 | 0.443 | 0.1231 | 4856 | 4968 | 0.0618 | 336 | 792 | 1174 |
| 3 | 0.439 | 0.1220 | 4856 | 4924 | 0.0376 | 205 | 801 | 1187 |
| 2 | 0.435 | 0.1208 | 4856 | 4875 | 0.01930 | 104.9 | 770 | 1143 |
| 1 | 0.433 | 0.1203 | 4954 | 4954 | 0.00707 | 38.4 | 1138 | 1440 |
| Story | ||||||||
|---|---|---|---|---|---|---|---|---|
| 9 | 0.690 | 0.1918 | 5248 | 5245 | 0.275 | 2368 | 483 | 190 |
| 8 | 0.717 | 0.1991 | 4856 | 5039 | 0.213 | 1840 | 1146 | 450 |
| 7 | 0.714 | 0.1982 | 4856 | 5016 | 0.1674 | 1443 | 1387 | 545 |
| 6 | 0.710 | 0.1973 | 4856 | 4993 | 0.1267 | 1093 | 1342 | 527 |
| 5 | 0.707 | 0.1963 | 4856 | 4967 | 0.0915 | 789 | 1665 | 654 |
| 4 | 0.703 | 0.1952 | 4856 | 4939 | 0.0619 | 533 | 1712 | 672 |
| 3 | 0.698 | 0.1939 | 4856 | 4907 | 0.0378 | 326 | 1716 | 674 |
| 2 | 0.693 | 0.1925 | 4856 | 4871 | 0.01943 | 167.5 | 1617 | 635 |
| 1 | 0.691 | 0.1919 | 4954 | 4954 | 0.00712 | 61.4 | 2437 | 816 |
| Story | ||||||||
|---|---|---|---|---|---|---|---|---|
| 9 | 0.252 | 0.0699 | 5248 | 3879 | 0.205 | 875 | 81.1 | 120 |
| 8 | 0.403 | 0.1119 | 4856 | 5744 | 0.245 | 1049 | 262 | 389 |
| 7 | 0.392 | 0.1088 | 4856 | 5583 | 0.1879 | 803 | 362 | 537 |
| 6 | 0.380 | 0.1054 | 4856 | 5411 | 0.1385 | 592 | 384 | 569 |
| 5 | 0.366 | 0.1018 | 4856 | 5224 | 0.0971 | 415 | 470 | 698 |
| 4 | 0.352 | 0.0978 | 4856 | 5019 | 0.0634 | 271 | 490 | 727 |
| 3 | 0.336 | 0.0934 | 4856 | 4794 | 0.0372 | 159.1 | 495 | 734 |
| 2 | 0.319 | 0.0886 | 4856 | 4546 | 0.01829 | 78.1 | 475 | 705 |
| 1 | 0.341 | 0.0946 | 4954 | 4954 | 0.00718 | 30.7 | 702 | 889 |
| Story | ||||||||
|---|---|---|---|---|---|---|---|---|
| 9 | 0.354 | 0.0984 | 5248 | 4022 | 0.214 | 1233 | 100.9 | 40 |
| 8 | 0.531 | 0.1474 | 4856 | 5576 | 0.240 | 1382 | 366 | 144 |
| 7 | 0.518 | 0.1440 | 4856 | 5447 | 0.1849 | 1064 | 485 | 191 |
| 6 | 0.505 | 0.1403 | 4856 | 5307 | 0.1370 | 788 | 483 | 190 |
| 5 | 0.490 | 0.1362 | 4856 | 5155 | 0.0966 | 556 | 613 | 241 |
| 4 | 0.474 | 0.1318 | 4856 | 4987 | 0.0635 | 366 | 631 | 248 |
| 3 | 0.456 | 0.1268 | 4856 | 4798 | 0.0376 | 216 | 631 | 248 |
| 2 | 0.436 | 0.1212 | 4856 | 4585 | 0.01860 | 107.0 | 591 | 232 |
| 1 | 0.462 | 0.1283 | 4954 | 4954 | 0.00724 | 41.7 | 895 | 300 |
References
- ASCE/SEI 7-22; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2022. Available online: https://ascelibrary.org/doi/book/10.1061/9780784415788 (accessed on 1 July 2023).
- Fan, W.; McGuire, J.J.; de Groot-Hedlin, C.D.; Hedlin, M.A.H.; Coats, S.; Fiedler, J.W. Stormquakes. Geophys. Res. Lett. 2019, 46, 12909–12918. [Google Scholar] [CrossRef]
- Duthinh, D.; Simiu, E. Safety of structures in strong winds and earthquakes: Multihazard considerations. J. Struct. Eng. 2010, 136, 330–333. [Google Scholar] [CrossRef]
- Crosti, C.; Duthinh, D.; Simiu, E. Risk consistency and synergy in multihazard design. J. Struct. Eng. 2011, 137, 844–849. [Google Scholar] [CrossRef]
- Aly, A.M. Design of buildings for wind and earthquake. In Proceedings of the 2014 World Congress on Advances in Civil, Environmental, and Materials Research, ACEM14, Busan, Republic of Korea, 24–28 August 2014. [Google Scholar]
- Aly, A.M.; Abburu, S. On the design of high-rise buildings for multihazard: Fundamental differences between wind and earthquake demand. Shock. Vib. 2015, 2015, 148681. [Google Scholar] [CrossRef]
- Thilakarathna, S.N.; Anwar, N.; Norachan, P.; Naja, F.A. The effect of wind loads on the seismic performance of tall buildings. Athens J. Technol. Eng. 2018, 5, 251–276. [Google Scholar] [CrossRef]
- Mazza, F.; Vulcano, A. Control of the earthquake and wind dynamic response of steel-framed buildings by using additional braces and/or viscoelastic dampers. Earthq. Eng. Struct. Dyn. 2011, 40, 155–174. [Google Scholar] [CrossRef]
- Kwag, S.; Gupta, A.; Baugh, J.; Kim, H.-S. Significance of multi-hazard risk in design of buildings under earthquake and wind loads. Eng. Struct. 2021, 243, 112623. [Google Scholar] [CrossRef]
- Roy, T.; Saito, T.; Matsagar, V. Multihazard framework for investigating high-rise base-isolated buildings under earthquakes and long-duration winds. Earthq. Eng. Struct. Dyn. 2010, 50, 1334–1357. [Google Scholar] [CrossRef]
- FEMA 356; Prestandard and Commentary for the Seismic Rehabilitation of Buildings. Federal Emergency Management Agency: Washington, DC, USA, 2010.
- Fujimoto, M.; Wada, A.; Saeki, E.; Watanabe, A.; Hitomi, Y. A study on the unbonded brace encased in buckling-restraining concrete and steel tubes. J. Struct. Constr. Eng. 1988, 34B, 249–258. (In Japanese) [Google Scholar]
- Fujimoto, M.; Wada, A.; Saeki, E.; Watanabe, A.; Hitomi, Y. A study on brace enclosed in buckling-restrained mortar and steel Tubes (Part 1). In Annual Research Meeting Architectural Institute of Japan; Architectural Institute of Japan: Tokyo, Japan, 1988. (In Japanese) [Google Scholar]
- Fujimoto, M.; Wada, A.; Saeki, E.; Watanabe, A.; Hitomi, Y. A study on brace enclosed in buckling-restrained mortar and steel tubes (Part 2). In Annual Research Meeting Architectural Institute of Japan; Architectural Institute of Japan: Tokyo, Japan, 1988. (In Japanese) [Google Scholar]
- Zhou, Y.; Shao, H.; Cao, Y.; Lui, E.M. Application of buckling-restrained braces to earthquake-resistant design of buildings: A review. Eng. Struct. 2021, 246, 112991. [Google Scholar] [CrossRef]
- International Building Code; International Code Council: Washington DC, USA, 2024.
- Holmes, J.D.; Bekele, S. Wind Loading of Structures, 4th ed.; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar] [CrossRef]
- Kubo, Y. Structure Configuration Based on Wind Engineering, 2nd ed.; Chapter 13, Handbook of Structural Engineering; Chen, W.F., Lui, E.M., Eds.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Martinez-Vazquez, P. Wind design spectra for generalisation. Wind. Struct. 2020, 30, 155–163. [Google Scholar] [CrossRef]
- Von Kármán, T. Progress in the statistical theory of turbulence. Proc. Natl. Acad. Sci. USA 1948, 34, 530–539. [Google Scholar] [CrossRef] [PubMed]
- Davenport, A.G. The spectrum of horizontal gustiness near the ground in high winds. J. R. Meteorol. Soc. 1961, 87, 194–211. [Google Scholar] [CrossRef]
- Harris, R.I. The nature of the wind. In The Modern Design of Wind-Sensitive Structures; Construction Industry Research and Information Association: Chicago, IL, USA, 1971. [Google Scholar]
- Hino, M. Spectrum of gusty wind. In Proceedings of the Third International Conference on Wind Effects on Buildings and Structures, Tokyo, Japan, 26–28 February 1971; pp. 69–77. [Google Scholar]
- Kaimal, J.C.; Wyngaard, J.C.; Izumi, Y.; Coté, O.R. Spectral characteristics of surface-layer turbulence. J. R. Meteorol. Soc. 1972, 98, 563–589. [Google Scholar] [CrossRef]
- Simiu, E. Wind spectra and dynamic alongwind response. J. Struct. Div. 1974, 100, 1897–1910. [Google Scholar] [CrossRef]
- Safak, E.; Foutch, D.A. Vibration of Buildings under Random Wind Loads; Civil Engineering Studies SRS-480; University of Illinois: Urbana-Champaign, IL, USA, 1980; Available online: http://hdl.handle.net/2142/14087 (accessed on 1 July 2023).
- Solari, G. Wind response spectrum. J. Eng. Mech. 1989, 115, 2057–2073. [Google Scholar] [CrossRef]
- Jang, J.-J.; Lee, Y.-L. A study of along wind speed power spectrum for Taiwan area. J. Mar. Sci. Technol. 1998, 6, 2522. [Google Scholar] [CrossRef]
- Mihanović, A.; Nikolić, Ž.; Smoljanović, H. Response spectrum of the Jugo wind force. Int. J. Eng. Model. 2008, 1, 33–41. [Google Scholar]
- Kaimal, J.C.; Finnigan, J.J. Spectra and Cospectra Over Flat Uniform Terrain. In Atmospheric Boundary Layer Flows; Oxford University Press: Oxford, UK, 1994. [Google Scholar] [CrossRef]
- SAC. SAC Steel Project Memorandum. 1994. Available online: https://www.sacsteel.org (accessed on 1 July 2023).
- Menegotto, M.; Pinto, P.E. Method of Analysis of Cyclically Loaded RC Plane Frames including Changes in Geometry and Non-Elastic Behavior of Elements under Normal Force and Bending; Preliminary Report IABSE; IABSE: Manchester, UK, 1973; Volume 13. [Google Scholar]
- Filippou, F.C.; Popov, E.P.; Bertero, V.V. Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints; Report EERC 83-19; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1983. [Google Scholar]
- Zsarnóczay, A.; Baker, J.W. Using model error in response history analysis to evaluate component calibration methods. Earthq. Eng. Struct. Dyn. 2020, 49, 175–193. [Google Scholar] [CrossRef]
- Upadhyay, A.; Pantelides, C.P.; Ibarra, L. Residual drift mitigation for bridges retrofitted with buckling restrained braces or self centering energy dissipation devices. Eng. Struct. 2019, 199, 109663. [Google Scholar] [CrossRef]
- Xu, W.; Pantelides, C.P. Strong-axis and weak-axis buckling and local bulging of buckling-restrained braces with prismatic core plates. Eng. Struct. 2017, 153, 279–289. [Google Scholar] [CrossRef]
- ANSI/AISC 341-22; Seismic Provisions for Structural Steel Buildings. American Institute of Steel Construction: Chicago, IL, USA, 2022.
- Kersting, R.A.; Fahnestock, L.A.; Lopez, W.A. Seismic Design of Steel Buckling-Restrained Braced Frames: A Guide for Practicing Engineers; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015; p. NIST GCR 15-917-34. [Google Scholar] [CrossRef]



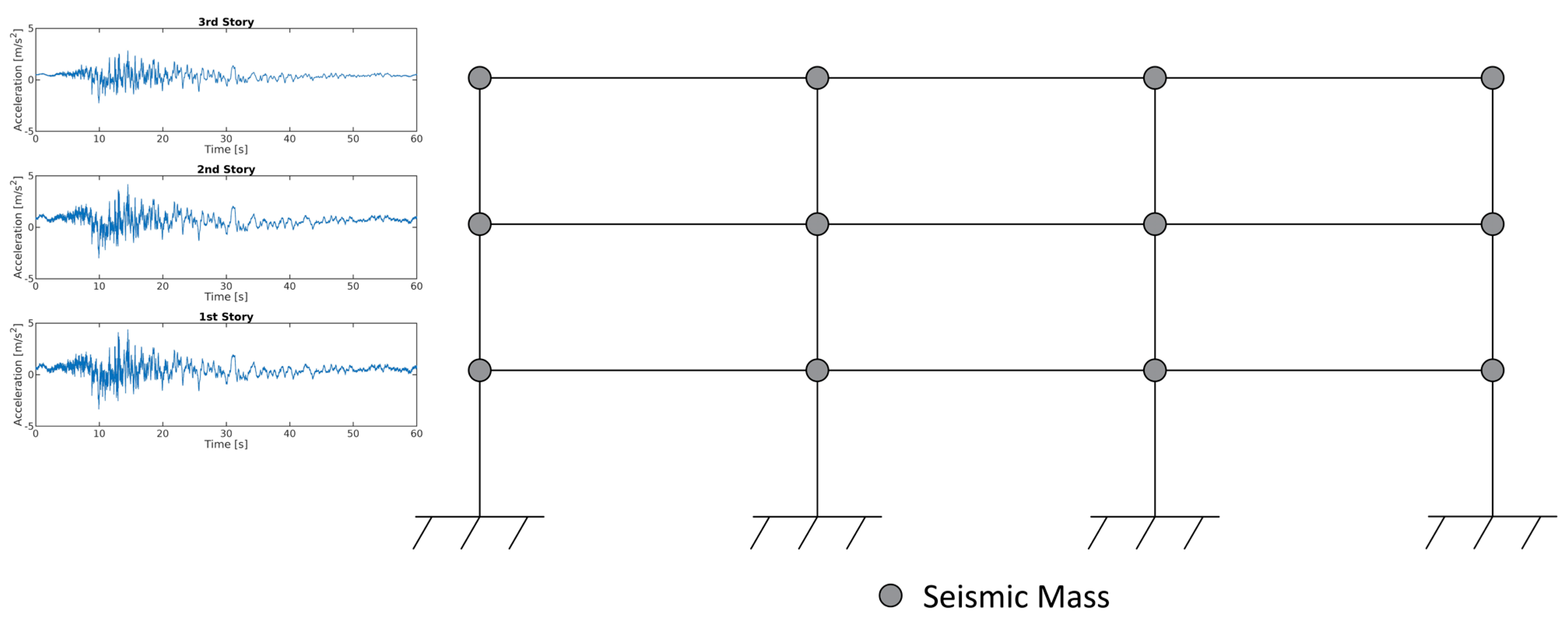








| Steel Frame Type | Immediate Occupancy (IO) | Life Safety (LS) | ||
|---|---|---|---|---|
| Peak Drift | Residual Drift | Peak Drift | Residual Drift | |
| Moment frames | 0.7% | Negligible | 2.5% | 1% |
| Braced frames | 0.5% | Negligible | 1.5% | 0.5% |
| Los Angeles | Charleston | |
|---|---|---|
| Immediate Occupancy (IO) | 41 | 62 |
| Life Safety (LS) | 46 | 72 |
| Parameters | Tension | Compression |
|---|---|---|
| Initial (elastic) stiffness of BRB, | ||
| Stiffness modification factor, | 1.39 | 1.39 |
| Elastic modulus of steel, | 200 GPa | 200 GPa |
| Yield strength of BRB steel core, | ||
| Material overstrength factor, | 1.11 | 1.11 |
| Yield strength of steel, | 248 MPa | 248 MPa |
| Kinematic hardening ratio, | 0.5% | 2.5% |
| Shape parameter *, | 26 | 26 |
| Shape parameter *, | 0.91 | 0.89 |
| Shape parameter *, | 0.10 | 0.02 |
| Initial hardening ratio for isotropic materials, | 0.25% | 0.6% |
| Saturated hardening ratio for isotropic materials, | 0.01% | 0.03% |
| Intersection point between and , | 0.8 | 0.3 |
| Isotropic transition parameter, | 3.0 | 3.0 |
| Length of the yield plateau, | 1.0 | 1.0 |
| Ultimate strength of BRB steel core, | ||
| Kinematic hardening to perfectly plastic transition parameter, | 2.0 | 2.0 |
| Model | Configuration | |
|---|---|---|
| Los Angeles for IO | 387 | 2-bay |
| Los Angeles for LS | 206 | 2-bay |
| Charleston for IO | 206 | 1-bay |
| Charleston for LS | 71 | 1-bay |
| Model | Configuration | ||||
|---|---|---|---|---|---|
| Story | 1st | 2nd–5th | 6th–8th | 9th | |
| Los Angeles for IO | 84 | 219 | 310 | 361 | 4-bay |
| Los Angeles for LS | 65 | 181 | 232 | 284 | 3-bay |
| Charleston for IO | 42 | 168 | 245 | 310 | 3-bay |
| Charleston for LS | 21 | 90 | 123 | 155 | 2-bay |
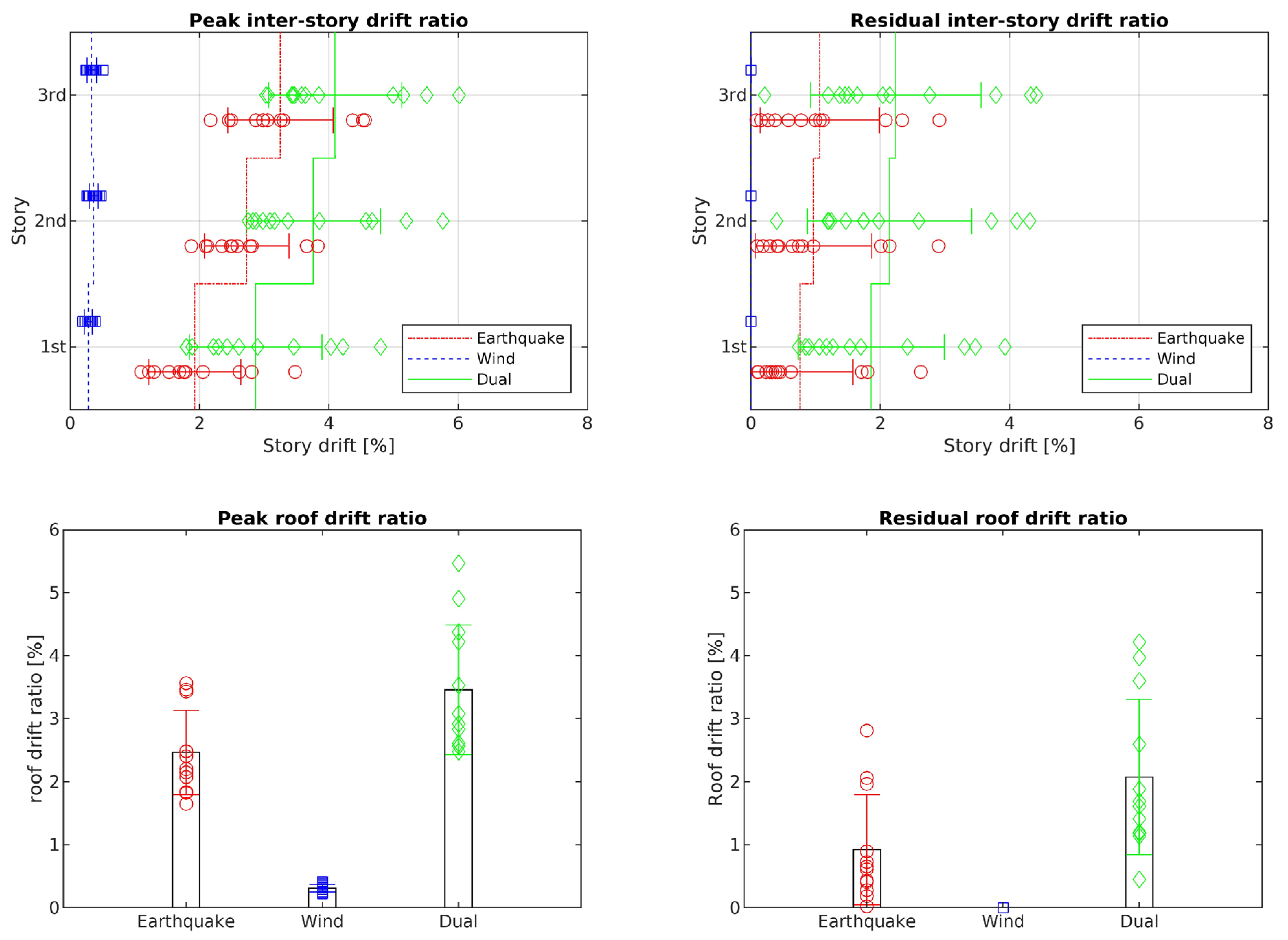
| City | Performance Level | Hazard | Peak Inter-Story | Residual Inter-Story | Peak Roof | Residual Roof |
|---|---|---|---|---|---|---|
| Los Angeles | IO | Earthquake | 3.25% | 1.06% | 2.47% | 0.92% |
| Wind | 0.36% | ≈0% | 0.31% | ≈0% | ||
| Dual | 4.10% | 2.24% | 3.46% | 2.08% | ||
| LS | Earthquake | 6.80% | 4.52% | 5.94% | 4.32% | |
| Wind | 0.47% | ≈0% | 0.40% | ≈0% | ||
| Dual | 11.63% | 10.40% | 10.99% | 10.08% | ||
| Charleston | IO | Earthquake | 1.14% | 0.083% | 0.96% | 0.06% |
| Wind | 0.93% | 0.11% | 0.78% | 0.09% | ||
| Dual | 1.93% | 0.93% | 1.65% | 0.75% | ||
| LS | Earthquake | 1.75% | 0.32% | 1.39% | 0.24% | |
| Wind | 1.35% | 0.42% | 1.14% | 0.36% | ||
| Dual | 3.57% | 2.62% | 3.27% | 2.42% |
| City | Performance Level | Hazard | Peak Inter-Story | Residual Inter-Story | Peak Roof | Residual Roof |
|---|---|---|---|---|---|---|
| Los Angeles | IO | Earthquake | 2.52% | 1.00% | 1.82% | 0.74% |
| Wind | 0.77% | ≈0% | 0.61% | ≈0% | ||
| Dual | 10.4% | 9.83% | 6.72% | 6.19% | ||
| LS | Earthquake | 4.36% | 2.83% | 3.20% | 2.19% | |
| Wind | 1.08% | 0.35% | 0.78% | 0.14% | ||
| Dual | C * | C * | C * | C * | ||
| Charleston | IO | Earthquake | 1.30% | 0.16% | 0.84% | 0.08% |
| Wind | 9.40% | 8.70% | 4.92% | 4.38% | ||
| Dual | C * | C * | C * | C * | ||
| LS | Earthquake | 1.71% | 0.41% | 1.18% | 0.26% | |
| Wind | C * | C * | C * | C * | ||
| Dual | C * | C * | C * | C * |
| City | Performance Level | Frame Type | Peak Inter-Story | Residual Inter-Story | Peak Roof | Residual Roof |
|---|---|---|---|---|---|---|
| Los Angeles | IO | MRF | 4.10% | 2.24% | 3.46% | 2.08% |
| BRBF | 0.27% | 0.01% | 0.27% | 0.01% | ||
| LS | MRF | 11.65% | 10.40% | 10.99% | 10.08% | |
| BRBF | 0.80% | 0.14% | 0.52% | 0.06% | ||
| Charleston | IO | MRF | 1.93% | 0.93% | 1.65% | 0.75% |
| BRBF | 0.27% | ≈0% | 0.25% | ≈0% | ||
| LS | MRF | 3.57% | 2.62% | 3.27% | 2.42% | |
| BRBF | 0.86% | 0.20% | 0.66% | 0.14% |
| City | Performance Level | Frame Type | Peak Inter-Story | Residual Inter-Story | Peak Roof | Residual Roof |
|---|---|---|---|---|---|---|
| Los Angeles | IO | MRF | 10.40% | 9.83% | 6.72% | 6.19% |
| BRBF | 0.64% | 0.05% | 0.56% | 0.05% | ||
| LS | MRF | C * | C * | C * | C * | |
| BRBF | 1.33% | 0.50% | 0.80% | 0.21% | ||
| Charleston | IO | MRF | C * | C * | C * | C * |
| BRBF | 0.30% | ≈0% | 0.26% | ≈0% | ||
| LS | MRF | C * | C * | C * | C * | |
| BRBF | 1.41% | 0.76% | 0.89% | 0.33% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, T.; Lui, E.M. Energy-Based Design of Buckling-Restrained Steel Braced Frames for Concurrent Occurrences of Earthquake and Wind. CivilEng 2024, 5, 343-377. https://doi.org/10.3390/civileng5020018
Shan T, Lui EM. Energy-Based Design of Buckling-Restrained Steel Braced Frames for Concurrent Occurrences of Earthquake and Wind. CivilEng. 2024; 5(2):343-377. https://doi.org/10.3390/civileng5020018
Chicago/Turabian StyleShan, Taonian, and Eric M. Lui. 2024. "Energy-Based Design of Buckling-Restrained Steel Braced Frames for Concurrent Occurrences of Earthquake and Wind" CivilEng 5, no. 2: 343-377. https://doi.org/10.3390/civileng5020018
APA StyleShan, T., & Lui, E. M. (2024). Energy-Based Design of Buckling-Restrained Steel Braced Frames for Concurrent Occurrences of Earthquake and Wind. CivilEng, 5(2), 343-377. https://doi.org/10.3390/civileng5020018









