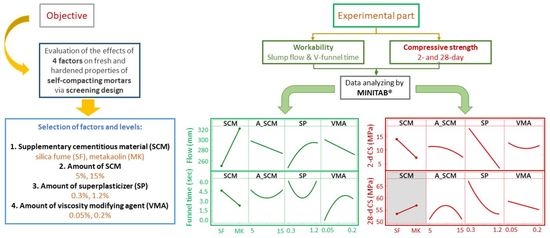
Optimization of Workability and Compressive Strength of Self-Compacting Mortar Using Screening Design
Abstract
:1. Introduction
1.1. Background
1.2. Design of Experiments (DOE)
2. Materials and Methods
2.1. Composition and Mix Design
2.2. Analytical Methods
- The slump flow test
- V-funnel test
- Strength test
- Minitab
3. Results
3.1. Fresh Properties
- Slump flow and V-funnel time
+ 19 SCM*A_SCM − 14.5 SCM*SP
− 1.8 VMA*VMA + 0.8 SCM*
3.2. Solid State Properties
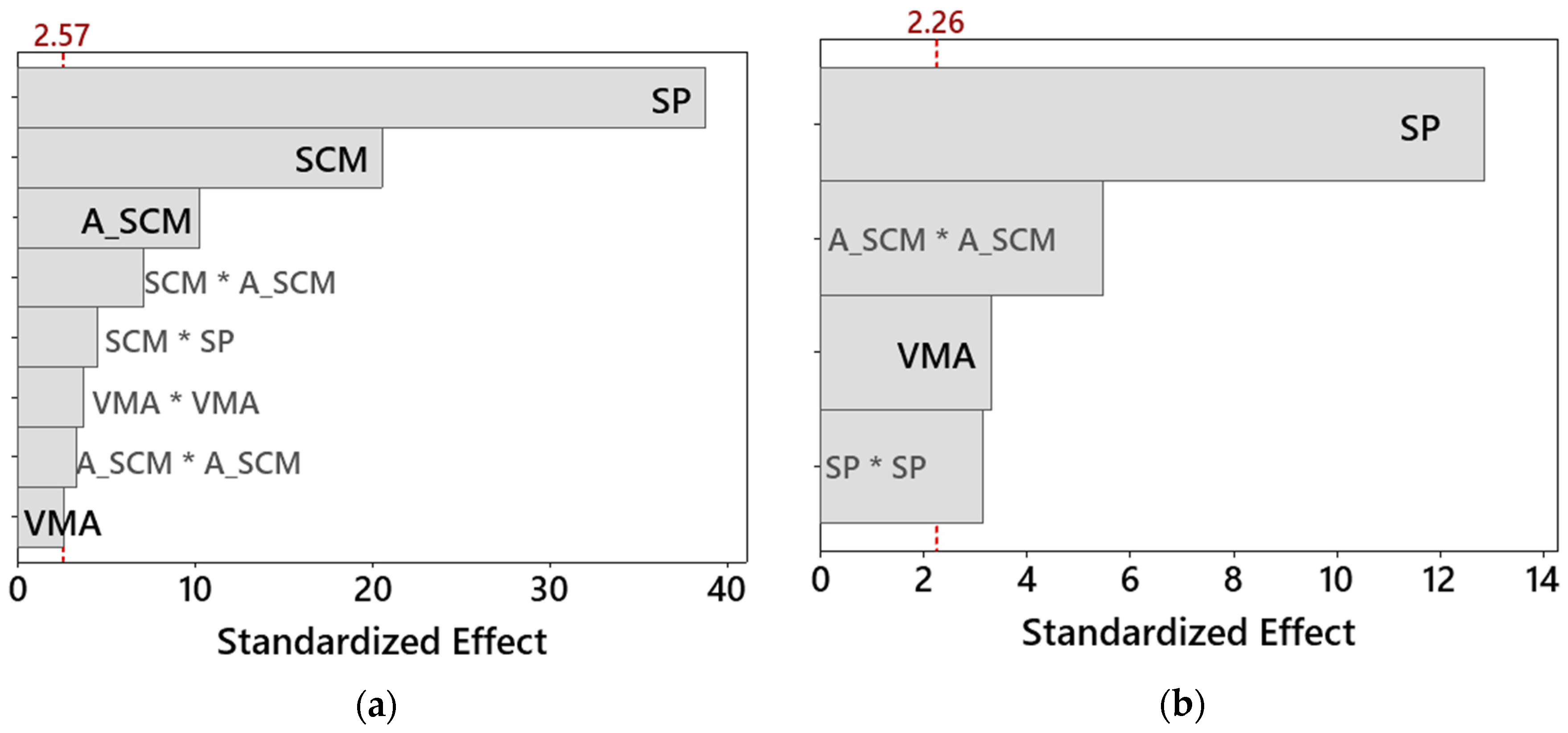
- Compressive strength
− 1.3 A_SCM*A_SCM + 1.5 VMA*VMA − 1.4 SCM*A_SCM − 1.1 SCM*SP
4. Discussion
5. Conclusions
- Screening the design allows a simple, less costly method to determine the composition of self-compacting mortars and concrete.
- The amounts of admixtures necessary for an optimal or specified workability can be determined with just a few experimental runs.
- Specifically, for the study presented:
- ○
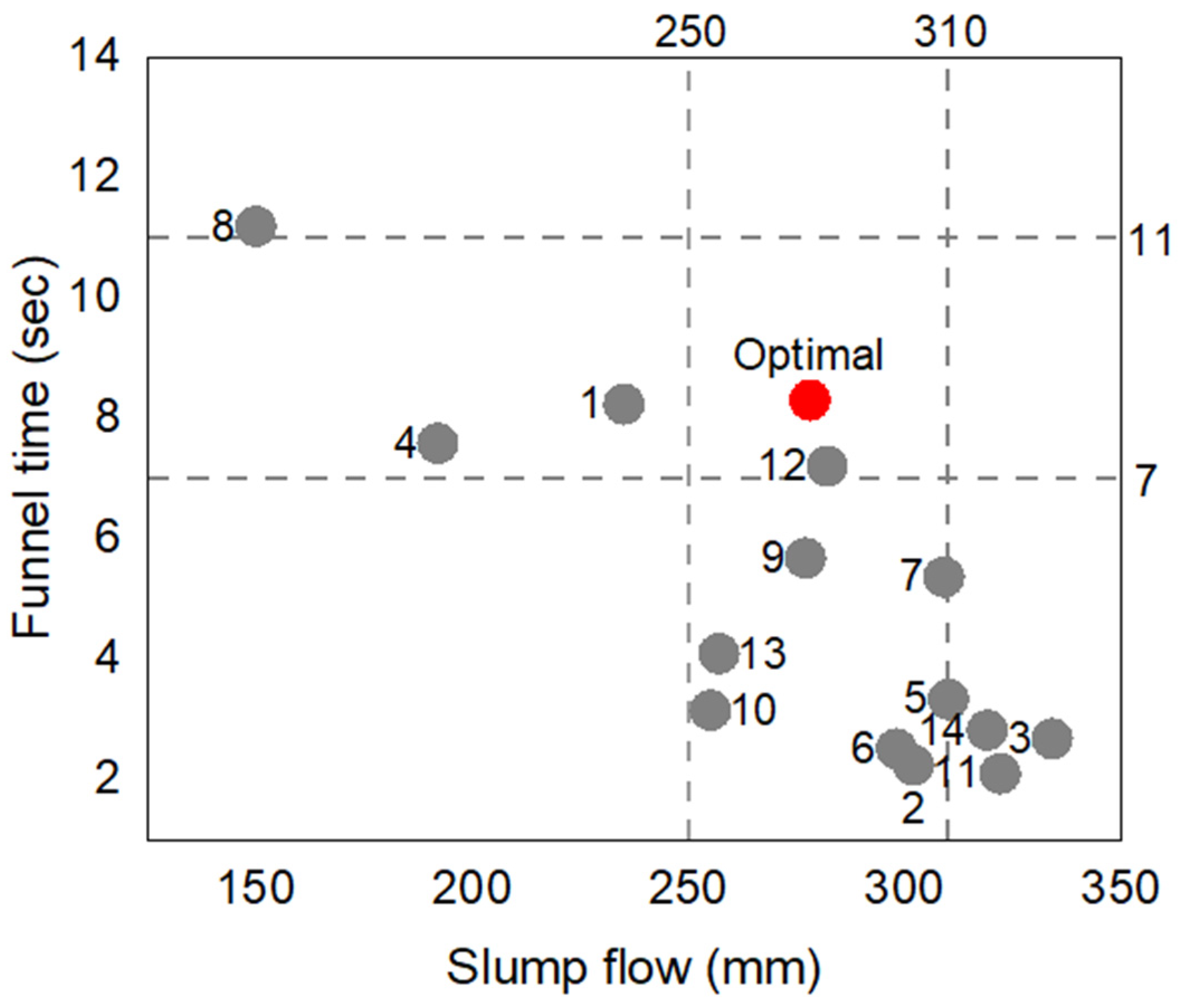
- The desired conditions for optimal workability were found to be 8.84% silica fume, 1.2% SP and 0.15% VMA at w/p = 0.6.
- ○
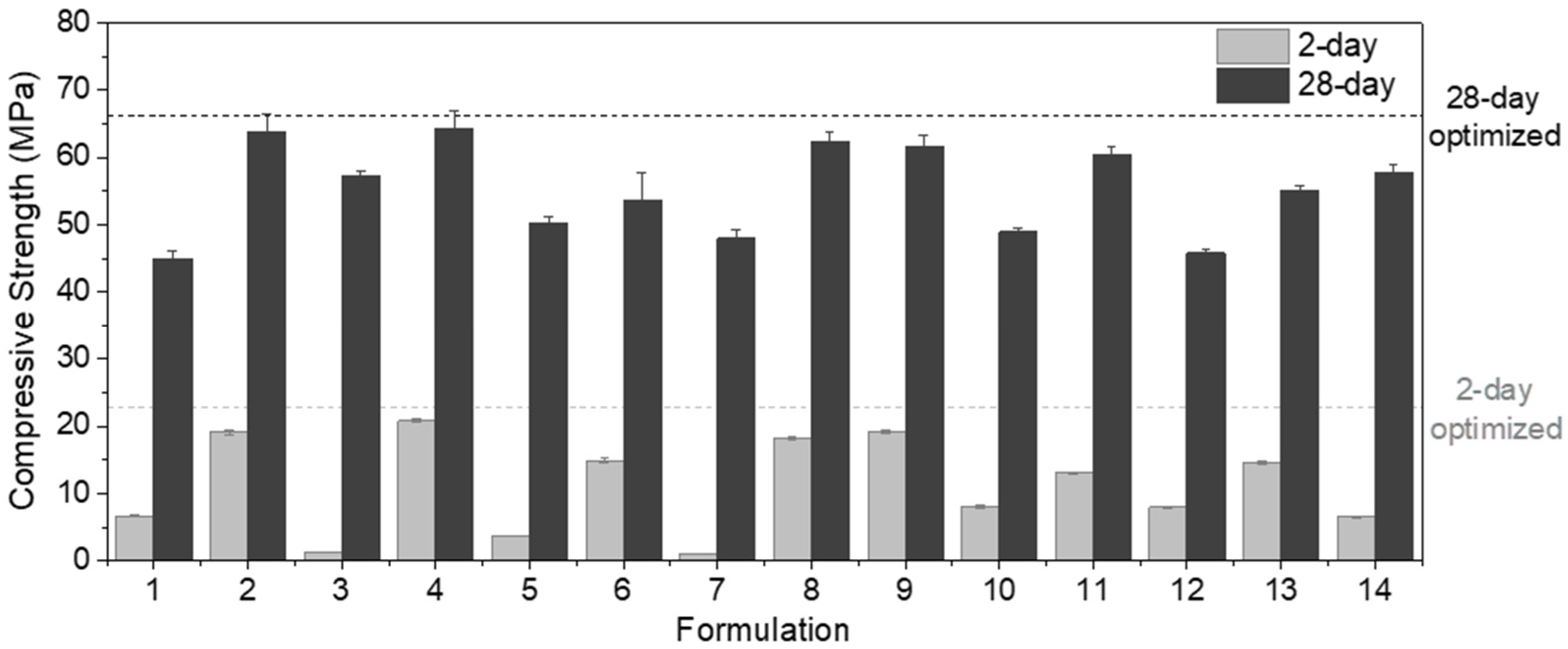
- The maximal values of strength can be achieved by using 9–9.8% silica fume, 0.3% SP and 0.05% VMA.
- In general, the influence of various constituents of self-compacting mortars on the workability and strength could clearly be identified or confirmed, respectively:
- ○
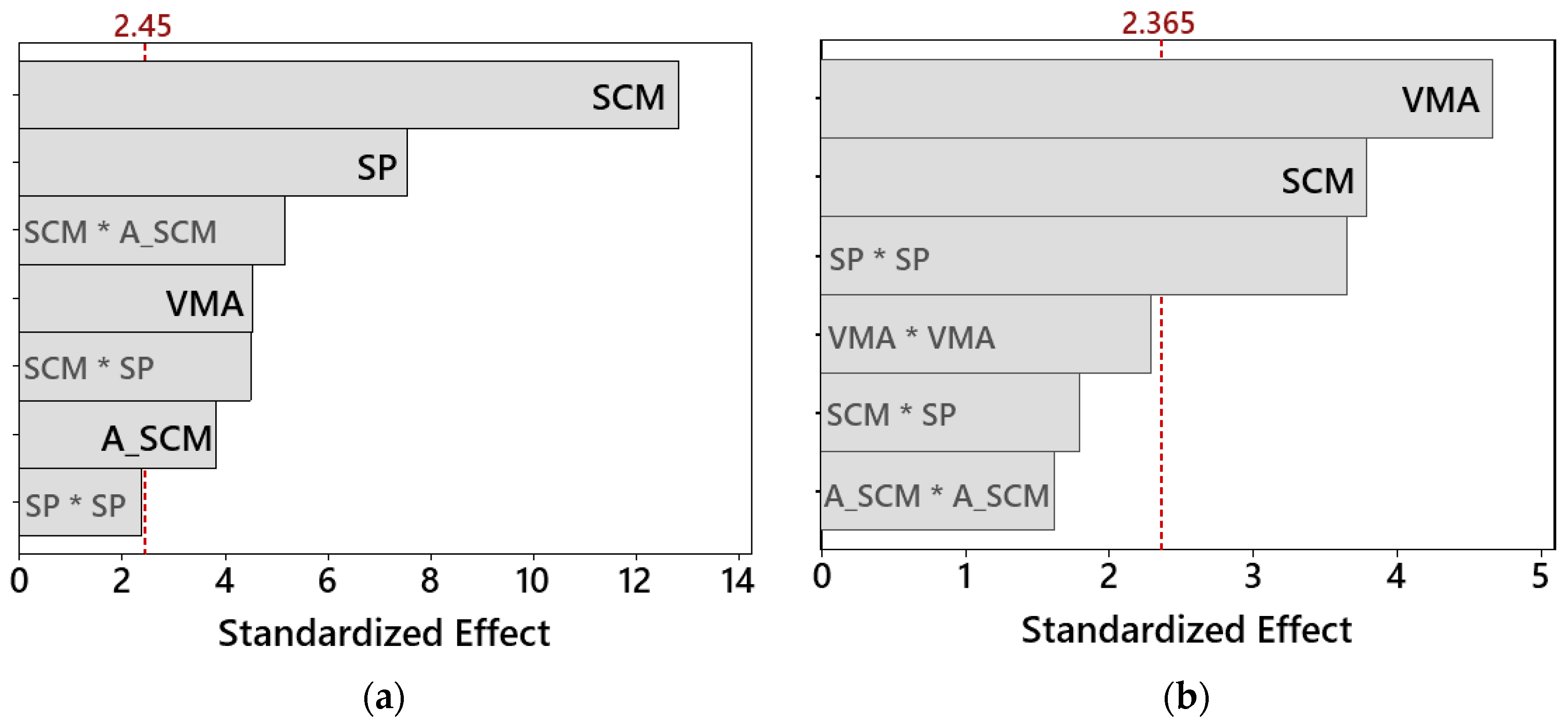
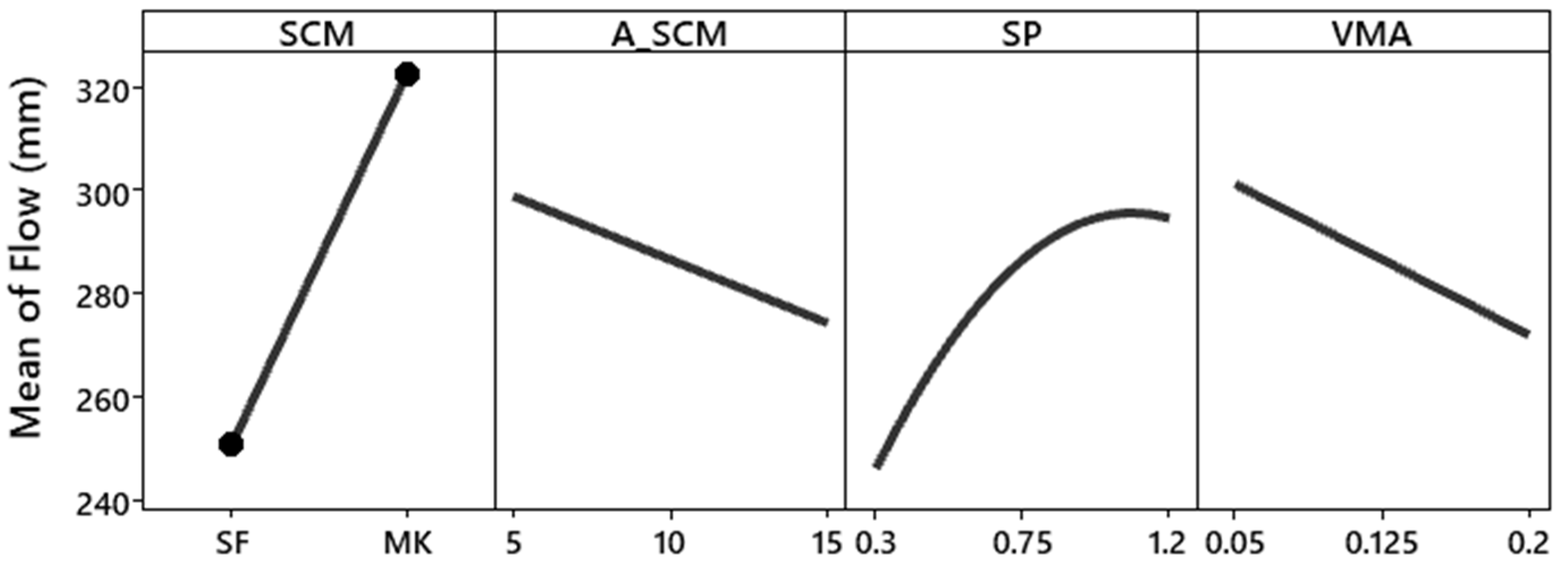
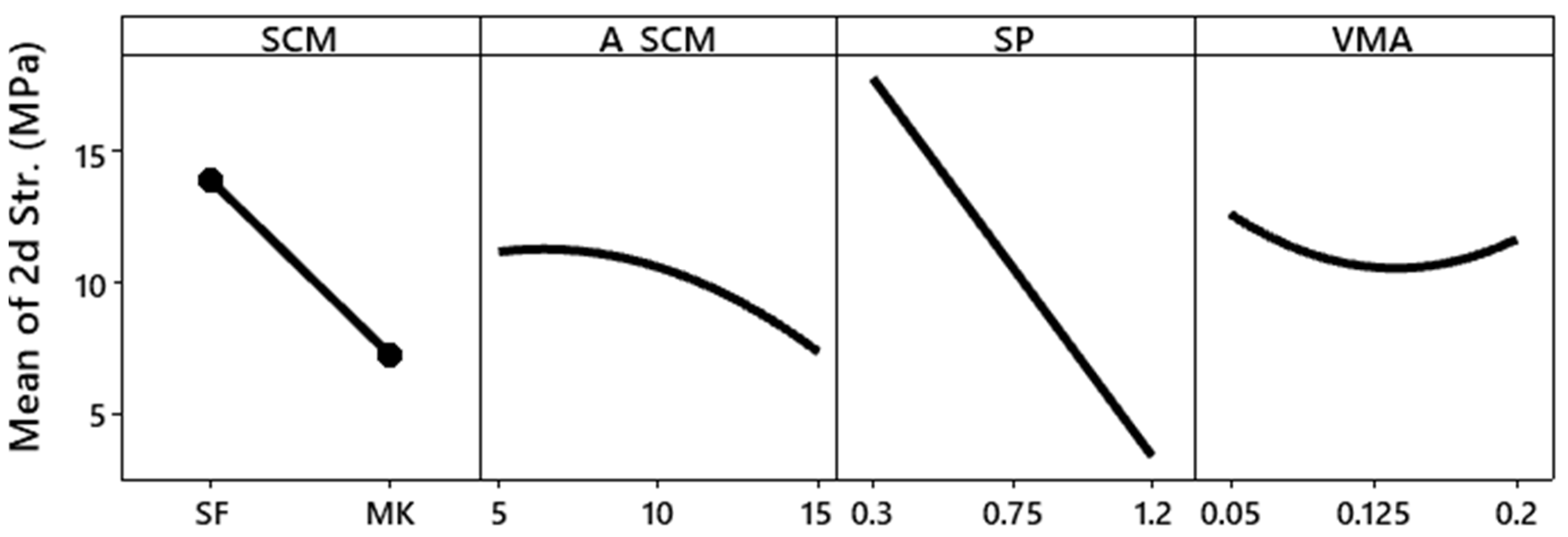
- The slump flow values increase with the increase in the SP dosage and decrease with the increase in the VMA.
- ○
- VMA has the highest impact on the funnel time, increasing it according to an almost linear function with an optimum at 0.15%.
- ○
- SP has the highest effect on the compressive strength. For any given type and amount of SCM, the increase in SP leads to a decrease in strength.
- ○
- The dosage of VMA showed no significant effect on the compressive strength.
- ○
- The type of SCM used has a considerable impact on the slump flow and funnel time. The use of MK as compared to SF increases the slump flow and decreases the funnel time.
- ○
- The increasing substitution of SCM has a negative effect on the spread flow values of the mortar and no considerable effect on the funnel time.
- ○
- The type and dosage of SCM necessary for optimum strength values can be determined by the screening method used.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Okamura, H.; Ouchi, M. Self-Compacting Concrete. J. Adv. Concr. Technol. 2003, 1, 5–15. [Google Scholar] [CrossRef]
- Su, Y.; Luo, B.; Luo, Z.; Huang, H.; Li, J.; Wang, D. Effect of Accelerators on the Workability, Strength, and Microstructure of Ultra-High-Performance Concrete. Materials 2022, 15, 159. [Google Scholar] [CrossRef] [PubMed]
- Leemann, A.; Winnefeld, F. Influence of workability and admixtures on the segregation of concrete during compaction. In Proceedings of the 2nd International Symposium on Advances in Concrete through Science and Engineering, Quebec City, QC, Canada, 11–13 September 2006. [Google Scholar]
- Ramanathan, P.; Baskar, I.; Muthupriya, P.; Venkatasubramani, R. Performance of self-compacting concrete containing different mineral admixtures. KSCE J. Civ. Eng. 2013, 17, 465–472. [Google Scholar] [CrossRef]
- Ozawa, K.; Sakata, N.; Okamura, H. Evaluation of Self-Compactibility of fresh concrete using the funnel test. Concr. Libr. JSCE 1994, 1994, 61–70. [Google Scholar]
- Sonebi, M.; Grünewald, S.; Walraven, J. Filling Ability and Passing Ability of Self-Consolidating Concrete. ACI Mater. J. 2007, 104, 162–170. [Google Scholar]
- Sonebi, M. Medium strength self-compacting concrete containing fly ash: Modelling using factorial experimental plans. Cem. Concr. Res. 2004, 34, 1199–1208. [Google Scholar] [CrossRef]
- Huseni, K.; Vilasrao, P.S.; Tamang, T.D.; Abdul Rahim, A. Optimization of strength properties for Self-Compacting Concrete byTaguchi Method. Int. J. Sci. Eng. Res. 2016, 7, 1719–1724. [Google Scholar] [CrossRef]
- Ding, X. The Optimization of Mix Proportion Design for SCC: Experimental Study and Grey Relational Analysis. Materials 2022, 15, 1305. [Google Scholar] [CrossRef]
- Mandal, A.; Roy, P. Modeling the compressive strength of molasses–cement sand system using design of experiments and back propagation neural network. J. Mater. Process. Technol. 2006, 180, 167–173. [Google Scholar] [CrossRef]
- Ghezal, A.; Khayat, K. Optimizing self-consolidating concrete with limestone filler by using statistical factorial design methods. ACI Mater. J. 2002, 99, 264–272. [Google Scholar]
- Shaheen, N.; Rizwan, S.A.; Khushnood, R.A.; Bier, T.A. Mechanical and energy performance of variably cured effective microorganisms cementitious composite designed via Taguchi. J. Clean. Prod. 2021, 310, 127350. [Google Scholar] [CrossRef]
- Siamardi, K. Optimization of fresh and hardened properties of structural light weight self-compacting concrete mix design using response surface methodology. Constr. Build. Mater. 2022, 317, 125928. [Google Scholar] [CrossRef]
- Suji, D.; Adesina, A.; Mirdula, R. Optimization of self-compacting composite composition using Taguchi-Grey relational analysis. Materialia 2021, 15, 101027. [Google Scholar] [CrossRef]
- Box, G.E.P.; Hunter, J.S.; Hunter, W.G. Statistics for Experimenters: Design, Innovation, and Discovery; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 672. [Google Scholar]
- Montgomery, D. Design and Analysis of Experiments, 9th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Barrentine, L.B. An Introduction to Design of Experiments: A Simplified Approach; ASQ Quality Press: Milwaukee, WI, USA, 1999; Volume 114. [Google Scholar]
- Cavazzuti, M. Optimization Methods; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Deming, S.N.; Morgan, S.L. Experimental Design: A Chemometric Approach, 2nd ed.; Elsevier Science: Amsterdam, The Netherlands, 1993; Volume 11, p. 436. [Google Scholar]
- Allen, T.T. Introduction to Engineering Statistics and Lean Sigma, 2nd ed.; Springer: London, UK, 2010; Volume 572. [Google Scholar]
- Box, G.E.P.; Meyer, R.D. Finding the Active Factors in Fractionated Screening Experiments. J. Qual. Technol. 1993, 25, 94–105. [Google Scholar] [CrossRef]
- Anderson, M.; Whitcomb, P. Screening process factors in the presence of interactions. In Annual Quality Congress Proceedings-American Society for Quality Control; ASQ: Milwaukee, WI, USA, 2004; pp. 471–480. [Google Scholar]
- Carlson, R. Preludes to a screening experiment: A tutorial. Chemom. Intell. Lab. Syst. 1992, 14, 103–114. [Google Scholar] [CrossRef]
- DIN EN 196-1: 1995-5; Methods of Testing Cement-Part 1: Determination of Strength. DIN Deutsches Institut für Normen: Berlin, Germany, 2005.
- EFNARC. Specification and Guidelines for Self-Compacting Concrete, European Federation of Producers and Applicators of Specialist Product for Structures; EFNARC: Norfolk, UK, 2002. [Google Scholar]
- Mathews, P.G. Design of Experiments with MINITAB; ASQ: Milwaukee, WI, USA, 2004. [Google Scholar]
- Sawyer, S.F. Analysis of Variance: The Fundamental Concepts. J. Man. Manip. Ther. 2009, 17, 27E–38E. [Google Scholar] [CrossRef]
- Bass, I. Six Sigma Statistics with Excel and Minitab, 1st ed.; Mcgraw-Hill Professional: New York, NY, USA, 2007; Volume 353. [Google Scholar]
- Larose, D.T. Data Mining Methods and Models, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2006; Volume 344. [Google Scholar]
- Srivastava, A.K.; Srivastava, V.K.; Ullah, A. The coefficient of determination and its adjusted version in linear regression models. Econom. Rev. 1995, 14, 229–240. [Google Scholar] [CrossRef]
- Akossou, A.; Palm, R. Impact of data structure on the estimators R-square and adjusted R-square in linear regression. Int. J. Math. Comput. 2013, 20, 84–93. [Google Scholar]
- Ferrari, L.; Kaufmann, J.; Winnefeld, F.; Plank, J. Multi-method approach to study influence of superplasticizers on cement suspensions. Cem. Concr. Res. 2011, 41, 1058–1066. [Google Scholar] [CrossRef]
- Leemann, A.; Winnefeld, F. The effect of viscosity modifying agents on mortar and concrete. Cem. Concr. Compos. 2007, 29, 341–349. [Google Scholar] [CrossRef]
- Rasheed, A.; Usman, M.; Farooq, H.; Hanif, A. Effect of Super-plasticizer Dosages on Fresh State Properties and Early-Age Strength of Concrete. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 431. [Google Scholar]
- Li, Z.; Ding, Z. Property improvement of Portland cement by incorporating with metakaolin and slag. Cem. Concr. Res. 2003, 33, 579–584. [Google Scholar] [CrossRef]


| Formulation | PC (%) | Aggregate (%) | SCM (%) |
|---|---|---|---|
| 1 | 23.75 | 71.25 | 5 |
| 2 | 22.50 | 67.50 | 10 |
| 3 | 21.25 | 63.75 | 15 |
| PC (%) | SF (%) | MK (%) | PC (%) | SF (%) | MK (%) | ||
|---|---|---|---|---|---|---|---|
| C3S | 55.2 | 62.2 | 0.1 | 0.1 | |||
| C2S | 16.4 | 20.0 | 97.4 | 54.2 | |||
| C4AF | 14.8 | 3.8 | 0.5 | ||||
| C3Acubic | 5.3 | 1.4 | 0.4 | ||||
| C3Aorth | 1.3 | 4.8 | 1.1 | 42.9 | |||
| C | 0.5 | 0.9 | 0.8 | 2.0 | |||
| CH0.5 | 1.6 | 2.7 | 0.2 | 0.2 | |||
| CaCO3 | 1.4 | 0.1 | |||||
| Arcanite | 0.6 | 0.2 | |||||
| Quartz | 3.5 | ||||||
| Feldspares (Microcline, orthoclase) | 9.9 | ||||||
| Illite | 4.0 | ||||||
| Amorphous | 2.8 | 100 | 82.6 |
| Factor | Low Level | Center Level | High Level |
|---|---|---|---|
| Supplementary cementitious material (SCM) | SF | - | MK |
| Amount of SCM (A_SCM) (%) | 5 | 10 | 15 |
| Superplasticizer (SP) (%) | 0.30 | 0.75 | 1.20 |
| Viscosity modifying agent (VMA) (%) | 0.05 | 0.12 | 0.20 |
| The Factor Levels | ||||
|---|---|---|---|---|
| Run | SCM | A_SCM | SP | VMA |
| 1 | SF | 15 | 1.20 | 0.20 |
| 2 | MK | 5 | 0.30 | 0.05 |
| 3 | MK | 10 | 1.20 | 0.05 |
| 4 | SF | 10 | 0.30 | 0.20 |
| 5 | MK | 15 | 0.75 | 0.20 |
| 6 | SF | 5 | 0.75 | 0.05 |
| 7 | MK | 5 | 1.20 | 0.12 |
| 8 | SF | 15 | 0.30 | 0.12 |
| 9 | MK | 5 | 0.30 | 0.20 |
| 10 | SF | 15 | 1.20 | 0.05 |
| 11 | MK | 15 | 0.30 | 0.05 |
| 12 | SF | 5 | 1.20 | 0.20 |
| 13 | SF | 10 | 0.75 | 0.12 |
| 14 | MK | 10 | 0.75 | 0.12 |
| Factor Levels | Results | |||||
|---|---|---|---|---|---|---|
| Run | SCM | A_SCM | SP | VMA | Slump Flow (mm) | Funnel Time (s) |
| 1 | SF | 15 | 1.20 | 0.20 | 235 | 8.2 |
| 2 | MK | 5 | 0.30 | 0.05 | 302 | 2.3 |
| 3 | MK | 10 | 1.20 | 0.05 | 334 | 2.7 |
| 4 | SF | 10 | 0.30 | 0.20 | 192 | 7.6 |
| 5 | MK | 15 | 0.75 | 0.20 | 310 | 3.3 |
| 6 | SF | 5 | 0.75 | 0.05 | 298 | 2.5 |
| 7 | MK | 5 | 1.20 | 0.12 | 309 | 5.4 |
| 8 | SF | 15 | 0.30 | 0.12 | 150 | 11.2 |
| 9 | MK | 5 | 0.30 | 0.20 | 277 | 5.7 |
| 10 | SF | 15 | 1.20 | 0.05 | 255 | 3.2 |
| 11 | MK | 15 | 0.30 | 0.05 | 322 | 2.1 |
| 12 | SF | 5 | 1.20 | 0.20 | 282 | 7.2 |
| 13 | SF | 10 | 0.75 | 0.12 | 257 | 4.1 |
| 14 | MK | 10 | 0.75 | 0.12 | 319 | 2.8 |
| Term | Slump Flow (mm) | Funnel Time (s) | ||||||
|---|---|---|---|---|---|---|---|---|
| Coef | SE Coef | T-Value | p-Value | Coef | SE Coef | T-Value | p-Value | |
| Constant | 286.5 | 5.3 | 53.8 | 0.000 | 3.5 | 0.8 | 4.3 | 0.003 |
| SCM | 35.8 | 2.8 | 12.8 | 0.000 | −1.2 | 0.3 | −3.8 | 0.007 |
| A_SCM | −12.2 | 3.2 | −3.8 | 0.009 | ||||
| SP | 24.1 | 3.2 | 7.5 | 0.000 | ||||
| VMA | −14.5 | 3.2 | −4.5 | 0.004 | 1.7 | 0.4 | 4.7 | 0.002 |
| A_SCM*A_SCM | 1.3 | 0.8 | 1.6 | 0.149 | ||||
| SP*SP | −16.2 | 6.8 | −2.4 | 0.056 | 2.7 | 0.7 | 3.6 | 0.008 |
| VMA*VMA | −1.8 | 0.8 | −2.3 | 0.056 | ||||
| SCM*A_SCM | 19.0 | 3.7 | 5.2 | 0.002 | ||||
| SCM*SP | −14.5 | 3.2 | −4.5 | 0.004 | 0.8 | 0.5 | 1.8 | 0.116 |
| Setting | Solution | |||
|---|---|---|---|---|
| Response | ||||
| Slump Flow (mm) | V-Funnel Time (s) | SCM | Silica Fume | |
| Goal | Target | Target | A_SCM | 8.84% |
| Lower | 150 | 2.1 | SP | 1.20% |
| Target | 280 | 9 | VMA | 0.15% |
| Upper | 334 | 11.2 | Funnel time fit | 8.5 s |
| Weight | 1 | 1 | Slump flow fit | 280 mm |
| Importance | 1 | 1 | D | 0.96 |
| Factor Levels | Results on Compressive Strength (MPa) | |||||
|---|---|---|---|---|---|---|
| Run | SCM | A_SCM | SP | VMA | 2-Day | 28-Day |
| 1 | SF | 15 | 1.20 | 0.20 | 6.7 | 44.9 |
| 2 | MK | 5 | 0.30 | 0.05 | 19.2 | 63.9 |
| 3 | MK | 10 | 1.20 | 0.05 | 1.3 | 57.3 |
| 4 | SF | 10 | 0.30 | 0.20 | 20.8 | 64.3 |
| 5 | MK | 15 | 0.75 | 0.20 | 3.7 | 50.1 |
| 6 | SF | 5 | 0.75 | 0.05 | 14.9 | 53.7 |
| 7 | MK | 5 | 1.20 | 0.12 | 1.0 | 48.0 |
| 8 | SF | 15 | 0.30 | 0.12 | 18.2 | 62.2 |
| 9 | MK | 5 | 0.30 | 0.20 | 19.1 | 61.6 |
| 10 | SF | 15 | 1.20 | 0.05 | 8.1 | 48.9 |
| 11 | MK | 15 | 0.30 | 0.05 | 13.1 | 60.4 |
| 12 | SF | 5 | 1.20 | 0.20 | 8.0 | 45.7 |
| 13 | SF | 10 | 0.75 | 0.12 | 14.5 | 55.2 |
| 14 | MK | 10 | 0.75 | 0.12 | 6.5 | 57.7 |
| Compressive Strength | ||||||||
|---|---|---|---|---|---|---|---|---|
| Term | 2-Day | 28-Day | ||||||
| Coef | SE Coef | T-Value | p-Value | Coef | SE Coef | T-Value | p-Value | |
| Constant | 10.6 | 0.4 | 26.4 | 0.000 | 57.0 | 1.0 | 58.3 | 0.000 |
| SCM | −3.3 | 0.2 | −20.5 | 0.000 | ||||
| A_SCM | −1.9 | 0.2 | −10.3 | 0.000 | ||||
| SP | −7.2 | 0.2 | −38.7 | 0.000 | −6.7 | 0.5 | −12.9 | 0.000 |
| VMA | −0.5 | 0.2 | −2.6 | 0.048 | −1.7 | 0.5 | −3.3 | 0.009 |
| A_SCM*A_SCM | −1.3 | 0.4 | −3.3 | 0.021 | −5.6 | 1.0 | −5.5 | 0.000 |
| SP*SP | 3.2 | 1.0 | 3.1 | 0.012 | ||||
| VMA*VMA | 1.5 | 0.4 | 3.7 | 0.013 | ||||
| SCM*A_SCM | −1.4 | 0.2 | −7.2 | 0.001 | ||||
| SCM*SP | −1.1 | 0.2 | −4.5 | 0.006 | ||||
| R2 = 99.7%, R2(adj) = 99.3%, R2(pred) = 98.3% | R2 = 96%, R2(adj) = 94%, R2(pred) = 88% | |||||||
| Setting | Solution | ||||
|---|---|---|---|---|---|
| Compressive Strength (MPa) | 2-Day | 28-Day | |||
| Response | 2-day | 28-day | SCM | Silica fume | Silica fume |
| Goal | Maximum | Maximum | A_SCM | 9.04% | 9.75% |
| Lower | 1.0 | 44.9 | SP | 0.30% | 0.30% |
| Upper | 20.9 | 64.3 | VMA | 0.05% | 0.05% |
| Weight | 1 | 1 | Comp. streng. fit | 22.1 MPa | 68.8 MPa |
| Importance | 1 | 1 | D | 1 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qorllari, A.; Bier, T.A. Optimization of Workability and Compressive Strength of Self-Compacting Mortar Using Screening Design. CivilEng 2022, 3, 998-1012. https://doi.org/10.3390/civileng3040056
Qorllari A, Bier TA. Optimization of Workability and Compressive Strength of Self-Compacting Mortar Using Screening Design. CivilEng. 2022; 3(4):998-1012. https://doi.org/10.3390/civileng3040056
Chicago/Turabian StyleQorllari, Anxhelina, and Thomas A. Bier. 2022. "Optimization of Workability and Compressive Strength of Self-Compacting Mortar Using Screening Design" CivilEng 3, no. 4: 998-1012. https://doi.org/10.3390/civileng3040056
APA StyleQorllari, A., & Bier, T. A. (2022). Optimization of Workability and Compressive Strength of Self-Compacting Mortar Using Screening Design. CivilEng, 3(4), 998-1012. https://doi.org/10.3390/civileng3040056