Dynamic Damage Quantification of Slab Tracks—Finite Element Models on Winkler Soil and Finite-Element Boundary-Element Models on Continuous Soil
Abstract
1. Introduction
2. Slab Tracks and Four Measurement Sites: G, S, W, and T
3. Methods for the Calculation of Displacements of Railway Tracks
3.1. Finite-Element Method for a Slab Track on Winkler Soil
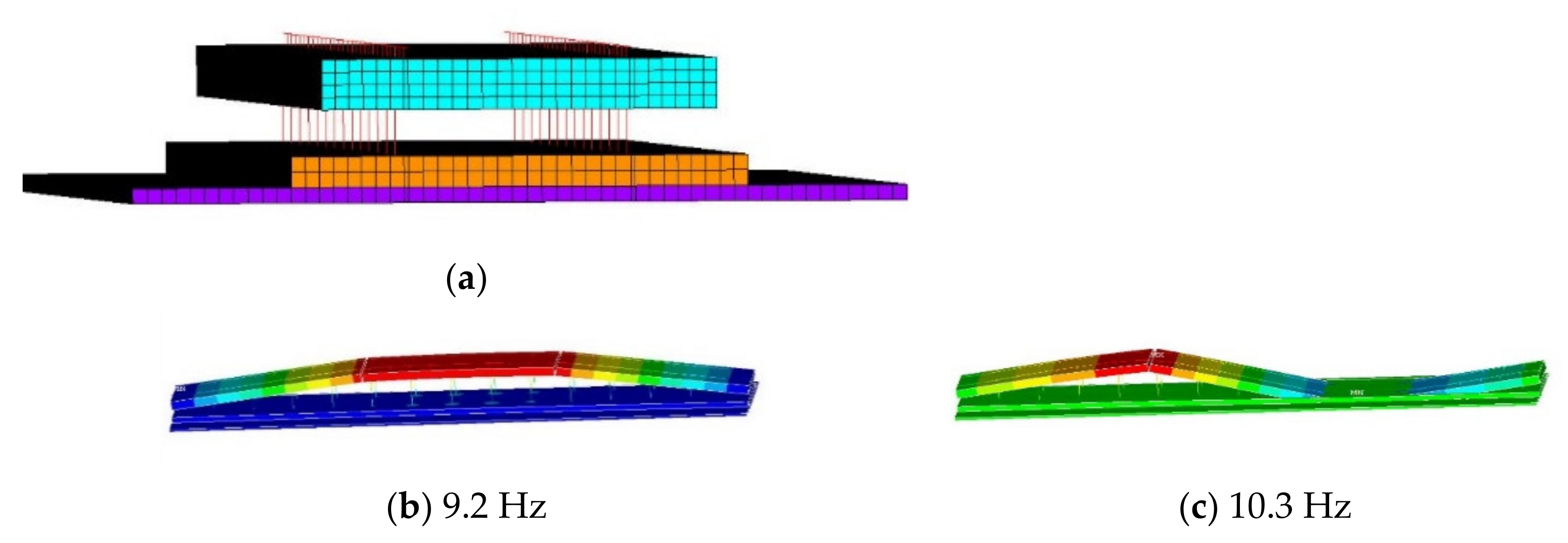
3.2. Modelling Details of the Finite-Element Slab Track
3.3. Finite-Element Boundary-Element Method (FEBEM) for a Slab Track on Continuous Soil
3.4. Special Methods for Train Passages over the Track
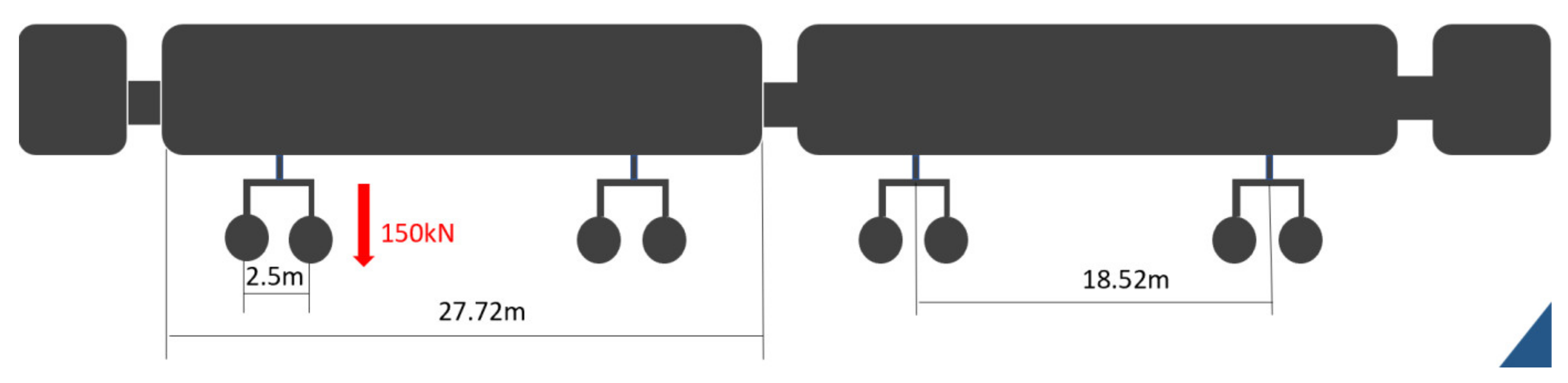
4. Experimental Methods
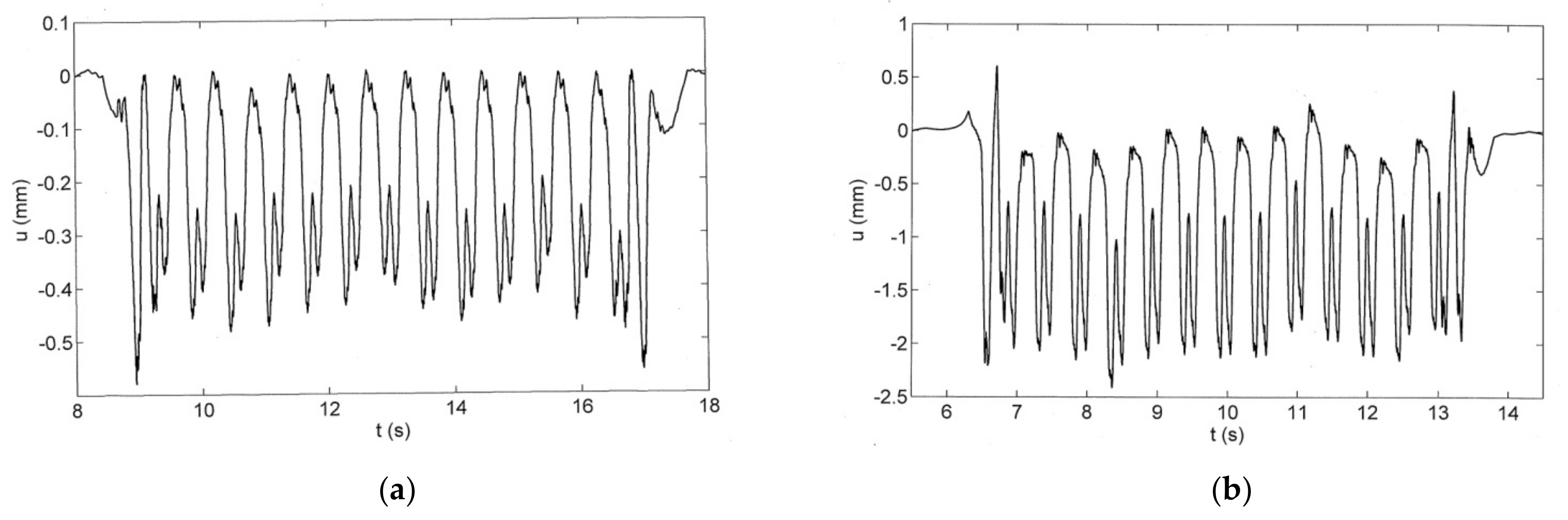
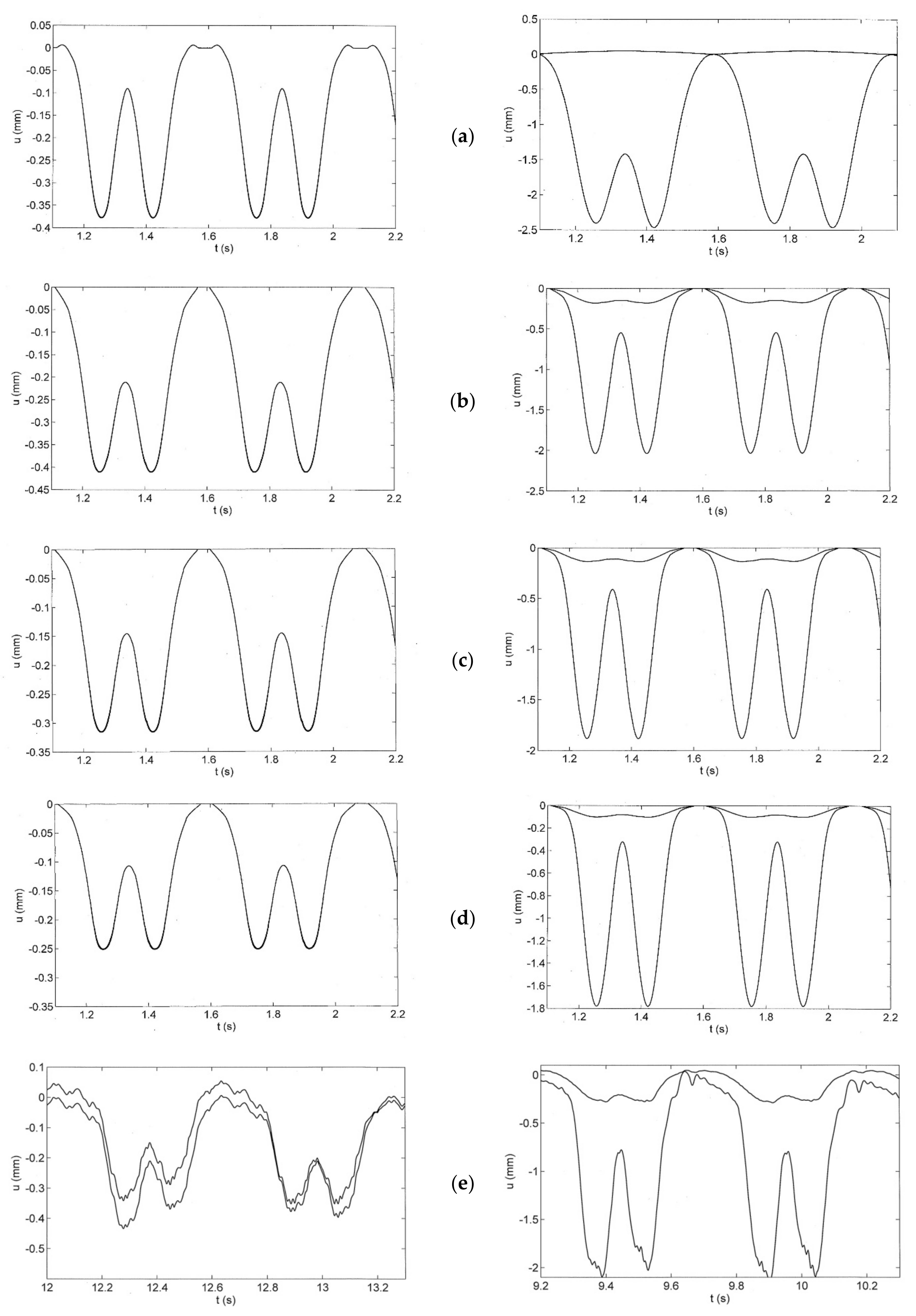
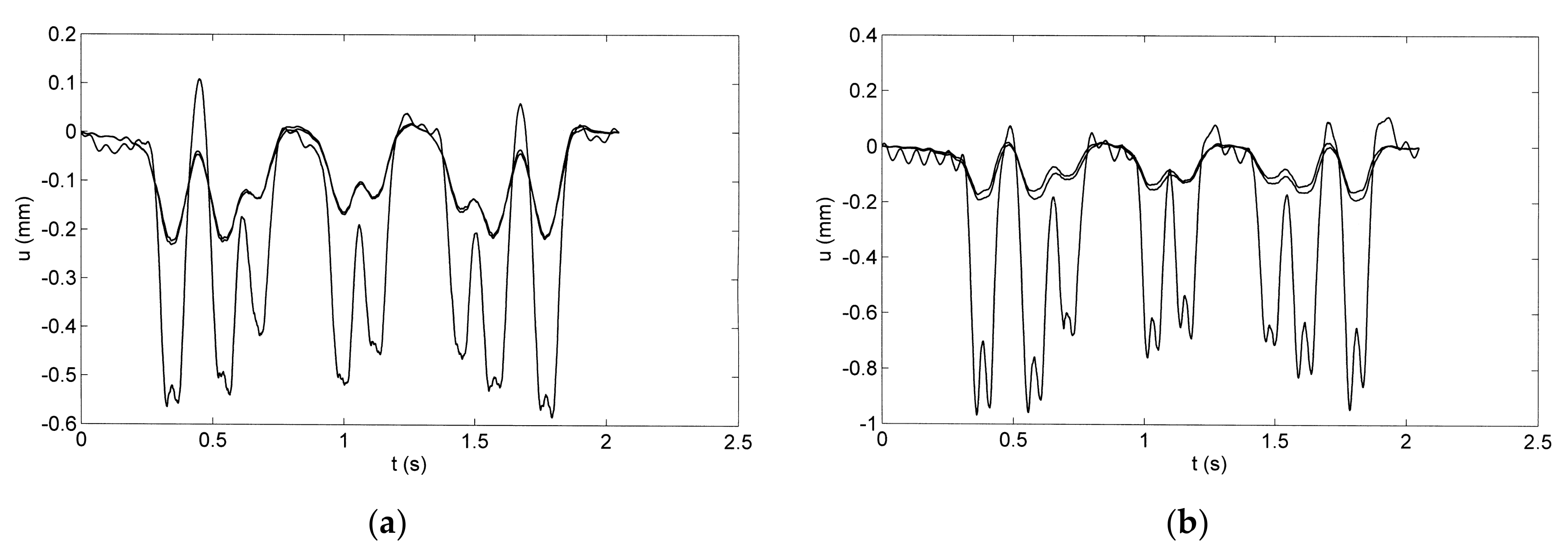
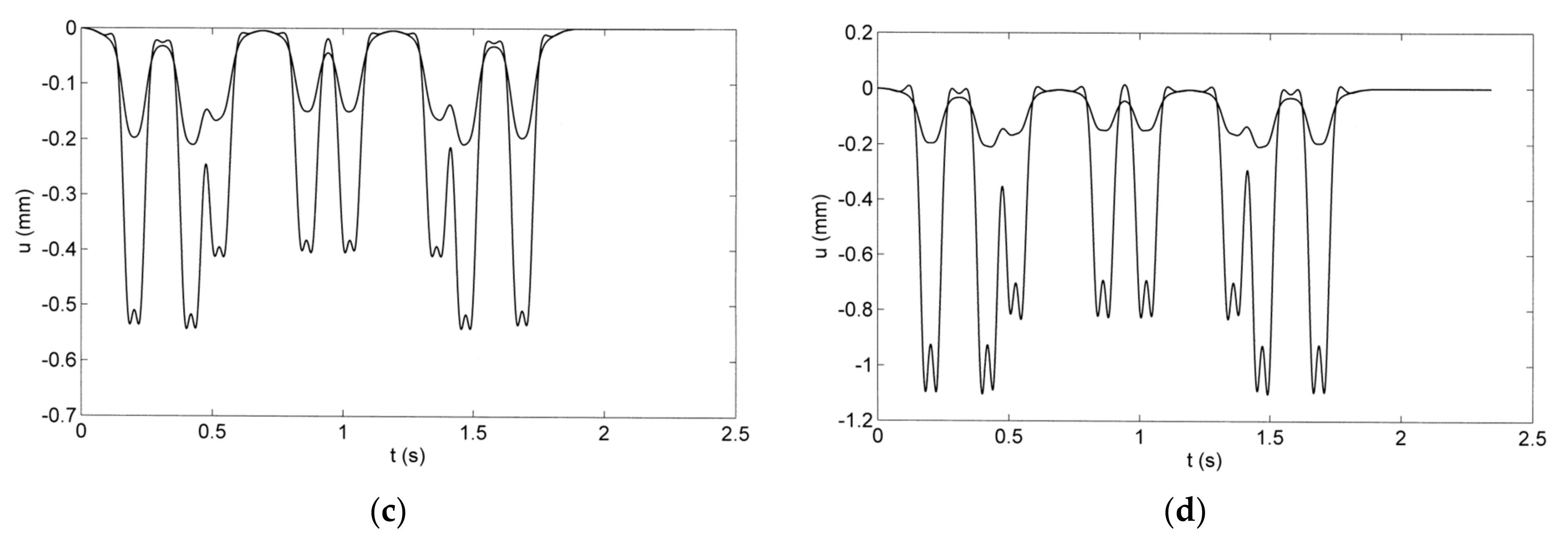
5. Measured Train Passages over Intact and Damaged Slab Tracks at Site G
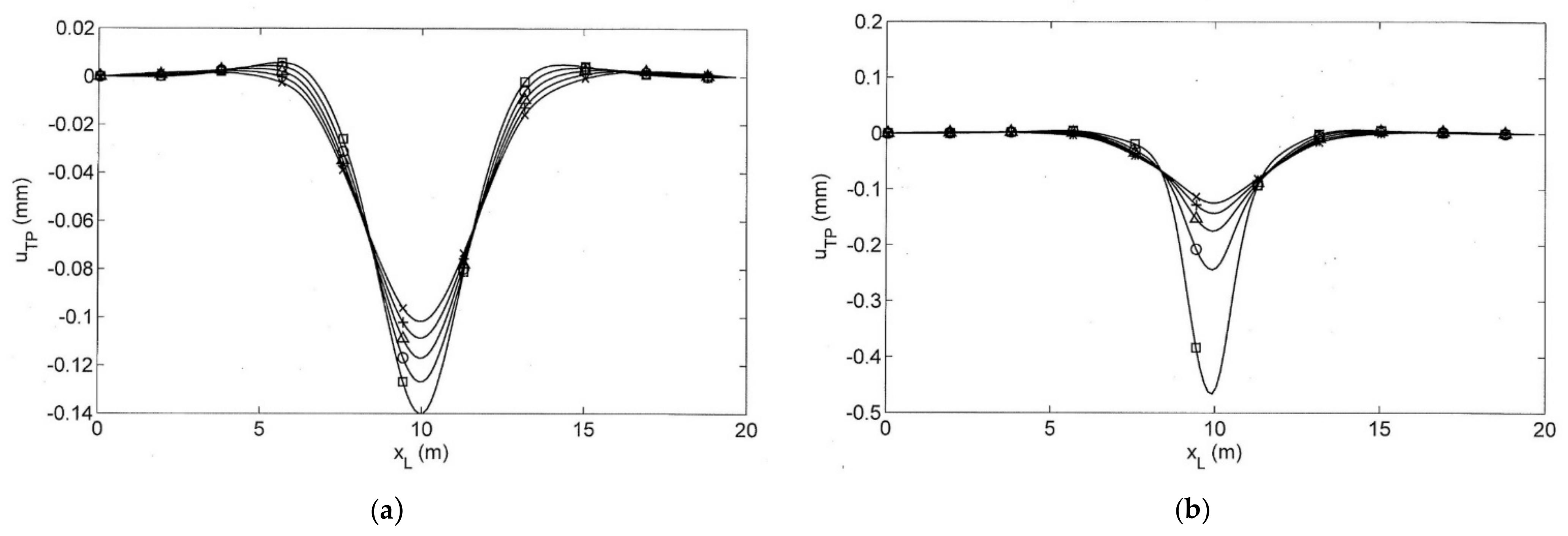
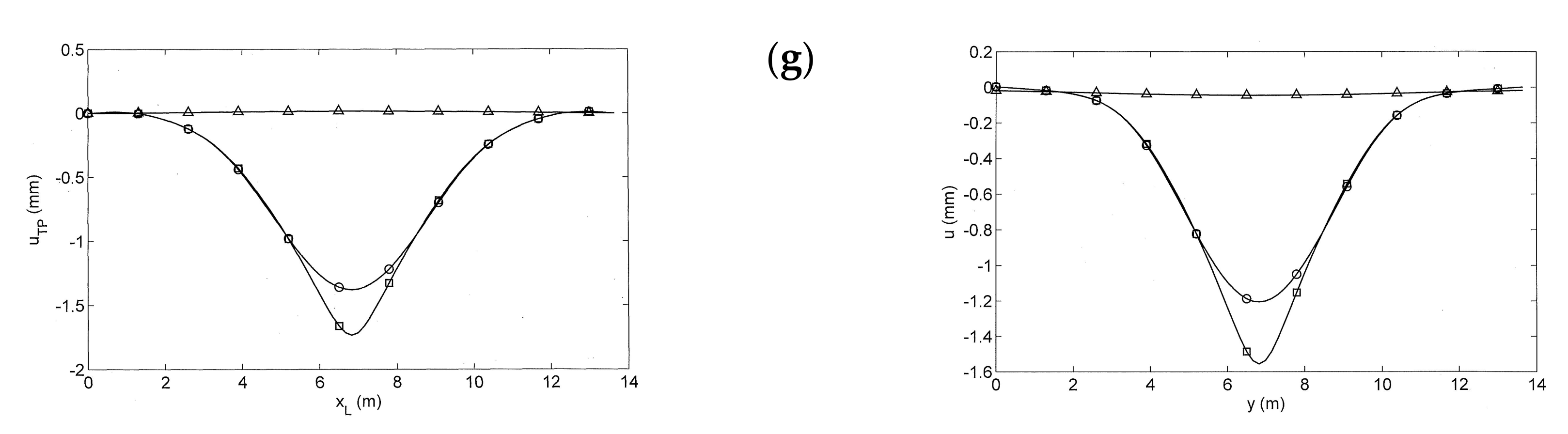
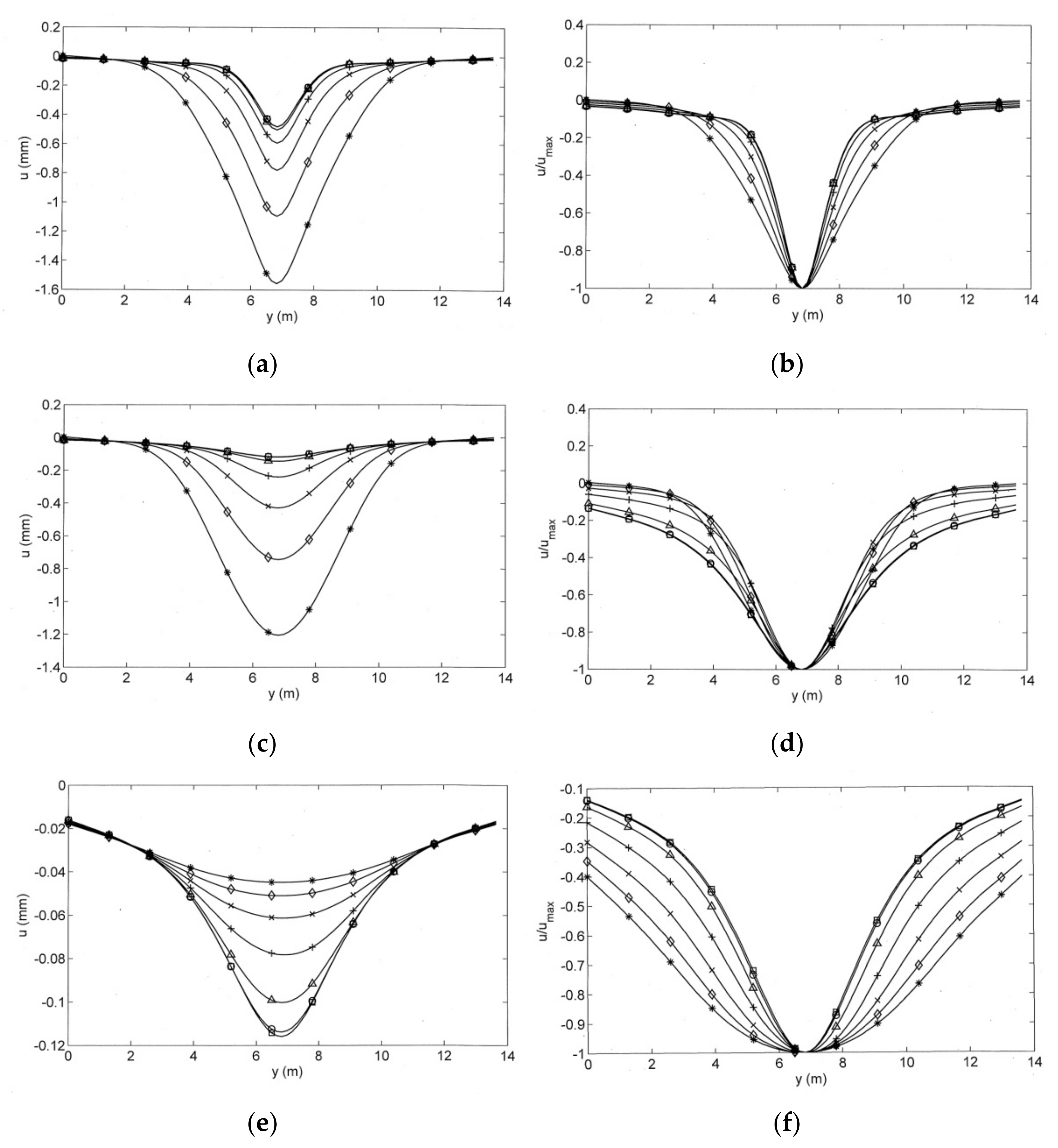
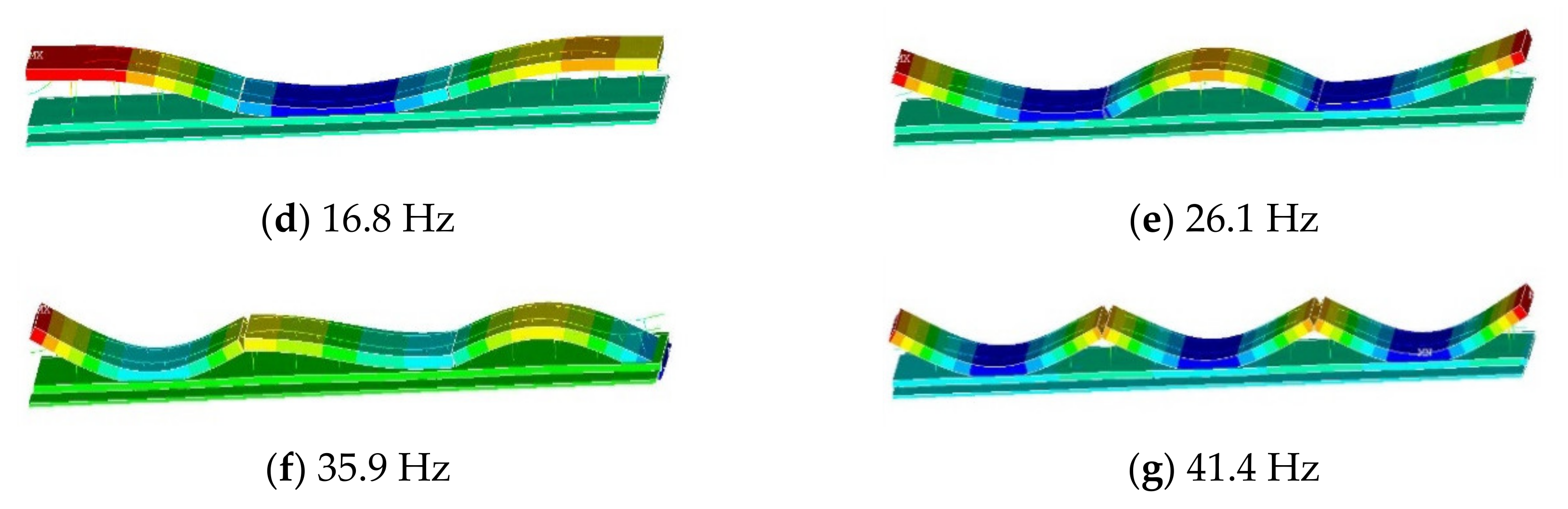
6. Calculated Displacement Distribution along the Slab Track
7. Calculated Train Passages over Intact and Damaged Slab Tracks
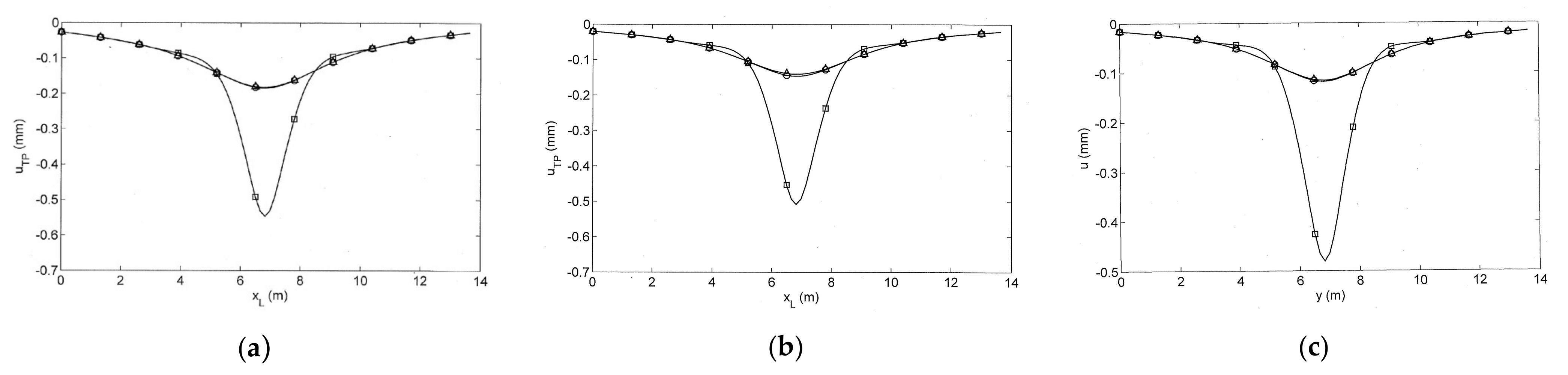
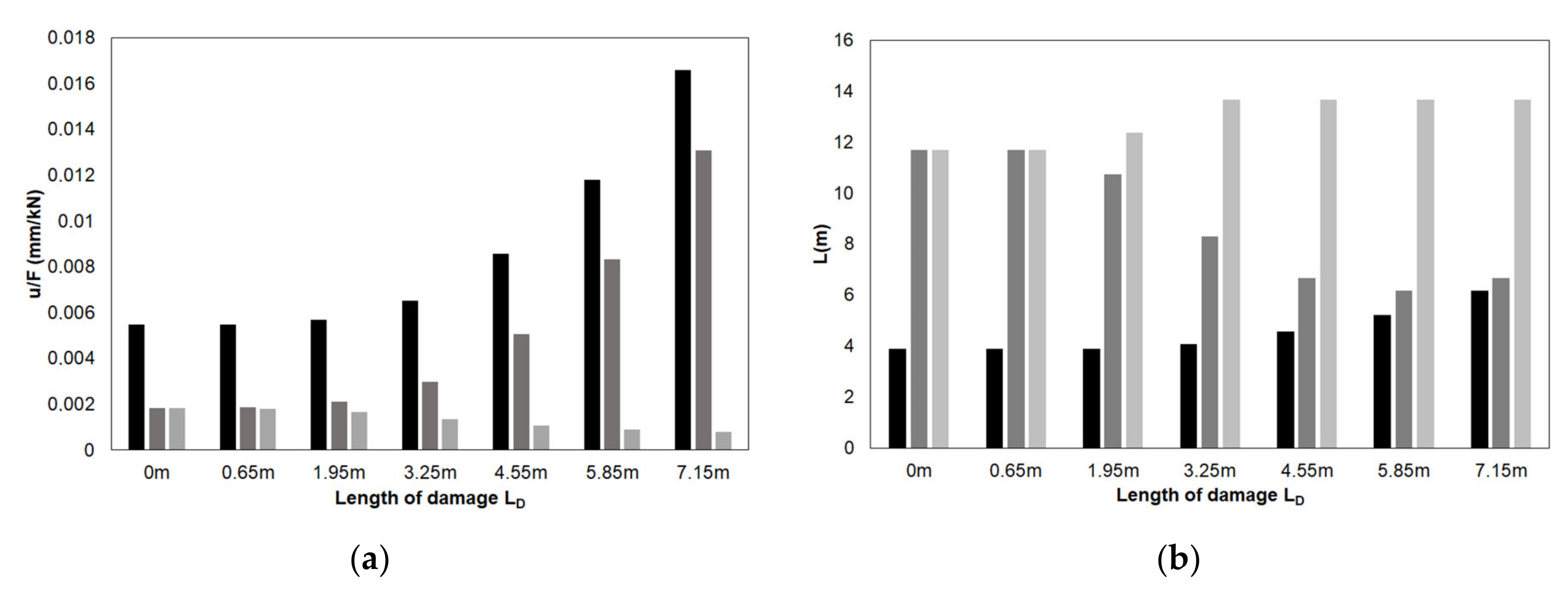
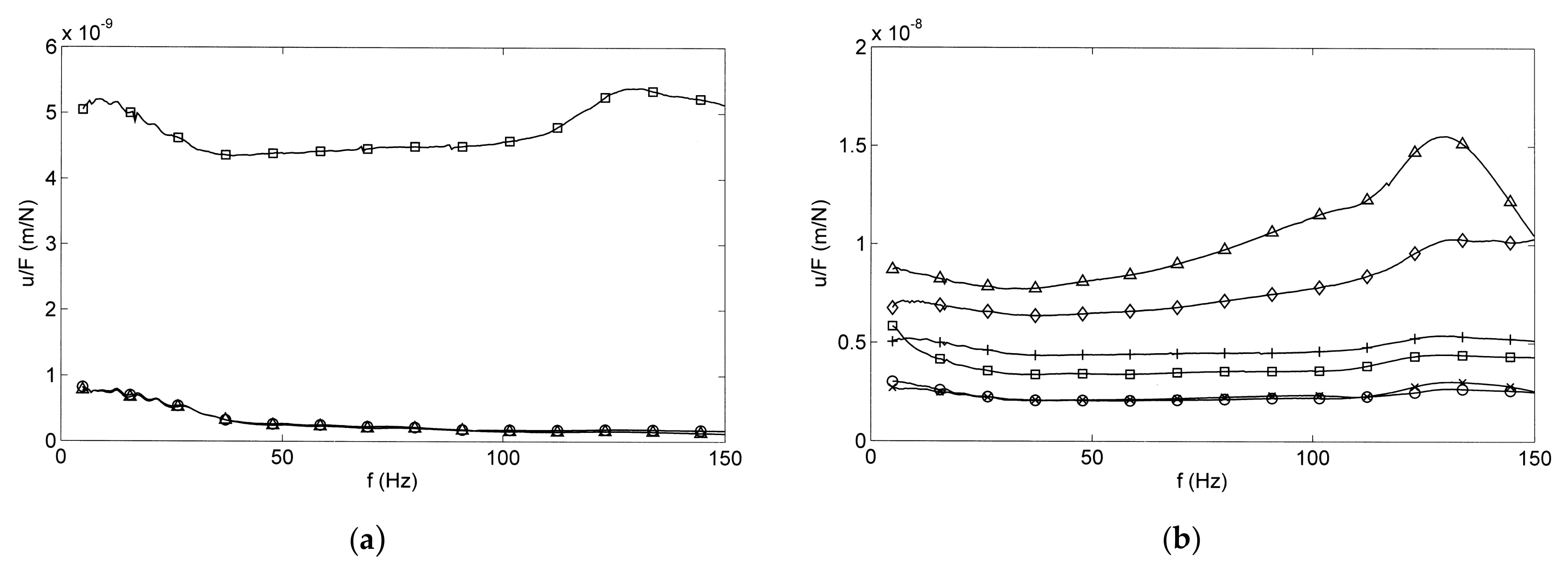
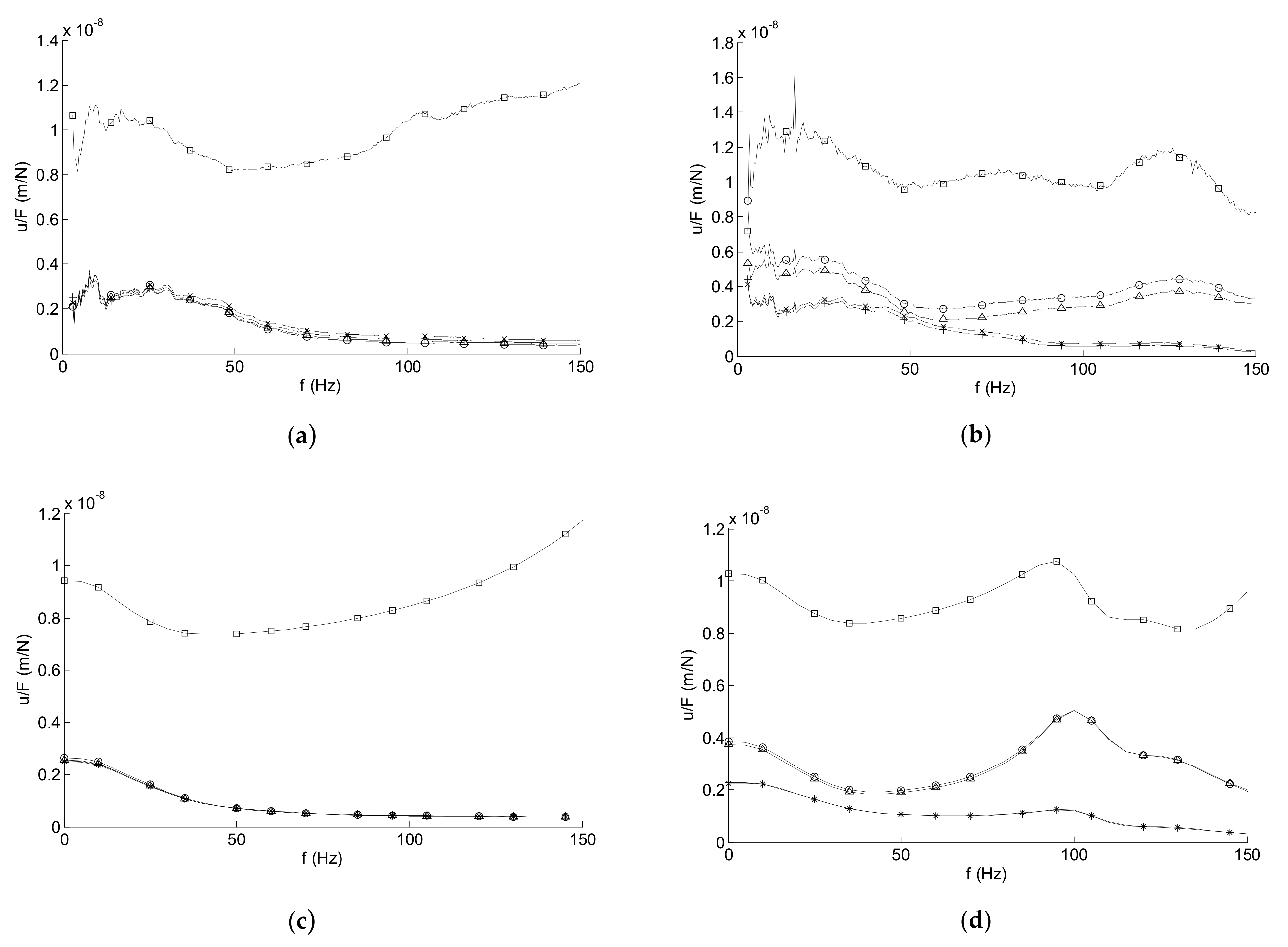
8. Comparison of the FEM on Winkler Soil with the FEBEM with Continuous Soil
9. Further Example Applications to the Three Sites: S, W, and T
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Auersch, L.; Said, S. Track-soil dynamics—Calculation and measurement of damaged and repaired slab tracks. Transp. Geotech. 2017, 12, 1–14. [Google Scholar] [CrossRef]
- Song, J. Research on Isolator Damping in Floating Slab and Its Influence on Dynamic Response. Master’s Thesis, Tongji University, Shanghai, China, 2019. [Google Scholar]
- Xu, H.; Wang, P.; Xu, J. Analysis of cement emulsified asphalt mortar gap on CRTS II slab ballastless track. Appl. Mech. Mater. 2013, 405–408, 1834–1838. [Google Scholar] [CrossRef]
- Song, X.; Zhao, C.; Zhu, X. Temperature-induced deformation of CRTS II slab track and its effect on track dynamical properties. Sci. China Technol. Sci. 2014, 57, 1917–1924. [Google Scholar] [CrossRef]
- Zhu, S.; Cai, C. Interface damage and its effect on vibrations of slab track under temperature and vehicle dynamic loads. Int. J. Non-Linear Mech. 2014, 58, 222–232. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Y.; Wu, T.; Wu, X. Performance of cement asphalt mortar in ballastless slab track over high-speed railway under extreme climate conditions. Int. J. Geomech. 2019, 19, 04019037. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, M.; Zhai, W.; Cai, C.; Zhao, C.; Zeng, D.; Zhang, J. Mechanical property and damage evolution of concrete interface of ballastless track in high-speed railway: Experiment and simulation. Constr. Build. Mater. 2018, 187, 460–473. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, K.; Gao, L.; Yan, S.; Cai, X. Study on the interlayer debonding and its effects on the mechanical properties of CRTS II slab track based on viscoelastic theory. Constr. Build. Mater. 2019, 224, 387–407. [Google Scholar] [CrossRef]
- Ren, J.; Ji, W.; Xiao, L.; Wei, K.; Haolan, L.; Shijie, D. Influence of cement asphalt mortar debonding on the damage distribution and mechanical responses of CRTS I prefabricated slab. Constr. Build. Mater. 2020, 230, 116995. [Google Scholar] [CrossRef]
- Zhong, Y.; Gao, L.; Cai, X.; An, B.; Zhang, Z.; Lin, J.; Qin, Y. An improved cohesive zone model for interface mixed-mode fractures of railway slab tracks. Appl. Sci. 2021, 11, 456. [Google Scholar] [CrossRef]
- Wang, P.; Xu, H.; Chen, R. Effect of cement asphalt mortar debonding on dynamic properties of CRTS II slab ballastless track. Adv. Mater. Sci. Eng. 2014, 2014, 193128. [Google Scholar] [CrossRef]
- Zhu, S.; Fu, Q.; Cai, C.; Spanos, D. Damage evolution and dynamic response of cement asphalt mortar layer of slab track under vehicle dynamic load. Sci. China Technol. Sci. 2014, 57, 1883–1894. [Google Scholar] [CrossRef]
- Ren, J.; Yang, R.; Wang, P.; Dai, F.; Yan, X. Influence of contact loss underneath concrete underlayer on dynamic performance of prefabricated concrete slab track. Rail Rapid Transp. 2017, 231, 1. [Google Scholar]
- Han, J.; Zhao, G.; Xiao, X.; Wen, Z.; Guan, Q.; Jin, X. Effect of softening of cement asphalt mortar on vehicle operation safety and track dynamics. J. Zhejiang Univ.-Sci. A Appl. Phys. Eng. 2015, 16, 976–986. [Google Scholar] [CrossRef]
- Xu, J.; Wang, P.; Liu, H.; Hu, Z.; Chen, R. Identification of internal damage in ballastless tracks based on Gaussian curvature mode shapes. J. Vibroeng. 2016, 18, 5217–5229. [Google Scholar] [CrossRef][Green Version]
- Ulriksen, M.; Bernal, D.; Damkilde, L. Shaped input distributions for structural damage localization. Mech. Syst. Signal Processing 2018, 110, 499–508. [Google Scholar] [CrossRef]
- Yan, A.; Golinval, J. Null subspace-based damage detection of structures using vibration measurements. Mech. Syst. Signal Process. 2006, 20, 611–626. [Google Scholar] [CrossRef]
- Döhler, M.; Mevel, L.; Hille, F. Subspace-based damage detection under changes in the ambient excitation statistics. Mech. Syst. Signal Process. 2014, 45, 207–224. [Google Scholar] [CrossRef]
- Ha, N.; Golinval, J. Localization and quantification of damage in beam-like structures using sensitivities of principal component analysis results. Mech. Syst. Signal Process. 2010, 24, 1831–1843. [Google Scholar]
- Zimmermann, H. Die Berechnung des Eisenbahnoberbaus; Ernst & Korn: Berlin, Germany, 1888. [Google Scholar]
- Winkler, E. Die Lehre von der Elastizität und Festigkeit; Dominicus: Prague, Czech Republic, 1867. [Google Scholar]
- Zhai, W. The Vertical Coupling Dynamics of Vehicle and Track as an Integral System. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 1991. [Google Scholar]
- Knothe, K.; Grassie, S. Modelling of railway track and vehicle/track interaction at high frequencies. Veh. Syst. Dyn. 1993, 22, 209–262. [Google Scholar] [CrossRef]
- Takemiya, H.; Bian, X. Substructure simulation of inhomogeneous track and layered ground dynamic interaction under train passage. J. Eng. Mech. ASCE 2005, 131, 699–711. [Google Scholar] [CrossRef]
- Jones, C. Use of numerical models to determine the effectiveness of anti-vibration system for railways. Proc. Inst. Civ. Eng. Transp. 1994, 105, 43–51. [Google Scholar] [CrossRef]
- Sheng, X.; Jones, C.; Petyt, M. Ground vibration generated by a load moving along a railway track. J. Sound Vib. 1999, 225, 129–156. [Google Scholar] [CrossRef]
- Lombaert, G.; Degrande, G. Ground-borne vibration due to static and dynamic axle loads of InterCity and high-speed trains. J. Sound Vib. 2009, 319, 1036–1066. [Google Scholar] [CrossRef]
- Auersch, L. Static and dynamic behaviours of isolated and un-isolated ballast tracks using a fast wavenumber domain method. Arch. Appl. Mech. 2017, 87, 555–574. [Google Scholar] [CrossRef]
- Ju, S.; Lin, H. Experimentally investigating finite element accuracy for ground vibrations induced by high-speed trains. Eng. Struct. 2008, 30, 733–746. [Google Scholar] [CrossRef]
- Auersch, L. Dynamics of the railway track and the underlying soil: The boundary-element solution, theoretical results and their experimental verification. Veh. Syst. Dyn. 2005, 43, 671–695. [Google Scholar] [CrossRef]
- Galvin, P.; Romero, A.; Dominguez, J. Fully three-dimensional analysis of high-speed train-track-soil-structure dynamic interaction. J. Sound Vib. 2010, 329, 5147–5163. [Google Scholar] [CrossRef]
- Lombaert, G.; Degrande, G.; Vanhauwere, B.; Vandeborght, B.; François, S. The control of ground-borne vibrations from railway traffic by means of continuous floating slabs. J. Sound Vib. 2006, 297, 946–961. [Google Scholar] [CrossRef]
- Steenbergen, M.; Metrikine, A.; Esveld, C. Assessment of design parameters of a slab track railway system from a dynamic viewpoint. J. Sound Vib. 2007, 306, 361–371. [Google Scholar] [CrossRef]
- Galvin, P.; Romero, A.; Dominguez, J. Vibrations induced by HST passage on ballast and non-ballast tracks. Soil Dyn. Earthq. Eng. 2010, 30, 862–873. [Google Scholar] [CrossRef]
- Auersch, L. The dynamic behaviour of slab tracks on homogeneous and layered soils and the reduction of ground vibration by floating slab tracks. J. Eng. Mech. 2012, 138, 923–933. [Google Scholar]
- Shih, J.; (University of Birmingham, Birmingham, UK), Approximate Soil Layers. Private communication, 2019.
- Milne, D.; Pen, L.; Thompson, D.; Powrie, W. Automated processing of railway track deflection signals obtained from velocity and accelerometer mesurements. Rail Rapid Transp. 2018, 232, 2097–2110. [Google Scholar] [CrossRef] [PubMed]








| Parts | Parameters | Values |
|---|---|---|
| Rails | bending stiffness of the rails (UIC60) | EI = 12.6 × 106 Nm2 |
| mass per length of the rails | m’R = 2 × 60 kg/m | |
| Slab track | distance of the rail supports | d = 0.65 m |
| stiffness of the rail pads | kR = 60 × 106 N/m | |
| hysteretic damping of the rail pads | DR = 10% | |
| modulus of elasticity of concrete | E = 3.6 × 1010 N/m2 | |
| mass density of concrete | ρ = 2.5 103 kg/m3 | |
| width of the track plate | aP = 2.8 m | |
| height of the track plate | hP = 0.1, 0.15, 0.2, 0.25, 0.3 m | |
| modulus of elasticity of the mortar | EM = 5 × 109 N/m2 | |
| modulus of elasticity of the base layer | EL = 5 × 109 N/m2 | |
| width of the base layer | aL = 3.5 m | |
| height of the base layer | hL = 0.3 m | |
| Soil | shear modulus of the soil | G = 4.5, 6.125; 8 × 107 N/m2 |
| shear wave velocity of the soil | vS = 150, 175, 200 m/s | |
| mass density of the soil | ρB = 2 × 103 kg/m3 | |
| Poisson’s ratio of the soil | νB = 0.33 | |
| hysteretic damping of the soil | DB = 2.5% |
| Components | Site W | Site S | Site T |
|---|---|---|---|
| Track plate | h1 = 0.15 m | h1 = 0.15 m | h1 = 0.325 m |
| Base plate | h2 = 0.17 m | h2 = 0.15 m | h2 = 0.2 m |
| Base layer | h3 = 0.3 m | h3 = 0.3 m | h3 = 0.1 m |
| Elastic layer | Soil | Rubber | Steel springs |
| Stiffness k | - | - | k = 6 × 106 N/m |
| Damping c | - | - | c = 6 × 103 Ns/m |
| Stiffness per track length | - | k’ = 4.5 × 108 N/m2 | k’ = 8 × 106 N/m2 |
| Stiffness per track area | - | k’’ = 1.5 × 108 N/m3 | k’’ = 3 × 106 N/m3 |
| Shear modulus of the soil | G = 6 × 107 N/m2 | G = 13 × 107 N/m2 | - |
| Mass of floating slab per track length | - | m’R = 1050 kg/m | m’R = 2200 kg/m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Auersch, L.; Song, J. Dynamic Damage Quantification of Slab Tracks—Finite Element Models on Winkler Soil and Finite-Element Boundary-Element Models on Continuous Soil. CivilEng 2022, 3, 979-997. https://doi.org/10.3390/civileng3040055
Auersch L, Song J. Dynamic Damage Quantification of Slab Tracks—Finite Element Models on Winkler Soil and Finite-Element Boundary-Element Models on Continuous Soil. CivilEng. 2022; 3(4):979-997. https://doi.org/10.3390/civileng3040055
Chicago/Turabian StyleAuersch, Lutz, and Jiaojiao Song. 2022. "Dynamic Damage Quantification of Slab Tracks—Finite Element Models on Winkler Soil and Finite-Element Boundary-Element Models on Continuous Soil" CivilEng 3, no. 4: 979-997. https://doi.org/10.3390/civileng3040055
APA StyleAuersch, L., & Song, J. (2022). Dynamic Damage Quantification of Slab Tracks—Finite Element Models on Winkler Soil and Finite-Element Boundary-Element Models on Continuous Soil. CivilEng, 3(4), 979-997. https://doi.org/10.3390/civileng3040055






