1. Introduction
Orthotropic steel decks did not find popular use in bridges in North America during the 20th century despite their advantages over comparable concrete slabs [
1] and early encouragement for their use [
2]. This is primarily due to higher overall construction costs as compared to concrete decks. However, with the spread of cable-stayed and suspension bridges, the use of orthotropic decks has increased rapidly because of their lighter weight, especially for medium- and long-span bridges [
3,
4]. In particular, steel orthotropic decks have the potential to save up to 50% in weight compared to the concrete decks they replace [
5]. Additionally, they have other advantages such as rapid construction, long life, low maintenance costs and potential for design standardization [
6]. These benefits have led to the replacement of existing concrete decks with orthotropic steel counterparts for a few bridges such as the Williamsburg, Bronx-Whitestone [
7] and Benjamin Franklin Bridges [
8].
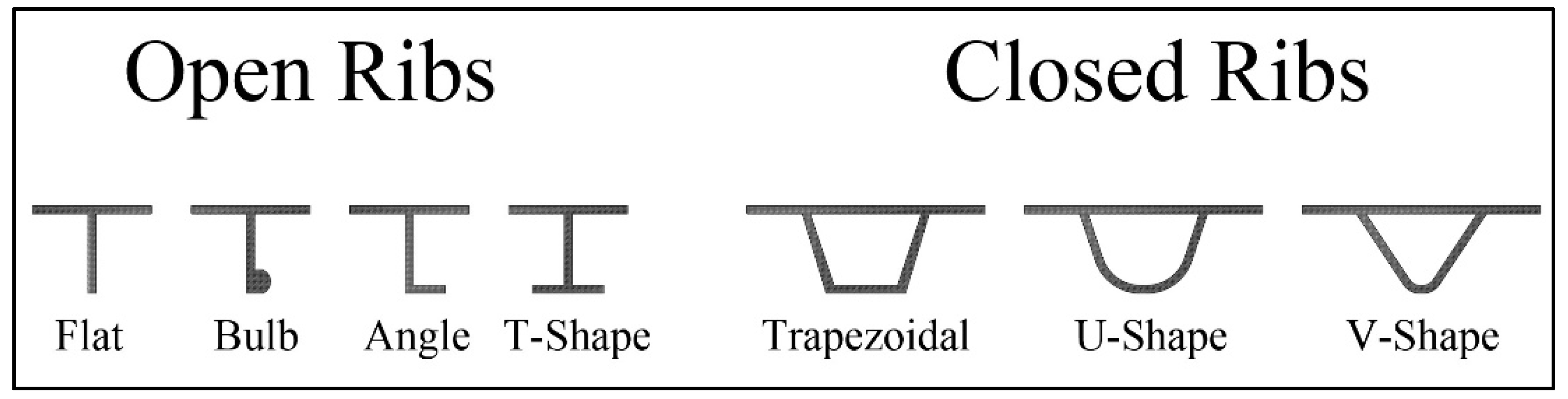
Orthotropic steel decks are composed of a panel that is stiffened in the longitudinal direction by ribs. The steel ribs help distribute the wheel loads, as well as provide additional stiffness. Based on the panel/rib connection, steel decks are usually classified as open-rib or closed-rib.
Figure 1 below shows examples of common open and closed steel rib configurations. According to a recent study conducted the by United States Federal Highway Administration (FHWA) on closed-rib connections [
9], closed-rib decks have many advantages over their open-rib counterparts. In particular, closed ribs have much higher rigidity which allows the use of longer spans, i.e., lesser girders or floor-beams [
6]. Additionally, closed orthotropic decks have improved wheel load transfer to girders which enables an increase in rib spacing or a decrease in panel thickness. The above two advantages save significant material weight by reducing the number of ribs and girders needed in the bridge. Moreover, closed ribs save half of the weld lines because they are completed from one-side (note that a single closed rib is compared with two open ribs). However, the use of a one-sided weld generally requires it to be a groove type with a relatively deep penetration. Additionally, one-sided welds limit visual inspection to the outside only, whereas many fatigue studies showed that the weld root is a possible fatigue crack initiation point [
10,
11]. Hence, open ribs allow for better observation and maintenance.
In addition to the characteristics of open and closed-rib decks mentioned above, both decks are considered labor-intensive. More specifically, the use of steel decks requires the fabrication of customized diaphragms that are welded with the panel, rib and girder. They are needed to improve the load transfer and distribution, as well as reduce stress concentrations. Many recent studies have been conducted on identifying and reducing diaphragm fatigue problems [
12,
13,
14]. This paper discusses classical orthotropic steel decks and introduces a new type of closed-rib section, i.e., a built-up section which represents a possible solution that minimizes the disadvantages of classical closed-rib decks. Moreover, this paper compares the behavior of typical open and closed steel rib sections with a suggested newer design, using finite element (FE) simulations and the Benjamin Franklin Bridge deck as a case study.
2. Classical Steel Orthotropic Decks
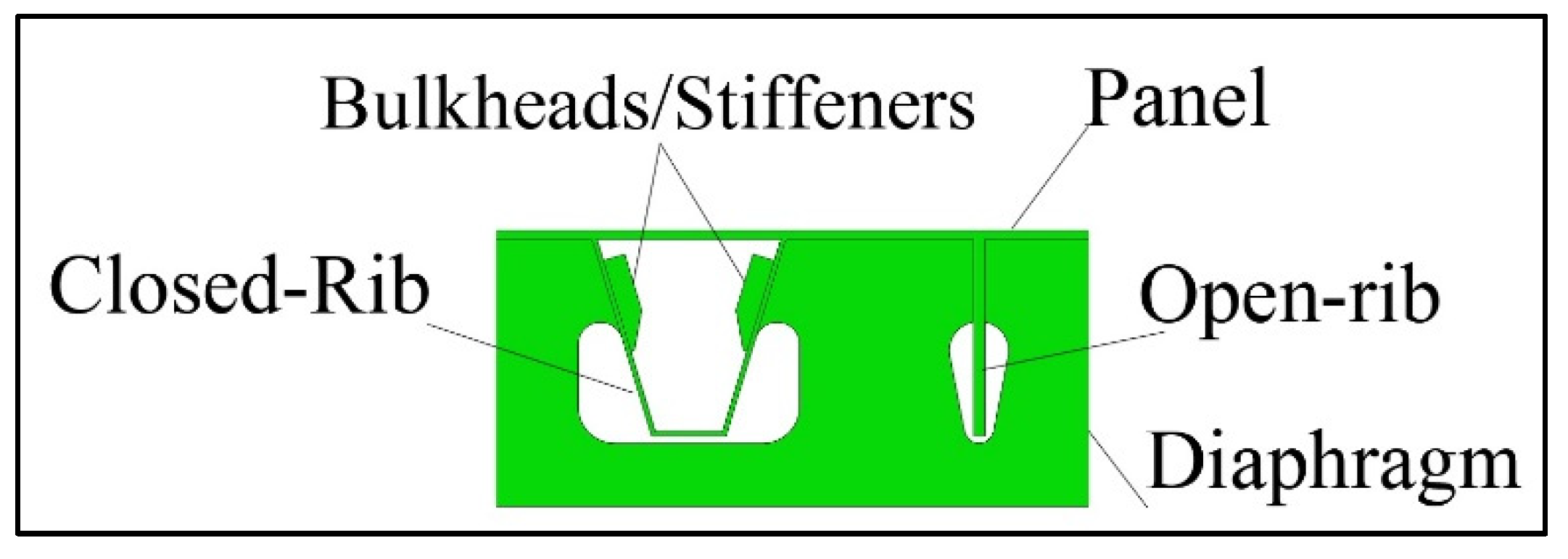
The Orthotropic steel decks have higher initial cost as compared to their concrete counterparts due to their fabrication complexity which makes them somewhat labor-intensive. Unlike their concrete counterparts, steel decks have structural details that require both off-site and on-site works. Steel decks usually need diaphragms to improve the rib bending performance, and to smoothly transfer the load from decks to supporting beams. Diaphragms can also be used to provide torsional bracing, especially for open ribs at midspans. These diaphragms have to be accurately cut to fit. Moreover, they also require manual welding as well as the welding of bulkheads/stiffeners where needed.
Figure 2 shows a typical diaphragm for trapezoidal and flat rib sections. Deck diaphragm welded connections are prone to stress concentrations when wheel loads are directly above the diaphragm [
15]. The 2016 Specification for Structural Steel Buildings Appendix 3 [
16] provided fatigue threshold stress, potential crack location and allowable stress calculations for various welded connections. However, American Association of State Highway and Transportation Officials (AASHTO) [
17] added special fatigue categories for steel orthotropic deck diaphragms (in their fatigue category table section 8 cases). Extensive studies have been conducted to identify hot-spots and reduce the potential for fatigue cracking at the welds by studying the effects of different diaphragm cutouts [
18], various weld penetration depths [
19], and changing the metal thickness at welded connection [
3].
Welded connections are exposed to many flaws, including but not limited to lack of fusion, partial penetration, porosity, arc strike and residual stress that affect their fatigue resistance. It is well known experimentally that fatigue cracks start at weld discontinuity locations [
20]. According to the AASHTO specification, continuous longitudinal welds are classified as category B with a fatigue threshold stress of 110.32 MPa (16 ksi) if parallel to the direction of the applied stress. These may be considered category C (adjusted) with a 68.95 MPa (10 ksi) threshold stress if the weld is discontinuous or normal to the direction of primary stress, and depending on the details it may fall under category D or E. However, one-sided longitudinal groove welds for orthotropic decks are considered category C with a fatigue threshold of 68.95 MPa (10 ksi). This gives the open ribs (which have double-sided welds) an advantage over closed ribs in terms of fatigue capacity at rib/panel connections, especially when the primary stress is parallel to the welds. Furthermore, AASHTO requires minimum penetration of 60% (which used to be 80%) and a root gap equal or less than 0.51 mm (0.02 in.) for the one-sided groove weld to be considered in category C. However, ensuring that the percent penetration is satisfied after welding may be problematic, relying on previously established weld procedures.
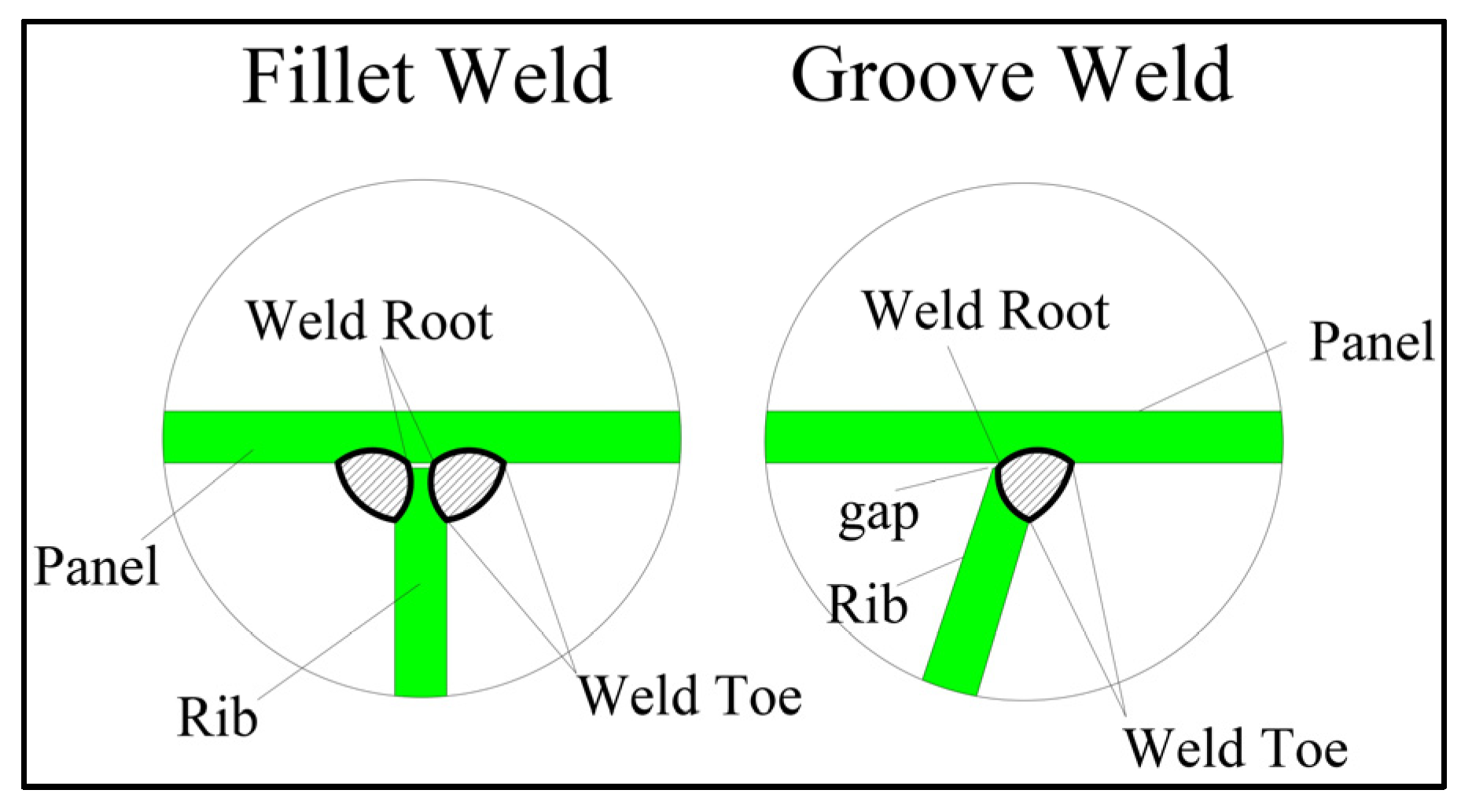
Fatigue cracks develop at stress concentration regions and propagate under live load stress fluctuation at the weld toe or bending in the ribs due to direct wheel loads (through the throat. The location and characteristics of these cracks depends on several factors including the detail type, the weld size compared to plate thickness, the weld penetration, the stress range and direction, and plate to rib gap and angle [
21]. In orthotropic decks, stress concentrations at rib/panel connections are a function of the local geometry and the elevated stresses that develop from local bending in the ribs due to direct wheel loads [
17]. Cracks may propagate from the weld toe or from the root through the weld throat (see
Figure 3). From a maintenance perspective, it is essential to avoid cracks growing from weld root through the deck plate because the deck plate is usually covered either with epoxy or concrete; hence, the crack may develop long before it is discovered. On the other hand, cracks that initiate at the weld toe may be observed and repaired before they spread. Although it is expected for groove welds to have cracks initiate at the weld toe if penetration and gap requirements are satisfied when stresses higher than threshold stress are applied, many steel decks with groove welds have suffered fatigue cracks which started at the root [
22]. On the contrary, root cracks may be less common in fillet-welded connections provided the welds have adequate throat thickness and the penetration is directed into the intersecting corner.
3. Built-Up Ribs
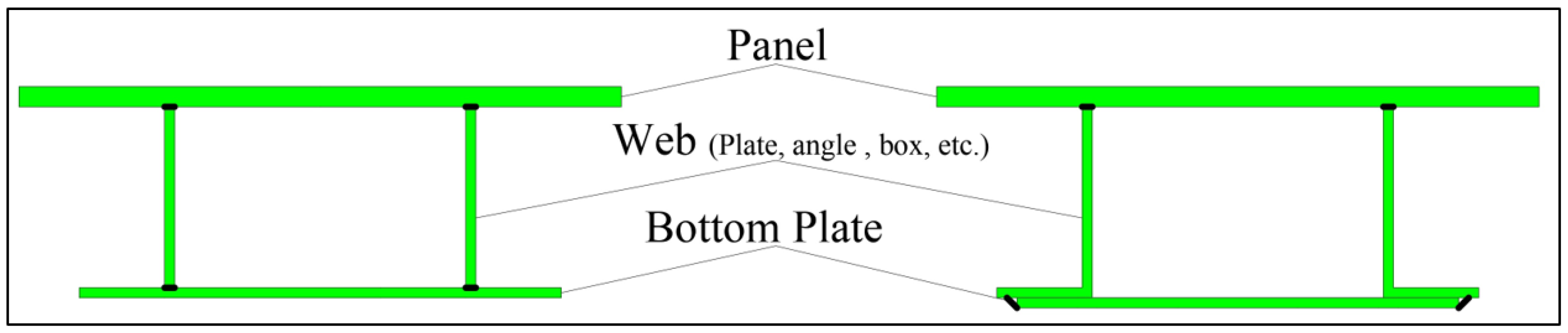
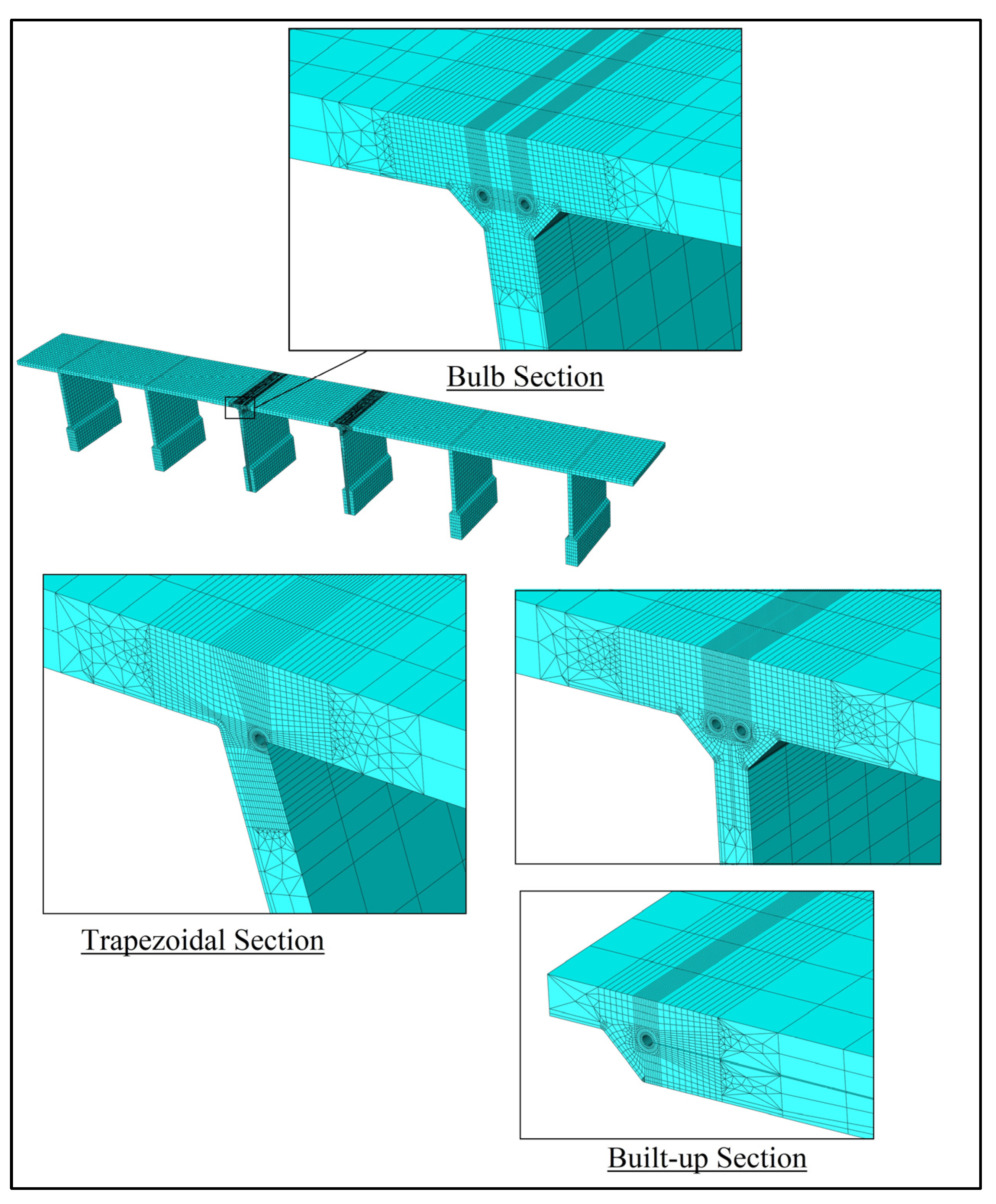
In light of the above discussion, a new built-up closed-rib section is presented in
Figure 4 which provides the required stiffness with better fatigue resistance and less fabrication complexity. The built-up rib is composed of three separate parts, i.e., two webs and a plate. The webs are suggested to be whole (such as angle or W shape sections) or partial (such as angle shapes cut from C or box sections) standard hot-rolled steel sections that have double fillet welds connecting them to the panel. The bottom plate connects the two webs by fillet welds and allows for relatively easy connection with floor-beams. The fillet welds at the bottom plate are expected to have lower stress concentration compared to the top plate due to wheel; hence, lower fatigue concerns are proposed, which leads to optimized weld design for economical purposes.
The bottom plate eliminates the need for diaphragms between decks and beams by providing a plane surface for bolted connections between the bottom plate and floor-beam flange. Additionally, by providing a sufficient torsional stiffness, built-up decks may avoid the need for intermediate diaphragms. However, for long spans where intermediate diaphragms are needed, the straight edges of the built-up ribs allow for easy installation of the rectangular stiffeners to connect the ribs without the need for customized cuts.
The built-up deck provides a viable economic replacement for existing steel and concrete decks. However, concrete decks are often supported by separate steel beams, which makes replacement easier than their steel deck counterparts, especially for steel decks where the panel is shared with floor-beams as a flange. The Benjamin Franklin Bridge was originally built with a concrete deck in 1927 [
8]. Due to severe deterioration in the concrete, renewing the deck system was necessary in 1982. An ASTM A36 steel [
23], open-rib bulb section was designed and eventually constructed. Although a closed-rib system replacement has less weight, the open system was used to avoid the complicated details and to provide a better fatigue resistance.
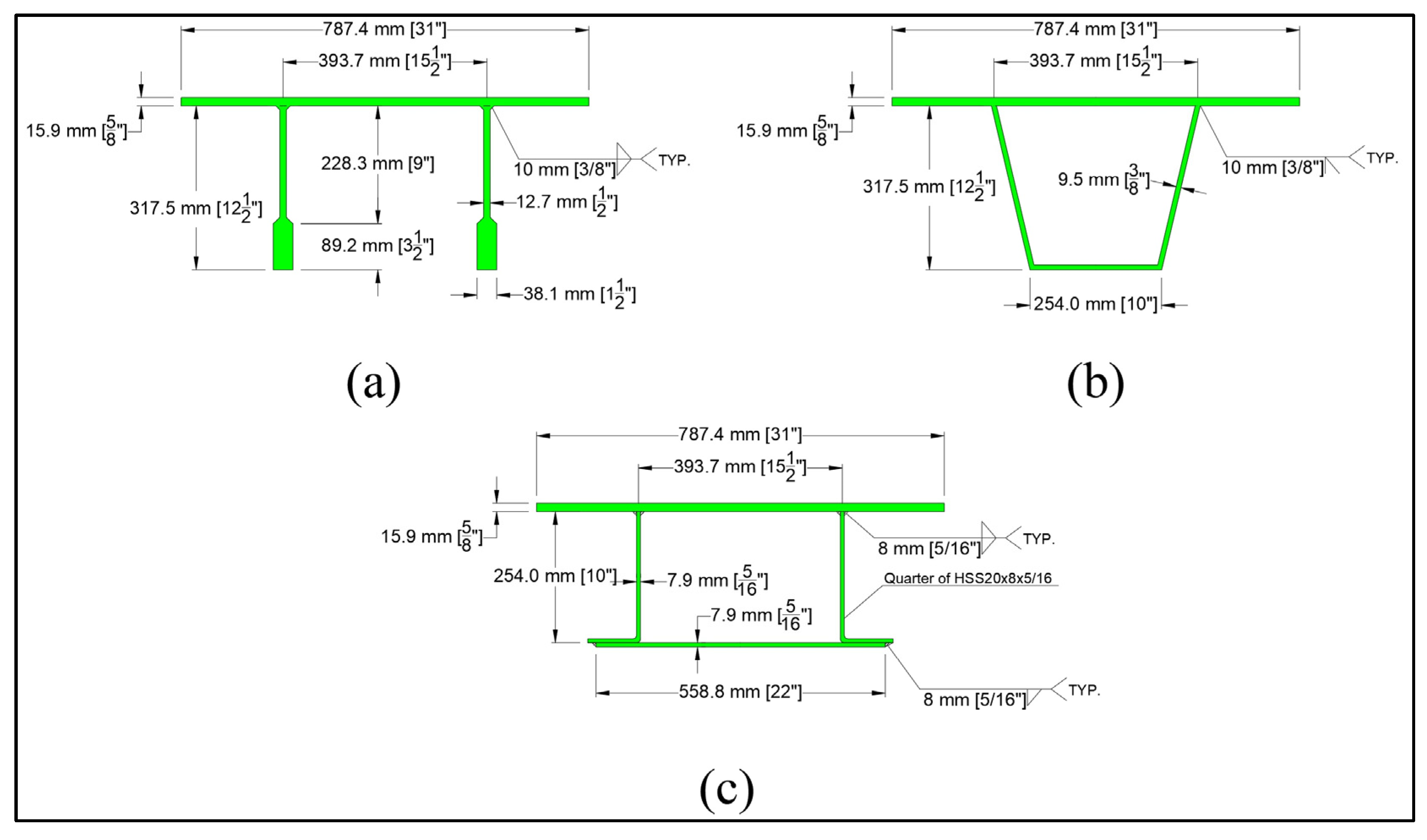
Figure 5a shows the details of the bulb section used to replace the concrete deck. The replacement section has 16 mm (5/8 in.) panel thickness with a maximum rib spacing of 393.7 mm (15.5 in.) and a maximum span of 6.78 m (22 ft–3 in.). A typical trapezoidal closed-rib replacement is presented in
Figure 5b. This section might serve the same span and provide weight savings but has several of the disadvantages mentioned earlier. Note that with closed ribs, the panel thickness can be reduced because of the torsional stiffness provided by the closed rib. Finally, a built-up closed-rib alternative section is presented in
Figure 5c. The rib is composed of two quarter-HSS webs that are cut from an HSS 20 × 8 × 5/16 hot-rolled section. The bottom plate has a width of 558.8 mm (22 in.) and a thickness of 8 mm (5/16 in.) as seen in
Figure 5c. The built-up section is lighter than the bulb, but slightly heavier than the trapezoidal one. In particular, the rib cross sectional areas of bulb, trapezoidal and built-up sections are 12,903 mm
2 (20 in.
2), 8645 mm
2 (13.4 in.
2) and 10,064 mm
2 (15.6 in.
2), respectively, which translate to estimated weight per plan area of 256.8 kg/m
2 (52.6 lb/ft
2), 216.3 kg/m
2 (44.3 lb/ft
2), and 224.6 kg/m
2 (46.0 lb/ft
2) including diaphragms for bulb, trapezoidal and built-up sections, respectively.
The typical trapezoidal section and the built-up section were design based on similar flexural stiffness criteria to that of the bulb section, and by optimizing the weight for each section. Although the built-up section has slightly higher weight than the trapezoidal section, it can be connected to floor-beams directly without the need of a complex diaphragm (see suggested bolt locations for deck to floor-beam flange connection in
Figure 5c). From a practical point of view, built-up decks have several economic advantages. According to an orthotropic steel decks constructability study [
24], increasing the fillet weld size has an exponential effect on cost since it may require several passes to fill the gap. A 10 mm (3/8 in.) fillet weld size in the bulb section may require two or three more passes than the 8 mm (5/16 in.) groove weld in the built-up section which justifies the additional weld lines in the built-up section. The weld cost may increase for the 10 mm (3/8 in.) groove weld of the trapezoidal section depending on the edge preparation type. Moreover, the complex cuts for the diaphragms require manual out-of-position welding rather than welding that can be automated. Out-of-position welding requires qualified welders and takes longer to achieve which further increases the cost. Finally, the built-up section is made from standard hot-rolled steel sections that may be manufactured with longer lengths as compared to the bent plates of typical trapezoidal sections, which are restricted by industrial capabilities. As a result, additional splices may be needed for trapezoidal sections.
4. Modeling
Finite element simulation finds extensive use in the analysis of physical phenomena, including structural behavior. With the increase in computational capabilities, simulation has become an essential step in designing complex structural and mechanical components before manufacturing and testing. Therefore, several simulations have been conducted to study the behavior of the three orthotropic steel sections presented above using ABAQUS software [
25]. The analyses focused on local bending in the deck sections webs as well as the stress concentrations at welded joints, which are directly related to fatigue life. In all analyses, small deformation and linear elastic steel assumptions were considered with elastic modulus of 200 GPa (29,000 ksi) and Poisson’s ratio of 0.26 for all components (steel base metal and weld). Moreover, AASHTO’s fatigue design truck for orthotropic decks was used for the load’s footprint, i.e., a single footprint of 17.8 kN (4 kips) over a 254 mm × 254 mm (10 in. × 10 in.) area for steering load and two footprints of 35.6 kN (8 kips) over 508 mm × 254 mm (20 in. × 10 in.) for rear load. Additionally, dynamic allowance for general fatigue and fracture limit state of 15% increase was used. For comparison purposes, higher factors, such as 75% with additional factor of 1.3, were not considered in order not to exceed yielding limit.
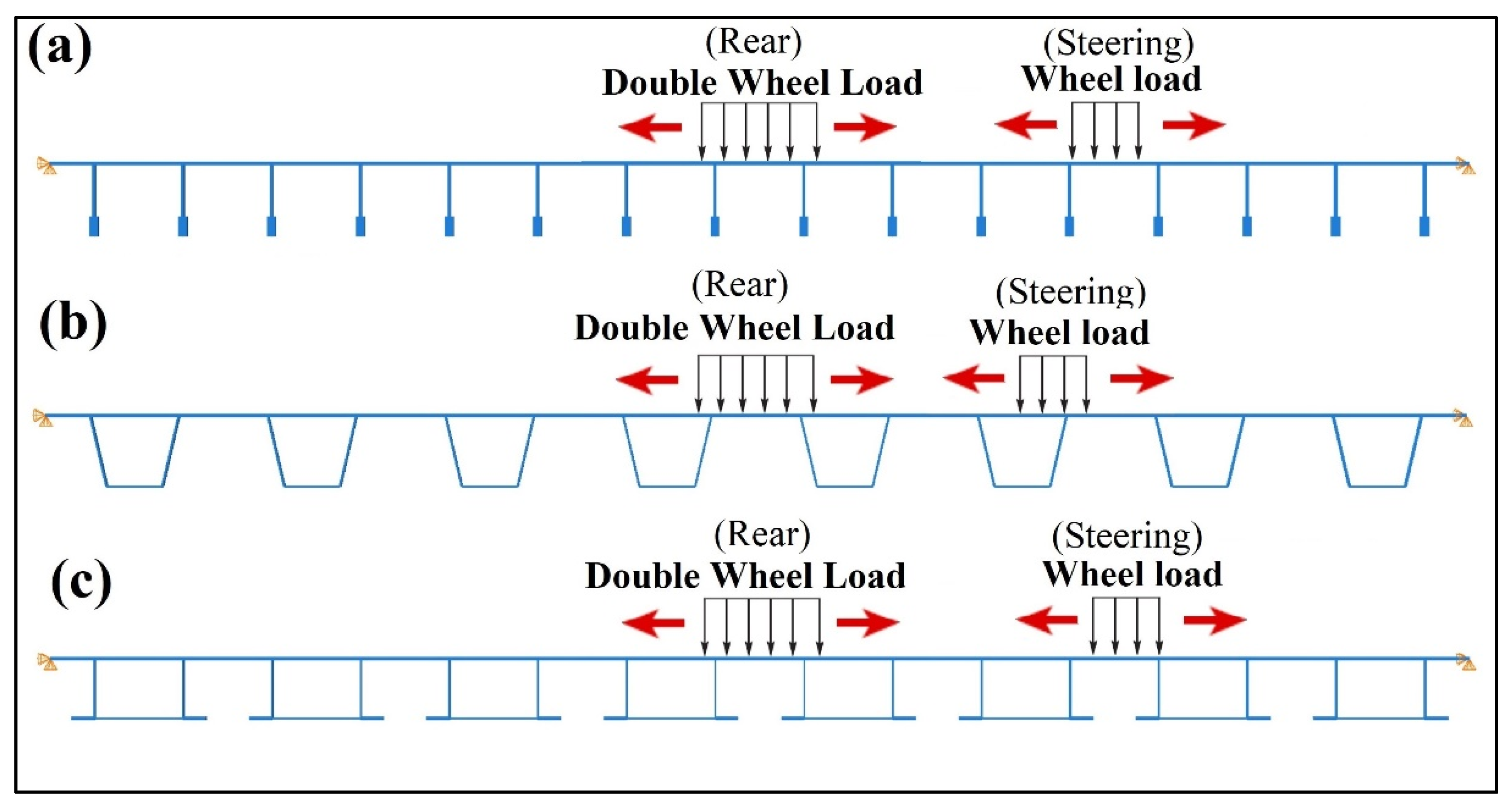
Transverse bending moments in the deck around the rib-to-deck weld is one of the main sources of stress concentration at the weld root and toe. Other stress concentrations occur due to direct wheel loading and geometric irregularity at diaphragms and floor-beams. In order to find the optimal location that results in the highest localized bending moment, two-dimensional frame influence line analysis has been carried out for each deck section. ABAQUS two-dimensional beam elements, type B23, were used with a 12.7 mm (0.5 in.) uniform element size. Frame vertical and horizontal translations were restrained at the far ends, and a moving distributed load was applied along the deck.
Figure 6 shows the loaded assembly (with rendered beam thickness) for each of the three sections. Note that the steering load patches were applied separately. In particular, the distributed load length was 254 mm (10 in.) and 508 mm (20 in.) for the steering (single wheel) and rear (double wheel) cases, respectively.
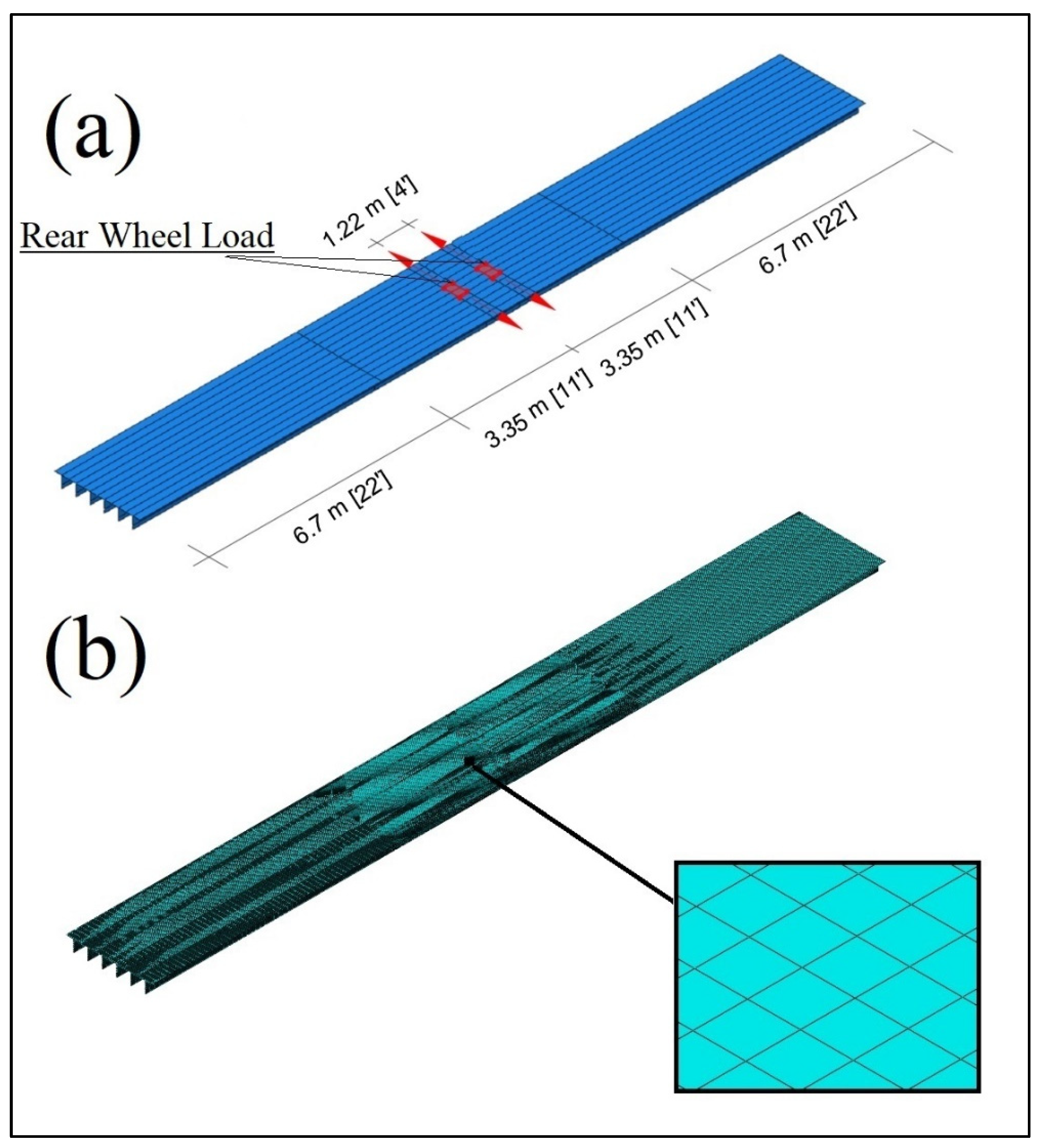
For a more accurate analysis and comparison, three-dimensional simulations of the different decks covering three spans were conducted using shell elements. The decks were loaded by uniformly distributed surface pressures positioned in the middle of the second span to create the highest positive bending moment on the deck. Both steering and rear tire patch loads were considered separately. Moreover, several load positions across the deck panels were analyzed.
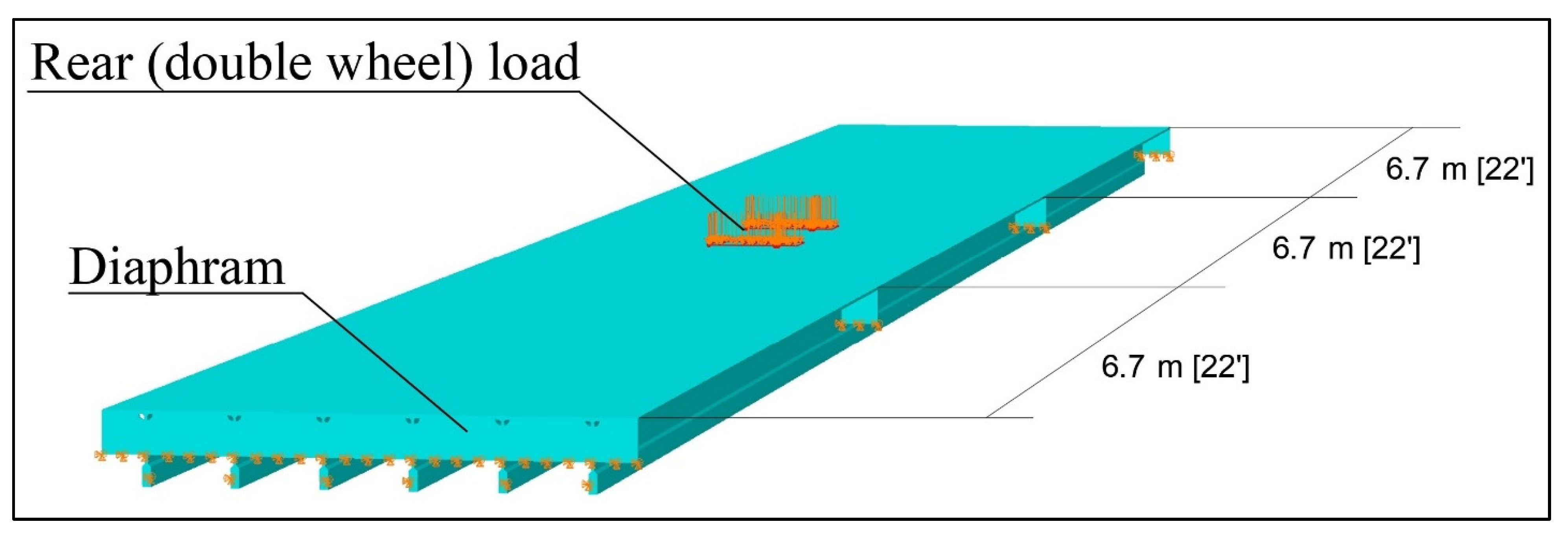
Figure 7a shows the rear load assembly of the three-span orthotropic bulb deck, in which six bulb ribs were assumed across the width (three ribs were assumed for the closed-rib sections). ABAQUS three-dimensional four-node shell elements, type S4, were used with a 50.8 mm (2 in.) uniform element size, as shown in
Figure 7b.
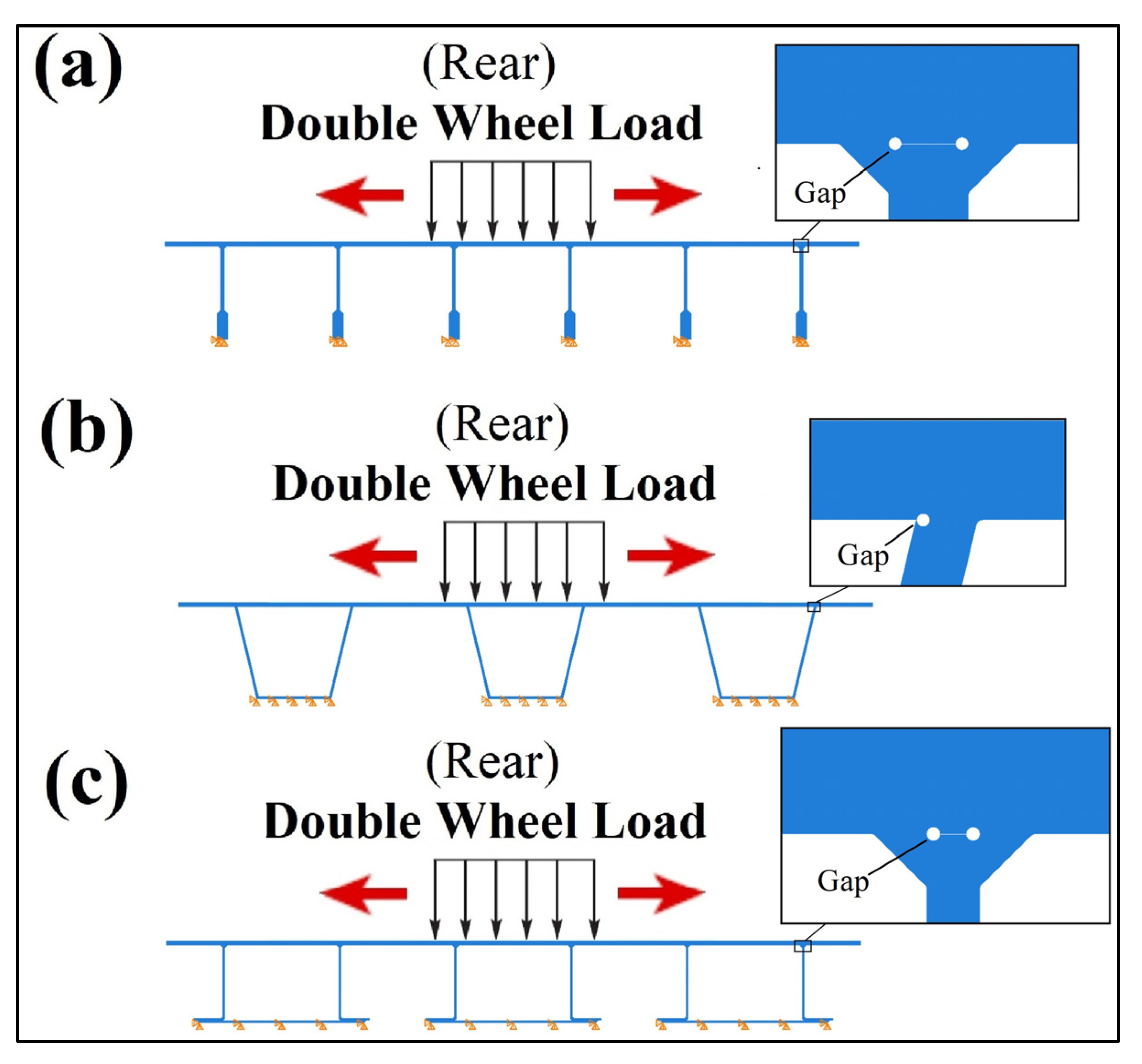
To study the stress concentration at the different welded joints, plane strain simulations were conducted using detailed models of the welded connections. These simulations also help finding optimal loading locations considering connection details.
Figure 8 shows the load assembly for each of the three sections. In particular, each model has been loaded with steering and rear loads at different positions to achieve the highest possible stress at the welded joints. Additionally, the rib translations were restrained at the bottom surface to allow local bending. Moreover, welds details have been considered for each section assuming a full gap between the web and top plate for fillet weld, and 20% gap in the web for grove weld. Weld sizes were 10 mm (3/8 in.) for the double fillet, 10 mm (3/8 in.) for the groove and 8 mm (5/16 in.) for the double fillet used for the bulb, trapezoidal and built-up sections, respectively (see
Figure 5 in
Section 3).
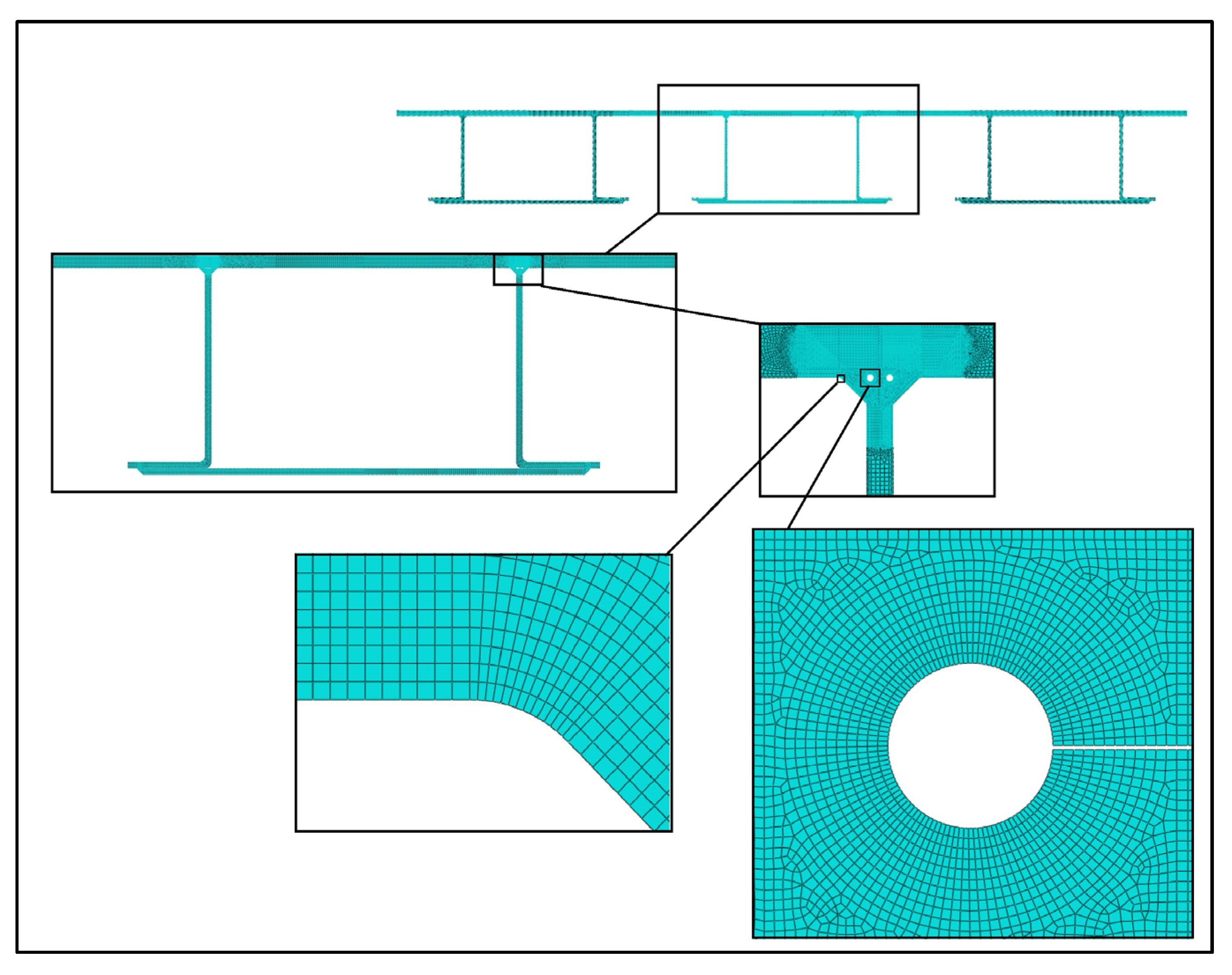
ABAQUS 4-node CPE4 and 3-node CPE3 plane strain continuum elements were used with various sizes that start at 0.127 mm (0.005 in.) for the region adjacent the joints and increases to 1.27 mm (0.05 in.) in the areas around the connection as seen in
Figure 9. The refinement around the joint was made to assure an accurate stress distribution. Weld root and toe details and meshing guidelines as developed by Hobbacher [
26] were considered. In particular, a notch radius of 1.016 mm (0.04 in.) was used for the weld toes and the weld roots consisted of 360° keyhole arcs. Further mesh refinement at the weld arcs were considered to satisfy the minimum recommended number of elements (i.e., 5 at toe’s arc and 40 at the root’s arc).
The above frame, shell and plane strain analyses were used to guide a series of three-dimensional continuum simulations that include extensive detail for better comparisons between the three deck sections. In particular, both three-span and two-span deck models were constructed and subjected to the various load cases shown in
Figure 10 as follows: (i) In case 1, three-span decks were loaded by distributed surface pressures at the middle of the intermediate span, providing maximum positive bending moment in the deck. Both steering and rear loads were considered separately and applied at positions where the highest stress concentration at a panel/rib connection is expected (positions obtained from previous analyses). This includes three load positions for case I, i.e., REI position where the rear tire load footprint starts at the panel/rib connection and is directed to the inside region of a closed rib; the RC position where the rear tire load footprint is centered on the panel/rib connection axis; and the SI position where the steering tire patch footprint center is located at 42% of the web spacing away from the panel/rib connection (inside closed rib region).
Figure 11 shows load case 1, including supports and the applied REI rear load patch on the three-span bulb deck; (ii) Case 2 configurations are similar to case 1, but is applied only to the decks with closed ribs (trapezoidal and built-up ribs). The wheel load position in case 2 was selected to develop the highest expected tension stress adjacent the weld root/toe inside of the closed rib (unreachable from outside). Hence, two positions for case II were considered, i.e., the REO position where the rear load tire footprint starts at the panel/rib connection and extends to the outside region of a closed rib; and the SO position where the steering load tire footprint center is located at 42% of the web spacing from panel/rib connection (outside closed rib region); (iii) Case 3 considers the orthotropic decks covering two spans, with rear tire patch loads located at 2.84 m (112 in.) from the intermediate floor-beam to create the highest negative bending moment in the deck (i.e., at 42% of span length). Wheel load positions were similar to case 1 counterparts (i.e., REI and RC positions); (iv) Finally, cases 4 and 5 had similar configurations to case 3, but the wheel loads were applied directly above an intermediate floor-beam. Case 4 is intended to simulate a rear axle sitting straddling a floor-beam, whereas case 5 examines the case when rear tire load footprint is directly above the floor-beam.
The 5 cases were simulated using ABAQUS eight-node C3D8 and six-node C3D6 three-dimensional continuum elements with sizes that varied from 1.27 mm (0.05 in.) at the joint of the rib under the wheel load to 12.7 mm (0.5 in.) in the area around it.
Figure 12 shows part of the three-dimensional continuum mesh of the three deck sections where wedge elements (six-node) were used to enlarge the mesh size around the joints. Moreover, the weld toe and root recommended notch radius and element size were considered similar to plane strain simulations.
5. Results and Comparisons
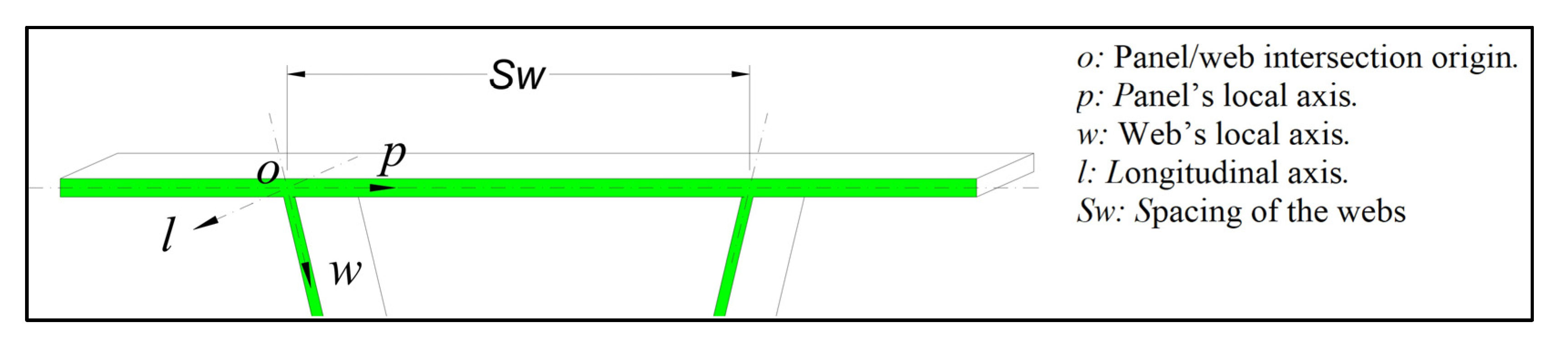
To facilitate the discussion of the results, local axes of the panel and web are defined in
Figure 13, where
o,
p,
w,
l and
Sw are the panel/web intersection origin, the panel’s local axis, the web’s local axis, the longitudinal axis and spacing of the webs, respectively. Influence line analyses showed that the optimal wheel load location resulting in a maximum local bending moment (about
l axis) in the web (M
W) to local panel’s bending moment (M
P) ratio for closed ribs was found when the center of the steering wheel load is located at 0.42
Sw away from the joint center
o, and when the rear wheel load edge is located at the joint (
o). Other less critical load locations were noted as well.
Table 1 shows comparisons between M
W/M
p as well as the normalized maximum deflections between the three deck types. It should be noted that the bulb web has a zero-local moment as expected in a two-dimensional analysis, which reduces the stress at the panel/web connection and gives it an advantage over the other sections. However, closed-rib decks benefit from additional stiffness that reduces the deflection, and hence allows for a reduction in panel thickness.
The results from the frame analyses show an advantage for the bulb rib deck over the closed sections in the distribution of local bending moment. However, open sections have lower torsional stiffness and lateral buckling capacity that may limit bending strength. Hence, open-rib sections may still experience local bending in the rib webs, and three-dimensional shell analyses were necessary for more accurate bending comparisons.
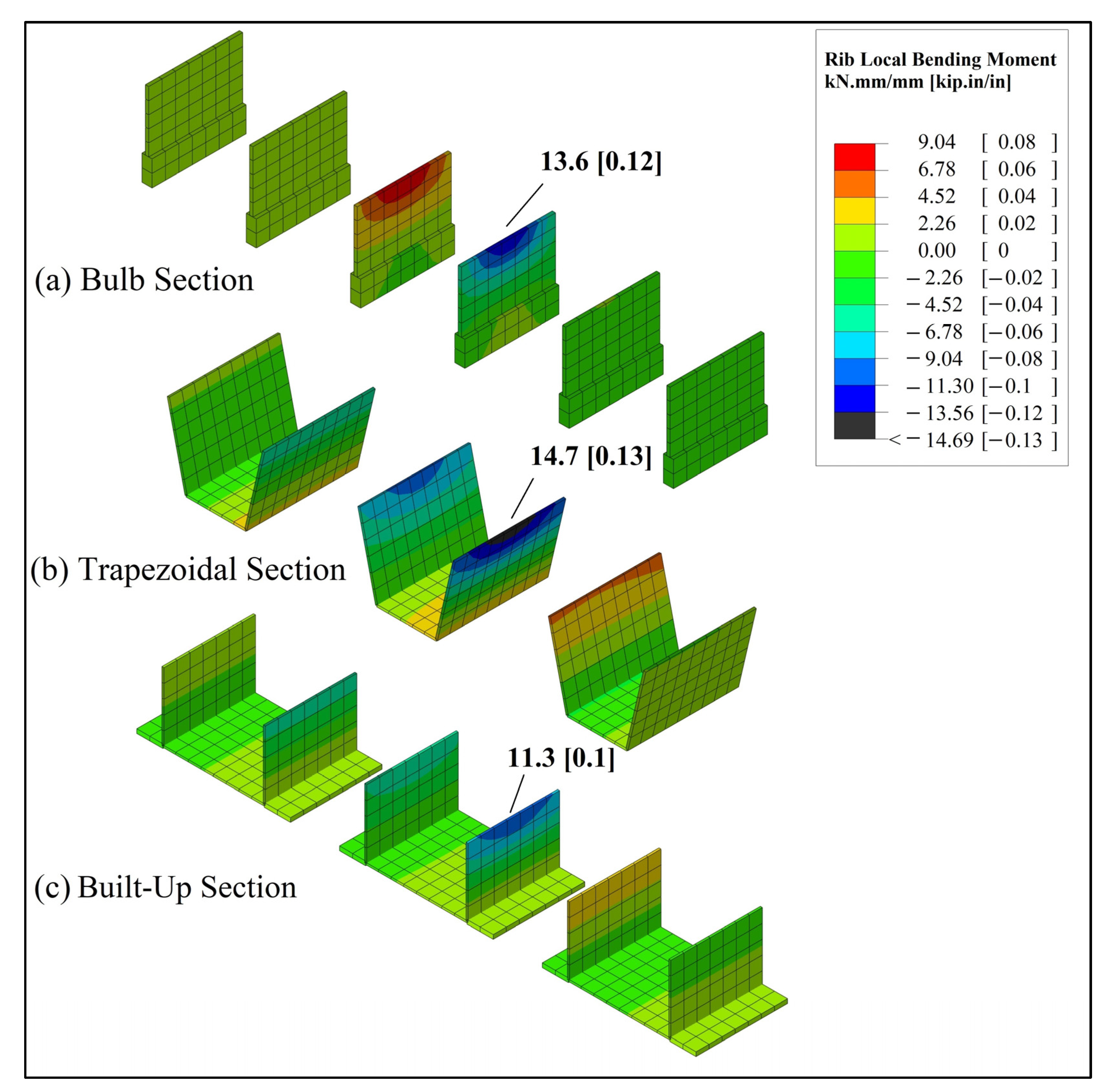
Figure 14 compares the local bending moment distribution for the three ribs at a wheel load footprint location, which generates the peak localized moments. It is observed that the highest local bending was generated in the trapezoidal section with a value of 14.7 kN·mm/mm (0.13 kip.in./in.), followed by the bulb section with a maximum moment of 13.6 kN·mm/mm (0.12 kip.in./in.), and the smallest belonged to the built-up section with a local moment of 11.3 kN·mm/mm (0.1 kip.in./in.) Moreover,
Table 2 compares between the maximum web’s local bending moment (Mw) of the three sections in both the steering and rear wheel loading cases. The open-rib bulb section has a significant local bending moment in the web despite being assumed free from local flexural stresses. Still, the local bending moment distribution and rib thickness/stiffness are related.
Local stress concentrations maybe used to evaluate fatigue life. The stress distribution due to local bending in the deck, considering the fine detail of the welded connections were obtained from plane strain simulations with a wheel load directly above the rib.
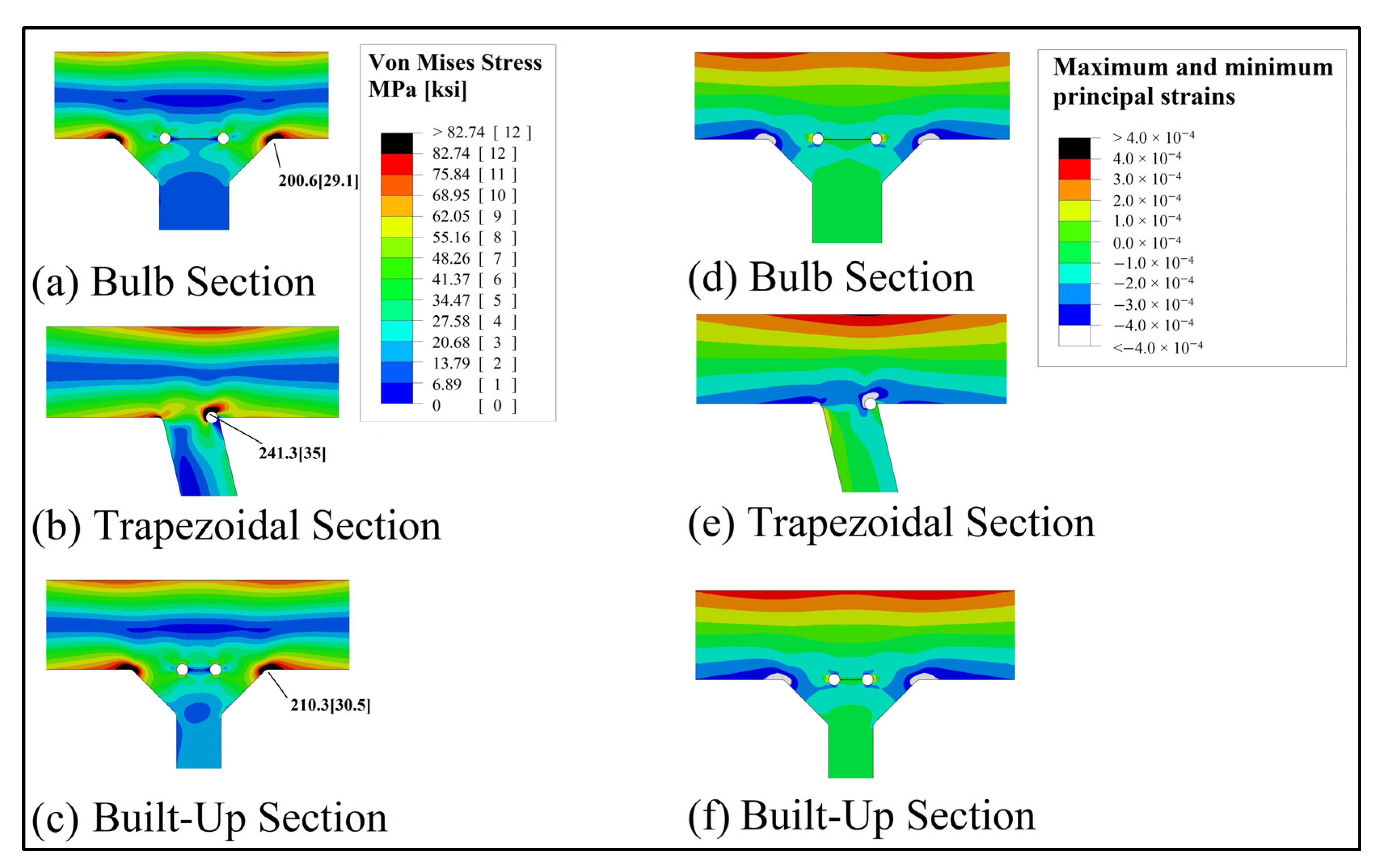
Figure 15 shows stresses and strains of the plane strain analysis that results in highest stresses at joints for each deck section. In particular,
Figure 15a–c show the Von Mises stress distribution at the welded joints for the bulb, trapezoidal and built-up sections, respectively.
Figure 15d–f show the maximum and minimum principal strains at the joint for the bulb, trapezoidal and built-up sections, respectively. The above results are obtained when the rear load footprint is centered on the web’s axis (RC position).
The maximum stress concentration is generated at the weld root in the trapezoidal section and at the toes of the bulb and built-up sections. Moreover, the maximum stresses from each section are tabulated in
Table 3 for steering and rear wheel load cases. Although the absolute applicability of the plane strain analysis may be debated, the significant difference between the sections stresses remains. Bulb and built-up sections have relatively lower maximum stresses as compared to the trapezoidal section. Plane strain analysis also predicts optimal load locations that may result in the highest stress concentration for three-dimensional simulations.
A better comparison between deck sections was accomplished using three-dimensional continuum simulations.
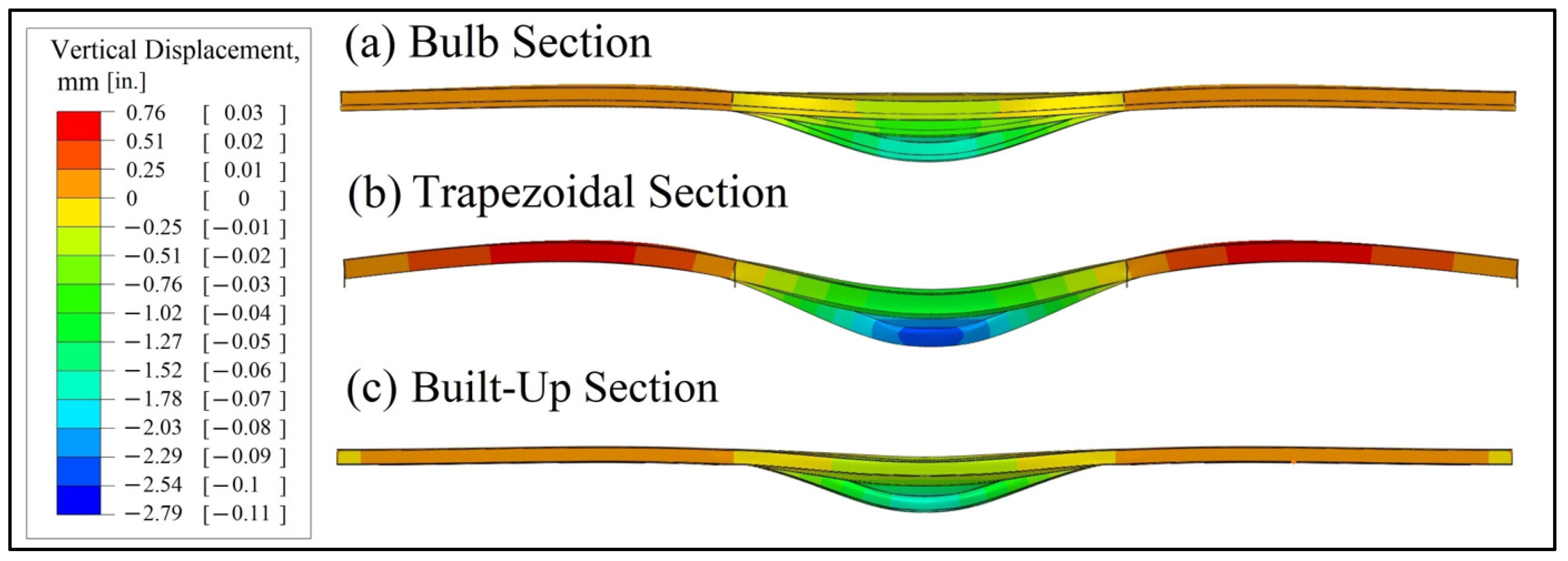
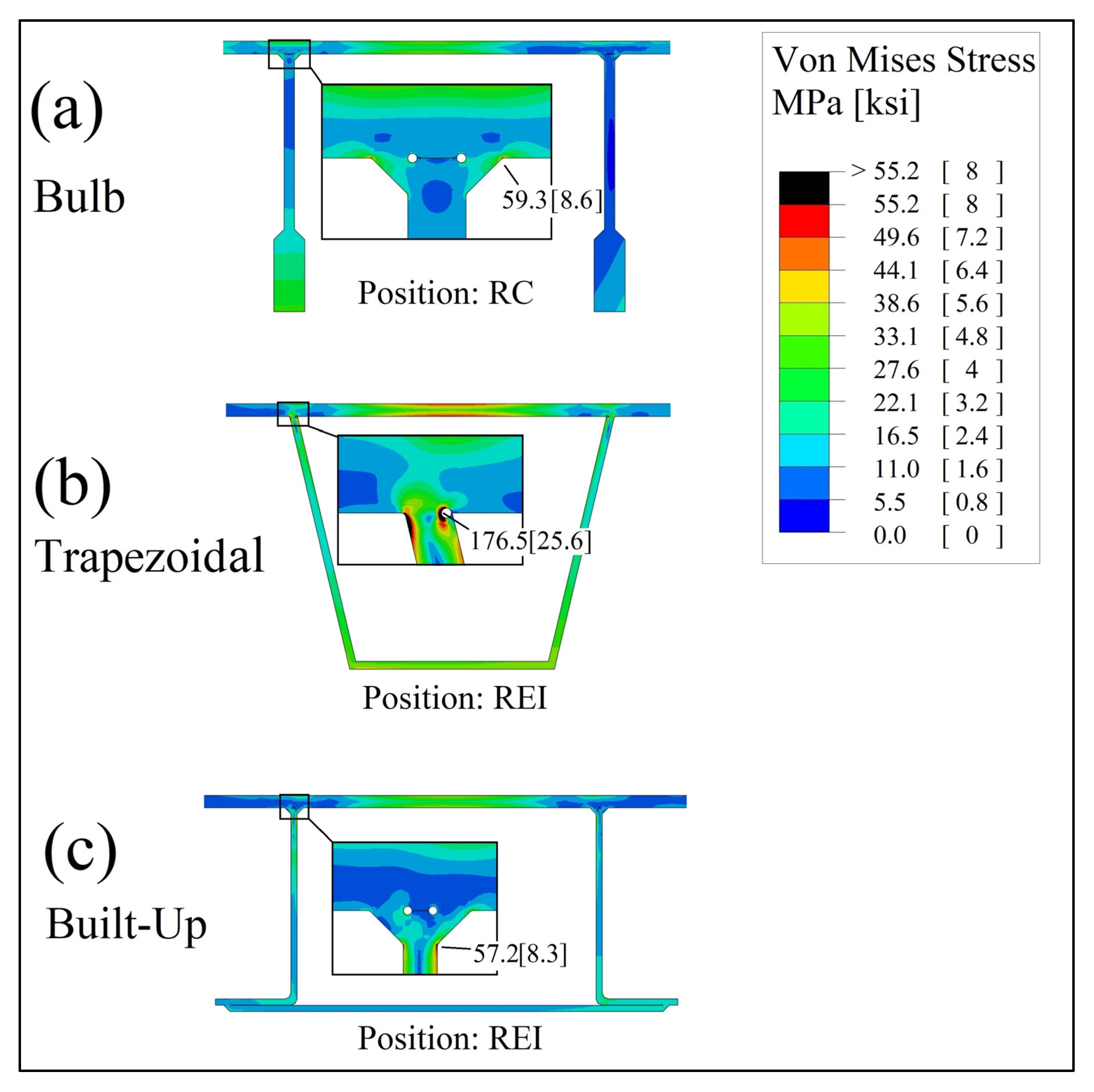
Figure 16 shows the deflected shape for each deck type under REI rear wheel loads as defined in case 1. The trapezoidal section had a vertical deflection of 2.67 mm (0.105 in.) which was larger than both the deflection of the bulb (1.96 mm [0.077 in.]) and built-up (1.88 mm [0.074 in.]) sections. Similarly, comparisons of the Von Mises stress distribution and maximum stress concentration are shown in
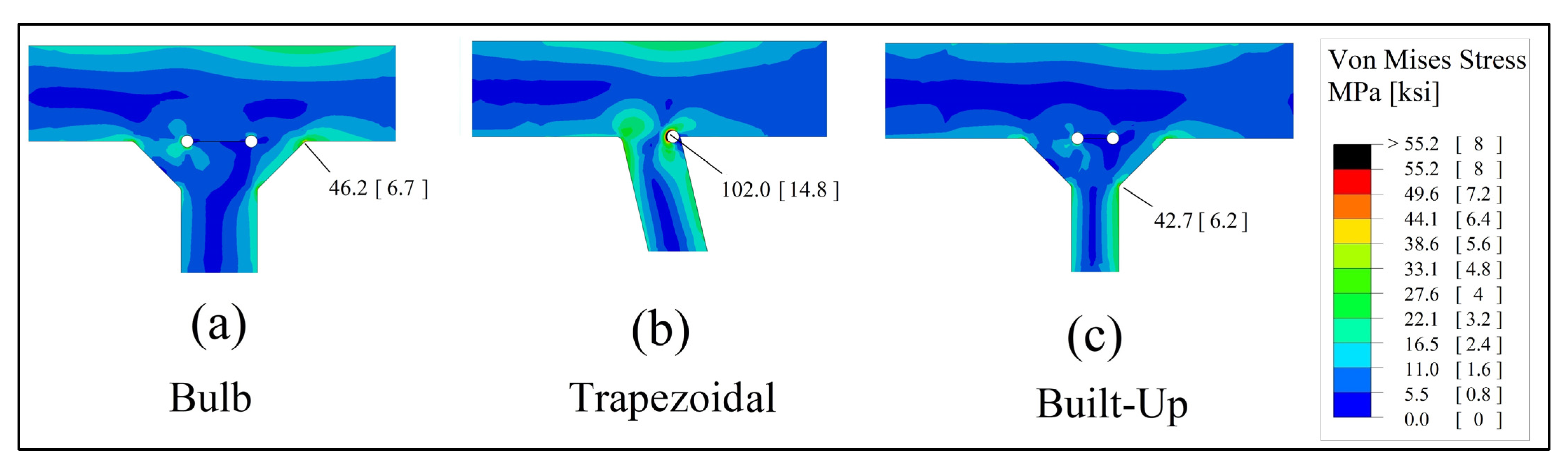
Figure 17 for load case 1 under rear load (showing distributions from cases with higher maximum stress among REI and RC positions). The maximum stress was 176.5 MPa (25.6 ksi) at the weld root of the trapezoidal section, whereas the maximum stresses for the bulb and built-up sections at the weld toe were 59.3 MPa (8.6 ksi) and 57.2 MPa (8.3 ksi), respectively. On the other hand,
Figure 18 shows the stress distribution at the welded connection under the steering wheel load for the three deck sections for load case 1 (SI position). The maximum stresses followed a similar pattern, with 102 MPa (14.8 ksi), 46.2 MPa (6.7 ksi) and 42.7 MPa (6.2 ksi) for the trapezoid, bulb and built-up sections, respectively.
Case 2 was exclusive for closed-rib sections (trapezoidal and built-up), in which the load was applied to create tension stress at the inside side of the welded connection (unobservable from outside).
Figure 19 shows a comparison between the trapezoidal and built-up sections under rear and steering loads in case 2. In particular, Von Mises stress distributions are shown in
Figure 19a,b for rear load, as well as
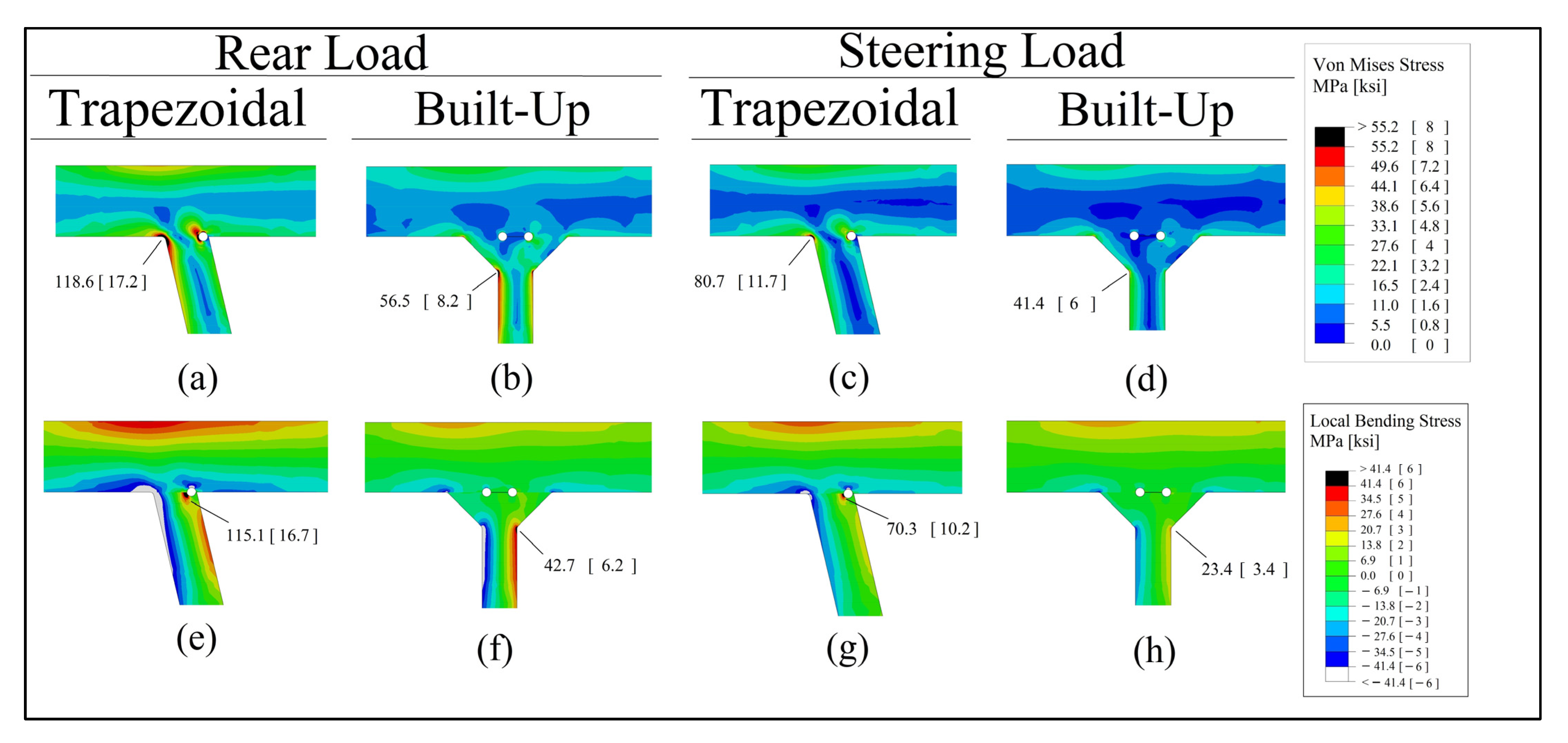
Figure 19c,d for steering load. In both cases, the trapezoidal section had higher stress concentration than the built-up section, with maximum stress concentrations of 118.6 MPa (17.2 ksi) and 80.7 MPa (11.7 ksi) at the weld toe for rear and steering load cases, respectively. On the other hand, the built-up section had stress concentrations of 56.5 MPa (8.2 ksi) and 41.4 MPa (6 ksi) for rear and steering load cases, respectively. The stress concentration values were comparable but lesser than case 1, as expected. However, this case was used to compare the local bending tension stress inside the closed rib which is shown in
Figure 19e,f for rear load, along with
Figure 19g,h for steering load. For both loads, the trapezoidal section had larger local bending tensional stress than the built-up counterpart, with maximum stress of 115.1 MPa (16.7 ksi) and 70.3 MPa (10.2 ksi) at the weld root for rear and steering load cases, respectively. By comparison, the built-up section had maximum tension stresses of 42.7 MPa (6.2 ksi) and 23.4 MPa (3.4 ksi) at the weld toe for rear and steering load cases, respectively.
Case 3 was intended to examine the response under the largest negative bending moment at an intermediate support where only rear wheel load was applied.
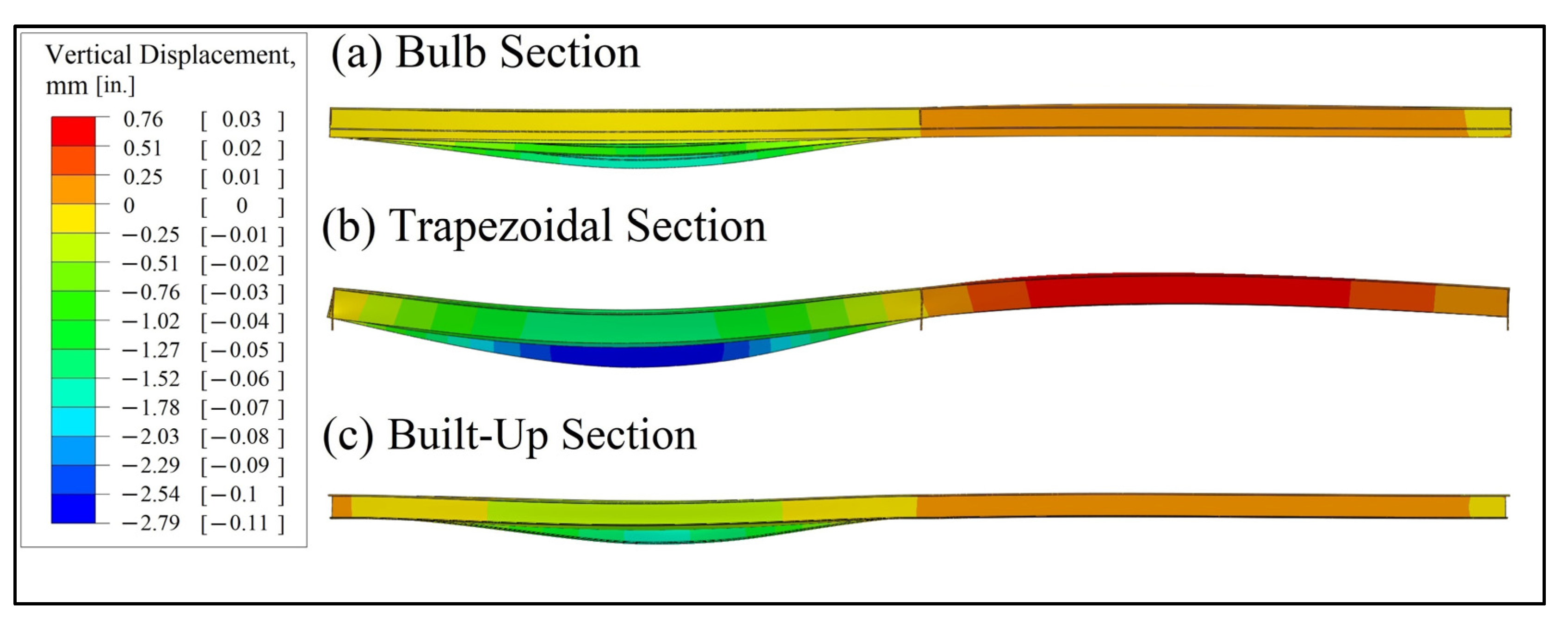
Figure 20 shows the deflected shapes of the three sections. The trapezoidal section had a maximum vertical deflection of 2.95 mm (0.116 in.), larger than either the deflection of the bulb (1.57 mm [0.062 in.]) or built-up (1.22 mm [0.048 in.]) sections.
Figure 21 shows Von Mises stress distribution comparisons at the intermediate floor-beam axis and at 254 mm (10 in.) away from the floor-beam for the three rib sections for cases with maximum stress concentrations. At the floor-beam, the bulb and trapezoidal sections need a diaphragm to transfer the load. The local stresses for those section at the weld details which connect the diaphragm and the ribs are presented in
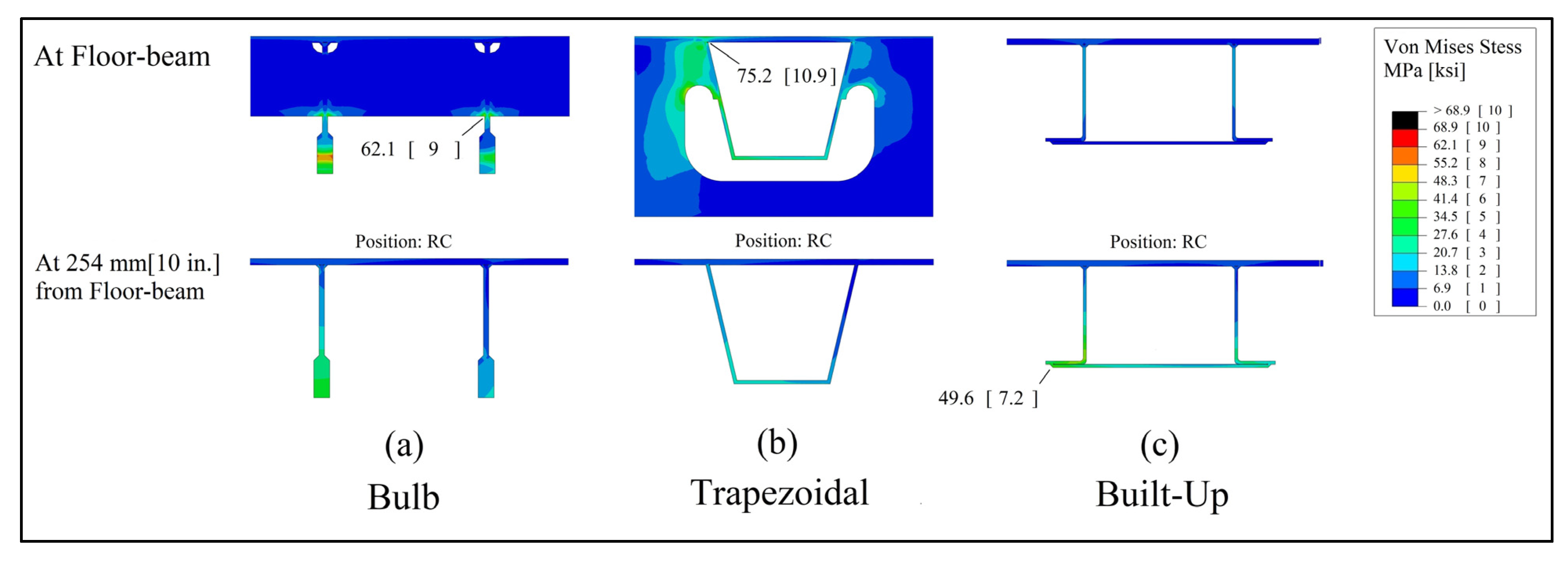
Figure 21. In particular, the trapezoidal and bulb sections had maximum stresses of 75.1 MPa (10.9 ksi) and 62 MPa (9 ksi) at the rib/diaphragm connection, respectively. The built-up section, however, had much lower stresses as it was supported directly on the floor-beam flange. On the other hand, at 254 mm (10 in.) away from the floor-beam, the built-up section had a slightly higher stress 49.6 MPa (7.2 ksi) as compared to the bulb and trapezoidal sections.
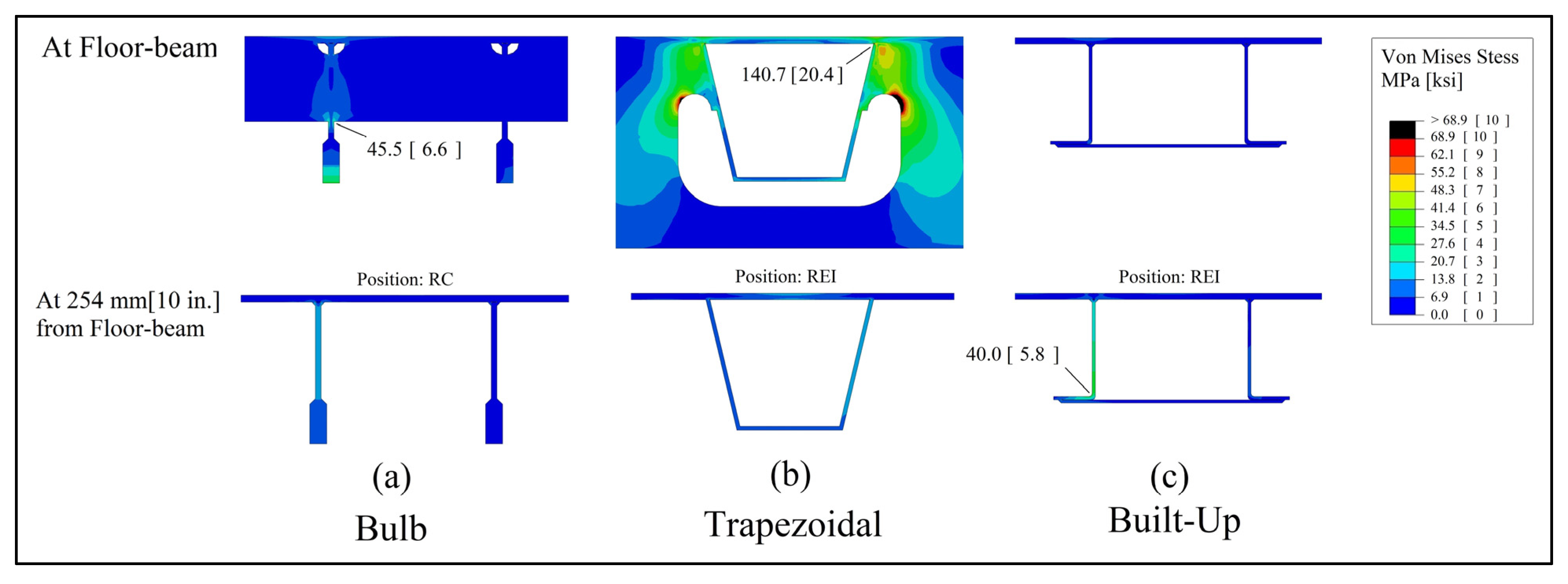
Direct loading from the rear wheels, where the tandem axle was directly above the floor-beam (wheel footprints are 609 mm [2 ft] away from each side), was analyzed in case 4. This loading created high stresses at the rib/diaphragm connection for the bulb and trapezoidal sections.
Figure 22 shows the Von Mises stress distributions for each of the decks in case 4 at the intermediate floor-beam and at 254 mm (10 in.) away from the beam axis. The trapezoidal section had the highest stresses with a maximum of 140.6 MPa (20.4 ksi), followed by the open bulb deck with maximum stress of 45.5 MPa (6.6 ksi). On the other hand, the built-up section had significantly smaller stresses adjacent to the floor-beam. Moreover, case 5 presents another critical loading scenario of direct loading at floor-beam where one of the rear footprints is directly above floor-beam axis. The Von Mises stress distributions for three decks at the intermediate floor-beam at 254 mm (10 in.) away from the beam’s axis (on the side of the other rear footprint) are shown in
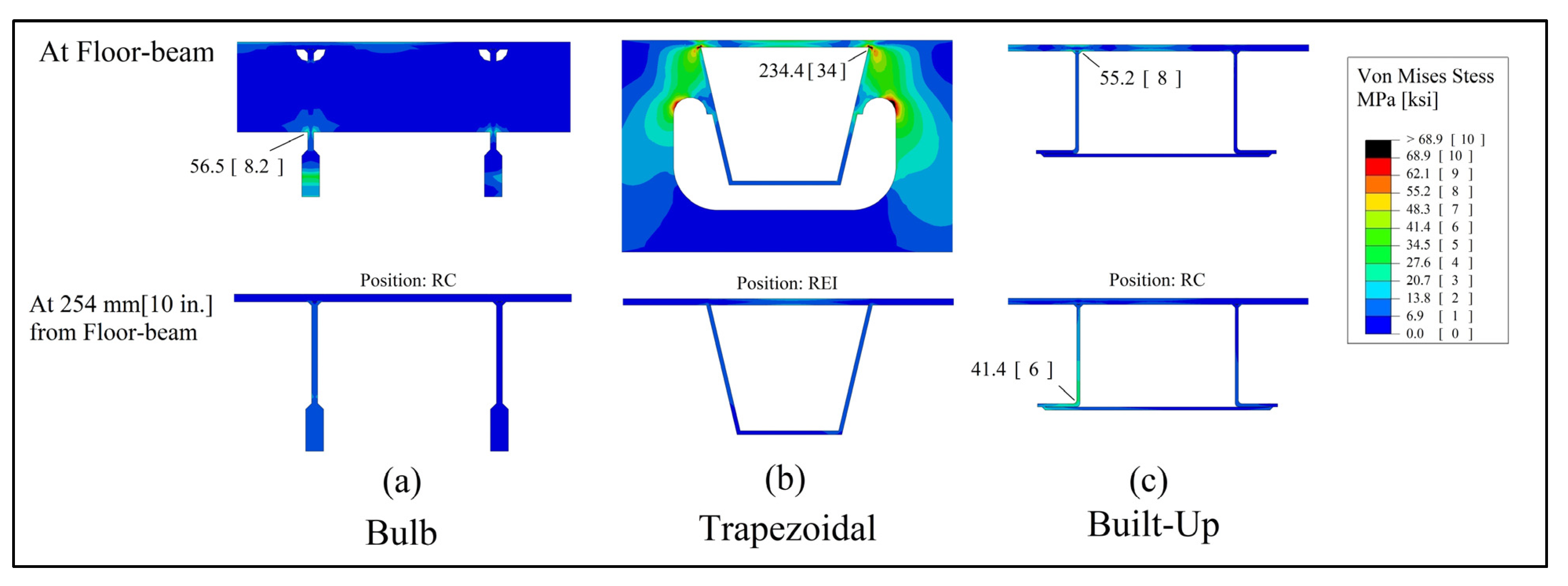
Figure 23 for case 5. Similar to the previous case, the trapezoidal section had the maximum stress concentration of 234.4 MPa (34 ksi), which was followed by the bulb section at 56.5 MPa (8.2 ksi), then the built-up section at 55.2 MPa (8 ksi).
Table 4 summarizes the maximum Von Mises stress concentrations at the weld connections for all four load cases using the three-dimensional continuum simulations. It may be noticed that the built-up section had a clear advantage considering the stress concentrations which may be used as an indicator of fatigue life.