Optimizing Design Parameters of PLA 3D-Printed Scaffolds for Bone Defect Repair
Abstract
:1. Introduction
2. Materials and Methods
2.1. CAD Design
2.2. Finite Element Simulations of Compression Testing
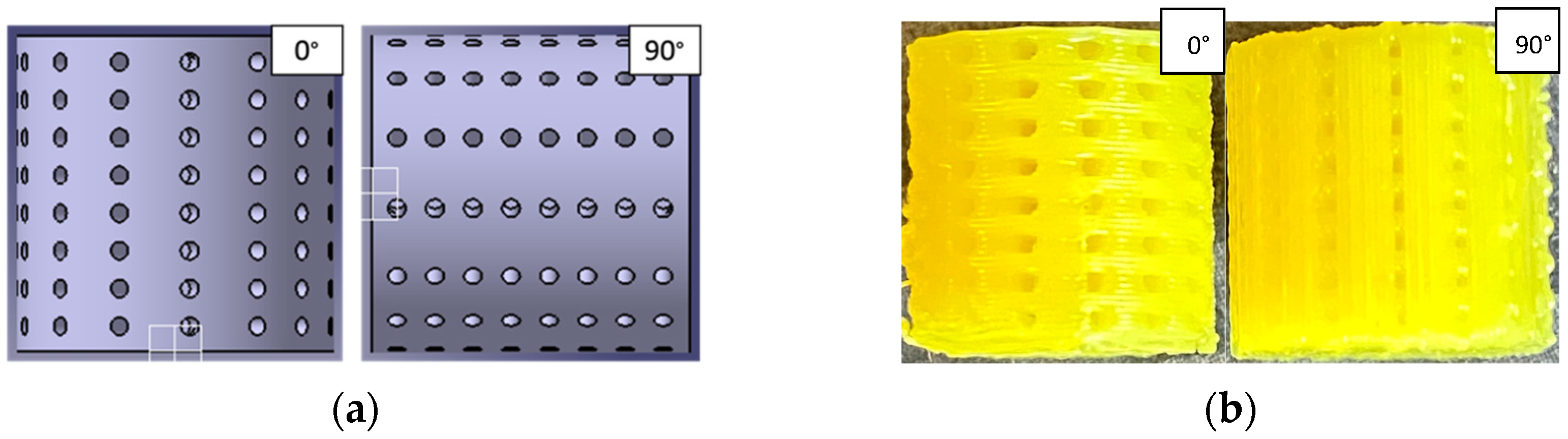
2.3. Printing and Experimental Compression Testing
2.4. Analysis
2.4.1. Simulations
2.4.2. Experimental Testing
2.4.3. Statistical Analyses
3. Results
3.1. Results from Simulations
3.2. Results from Experimental Testing
3.2.1. Printing
3.2.2. Experimental Testing
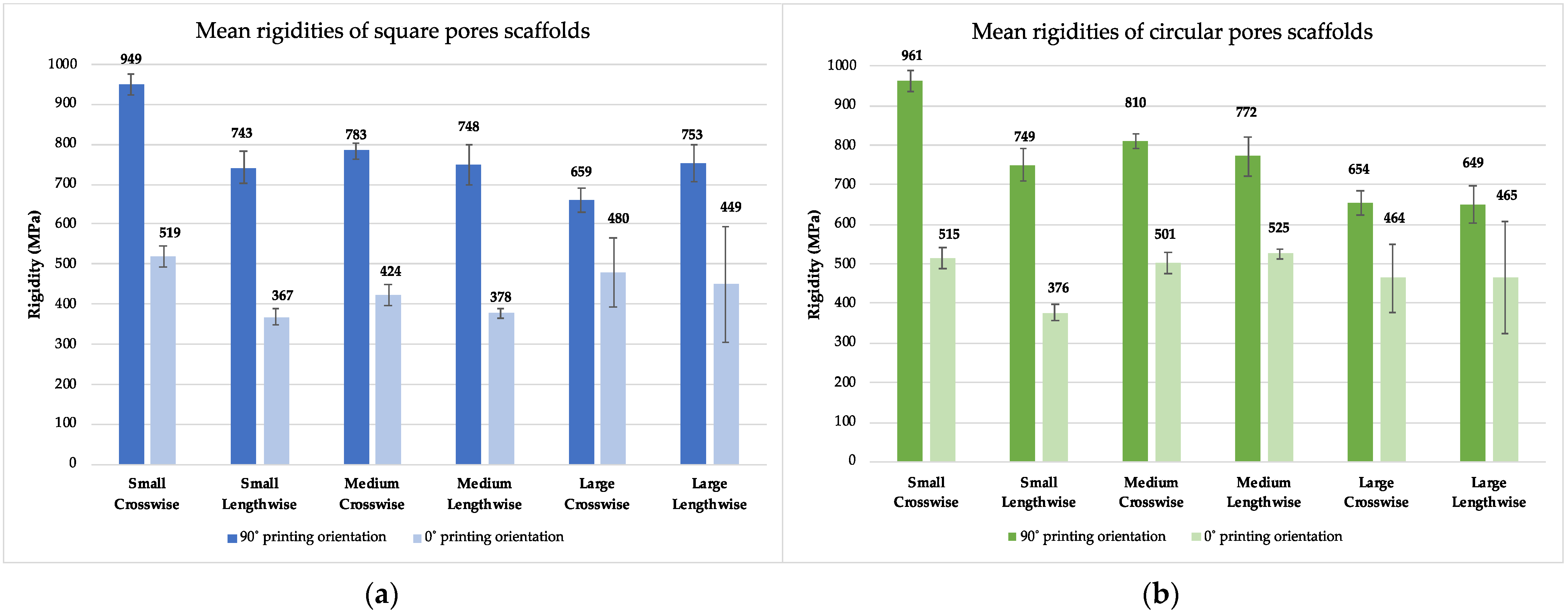
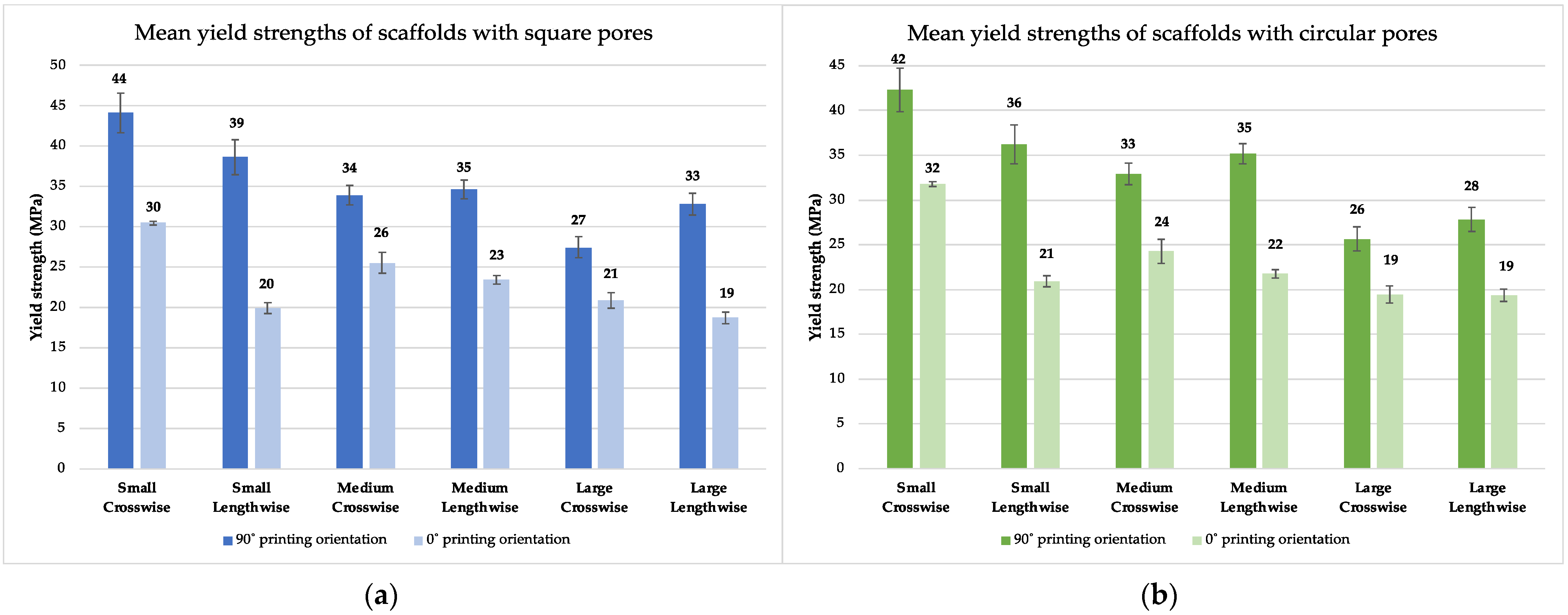
3.3. Comparative Analysis of Rigidity and Yield Strength
4. Discussion
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fairag, R.; Rosenzweig, D.H.; Ramirez-Garcialuna, J.L.; Weber, M.H.; Haglund, L. Three-Dimensional Printed Polylactic Acid Scaffolds Promote Bone-like Matrix Deposition in Vitro. ACS Appl. Mater. Interfaces 2019, 10, 15306–15315. [Google Scholar] [CrossRef] [PubMed]
- Baptista, R.; Guedes, M. Morphological and Mechanical Characterization of 3D Printed PLA Scaffolds with Controlled Porosity for Trabecular Bone Tissue Replacement. Mater. Sci. 2021, 118, 111528. [Google Scholar] [CrossRef] [PubMed]
- Roseti, L.; Parisi, V.; Petretta, M.; Cavallo, C.; Desando, G.; Bartolotti, I.; Grigolo, B. Scaffolds for Bone Tissue Engineering: State of the Art and New Perspectives. Mater. Sci. Eng. C 2017, 78, 1246–1262. [Google Scholar] [CrossRef] [PubMed]
- O’Keefe, R.J.; Mao, J. Bone Tissue Engineering and Regeneration: From Discovery to the Clinic—An Overview. Tissue Eng. Part B Rev. 2011, 17, 389–392. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oladapo, B.I.; Zahedi, S.A.; Adeoye, A.O.M. 3D Printing of Bone Scaffolds with Hybrid Biomaterials. Compos. Part B 2019, 158, 428–436. [Google Scholar] [CrossRef]
- Su, X.; Wang, T.; Guo, S. Applications of 3D Printed Bone Tissue Engineering Scaffolds in the Stem Cell Field. Regen. Ther. 2021, 16, 63–72. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yang, G.; Johnson, B.N.; Jia, X. Three-Dimensional (3D) Printed Scaffold and Material Selection for Bone Repair. Acta Biomater. 2019, 84, 16–33. [Google Scholar] [CrossRef]
- Murphy, S.V.; Atala, A. 3D Bioprinting of Tissues and Organs. Nat. Biotechnol. 2014, 32, 773–785. [Google Scholar] [CrossRef]
- Dong, Q.; Zhang, M.; Zhou, X.; Shao, Y.; Li, J.; Wang, L.; Chu, C.; Xue, F.; Yao, Q.; Bai, J. 3D-Printed Mg-Incorporated PCL-Based Scaffolds: A Promising Approach for Bone Healing. Mater. Sci. 2021, 129, 112372. [Google Scholar] [CrossRef]
- Boskey, A.L.; Roy, R. Cell Culture Systems for Studies of Bone and Tooth Mineralization. Chem. Rev. 2008, 108, 4716–4733. [Google Scholar] [CrossRef] [Green Version]
- Turnbull, G.; Clarke, J.; Picard, F.; Riches, P.; Jia, L.; Han, F.; Li, B.; Shu, W. 3D Bioactive Composite Scaffolds for Bone Tissue Engineering. Bioact. Mater. 2018, 3, 278–314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, B.; Wang, L.; Song, P.; Pei, X.; Sun, H.; Wu, L.; Zhou, C.; Wang, K.; Fan, Y.; Zhang, X. 3D Printed Bone Tissue Regenerative PLA/HA Scaffolds with Comprehensive Performance Optimizations. Mater. Des. 2021, 1, 109490. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, W.; Wu, S.; Kuss, M.; Jiang, X.; Untrauer, J.B.; Reid, S.P.; Duan, B. 3D Printed Composite Scaffolds with Dual Small Molecule Delivery for Mandibular Bone Regeneration. Biofabrication 2021, 12, 035020. [Google Scholar] [CrossRef] [PubMed]
- Bordea, I.R.; Candrea, S.; Alexescu, G.T.; Bran, S.; Băciuț, M.; Băciuț, G.; Lucaciu, O.; Dinu, C.M.; Todea, D.A. Nano-Hydroxyapatite Use in Dentistry: A Systematic Review. Drug Metab. Rev. 2020, 52, 319–332. [Google Scholar] [CrossRef] [PubMed]
- Stryker’s Spine Division Receives FDA Clearance for 3D-Printed Tritanium TL Curved Posterior Lumbar Cage. Available online: https://www.stryker.com/us/en/about/news/2018/stryker_s-spine-division-receives-fda-clearance-for-3d-printed-t.html (accessed on 21 June 2022).
- Haglund, L.; Ahanger, P.; Rosenzweig, D.H. Advancements in 3D Printed Scaffolds to Mimic Matrix Complexities for Musculoskeletal Repair. Curr. Opin. Biomed. Eng. 2019, 10, 142–148. [Google Scholar] [CrossRef]
- Polo-Corrales, L.; Latorre-Esteves, M.; Ramirez-Vick, J.E. Scaffold Design for Bone Regeneration. J. Nanosci. Nanotechnol. 2014, 14, 15–56. [Google Scholar] [CrossRef] [Green Version]
- Grémare, A.; Guduric, V.; Bareille, R.; Heroguez, V.; Latour, S.; L’heureux, N.; Fricain, J.-C.; Catros, S.; Le Nihouannen, D. Characterization of Printed PLA Scaffolds for Bone Tissue Engineering. J. Biomed. Mater. Res. Part A 2018, 106, 8. [Google Scholar] [CrossRef]
- Gregor, A.; Filova, E.; Novak, M.; Kronek, J.; Chlup, H.; Buzgo, M.; Blahnova, V.; Lukasova, V.; Bartos, M.; Necas, A.; et al. Designing of PLA Scaffolds for Bone Tissue Replacement Fabricated by Ordinary Commercial 3D Printer. J. Biol. Eng. 2017, 11, 31. [Google Scholar] [CrossRef] [Green Version]
- Velioglu, Z.B.; Pulat, D.; Demirbakan, B.; Ozcan, B.; Bayrak, E.; Erisken, C. 3D-Printed Poly(Lactic Acid) Scaffolds for Trabecular Bone Repair and Regeneration: Scaffold and Native Bone Characterization. Connect. Tissue Res. 2019, 60, 274–282. [Google Scholar] [CrossRef]
- Holzapfel, B.M.; Rudert, M.; Hutmacher, D.W. Gerüstträgerbasiertes Knochen-Tissue-Engineering. Orthopedics 2017, 46, 701–710. [Google Scholar] [CrossRef]
- Leukers, B.; Gülkan, H.; Irsen, S.H.; Milz, S.; Tille, C.; Schieker, M.; Seitz, H. Hydroxyapatite Scaffolds for Bone Tissue Engineering Made by 3D Printing. J. Mater. Sci. Mater. Med. 2005, 16, 1121–1124. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Zhao, H.; Chen, K.-M.; Li, X.-S.; Gao, M.; Zhou, J.; Ma, X. The Preliminary Performance Study of the 3D Printing of a Tricalcium Phosphate Scaffold for the Loading of Sustained Release Anti-Tuberculosis Drugs. J. Mater. Sci. 2014, 50, s10853–s014. [Google Scholar] [CrossRef]
- Esposito Corcione, C.; Gervaso, F.; Scalera, F.; Padmanabhan, S.K.; Madaghiele, M.; Montagna, F.; Sannino, A.; Licciulli, A.; Maffezzoli, A. Highly Loaded Hydroxyapatite Microsphere/ PLA Porous Scaffolds Obtained by Fused Deposition Modelling. Thermophys. Asp. Funct. Ceram. Surf. 2019, 45, 2803–2810. [Google Scholar] [CrossRef]
- Wang, M.O.; Vorwald, C.E.; Dreher, M.L.; Mott, E.J.; Cinar, A.; Mehdizadeh, H.; Somo, S.; Dean, D.; Brey, E.M.; Fisher, J.P. Evaluating 3D Printed Biomaterials as Scaffolds for Vascularized Bone Tissue Engineering. Adv. Mater. 2016, 15, 138–144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, B.; Guo, L.; Chen, H.; Ventikos, Y.; Narayan, R.J. Finite Element Evaluations of the Mechanical Properties of Polycaprolactone/Hydroxyapatite Scaffolds by Direct Ink Writing: Effects of Pore Geometry. J. Mech. Behav. Biomed. Mater. 2020, 104, 103665. [Google Scholar] [CrossRef] [PubMed]
- Zeltinger, J.; Sherwood, J.K.; Graham, D.A.; Müeller, R.; Griffith, L.G. Effect of Pore Size and Void Fraction on Cellular Adhesion, Proliferation, and Matrix Deposition. Tissue Eng. 2001, 7, 557–572. [Google Scholar] [CrossRef]
- O’Brien, F.J.; Harley, B.A.; Yannas, I.V.; Gibson, L.J. The Effect of Pore Size on Cell Adhesion in Collagen-GAG Scaffolds. Biomaterials 2005, 26, 433–441. [Google Scholar] [CrossRef]
- Rosenzweig, D.H.; Carelli, E.; Steffen, T.; Jarzem, P.; Haglund, L. 3D-Printed ABS and PLA Scaffolds for Cartilage and Nucleus Pulposus Tissue Regeneration. Int. J. Mol. Sci 2015, 16, 15118–15135. [Google Scholar] [CrossRef] [Green Version]
- Yan, Y.; Chen, H.; Zhang, H.; Guo, C.; Yang, K.; Chen, K.; Cheng, R.; Qian, N.; Sandler, N.; Zhang, Y.S.; et al. Vascularized 3D Printed Scaffolds for Promoting Bone Regeneration. Biomaterials 2019, 190, 97–110. [Google Scholar] [CrossRef]
- Olubamiji, A.D.; Izadifar, Z.; Si, J.L.; Cooper, D.L.M.; Eames, B.F.; Chen, D.X. Modulating Mechanical Behaviour of 3D-Printed Cartilage-Mimetic PCL Scaffolds: Influence of Molecular Weight and Pore Geometry. Biofabrication 2016, 8, 025020. [Google Scholar] [CrossRef]
- Jeong, H.-J.; Gwak, S.-J.; Seo, K.D.; Lee, S.; Yun, J.-H.; Cho, Y.-S.; Lee, S.-J. Fabrication of Three-Dimensional Composite Scaffold for Simultaneous Alveolar Bone Regeneration in Dental Implant Installation. Int. J. Mol. Sci 2020, 21, 1863. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahangar, P.; Aziz, M.; Rosenzweig, D.H.; Weber, M.H. Advances in Personalized Treatment of Metastatic Spine Disease. Ann. Transl. Med. 2019, 7, 14. [Google Scholar] [CrossRef] [PubMed]
- Shuhua, W.; Qiaoli, X.; Fen, L.; Jinming, D.; Husheng, J.; Bingshe, X. Preparation and Properties of Cellulose-Based Carbon Microsphere/Poly(Lactic Acid) Composites. J. Compos. Mater. 2014, 48, 1297–1302. [Google Scholar] [CrossRef]
- Pitaru, A.A.; Lacombe, J.-G.; Cooke, M.E.; Beckman, L.; Steffen, T.; Weber, M.H.; Martineau, P.A.; Rosenzweig, D.H. Investigating Commercial Filaments for 3D Printing of Stiff and Elastic Constructs with Ligament-Like Mechanics. Micromachines 2020, 11, 846. [Google Scholar] [CrossRef] [PubMed]
- Cubo-Mateo, N.; Rodríguez-Lorenzo, L.M. Design of Thermoplastic 3D-Printed Scaffolds for Bone Tissue Engineering: Influence of Parameters of “Hidden” Importance in the Physical Properties of Scaffolds. Polymers 2020, 12, 1546. [Google Scholar] [CrossRef]
- Baptista, R.; Guedes, M. Porosity and Pore Design Influence on Fatigue Behavior of 3D Printed Scaffolds for Trabecular Bone Replacement. J. Mech. Behav. Biomed. Mater. 2021, 117, 104378. [Google Scholar] [CrossRef]
- Gong, B.; Cui, S.; Zhao, Y.; Sun, Y.; Ding, Q. Strain-Controlled Fatigue Behaviors of Porous PLA-Based Scaffolds by 3D-Printing Technology. J. Biomater. Sci. Polym. Ed. 2017, 28, 2196–2204. [Google Scholar] [CrossRef]
- Buyuksungur, S.; Endogan Tanir, T.; Buyuksungur, A.; Bektas, E.I.; Torun Kose, G.; Yucel, D.; Beyzadeoglu, T.; Cetinkaya, E.; Yenigun, C.; Tönük, E.; et al. 3D Printed Poly(ε-Caprolactone) Scaffolds Modified with Hydroxyapatite and Poly(Propylene Fumarate) and Their Effects on the Healing of Rabbit Femur Defects. Biomater. Sci. 2017, 5, 2144–2158. [Google Scholar] [CrossRef]
- Trachtenberg, J.E.; Placone, J.K.; Smith, B.T.; Fisher, J.P.; Mikos, A.G. Extrusion-Based 3D Printing of Poly(Propylene Fumarate) Scaffolds with Hydroxyapatite Gradients. J. Biomater. Sci. Polym. Ed. 2017, 28, 532–554. [Google Scholar] [CrossRef] [Green Version]
- Nyberg, E.; Holmes, C.; Witham, T.; Grayson, W.L. Growth Factor-Eluting Technologies for Bone Tissue Engineering. Drug Deliv. Transl. Res. 2016, 6, 184–194. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Shie, M.-Y.; Lai, Y.-H.; Foo, N.-P.; Lee, M.-J.; Yao, C.-H. Fabrication of 3D Printed Poly(Lactic Acid)/Polycaprolactone Scaffolds Using TGF-Β1 for Promoting Bone Regeneration. Polymer 2021, 13, 3731. [Google Scholar] [CrossRef] [PubMed]
- Barati, D.; Shariati, S.R.P.; Moeinzadeh, S.; Melero-Martin, J.M.; Khademhosseini, A.; Jabbari, E. Spatiotemporal Release of BMP-2 and VEGF Enhances Osteogenic and Vasculogenic Differentiation of Human Mesenchymal Stem Cells and Endothelial Colony-Forming Cells Co-Encapsulated in a Patterned Hydrogel. J. Control. Release Off. J. Control. Release Soc. 2016, 223, 126–136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aravamudhan, A.; Ramos, D.M.; Nip, J.; Subramanian, A.; James, R.; Harmon, M.D.; Yu, X.; Kumbar, S.G. Osteoinductive Small Molecules: Growth Factor Alternatives for Bone Tissue Engineering. Curr. Pharm. Des. 2013, 19, 3420–3428. [Google Scholar] [CrossRef] [PubMed]
- Ji, X.; Yuan, X.; Ma, L.; Bi, B.; Zhu, H.; Lei, Z.; Liu, W.; Pu, H.; Jiang, J.; Jiang, X.; et al. Mesenchymal Stem Cell-Loaded Thermosensitive Hydroxypropyl Chitin Hydrogel Combined with a Three-Dimensional-Printed Poly(ε-Caprolactone) /Nano-Hydroxyapatite Scaffold to Repair Bone Defects via Osteogenesis, Angiogenesis and Immunomodulation. Theranostics 2020, 10, 16. [Google Scholar] [CrossRef] [PubMed]
- Ferlin, K.M.; Prendergast, M.E.; Miller, M.L.; Kaplan, D.S.; Fisher, J.P. Influence of 3D Printed Porous Architecture on Mesenchymal Stem Cell Enrichment and Differentiation. Acta Biomater. 2016, 32, 161–169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, H.; Zhang, L.; Qiu, G.; Huang, W.; Zhou, K.; Zhang, X.; Wu, Z. Effects of bore diameter of porous hydroxyapatite scaffolds on three-dimensional dynamic cultivation of osteoblasts. Zhonghua Yi Xue Za Zhi 2014, 94, 3098–3101. [Google Scholar]
- Bahraminasab, M. Challenges on Optimization of 3D-Printed Bone Scaffolds. Biomed. Eng. Online 2020, 19, 69. [Google Scholar] [CrossRef]
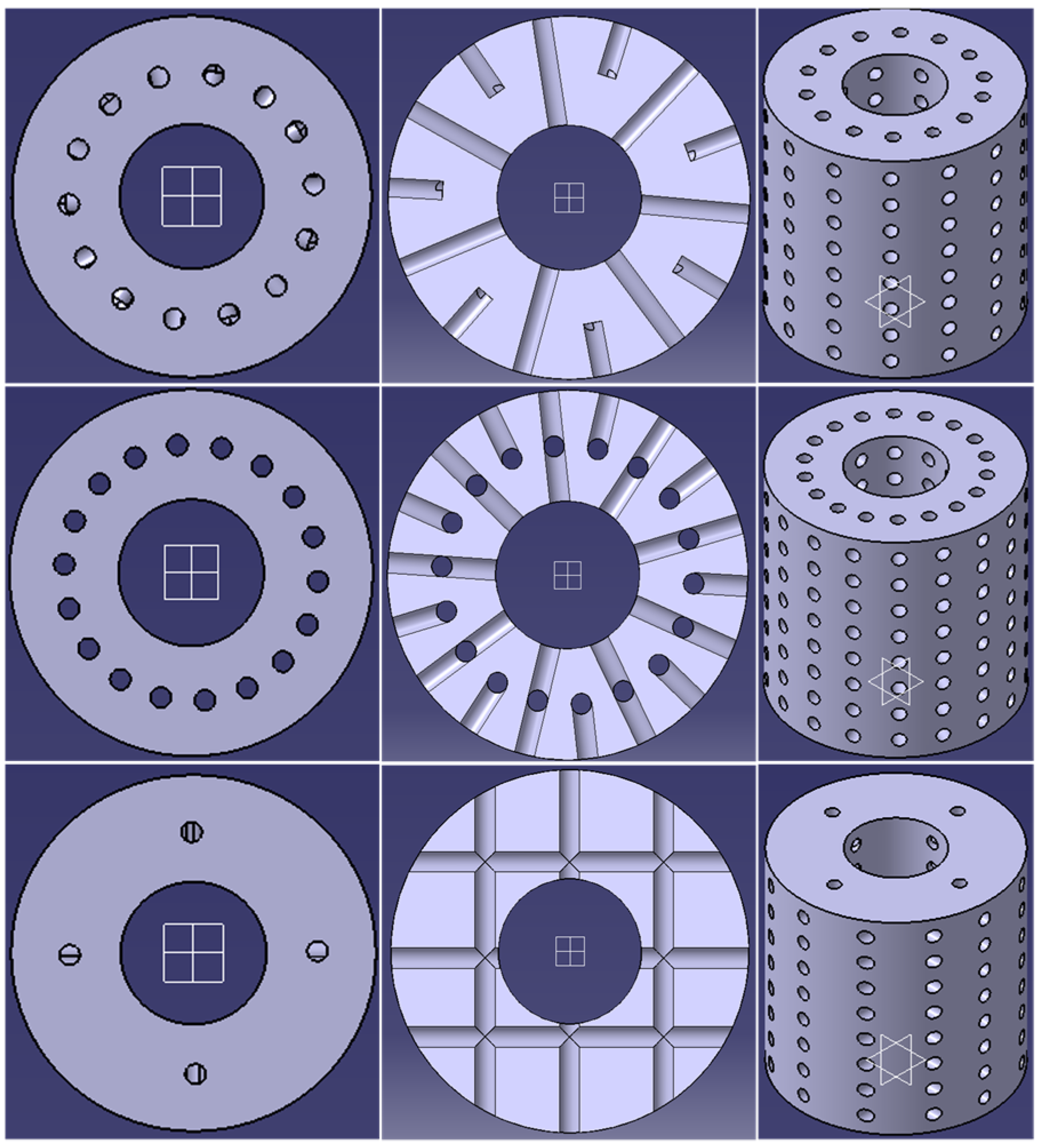

| Pore Size (Surface Area) | Pore Shape | Crosswise | Lengthwise | Eccentric |
|---|---|---|---|---|
| Small (0.25 mm2) | Square | 15 | 21 | 16 |
| Circular | 15 | 21 | 16 | |
| Triangular | 16 | 21 | 16 | |
| Medium (0.56 mm2) | Square | 24 | 26 | 29 |
| Circular | 25 | 26 | 30 | |
| Triangular | 25 | 26 | 31 | |
| Large (1 mm2) | Square | 36 | 37 | 49 |
| Circular | 35 | 37 | 47 | |
| Triangular | 35 | 36 | 52 |
| Pore Size (Surface Area) | Pore Shape | Crosswise | Lengthwise | Eccentric |
|---|---|---|---|---|
| Small (0.25 mm2) | Square | 802 MPa | 800 MPa | 768 MPa |
| Circular | 797 MPa | 808 MPa | 763 MPa | |
| Triangular | 641 MPa | Not converging | Not converging | |
| Medium (0.56 mm2) | Square | 758 MPa | 799 MPa | 710 MPa |
| Circular | 773 MPa | 804 MPa | 694 MPa | |
| Triangular | 606 MPa | 675 MPa | Not converging | |
| Large (1 mm2) | Square | 725 MPa | 782 MPa | 618 MPa |
| Circular | 726 MPa | 786 MPa | 618 MPa | |
| Triangular | 558 MPa | 653 MPa | Not converging |
| Pore Size (Surface Area) | Pore Shape | Crosswise | Lengthwise | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| FEA | Exp. Res. 90° | Exp. Res. 0° | Yield Str. 90° | Yield Str. 0° | FEA | Exp. Res. 90° | Exp. Res. 0° | Yield Str. 90° | Yield Str. 0° | ||
| Small (0.25 mm2) | Square | 802 | 949 | 519 | 44 | 30 | 800 | 743 | 367 | 39 | 20 |
| Circular | 797 | 961 | 515 | 42 | 32 | 808 | 749 | 376 | 36 | 21 | |
| Medium (0.56 mm2) | Square | 758 | 783 | 424 | 34 | 26 | 799 | 748 | 378 | 35 | 23 |
| Circular | 773 | 810 | 501 | 33 | 24 | 804 | 772 | 525 | 35 | 22 | |
| Large (1 mm2) | Square | 725 | 659 | 480 | 27 | 21 | 782 | 753 | 449 | 33 | 19 |
| Circular | 726 | 654 | 464 | 24 | 19 | 786 | 649 | 465 | 28 | 19 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dussault, A.; Pitaru, A.A.; Weber, M.H.; Haglund, L.; Rosenzweig, D.H.; Villemure, I. Optimizing Design Parameters of PLA 3D-Printed Scaffolds for Bone Defect Repair. Surgeries 2022, 3, 162-174. https://doi.org/10.3390/surgeries3030018
Dussault A, Pitaru AA, Weber MH, Haglund L, Rosenzweig DH, Villemure I. Optimizing Design Parameters of PLA 3D-Printed Scaffolds for Bone Defect Repair. Surgeries. 2022; 3(3):162-174. https://doi.org/10.3390/surgeries3030018
Chicago/Turabian StyleDussault, Alexandrine, Audrey A. Pitaru, Michael H. Weber, Lisbet Haglund, Derek H. Rosenzweig, and Isabelle Villemure. 2022. "Optimizing Design Parameters of PLA 3D-Printed Scaffolds for Bone Defect Repair" Surgeries 3, no. 3: 162-174. https://doi.org/10.3390/surgeries3030018
APA StyleDussault, A., Pitaru, A. A., Weber, M. H., Haglund, L., Rosenzweig, D. H., & Villemure, I. (2022). Optimizing Design Parameters of PLA 3D-Printed Scaffolds for Bone Defect Repair. Surgeries, 3(3), 162-174. https://doi.org/10.3390/surgeries3030018








