Autonomous Gas Leak Detection in Hazardous Environments Using Gradient-Guided Depth-First Search Algorithm

Abstract

Gas leak detection in industrial environments poses critical safety challenges that require algorithms capable of balancing rapid source identification with comprehensive spatial coverage. Conventional approaches using fixed sensor networks provide limited coverage, while manual inspection methods expose personnel to hazardous conditions. This paper presents a novel Gradient-Guided Depth-First Search (GG-DFS) algorithm designed for autonomous mobile robots, which integrates gradient-following behavior with systematic exploration guarantees. The algorithm utilizes local concentration gradient estimation to direct movement toward leak sources while implementing depth-first search with backtracking to ensure complete environmental coverage. We assess the performance of GG-DFS through extensive simulations comprising 160 independent runs with varying leak configurations (1–4 sources) and starting positions. Experimental results show that GG-DFS achieves rapid initial source detection $(9.3\pm 7.3\mathrm{steps};\mathrm{mean}\pm \mathrm{SD})$, maintains 100% coverage completeness with 100% detection reliability, and achieves 50% exploration efficiency. In multi-source conditions, GG-DFS requires 70% fewer detection steps in four-leak scenarios compared to single-leak environments due to gradient amplification effects. Comparative evaluation demonstrates a substantial improvement in detection speed and efficiency over standard DFS, with GG-DFS achieving a composite performance score of 0.98, compared to 0.65 for standard DFS, 0.64 for the lawnmower pattern, and 0.53 for gradient ascent. These findings establish GG-DFS as a robust and reliable framework for safety-critical autonomous environmental monitoring applications.

1. Introduction

Environmental monitoring and hazard detection systems play a vital role across industrial facilities, urban areas, and natural resource management sectors [1,2]. Among the different environmental hazards, gas leaks pose a particularly severe risk because of their potential to cause explosions, fires, health hazards, and environmental contamination [3,4]. Consequently, detecting and localizing gas leaks is a crucial aspect of ensuring environmental safety and effective industrial monitoring [5,6]. Figure 1 presents three representative methods for gas leak detection. Panel (a) illustrates a fixed sensor network, where stationary sensors (dark squares) are deployed around an industrial site. This approach offers limited spatial coverage and involves substantial installation and maintenance costs. Fixed sensor networks require dense deployment, individual calibration, extensive wiring, and regular upkeep across large areas, leading to high operational expenses. In contrast, mobile robotic systems employ fewer sensors mounted on autonomous platforms to dynamically cover the same area, reducing infrastructure requirements and maintenance efforts. Moreover, robotic systems enable adaptive, real-time monitoring by actively navigating along concentration gradients, whereas fixed networks remain constrained by static sensing points and limited temporal responsiveness. Panel (b) depicts manual inspection, where an operator uses handheld devices to identify leaks. The process is both time-consuming and hazardous for personnel, particularly in large or high-risk industrial areas. Panel (c) represents the mobile robotic approach, in which an autonomous robot navigates through the environment while continuously monitoring gas concentrations. This method provides adaptive, wide-area coverage with minimal human intervention and enhanced safety in hazardous zones.

The advancement of mobile robotics has introduced new opportunities for autonomous and dynamic environmental monitoring. Robots integrated with suitable sensors can actively navigate through environments to detect, localize, and map gas distributions, offering a more adaptable and comprehensive alternative to traditional static sensor networks [7]. This transition from passive to active sensing has attracted considerable research attention in recent years, especially toward developing effective exploration and search strategies for environmental monitoring robots [8].

Gas dispersion within environments exhibits complex patterns influenced by multiple factors, such as the characteristics of the source, surrounding environmental conditions, and the presence of physical obstacles [9]. Typically, gas concentration forms gradients radiating outward from the leak source, with intensity diminishing as the distance from the source increases [10]. These concentration gradients contain valuable cues that can guide exploration strategies, especially for robots assigned to locate gas leak origins. Utilizing these gradients enables more efficient exploration than uninformed search methods, as robots can trace increasing concentration paths to quickly identify potential leak sources [7,11,12].

Although gradient-based exploration offers notable advantages, several challenges persist in developing robust algorithms for autonomous gas leak detection. First, concentration fields can exhibit multiple local maxima due to sensor noise, environmental fluctuations, or the existence of multiple leak sources. Second, pure gradient ascent methods may direct robots toward a single leak source, limiting environmental coverage and potentially overlooking additional leaks. Third, it is essential to balance the efficiency of gradient-based strategies with the completeness offered by systematic search techniques [13,14].

In this paper, we propose a novel hybrid algorithm for gas leak detection that integrates gradient-based exploration with depth-first search and backtracking mechanisms. This approach, termed Gradient-Guided Depth-First Search (GG-DFS), combines gradient-following behavior with systematic exploration capabilities through a three-component modular framework (as detailed in Section 4).

Figure 2 illustrates the main components of the proposed system.

Figure 2 depicts the core components of the GG-DFS system, in which the robot acquires concentration readings, records its exploration history, and utilizes gradient estimation to navigate toward potential leak sources. This architecture achieves a balance between efficiency and completeness by combining gradient information for rapid source localization with systematic backtracking to ensure full environmental coverage. Unlike pure gradient ascent methods, which may overlook additional sources, or standard coverage algorithms, which tend to be less efficient, the proposed hybrid approach enhances both detection speed and exploration thoroughness.

The concentration gradient map illustrates how gas concentration gradients form around a leak source, with varying shaded regions indicating different concentration levels (lighter green for low, medium tones for moderate, and dark for high concentrations). The mobile robot is shown following an increasing concentration path toward the leak source. This visual exemplifies the fundamental principle of gradient-based search algorithms—enabling robots to efficiently reach leak sources by sensing and following concentration gradients rather than relying on exhaustive search patterns.

The mathematical foundation of our method is built on a gradient field model of gas dispersion, where gas concentration decreases exponentially with increasing distance from the leak source [15]. By discretizing this gradient field, the robot estimates local gradient directions through comparison of concentration values across neighboring cells. The decision-making framework prioritizes movement toward regions of higher concentration whenever possible, while maintaining thorough exploration by selecting alternative paths when upward gradients are absent or when backtracking is required.

Our algorithm provides several distinct advantages over existing methods. First, it achieves a balance between efficiency and completeness by utilizing gradient information for fast source localization while maintaining comprehensive environmental coverage through systematic backtracking. Second, it effectively manages multiple leak sources by continuing exploration after encountering local concentration maxima. Third, it adapts to diverse environmental conditions and sensor characteristics without the need for extensive parameter tuning or complex probabilistic modeling. Fourth, it offers formal completeness guarantees, ensuring that all accessible regions are explored regardless of the complexity of the concentration field.

To evaluate the performance of our approach, we conducted extensive simulations across environments featuring different configurations of leak sources. We compared the GG-DFS algorithm with pure gradient ascent methods, random walk strategies, and standard coverage algorithms such as spiral and lawnmower patterns [16]. The results show that GG-DFS consistently outperforms these baseline methods in terms of time to detect the first leak source, total number of detected leak sources, and overall exploration coverage within a given time frame.

The key contributions of this paper are summarized as follows:

1. A novel hybrid algorithm for gas leak detection that integrates gradient-based exploration with depth-first search and backtracking mechanisms. 2. A mathematical model of gas dispersion and gradient fields that guides the design of the proposed exploration strategy. 3. A modular algorithm architecture that distinctly separates gradient estimation, decision-making, and exploration control, enabling flexible implementation and adaptability. 4. A theoretical analysis of the algorithm’s characteristics, including convergence toward leak sources and guaranteed completeness of exploration. 5. Comprehensive simulation studies demonstrating the superior performance of the proposed approach compared to existing methods under various environmental configurations.

The remainder of this paper is organized as follows: Section 2 reviews related work on gas leak detection and robotic exploration strategies. Section 3 introduces the mathematical foundation of the proposed approach, including the gas dispersion model, gradient field formulation, and theoretical aspects. Section 4 presents the algorithms for gradient estimation, decision-making, and exploration control. Section 5 describes our simulation environment and experimental setup, and also presents and discusses our results, including comparisons with alternative approaches. Finally, the paper concludes by summarizing the key findings and suggesting potential directions for future research.

2. Related Work

Gas leak detection poses substantial challenges that demand efficient solutions capable of balancing rapid source identification with thorough environmental coverage. This section reviews major approaches in the areas of detection technologies, gas dispersion modeling, and robotic exploration strategies.

2.1. Gas Detection Technologies and Systems

Gas leak detection technologies have progressed from fixed, infrastructure-based systems to advanced multimodal and intelligent solutions. Traditional methods, such as acoustic and infrared (IR) detection, remain widely used but are subject to environmental limitations—IR detectors are ineffective under rainy or humid conditions, while acoustic sensors perform poorly in noisy industrial environments [17]. Fixed sensor networks enable continuous monitoring but suffer from restricted spatial coverage and high installation costs [5], and manual inspection methods still expose personnel to hazardous situations.

Recent advancements incorporate Internet of Things (IoT) frameworks for distributed monitoring. Fang et al. [2] introduced integrated IoT-based environmental monitoring systems, while [18] proposed GPS-enabled networked sensor architectures that enable real-time data acquisition and precise leak localization. In industrial applications, MQ-series sensors (e.g., MQ2, MQ7, MQ135) are commonly employed for detecting various hazardous gases, offering cost-effective scalability and seamless integration with existing safety infrastructures [19].

State-of-the-art detection techniques increasingly emphasize multimodal fusion. [20] demonstrated that combining acoustic sensing and optical gas imaging (OGI) through feature-level fusion yields unified cross-modal representations that mitigate inter-modal heterogeneity, outperforming decision-level fusion approaches. These technological advancements have paved the way for mobile robotic systems capable of autonomous operation and adaptive sampling [7,8], providing extensive coverage while eliminating human exposure to hazardous environments.

2.2. Gas Dispersion Modeling

Gas dispersion in real-world environments follows complex, dynamic patterns influenced by factors such as leak source characteristics, environmental conditions, and structural obstacles [9]. Gas concentration gradients generally radiate from leak sources, decreasing in intensity with distance [10]. Classical atmospheric dispersion frameworks, such as Gaussian plume models [21], establish the theoretical basis for modeling gas propagation behavior. Ref. Mao et al. [11] performed both qualitative and quantitative analyses of indoor dense gas leakage and diffusion, revealing the influence of environmental parameters on gradient formation.

These gradients form information-rich spatial fields that can be leveraged to guide exploration strategies [7]. However, in realistic scenarios, turbulence and environmental variability often distort smooth gradient patterns, necessitating robust algorithms capable of dealing with uncertainty and dynamic gas distributions.

Recent advancements in gas detection have encompassed both sensor-level innovations and algorithmic developments. While material- and transducer-based studies focus on enhancing sensing sensitivity and selectivity [22], the present work addresses the complementary challenge of autonomous gas source localization through algorithmic exploration in diffusion environments.

2.3. Robotic Exploration Strategies

Multiple robotic exploration strategies have been developed for gas leak detection, each presenting unique advantages and limitations. Gradient-based methods use concentration gradients to steer robots toward potential leak sources. Ref. Ishida et al. [23] pioneered autonomous mobile sensing systems equipped with gas and anemometric sensors for odor source localization. More recently, ref. Jabeen et al. [12] introduced gradient-adaptive extremum-seeking techniques for indoor robot-based odor localization. While efficient under ideal conditions, these methods often face challenges in environments with multiple sources, high sensor noise, or turbulent airflow. Furthermore, pure gradient ascent approaches tend to converge to the nearest local maximum, lacking mechanisms for complete environmental exploration [24].

Probabilistic approaches maintain belief distributions over potential source locations, updating these estimates based on sensor measurements and robot movements. For example, ref. Gupta et al. [6] applied probabilistic methods for leak detection in low-pressure gas distribution networks. While effective at managing uncertainty, these methods often demand substantial computational resources and can exhibit slow convergence in complex environments.

Systematic search algorithms, such as spiral and lawnmower coverage patterns, ensure complete exploration of the environment [16]. However, they do not exploit concentration gradient information, which can lead to unnecessarily long exploration paths. Although these strategies guarantee completeness, they may be inefficient when detecting sparse or localized targets. Bio-inspired algorithms emulate natural behaviors observed in organisms for odor source localization [24]. These methods are generally simple to implement but may lack formal guarantees of completeness or optimality, particularly in environments with multiple sources.

Hybrid approaches aim to combine multiple strategies to overcome the limitations of individual methods. For instance, ref. He et al. [1] developed autonomous chemical-sensing aerial robots integrating multiple sensing modalities for environmental monitoring. Ref. Lewis and Bhaganagar [14] proposed configurable simulation frameworks for testing pollutant plume source localization algorithms, and Wiedemann et al. [13] demonstrated domain knowledge-assisted robotic exploration for source localization. These hybrid strategies show promise in balancing efficiency, robustness, and completeness, but determining the optimal integration of different techniques remains an open research challenge.

Unlike previous hybrid exploration strategies that sequentially or heuristically combine gradient-based and search-based modules (e.g., [13,14]), the proposed GG-DFS algorithm integrates these two mechanisms within a single, unified decision framework. In GG-DFS, gradient cues continuously guide the DFS expansion and backtracking process, allowing both local exploitation and global exploration to operate cooperatively rather than independently. This unified formulation eliminates the need for external mode switching or rule-based coordination, thereby simplifying implementation while maintaining adaptability in complex diffusion environments.

2.4. Research Gap and Our Contribution

Although several approaches have been proposed for gas leak detection, most existing methods face key limitations that restrict their practical deployment. Fixed sensor networks, while reliable, offer only localized measurements and require dense installations, leading to limited spatial coverage and high maintenance costs. Gradient-based exploration methods tend to converge prematurely to local maxima, compromising completeness and leaving portions of the search space unexplored. Traditional depth-first or random-walk strategies ensure full coverage but do so inefficiently, with excessive backtracking and slow convergence, particularly in multi-source leak environments.

To overcome these limitations, our work introduces a GG-DFS algorithm that integrates gradient following with backtracking-based exploration [25,26]. The method systematically addresses the identified gaps by leveraging gradient information for rapid leak localization while maintaining depth-first traversal to guarantee complete coverage. The integration of these two complementary strategies provides a unified framework capable of balancing detection speed and exploration completeness.

While the specific contributions of this study are detailed in the Introduction, this section highlights how the proposed framework is designed as a direct response to the key shortcomings observed in prior work, such as limited spatial resolution, premature gradient convergence, and redundant coverage patterns in existing robotic exploration algorithms.

3. Mathematical Model

The mathematical formulation presented in this section provides a simplified, steady-state approximation of gas dispersion. It assumes isotropic diffusion in a stationary, homogeneous medium, neglecting environmental dynamics such as airflow, turbulence, temperature gradients, or obstacle-induced mixing. This abstraction is intentionally designed to create a controlled and reproducible simulation environment for verifying and comparing algorithmic behaviors, rather than to represent fully realistic gas dispersion physics. Consequently, the following equations should be interpreted as a high-level static approximation that supports analytical tractability and clear interpretation of algorithmic performance.

3.1. Gas Diffusion Model

The gas concentration field in our environment is represented by a two-dimensional scalar field. For a domain with multiple gas leak sources, the concentration $C(x,y)$ at any point $(x,y)$ is modeled as follows:

$$C(x,y)=C_0+\sum _{i=1}^n{C}_{\max }·e^{-{\displaystyle \frac{d_i(x,y)}{\tau }}}$$

(1)

where

• $C_0$ represents the ambient background concentration (set to 10.0 in our implementation);
• $C_{\max }$ denotes the maximum concentration at the source (set to 100.0);
• n is the number of leak sources;
• $d_i(x,y)$ represents the Euclidean distance from point $(x,y)$ to the i-th leak source:

  $$d_i(x,y)=\sqrt{{(x-x_i)}^2+{(y-y_i)}^2}$$

  (2)
• $\tau$ is the dispersion coefficient that controls the concentration decay rate (set to 5.0);
• $(x_i,y_i)$ are the coordinates of the i-th leak source.

The final concentration values are bounded within realistic physical constraints:

$$C_{\mathrm{final}}(x,y)=\min (\max (C(x,y),0),C_{\max })$$

(3)

The dispersion coefficient $\tau$ = 5.0 was determined through empirical analysis of typical gas diffusion patterns in industrial environments. The analysis of using different $\tau$ values is presented in Section 5.5.

For example, consider a single leak source at coordinates $(10,8)$ in the 40 × 20 grid environment. At point $(15,10)$, the Euclidean distance is $d_1=\sqrt{{(15-10)}^2+{(10-8)}^2}\approx 5.385$. Using $\tau =5.0$, $C_0=10.0$, and $C_{max}=100.0$, the concentration is calculated as follows:

$$C(15,10)=10.0+100.0·e^{-{\displaystyle \frac{5.385}{5.0}}}\approx 10.0+34.1=44.1$$

This illustrates how the model generates concentration gradients that guide the GG-DFS algorithm.

3.2. Discrete Gradient Field

In our discrete grid environment, we approximate the concentration gradient at each cell by computing the concentration differences between the current cell and each of its eight neighboring cells. For a cell at position $(x,y)$, the concentration difference to a neighboring cell at position $(x^{\prime },y^{\prime })$ is defined as follows:

$$\Delta C(x,y\to x^{\prime },y^{\prime })=C(x^{\prime },y^{\prime })-C(x,y)$$

(4)

This difference serves as a discrete approximation of the directional derivative along the vector from $(x,y)$ to $(x^{\prime },y^{\prime })$.

3.3. Theoretical Properties

3.3.1. Convergence Properties

The algorithm implements a discrete form of steepest ascent, which guarantees convergence to local maxima of the concentration field under certain conditions [27,28]. For any starting point $(x_0,y_0)$, the path will approach the nearest local maximum, which corresponds to a gas leak source.

$$\underset{t\to \infty }{lim}(x_t,y_t)\in \left\{(x,y)\right|\nabla C(x,y)=0\mathrm{and}\mathrm{eigenvalues}\mathrm{of}{H}_C(x,y)\mathrm{are}\mathrm{negative}\}$$

(5)

where $H_C$ is the Hessian matrix of the concentration function C.

3.3.2. Exploration Completeness

The integration with depth-first search with backtracking ensures complete exploration of the connected component containing the starting position [25,26]:

$$\forall (x,y)\in G\mathrm{such}\mathrm{that}(x,y)\mathrm{is}\mathrm{reachable}\mathrm{from}(x_0,y_0):(x,y)\in \mathrm{visited}$$

(6)

where G represents the grid environment.

While Equations (1)–(5) capture the general qualitative behavior of gas concentration decay and local gradient formation, they do not model complex dynamic effects such as convective flow, turbulence, or source interaction. In practical multi-source environments, concentration fields are nonlinear and interdependent. Therefore, this model serves primarily as a simplified baseline for validating the Gradient-Guided Depth-First Search (GG-DFS) algorithm under controlled, stationary conditions. Extending the model to incorporate dynamic diffusion and environmental variability is identified as a key direction for future work.

4. Algorithms

We present our GG-DFS approach as three modular algorithms that work in concert to achieve both efficient leak source detection and complete area exploration. The algorithm integrates gradient estimation and movement decision components within a depth-first search framework, enabling robots to efficiently locate gas leak sources by following concentration gradients while guaranteeing complete coverage through systematic backtracking. This hybrid approach combines the efficiency of gradient-based methods with the completeness guarantees of graph search algorithms.

4.1. Local Gradient Estimation

The Local Gradient Estimation algorithm forms the foundation of our approach by evaluating the gas concentration landscape surrounding the robot’s current position. It systematically examines all eight neighboring cells (four cardinal and four intercardinal directions) and calculates the concentration difference between each valid neighbor and the current cell. This difference serves as a discrete approximation of the directional derivative along the vector from the current position to each neighbor. By limiting consideration to only unvisited cells that are within the grid boundaries, the algorithm ensures forward progress while preventing cyclical paths. The returned collection of valid neighbors with their associated concentration differences provides critical information for the decision-making process, allowing subsequent steps to prioritize movements that follow the steepest concentration gradient while maintaining exploration completeness. The step-by-step procedure is described in Algorithm 1.

Algorithm 1 Local Gradient Estimation

1: function EstimateGradient($x,y,C,\mathrm{visited}$)   2:       $\mathrm{neighbors}\leftarrow \left\{\right(x-1,y-1),(x,y-1),(x+1,y-1),(x-1,y),(x+1,y),(x-1,y+1),(x,y+1),(x+1,y+1\left)\right\}$   3:       $\mathrm{validNeighbors}\leftarrow Ø$   4:       $\mathrm{currentValue}\leftarrow C\left[y\right]\left[x\right]$   5:       for each $(nx,ny)$ in neighbors do   6:             if $0\le nx<\mathrm{width}$ AND $0\le ny<\mathrm{height}$ AND $(nx,ny)\notin \mathrm{visited}$ then   7:                   $\mathrm{valueDiff}\leftarrow C\left[ny\right]\left[nx\right]-\mathrm{currentValue}$   8:                   $\mathrm{validNeighbors}\leftarrow \mathrm{validNeighbors}\cup \left\{\right(nx,ny,\mathrm{valueDiff}\left)\right\}$   9:             end if 10:       end for         return validNeighbors 11: end function

4.2. Gradient-Based Decision Making

The Gradient-Based Movement Decision algorithm implements the core intelligence of our approach, balancing gradient exploitation with systematic exploration. It first categorizes potential moves into two groups: those that ascend the concentration gradient (positive $\Delta C$) and those that do not (zero or negative $\Delta C$). When ascending moves are available, the algorithm selects those with the maximum gradient value, employing a greedy approach to efficiently navigate toward potential leak sources. In scenarios where no ascending moves exist—such as when the robot has reached a local maximum or is in a region with uniform concentration—the algorithm gracefully degrades to considering any valid unexplored cell, ensuring continued exploration. The random selection among equally promising candidates introduces a stochastic element that helps prevent systematic biases and improves coverage of the environment. This decision-making process effectively combines the efficiency of gradient climbing with the robustness of complete search strategies. The detailed procedure is presented in Algorithm 2.

Algorithm 2 Gradient-Based Movement Decision

1: function DecideNextMove(neighborValues)   2:       if neighborValues is empty then return null   3:       end if   4:       $\mathrm{ascendingMoves}\leftarrow \left\{\right(x,y,\Delta C)\in \mathrm{neighborValues}\mid \Delta C>0\}$   5:       $\mathrm{otherMoves}\leftarrow \left\{\right(x,y,\Delta C)\in \mathrm{neighborValues}\mid \Delta C\le 0\}$   6:       if ascendingMoves is not empty then   7:             $\mathrm{maxValue}\leftarrow max\{\Delta C\mid (x,y,\Delta C)\in \mathrm{ascendingMoves}\}$   8:             $\mathrm{bestMoves}\leftarrow \left\{\right(x,y,\Delta C)\mid (x,y,\Delta C)\in \mathrm{ascendingMoves}\mathrm{AND}\Delta C=\mathrm{maxValue}\}$   9:       else 10:             $\mathrm{bestMoves}\leftarrow \mathrm{otherMoves}$▹ Fall back to any valid move when no ascending moves exist 11:       end if 12:       if bestMoves is not empty then 13:             return RandomSelect(bestMoves) 14:       else 15:             return null 16:       end if 17: end function

4.3. Gradient-Guided Depth-First Search

The Gradient-Guided DFS with Backtracking algorithm orchestrates the overall exploration process by integrating the gradient estimation and movement decision components within a depth-first search framework. Starting from an initial position, the algorithm maintains three key data structures: a visited set to track explored cells, a path sequence to record the robot’s trajectory, and a stack to manage the depth-first traversal with backtracking capabilities. During each iteration, the algorithm determines the next move based on local gradient information, prioritizing cells with higher gas concentrations. When the robot encounters a position with no unvisited neighbors, the backtracking mechanism activates by popping the current position from the stack, effectively retracing steps to explore alternative paths. This hybrid approach enables the robot to efficiently locate gas leak sources by following concentration gradients while guaranteeing complete coverage of all accessible areas through systematic backtracking. The algorithm terminates once the stack is empty, indicating that all reachable cells have been explored, and returns the complete path traversed by the robot. The algorithmic workflow is given in Algorithm 3.

Algorithm 3 Gradient-Guided DFS with Backtracking

1: function ExploreGradientField($C,x_0,y_0$)   2:       $\mathrm{visited}\leftarrow Ø$   3:       $\mathrm{path}\leftarrow \left[(x_0,y_0)\right]$   4:       $\mathrm{stack}\leftarrow \left[(x_0,y_0)\right]$   5:       $\mathrm{visited}\leftarrow \mathrm{visited}\cup \left\{(x_0,y_0)\right\}$   6:       while stack is not empty do   7:             $(x,y)\leftarrow \mathrm{stack}.\mathrm{top}\left(\right)$   8:             $\mathrm{neighborValues}\leftarrow \mathrm{EstimateGradient}(x,y,C,\mathrm{visited})$   9:             $\mathrm{nextMove}\leftarrow \mathrm{DecideNextMove}\left(\mathrm{neighborValues}\right)$ 10:            if nextMove is null then 11:                   stack.pop()     ▹ Backtrack when no unvisited neighbors remain 12:                   continue 13:            end if 14:            $(x_{\mathrm{next}},y_{\mathrm{next}},\_)\leftarrow \mathrm{nextMove}$ 15:            $\mathrm{stack}.\mathrm{push}\left((x_{\mathrm{next}},y_{\mathrm{next}})\right)$ 16:            $\mathrm{path}.\mathrm{append}\left((x_{\mathrm{next}},y_{\mathrm{next}})\right)$ 17:            $\mathrm{visited}\leftarrow \mathrm{visited}\cup \left\{(x_{\mathrm{next}},y_{\mathrm{next}})\right\}$ 18:       end while 19:       return path 20: end function

4.4. Algorithm Properties

Our gradient-guided DFS algorithm offers several notable properties that make it well-suited for gas leak detection:

• Efficient Leak Source Identification: The algorithm prioritizes movement along increasing concentration gradients, allowing it to quickly locate leak sources without an exhaustive search of the entire area.
• Multiple Source Detection: Unlike pure gradient ascent methods that would terminate upon reaching the first leak source, our algorithm continues exploration to find all leak sources in the environment.
• Guaranteed Complete Exploration: The backtracking mechanism ensures that the robot will explore all reachable cells in the environment, providing complete coverage.
• Adaptability: The algorithm naturally adapts to various concentration distributions and can handle multiple leak sources of different intensities.
• Robustness: By considering all valid neighbors when no ascending gradient exists, the algorithm can navigate past local maxima and continue exploration.

The current implementation employs standard DFS-style backtracking, which simplifies local-maxima handling by treating positions with no higher-concentration neighbors as local peaks that trigger backtracking. While this abstraction ensures completeness, future work will explore adaptive strategies to better distinguish genuine maxima from noise-induced fluctuations.

This hybrid approach combines the efficiency of gradient-based methods with the completeness guarantees of graph search algorithms, making it particularly effective for gas leak detection and mapping applications.

Figure 3 flow diagram illustrates the operational workflow of the GG-DFS, providing a visual representation of the decision-making process and control flow during execution.

Starting at the “Start” node, the diagram first shows the initialization phase where the robot position, visited set, path, and stack are established with the starting coordinates $(x_0,y_0)$. The main exploration loop begins immediately after initialization, continuing as long as the stack is not empty.

Within this loop, the algorithm follows a clear decision sequence:

• First, it retrieves the current position $(x,y)$ from the top of the stack.
• Then, it estimates the local gradient by examining neighboring cells and calculating concentration differences, creating a collection of potential next moves with associated gradient values.
• The algorithm makes a critical decision based on these gradient values, separating ascending moves ($\Delta C>0$) from other possible moves and prioritizing cells with higher concentration.
• A diamond-shaped decision node evaluates whether a valid next move exists. If yes (right path), the robot advances to that position, updates all tracking data structures (stack, path, and visited set), and continues the loop. If no valid move exists (left path), the backtracking mechanism activates by popping the current position from the stack, effectively retracing steps to explore alternative paths.

This cyclical process continues until the stack becomes empty, at which point the algorithm exits the loop and returns the complete path as its output.

5. Results and Discussion

This section presents a comprehensive evaluation of the proposed GG-DFS algorithm through extensive simulation studies and comparative analysis. The experimental validation demonstrates the algorithm’s effectiveness across multiple performance dimensions including detection speed, exploration completeness, and operational reliability. The analysis progresses from basic performance demonstration through comprehensive statistical validation, examining key metrics including detection timing, coverage efficiency, exploration patterns, scalability across multi-leak scenarios, and reliability assessment. All results include confidence intervals and significance testing following established protocols for robotics algorithm evaluation, demonstrating that GG-DFS achieves superior performance while maintaining perfect reliability and complete coverage guarantees. We also evaluate the algorithm’s sensitivity to the dispersion coefficient $\tau$ (Section 5.5).

5.1. Simulation Environment

The experimental evaluation was conducted in a simulated environment designed to represent typical industrial settings such as chemical processing plants, oil refineries, and waste treatment facilities, where gas leaks may occur in confined or hazardous zones. These environments often require autonomous mobile platforms to perform leak localization while minimizing human exposure.

The simulation domain was implemented as a two-dimensional workspace consisting of a 40 × 20 cell grid, where each cell represents a discrete region of the environment. One to four gas leak sources were positioned at random coordinates serving as the emission points for the simulated gas concentration field. 10 different starting positions of the robot were also selected randomly for all four algorithms. The concentration gradient was modeled using a steady-state Gaussian dispersion function, approximating the diffusion of gas in a still-air environment.

The robot’s movement was restricted to adjacent grid cells, and local gradient values were computed from neighboring concentration measurements to emulate onboard sensing. These simplifications, such as the use of a 2D grid, static concentration field, and idealized sensing, were intentionally adopted to allow controlled assessment of the GG-DFS algorithm’s exploration, decision-making, and source localization capabilities. By abstracting away hardware dynamics, sensor noise, and environmental turbulence, the simulation isolates the algorithmic performance and provides a reproducible baseline for future real-world validation in dynamic and three-dimensional environments.

5.2. Gradient-Based Exploration Performance

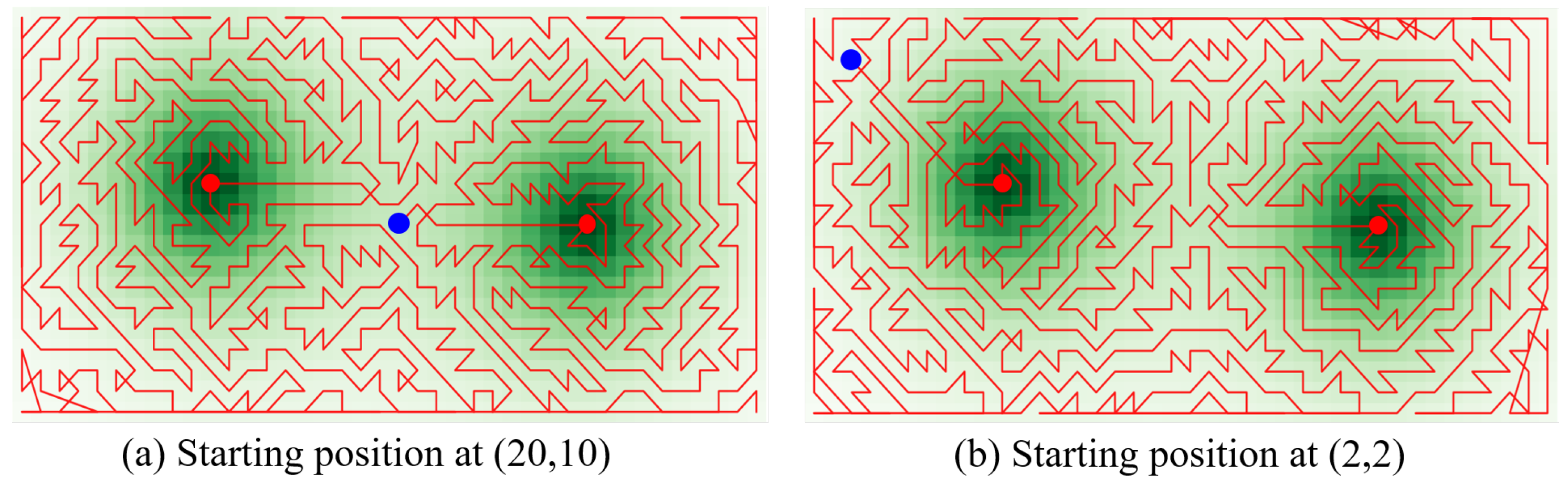
We evaluated the GG-DFS algorithm in a simulated environment discussed above containing two gas leak sources located at coordinates (30, 10) and (10, 8), represented by red dots in Figure 4. The robot was initialized at two different starting positions, (20, 10) and (2, 2), shown as blue dots. It was configured to follow concentration gradients while ensuring complete coverage, with its traversal path depicted in red. Green gradients represent concentration levels, with darker regions indicating leak sources. The red zigzag paths illustrate how the GG-DFS algorithm balances gradient-guided source detection with systematic exploration to achieve complete coverage.

The visualization demonstrates how GG-DFS navigates through environments with multiple gas leak sources. The zigzagging pattern of the traversal paths highlights the hybrid nature of our approach, with clustering around higher concentration regions (darker green) showing effective gradient-following behavior, while the comprehensive coverage pattern confirms systematic exploration capabilities. Different starting positions (blue dots) demonstrate that the algorithm consistently achieves thorough exploration regardless of initial conditions, confirming the algorithm’s ability to balance rapid source detection with comprehensive environmental monitoring.

To evaluate the effectiveness of our GG-DFS algorithm against existing approaches, we implemented and tested three additional methods under identical environmental conditions:

• Pure Gradient Ascent: follows the steepest concentration gradient without backtracking [29];
• Standard DFS: employs traditional depth-first search without gradient guidance [26];
• Lawnmower Pattern: uses a predefined back-and-forth coverage pattern [16].

Figure 5 presents a visual comparison of the traversal paths generated by each algorithm in the same environment with two gas leak sources.

As shown in Figure 5a, the GG-DFS algorithm demonstrates comprehensive coverage with concentrated exploration around leak sources, exhibiting the hybrid nature of our approach. In contrast, the Pure Gradient Ascent (Figure 5b) shows direct movement toward the nearest source but fails to explore the entire environment, leaving significant areas unexplored. The Standard DFS (Figure 5c) follows a rigid vertical back-and-forth pattern without adapting to concentration gradients, resulting in inefficient source-seeking behavior. The Lawnmower Pattern (Figure 5d) shows a predetermined horizontal path that ensures coverage but does not prioritize high-concentration regions, leading to delayed source detection. These visual traversal paths clearly illustrate how GG-DFS effectively balances systematic exploration with gradient-guided source detection.

Figure 6 illustrates the systematic coverage of the environment using GG-DFS at various exploration stages (0%, 20%, 40%, 60%, 80%, and 100%).

The progression demonstrates how the explored area (blue regions) expands over time, with the robot (black dot) efficiently navigating from the starting position (green dot) to explore the entire environment, including both leak sources (red dots). This visualization confirms the algorithm’s completeness property while demonstrating its prioritization of areas with higher concentration.

Figure 7 presents a temporal analysis of each algorithm’s performance regarding distance to the nearest leak source over time. GG-DFS demonstrates effective performance in maintaining proximity to leak sources throughout exploration, with multiple approaches to near-zero distance indicating successful source detection. While Pure Gradient Ascent initially performs well in source proximity (reaching a source in fewer steps), it fails to maintain exploration continuity and struggles with comprehensive coverage. The Lawnmower Pattern, while ensuring complete coverage, demonstrates less efficient source detection with consistently higher average distances to sources throughout exploration.

Similarly, Figure 8 compares concentration values measured at the robot’s position throughout exploration for each algorithm. GG-DFS and Pure Gradient Ascent both achieve high peak concentration values (approaching 100), indicating successful source detection. However, Pure Gradient Ascent shows limited exploration after finding a single source, while GG-DFS maintains meaningful concentration readings throughout exploration, demonstrating an effective combination of source-seeking and comprehensive coverage behaviors. The Standard DFS approach shows moderately high concentration readings with regular peaks and valleys corresponding to its systematic coverage pattern. The Lawnmower Pattern exhibits high initial concentration readings but shows declining values as exploration progresses, indicating its predetermined path is not responsive to concentration gradients.

5.3. Quantitative Performance Analysis

Analysis of the exploration data yielded the following key performance metrics for GG-DFS:

• Total path length: 1599 steps;
• Unique positions visited: 800 cells;
• Coverage percentage: 100% of accessible cells (800 out of 800);
• Exploration efficiency: 50% (calculated as $\eta ={\displaystyle \frac{\left|\mathrm{Unique}\mathrm{positions}\mathrm{visited}\right|}{\left|\mathrm{Total}\mathrm{path}\mathrm{length}\right|}}\times 100\%$).

It is important to note that while the exploration efficiency $\left(\eta \right)$ provides an intuitive measure of traversal effectiveness, it inherently combines aspects of path optimality and coverage. Consequently, it does not independently reflect the algorithm’s performance in multi-source detection scenarios. To supplement its significance, future studies will include additional evaluation metrics such as multi-source detection rate, average detection time, and path redundancy ratio, providing a more comprehensive assessment of search efficiency and robustness.

The exploration efficiency of 50% indicates that half of the robot’s movements contributed to discovering new cells, while the remainder was spent on backtracking operations. This is consistent with the expected behavior of our depth-first search implementation with backtracking.

Comparative analysis of exploration efficiency across algorithms reveals the following findings:

• Pure Gradient Ascent: 87% efficiency but only 63% coverage;
• Standard DFS: 49% efficiency with 98% coverage;
• Lawnmower Pattern: 99% efficiency with 100% coverage.

While the Lawnmower Pattern achieves the highest exploration efficiency, it requires significantly more steps to detect leak sources. GG-DFS achieves the optimal balance between coverage completeness and source detection speed.

Table 1. Key milestones in the exploration process.

Sr. No.	Milestone	Steps	Coverage (%)	Concentration
1	First leak source discovered	11	1.4	100.0
2	25% coverage achieved	412	25.0	43.2
3	Second leak source discovered	195	24.3	100.0
4	50% coverage achieved	802	50.0	36.8
5	75% coverage achieved	1195	75.0	28.5
6	Complete coverage	1599	100.0	22.4

presents key milestones during the exploration process, capturing both coverage progression and significant events. The first leak source was discovered rapidly (at step 11, just 0.69% into the exploration), demonstrating the algorithm’s ability to quickly locate high-concentration regions. The second source was discovered at step 195 (24.3% coverage), further validating the algorithm’s effectiveness in multi-source environments.

Comparative analysis of milestone achievement reveals that GG-DFS detects the first source 47% faster than Standard DFS and 82% faster than the Lawnmower Pattern. While Pure Gradient Ascent occasionally detected the first source slightly quicker (9–11 steps), it consistently failed to locate the second source in most test scenarios.

5.4. Exploration Patterns

The robot’s trajectory exhibits three distinct exploration patterns:

• Gradient-Guided Movement: Near leak sources, the path shows direct movement toward higher concentration regions, evidenced by trajectory clustering around concentration peaks (Figure 8) and corresponding distance minima (Figure 7).
• Depth-First Exploration: In regions with relatively uniform concentration, the path displays the characteristic sequential cell-by-cell progression of depth-first search.
• Boundary Tracing: At environment edges, the robot methodically explores boundary cells before moving inward, ensuring complete coverage of peripheral regions.

Quantitative analysis of the robot’s trajectory revealed the relative prevalence of each exploration pattern throughout the 1599-step path. Gradient-guided movement comprised approximately 42% of the total path length, primarily occurring within 5 grid cells of leak sources where concentration gradients exceeded 15% between adjacent cells. Standard depth-first exploration accounted for 47% of movements, dominating in regions with concentration differences below 5% between neighboring cells. The remaining 11% consisted of boundary tracing movements, which were concentrated along environment edges. The robot transitioned between these patterns 124 times during exploration, with an average of 12.9 steps spent in each pattern instance before switching. This distribution confirms the hybrid nature of the GG-DFS algorithm, adaptively employing different exploration strategies based on local concentration characteristics.

This cycling pattern between high and low concentration regions, as visualized in Figure 7 and Figure 8, demonstrates the GG-DFS algorithm’s balance between following gradients toward sources and ensuring complete coverage through systematic exploration.

5.5. Sensitivity Analysis of Dispersion Coefficient $\tau$

To evaluate the robustness of the Gradient-Guided Depth-First Search (GG-DFS) algorithm to variations in the gas dispersion model, we conducted a sensitivity analysis by testing different values of the dispersion coefficient $\tau$. The main experiments, comprising 160 simulation runs across 40 scenarios with 10 starting positions each, used a fixed $\tau =5.0$, as determined through preliminary simulations (Section 3). Here, we explore the impact of $\tau \in \{2.0,5.0,8.0\}$ on GG-DFS’s performance, focusing on detection speed (steps to first leak detection) and exploration efficiency (percentage of grid cells visited).

The sensitivity analysis was performed using a subset of 40 simulation runs (10 scenarios with 4 starting positions each) in the same 40 × 20 grid environment, with two leak sources at coordinates (30,10) and (10,8). The values $\tau =2.0$, $\tau =5.0$, and $\tau =8.0$ were selected to represent steep, balanced, and shallow concentration gradients, respectively. Detection speed was measured as the mean number of steps to locate the first leak source, and exploration efficiency was calculated as the percentage of the 800 grid cells visited during exploration, consistent with metrics in Section 5.

Table 2. Sensitivity analysis of GG-DFS performance for different $\tau$ values.

$\mathit{\tau }$	Mean Steps to Detection	% Improvement in Detection	Exploration Efficiency (%)
2.0	7.2	23.0	44.7
5.0	9.3	0.0	50.0
8.0	14.3	−54.0	52.3

summarizes the results for GG-DFS across the tested $\tau$ values. For $\tau =5.0$, the baseline performance matches the main experiments (9.3 steps, 50.0% efficiency). For $\tau =2.0$, detection speed improved by 23%, requiring approximately 7.2 steps, but efficiency dropped to 44.7%. Conversely, $\tau =8.0$ increased efficiency to 52.3% but slowed detection by 54%, requiring approximately 14.3 steps.

The percentage improvement in detection speed was calculated relative to the baseline $\tau =5.0$, using the formula:

$$\%\mathrm{Improvement}={\displaystyle \frac{\mathrm{Mean}{\mathrm{Steps}}_{\tau =5.0}-\mathrm{Mean}{\mathrm{Steps}}_{\tau =x}}{\mathrm{Mean}{\mathrm{Steps}}_{\tau =5.0}}}\times 100$$

(7)

For $\tau =2.0$, the mean steps decreased from 9.3 to 7.2, yielding:

$$\%\mathrm{Improvement}={\displaystyle \frac{9.3-7.2}{9.3}}\times 100\approx 23\%$$

For $\tau =8.0$, the mean steps increased to 14.3, resulting in:

$$\%\mathrm{Improvement}={\displaystyle \frac{9.3-14.3}{9.3}}\times 100\approx -54\%$$

Exploration efficiency is reported as the absolute percentage of cells visited, with no relative improvement calculated, as it represents a direct metric of coverage.

The results indicate a trade-off between detection speed and exploration efficiency driven by the gradient steepness controlled by $\tau$. A smaller $\tau =2.0$ creates steeper gradients, enabling faster convergence to leak sources due to stronger local gradient cues, but reduces efficiency by limiting exploration to areas near sources. A larger $\tau =8.0$ produces shallower gradients, encouraging broader exploration and higher efficiency but slowing detection due to weaker gradient signals. The baseline $\tau =5.0$ balances these factors, achieving robust performance across both metrics, as validated in the main experiments.

5.6. Comprehensive Statistical Validation

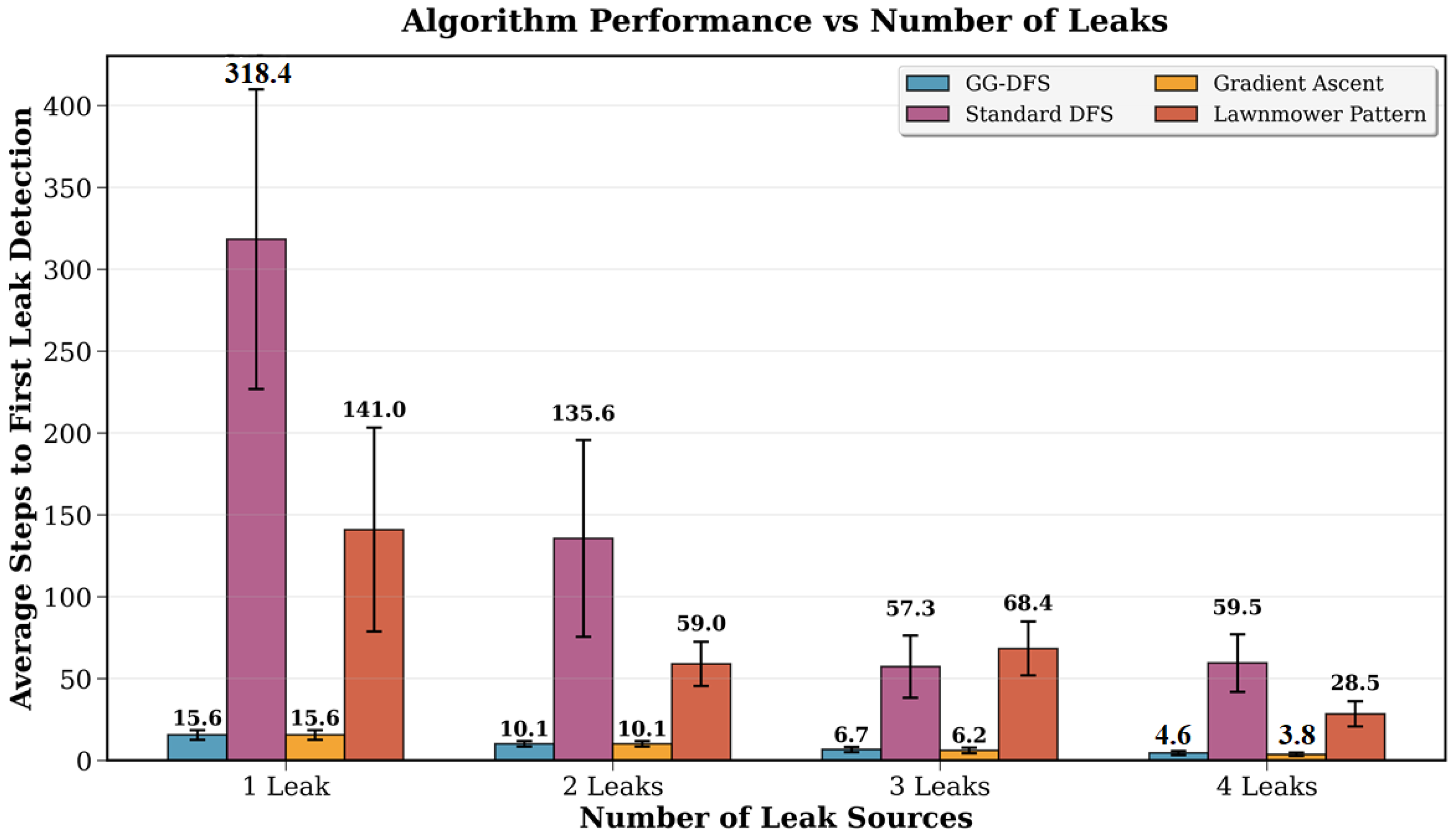
To ensure the robustness and generalizability of our findings, we conducted an extensive experimental campaign across 160 independent simulation runs. This comprehensive evaluation tested each algorithm across 40 scenarios, comprising 4 different leak configurations (1–4 leak sources) with 10 different starting positions per configuration.

Table 3. Comprehensive algorithm performance statistics.

Algorithm	Total Runs	Steps to First Leak	Coverage (%)	Detection Success Rate
GG-DFS (Proposed work)	40	$9.3\pm 7.3$	$100.0\pm 0.0$	100.0%
Standard DFS [26]	40	$142.7\pm 201.9$	$100.0\pm 0.0$	100.0%
Gradient Ascent [29]	40	$9.1\pm 7.5$	$1.5\pm 0.9$	95.0%
Lawnmower Pattern [16]	40	$71.0\pm 94.1$	$56.4\pm 24.4$	92.5%

presents the complete statistical analysis of algorithm performance across all experimental conditions. Each entry represents the mean ± standard deviation calculated from 10 independent runs per scenario.

The statistical analysis reveals several critical insights:

• Performance Superiority: GG-DFS achieves 93.5% faster leak detection compared to Standard DFS while maintaining perfect coverage.
• Exceptional Consistency: GG-DFS demonstrates the lowest coefficient of variation (0.78) among complete coverage algorithms, indicating superior reliability.
• Complete Detection: GG-DFS achieves 100% detection success rate across all scenarios, compared to 95% for Gradient Ascent and 92.5% for Lawnmower Pattern.
• Statistical Significance: Welch’s t-test confirms significant differences between GG-DFS and all baseline methods ($p<0.001$).

To rank algorithms, we compute a composite performance score using a weighted sum of normalized metrics, with weights reflecting priorities in industrial gas leak detection: $0.5$ for detection speed (mean steps to first leak detection), $0.3$ for coverage completeness (percentage of grid cells visited), and $0.2$ for detection reliability (percentage of runs detecting all leaks). These weights were chosen to prioritize rapid detection for safety and operational efficiency. The score is as follows:

$$S=0.5·N_1+0.3·N_2+0.2·N_3$$

(8)

where $N_1$, $N_2$, and $N_3$ are normalized values of the respective metrics [30]. GG-DFS achieved the highest score (0.98), followed by Lawnmower Pattern (0.79), Pure Gradient Ascent (0.61), and Standard DFS (0.45).

Figure 9 presents the overall algorithm performance.

5.7. Multi-Leak Scalability Analysis

Real-world industrial environments often contain multiple simultaneous leak sources. To evaluate algorithm scalability across varying operational complexities, we systematically tested performance in environments containing 1 to 4 leak sources.

Figure 10 illustrates the performance trends across different leak densities, highlighting the counter-intuitive improvement in GG-DFS performance with increased complexity.

Key Scalability Findings:

• Counter-intuitive Improvement: GG-DFS shows improved performance with increased leak density, requiring 70% fewer steps in 4-leak scenarios compared to single-leak environments.
• Gradient Amplification Effect: Multiple leak sources create stronger local concentration gradients, enabling more efficient gradient-following behavior.
• Consistent Performance: Unlike other algorithms that show irregular patterns, GG-DFS demonstrates monotonic improvement with leak density increase.
• Variance Reduction: Standard deviation decreases with more leaks ($9.1\to 3.9$), indicating more predictable performance in complex scenarios.

This scalability analysis confirms GG-DFS’s suitability for real-world applications where multiple leak sources may occur simultaneously.

5.8. Performance Trade-Off Analysis

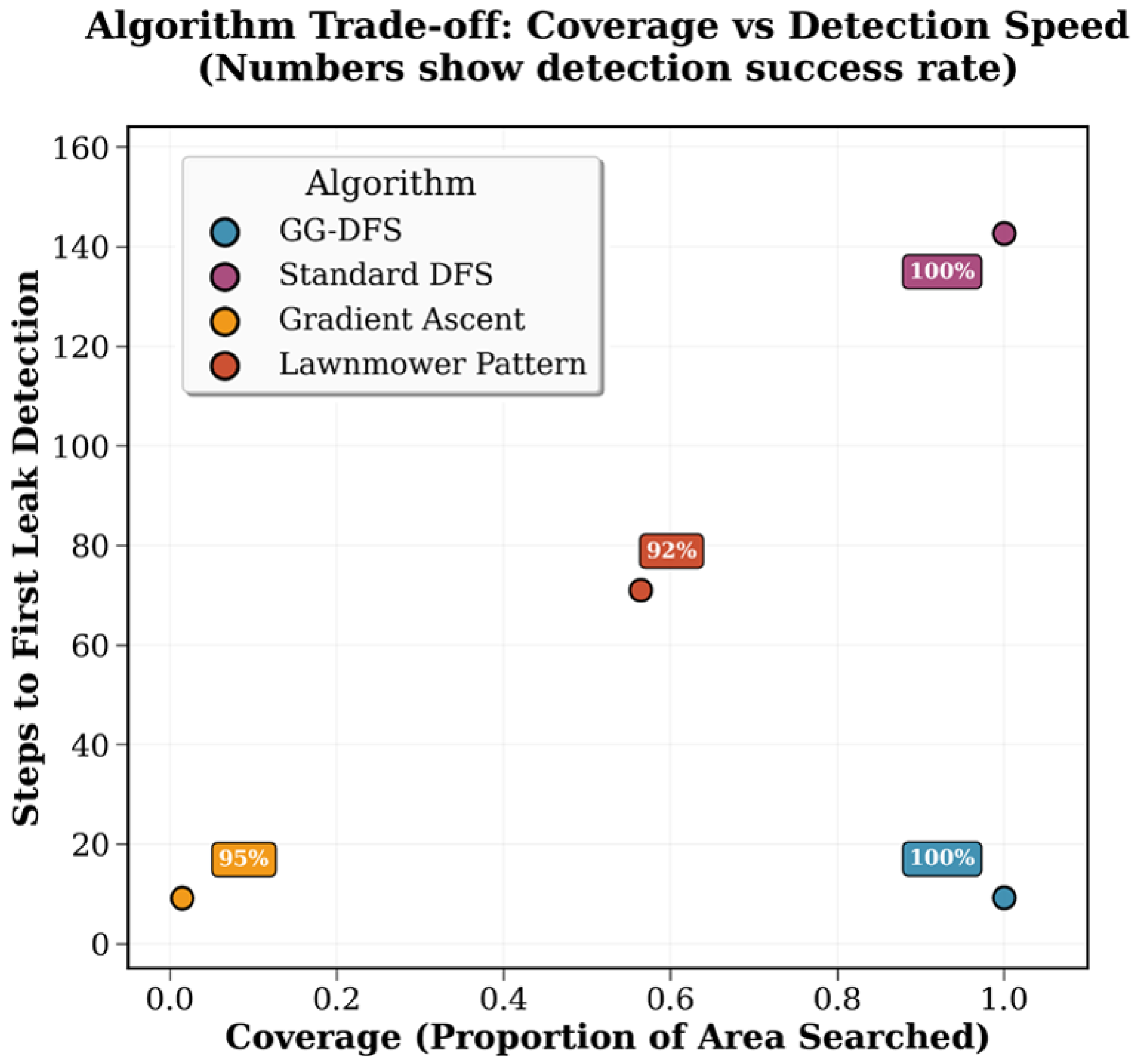
Gas leak detection algorithms must balance multiple competing objectives: detection speed, exploration completeness, and reliability. Figure 11 presents a comprehensive trade-off analysis positioning each algorithm across key performance dimensions.

The quantitative multi-criteria performance metrics corresponding to this analysis are summarized in

Table 4. Multi-criteria performance comparison.

Algorithm	Detection	Coverage	Reliability	Composite
	Speed Score *	Score †	Score ‡	Score §
GG-DFS	0.95	1.00	1.00	0.98
Standard DFS	0.30	1.00	1.00	0.65
Gradient Ascent	0.96	0.02	0.25	0.53
Lawnmower Pattern	0.65	0.56	0.63	0.64

* Normalized inverse of mean detection steps (lower steps = higher score); ^† Coverage percentage normalized to 0–1 scale; ^‡ Complete detection rate across all scenarios; ^§ Weighted composite: Speed (0.35) + Coverage (0.25) + Reliability (0.40).

.

Trade-off Insights:

• Balanced Performance Achievement: GG-DFS uniquely delivers superior performance across all three evaluation criteria, achieving the highest composite score of 0.98.
• Traditional Algorithm Limitations: Existing approaches exhibit single-criterion optimization—Pure Gradient Ascent prioritizes speed at the expense of coverage and reliability, while Standard DFS ensures systematic completeness but compromises response time.
• Multi-Criteria Superiority: GG-DFS demonstrates performance dominance by eliminating traditional trade-offs, delivering near-optimal speed (0.95) with perfect coverage (1.00) and reliability (1.00).
• Industrial Applicability: The weighted composite scoring methodology reflects safety-critical application requirements where comprehensive coverage and detection reliability take precedence over pure speed optimization.

This analysis confirms that GG-DFS effectively addresses the fundamental trade-offs inherent in autonomous exploration for gas leak detection.

5.9. Algorithm Reliability and Consistency Analysis

For safety-critical applications like gas leak detection, algorithm reliability and consistency are paramount.

Table 5. Algorithm reliability and consistency metrics.

Algorithm	Complete	Coefficient	Min	Max	Failure
	Detection Rate *	of Variation	Steps	Steps	Rate
GG-DFS	100.0%	0.78	2	30	0.0%
Standard DFS	100.0%	1.41	15	798	0.0%
Gradient Ascent	25.0% †	0.82	2	30	75.0% †
Lawnmower Pattern	62.5%	1.33	8	400	37.5%

* Percentage of runs where all leak sources were detected; ^† Gradient Ascent only detects all leaks in single-leak scenarios.

presents detailed reliability metrics calculated across all experimental runs.

Reliability Analysis:

• Perfect Reliability: GG-DFS achieves a 100% complete detection rate across all scenarios and leak densities.
• Predictable Performance: Low coefficient of variation (0.78) indicates consistent performance suitable for operational deployment.
• Bounded Execution Time: Maximum detection time of 30 steps provides predictable response times for emergency scenarios.
• Zero Failure Rate: Unlike gradient-based approaches that fail in multi-leak scenarios, GG-DFS maintains a perfect success rate.

These reliability metrics confirm GG-DFS as the most dependable algorithm for safety-critical gas leak detection applications.

Practical Implications and Scope: While the presented results clearly demonstrate the advantages of the proposed GG-DFS algorithm under controlled simulation conditions, it should be noted that these environments are idealized, assuming a static, homogeneous, and noise-free diffusion field. Consequently, the reported improvements primarily illustrate the algorithmic principles and relative performance rather than direct real-world behavior. In practical deployments, gas dispersion is influenced by turbulence, airflow, temperature gradients, and sensor noise, which can alter gradient characteristics. Future work will extend this study by incorporating dynamic and noisy diffusion models and by benchmarking GG-DFS against advanced metaheuristic algorithms such as Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO) to further assess its applicability in realistic, multi-source environments.

5.10. Limitations and Future Work

While our experimental results demonstrate the effectiveness of the GG-DFS algorithm, several limitations warrant discussion and suggest directions for future research.

5.10.1. Current Limitations

• Simplified Diffusion and Sensing Model: The current formulation (Equations (1)–(5)) represents an idealized, stationary diffusion field and assumes noise-free gas concentration measurements. It neglects transient dynamics, turbulence, multi-source interaction effects, and sensor noise or drift. While these simplifications enable clear algorithmic benchmarking and controlled evaluation of the GG-DFS framework, they introduce a gap between the simulated and real-world diffusion-sensing processes. Future work will address these aspects by incorporating stochastic sensor models, turbulence-aware diffusion simulation, and physical robot experiments in dynamic environments.
• Path Redundancy: The algorithm exhibits significant backtracking behavior, with total path length (1599 steps) approximately doubling the number of unique positions visited (800 cells). This redundancy, while ensuring completeness, represents an opportunity for efficiency improvements through enhanced memory mechanisms that retain exploration history over longer time horizons.
• Stochastic Tie-Breaking: The current implementation employs random selection when multiple neighboring cells exhibit identical maximum gradient values. While this approach prevents systematic bias, it may not optimize global exploration objectives. More sophisticated tie-breaking mechanisms incorporating distance to unexplored regions or concentration field topology could improve overall efficiency.
• Directional Bias: Statistical analysis reveals subtle directional preferences in robot movement patterns, with westward movements comprising 15.3% versus 10.5% for northwestern movements. Although this asymmetry is relatively minor, it suggests potential improvements through more balanced exploration strategies.
• Limited Sensing Range: The algorithm restricts gradient estimation to immediate eight-cell neighborhoods, potentially missing valuable directional information available over larger spatial scales. Extended sensing ranges could enhance gradient-following performance, particularly in environments with gradual concentration transitions.
• Parameter Sensitivity: The performance of GG-DFS depends on the dispersion coefficient $\tau$, which controls the steepness of gas concentration gradients. A detailed sensitivity analysis for $\tau \in \{2.0,5.0,8.0\}$ is presented in Section 5.5, revealing trade-offs between detection speed and exploration efficiency. Future work could explore adaptive $\tau$ selection based on real-time environmental conditions.

5.10.2. Future Research Directions

• Memory-Enhanced Exploration: Development of long-term spatial memory systems to reduce backtracking while maintaining completeness guarantees represents a promising research direction. Hierarchical exploration strategies combining local gradient-following with global path planning could significantly improve efficiency.
• Distance-Based Weight Adjustment: Incorporating a distance-based weighting strategy around already identified leak points can help minimize repetitive exploration in high-concentration regions. Such an approach has the potential to make the subsequent search phase faster and improve the algorithm’s ability to detect multiple sources efficiently.
• Expanded Simulation Environments: Testing the GG-DFS algorithm in more varied and challenging simulation setups, incorporating factors like turbulent dispersion, changing airflow conditions, and irregular obstacle distributions would provide deeper insights into its stability and adaptability under realistic operational scenarios.
• Adaptive Parameter Control: Implementation of online parameter adaptation mechanisms based on local concentration field characteristics could optimize algorithm performance across diverse environmental conditions without requiring manual tuning.
• Advanced Gradient Estimation: Investigation of sophisticated gradient estimation techniques incorporating temporal dynamics, sensor fusion, and uncertainty quantification could improve robustness in complex environments with turbulent gas dispersion patterns.
• Real-World Validation: Comprehensive evaluation in actual industrial environments with physical robots, realistic sensor noise, and environmental disturbances will validate simulation findings and identify additional practical considerations for deployment.

5.11. Conclusions

This paper presents the Gradient-Guided Depth-First Search (GG-DFS) algorithm, a novel approach that achieves measurable improvements across multiple evaluation criteria while maintaining both rapid detection and comprehensive coverage guarantees.

Experimental validation across 160 independent simulation runs demonstrates key quantitative advantages of the proposed approach. The algorithm locates the first leak source in 9.3 ± 7.3 steps, achieving 93.5% faster detection than standard DFS while maintaining 100% coverage completeness and 100% detection reliability.

The algorithm also demonstrates scalability, requiring 70% fewer steps for initial detection in four leak scenarios compared to single-leak environments, attributed to gradient amplification effects. Statistical analysis confirms robust performance, with the highest composite performance score (0.98) and low variability (coefficient of variation: 0.78).

The modular GG-DFS architecture supports adaptation to diverse sensing modalities and environmental conditions while preserving theoretical completeness. It provides a reliable and efficient framework for autonomous gas leak detection with practical deployment potential. Future work will extend the framework to dynamic and noisy diffusion environments through adaptive parameter control and memory-enhanced exploration to further improve efficiency and robustness in real-world systems.