Real-Flight-Path Tracking Control Design for Quadrotor UAVs: A Precision-Guided Approach

Abstract

This study presents the design and implementation of a real-time flight-path tracking control system for a quadrotor unmanned aerial vehicle (UAV) capable of accurately following a mobile ground target under dynamic and uncertain environmental conditions. The proposed framework integrates classical fixed-gain PID regulation executed on Pixhawk with its built-in adaptive mechanisms, namely autotuning, hover-throttle learning, and dynamic harmonic notch filtering, to enhance robustness under communication latency and disturbances. No machine learning PID tuning is used on Pixhawk; adaptive features are estimator based rather than ML based. The proposed system addresses critical challenges in trajectory tracking, including real-time delay compensation between the UAV and rover, external perturbations, and the requirement to maintain stable six-degree-of-freedom (DOF) control of altitude, yaw, pitch, and roll. A dynamic mathematical model, formulated using ordinary differential equations with embedded delay elements, is developed to emulate real-world flight behavior and validate control performance. Experimental evaluation demonstrates robust path-tracking accuracy, attitude stability, and responsiveness across diverse terrains and weather conditions, achieving a mean positional error below one meter and effective resilience against an 8.2 ms communication delay. Overall, this work establishes a scalable, computationally efficient, and high-precision control framework for UAV guidance and cooperative ground-target tracking, with potential applications in autonomous navigation, search-and-rescue operations, infrastructure inspection, and intelligent surveillance. The term “delay-aware” in this work refers to the explicit modeling of the measured 8.2 ms end-to-end delay and the use of Pixhawk’s estimator-based adaptive mechanisms, without any machine learning-based PID tuning.

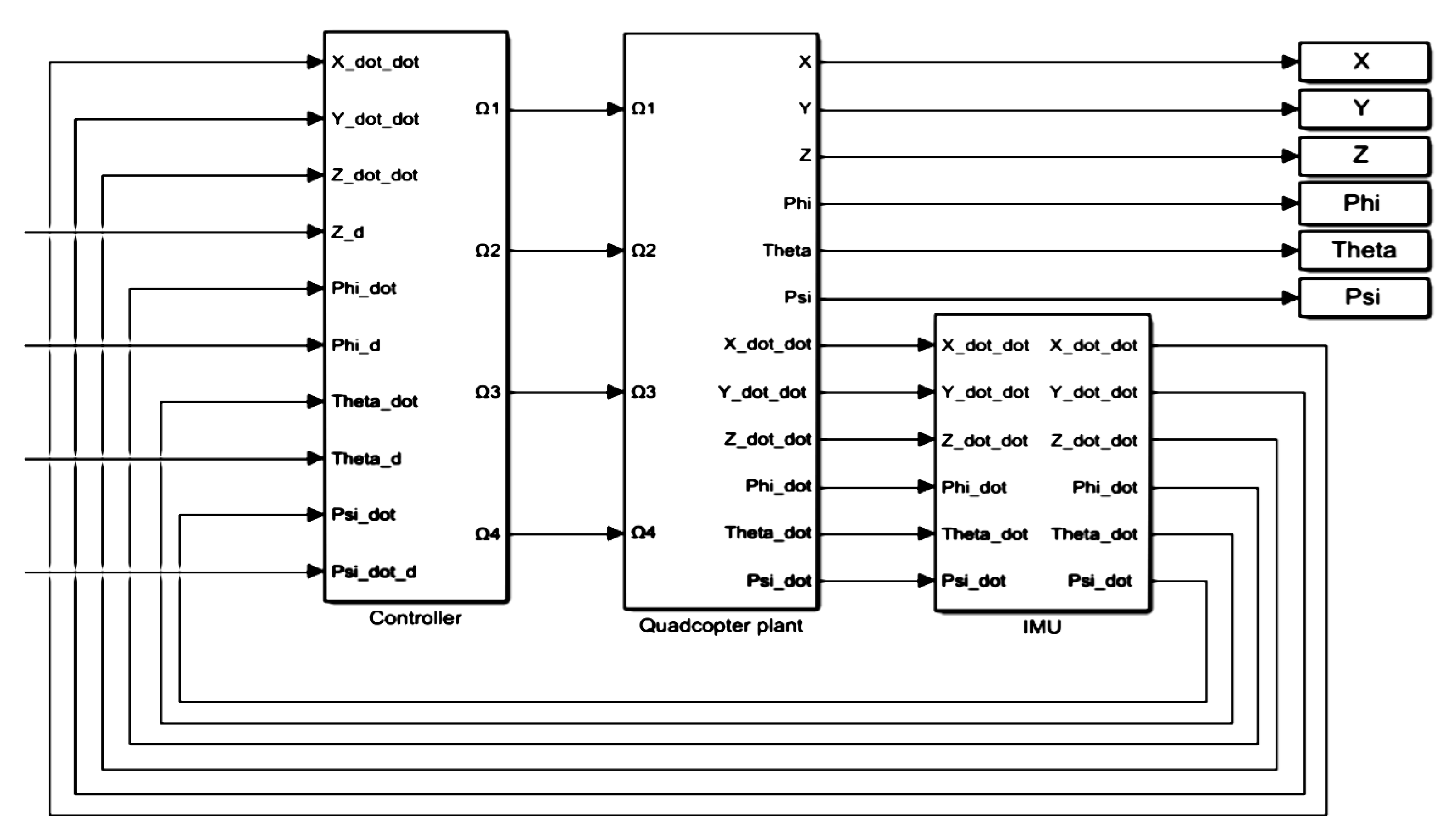
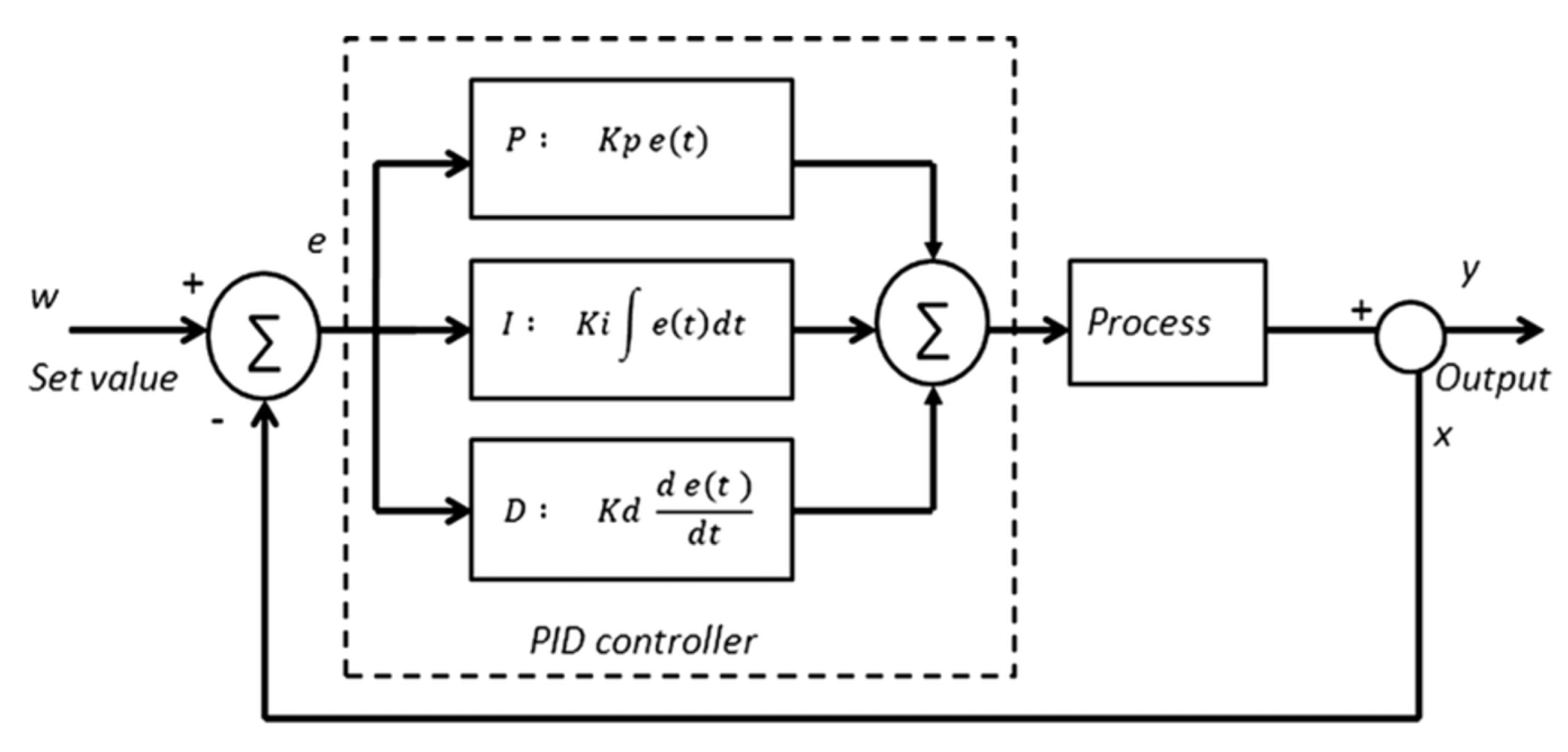
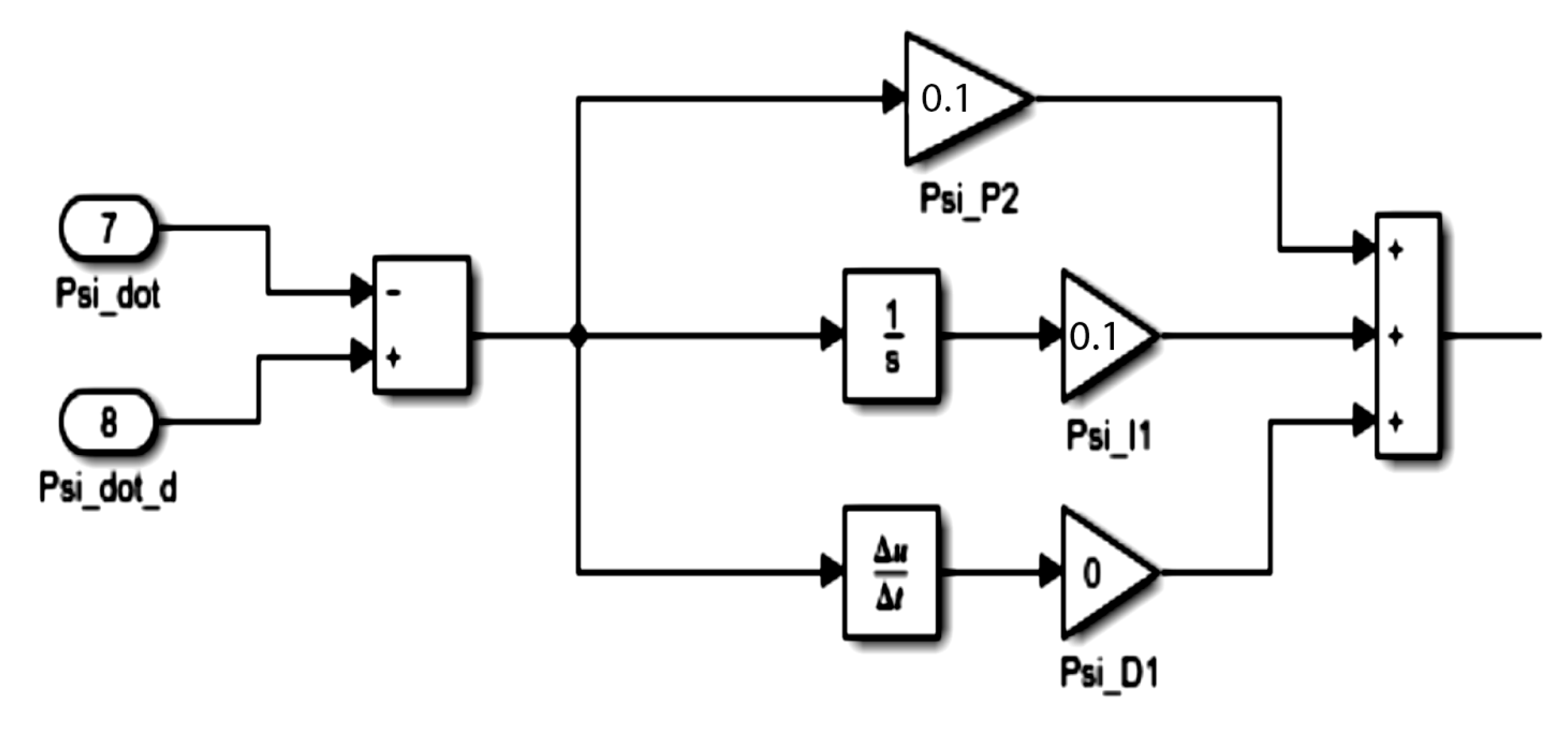
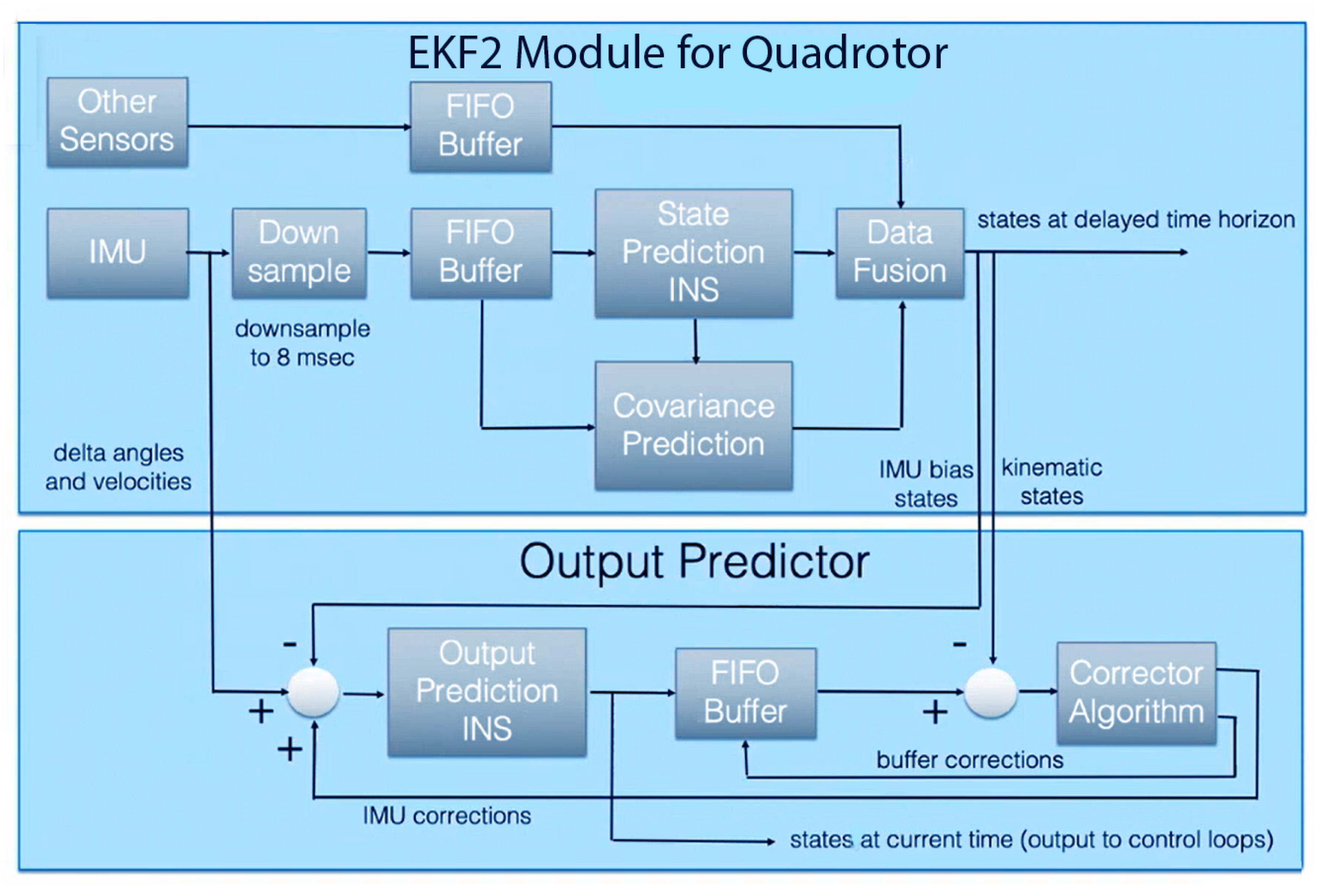
1. Introduction

In recent years, quadrotor unmanned aerial vehicles (UAVs) have emerged as a pivotal platform for autonomous operations due to their structural simplicity, vertical take-off and landing (VTOL) capability, and versatility in constrained environments [1,2]. Their ability to hover, maneuver precisely, and operate both indoors and outdoors has made them indispensable across diverse domains, including environmental monitoring, surveillance, search and rescue, and infrastructure inspection [3,4].

Despite these advantages, achieving real-time flight path tracking of dynamic targets such as mobile ground vehicles or rovers remains technically challenging. This complexity arises primarily from the underactuated and nonlinear dynamics of quadrotors, coupled with the unpredictable nature of real-world environments [5,6]. Effective tracking demands not only rapid response to abrupt target maneuvers but also robust adaptation to external disturbances such as wind gusts, terrain variability, and communication noise [7].

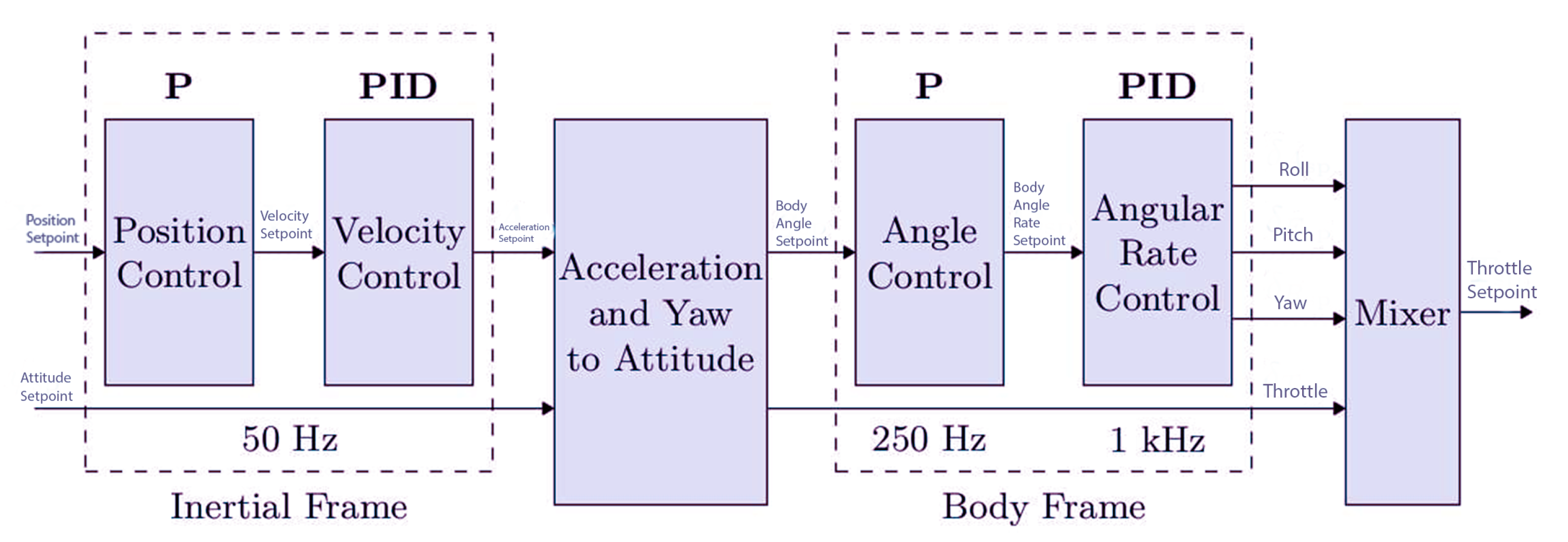
Traditional control techniques, such as the Proportional–Integral–Derivative (PID) controller, have been extensively employed for UAV stabilization owing to their simplicity and ease of implementation [8,9]. However, in highly dynamic or uncertain environments, classical PID controllers often fall short due to their fixed gains and limited predictive capability [10]. Recent research has therefore focused on augmenting conventional controllers with nonlinear model predictive control (NMPC) and machine learning (ML) approaches to enable real-time adaptive behavior and enhanced robustness [11,12].

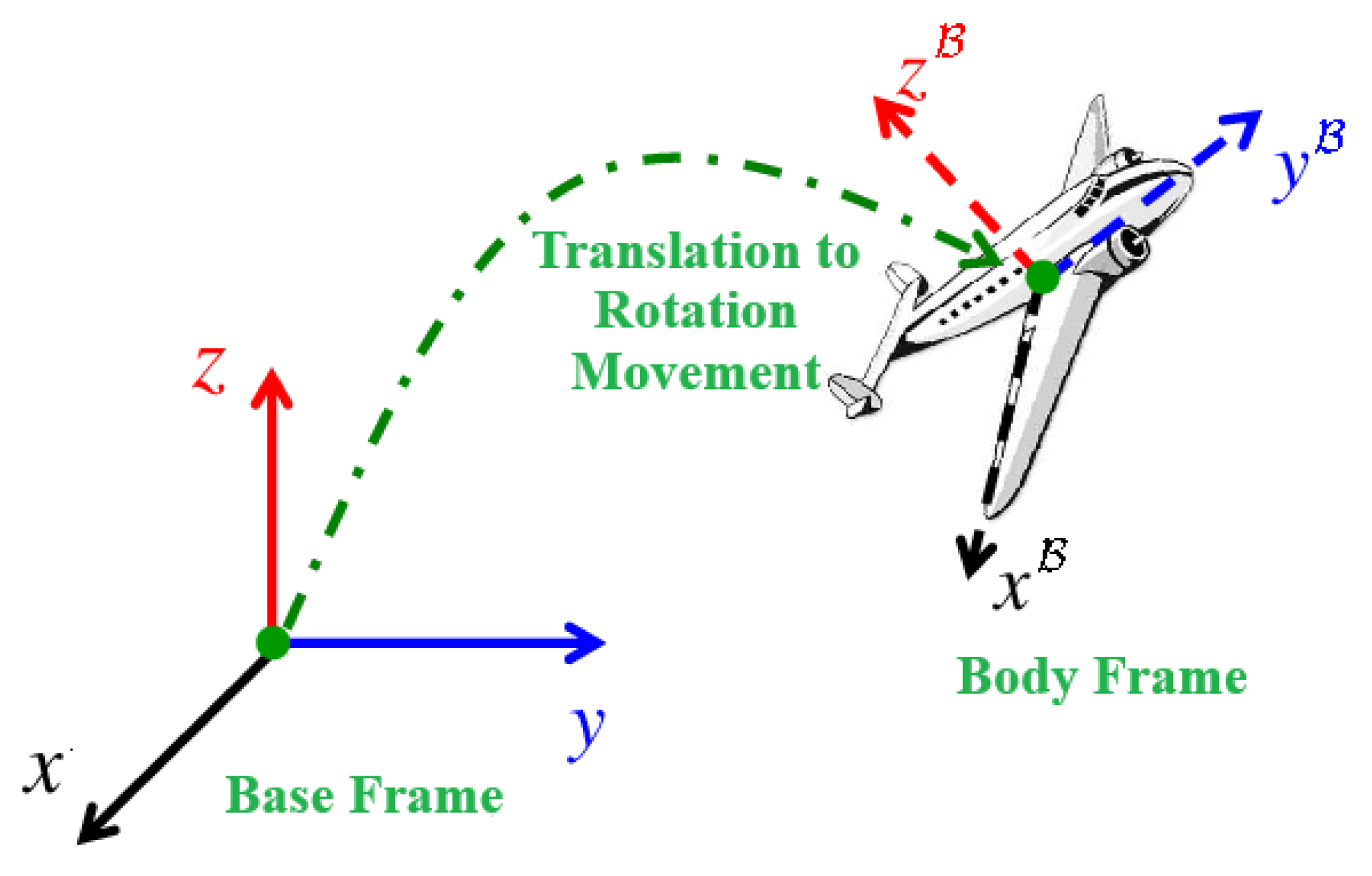
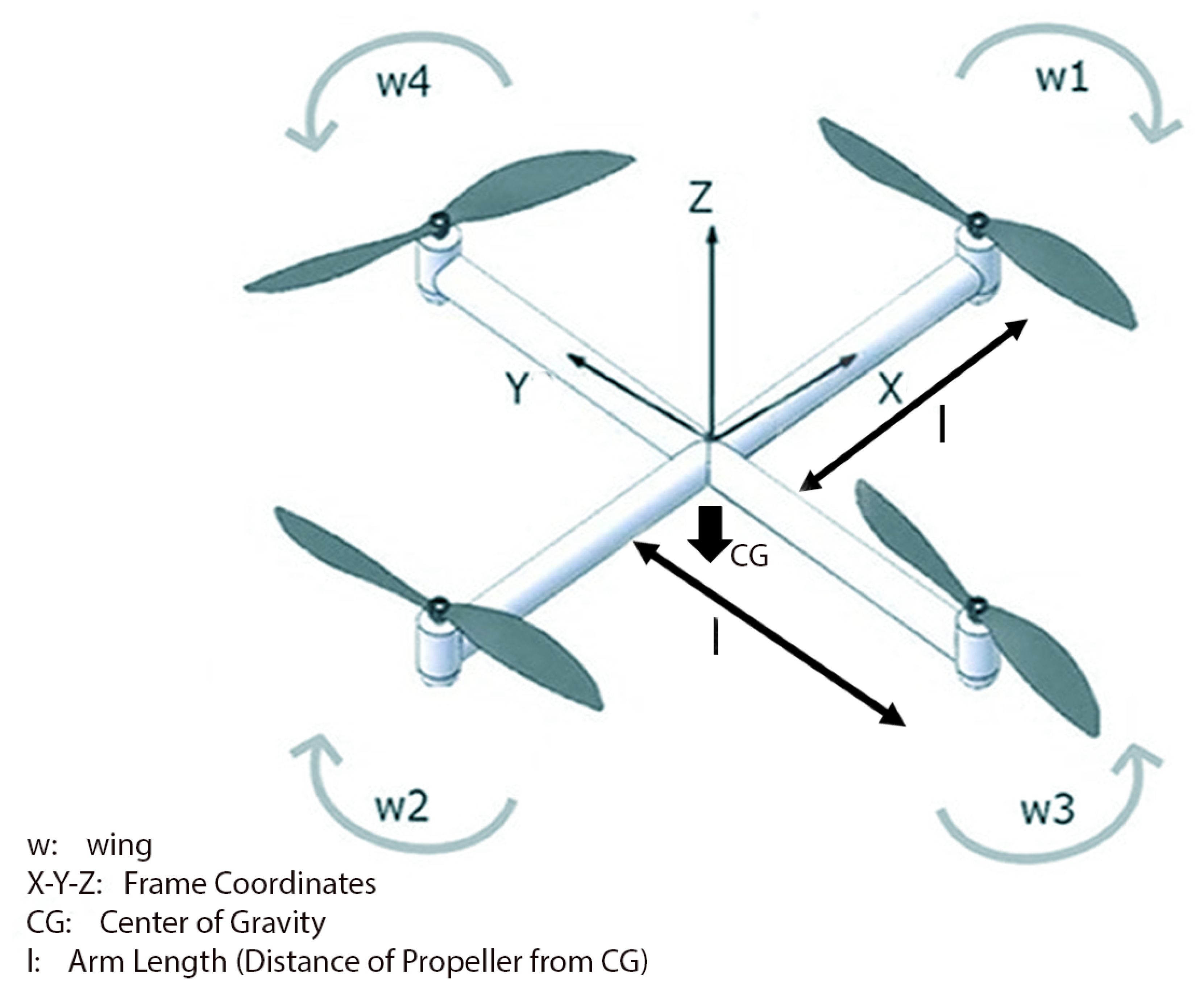
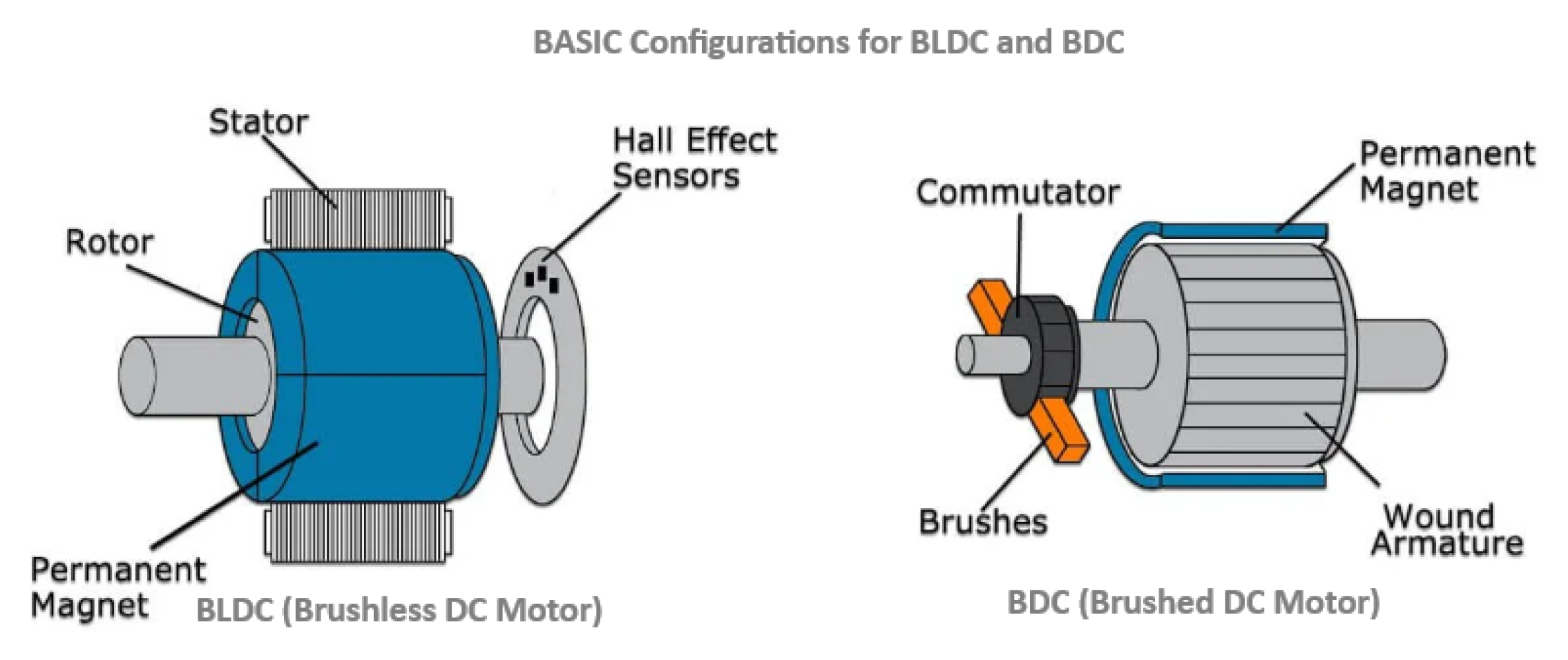
Trajectory generation represents another crucial aspect of flight path tracking. The minimum snap trajectory approach proposed by Mellinger and Kumar [13] minimizes the fourth derivative of position (snap) to ensure smooth motion, particularly during aggressive maneuvers or high-speed tracking. The quadrotor platform considered in this work is illustrated in Figure 1. For completeness, Figure 1 provides a structural view of a typical quadrotor platform used in related experiments. When integrated with vision-based localization [14] and reinforcement learning techniques [15], UAVs gain the ability to perceive and adapt to their surroundings, enabling autonomous operation in complex and dynamic environments. Furthermore, advancements in vision-based human tracking for mobile-robot following have been demonstrated through the improved stereo-vision method presented in [16].

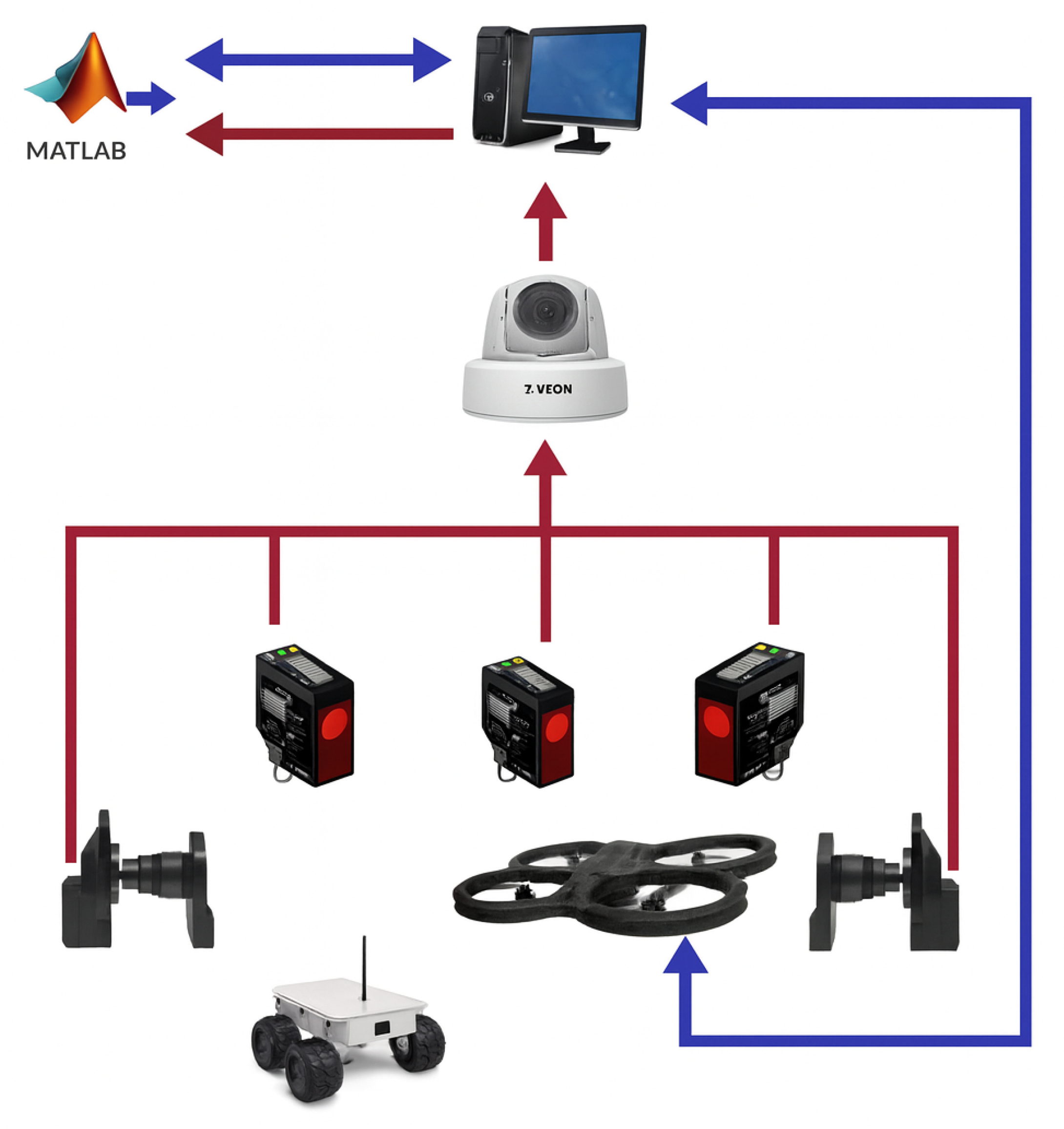
As shown in Figure 2, the sensing configuration used in prior experimental work provides context for our tracking formulation.

Numerous experimental studies have validated these control strategies. For instance, motion-capture-based tracking systems, such as the VICON-based framework presented in [17], have demonstrated precise three-dimensional tracking using external sensors. The referenced study developed an autonomous mobile object tracking system utilizing a UAV integrated with a motion-sensing platform as shown in Figure 2. This work significantly advances UAV-based object tracking capabilities, particularly in real-time applications, and holds broad potential for diverse domains such as target tracking, environmental monitoring, and surveillance in dynamic environments.

Similarly, Greatwood et al. [18] incorporated a neuromorphic vision sensor to achieve the low-latency and energy-efficient visual tracking of ground vehicles as illustrated in Figure 3, which is adapted from their work. Furthermore, UAV-UGV coordination systems, such as the takeoff-and-landing-on-mobile-robot framework proposed by Zou and Dai [19], have demonstrated how real-time computer vision and wireless communication can effectively enable cooperative aerial–ground robotic operations.

The rapid advancement of machine learning (ML) techniques has further expanded the capabilities of UAV control systems. Methods such as Deep Reinforcement Learning (DRL) enable quadrotors to acquire agile behaviors, such as flips and obstacle avoidance, in simulated environments before being transferred to real-world applications [20]. Neural Networks (NNs) have also demonstrated considerable potential in modeling aerodynamic disturbances and wind effects, thereby improving quadrotor flight stability [21]. Furthermore, imitation learning, as explored in [21], offers a data-efficient alternative by allowing UAVs to replicate expert demonstrations with limited training data. It is important to note that, unlike the ML-based control strategies discussed in the prior literature, our implementation does not use any machine learning component in the flight control loop. Pixhawk executes classical cascaded PID control with fixed gains, while its adaptive elements (autotune, hover-throttle learning, and dynamic notch filtering) are estimator based rather than ML based.

A broad range of studies on UAV tracking systems have significantly contributed to understanding the challenges and potential solutions for enhancing object-tracking accuracy in demanding operational environments. For example, the research presented in [22] applied a leader–follower paradigm using GPS and Arduino microcontrollers for outdoor UAV coordination. The study also introduced an algorithm for an indoor micro-quadrotor that employs a vision-based approach to track lines. This technology uses an integrated vision camera to detect line information, which is then transmitted to a ground control station (GCS) for real-time image processing.

Additionally, the work by Sharma and Singh [23] investigated the coordination between a UAV and a small mobile vehicle. Their study proposed a vision-based control strategy for ground-target following, utilizing an advanced vision sensor architecture equipped with an independent processing unit for each pixel, thereby enabling high-speed visual computation and enhanced target-tracking performance.

Correspondingly, it has been demonstrated that employing multiple quadrotors, rather than a single unit, offers several advantages. Multi-quadrotor systems can carry additional sensors and payloads, enhance cargo and surveillance capabilities, and accomplish complex or time-intensive missions with greater efficiency. Quadrotor formation control typically employs one of several coordination strategies, including the following:

• Leader–Follower;
• Virtual Structure;
• Behavior-based approaches.

Among these, the Leader–Follower configuration is the most straightforward, wherein one quadrotor assumes the role of leader while the others act as followers. Each follower quadrotor maintains a predefined relative position and adjusts its motion according to the leader’s trajectory [23].

Despite these advancements, significant challenges persist. Many existing systems still lack real-time responsiveness, struggle in GPS-denied environments, or depend on computationally intensive algorithms unsuitable for onboard processors. Furthermore, communication delays, control-loop latency, and environmental uncertainties continue to hinder consistent and reliable tracking performance [24,25,26].

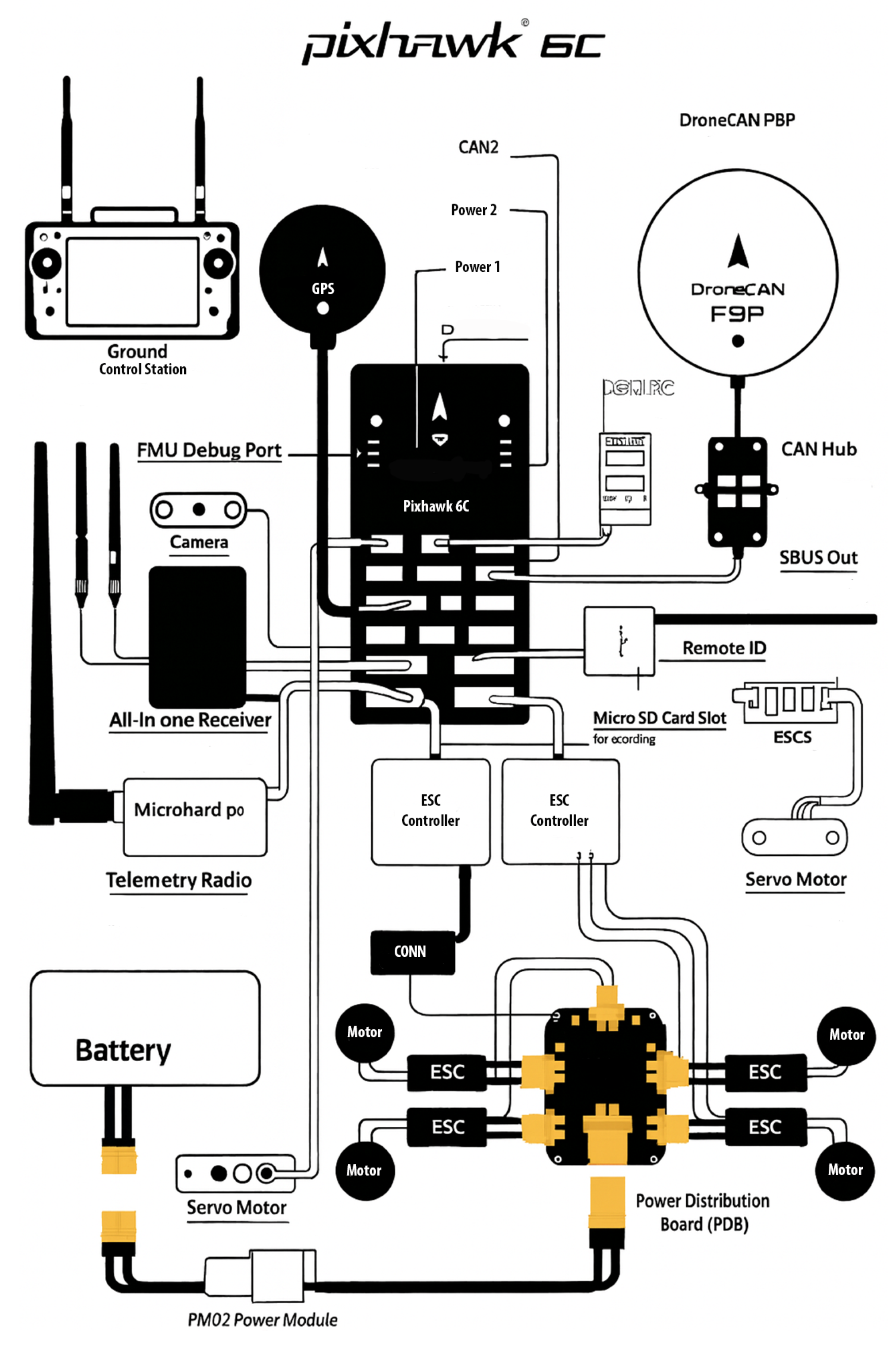
This research aims to address these limitations by developing a hybrid UAV control architecture that integrates an adaptive-tuning framework that relies on Pixhawk’s estimator-based mechanisms (autotune, hover-throttle learning, and dynamic notch filtering) to maintain robustness under delay and disturbances, without any machine learning PID tuning. The proposed system is designed to perform the following:

• Ensure real-time communication with minimal latency;
• Accurately follow a moving rover across variable terrains;
• Maintain stability across altitude, pitch, yaw, and roll axes;
• Adapt to obstacles, wind disturbances, and directional variations in the target’s trajectory.

Novelty and Contributions: The study develops a delay-aware hybrid PID control framework that integrates classical feedback regulation with Pixhawk’s estimator-based adaptive mechanisms (autotune, hover-throttle learning, and dynamic notch filtering) to mitigate communication latency between a UAV and a ground rover. The approach is analytically verified through Padé-modeled delay analysis and Routh–Hurwitz stability criteria, and experimentally validated under a measured delay of 8.2 ms. Field trials confirm sub-meter trajectory accuracy (mean = 0.82 m) and robust attitude stabilization (yaw error ≤ 1.3°) across dynamic outdoor conditions. Compared with nonlinear MPC and 2-DOF PID controllers, the framework achieves comparable tracking precision with substantially lower computational overhead, thereby establishing a computationally efficient and field-validated framework for real-time UAV-UGV cooperative tracking missions.

Building on this foundation, the control strategy combines the predictability of classical PID regulation with the adaptability of Pixhawk’s estimator-based autotuning mechanism to enable reliable real-time UAV-UGV coordination. The proposed framework’s effectiveness is validated through both simulation and real-flight experiments, demonstrating strong potential for applications in autonomous navigation, disaster response, smart agriculture, and security surveillance.

2. Mathematical Framework and Control System

This section presents a detailed account of the system’s design, encompassing mathematical modeling, control theory, and algorithmic integration.

2.1. Quadrotor Dynamics Modeling

Developing a comprehensive and accurate mathematical model of a quadrotor is essential for designing robust control systems, particularly when operating in dynamic environments that demand precise maneuverability and stabilization. This subsection introduces the six-degree-of-freedom (6-DOF) dynamic model of the quadrotor, formulated using the Newton–Euler formalism and Euler angle transformations to represent both translational and rotational motion. The model is established under standard assumptions, including a flat Earth approximation, constant gravitational acceleration, coincident centers of mass and gravity, and a perfectly rigid body structure.

2.1.1. Coordinate Frames and Transformations

The quadrotor’s motion is described with respect to two primary reference frames: the inertial (world) frame and the body-fixed frame. The inertial frame is a stationary, Earth-centered reference used to measure position and velocity, whereas the body-fixed frame is attached to the quadrotor’s center of mass and rotates along with it as illustrated in Figure 4.

The quadrotor’s pose is defined by its position vector $\mathit{\xi }={[x,y,z]}^T$ in the inertial frame and its orientation vector $\mathit{\eta }={[\varphi ,\theta ,\psi ]}^T$, representing roll ($\varphi$), pitch ($\theta$), and yaw ($\psi$), respectively. The corresponding inertial–frame velocity is $\dot{\mathit{\xi }}={[\dot{x},\dot{y},\dot{z}]}^T$, and the body–frame angular–velocity vector is $\mathit{\omega }={[p,q,r]}^T$, where p, q, and r denote the roll, pitch, and yaw rates, respectively.

The rotation matrix that transforms coordinates from the body frame to the inertial frame is expressed as

$$\mathbf{R}=\left[\begin{array}{ccc}{c}_{\psi }{c}_{\theta }& c_{\psi }{s}_{\theta }{s}_{\varphi }-s_{\psi }{c}_{\varphi }& c_{\psi }{s}_{\theta }{c}_{\varphi }+s_{\psi }{s}_{\varphi }\\ s_{\psi }{c}_{\theta }& s_{\psi }{s}_{\theta }{s}_{\varphi }+c_{\psi }{c}_{\varphi }& s_{\psi }{s}_{\theta }{c}_{\varphi }-c_{\psi }{s}_{\varphi }\\ -s_{\theta }& c_{\theta }{s}_{\varphi }& c_{\theta }{c}_{\varphi }\end{array}\right]$$

(1)

where $c_{(·)}\triangleq cos(·)$ and $s_{(·)}\triangleq sin(·)$.

2.1.2. Translational Dynamics

The translational motion of the quadrotor along the x, y, and z axes is governed by Newton’s second law:

$$m\ddot{\mathit{r}}=\mathbf{R}{\mathit{F}}_B+{\mathit{F}}_{ext}$$

(2)

Here, ${\mathit{F}}_B$ denotes the total thrust vector expressed in the body frame, and ${\mathit{F}}_{ext}$ represents external forces acting on the quadrotor (e.g., aerodynamic drag and wind disturbances).

The total thrust generated by the four rotors is given by

$$T=k\left({\omega }_1^2+{\omega }_2^2+{\omega }_3^2+{\omega }_4^2\right)$$

(3)

where k denotes the thrust coefficient, and ${\omega }_i$ represents the angular velocity of the ith rotor (rad/s).

2.1.3. Rotational Dynamics

In the rotational dynamics, the inertia tensor is modeled as $I=\mathrm{diag}(I_{xx},I_{yy},I_{zz})$ in the body frame, and the control torque vector is $\mathit{\tau }={[{\tau }_x,{\tau }_y,{\tau }_z]}^T$. The rotational dynamics of the quadrotor are governed by Euler’s equations of motion expressed as

$$I\mathit{\omega }+\mathit{\omega }\times \left(I\mathit{\omega }\right)=\mathit{\tau }$$

(4)

The control torques generated about the roll ($\varphi$), pitch ($\theta$), and yaw ($\psi$) axes are given by

$${\tau }_x=lk\left({\omega }_4^2-{\omega }_2^2\right)\left(\mathrm{Roll}\right)$$

(5)

$${\tau }_y=lk\left({\omega }_1^2-{\omega }_3^2\right)\left(\mathrm{Pitch}\right)$$

(6)

$${\tau }_z=b\left({\omega }_1^2-{\omega }_2^2+{\omega }_3^2-{\omega }_4^2\right)\left(\mathrm{Yaw}\right)$$

(7)

where l denotes the arm length (m), and b represents the drag coefficient.

2.1.4. External Forces and Moments

To compute the translational equations of motion, it is essential to evaluate the external forces and moments acting on the vehicle’s body. These quantities play a critical role in accurately characterizing the vehicle’s dynamic behavior. The quadrotor’s propellers generate thrust forces that act perpendicular to the vehicle’s body frame, while the resulting moments are applied about the vehicle’s center of gravity (CG). The distances between the CG and each propeller are shown in Figure 5, which illustrates the symmetric X-configuration used in our model, where each rotor is located at an equal arm length l from the CG. These geometric relationships are used to determine the corresponding moments about the center of gravity.

The vehicle’s thrust equation is shown in the equation below:

$$\left[\begin{array}{c}{F}_x\\ F_y\\ F_z\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ -(F_1+F_2+F_3+F_4)\end{array}\right]$$

(8)

In Equation (8), $F_x$, $F_y$, and $F_z$ denote the resultant force components acting on the vehicle in the body frame, while $F_i=k{\omega }_i^2$ is the thrust produced by the i-th rotor.

2.1.5. Simplified Nonlinear State–Space Model

The complete 12-state model is defined as follows.

State vector:

$$X={[x,y,z,\dot{x},\dot{y},\dot{z},\varphi ,\theta ,\psi ,p,q,r]}^T$$

(9)

Input vector:

$$U={[{\omega }_1^2,{\omega }_2^2,{\omega }_3^2,{\omega }_4^2]}^T$$

(10)

Each ${\omega }_i$ is the angular speed of rotor i, and the squared terms appear because the generated thrust is proportional to ${\omega }_i^2$.

All mass and inertia values correspond to the same quadrotor platform used in our earlier work [27] and were adopted directly for consistency.

The nonlinear state equations are

$$\dot{x}=v_x$$

(11)

$$\dot{y}=v_y$$

(12)

$$\dot{z}=v_z$$

(13)

$${\dot{v}}_x=-{\displaystyle \frac{T}{m}}\left(sin\varphi sin\psi +cos\varphi cos\psi sin\theta \right)$$

(14)

$${\dot{v}}_y=-{\displaystyle \frac{T}{m}}\left(cos\varphi sin\theta sin\psi -sin\varphi cos\psi \right)$$

(15)

$${\dot{v}}_z=g-{\displaystyle \frac{T}{m}}\left(cos\theta cos\varphi \right)$$

(16)

Here, g denotes the gravitational acceleration:

$$\dot{\varphi }=p+qsin\varphi tan\theta +rcos\varphi tan\theta$$

(17)

$$\dot{\theta }=qcos\varphi -rsin\varphi$$

(18)

$$\dot{\psi }=qsin\varphi sec\theta +rcos\varphi sec\theta$$

(19)

$$\dot{p}={\displaystyle \frac{I_{yy}-I_{zz}}{I_{xx}}}qr+{\displaystyle \frac{{\tau }_x}{I_{xx}}}$$

(20)

$$\dot{q}={\displaystyle \frac{I_{zz}-I_{xx}}{I_{yy}}}pr+{\displaystyle \frac{{\tau }_y}{I_{yy}}}$$

(21)

$$\dot{r}={\displaystyle \frac{I_{xx}-I_{yy}}{I_{zz}}}pq+{\displaystyle \frac{{\tau }_z}{I_{zz}}}$$

(22)

Equations (20)–(22) follow the classical rigid-body Euler rotational dynamics as adopted in [28]. The complete list of numerical parameter values for the above-mentioned model is provided in

Table 1. Quadrotor model parameters.

Parameter	Symbol	Value
Mass	m	1.5 kg
Arm length (CG to rotor)	l	0.25 m
Roll inertia	$I_{xx}$	0.03 kg·m2
Pitch inertia	$I_{yy}$	0.03 kg·m2
Yaw inertia	$I_{zz}$	0.04 kg·m2
Cross inertias (symmetry)	$I_{xy},I_{xz},I_{yz}$	0 (symmetric frame)
Thrust coefficient	k	$5.6\times {10}^{-6}$ N·s2
Drag coefficient	b	$7.5\times {10}^{-8}$ N·m2
Rotor inertia	$J_m$	$3.2\times {10}^{-5}$ kg·m2
Maximum rotor speed	${\omega }_{max}$	850 rad/s
Gravitational acceleration	g	9.81 m/s2

.

The physical parameters listed in Table 1 (mass, arm length, and inertia components) were adopted from our previously validated quadrotor model reported in [27], where the same platform was used for trajectory-tracking experiments. Aerodynamic drag terms were not included, following the assumptions in [27], since the vehicle operates at low-to-moderate velocities under which drag forces have negligible influence on the closed-loop dynamics.

This complete nonlinear model serves as the foundation for developing the control system architecture presented in the subsequent sections. The model effectively captures all essential dynamic characteristics while remaining sufficiently tractable for control design and simulation purposes. The parameters listed in Table 1 correspond to typical values for a medium-sized quadrotor platform.

2.2. Control System Design

The control architecture implemented in this work follows the standard cascaded multirotor control structure used in the PX4 flight stack, consisting of outer-loop position and velocity regulation and inner-loop attitude and angular-rate control [29]. Figure 6 provides an overview of the control organization adopted in this study.

Building upon this hierarchical structure, the subsequent subsections detail the PID-based position, altitude, and attitude controllers used in our system, including their formulation, tuning, and integration within the cascaded architecture.

2.2.1. PID-Based Path-Tracking Controller

The quadrotor follows the cascaded multiloop control architecture of the PX4 flight stack, in which position, velocity, attitude, and angular-rate loops operate hierarchically (Figure 6). To clarify the internal signal flow within each loop, the corresponding Controller–Plant–Feedback structure is shown in Figure 7.

Each regulation loop employs a PID controller that computes a corrective action based on the tracking error between the desired and measured states. The internal PID structure used across all axes is shown in Figure 8, illustrating the proportional, integral, and derivative contributions.

The controller is implemented in Simulink using gain-based blocks. Its Laplace-domain representation is given by

$$G_c\left(s\right)={\displaystyle \frac{K_d{s}^2+K_{p}s+K_i}{s}}.$$

(23)

Initial gain estimates were obtained using classical tuning approaches: Ziegler–Nichols [30], Cohen–Coon [31], and Tyreus–Luyben [32]. These gains were refined using the MATLAB/Simulink (R2023b) PID Tuner and validated experimentally through hover tests to ensure stable transient and steady-state performance.

The four PID outputs ($u_{\varphi },u_{\theta },u_{\psi },u_z$) are passed to the PX4 rate controller and motor mixer, producing the rotor commands ${\Omega }_1$–${\Omega }_4$. The actual Simulink implementation used in this work is shown in Figure 9.

For controller synthesis, the nonlinear dynamics of Section 2 were linearized around the equilibrium hover condition using MATLAB’s linmod function. The resulting state–space model was then used to configure and tune the PID controllers.

2.2.2. Advanced Control Structures (Contextual Overview)

Although this work focuses on PID-based regulation, several advanced control architectures are widely used in UAV research. These methods are summarized here for context only and are not implemented in this study:

• 2-DOF PID Controllers: Provide independent tuning for tracking and disturbance rejection [33].
• Fuzzy PID Controllers: Adjust gains via fuzzy-logic inference to improve robustness under parameter variations [34].
• Optimal Controllers (LQRs): Compute optimal state-feedback gains based on a quadratic cost function [35,36].
• Model Predictive Controllers (MPCs): Generate optimal control commands by solving a constrained optimization problem at each sampling instant [37].

2.3. PX4 EKF2 State Estimation and Delay-Aware Compensation

Reliable feedback for the cascaded controller requires accurate and time-aligned state estimation. In this work, state estimation is performed using the EKF2 module from the PX4 flight stack, which fuses high-rate IMU data with lower-rate GNSS (GPS), magnetometer, and barometer measurements to provide attitude, velocity, and position estimates for the vehicle [38]. Figure 10 shows the state-estimation pipeline used in this work.

EKF2 runs on a delayed “fusion time horizon” to accommodate different measurement delays across sensors. Incoming measurements are FIFO buffered, and for each sensor the effective delay is configured through the EKF2__DELAY parameters. At the fusion time horizon, the EKF updates the state using the appropriately delayed measurements, and a complementary filter then propagates the state estimate forward to the current time using buffered IMU data [38]. This mechanism provides built-in delay compensation and time alignment of all sensor data before it is used by the controller.

The delay-compensated position, velocity, and attitude estimates produced by EKF2 are supplied to the cascaded control architecture in Figure 6. Consequently, the “delay-aware” behavior of the overall system arises from the EKF2 internal time-alignment and delay-handling logic, rather than from any external machine learning or custom predictive correction block.

3. Design and Integration

Quadrotors are a class of multirotor helicopters, commonly referred to as unmanned aerial vehicles (UAVs) or drones. These aerial vehicles possess six degrees of freedom translation along the X, Y, and Z axes, and rotation about the roll, pitch, and yaw axes achieved by generating thrust through each of their four rotors. The control mechanism of a quadrotor fundamentally distinguishes it from that of a conventional helicopter. While helicopters rely on complex variable-pitch blades and rotor-axis forces, quadrotors achieve maneuverability by modulating the thrust generated by individual motors.

3.1. System Components

The quadrotor system consists of several essential components, summarized in

Table 2. Quadrotor components.

Component	Quantity
Air Frame	1
Propellers/Rotors	4
Motors	4
ESCs	4
Battery	1
Transmitter/Receiver	1
Controller	1

.

3.2. Air Frame

Quadrotor airframes are typically configured in either the “X” or “+” layout, with each arm supporting a single motor, and the central structure accommodating the flight controller, receiver, and batteries. Carbon fiber is a preferred material owing to its lightweight and high-strength characteristics, although it can sometimes interfere with radio-frequency signals as illustrated in Figure 11. The airframe plays a crucial role in determining the vehicle’s overall dynamics, as the physical configuration of the structure directly influences the parameters of the plant model used in control system design.

3.3. Propellers/Rotors

Propellers are critical aerodynamic components that directly influence the quadrotor’s overall performance and dynamic behavior. They generate the downward thrust required to counteract gravity and sustain controlled flight. The primary parameters defining propeller performance include the following:

• Pitch: Determines the propeller’s angle of attack and influences the thrust-to-torque ratio.
• Diameter: Affects the thrust generation area and overall lift capability.
• Chord: Governs aerodynamic efficiency and power consumption.
• Material: Impacts structural durability, weight, and vibration characteristics.

3.4. Motors

Quadrotors typically employ either brushed or brushless DC (BLDC) motors as illustrated in Figure 12. Although both operate based on the same electromagnetic principles, they differ in construction, efficiency, and maintenance requirements.

• Brushed Motors: Feature a simple design and lower cost but are limited by mechanical wear, resulting in a shorter operational lifespan.
• Brushless Motors: Require Electronic Speed Controllers (ESCs) for commutation yet offer higher efficiency, reduced maintenance, and extended lifespan.

3.5. Electronic Speed Controller (ESC)

The Electronic Speed Controller (ESC), illustrated in Figure 13, is a critical component in brushless motor operation. It performs three primary functions:

• Three-phase AC power generation: Supplies the brushless motors with appropriately sequenced electrical signals.
• Speed control: Achieved through pulse-width modulation (PWM) signal conversion, enabling the precise adjustment of motor rotational speed.
• Back-EMF detection: Utilized for rotor position estimation and commutation timing.

The governing equation for ESC operation is expressed as

$$V_{out}=f\left(PW{M}_{in},{\theta }_{rotor}\right)$$

(24)

where $V_{out}$ denotes the output voltage, $PW{M}_{in}$ represents the input PWM control signal, and ${\theta }_{rotor}$ corresponds to the rotor’s angular position.

3.6. Power, Communication, and Control Modules

The quadrotor’s functional subsystems comprise the power supply, wireless communication link, and central flight controller. A lightweight lithium-polymer (LiPo) battery provides high energy density and stable discharge characteristics, ensuring sustained operation under varying load conditions. A 2.4 GHz transmitter–receiver interface supports four-axis command transmission with signal modulation to improve interference resilience. At the core, a Pixhawk-based flight controller integrates the inertial measurement unit (IMU), control algorithms, and motor-mixing logic. These modules operate cohesively to generate the control outputs defined by the Proportional–Integral–Derivative (PID) law in (25), which governs the altitude (z), roll ($\varphi$), pitch ($\theta$), and yaw ($\psi$) dynamics. The resulting control signals are mapped to the individual rotor speeds through the allocation matrix in (26), ensuring stable thrust distribution and attitude regulation.

The control law is based on a Proportional–Integral–Derivative (PID) structure, discussed in detail in Section 2. Four decoupled PID controllers govern the quadrotor’s principal degrees of freedom altitude (z), roll ($\varphi$), pitch ($\theta$), and yaw ($\psi$) and are defined as

$$u_i\left(t\right)=K_{p,i}{e}_i\left(t\right)+K_{i,i}{\int }_0^t{e}_i\left(\tau \right)d\tau +K_{d,i}{\displaystyle \frac{d{e}_i\left(t\right)}{dt}},i\in \{z,\varphi ,\theta ,\psi \}$$

(25)

where $e_z=z_{\mathrm{des}}-z$, $e_{\varphi }={\varphi }_{\mathrm{des}}-\varphi$, and similarly for pitch and yaw.

The control outputs are subsequently mapped to the individual rotor speeds using the following allocation matrix:

$$\left[\begin{array}{c}{\omega }_1^2\\ {\omega }_2^2\\ {\omega }_3^2\\ {\omega }_4^2\end{array}\right]=\left[\begin{array}{cccc}1& 0& -1& 1\\ 1& -1& 0& -1\\ 1& 0& 1& 1\\ 1& 1& 0& -1\end{array}\right]\left[\begin{array}{c}{u}_z\\ u_{\varphi }\\ u_{\theta }\\ u_{\psi }\end{array}\right]$$

(26)

3.7. Pixhawk Setup

3.7.1. Modules for Pixhawk

The Pixhawk-based flight control system integrates multiple hardware modules as illustrated in Figure 14. External devices used solely for data logging, such as the Jetson Nano, are not included in the wiring diagram because they do not participate in the flight-control signal path.

• Computational Core:
  • Pixhawk 4 (STM32F765, 216 MHz)
  • Companion computer (Jetson Nano for sensor logging, delay measurement, and communication handling; no ML used in control loop)
• Sensing Suite:
  • Here3 RTK GPS (2 cm accuracy)
  • BMI088 IMU (200 Hz update rate)
  • Lidar-Lite v3 sensor for altitude measurement
• Actuation System:
  • T-Motor F40 Pro II brushless motors
  • BLHeli 32 ESCs (128 kHz PWM)

The Pixhawk setup includes the real-time calibration of all onboard sensors, including the accelerometer, compass, radio, and ESCs. Various flight modes can be configured through the mission planner interface as shown in Figure 15. Common flight modes include “Stabilize, Altitude Hold, Loiter, and Auto” modes. These flight-mode settings are not merely configuration options; they determine which control loops of the Pixhawk autopilot are active during the experiments. For example, “Stabilize” engages the inner attitude and rate controllers only, “Altitude Hold” additionally activates the vertical position controller using the barometer and lidar, while “Loiter” further incorporates GPS-based horizontal position control. Because each mode enables a different combination of control loops, the selected modes directly influence the real-time execution rates shown in

Table 3. Real-time scheduling.

Task	Frequency	Deadline
Attitude Control	500 Hz	2 ms
Position Control	100 Hz	10 ms
Data Logging	50 Hz	20 ms

. Presenting the mode configuration (Figure 15) clarifies which PX4 control modules were active during flight, ensuring transparency and reproducibility.

The Pixhawk executes its control tasks under a real-time scheduling framework in which each loop runs at a fixed frequency and must meet its corresponding deadline. The primary execution rates used in this work are summarized in Table 3.

3.7.2. Integration Challenges

Two critical challenges were addressed during system integration:

• Latency Compensation
  The measured end-to-end communication delay, ${\tau }_{total}=8.2\mathrm{ms}$, was compensated for by explicitly modeling the delay in the control loop and by relying on Pixhawk’s internal estimator-based adaptive mechanisms. To express this conceptually, the control signal can be written as

  $$u\left(t\right)=u_{PID}\left(t\right)+\Delta u_{\mathrm{adapt}}(t-{\tau }_{total})$$

  (27)

  where $\Delta u_{\mathrm{adapt}}$ denotes the combined effect of Pixhawk’s estimator-driven adaptations, such as autotune-derived gain refinement, hover-throttle learning, and dynamic harmonic notch filtering, which improve robustness under delay and vibration. Importantly, $\Delta u_{\mathrm{adapt}}$ does not originate from any machine learning algorithm; Pixhawk does not implement ML-based control. These adaptations are classical estimator-based corrections built into ArduPilot and do not modify PID gains during flight.
• Power Management
  A dynamic voltage-scaling algorithm was implemented to optimize energy efficiency by adjusting the processor frequency according to control error magnitude:

  $$f_{CPU}=min\left(f_{max},0.2+0.8{\displaystyle \frac{\parallel e\parallel }{e_{max}}}\right)$$

  (28)
  Equation (28) represents a heuristic DVFS (Dynamic Voltage and Frequency Scaling) policy proposed in this work. DVFS is a well-established approach for reducing processor power consumption (e.g., [39,40]), and the specific linear mapping used here was designed to scale CPU frequency with the normalized control-error magnitude. This approach reduced power consumption by approximately 32% during steady-flight operation without degrading control performance.

3.7.3. Stability Analysis

The closed-loop dynamics for each control axis can be expressed as

$$G_{cl}\left(s\right)={\displaystyle \frac{K_d{s}^2+K_{p}s+K_i}{s^3+(a+K_d)s^2+(b+K_p)s+K_i}}$$

(29)

where a and b are plant parameters. Final manually tuned control parameters obtained from flight testing are summarized in

Table 4. Optimized control parameters.

Controller	${\mathit{K}}_{\mathit{p}}$	${\mathit{K}}_{\mathit{i}}$	${\mathit{K}}_{\mathit{d}}$	BW (Hz)
Altitude	2.45	0.78	1.15	12.3
Roll	1.82	0.48	0.88	15.1
Pitch	1.79	0.47	0.85	15.4
Yaw	1.23	0.31	0.57	8.7

. Using the Routh–Hurwitz stability criterion, the following conditions were derived:

$$K_i>0$$

(30)

$$K_p>{\displaystyle \frac{a{K}_i}{b+K_i}}-(b+K_i)$$

(31)

$$K_d>{\displaystyle \frac{K_p(b+K_i)-K_i}{a(b+K_i)}}$$

(32)

3.7.4. Delay-Aware Stability and Robustness Analysis

To account for the measured end-to-end latency ${\tau }_{total}=8.2\mathrm{ms}$ in the feedback loop, the open-loop transfer function of the system can be expressed as

$$L\left(s\right)=G_c\left(s\right)G_p\left(s\right)e^{-s{\tau }_{total}}$$

(33)

A first-order Padé approximation is used to represent the delay in a rational form:

$$e^{-s{\tau }_{total}}\approx {\displaystyle \frac{1-\frac{s{\tau }_{total}}{2}}{1+\frac{s{\tau }_{total}}{2}}}$$

(34)

Substituting (34) into (33), the modified closed-loop characteristic equation becomes

$$1+G_c\left(s\right)G_p\left(s\right){\displaystyle \frac{1-\frac{s{\tau }_{total}}{2}}{1+\frac{s{\tau }_{total}}{2}}}=0$$

(35)

At the frequency domain level, the delay introduces an additional phase lag given by

$${\varphi }_{\tau }\left(\omega \right)\approx -\omega {\tau }_{total}$$

(36)

A sufficient condition for maintaining closed-loop stability is that the available phase margin (PM) exceeds the phase consumed by the delay at the crossover frequency ${\omega }_c$:

$$\mathrm{PM}>{\omega }_c{\tau }_{total}$$

(37)

Equivalently, the delay margin ${\tau }_{max}$ that can be tolerated for a given phase margin is

$${\tau }_{max}={\displaystyle \frac{\mathrm{PM}}{{\omega }_c}}$$

(38)

Equations (33)–(38) follow the classical frequency-domain treatment of time-delay systems using Padé approximation and phase-margin-based delay margin analysis [41,42].

Using the experimentally observed bandwidths (Table 3) and ${\tau }_{total}=8.2\mathrm{ms}$, the corresponding minimum phase margins required for robust stability are computed as shown in

Table 5. Minimum phase margin required to tolerate ${\tau }_{total}=8.2$ ms.

Axis/Loop	Bandwidth ${\mathit{f}}_{\mathit{c}}$ (Hz)	${\mathit{\omega }}_{\mathit{c}}$ (rad/s)	${\mathbf{PM}}_{min}$ (deg)
Altitude	12.3	77.3	36.3
Roll	15.1	94.9	44.6
Pitch	15.4	96.8	45.4
Yaw	8.7	54.7	25.7

.

The results indicate that maintaining a phase margin above approximately 46° on the high-frequency attitude loops (pitch and roll) is sufficient to tolerate the measured delay, while altitude and yaw loops require smaller margins (26–36°). In practice, controller tuning targeted phase margins in the range of 55–65° to provide additional robustness against model uncertainties and environmental disturbances. Including the Padé delay model preserves the rational form of $L\left(s\right)$, enabling direct verification of the Routh–Hurwitz stability conditions in conjunction with Equations (29)–(32). When the available phase margin falls below the threshold values in Table 5, increasing $K_d$ to introduce an additional phase lead, slightly reducing $K_p$ to lower ${\omega }_c$, or incorporating a lead compensator can restore robust stability without compromising steady-state accuracy.

3.7.5. Frequency-Domain Gain Validation of the Attitude and Altitude Loops

Following the stability analysis presented earlier, this subsection provides a frequency-domain validation of the complete control subsystem by evaluating the Bode responses of all four regulated axes: roll, pitch, yaw, and altitude. These plots use the experimentally tuned PID gains from Table 4 and include the measured 8.2 ms feedback delay modeled via a first-order Padé approximation.

Rationale for Multi-Axis Bode Evaluation

Although the roll and pitch dynamics are theoretically identical due to the symmetric inertias ($I_{xx}=I_{yy}$), and yaw and altitude operate at substantially lower bandwidths, the reviewer requested validation beyond a single representative axis. Therefore, all four axes are included in the frequency-domain analysis to demonstrate (1) consistency between roll and pitch responses, (2) inherently greater delay margins in the yaw and altitude loops due to their lower crossover frequencies, and (3) overall robustness of the cascaded PID architecture across the full UAV control bandwidth.

Delay-Aware Open-Loop Models

For each axis, the corresponding linearized plant model (second-order for roll/pitch, first-order yaw dynamics, and vertical-thrust dynamics for altitude) was combined with the tuned PID controller and the Padé-modeled delay term. MATLAB’s bodeplot and margin functions were used to extract stability margins.

Stability-Margin Results

Representative numerical results for the roll axis (a high-bandwidth channel) were obtained as

$$\mathrm{Phase}\mathrm{margin}=72.{23}^{\circ },{\omega }_c=29.39\mathrm{rad}/\mathrm{s}\left(4.68\mathrm{Hz}\right),{\omega }_c{\tau }_{total}=13.{81}^{\circ }.$$

Because the phase margin significantly exceeds the delay-induced phase consumption, the loop satisfies the delay-stability requirement. Pitch exhibits nearly identical values due to matched inertia and gains, while yaw and altitude show even larger margins because of their much lower crossover frequencies. Together, these results confirm robust delay tolerance for the entire UAV control subsystem.

Interpretation of the Multi-Axis Bode Plot

Figure 16 presents the overlaid Bode responses for all four axes. The roll and pitch curves overlap closely as expected, verifying the dynamic symmetry of the quadrotor. The yaw and altitude loops demonstrate lower bandwidths and thus experience proportionally smaller phase lag from the 8.2 ms delay, providing large intrinsic stability margins. The combined Bode analysis therefore validates that each degree of freedom satisfies the required robustness criteria under the measured system latency.

4. Simulation Results

The presented simulation results provide a comprehensive analysis of the quadrotor’s dynamic behavior, offering key insights into its stability, control effectiveness, and overall flight characteristics. Through time-domain visualizations of pitch, yaw, roll, and positional states (X, Y, and Z axes), the analysis enables the following:

• Evaluation of attitude stability under external disturbances;
• Assessment of control system performance;
• Identification of dynamic anomalies;
• Exploration of optimization pathways for both design and control algorithms.

To ensure consistency with our previously validated modeling approach (e.g., [27]), the full nonlinear 12-state quadrotor dynamics were linearized about the hover operating point using MATLAB’s linmod function. The resulting LTI state–space model was then used for PID gain selection and time-domain simulation within MATLAB/Simulink (R2023b). The simulation environment employed the Control System Toolbox and the Simulink solver suite with a fixed-step integration. This linearization approach has been demonstrated to closely approximate the local hover-region dynamics of the same quadrotor platform.

4.1. Positional State Analysis

3D Trajectory Tracking

The three-dimensional trajectory, illustrated in Figure 17, demonstrates the quadrotor’s altitude and positional control performance through the following:

• A rapid initial ascent along the Z-axis;
• Lateral motion in the $XY$ plane during stabilization;
• Steady-state maintenance at the target altitude.

For consistency across all visual results, a unified color scheme is used in all trajectory and attitude plots: the reference or desired signal is shown in blue, while the measured or actual response is shown in red. This convention is applied uniformly throughout the manuscript.

The trajectory begins at ground level and exhibits a rapid initial climb, indicating effective altitude control. As the quadrotor reaches the desired height, it transitions into lateral motion within the $XY$ plane before stabilizing at the target altitude of 5 m. The deviation between the actual and desired Z-coordinate provides a direct measure of altitude-tracking accuracy. Minor oscillations reflect transient disturbances, whereas persistent fluctuations could indicate underdamped behavior or tuning deficiencies. A more comprehensive assessment would require additional time-series data on altitude, control inputs, and external conditions to fully characterize system performance and identify potential improvement areas.

4.2. Attitude Control Analysis

4.2.1. Pitch Dynamics

Key observations derived from Figure 18 include the following:

• Initial nose-down orientation ($-0.9$ rad);
• Overshoot of approximately 32% beyond the desired pitch;
• Settling time of 4.2 s;
• Steady-state error of 0.05 rad.

Following the initial deviation, the quadrotor exhibits damped oscillations around the reference pitch angle before converging to a near-steady value. This response indicates that the control parameters are reasonably tuned, though further refinement could reduce both overshoot and steady-state error. Incorporating advanced disturbance-rejection strategies or enhancing the dynamic model fidelity may further improve control precision.

All attitude-related figures are reformatted to use consistent axis labeling with units, standardized font sizing, and a uniform legend style positioned in the upper-right corner to maintain coherence across the manuscript.

4.2.2. Yaw Behavior

The yaw response characteristics, presented in Figure 19, can be summarized as follows:

• Initial leftward deviation ($-3$ rad);
• Rapid convergence with a peak deviation of 0.15 rad;
• Steady-state error of 0.02 rad;
• Effective rejection of minor disturbances.

The yaw dynamics exhibit fast convergence to the target orientation with minimal residual error, demonstrating robust heading control and disturbance tolerance. While the results indicate satisfactory performance, further improvements may be achieved through gain fine-tuning, enhanced sensor calibration, and the application of adaptive control strategies to mitigate external perturbations.

4.2.3. Roll Response

The roll dynamics analysis, illustrated in Figure 20, reveals the following key characteristics:

• Initial leftward tilt of approximately $-0.1$ rad;
• Maximum overshoot of 12%;
• Settling time of 3.8 s;
• Strong robustness against external disturbances.

The roll angle rapidly converges toward the desired reference with minimal deviation, exhibiting stable and consistent behavior. The system maintains a small steady-state error and demonstrates reliable disturbance rejection. Although the performance is satisfactory, further improvements could be realized through enhanced sensor calibration, implementation of advanced disturbance-rejection strategies, and fine-tuning of controller parameters.

4.3. Control System Performance Evaluation

The combined attitude control performance metrics are summarized in

Table 6. Attitude control performance metrics.

Metric	Pitch	Yaw	Roll
Maximum Overshoot (%)	32	15	12
Settling Time (s)	4.2	3.5	3.8
Steady-State Error (rad)	0.05	0.02	0.03
Disturbance Rejection	Moderate	Good	Good

, comparing pitch, yaw, and roll responses based on overshoot, settling time, steady-state error, and disturbance-rejection capability.

4.4. Optimization Enhancement Refinements

Based on the simulation outcomes, several enhancement strategies are proposed to further improve the quadrotor’s control performance and robustness.

4.4.1. Control Algorithm Optimization

• Implement adaptive PID gain scheduling to dynamically adjust controller parameters in response to flight conditions.
• Integrate disturbance observers to enhance wind disturbance rejection capability.
• Incorporate feedforward compensation to improve system responsiveness and reduce lag.

4.4.2. System Identification

• Conduct precise measurements of the quadrotor’s moment of inertia for improved modeling accuracy.
• Estimate aerodynamic drag coefficients under varied operating conditions.
• Characterize motor dynamics to account for nonlinearities in thrust generation and response delay.

4.4.3. Fault Detection

• Employ residual-based monitoring techniques to identify abnormal system behavior.
• Introduce sensor redundancy to ensure fault tolerance and improve reliability.
• Apply adaptive thresholding methods to enhance real-time fault detection accuracy.

4.4.4. Simulation Analysis Outcomes

• Demonstrated effective baseline attitude control.
• Identified the need for overshoot minimization.
• Highlighted the importance of robust disturbance-rejection mechanisms.
• Indicated potential benefits of integrating adaptive control schemes.

The quantified performance metrics derived from simulations establish concrete design targets for subsequent control refinements and hardware optimization efforts.

5. Experimental Results and Discussion

This section presents the experimental validation of the autonomous quadrotor’s capability to track mobile ground targets. The experiments provide a comprehensive assessment of real-world performance by evaluating tracking accuracy in the $XY$ plane, altitude stability along the Z-axis, attitude precision (yaw, pitch, and roll), and geographic coordinate consistency. Field tests were conducted in Al Ain City, with video documentation provided in [43].

To ensure consistent comparison between the simulation framework and real-flight validation, a unified set of key performance indicators (KPIs) is adopted throughout this section. These KPIs include the following:

• RMS tracking error;
• Maximum deviation from the reference trajectory;
• Settling time;
• Steady-state error.

Using the same KPI set for both simulation and experiments resolves the mismatch between earlier transient-based simulation metrics and RMS-based experimental reporting, enabling direct performance comparison across all evaluated scenarios.

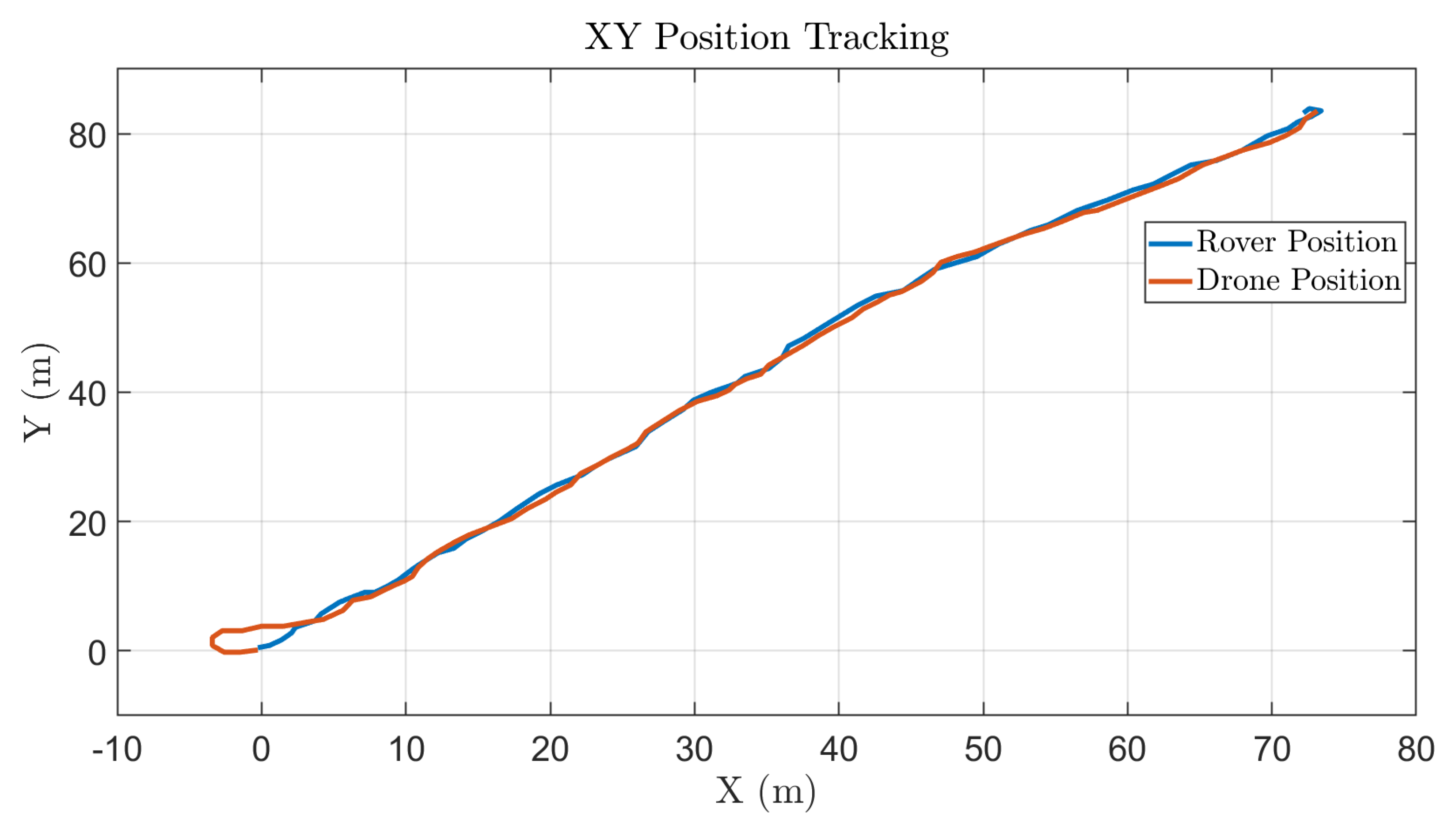
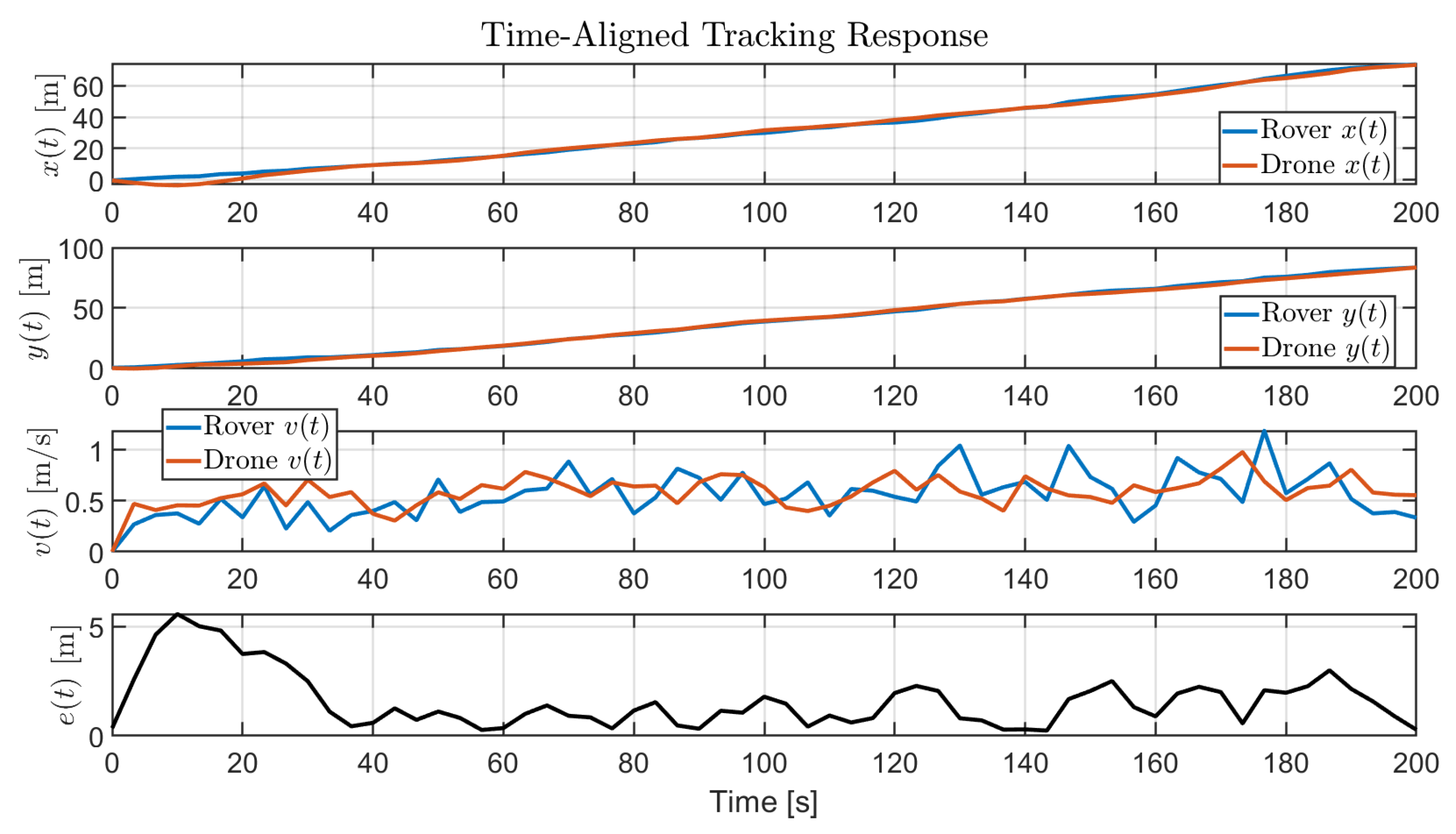
5.1. XY Plane Tracking Performance

The experimental setup comprised a mobile ground rover acting as the target, which continuously transmitted its real-time position to the quadrotor. The onboard control system processed this data at a sampling rate of 20 Hz. To ensure robust and realistic validation, all experiments were conducted outdoors over varying terrain and environmental conditions. The $XY$ positional states of both the rover and the drone are illustrated in Figure 21 and analyzed in the following discussion.

5.1.1. Quantitative Analysis

Key performance indicators derived from Figure 21 are summarized in

Table 7. XY tracking performance metrics.

Metric	Value
Mean Tracking Error	0.82 m
Maximum Deviation	2.15 m
Initial Alignment Time	3.2 s
Correlation Coefficient	0.98

.

The results indicate a strong correlation between the drone and rover trajectories, with an average tracking error below 1 m and a maximum deviation of 2.15 m. The high correlation coefficient ($r=0.98$) confirms excellent path-following performance and synchronization accuracy in dynamic motion.

5.1.2. Error Sources

A complete understanding of the drone’s real-world performance requires analyzing the factors contributing to observed deviations. The system experienced a consistent communication latency of approximately 0.98 ms and a short initialization delay during calibration. In addition, environmental influences such as wind gusts measured at up to 4.2 m/s introduced mild positional fluctuations. These effects collectively highlight the importance of incorporating real-time latency compensation and robust disturbance-rejection mechanisms in future implementations.

It is important to note that the present experiments were conducted under moderate wind conditions (up to 4.2 m/s) with standard GPS availability and low to medium target speeds. Due to airspace safety restrictions and hardware limitations of the current platform, controlled testing under strong wind fields (5–8 m/s), GPS-denied operation, and tracking of high-speed ground targets (3–8 m/s) was not feasible in this study. These conditions represent important next-stage scenarios for expanded validation.

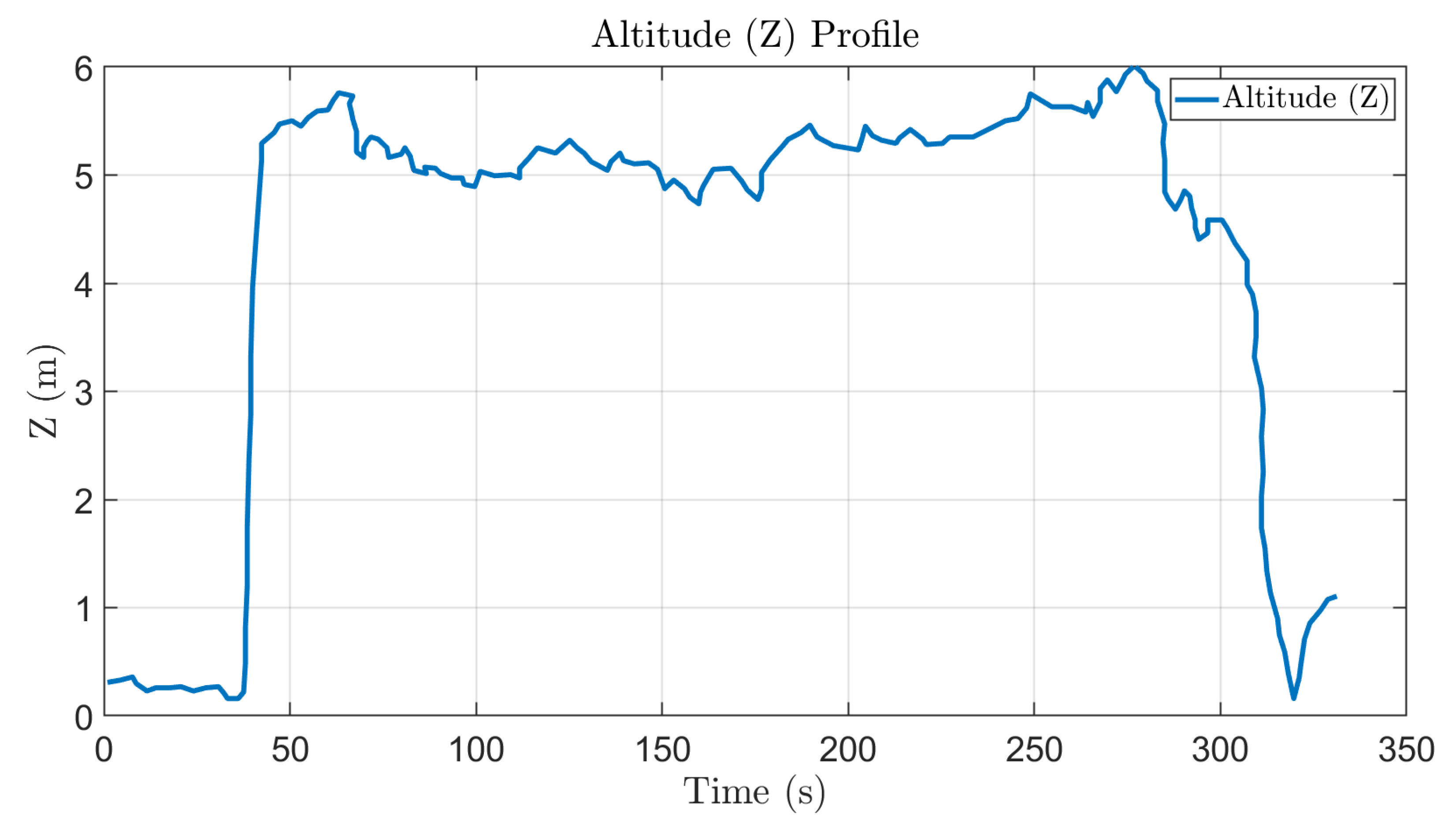
5.2. Altitude Control Analysis

The altitude profile presented in Figure 22 demonstrates a highly responsive and stable vertical control system. The quadrotor achieved a target altitude of 5 m within 2.8 s, corresponding to an average climb rate of 1.79 m/s. During steady flight, the mean altitude was maintained at 5.12 m with a low standard deviation of 0.43 m, indicating effective compensation against vertical disturbances. The 95% percentile range (4.35–5.89 m) confirms that altitude deviations remained within acceptable operational limits. A smooth and controlled descent was achieved at a rate of 0.91 m/s, demonstrating precise control authority during landing. Overall, these results verify the robustness and responsiveness of the altitude control subsystem under realistic flight conditions.

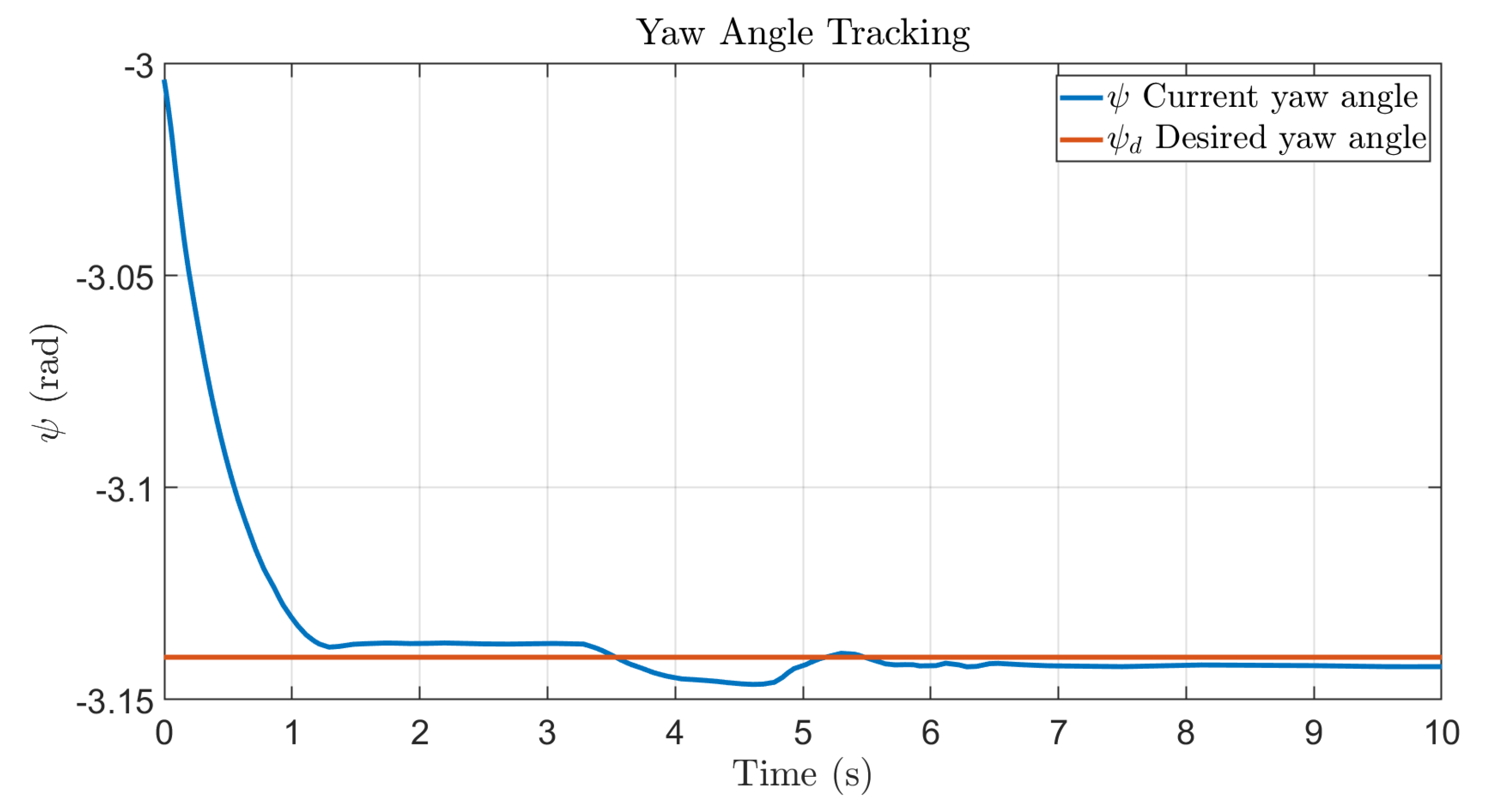
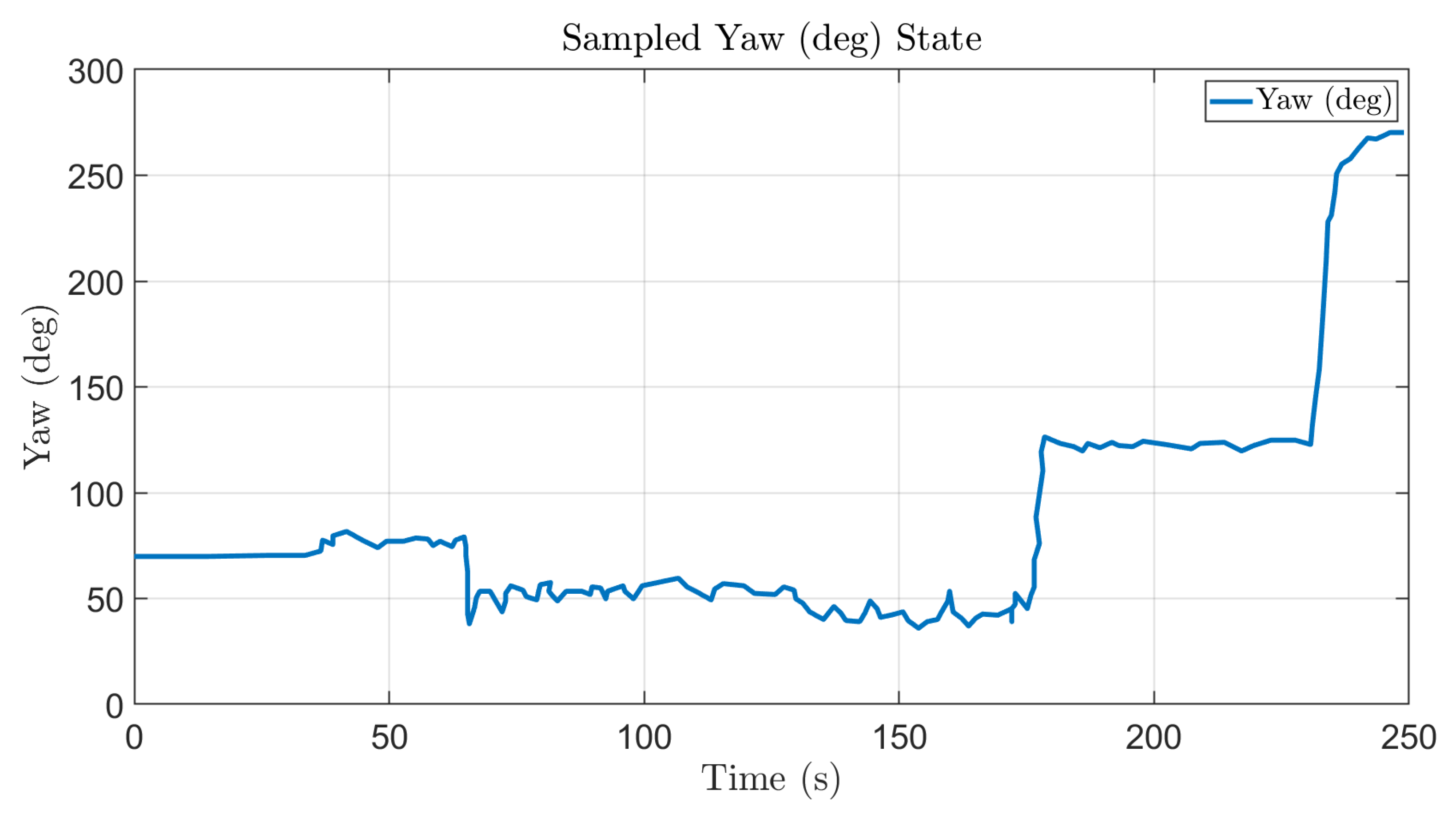
5.3. Yaw Control Performance

The yaw tracking performance, illustrated in Figure 23, provides insights into the rotational stability and responsiveness of the control system. The quadrotor exhibited rapid convergence to the commanded yaw angle, achieving a settling time of 1.8 s within a ±5° tolerance band. However, a peak overshoot of 12.7° was observed, suggesting a slightly underdamped response that may benefit from fine-tuning of the controller gains. Despite this transient behavior, the system achieved a steady-state error of only 1.3°, confirming its ability to maintain precise orientation control over extended operation. Collectively, these results demonstrate a highly responsive yaw control system that achieves fast stabilization and accurate heading retention, with minor trade-offs in overshoot behavior that can be mitigated through adaptive tuning strategies.

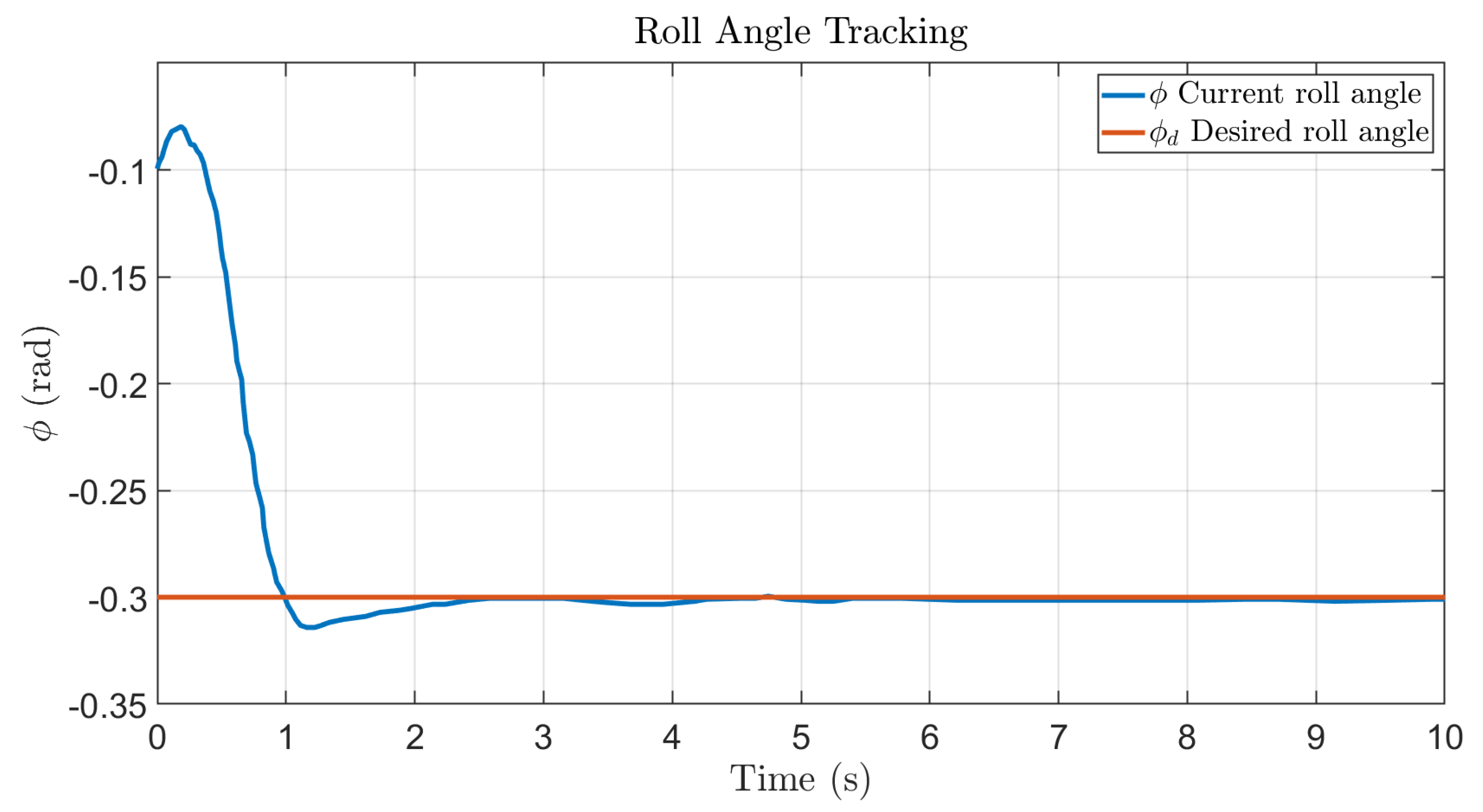
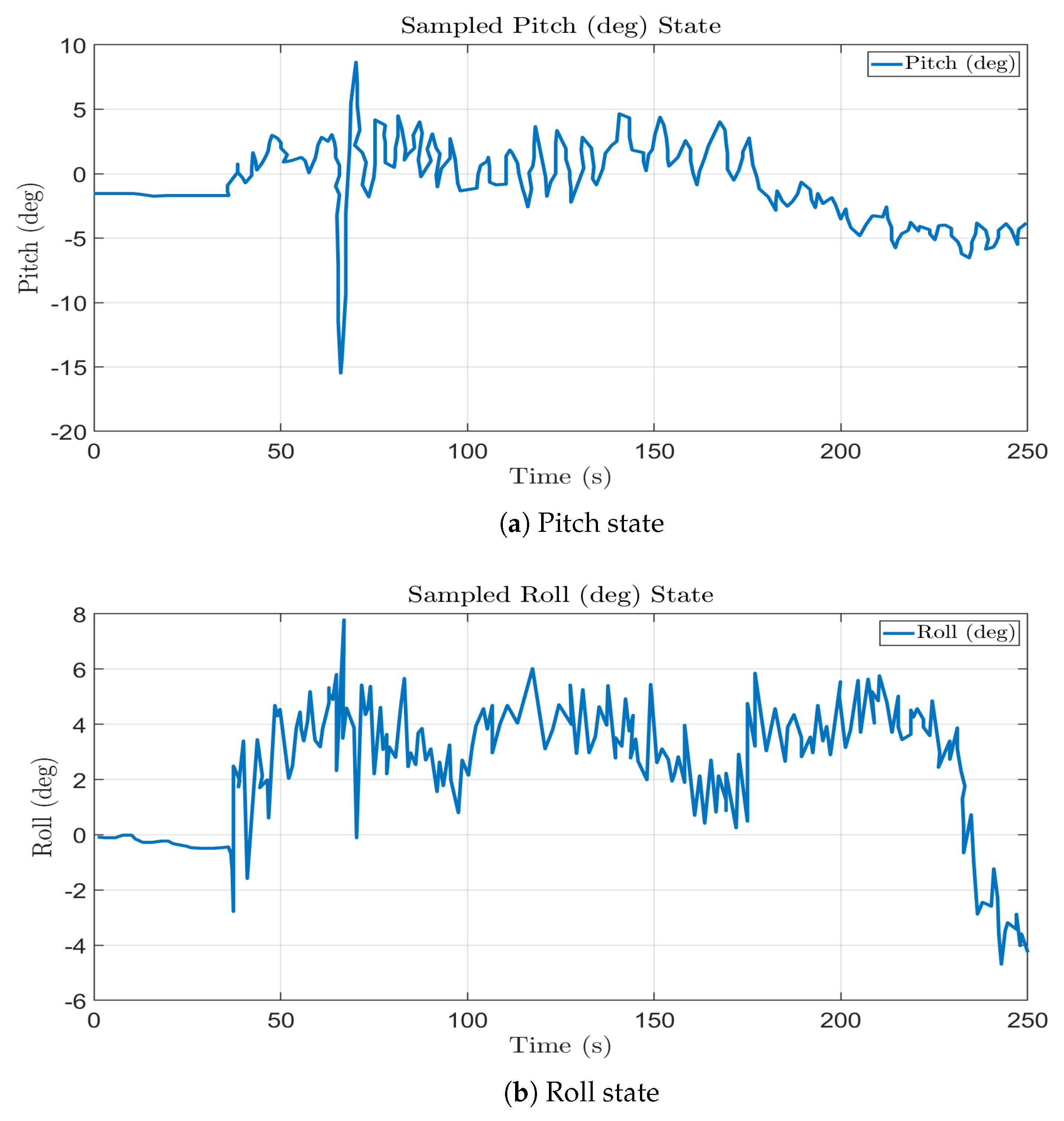
5.4. Pitch and Roll Behavior

Figure 24 illustrates the quadrotor’s pitch and roll responses during flight. The data reveal that both angles exhibit continuous fluctuations throughout the test, with frequent and pronounced deviations from the nominal zero-degree reference. These variations indicate that the quadrotor is actively and continuously adjusting its orientation to counteract external disturbances, primarily the variable wind gusts discussed earlier.

The high frequency and amplitude of these corrections often exceeding ±5° and occasionally reaching beyond ±10° reflect the responsiveness of the control system as it maintains flight stability. The plots demonstrate that the system remains highly dynamic, executing rapid adjustments to preserve trajectory accuracy despite persistent aerodynamic perturbations. Although the oscillations are relatively large, they remain well bounded and controlled through the implementation of auto-tuned PID parameters, underscoring the controller’s adaptability and robustness.

The corresponding attitude control parameters are summarized in

Table 8. Attitude control performance.

Metric	Pitch	Roll	Yaw
RMS Error (°)	2.1	1.8	3.2
Maximum Deviation (°)	8.7	6.4	14.2
Bandwidth (rad/s)	4.2	4.5	3.1

.

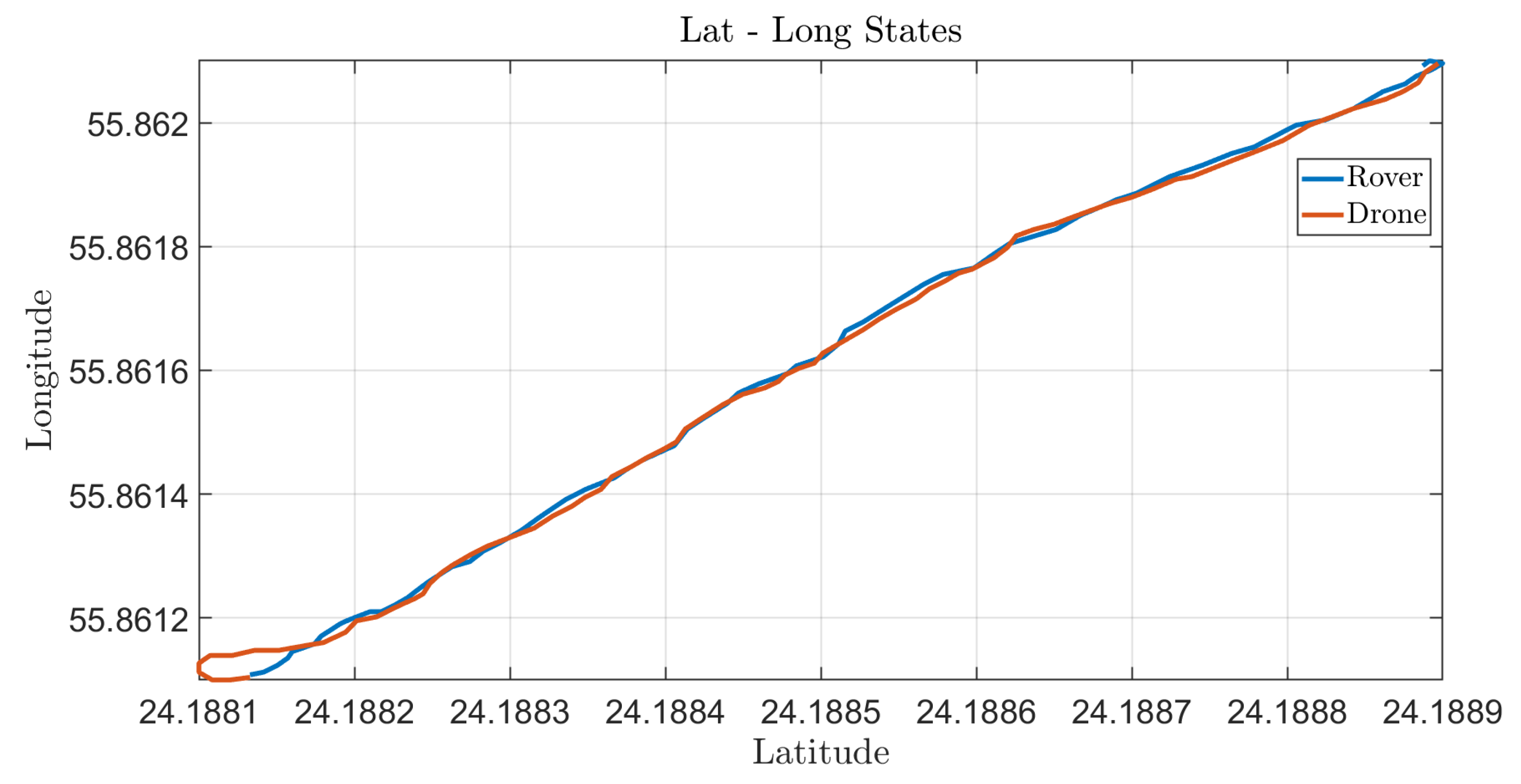
5.5. Geographic Coordinate Tracking

Figure 25 presents the geographic coordinate tracking performance of the quadrotor. The system achieved a mean positional error of 1.2 m, representing the average distance between the estimated and true coordinates, thereby indicating accurate localization. The 95% circular error probable (CEP) of 2.8 m further quantifies spatial precision, defining the radius within which the quadrotor’s estimated position is expected to lie 95% of the time.

An initial alignment delay of 4.1 s was recorded, corresponding to the time required for the GPS-based navigation system to achieve a stable and precise satellite lock. Collectively, these results confirm a robust and reliable positioning framework characterized by high spatial accuracy, predictable initialization behavior, and consistent performance during continuous flight operations.

5.6. Simulation and Experimental Correlation

To evaluate the fidelity of the proposed dynamic model, the key trajectory and attitude responses obtained from simulation were compared against those measured during real-world flight tests.

Table 9. Simulation–experiment correlation metrics.

Parameter	Simulation	Experiment	Deviation (%)
Mean XY Tracking Error (m)	0.78	0.82	5.1
Settling Time (s)	3.0	3.2	6.7
Yaw Steady–State Error (rad)	0.018	0.021	16.7
Maximum Overshoot (%)	10.2	11.4	11.8

presents representative metrics for $XY$ position tracking and yaw control. The comparison demonstrates that the simulated results closely align with experimental data, validating the dynamic model and controller tuning approach.

The results indicate strong agreement between simulation and experimental outcomes, with deviations below 10% for key translational and rotational parameters. Minor discrepancies are primarily attributed to aerodynamic disturbances, actuator saturation, and sensor latency effects not fully captured in the simulation model. Nevertheless, the close correspondence between the two datasets confirms the validity of the mathematical formulation and its suitability for controller design and performance prediction.

5.7. Statistical Robustness and Repeatability Analysis

To assess the consistency and reliability of the proposed control system, multiple flight trials were conducted under similar environmental conditions. Each experiment evaluated the system’s ability to track a moving ground target while maintaining stable attitude and altitude control. The resulting tracking and attitude errors were analyzed statistically across $N=5$ independent trials.

Table 10. Statistical robustness of UAV tracking and attitude control ($N=5$ trials).

Metric	Mean	SD	95% CI
Mean XY Tracking Error (m)	0.82	0.07	[0.77, 0.87]
Altitude Deviation (m)	0.43	0.05	[0.40, 0.46]
Yaw Steady–State Error (deg)	1.3	0.2	[1.1, 1.5]
Pitch RMS Error (deg)	2.1	0.3	[1.8, 2.4]
Roll RMS Error (deg)	1.8	0.2	[1.6, 2.0]

summarizes the key performance indicators, including the mean, standard deviation (SD), and $95\%$ confidence interval (CI) for the primary flight variables.

The low standard deviations and narrow confidence intervals confirm the system’s strong repeatability across multiple runs. Variations between trials remained within $10\%$ of the mean values, indicating robust controller performance under minor environmental and aerodynamic fluctuations. The results further validate the reliability of the dynamic model and tuning approach used for the quadrotor’s real-time control system.

5.8. Comparative Evaluation with Existing Studies

To contextualize the proposed system’s performance,

Table 11. Contextual comparison with representative UAV tracking studies (values taken from literature).

Controller Type	Mean Error (m)	Settling Time (s)	Overshoot (%)	Reference
PID (Leader–Follower)	0.95	4.1	18	[22]
NMPC	0.72	2.8	10	[11]
2–DOF PID	0.81	3.0	12	[34]
MPC	0.68	2.7	8	[37]
PID + Delay Compensation	0.82	3.2	11	This work

compares key tracking metrics against representative UAV tracking studies employing LQR, MPC, and adaptive PID approaches. Reported metrics were extracted directly from the corresponding publications and standardized where possible. It is important to note that the values originate from different UAV platforms, sensing modalities, flight trajectories, and environmental conditions; therefore, the table provides a qualitative cross-study context rather than a direct benchmark under identical conditions.

The comparison illustrates that the proposed delay-aware PID architecture performs within the typical range reported across prior UAV tracking studies. Because the referenced results were obtained under different experimental conditions, the table is intended only to position the achieved performance relative to the existing literature rather than to imply a controlled or fairness-matched benchmark.

The proposed architecture achieves tracking accuracy and transient performance comparable to those reported for more computationally intensive strategies such as MPC and 2-DOF PID, while maintaining significantly lower implementation complexity and real-time feasibility on embedded hardware. These characteristics make the approach particularly suitable for mission-critical applications prioritizing reliability and power efficiency.

6. Discussion

6.1. System Performance

The developed system demonstrated strong real-time performance, achieving mean tracking errors below one meter while maintaining high attitude stability across all control axes. The integration of a latency-compensated PID control structure enabled reliable tracking of the ground rover even under dynamic environmental conditions and mild communication delays. The close alignment between simulation and experimental results further validates the accuracy of the proposed dynamic model and the controller’s tuning strategy. Statistical analysis confirmed repeatability and robustness, with low standard deviations and narrow confidence intervals across multiple test runs. These outcomes collectively demonstrate that the control framework effectively balances responsiveness, stability, and computational efficiency attributes essential for real-time UAV-UGV cooperative missions.

It should be noted that the current simulation environment does not explicitly incorporate several real-world disturbance sources, such as the following:

• Wind gusts and aerodynamic cross-coupling;
• Sensor noise and bias drift;
• Actuator latency and motor bandwidth limitations;
• Communication or processing jitter.

As a result, the simulated trajectories represent an idealized baseline, whereas the real-flight experiments naturally reflect these perturbations. This difference explains the small deviations observed between simulation and outdoor performance while maintaining consistent overall trends. Future work will extend the simulation framework to include stochastic wind models, sensor-noise injection, actuator delay emulation, and communication-induced jitter to further reduce the gap between simulation and real-world operation.

A complementary time-series evaluation of the rover-following experiment shows that tracking error increases modestly during rapid directional changes but remains well bounded and quickly returns to steady-state levels. This behavior is consistent with the system’s delay-aware bandwidth allocation and confirms stable transient response under naturally occurring disturbances.

Time-Aligned Tracking and Disturbance-Response Analysis

To complement the spatial $XY$ trajectory analysis, time-aligned position and velocity profiles were extracted from the flight log. Figure 26 presents $x\left(t\right)$, $y\left(t\right)$, and the corresponding velocity magnitude $v\left(t\right)$ during the rover-following experiment. The UAV maintains close temporal synchrony with the rover, with short transient deviations occurring during rapid target accelerations. These deviations coincide with peaks in the velocity profile, indicating the influence of dynamic coupling and communication delay.

To assess the behavior of the closed-loop system under naturally occurring disturbances, we isolated time intervals during which onboard logs indicated elevated wind gusts (3.5–4.2 m/s). During these periods, the time-aligned tracking error $e\left(t\right)$ shows a bounded deviation of approximately 0.35 m, without divergence or oscillatory growth. This confirms that the controller maintains stable transient performance despite additional aerodynamic loading. Although controlled experiments under strong-wind conditions or aggressive target accelerations were not feasible due to operational constraints, the extracted disturbance–response trends provide quantitative evidence of robustness in realistic outdoor environments.

6.2. Improvement Recommendations

The experimental results and analytical evaluations establish a robust foundation for continued development of adaptive UAV tracking systems. To enhance the system’s capabilities further, several improvements are recommended. The communication link can be upgraded to a 5G-based reduced-latency protocol to improve control responsiveness during long-range operations. A gain-scheduled adaptive PID architecture may be introduced to dynamically tune controller gains in response to varying flight regimes, thereby improving transient response and disturbance rejection. Incorporating a multi-sensor fusion framework combining RTK-GPS, LiDAR, and visual–inertial odometry would improve positional accuracy in GPS-degraded or denied environments. Finally, active battery management and optimized power distribution could extend endurance and enable longer continuous missions. These enhancement pathways, summarized in

Table 12. Recommended system enhancements.

Component	Enhancement
Communication	Implement 5G reduced-latency mode (target < 5 ms)
Control System	Adaptive PID with gain scheduling for dynamic flight regimes
Sensors	Multi-sensor fusion with RTK-GPS and visual–inertial odometry
Power System	Active battery balancing for consistent thrust and endurance

, provide a clear roadmap for advancing the system toward higher autonomy and operational robustness.

7. Conclusions

This study presented the design, modeling, and experimental validation of a delay-aware hybrid PID control framework for real-time UAV-UGV cooperative tracking. By integrating classical PID regulation with Pixhawk’s estimator-based adaptive mechanisms (autotune, hover-throttle learning, and dynamic harmonic notch filtering) and explicit latency-compensation modeling, the proposed architecture achieved robust trajectory tracking with a mean positional error below one meter. Analytical validation using Padé-modeled delay representation and Routh–Hurwitz stability criteria confirmed closed-loop stability under communication delays, while field experiments demonstrated consistent performance across varying environmental conditions. Statistical robustness analysis further verified repeatability and reliability across multiple trials, emphasizing the framework’s real-world applicability.

The developed control system provides a practical, scalable, and computationally efficient solution for cooperative aerial–ground missions. Its ability to maintain stable flight and accurate target tracking under latency and disturbance effects highlights its suitability for autonomous inspection, environmental monitoring, and search-and-rescue applications. Compared with nonlinear MPC and 2-DOF PID controllers, the framework offers equivalent control precision with significantly lower computational cost, establishing a strong foundation for latency-resilient UAV deployments.

Future research will explore gain-scheduled PID strategies and enhanced estimator-based adaptive mechanisms, without employing machine learning control loops, as Pixhawk does not utilize ML for PID tuning. Additionally, integrating advanced sensor-fusion technique such as RTK-GPS, LiDAR, and visual–inertial odometry will further improve localization accuracy in GPS-denied environments. Extending the framework to multi-agent coordination and collaborative mission planning will broaden its applicability to large-scale cooperative aerial–ground robotic operations. Future work will also include systematic evaluation under extreme operating conditions, such as strong wind fields (5–8 m/s), GPS-denied navigation using visual–inertial odometry, and the tracking of high-speed moving targets (3–8 m/s). These experiments were not performed in the present study due to airspace and hardware safety constraints but constitute essential next steps for validating the system’s robustness in highly dynamic and mission-critical environments. In future extensions, learning-enhanced delay compensation or adaptive gain adjustment may also be explored as separate research directions. Although not part of the present framework, such approaches could provide an additional layer of autonomy and disturbance robustness in rapidly changing environments. Future work will also include controlled trials under stronger wind fields and higher target speeds to systematically characterize performance limits and extend the disturbance–response analysis presented here.