Particle Swarm Optimization-Enhanced Fuzzy Control for Electrical Conductivity Regulation in Integrated Water–Fertilizer Irrigation Systems
Abstract
1. Introduction
2. Materials and Methods
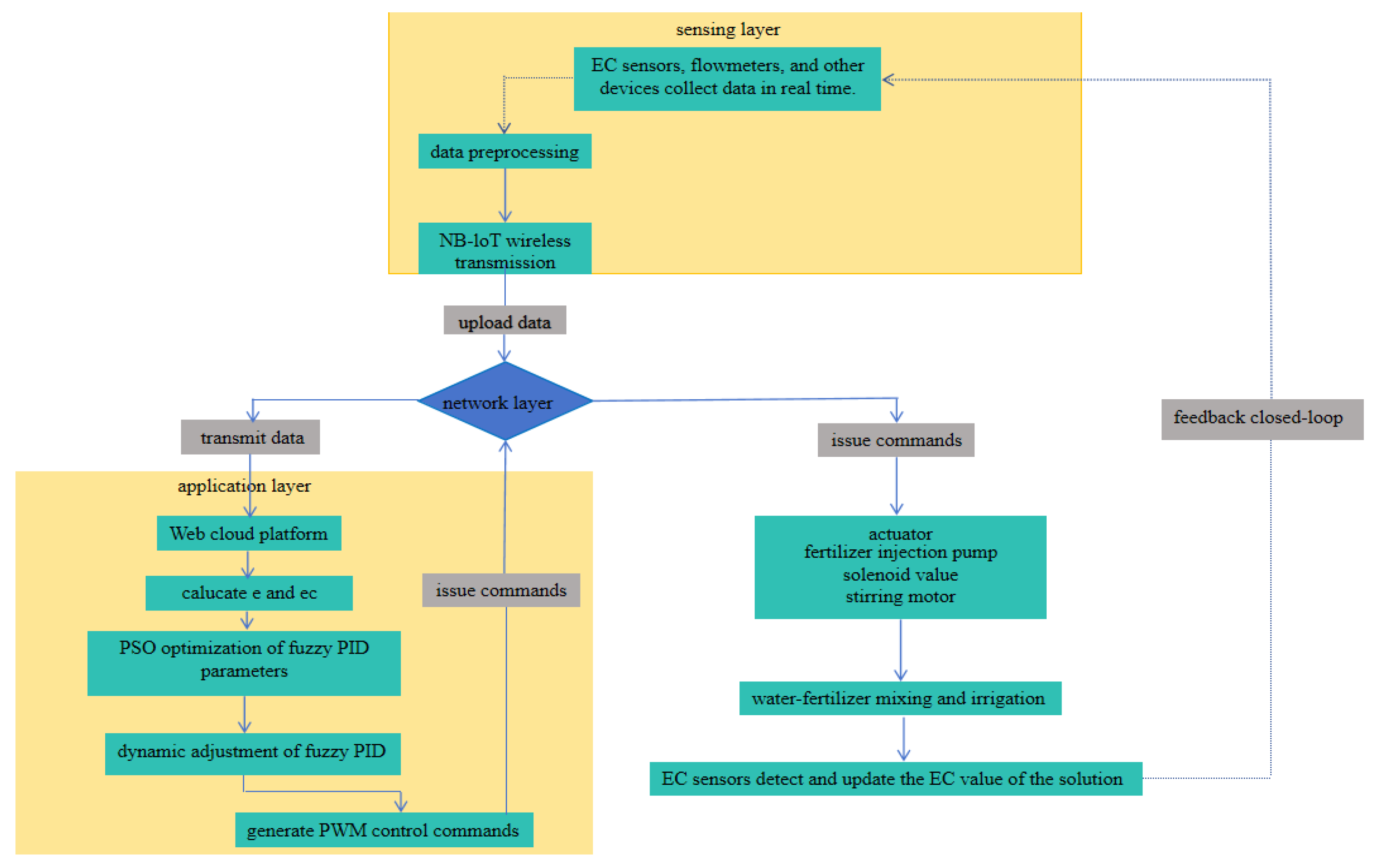
2.1. System Hardware Architecture
2.2. Control Algorithm Design
2.2.1. Conventional PID Controller
2.2.2. Fuzzy PID Controller
- Dynamic adjustment of inertia weight: Adjust w based on the particle fitness value. Particles with poor fitness have an increased w to expand the search range, while particles with good fitness have a decreased w for fine search. The formula is:
- 2.
- Adaptive change of learning factors: Increase in the early iteration stage to enhance individual cognition, and increase in the later stage to enhance global collaboration. The formulas are:
- (1)
- Initialize the particle swarm. The spatial dimension is set to 5, the swarm size to 80, and the maximum number of iterations to 80. Subsequently, parameters including the inertia weight, cognitive coefficient, and social coefficient are defined. The particle swarm [29] is initialized within the search space, and the initial position and velocity of each particle are assigned.
- (2)
- Evaluate fitness. Each particle in the swarm is passed to a fuzzy PID controller, where its corresponding fitness value is computed based on the Integral of Time multiplied by Absolute Error (ITAE) performance criterion. The fitness of each particle is compared with its previous best value to update the personal best () and the global best ().
- (3)
- Update particle position and velocity. The inertia weight is calculated using a weighting strategy [30], and the cognitive and social learning factors are determined. These values are then substituted into Equations (5) and (6) to update the current velocity and position of each particle.
- (4)
- Check termination condition. If the target criterion is satisfied, the algorithm terminates and returns the optimal solution. Otherwise, the process returns to Step (2) to continue the optimization until the maximum number of iterations is reached, at which point the current global best solution is output.
2.3. Experimental Design and Data Collection
2.3.1. Overall Experimental Methodology
2.3.2. Simulation Design Experiment
2.3.3. Field Experiment Setup and Performance Metrics
3. Results
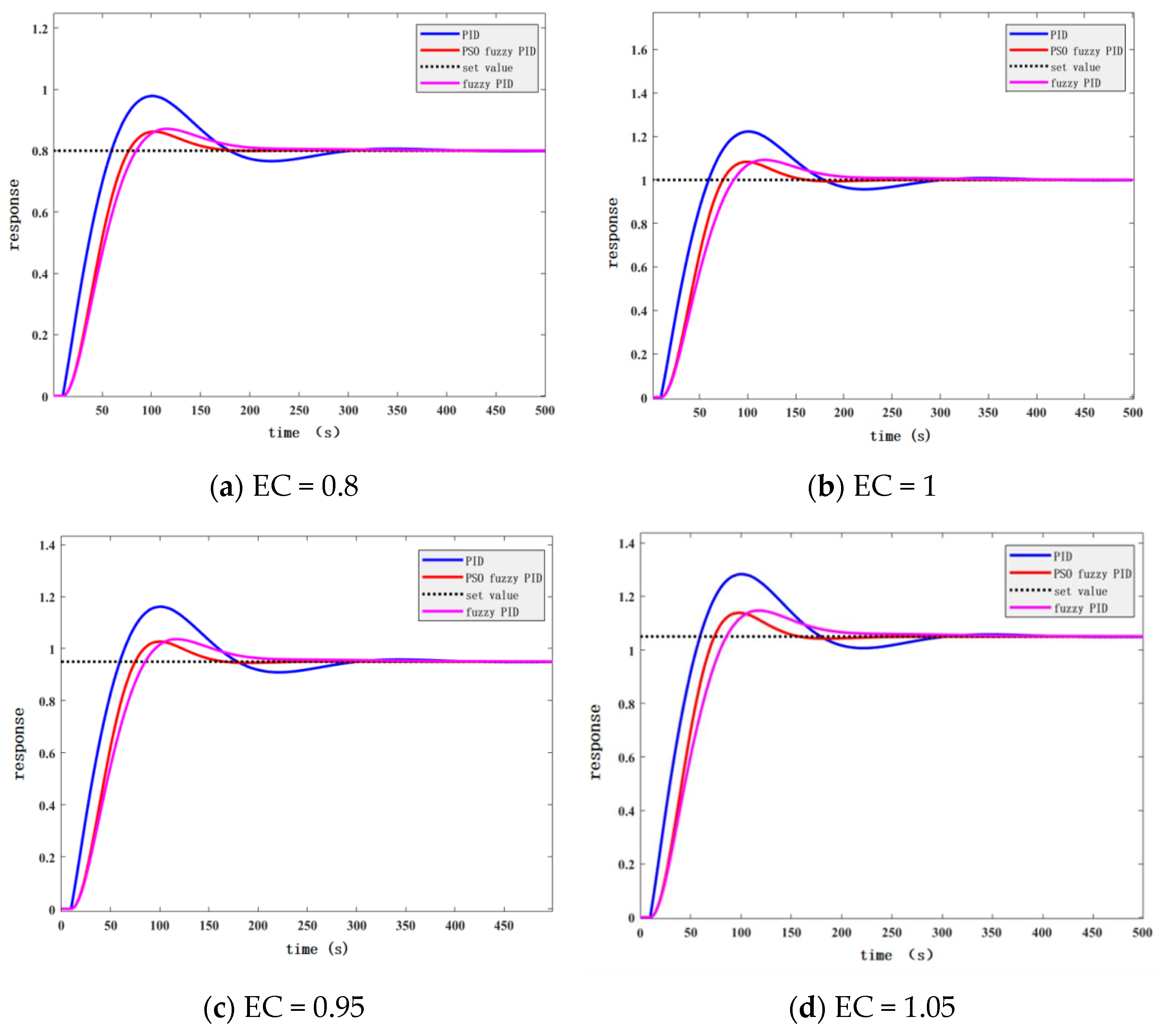
3.1. Simulation Results
3.2. EC Control Accuracy
EC Control and Soil Nutrient Correlation
3.3. Irrigation Performance
4. Discussion
4.1. Superiority of the PSO-Fuzzy PID Controller
4.2. System Integration and Agricultural Practicality
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gunarasan, C.P.J.; Lee, W.J. Biomimetic materials for fog harvesting: Prospects and challenges. Desalination 2025, 615, 119324. [Google Scholar] [CrossRef]
- Kopittke, P.M.; Harper, S.M.; Asio, L.G.; Asio, V.B.; Batalon, J.T.; Batuigas, A.M.T.; Gonzaga, A.B.; Gonzaga, N.R.; de Guzman, M.T.L.; Lumanao, D.M.; et al. Soil degradation: An integrated model of the causes and drivers. Int. Soil Water Conserv. Res. 2025, 13, 744–755. [Google Scholar] [CrossRef]
- Kohtaro, I.; Kenta, I.; Joseph, B.B. Heterogeneity effects of plant density and fertilizer application on cowpea grain yield in soil types with different physicochemical characteristics. Field Crops Res. 2023, 292, 108825. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, X.; Wang, X. Enhancing soil health and crop yields through water-fertilizer coupling technology. Front. Sustain. Food Syst. 2024, 8, 1494819. [Google Scholar] [CrossRef]
- Jain, S.; Kaur, M. Design and Implementation of an IoT-based automated EC and pH Control System in an NFT-based Hydroponic Farm. Eng. Technol. Appl. Sci. Res. 2024, 14, 13078–13081. [Google Scholar] [CrossRef]
- Liu, H.P.; Long, C.J.; Wan, P.; Wang, X.Y.; Hu, B. Fuzzy PID control of plant protection quadrotor aircraft. Trans. Chin. Soc. Agric. Eng. 2015, 31, 71–77. [Google Scholar]
- Li, L.; Wang, J.H.; Meng, F.J.; Mu, Y.H.; Yuan, H.B.; Wang, H.H.; Sigrimis, N. Nutrient solution regulation model based on quadratic hybrid mechanism and PID algorithm implementation. Trans. Chin. Soc. Agric. Eng. 2016, 32, 100–106. [Google Scholar]
- Yao, J.F.; Lu, J.; Zheng, Y.L.; Wang, X.F.; Zhao, Y.D.; Chen, X.C.; Lei, G.N.; Tang, S.Z. DC motor speed control of tree ring measuring instrument based on variable universe fuzzy control algorithm. Trans. Chin. Soc. Agric. Eng. 2019, 35, 57–63. [Google Scholar]
- Yan, L.; Webber, J.L.; Mehbodniya, A.; Moorthy, B.; Sivamani, S.; Nazir, S.; Shabaz, M. Distributed optimization of heterogeneous UAV cluster PID controller based on machine learning. Comput. Electr. Eng. 2022, 101, 108059. [Google Scholar] [CrossRef]
- Mohindru, P. Review on PID, fuzzy and hybrid fuzzy PID controllers for controlling non-linear dynamic behaviour of chemical plants. Artif. Intell. Rev. 2024, 57, 97. [Google Scholar] [CrossRef]
- Kok, C.L.; Heng, J.B.; Koh, Y.Y.; Teo, T.H. Energy-, Cost-, and Resource-Efficient IoT Hazard Detection System with Adaptive Monitoring. Sensors 2025, 25, 1761. [Google Scholar] [CrossRef]
- Jain, M.; Saihjpal, V.; Singh, N.; Singh, S.B. An overview of variants and advancements of PSO algorithm. Appl. Sci. 2022, 12, 8392. [Google Scholar] [CrossRef]
- Don Chua, W.F.; Lim, C.L.; Koh, Y.Y.; Kok, C.L. A Novel IoT Photovoltaic-Powered Water Irrigation Control and Monitoring System for Sustainable City Farming. Electronics 2024, 13, 676. [Google Scholar] [CrossRef]
- Mondal, P.; Basu, M. Adoption of precision agriculture technologies in India and in some developing countries: Scope, present status and strategies. Prog. Nat. Sci. 2009, 19, 659–666. [Google Scholar] [CrossRef]
- Dan, Z. Problems and Development Countermeasures of Agricultural Water-Saving Irrigation. Meteorol. Environ. Res. 2018, 9, 101–104, 108. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Hussain, S.M.S.; Ustun, T.S.; Sarker, M.R.; Hannan, M.A.; Mohamed, R.; Ali, J.A.; Mekhilef, S.; Milad, A. Artificial neural networks based optimization techniques: A review. Electronics 2021, 10, 2689. [Google Scholar] [CrossRef]
- Miao, C.; Chen, G.; Yan, C.; Wu, Y. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm. Comput. Ind. Eng. 2021, 156, 107230. [Google Scholar] [CrossRef]
- SS, V.C.; Hareendran, A.; Albaaji, G.F. Precision farming for sustainability: An agricultural intelligence model. Comput. Electron. Agric. 2024, 226, 109386. [Google Scholar] [CrossRef]
- Khattak, H.A.; Shah, M.A.; Khan, S.; Ali, I.; Imran, M. Perception layer security in Internet of Things. Future Gener. Comput. Syst. 2019, 100, 144–164. [Google Scholar] [CrossRef]
- Bhagwat, P.; Perkins, C.; Tripathi, S. Network layer mobility: An architecture and survey. IEEE Pers. Commun. 2002, 3, 54–64. [Google Scholar] [CrossRef]
- Karagiannis, V.; Chatzimisios, P.; Vázquez-Gallego, F.; Alonso-Zárate, J. A survey on application layer protocols for the internet of things. Trans. IoT Cloud Comput. 2015, 3, 11–17. [Google Scholar]
- Bañón, S.; Álvarez, S.; Bañón, D.; Ortuño, M.F.; Sánchez-Blanco, M.J. Assessment of soil salinity indexes using electrical conductivity sensors. Sci. Hortic. 2021, 285, 110171. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Yang, X.; Li, Z.; Cheng, Y.; Zheng, J.; Han, X.; Wang, J. Standard nutrient-solution-based fish-tail-water-fertilizer machine: Design, control, and decision. Comput. Electron. Agric. 2025, 238, 110774. [Google Scholar] [CrossRef]
- Cheng, S.; Gao, Y.; Liu, J.; Guo, C.; Xu, F.; Fu, L. An Optimal Control Strategy Considering Fatigue Load Suppression for Wind Turbines with Soft Switch Multiple Model Predictive Control Based on Membership Functions. Energies 2025, 18, 4695. [Google Scholar] [CrossRef]
- Vadood, M.; Haji, A. Prediction of Color Coordinates of Polyester Fabrics Dyed with Madder Using Mamdani-Fuzzy Logic and Optimization Algorithm. Fibers Polym. 2025, 26, 3463–3472. [Google Scholar] [CrossRef]
- Shoaip, N.; El-Sappagh, S.; Abuhmed, T.; Elmogy, M. A dynamic fuzzy rule-based inference system using fuzzy inference with semantic reasoning. Sci. Rep. 2024, 14, 4275. [Google Scholar] [CrossRef]
- Stamenov, D.; Rogne, Ø.; Abbiati, G.; Sauder, T. Comparison of empirical methods for estimation of quadratic transfer functions of low-frequency hydrodynamic loads. Ocean Eng. 2025, 341 Pt 3, 122582. [Google Scholar] [CrossRef]
- Chang, L.; Li, Y.; Li, D.; Zhang, M.; Du, W.; Cheng, K. Spatiotemporal representation of internal fracture sources using dual-surface infrared radiation and particle swarm optimization algorithm. Theor. Appl. Fract. Mech. 2026, 141 Pt A, 105249. [Google Scholar] [CrossRef]
- Cui, D.; Mo, Y.; Yuan, X.; Ye, L.; Wang, K.; Shen, F.; Wang, Y.; Yang, C.; Gui, W. Deep learning-based model predictive control with exponential weighting strategy and its application in energy management systems. J. Process Control 2025, 155, 103542. [Google Scholar] [CrossRef]
- Ali, A.; Majhi, S. PI/PID controller design based on IMC and percentage overshoot specification to controller setpoint change. ISA Trans. 2009, 48, 10–15. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Jiang, J.; Peng, J.; Zheng, J.; Hong, X.; Tang, D.; Peng, X.; Yu, H.; Xu, D.; Zhou, Z. Corrigendum to ‘Study on the steady-state performance and condensation phase change flow of steam hydrostatic dry gas seals’ [Thermal Sci. Eng. Prog. 65(2025) September 103931]. Therm. Sci. Eng. Prog. 2025, 67, 104086. [Google Scholar] [CrossRef]
- Zhang, Q.M. Green cultivation technology and promotion of wheat. Guangdong Canye 2022, 56, 54–56. [Google Scholar]
- Xu, S.D. Wheat cultivation management and pest control technology. Agric. Dev. Equip. 2022, 12, 226–227. [Google Scholar]










| ec | e | ||||||
|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PB | PB | PM | PM | PS | ZO | ZO |
| NM | PB | PB | PM | PS | PS | ZO | NS |
| NS | PM | PM | PM | PS | ZO | NS | NS |
| ZO | PM | PM | PS | ZO | NS | NS | NM |
| PS | PS | PS | ZO | NS | NS | NM | NM |
| PM | PS | ZO | NS | NM | NM | NM | NB |
| PB | ZO | ZO | NM | NM | NM | NB | NB |
| ec | e | ||||||
|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | NB | NB | NM | NM | NS | ZO | ZO |
| NM | NB | NB | NM | NS | NS | ZO | ZO |
| NS | NM | NM | NS | NS | ZO | PS | PS |
| ZO | NM | NM | NS | ZO | PS | PM | PM |
| PS | NM | NS | ZO | PS | PS | PM | PB |
| PM | ZO | ZO | PS | PS | PM | PB | PB |
| PB | ZO | ZO | PS | PM | PM | PB | PB |
| ec | e | ||||||
|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PS | NS | NB | NB | NB | NM | PS |
| NM | PS | NS | NB | NM | NM | NS | ZO |
| NS | ZO | NS | NM | NM | NS | NS | ZO |
| ZO | ZO | NS | NS | NS | NS | NM | ZO |
| EC Value | PSO-Fuzzy PID Controller | Fuzzy PID Controller | PID Controller | |||
|---|---|---|---|---|---|---|
| Overshoot | Settling Time | Overshoot | Settling Time | Overshoot | Settling Time | |
| 0.8 | 7.64% | 272 s | 8.67% | 288.4 s | 22.84% | 344.8 s |
| 0.95 | 7.96% | 280 s | 11.8% | 297.8 s | 23.56% | 345.95 s |
| 1 | 8.152% | 286.3 s | 9.34% | 313.6 s | 23.56% | 345.95 s |
| 1.05 | 8.152% | 295 s | 9.66% | 315 s | 28.7% | 346.5 s |
| Performance Metrics | Degrees of Freedom | F Value | p Value |
|---|---|---|---|
| Overshoot | 2 | 108.3 | <0.001 |
| Setting time | 2 | 72.25 | <0.001 |
| Steady-state error | 2 | 33.75 | <0.001 |
| EC Target Value | Number of Samples | Actual Measured Value | Deviation |
|---|---|---|---|
| 1 | 0.784 ms/cm | −0.016 ms/cm | |
| 0.8 ms/cm | 2 | 0.787 ms/cm | −0.013 ms/cm |
| 3 | 0.789 ms/cm | −0.011 ms/cm | |
| 1 | 0.949 ms/cm | −0.001 ms/cm | |
| 0.95 ms/cm | 2 | 0.949 ms/cm | −0.001 ms/cm |
| 3 | 0.949 ms/cm | −0.001 ms/cm | |
| 1 | 1.0 ms/cm | 0.000 ms/cm | |
| 1.0 ms/cm | 2 | 0.999 ms/cm | −0.001 ms/cm |
| 3 | 1.07 ms/cm | +0.070 ms/cm | |
| 1 | 1.04 ms/cm | −0.010 ms/cm | |
| 1.05 ms/cm | 2 | 1.05 ms/cm | 0.000 ms/cm |
| 3 | 1.06 ms/cm | +0.010 ms/cm |
| Error Metric | Value |
|---|---|
| RMSE (ms/cm) | 0.0217 |
| MAE (ms/cm) | 0.01125 |
| R2 | 0.9462 |
| Statistical Test | Teat Value | Result | p-Value | Conclusion |
|---|---|---|---|---|
| One-sample t-test | 0.02 ms/cm | t(11) = 8.37 | <0.001 | Significantly better than precision ag standard |
| One-way ANOVA | Between EC targets | F(3,8) = 1.24 | 0.36 | Consistent performance across operational range |
| Coefficient of variation | - | 0.32–0.45% | - | High reproducibility |
| Serial Number | Plant Height | SPAD Value | 1000-Grain Weight |
|---|---|---|---|
| 1 | 68.2 | 45.3 | - |
| 2 | 76.5 | 48.1 | 42.3 |
| Soil Moisture Before Irrigation | Rainfall Forecast | Crop Transpiration Prediction | Irrigation Volume | Soil Moisture After Irrigation | |
|---|---|---|---|---|---|
| Serial number | /% | /mm | /mm | /mm | /% |
| 1 | 15.8 | 0 | 4.5 | 16.55 | 20.7 |
| 2 | 18.1 | 0 | 5.3 | 11.35 | 21.2 |
| 3 | 20.6 | 1.3 | 1.6 | 0 | — |
| 4 | 18.4 | 0 | 4.3 | 13.75 | 22.1 |
| 5 | 20.7 | 0 | 2.8 | 0 | — |
| Indicator | Value | Evaluation |
|---|---|---|
| Christiansen’s Uniformity Coefficient (Cu) | 97.6% | Good |
| Average Soil Moisture after Irrigation | 21.3% | Within Optimal Range (19–25%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Li, X.; Zheng, Q.; Liu, L. Particle Swarm Optimization-Enhanced Fuzzy Control for Electrical Conductivity Regulation in Integrated Water–Fertilizer Irrigation Systems. Automation 2025, 6, 76. https://doi.org/10.3390/automation6040076
Yang J, Li X, Zheng Q, Liu L. Particle Swarm Optimization-Enhanced Fuzzy Control for Electrical Conductivity Regulation in Integrated Water–Fertilizer Irrigation Systems. Automation. 2025; 6(4):76. https://doi.org/10.3390/automation6040076
Chicago/Turabian StyleYang, Jin, Xue Li, Quan Zheng, and Lichao Liu. 2025. "Particle Swarm Optimization-Enhanced Fuzzy Control for Electrical Conductivity Regulation in Integrated Water–Fertilizer Irrigation Systems" Automation 6, no. 4: 76. https://doi.org/10.3390/automation6040076
APA StyleYang, J., Li, X., Zheng, Q., & Liu, L. (2025). Particle Swarm Optimization-Enhanced Fuzzy Control for Electrical Conductivity Regulation in Integrated Water–Fertilizer Irrigation Systems. Automation, 6(4), 76. https://doi.org/10.3390/automation6040076






