1. Introduction
Autonomous path planning has been a cornerstone of mobile robotics research for over three decades, reflecting the growing complexity of dynamic environments and the need for intelligent, real-time decision-making. The foundational work by Kosaka & Kak (1992) [
1] marked an early attempt to integrate vision and probabilistic models via the FINALE (Fast Indoor Navigation Allowing for Locational Errors) system, leveraging Kalman filters for indoor navigation under uncertainty. This seminal research laid the groundwork for later developments in map-based navigation and uncertainty handling. During the following decades, advances in localization, mapping, and real-time perception significantly shaped the path planning landscape. Patle et al. (2019) [
2] provided a comprehensive survey of path planning strategies, broadly classifying them into global and local methods, as well as static and dynamic planning. Their work emphasizes the rise in intelligent and bio-inspired approaches—such as genetic algorithm (GA), particle swarm optimization (PSO), colony optimization (ACO), and artificial bee colony (ABC)—for effective obstacle avoidance and trajectory generation in both static and uncertain environments. As robots became more autonomous, there was a pressing need to process environmental information more effectively and at higher speeds.
The evolution of robotic platforms also contributed to this progress. Taheri and Zhao. (2020) [
3] reviewed omnidirectional mobile robot systems that are capable of holonomic motion, allowing them to navigate in narrow and complex spaces with enhanced maneuverability and flexibility. In parallel, several intelligent decision-making frameworks have emerged, combining fuzzy logic, artificial neural networks, and optimization techniques to improve adaptiveness in robotics and control systems, as shown by Cebollada et al. (2021) [
4].
Real-world deployment scenarios such as intralogistics demanded new path planning paradigms that could operate under spatial and temporal constraints. Fragapane et al. (2021) [
5] discussed the role of agent-based simulations and decentralized control in warehouse intralogistics, where autonomous mobile robots interact and negotiate with each other to optimize task allocation, reflecting broader concerns for scalability and robustness in dynamic multi-agent environments. Simultaneously, robust localization remained a prerequisite for accurate path execution. Panigrahi & Bisoy (2022) [
6] categorized localization algorithms based on initial position awareness, and reviewed key methods including probabilistic approaches, simultaneous localization and mapping (SLAM), and AI-based techniques such as fuzzy logic, PSO, and neural networks. They emphasized the role of sensor fusion and feature-based mapping in reducing pose uncertainty and enhancing localization accuracy.
As robotic autonomy advanced, research began focusing on adaptable navigation systems capable of functioning in complex or partially known environments. Liu et al. (2023) [
7] discussed a hybrid topological–metric mapping framework based on Mixed Representation (MR), which integrates the global efficiency of topological planning with the local precision of metric modeling. Their layered navigation strategy—employing global topological maps alongside subregion-based metric detail—enables scalable and flexible path planning without requiring exhaustive prior environment modeling. Simultaneously, Singh et al. (2023) [
8] reviewed the transformative role of deep reinforcement learning (DRL) in mobile robot navigation. DRL enables robots to learn navigation strategies through interaction and feedback, often outperforming traditional planners in dynamic, unstructured environments. Further consolidating this shift, Loganathan & Ahmad (2023) [
9] reviewed the integration of advanced sensing, SLAM, and high-definition mapping technologies to construct autonomous navigation pipelines. They emphasized the need to integrate global and local path planning modules, enabling robots to achieve both optimal route planning and real-time obstacle avoidance—an essential feature in dynamic or unpredictable environments.
The frontier of robotic navigation now includes emerging domains such as construction robotics, where planners must dynamically adapt to evolving physical environments. Zhao et al. (2025) [
10] proposed a structured, three-phase planning framework—comprising construction task sequencing, element transit planning, and joint trajectory refinement—to coordinate high-level symbolic reasoning with low-level motion execution in autonomous in situ construction. Taleb et al. (2025) [
11] emphasized the integration of mapping, localization, and path planning as a unified triad. Their review explores SLAM, semantic-level perception, and learning-enhanced planning algorithms as core enablers of intelligent robot navigation, particularly in complex and dynamic environments such as hospitals or emergency zones.
The A* algorithm occupies a central position in path planning research, combining the accumulated cost function of Dijkstra’s algorithm with the heuristic-driven exploration of Best-First search. This hybrid formulation allows A* to achieve deterministic optimality under admissible heuristics while maintaining superior computational efficiency compared with Dijkstra, which, though optimal, suffers from exhaustive node expansion in large or dense graphs. In contrast, Best-First search offers faster convergence by following heuristic estimates alone, yet frequently sacrifices path quality and reliability in cluttered environments. A* therefore provides a balanced compromise, guiding the search efficiently toward the goal while preserving optimality. When contrasted with the Probabilistic Roadmap Method (PRM), A* represents a fundamentally different paradigm. PRM is designed for high-dimensional or continuous spaces, where it constructs a roadmap through random sampling and connection of collision-free nodes. While PRM offers probabilistic completeness and improved scalability for multi-degree-of-freedom robotic systems, it lacks the deterministic guarantees of A* and incurs significant preprocessing costs in dynamic environments. Overall, A* is best suited for structured, low-dimensional domains, whereas Dijkstra, Best-First, and PRM retain situational relevance depending on the requirements of speed, and scalability.
The A* search algorithm is a widely used and efficient pathfinding technique [
12]. Within the framework of the A* pathfinding algorithm, the evaluation function is explicitly defined in mathematical form as f(n) = g(n) + h(n) [
13], where f(n) represents the total estimated cost of traveling from the start node to the goal node through the intermediate node n. The term g(n) denotes the actual accumulated cost from the initial node n
0 to the current node n, calculated as
where c(n
k−1, n
k) is the movement cost between two consecutive nodes along the known path. The term h(n) serves as the heuristic function, providing an estimate of the remaining cost from node n to the goal node n
goal, typically modeled as the Euclidean distance,
or the Manhattan distance ∣x
n − x
g∣ + ∣y
n − y
g∣ among other metrics [
14], depending on the characteristics of the search space. This two-component structure allows A* to balance the accuracy of the known cost with the ability to predict the remaining cost, thereby improving search efficiency and preserving the optimality of the path compared with traditional exhaustive methods such as Dijkstra’s algorithm.
Choosing an appropriate heuristic is critical [
15]. A heuristic is admissible if it never overestimates the true cost and consistent if it obeys the triangle inequality. Common heuristics include Manhattan distance for grid maps or Euclidean distance for continuous spaces. A* guarantees optimality only when the heuristic is admissible. Implementation details, such as tie-breaking, grid connectivity (4-way, 8-way), and data structures (priority queues), significantly affect performance. Amit Patel suggests breaking ties in favor of nodes with higher g(n) to encourage smoother, less “zigzag” paths [
16].
In heuristic-based path planning, the choice of evaluation metric critically influences the efficiency and quality of the A* algorithm. The Manhattan distance, defined as the sum of absolute coordinate differences, is particularly suitable for four-connected grid environments where movement is constrained to orthogonal directions. Its computational simplicity is advantageous, though it often underestimates true path cost in scenarios involving diagonal movement. The Euclidean distance, by contrast, calculates the straight-line distance between two points, providing an admissible heuristic that better reflects continuous motion. However, in grid-based applications, Euclidean estimation can overemphasize diagonal proximity, leading to expanded nodes that do not align well with the allowed movement set. The octile distance addresses this limitation by integrating both orthogonal and diagonal movements into its formulation, assigning a weight of √2 for diagonals and 1 for straight moves. This produces a more accurate and admissible heuristic for eight-connected grids, striking a balance between accuracy and computational cost. Finally, the Chebyshev distance measures the maximum absolute difference across coordinates, effectively assuming unrestricted diagonal and orthogonal movement at equal cost. While computationally efficient, it may over-simplify environments with anisotropic motion constraints. Collectively, these metrics highlight the necessity of aligning heuristic design with the robot’s mobility model and grid topology to ensure both admissibility and search efficiency.
Path planning remains a core problem in mobile robotics, particularly in dynamic and partially observable environments. Traditional algorithms such as A* are widely adopted for global path planning in grid-based representations [
17]. Despite its widespread use, the traditional A* algorithm exhibits several limitations that hinder its application in real-world robotic systems. Firstly, A* does not account for the kinematic or dynamic constraints of vehicles—it only computes geometrically valid paths without considering turning radii, speed limits, or feasible angular transitions. As a result, the generated paths may include sharp, impractical turns that are infeasible for wheeled robots [
18]. Secondly, A* often produces jagged or sawtooth-like trajectories due to grid discretization, which reduces motion smoothness and increases friction, energy consumption, and mechanical wear [
19]. Third, A* focuses solely on minimizing distance to the goal and lacks obstacle avoidance buffers, causing paths to pass dangerously close to obstacles—an issue under positional uncertainty [
20]. Moreover, in large or complex environments, A* suffers from poor scalability, exploring many unnecessary nodes and consuming excessive memory and computation time. Its reliance on uniform grid structures also limits resolution and can result in “staircase” effects when using 4- or 8-connected grids [
21]. Additionally, A* lacks learning capability—it re-computes paths from scratch even for repetitive tasks in the same environment [
22]. Finally, A* is inherently an offline planner; it does not adapt to environmental changes, making it unsuitable for dynamic or partially observable settings unless combined with reactive or incremental methods [
23].
In a 2024 review, Xu et al. [
24] conducted a performance-oriented assessment of improved A* variants for robotic path planning, notably introducing the SBREA (Slide-Rail corner adjustment and Bi-directional Rectangular Expansion A*) algorithm. This method effectively enhanced path smoothness and reduced search redundancy by incorporating bidirectional rectangular expansion and an adaptive corner adjustment mechanism. Despite its contributions, the review lacked a systematic cross-comparison among studies, did not address hybrid algorithmic integrations, and overlooked the applicability of these methods in dynamic or large-scale environments.
To address these limitations, the present study provides a comprehensive and structured synthesis of 22 peer-reviewed articles, selected from an initial pool of 50 publications retrieved from the databases Scopus and Web of Science using targeted keywords such as “A* algorithm,” “improved A*,” “enhanced A*,” “hybrid A*,” “mixed A*,” and “combined A*.” The selected papers, published between 2020 and 2025, were classified into two principal categories. The first batch of 10 papers comprises A* enhancements focusing on structural and geometric optimizations, heuristic weighting schemes, and adaptive search strategies. The second batch of 12 papers involves hybrid A* algorithms that integrate A* with complementary techniques such as Dynamic Window Approach (DWA), Artificial Potential Field (APF), and Particle Swarm Optimization (PSO), etc.
Our review further introduces comparative tables presenting quantitative performance indicators—such as percentage reductions in path length, number of expanded nodes, and angular deviation—to support a rigorous performance analysis. Mathematical formulations of advanced heuristic evaluation functions and kinetic feasibility constraints are also analyzed to underscore practical applications in autonomous mobile robot navigation under dynamic and complex scenarios. Therefore, this work significantly extends existing literature by offering an application-driven, analytically grounded, and industry-relevant synthesis of recent advancements in A*-based path planning.
2. Improved A* Algorithm
Currently, classical path-planning approaches such as the traditional A* algorithm [
25], Rapidly exploring Random Tree (RRT) [
26], and the artificial potential field method [
27], etc., can be integrated to develop an improved A* algorithm that exploits the strengths of each technique while mitigating their individual limitations.
To begin with, we reviewed the first ten studies focusing on improved A* algorithms.
Table 1 presents a chronological list of these studies, highlighting the percentage improvements achieved by each modified algorithm compared to the traditional A* algorithm. The comparison is based on four key performance indicators, which correspond to the major limitations of the original A* algorithm: the number of expanded nodes, total path length, processing time, and path angularity. These metrics provide a comprehensive assessment of enhancements in terms of computational efficiency, trajectory optimality, and smoothness.
The evaluation function plays a pivotal role in the A* algorithm, and its formulation often reflects the core improvements proposed in a given study. Analyzing the evaluation function thus provides valuable insights into the optimization strategies employed.
Table 2 summarizes and compares the evaluation functions adopted in the selected ten studies, along with brief explanations of how each modification deviates from the traditional A* formulation and contributes to performance enhancement.
The ten selected studies were categorized into four methodological groups.
Group 1 (IDs 1.4 and 1.5) retains the traditional A* evaluation function; enhancements focus on other techniques rather than modifying the function itself, as detailed in later sections.
Group 2 (IDs 1.1, 1.3, 1.6, and 1.8) introduces a “guideline” mechanism to assist directional planning, which effectively reduces both the number of traversed nodes and processing time.
Group 3 (IDs 1.7, 1.9, and 1.10) involves modifications to the weighting parameters in the heuristic component h(n) to enhance performance in complex environments.
Group 4 comprises a single study (ID 1.2) that directly integrates the Artificial Potential Field (APF) method into the A* evaluation function. In this method, APF serves as an enhancement within the A* framework, distinguishing it from the hybrid approach discussed in
Section 2, where A* handles global path planning and APF performs local optimization. This layered combination aims to balance global optimality with real-time obstacle avoidance.
2.1. Group 1
Both studies (IDs 1.4 and 1.5) published in 2022 aim to overcome key limitations of the traditional A* algorithm, including inefficiency in large-scale environments and the generation of non-smooth, suboptimal paths. Although they share a common objective—improving path planning for mobile robots—they differ in methodology, target application, and evaluation criteria.
Wang et al. [
31] proposed the EBS-A* algorithm, integrating three main strategies: expansion distance, bidirectional search, and path smoothing. The expansion distance defines a safety buffer by marking adjacent nodes near obstacles as non-traversable, thus reducing collision risk and search space (Equation (3)). The buffer radius depends on robot velocity (
Vi), threshold velocity (
Vr), and safety radius (
r).
where
Vi is the current velocity,
Vr is the threshold velocity, and r is the robot’s safety radius.
Bidirectional search simultaneously grows the tree from start and goal nodes, reducing search depth and time complexity. Path smoothing is applied using Bezier curves and acute-angle decomposition, yielding continuous curvature and a maximum turning angle of 45°, thereby enhancing motion stability.
In contrast, Martins et al. [
32] introduced the IMOA* algorithm, which improves traditional A* by optimizing four criteria: processing time, path length, smoothness, and number of random points. A major innovation is the pre-serialization of the obstacle map using a pickle file, allowing instant retrieval in subsequent runs and reducing average processing time by 99.98%. A path–problem–aware executor then removes redundant intermediate points, improving smoothness by minimizing angle deviation. IMOA demonstrated several average improvements, including a 1.58% reduction in path length, 83.45% fewer sampling points, and a smoother trajectory characterized by a turning angle of 155°, compared to 135° for the traditional A algorithm. In contrast, EBS-A* does not rely on pre-stored maps but integrates both pre-processing and post-processing stages, thereby enhancing safety, reducing computation time, and producing a smoother path.
To enhance path quality, the authors introduced a path–problem–aware executor that evaluates the raw path and simplifies it by deleting unnecessary intermediate points. Given two path nodes
Pi and
Pi+1, the total path length is computed as:
Path smoothness is measured by minimizing deviations from 180°, using:
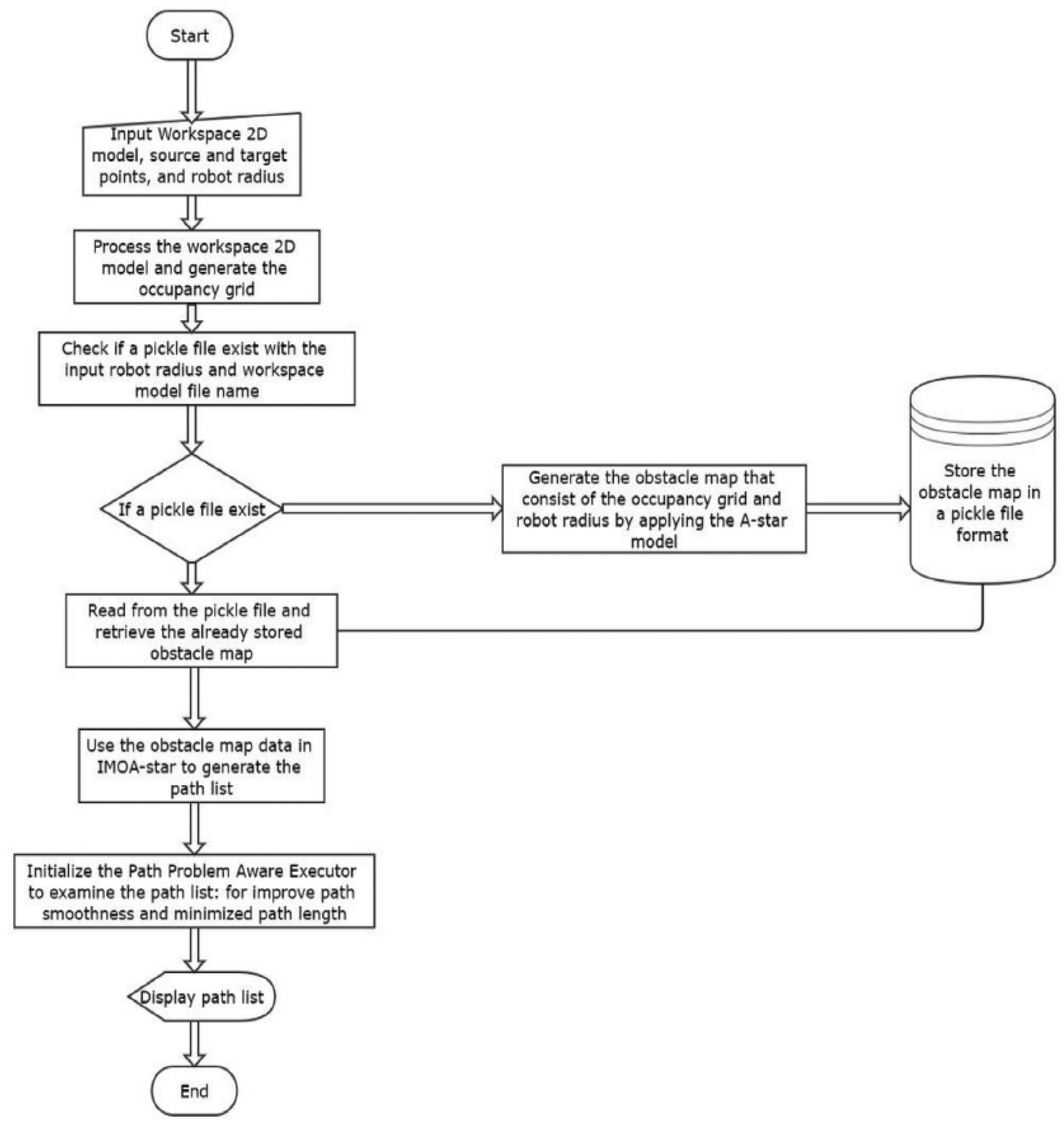
The algorithmic flowchart presented in paper ID 1.5 is illustrated in
Figure 1.
The EBS-A* algorithm enhances performance through three strategies: expansion distance, bidirectional search, and path smoothing. Expansion distance ensures a safety margin from obstacles, bidirectional search accelerates convergence, and smoothing eliminates sharp turns to provide more continuous and practical paths. These improvements make EBS-A* particularly suitable for industrial and service robotics in structured environments such as warehouses, airports, and healthcare facilities, where safety and reliable navigation are prioritized. However, these very improvements introduce important constraints. First, the algorithm assumes a static environment with a raster-type map, making it difficult to maintain performance when the operating space changes continuously or when map data are provided only partially—situations commonly encountered in outdoor applications or complex industrial settings. Second, the selection of the expansion–distance parameter depends directly on the robot’s geometric dimensions and kinematic characteristics (such as diameter and cruising speed) as well as on sensor accuracy. If this parameter is not properly tuned, it can either waste maneuvering space or, conversely, fail to provide a sufficient safety “buffer zone,” thereby reducing applicability in real operational contexts. Third, employing Bézier curves requires continuous computation and can increase the processing burden when applied to large maps or systems with limited computational resources. Consequently, EBS-A* is particularly well suited to scenarios in known indoor environments where the map is relatively stable and where optimizing trajectory smoothness and speed yields direct benefits for operational productivity.
In contrast, the IMOA* algorithm introduces a multi-objective optimization approach aimed at reducing computational overhead in large workspaces. By storing obstacle maps and incorporating a path–problem–aware executor, it significantly improves planning speed, smoothness, and energy efficiency for non-holonomic mobile robots. This design is highly applicable to large-scale logistics and industrial environments where computational speed and scalability are essential. Nevertheless, this advantage comes with several noteworthy limitations. First, the initial setup phase—the creation of the pickle file—can take several hours for a large workspace, which is incompatible with the need for rapid response in continuously changing environments. Moreover, IMOA* also assumes static obstacles and a fixed spatial configuration; any map variation requires a complete regeneration of the database, undermining the method’s time advantage. In addition, although the algorithm was demonstrated on powerful hardware (Intel Core i7), deploying it on resource-constrained computing devices (for example, low-cost robot embedded systems) may face challenges in terms of storage capacity and the bandwidth required to retrieve the pickle file.
In summary, EBS-A* is tailored for dynamic local navigation with real-time adaptation, while IMOA* targets large-scale environments requiring repeated queries and energy-efficient planning.
2.2. Group 2
All four studies in this group (IDs 1.1, 1.3, 1.6, and 1.8) incorporate a guideline—typically the axis between start and goal—to direct search trajectories and minimize unnecessary exploration. Each modifies the traditional A* evaluation function by embedding application-specific terms into the heuristic or as a separate penalty.
Erkel et al. [
28] proposed enhancements tailored for autonomous land vehicles, addressing A*’s inefficiencies in handling curves, obstacle anticipation, and fixed step size. Their revised function is:
where
G(
i) is the cumulative cost,
H1(
i) is the distance from node i to a guideline (expressing driver intent), and
H2(
i) is the distance from the nearest point g(i) on the guideline to the goal. The weights
α1 and
α2 balance spatial alignment and goal-directed efficiency. In the original article, the author used the subscript
i; however, in
Table 2, this has been replaced with n to ensure consistency with other published studies and to facilitate easier comparison. The meanings of these two indices are entirely equivalent.
Figure 2 describes the physical meaning for
H1 and
H2, as illustrated by Erke et al. [
28].
To enhance obstacle avoidance, the algorithm identifies key points near blocked guidelines and regenerates sub-guidelines that circumvent the obstruction. The best candidate is chosen based on virtual-speed-based cost–time.
Figure 3 shows the process of the key point-based A* algorithm, as proposed by Erke et al. [
28].
Furthermore, a variable-step strategy adjusts search resolution: longer steps in open areas improve efficiency, while shorter steps near obstacles enhance safety. Combined, these techniques reduce node expansion and planning time, enabling robust real-time path planning in complex urban environments.
In contrast, XiangRong et al. [
30] explicitly modify the evaluation function by appending a spatial constraint term
C(n) to guide the search trajectory. Their cost function is
f(n) = g(n) + h(n) + C(n). The function
C(n) quantifies the perpendicular distance between the current node n and a straight line—termed the “guide line”—connecting the start and goal positions. Mathematically, for a node
n = (xn,yn), start
s = (xs,ys), and goal
g = (xg,yg), the constraint is calculated as:
Figure 4 illustrates
C(n), as defined by XiangRong et al. [
30], representing a node’s deviation from the ideal trajectory. By penalizing nodes that deviate from the guide line, the algorithm minimizes unnecessary exploration, thereby reducing the search space and computational load. This constraint functions as a soft geometric prior, guiding the search toward globally aligned paths, even in complex obstacle environments.
Zhang et al. [
33] propose a similar yet subtly different improvement for unmanned surface vehicles (USVs) operating in marine environments. Their evaluation function extends A* by incorporating a linear deviation term
d(n), modulated by a tunable weight
λ:
f(n) = g(n) + h(n) + λd(n).
Figure 5 shows the node vertical distance diagram, as proposed by Zhang et al. [
33] Unlike
C(n), which uses Euclidean distance,
d(n) quantifies orthogonal deviation from a predefined navigation axis, measured relative to the grid. The weight λ adaptively controls the influence of this penalty, with higher values used in constrained environments such as narrow channels or dynamic obstacle zones. A directional smoothing filter is applied post-planning, highlighting that the evaluation function is part of a comprehensive trajectory optimization process.
Yin et al. [
35] proposed a mathematically rigorous enhancement by incorporating a directional angle cost
c(n) into the evaluation function:
where
c(n) = π − θ, and
θ is the angle between two vectors:
, from node
n to the start, and
, from
n to the goal. This formulation penalizes angular deviation, encouraging node selection aligned with the global path.
Figure 5 illustrates the node angle, as proposed by Yin et al. [
30]. This formulation favors nodes aligned with the global path (i.e., when
θ ≈
π). The weight μ adjusts the emphasis on angular consistency. This cost term proved effective in medical robotics, where smoother paths reduce mechanical strain and enhance the stability of sample transport. A cubic uniform B-spline smoothing stage is also applied to ensure physical feasibility for mobile platforms.
Study (ID 1.1) is applied in practice to autonomous land vehicles, enhancements such as guideline-based heuristics, key-point obstacle avoidance, and variable step sizes improve robustness and reduce computational cost, making the algorithm more adaptable to structured road environments. This approach helps stabilize the path and increase reliability, but it relies on the assumption of an available and trustworthy guideline—a condition difficult to achieve in dynamic environments or when map information is incomplete. In addition, selecting the optimal search-step parameter still requires experimentation and empirical tuning, thereby reducing the level of automation when scaling up. In static indoor settings, study (ID 1.3) reports improvements including bidirectional search, constraint functions, and guideline strategies effectively reduce memory consumption and limit unnecessary node expansion, enhancing efficiency for robots operating in constrained spaces. However, this method assumes that the straight line between the start and goal points is always geometrically valid and unobstructed by major obstacles. When the map has a complex layout or contains dynamic obstacles, the guide line may lose its validity, reducing the reliability of the solution and requiring the addition of a local replanning algorithm. In maritime applications, study (ID 1.6) applied the improved A* for unmanned surface vehicles integrates bidirectional search and spline-based smoothing, reducing inflection points and producing more navigable paths under complex sea conditions, which are critical for environmental monitoring tasks. Nevertheless, this method still relies on the assumption of a static environment and a rasterized grid. For dynamic marine areas with waves, moving obstacles, or incomplete map information, the solution lacks a real-time adaptation mechanism; moreover, the grid pre-processing steps and B-spline smoothing further increase the computational burden on resource-constrained embedded systems. Similarly, study (ID 1.8), conducted in medical testing laboratories, employed an enhanced evaluation function, bidirectional strategy, and B-spline smoothing to enable mobile robots to navigate efficiently in highly structured yet cluttered environments, thereby ensuring stability and reducing redundant nodes. However, this method strongly depends on an accurate grid map and a stable laboratory spatial configuration; any changes in the setup or equipment layout require remapping and a complete recomputation, thereby reducing flexibility in real operational environments that change continuously.
Although significant progress has been made, several common limitations persist. Many methods depend on accurate prior maps and demonstrate reduced adaptability in dynamic or rapidly changing environments. Moreover, path smoothing and optimization often increase computational complexity, limiting real-time responsiveness in large-scale scenarios. Overall, improved A* variants have shown strong potential in logistics, healthcare automation, and marine monitoring, and future work should integrate dynamic re-planning capabilities with multi-objective optimization to balance efficiency, safety, and adaptability in real-world applications.
These differences are reflected in the computational performance summarized in
Table 1. Erkel et al.’s algorithm achieved a 95.76% reduction in computational load (1.426 vs. 33.654) [
28]. XiangRong et al. [
30] reported average reductions of 65% in search area and 74.38% in processing time across two experiments. Zhang et al.’s hybrid method reduced the number of nodes traversed by 71.17% on 80 × 80 grid maps [
33], while Yin et al. [
35] showed a 52% reduction on 30 × 30 grid maps. All Group 2 studies achieved over 50% improvement, confirming the strong efficiency gains in expanded nodes—a key factor in optimizing time and memory consumption.
2.3. Group 3
Group 3 also modifies the evaluation function of traditional A*, but with a distinct focus on optimizing the weighting of the heuristic component
h(n). A comparative analysis of three recent algorithms [
34,
36,
37] reveals shared strategies—such as guided search, dynamic weighting, and heuristic refinement—alongside key differences in how the heuristic term is adaptively tuned to improve path quality and computational efficiency.
All three aim to reduce redundant node expansion, enhance heuristic flexibility, and apply post-processing smoothing. They start from the traditional A* formulation f(n) = g(n) + h(n), using Euclidean distance as h(n) for greater accuracy in continuous-space environments, compared to Manhattan or diagonal metrics.
The first aspect analyzed is heuristic weight adaptation, which balances search speed and accuracy. This strategy dynamically adjusts the weight of the heuristic function h(n) during the search, allowing the algorithm to emphasize global exploration or local refinement depending on goal proximity and environmental complexity.
These algorithms incorporate dynamic heuristic weighting to adjust the influence of h(n) throughout the search. For instance, Han et al. [
34] introduce a dynamic coefficient W in the evaluation function:
f(n) = g(n) + W ×
h(n).
In Zhang & Zhang [
37], a more structured weighting scheme is introduced:
where
R is the total distance between the start and goal, and r is the distance from the current node to the goal. This formulation prioritizes speed in the early search phase and accuracy in later phases.
Han et al. [
34] employ static weights for
W, manually tuned based on goal distance (see their
Table 2). In contrast, Zhang & Zhang [
37] implement real-time heuristic modulation via the ratio
(R + r)/
R, enabling automatic, environment-sensitive adaptation.
Zhao et al. [
36] introduced vector-based angular filtering, which restricts node expansion to directions aligned with the optimal search vector. Rather than evaluating 8, 16, or 24 neighbors, the algorithm limits the search to a six-directional neighborhood, defined as:
θ∈{[0°, 22.5°] ∪ (337.5°, 360°]; (22.5°, 90°]; (90°, 157.5°]; (157.5°, 202.5°]; (202.5°, 270°]; (270°, 337.5°]}
This directional constraint greatly reduces unnecessary lateral or regressive node expansions, cutting down on redundant processing without sacrificing path feasibility.
Secondly, we analyze differences in bidirectional search strategies. Unlike the traditional A*, which performs a unidirectional forward search, improved variants launch simultaneous searches from both the start and goal nodes. These converge mid-way, significantly reducing node expansion and computation time. The effectiveness of such strategies depends on how the meeting point is defined and how partial paths are merged, with implementations varying across studies.
Among the three, only Zhang & Zhang [
37] explicitly implement bidirectional A*, growing search trees from both start and goal nodes.
Thirdly, we examine differences in path smoothing. While all three algorithms apply post-processing to improve trajectory feasibility and motion stability, they adopt distinct mathematical approaches. These include strategies for reducing sharp turns, removing redundant waypoints, and ensuring curvature continuity. The next subsection outlines each method—such as Bezier curve fitting, angle-threshold filtering, and minimum snap optimization—highlighting their trade-offs in smoothness, computational cost, and real-time applicability.
Zhao et al. [
36] use second-order Bezier curves to connect segments of the raw path. The curve is defined by:
where
P0,
P1,
P2 are three sequential control points. This interpolation smooths sharp corners and provides continuous first- and second-order derivatives (velocity and acceleration), which are critical for real-time motion execution.
Instead of curve fitting, Zhang & Zhang [
37] employ an Inflection Point Elimination method using parent–grandparent filtering. This approach analyzes angular deviation among a node, its parent, and grandparent to identify and remove unnecessary inflection points. If a direct, obstacle-free line exists from
Pi to
Pi−2, the intermediate point
Pi−1 is eliminated. Iterative application of this rule yields a smoother, more direct path while preserving obstacle avoidance and geometric structure.
Han et al. [
34] introduced a Grouping-Based Node Consolidation method, dividing the minimal node set into seven segments and applying Bezier smoothing to each. This simple post-processing technique offers a balance between smoothness and structural fidelity, though it is less adaptive than Zhang & Zhang’s [
37] inflection point pruning.
In study (ID 1.7), the introduction of dynamic weighting and flexible neighborhood selection significantly improves computational efficiency while maintaining accuracy in large-scale environments. However, this method depends on properly tuning the weight coefficient W during the search phases; if W is not optimally chosen, the resulting path may not be truly shortest or may become unstable when the environment changes. In addition, the five search directions are constrained by the initial vector from the start to the goal point, so when the obstacle configuration is complex or there are many junctions, the narrowed search range may overlook feasible passages, reducing reliability in dynamic environments or irregular spaces. Similarly, algorithms in study (ID 1.10) that incorporate bidirectional search and refined evaluation functions achieve faster convergence and lower path costs, while the integration of Bezier or B-spline curves ensures smoother trajectories, which are critical for stable robot motion. Nevertheless, this approach still relies on the assumption of a static environment and complete map information; if obstacles move or the map is continuously updated, the bidirectional strategy will struggle to synchronize the searches from both sides. Moreover, the algorithm does not account for the vehicle’s kinematic constraints, so when applied to robots with limited turning radius or more complex dynamics, the smoothed path may still be mechanically infeasible. In off-road emergency rescue scenarios, study (ID 1.9) analyzed the inclusion of road and terrain factors allows the algorithm to generate feasible and time-efficient paths across unstructured environments, demonstrating adaptability to harsh and dynamic terrains. However, the fixed grid-based map model assumes a stable laboratory layout; any changes in the arrangement or equipment require remapping and a complete recomputation, limiting flexibility in environments that change frequently.
Despite these advances, several limitations remain. Many improved versions rely heavily on accurate environmental models, which may reduce effectiveness in dynamic or uncertain contexts. Furthermore, the additional computational overhead introduced by smoothing and evaluation refinements can limit scalability for real-time large-scale systems. In practice, these algorithms have shown promising applications in autonomous vehicles, logistics robots, marine and field exploration, and healthcare automation, where both safety and efficiency are paramount. Future research should aim to combine dynamic re-planning with multi-objective optimization to balance robustness, adaptability, and real-time performance in diverse operating environments.
As shown in
Table 1, algorithms in Group 3 demonstrate varying performance. Studies (IDs 1.7 and 1.9) achieved substantial reductions in processing time—82.07% and 88.2%, respectively. In contrast, study (ID 1.10) reported only a 20% reduction, indicating lower optimization effectiveness.
2.4. Group 4
The final study in this section (ID 1.2) distinguishes itself by prioritizing path smoothness over processing time or node expansion.
To enhance trajectory smoothness and control efficiency for autonomous land vehicles (ALVs), Zhang et al. [
29] proposed an improved A* algorithm that integrates an artificial potential field (APF) into the heuristic. Traditional A*, relying solely on distance-based heuristics, often produces paths with excessive turning points. To address this, the revised evaluation function is:
f(n) = g(n) + h′(n) + v(n); where
g(n) is the actual cost,
h′(n) is a diagonal-distance-based heuristic, and
v(n) represents APF-based repulsion from obstacles and attraction to the goal.
Specifically, the improved heuristic h′(n) is defined as:
Here,
xn and
yn represent the horizontal and vertical coordinates, respectively, of the current position
n, while
xe and
ye correspond to the horizontal and vertical coordinates of the target point. The potential field term
v(n) is computed via the projection of the synthetic force vector
(all repulsive forces and attraction) onto the direction vector
toward the neighbor:
The improved A* algorithm for autonomous land vehicles introduces a heuristic function combining distance and obstacle potential fields, enabling smoother and more practical paths. By reducing redundant turning points and integrating B-spline smoothing, the method enhances maneuverability and decreases posture adjustments, which is crucial for efficiency in logistics, rescue, and urban navigation. Its main advantage is improved path feasibility and stability, while the drawback lies in higher computational cost and longer planning times in dense environments. Nevertheless, this method still has clear limitations: (i) it relies heavily on the quality and accuracy of the static raster map; (ii) computing the potential field and performing B-spline path smoothing significantly increases planning time (doubling it in large-scale tests), making real-time applications challenging; and (iii) the well-known local minima problem of the potential field approach can cause the algorithm to become trapped.
When combined with quartic B-spline smoothing, it preserves path length similar to traditional A*, while reducing total turning angle by approximately 71–72%. Although computational time increases due to added complexity, overall ALV operation time decreases, as fewer directional adjustments are needed during execution.
4. Conclusions
The scalability of A* deteriorates significantly in larger or more complex environments due to several inherent limitations [
50]. First, the search space grows exponentially with map size: in two-dimensional grids, doubling the resolution quadruples the number of nodes, while in three-dimensional environments the growth is cubic. Second, the algorithm requires maintaining both open and closed lists, and priority queue operations become computational bottlenecks when managing hundreds of thousands of nodes. Third, redundant node expansions increase substantially in large maps, as A* explores numerous unnecessary states to guarantee global optimality. Fourth, the reliance on uniform grid discretization creates a trade-off: fine grids yield accurate paths but dramatically increase computational cost, whereas coarse grids reduce computation but produce unrealistic “staircase” trajectories that violate the kinematic feasibility of real robots. Finally, A* lacks adaptability; any environmental change necessitates recomputation from scratch, which is particularly prohibitive in large, dynamic scenarios such as warehouses, agricultural fields, or search-and-rescue operations.
In essence, A*’s poor scalability arises from its exhaustive search nature and uniform grid reliance. This is why researchers in robotics and automation have moved toward improved or hybrid A* variants (e.g., A* + DWA, A* + APF, A* + PSO, A* + RRT…), which incorporate adaptive heuristics, hierarchical maps, or learning-based strategies to significantly reduce computational load while maintaining path quality.
The findings indicate that while the traditional A* algorithm has its limitations—such as trajectory angularity, computational inefficiency, and lack of adaptability to dynamic or large-scale environments—have motivated diverse enhancements. Studies focusing on geometric and heuristic refinements have demonstrated significant reductions in node expansion, path angularity, and computation time, while hybrid frameworks that combine A* with methods such as DWA, APF, PSO, RRT, and Greedy algorithm have proven more robust in dynamic, uncertain, or multi-goal scenarios. Importantly, the hybrid approaches not only bridge global optimality with local adaptability but also offer improved safety margins and smoother trajectories, thereby moving closer to real-world applicability in autonomous mobile robots.
Despite these advances, several open challenges remain. First, most of the improvements have been validated in controlled simulation environments, with limited experimental evidence on physical robotic platforms operating in large-scale, unstructured, or highly dynamic environments. Second, many algorithms prioritize one performance metric (e.g., smoothness or computational efficiency) at the expense of others, leading to trade-offs that are not sufficiently addressed in a unified optimization framework. Third, current hybrid algorithms still lack generalization capability; their effectiveness is often contingent upon parameter tuning and problem-specific assumptions. Furthermore, the integration of learning-based methods, such as deep reinforcement learning, has only been explored in a limited capacity, leaving significant potential for adaptive and self-optimizing navigation strategies.
Future research should address these gaps through several promising directions. A first priority is the development of holistic evaluation benchmarks that incorporate path optimality, smoothness, safety, computation time, and energy efficiency under standardized testing scenarios. Such benchmarks will enable objective cross-comparison and accelerate the translation of algorithmic innovation into practical deployment. A second direction lies in the tight integration of A with machine learning and data-driven methods, enabling adaptive heuristic functions, real-time parameter optimization, and lifelong learning in continuously evolving environments. Third, multi-agent navigation represents a critical frontier, where collaborative path planning and decentralized control must ensure scalability and robustness in swarm robotics, warehouse intralogistics, and emergency rescue operations. Fourth, future systems must incorporate kinodynamic constraints and uncertainty modeling, ensuring that planned trajectories are not only geometrically optimal but also dynamically feasible and real-time movements under sensor noise, localization errors, and environmental disturbances. Lastly, hardware-in-the-loop validation and large-scale real-world experiments should become a standard component of evaluation to confirm robustness, safety, and computational feasibility in practical robotic systems.
In conclusion, the trajectory of research indicates that improved and hybridized A* algorithms will remain a cornerstone of autonomous navigation. Their continued evolution, coupled with advances in sensing, computation, and machine learning, promises to deliver intelligent, adaptive, and reliable robotic systems capable of safe and efficient operation in increasingly complex environments.





 −95.76%
−95.76%  −0.15%
−0.15%  −2.0%
−2.0%  unspecified
unspecified unspecified
unspecified −1% to −2%
−1% to −2%  Processing time doubled due to computational complexity
Processing time doubled due to computational complexity −71% to −72%
−71% to −72%  −65%
−65%  −11.41%
−11.41%  −74.38%
−74.38% unspecified
unspecified −62.52%
−62.52% −13.13%
−13.13% −82.21%
−82.21% −50%
−50% −83.45%
−83.45% −1.58%
−1.58% −99.8%
−99.8% unspecified
unspecified −71.17%
−71.17% −3.13%
−3.13% −49.9%
−49.9% −35.12%
−35.12% −86.57%
−86.57% unchanged
unchanged −82.07%
−82.07% The application of the Bézier curve; not quantified.
The application of the Bézier curve; not quantified. −52%
−52% −3.7%
−3.7% −49.4%
−49.4% 
 −13.4%
−13.4% +21.9%
+21.9% −88.2%
−88.2% unspecified
unspecified −48.31%
−48.31% −6.6%
−6.6% −20.00%
−20.00% −1.86%
−1.86% The reduction may be attributed to the nature of the RRT algorithm, which does not explore the entire space exhaustively but rather expands the tree through randomly sampled points; not quantified.
The reduction may be attributed to the nature of the RRT algorithm, which does not explore the entire space exhaustively but rather expands the tree through randomly sampled points; not quantified.  −51.7%
−51.7%  −70.9%
−70.9% In RRT, new nodes are generated along vectors directed toward the goal, which facilitates the formation of curved paths or paths with reduced angular deviations; not quantified.
In RRT, new nodes are generated along vectors directed toward the goal, which facilitates the formation of curved paths or paths with reduced angular deviations; not quantified.  unspecified
unspecified −22%
−22%  unspecified
unspecified −53%
−53% −88.85%
−88.85% −5.58%
−5.58% −77.05%
−77.05% unspecified
unspecified −13.9%
−13.9% insignificant change
insignificant change −36.6%
−36.6% Path smoothing is achieved using the Dynamic Tangent Method; not quantified.
Path smoothing is achieved using the Dynamic Tangent Method; not quantified.  −32%
−32% unspecified
unspecified −70%
−70% Path smoothing is achieved using the Least Squares method; not quantified.
Path smoothing is achieved using the Least Squares method; not quantified.  −17.2%
−17.2% −9.68%
−9.68% −24.54%
−24.54% −72.59%
−72.59% unchanged
unchanged −4.8%
−4.8% −16%
−16% −76%
−76% −58%
−58% −6.24%
−6.24% −12%
−12% −75%
−75% The reduction may be attributed to the decrease in the number of neighboring directions considered—from eight to five; not quantified.
The reduction may be attributed to the decrease in the number of neighboring directions considered—from eight to five; not quantified.  No path shortening was observed.
No path shortening was observed. The processing time is reduced; not quantified.
The processing time is reduced; not quantified.  −51.96%
−51.96%  −51.8%
−51.8% −17.9%
−17.9% −43.4%
−43.4% −53.5%
−53.5% unspecified
unspecified −5.5%
−5.5%  50.7 times higher in terms of random sampling and optimization time
50.7 times higher in terms of random sampling and optimization time The path curvature is significantly increased owing to the continuous circular arc technique applied at the junction of two straight segments.
The path curvature is significantly increased owing to the continuous circular arc technique applied at the junction of two straight segments. It decreases because random node selection is probabilistic, thereby avoiding excessive exploration around local optima.
It decreases because random node selection is probabilistic, thereby avoiding excessive exploration around local optima. unchanged
unchanged −12%
−12% −24%
−24%






