Optimized Adaptive Fuzzy Synergetic Controller for Suspended Cable-Driven Parallel Robots
Abstract
1. Introduction
2. Kinematic and Dynamic Modeling of a Suspended CDPR
2.1. Kinematic Modeling
2.2. Dynamic Modeling
3. Controller Design
3.1. Synergetic Controller
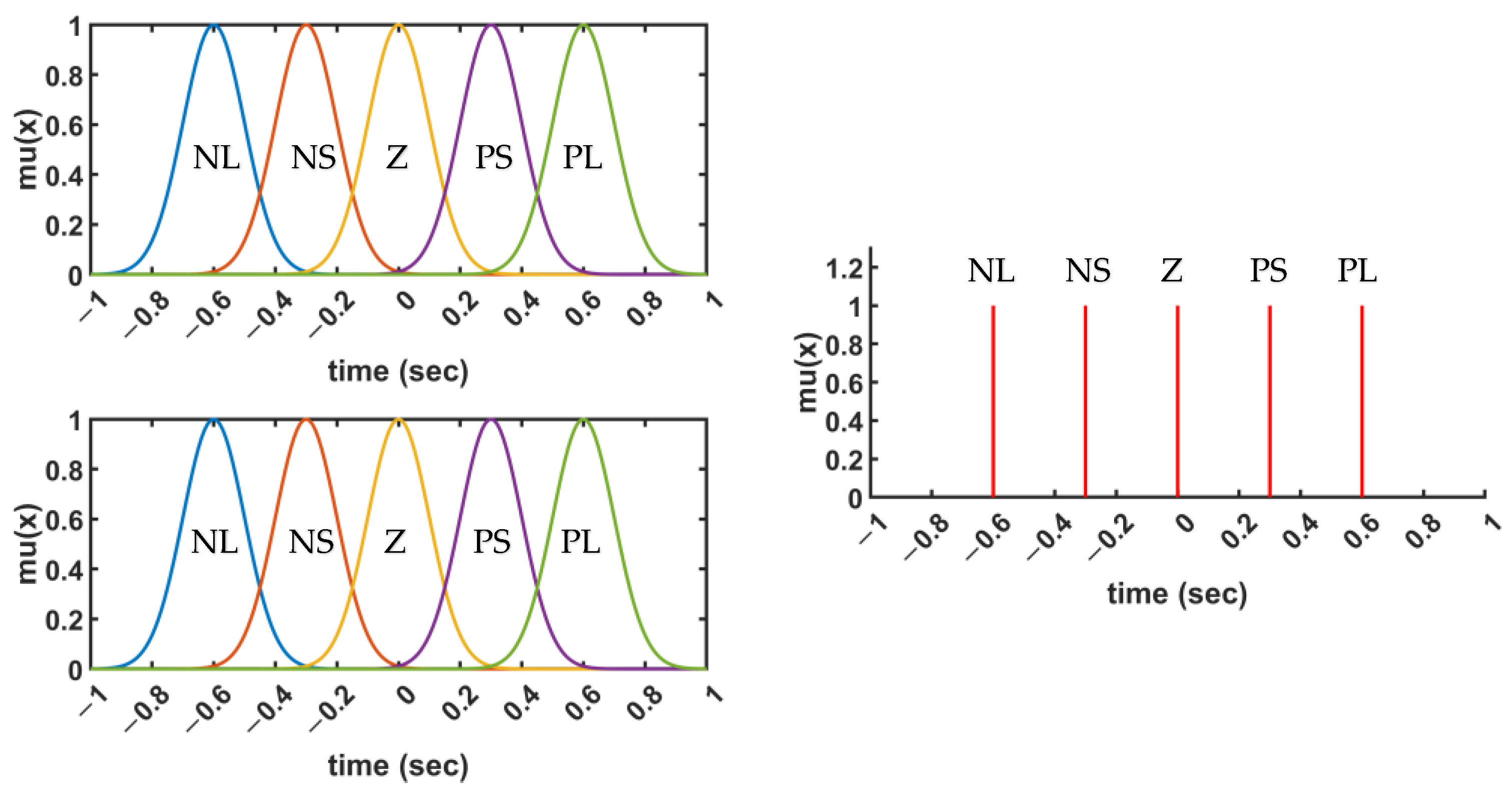
3.2. Fuzzy Basis System
3.3. AFSC
3.4. DA Optimization
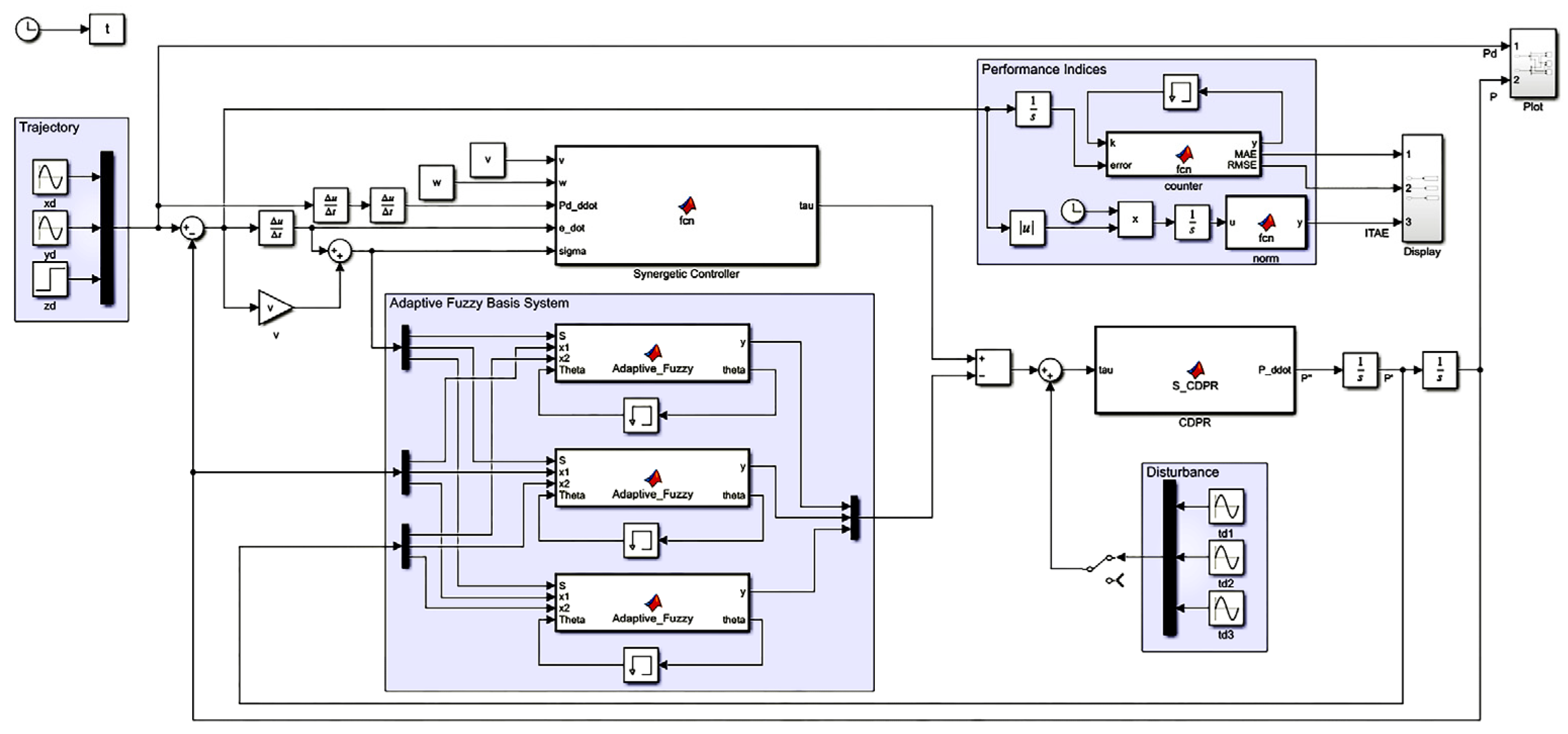
4. Results and Discussion
4.1. Scenario One: Without Disturbance and Parameter Uncertainities
4.2. Scenario Two: With Disturbance and Parameter Uncertainities
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jomartov, A.; Tuleshov, A.; Kamal, A.; Abduraimov, A. Simulation of Suspended Cable-Driven Parallel Robot on SimulationX. Int. J. Adv. Robot. Syst. 2023, 20, 172988062311614. [Google Scholar] [CrossRef]
- Tho, T.P.; Thinh, N.T. An Overview of Cable-Driven Parallel Robots: Workspace, Tension Distribution, and Cable Sagging. Math. Probl. Eng. 2022, 2022, 2199748. [Google Scholar] [CrossRef]
- Zhang, Z.; Shao, Z.; You, Z.; Tang, X.; Zi, B.; Yang, G.; Gosselin, C.; Caro, S. State-of-the-Art on Theories and Applications of Cable-Driven Parallel Robots. Front. Mech. Eng. 2022, 17, 37. [Google Scholar] [CrossRef]
- Picard, E.; Tahoumi, E.; Plestan, F.; Caro, S.; Claveau, F.A. New Control Scheme of Cable-Driven Parallel Robot Balancing Between Sliding Mode and Linear Feedback. IFAC Pap. 2020, 53, 9936–9943. [Google Scholar] [CrossRef]
- Ji, H.; Shang, W.; Cong, S. Adaptive Synchronization Control of Cable-Driven Parallel Robots with Uncertain Kinematics and Dynamics. IEEE Trans. Ind. Electron. 2021, 68, 8444–8454. [Google Scholar] [CrossRef]
- Liu, P.; Tian, H.; Cao, X.; Qiao, X.; Gong, L.; Duan, X.; Qiu, Y.; Su, Y. Pick-and-Place Trajectory Planning and Robust Adaptive Fuzzy Tracking Control for Cable-Based Gangue-Sorting Robots with Model Uncertainties and External Disturbances. Machines 2022, 10, 714. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, Y.; Zi, B.; Zhu, W. Fuzzy Adaptive Whale Optimization Control Algorithm for Trajectory Tracking of a Cable-Driven Parallel Robot. IEEE Trans. Autom. Sci. Eng. 2023, 21, 5149–5160. [Google Scholar] [CrossRef]
- Kolesnikov, A.; Veselov, G.; Kolesnikov, A. Modern Applied Control Theory: Synergetic Approach in Control Theory; TSURE Press: Moscow, Russia, 2000. [Google Scholar]
- Derkouche, D.; Kouzi, K. Optimized Synergetic Control Approach for a Six-Phase Asynchronous Generator Coupled to an Intelligent Flywheel Energy Storage System. Rom. J. Inf. Technol. Autom. Control 2022, 32, 103. [Google Scholar] [CrossRef]
- Erenturk, K.; Draou, A.; AlKassem, A. Design and Comparison of Different Types of Synergetic Controllers for Islanded DC Microgrids. Sustainability 2022, 14, 8792. [Google Scholar] [CrossRef]
- Khatir, A.; Bouchama, Z.; Benaggoune, S.; Zerroug, N. Indirect Adaptive Fuzzy Finite Time Synergetic Control for Power Systems. Electr. Eng. Electromechanics 2023, 1, 57–62. [Google Scholar] [CrossRef]
- Medjbeur, L.; Harmas, M.N. Adaptive Fuzzy Terminal Synergetic Control. In Proceedings of the 2011 International Conference on Communications, Computing and Control Applications (CCCA), Hammamet, Tunisia, 3–5 March 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Rebai, A.; Guesmi, K.; Gozim, D.; Hemici, B. Adaptive Fuzzy Synergetic Control of Nonlinear Systems with Unknown Backlash-Like Hysteresis. In Proceedings of the 19th International Conference on System Theory, Control and Computing (ICSTCC), Cheile Gradistei, Romania, 14–16 October 2015; pp. 213–218. [Google Scholar] [CrossRef]
- Abdelouaheb, B.; Farid, K.; Najib, E. Synergetic Adaptive Fuzzy Control for A Class of Nonlinear Discrete-Time Systems. Int. J. Control Autom. Syst. 2018, 16, 1981–1988. [Google Scholar] [CrossRef]
- Bouchama, Z.; Essounbouli, N.; Harmas, M.N.; Hamzaoui, A.; Saoudi, K. Reaching Phase Free Adaptive Fuzzy Synergetic Power System Stabilizer. Int. J. Electr. Power Energy Syst. 2016, 77, 43–49. [Google Scholar] [CrossRef]
- Sobhan, P.V.S.; Rambabu, C.; Padmavathi, S.V.; Bali, S.K.; Yaseen, M.D. Fuzzy Synergetic Control Based Thermoelectric Generator System for Waste Heat Recovery in Manufacturing Process. Int. J. Interact. Des. Manuf. 2022. [Google Scholar] [CrossRef]
- Babes, B.; Hamouda, N.; Albalawi, F.; Aissa, O.; Ghoneim, S.S.M.; Abdelwahab, S.A.M. Experimental Investigation of an Adaptive Fuzzy-Neural Fast Terminal Synergetic Controller for Buck DC/DC Converters. Sustainability 2022, 14, 7967. [Google Scholar] [CrossRef]
- Bouchama, Z.; Harmas, M.N. Optimal Robust Adaptive Fuzzy Synergetic Power System Stabilizer Design. Electr. Power Syst. Res. 2012, 83, 170–175. [Google Scholar] [CrossRef]
- Mirjalili, S.M. Dragonfly Algorithm: A New Meta-Heuristic Optimization Technique for Solving Single-Objective, Discrete, and Multi-Objective Problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Hosseini, M.I.; Harandi, M.; Khalilpour, S.A.; Taghirad, H. Adaptive Fast Terminal Sliding Mode Control of a Suspended Cable-Driven Robot. In Proceedings of the 27th Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, 30 April–2 May 2019; pp. 985–990. [Google Scholar] [CrossRef]
- Jomartov, A.; Tuleshov, A.; Kamal, A.; Abduraimov, A. Design of a Cable-Driven Parallel Robot for Landmine Detection. SN Appl. Sci. 2023, 5, 299. [Google Scholar] [CrossRef]
- Hasan, M.A.; Oglah, A.A.; Marie, M.J. Optimal FOPI-FOPD Controller Design for Rotary Inverted Pendulum System Using Grey Wolves’ Optimization Technique. Telkomnika 2023, 21, 657–666. [Google Scholar] [CrossRef]
- Lewis, F.L.; Dawson, D.M.; Abdallah, C.T. Robot Manipulator Control: Theory and Practice, 2nd ed.; Marcel Dekker: New York, NY, USA, 2004. [Google Scholar]
- Humaidi, A.J.; Ibraheem, I.K.; Azar, A.T.; Sadiq, M.E. A New Adaptive Synergetic Control Design for Single Link Robot Arm Actuated by Pneumatic Muscles. Entropy 2020, 22, 723. [Google Scholar] [CrossRef]
- Ben Hazem, Z.; Bingül, Z. A Comparative Study of Anti-Swing Radial Basis Neural-Fuzzy LQR Controller for Multi-Degree-of-Freedom Rotary Pendulum Systems. Neural Comput. Appl. 2023, 35, 17397–17413. [Google Scholar] [CrossRef]
- Lutfy, O.F.; Mohd, N.; Samsul, B.; Marhaban, M.H. A Simplified Adaptive Neuro-Fuzzy Inference System (ANFIS) Controller Trained by Genetic Algorithm to Control Nonlinear Multi-Input Multi-Output Systems. Sci. Res. Essays 2011, 6, 6475–6486. [Google Scholar] [CrossRef]
- Yoo, B.K.; Ham, W.C. Adaptive Control of Robot Manipulator Using Fuzzy Compensator. IEEE Trans. Fuzzy Syst. 2000, 8, 186–199. [Google Scholar]
- Zi, B. Fuzzy Control System Design and Analysis for Completely Restrained Cable-Driven Manipulators. In Fuzzy Logic-Controls, Concepts, Theories and Applications; Dadios, E., Ed.; InTech: Silverwater, Australia, 2012. [Google Scholar]
- Amini, Z.; Maeen, M.; Jahangir, M.R. Providing a Balancing Method Based on Dragonfly Optimization Algorithm for Resource Allocation in Cloud Computing. Int. J. Networked Distrib. Comput. 2017, 6, 35–42. [Google Scholar] [CrossRef]
- Rahman, C.M.; Rashid, T.A.; Alsadoon, A.; Bacanin, N.; Fattah, P.; Mirjalili, S. A Survey on Dragonfly Algorithm and Its Applications in Engineering. Evol. Intell. 2021, 16, 1–21. [Google Scholar] [CrossRef]
- Alshinwan, M.; Abualigah, L.; Shehab, M.; Abd Elaziz, M.; Khasawneh, A.M.; Alabool, H.; Al Hamad, H. Dragonfly Algorithm: A Comprehensive Survey of Its Results, Variants, and Applications. Multimed. Tools Appl. 2021, 80, 14979–15016. [Google Scholar] [CrossRef]
- Meraihi, Y.; Ramdane-Cherif, A.; Acheli, D.; Mahseur, M. Dragonfly Algorithm: A Comprehensive Review and Applications. Neural Comput. Appl. 2020, 32, 16625–16646. [Google Scholar] [CrossRef]
- Awouda, A.A.; Mamat, R.B. Refine PID Tuning Rule Using ITAE Criteria. In Proceedings of the 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 23–25 February 2019; pp. 171–176. [Google Scholar] [CrossRef]
- Chak, Y.-C. Fuzzy Control of a Double Integrator: A Performance Comparison of Four Basic Shapes of Fuzzy Sets. Res. Exp. Find. 2021, 10, 1–6. [Google Scholar] [CrossRef]
- Ghaleb, A.F.; Oglah, A.A.; Humaidi, A.J.; Al-Obaidi, A.S.M.; Ibraheem, I.K. Optimum of Fractional Order Fuzzy Logic Controller with Several Evolutionary Optimization Algorithms for Inverted Pendulum. Int. Rev. Appl. Sci. Eng. 2023, 14, 1–12. [Google Scholar] [CrossRef]
- Mirjalili, S.M. DA: Dragonfly Algorithm. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/51035-da-dragonfly-algorithm (accessed on 10 November 2024).
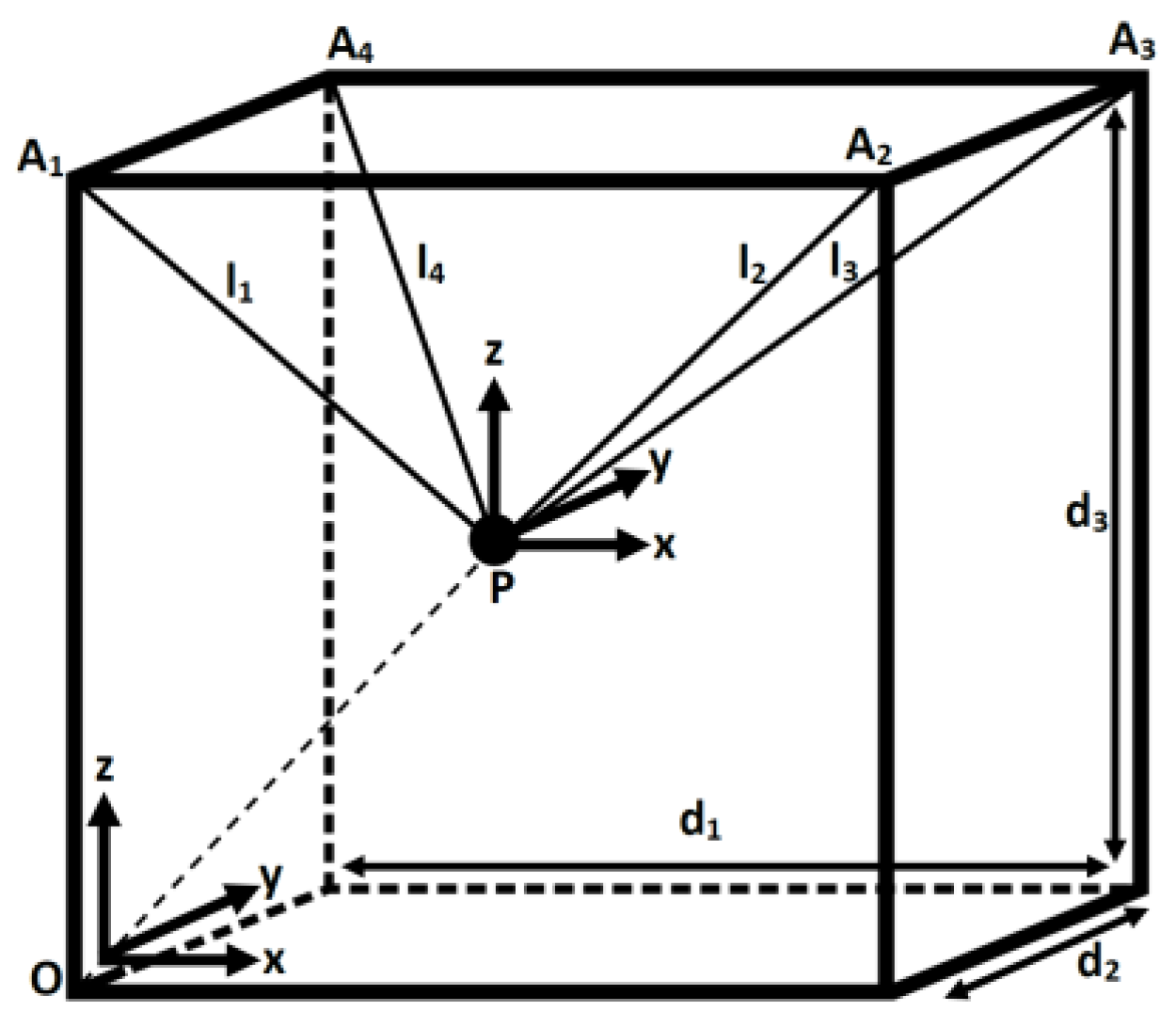
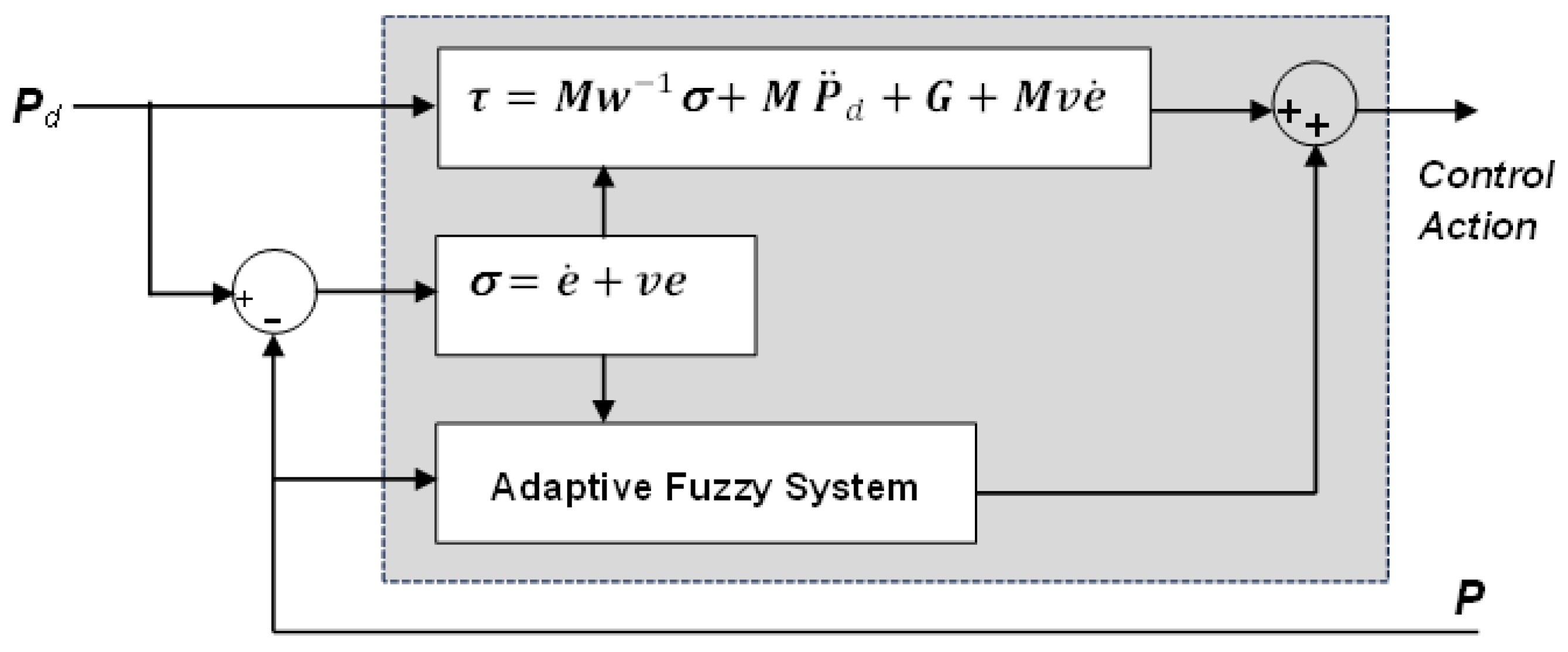



| Parameter | Symbol | Description |
|---|---|---|
| Frame Dimensions | Length, width, and height of the frame. | |
| Top plane’s corners | Positions of the top corners of the frame. | |
| EE position | position of the EE. | |
| Cable length | length of the cables. | |
| EE mass matrix | m is the mass of EE, and I is the identity matrix. | |
| EE gravity vector | ||
| Generalized force vector | Force in task space. | |
| Tension vector | Force in joint space. | |
| Jacobian matrix | Transformation matrix from joint space to task space. | |
| Disturbances and uncertainties component vector | bounded value. |
| Parameter | Symbol | Value |
|---|---|---|
| Vector A1 | [0, 0, d3] | [0, 0, 3] meters |
| Vector A2 | [0, d2, d3] | [0, 4, 3] meters |
| Vector A3 | [d1, 0, d3] | [4, 0, 3] meters |
| Vector A4 | [d1, d2, d3] | [4, 4, 3] meters |
| Mass of EE | m | 5 kg |
| NL | NS | Z | PS | PL | |
|---|---|---|---|---|---|
| NL | NL | NL | NL | NS | Z |
| NS | NL | NL | NS | Z | PS |
| Z | NL | NS | Z | PS | PL |
| PS | NS | Z | PS | PL | PL |
| PL | Z | PS | PL | PL | PL |
| Parameter | Symbol | Value (Case 1) |
|---|---|---|
| Number of variables to be optimized | s | 6 |
| Lower–upper bound of variables | lb, ub | 0.1, 100 |
| Nationhood hypersphere radius | r | |
| Inertia weight | ||
| Weight of separation, alignment, and cohesion | 2Rand. | |
| Weight of food factor | 2Rand. | |
| Weight of enemy factor | ||
| Random walk parameters | [] | [Rand., Rand., 1.5] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alwan, Y.H.; Oglah, A.A.; Croock, M.S. Optimized Adaptive Fuzzy Synergetic Controller for Suspended Cable-Driven Parallel Robots. Automation 2025, 6, 15. https://doi.org/10.3390/automation6020015
Alwan YH, Oglah AA, Croock MS. Optimized Adaptive Fuzzy Synergetic Controller for Suspended Cable-Driven Parallel Robots. Automation. 2025; 6(2):15. https://doi.org/10.3390/automation6020015
Chicago/Turabian StyleAlwan, Yasser Hatim, Ahmed A. Oglah, and Muayad Sadik Croock. 2025. "Optimized Adaptive Fuzzy Synergetic Controller for Suspended Cable-Driven Parallel Robots" Automation 6, no. 2: 15. https://doi.org/10.3390/automation6020015
APA StyleAlwan, Y. H., Oglah, A. A., & Croock, M. S. (2025). Optimized Adaptive Fuzzy Synergetic Controller for Suspended Cable-Driven Parallel Robots. Automation, 6(2), 15. https://doi.org/10.3390/automation6020015






