1. Introduction
As modern industry continues to advance, rotating machines have become crucial components that drive a wide range of applications, from energy production to manufacturing. Because these machines often operate under varying conditions, they are susceptible to failures that can result in system-wide breakdowns, leading to significant economic losses and even safety hazards [
1,
2]. Thus, research on fault diagnosis in rotating machines—especially in key components such as bearings and gearboxes—is essential for ensuring the reliability and efficiency of industrial processes.
In recent years, artificial intelligence methods have emerged as valuable tools for the fault diagnosis of rotating machines and their components. Among these, deep learning methods have gained increasing research interest because of their robust capabilities in feature extraction and fault classification [
2]. These methods require large amounts of labeled data for effective training; however, obtaining sufficient fault data in practical industrial environments is extremely challenging due to various intrinsic challenges associated with industrial operations. These challenges include the prevalence of healthy state data due to extended normal operation periods [
3], the infrequent occurrence of faults in well-maintained systems [
4], the impracticality of inducing faults for data collection due to costs and safety concerns [
5], and the complexity of collecting comprehensive fault data encompassing various fault types and severities [
6].
In addition, the scarcity of fault data leads to significant class imbalance in condition monitoring datasets, where healthy state data vastly outnumber fault data, with some fault classes being particularly underrepresented [
7]. This imbalance creates challenges for the deep learning models used for fault diagnosis. These models often favor the majority class (i.e., healthy state), leading to poor detection rates for the less common fault classes. The scarcity of fault data can lead to inadequate training of the model, resulting in overfitting and significantly limiting the use of deep learning models in industrial settings. In addition, the absence of diverse fault data hinders the ability of the model to identify new or unseen faults [
8]. This is particularly problematic given the wide variety of possible fault types and severities that can occur in rotating machinery. Standard evaluation metrics can also provide overly optimistic assessments of model performance when applied to imbalanced datasets, further complicating the assessment of deep learning-based fault diagnosis solutions. Thus, the issues of fault data scarcity and class imbalance present significant barriers to the development and deployment of effective and reliable intelligent fault diagnosis models in industrial settings.
Many researchers have employed the synthetic minority oversampling technique (SMOTE) and its improved variants [
9,
10,
11,
12] as data generation methods in fault diagnosis studies to resolve the issue of imbalanced data and improve diagnostic accuracy. However, while the SMOTE and its adaptations focus primarily on local information, they often produce synthetic data that lack realism and struggle to capture complex data distributions, resulting in a limited diversity of generated samples. Furthermore, these methods generate new samples through interpolation among existing samples, which can lead to overfitting. Thus, such oversampling techniques fall short of effectively utilizing fault information and expanding the dataset, making it challenging to provide the sufficient training data required by deep learning models.
Scholars have also turned to machine learning techniques to address the challenges of fault diagnosis with limited fault data. For example, Mao et al. [
13] developed an online sequential prediction framework that employs an extreme learning machine to address the fault diagnosis issue in situations with limited fault data. Leveraging the strong learning capabilities of deep learning models, He et al. [
14] constructed a transfer multi-wavelet auto-encoder to diagnose gearbox faults when faced with limited fault samples. Zhao et al. [
15] developed a normalized CNN aimed at diagnosing bearing faults to address the critical issue of data imbalance due to limited fault data. Similarly, Jia et al. [
16] proposed a deep normalized CNN to enhance the training process and implemented a weighted SoftMax loss to address the issue of imbalanced data. Nevertheless, these methods often require significant computational resources and may not generalize well to unseen fault conditions, thereby highlighting ongoing challenges in this research area.
Recently, generative adversarial networks (GANs), introduced by Goodfellow et al. [
17] in 2014, have become a prominent technique for data augmentation in fault diagnosis, specifically to address data imbalance issues. Unlike traditional data augmentation methods, GANs generate synthetic samples by learning the mapping between a prior distribution and the target data distribution [
18,
19]. However, standard GANs often encounter challenges, such as unstable training, which can lead to the generation of low-quality samples. Additionally, these models may struggle to produce multiple fault categories at once.
To overcome these limitations, recent research has focused on developing improved GAN architectures that can generate multiple categories of fault signals with stable training. For example, Wang et al. [
20] utilized a conditional GAN for augmenting fault data in bearing fault diagnosis. Similarly, Georgios and Bacao [
21] proposed a conditional GAN-based method that captures the real distribution of the minority class by adding extra conditional information. Jiang et al. [
22] introduced a variational information-constrained GAN aimed at addressing the issue of limited fault data in machine diagnosis. This approach incorporates an encoder into the discriminator to improve data synthesis capabilities. Wang et al. [
23] also applied a Wasserstein GAN (WGAN) to generate fault signals and employed a new loss function based on the Wasserstein distance that enhances model stability compared with traditional GANs. Following a similar approach, Gao et al. [
24] extended the WGAN with a gradient penalty to generate artificial data samples, thereby enriching datasets with limited samples and improving diagnostic accuracy. Additionally, Zhu et al. [
25] employed a conditional WGAN with a gradient penalty as a novel oversampling method to create synthetic samples for minority classes in imbalanced datasets. Zhang et al. [
26] introduced a multi-module GAN featuring an adaptive decoupling strategy to address the scarcity of fault samples, whereas Liu et al. [
27] utilized a deep feature-enhanced GAN to generate synthetic fault samples, expanding the training dataset for better fault diagnosis of rolling bearings. Huang et al. [
28] developed an improved GAN for bearing fault diagnosis to address challenges such as model collapse and gradient vanishing during training.
The review of the aforementioned studies exemplified the effectiveness of GANs in enriching training samples for fault diagnosis in rotating machines, but GANs still face the following limitations: (1) Most existing GANs often fail to capture the hierarchical characteristics of machinery vibration signals, which contain vital information across multiple time scales. (2) Although some research efforts have focused on integrating physical aspects into deep learning models [
29,
30,
31,
32], to the knowledge of the authors, existing GANs do not incorporate domain-specific knowledge or physical principles in the generation of synthetic samples. Thus, the generated signals may not accurately represent real-world fault conditions. (3) Many existing GAN models produce a limited diversity of samples, which poses challenges when simulating a wide range of fault conditions. Furthermore, these GANs often struggle to maintain consistent patterns in time-series data, resulting in difficulties in verifying the quality of the generated signals.
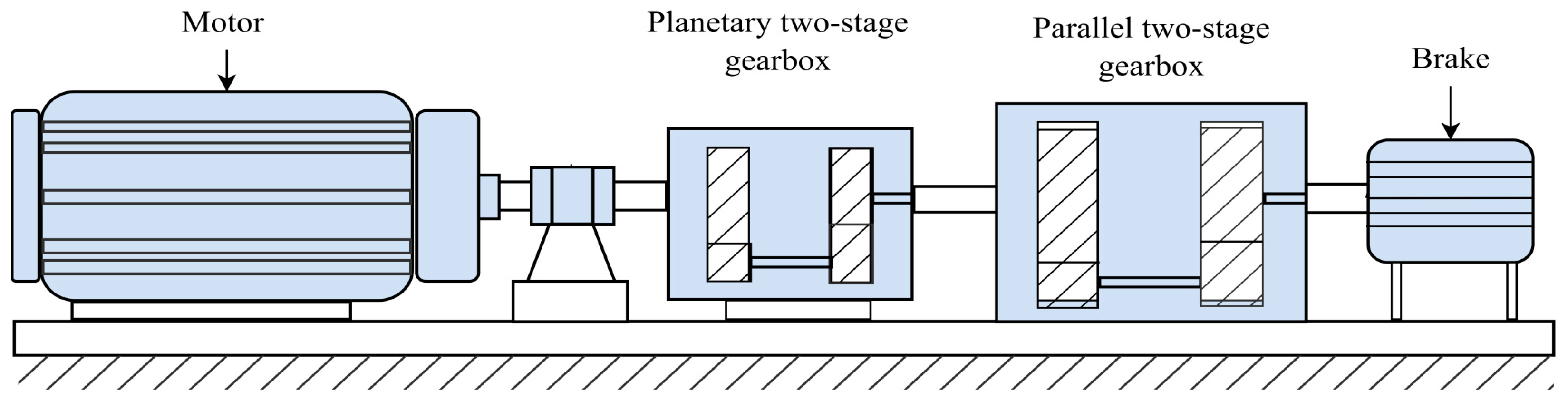
In this paper, a novel hierarchical adaptive wavelet-guided adversarial network with physics-informed regularization (HAWAN-PIR) is proposed. The objective of HAWAN-PIR is to generate high-quality, multiscale time-series vibration signals to enrich the training dataset for a one-dimensional convolutional network (1-D CNN). More importantly, HAWAN-PIR incorporates physics-informed regularization of machinery faults to ensure that the generated signals adhere to known physical knowledge and constraints. The 1-D CNN model autonomously extracts high-level features from the input data and uses these features to predict the health state of the target machinery. The effectiveness of HAWAN-PIR and the associated fault diagnosis process is validated through two experimental studies: motor rolling bearings and planetary gearboxes.
The main contributions of this study can be summarized as follows:
- (1)
A hierarchical wavelet-based imbalance severity score is introduced to quantify data imbalance across multiple scales in fault diagnosis datasets.
- (2)
A new hierarchical GAN architecture with physics-informed regularization is proposed that uses adaptive wavelet decomposition to generate realistic vibration signals at different scales, significantly enhancing fault diagnosis in rotating machinery.
- (3)
A multiscale synthesis quality index is developed to evaluate the quality of the generated fault data. This index assesses the fidelity and realism of synthetic data across different scales.
- (4)
A scale-aware dynamic mixing algorithm is presented to optimally integrate synthetic data with real data. This addresses how to effectively combine these datasets.
- (5)
In this paper, ablation studies are conducted to verify the effectiveness of the HAWAN-PIR framework. The studies analyze how different components of HAWAN-PIR contribute to the diagnostic performance of the 1-D CNN model.
The subsequent sections of this paper are organized as follows:
Section 2 details the proposed method,
Section 3 presents the experimental validation and analysis, and
Section 4 concludes this paper.
2. The Proposed Method
2.1. Network Architecture of HAWAN-PIR
To address the data imbalance problem and improve fault diagnosis performance, HAWAN-PIR is proposed in this paper. This framework generates additional multiscale time-series vibration signals, which are then utilized by a 1-D CNN for fault pattern recognition. The overall data generation strategy for the fault diagnosis task is depicted in
Figure 1.
The network architecture of HAWAN-PIR comprises two main components: the generator and the discriminator, as depicted in
Figure 1. The generator is structured as a four-layer network, with layer sizes set to 128, 256, 512, and 1024 units, respectively. The initial layer contains 128 units, which represent the combined dimensions of the noise vector and the label vector. In contrast, the discriminator is structured as a two-layer network, with units configured to 1024, 512, and 1 in each layer. The larger initial layer (i.e., 1024 units) of the discriminator captures complex features from the time series data, whereas the subsequent layers reduce to 512 and then 1 unit to enhance its classification ability. These parameters were determined through a series of iterative experiments.
The objective function of HAWAN-PIR is designed to ensure the generation of realistic and physically consistent synthetic fault data. This function can be mathematically expressed as:
where each component of this objective function serves a specific purpose in maintaining the integrity and quality of the generated data.
The multiscale adversarial loss (
) ensures that the generated data are indistinguishable from the real data across different scales. This loss is formulated as:
where
represents different scales,
is the scale-specific discriminator,
is the scale-specific generator,
denotes the real data at scale
, and
is the random noise input at scale
.
The reconstruction loss (
) ensures that the generator can accurately reconstruct input signals, which can be expressed as:
where
functions as an encoder that maps real signals into a latent space, whereas
reconstructs the signal from this latent representation.
The physics-informed regularization term () enforces physical constraints on the generated signals—emphasizing the features that contain the most relevant fault information—and is tailored for each case study.
The hierarchical structure is fundamentally linked to the wavelet transform, as wavelet decomposition captures multi-resolution features from the vibration signals, organizing these features in a way that prioritizes relevant fault characteristics. This hierarchy allows the model to effectively utilize information at different scales, enhancing diagnostic performance. By structuring the extracted features hierarchically, the model can leverage both general and specific fault-related information, leading to more accurate predictions.
In the case of rolling bearings, the physics-informed regularization can be expressed as:
where
represents the essential features that characterize the fault conditions in rolling bearings. These features are derived from the physical characteristics of the machinery and include parameters such as fault characteristic frequencies. In this work, we consider three types of bearing faults: inner race faults, outer race faults, and roller or ball faults. The fault characteristic frequency formulas for these types of bearing faults are as follows [
30]:
where
is the number of rolling elements,
is the diameter of the rolling element,
is the pitch diameter,
,
, and
are the fault characteristic frequencies of the inner race, outer race, and rolling element, respectively,
is the rotating frequency of the shaft, and
is the load angle relative to the radial plane.
For the planetary gearbox case, the physics-informed regularization can be expressed as:
where
includes features relevant to the gearbox, such as gear mesh frequencies, which are crucial for identifying faults in the gear system. The gear mesh frequency can be calculated as [
33]:
where
is the number of teeth on the gear,
is the rotational speed of the gear in the RPM, and
is the pitch diameter of the gear.
It is important to clarify that the features and do not imply a direct relationship with the process of obtaining harmonic amplitudes through Fast Fourier Transform (FFT). Instead, and include essential fault-related features that are extracted based on the physical characteristics of the machinery being analyzed. These features represent various aspects of the vibration signals, such as amplitudes at specific fault characteristic frequencies, which are crucial for diagnosing the health of the machinery.
The multiscale coherence loss (
) ensures consistency across different scales of the generated signals, which can be expressed as:
where
represents the wavelet transform applied at scale
. This integration allows for the analysis of signals across multiple scales. The term
denotes the generator output at scale
. This approach enables the effective capture of temporal and frequency characteristics of the data.
It is important to note that this formulation allows for the measurement of differences between the wavelet-transformed generated signals and the real signals at each scale. By enforcing coherence, the generated output aligns more closely with the characteristics of the real signals across different scales.
Finally, the entropy balancing loss (
) maintains the complexity and information content of the generated signals, which can be expressed as:
where
H is the Shannon entropy. This loss function ensures that the generated signals retain a similar level of complexity and information as the real signals, further enhancing the fidelity of the proposed HAWAN-PIR model.
2.2. Hierarchical Wavelet-Based Imbalance Severity Score
To quantify data imbalance across multiple scales and multiclass problems, the hierarchical wavelet-based imbalance severity score (HWISS) is presented. Particularly, for this work, the total number of classes is ten, i.e., one healthy class and nine fault classes. The HWISS is defined as:
where
represents the physics-informed weighting for scale
of class
.
The fault-to-normal sample ratio at scale
for class
can be expressed as:
Each sample undergoing the wavelet transform generates signals at different scales. The dependence of on arises because each scale captures different levels of detail in the vibration signals, leading to variations in the number of fault samples captured at each scale. This reflects the hierarchical nature of the vibration signals being analyzed.
The weighting is critical as it emphasizes the importance of features extracted at each scale for fault diagnosis. These weights are determined based on the relevance of the physical features, such as fault characteristic frequencies, to the specific fault conditions being analyzed. By incorporating these physics-informed weights, the HWISS provides a comprehensive measure of imbalance that considers both the scale-specific ratios and the hierarchical structure of the data. A higher HWISS indicates a more severe imbalance across the scales, which can significantly impact fault diagnosis.
2.3. Comprehensive Multiscale Synthesis Quality Index
The quality of generated data is a critical factor that impacts classification accuracy in the context of imbalanced diagnosis. To evaluate the quality of the generated data, the comprehensive multiscale synthesis quality index (CMSQI) is proposed in this study, which can be expressed as:
This index integrates three main components:
- (1)
The wavelet-based discriminative score (WDS) measures how well the synthetic data align with the real data in the wavelet domain;
- (2)
The physics-informed signal fidelity measure (PISFM) evaluates how well the synthetic data adhere to the known physical principles of rotating machinery;
- (3)
The class balance improvement metric (CBIM) quantifies how much the synthetic data improve the balance between fault and healthy classes.
The weights , and indicate the relative importance of each component in the overall quality evaluation. A higher CMSQI score signifies better quality of the generated data.
2.4. Scale-Aware Dynamic Mixing Algorithm
The scale-aware dynamic mixing (SADM) algorithm optimizes the integration of synthetic and real data for training 1-D CNN classifiers. The mixing ratio (MR) for each scale
can be calculated as:
where
is the imbalance severity score,
is the synthesis quality index, and
is a measure of the performance of the 1-D CNN on scale
data. If
is high,
is high, and
is low, the function
might return a high
to include more synthetic data. Conversely, if
is low,
is low, and
is high,
might return a low
to rely more on real data.
This adaptive mixing strategy ensures that more synthetic data are utilized where the imbalance is significant, higher-quality synthetic data are prioritized, and the mixing ratio is adjusted based on CNN performance. This creates a feedback loop that optimizes data generation for the specific classification task.
2.5. Training and Fault Classification Procedures
As mentioned earlier, the HAWAN-PIR framework is used to extend the training samples, and these samples, in combination with the real data, are then utilized by a 1-D CNN for fault pattern recognition.
The training process begins with the initialization of both the generator G and the discriminator D networks, which are set with random weights to facilitate effective learning during training iterations. In each iteration, real data and random noise are sampled. The generator uses this noise to create synthetic data G(z). The training involves calculating a total loss , which includes the following components: , , , and . The parameters of the discriminator are updated to minimize , whereas the parameters of the generator are adjusted to minimize . Thus, the fault data are generated.
Once the synthetic samples are generated, periodic assessments using the CMSQI metrics are performed to evaluate the quality of the synthetic data. After these evaluations, the SADM algorithm is applied to create an optimally mixed dataset of real and synthetic data for each scale.
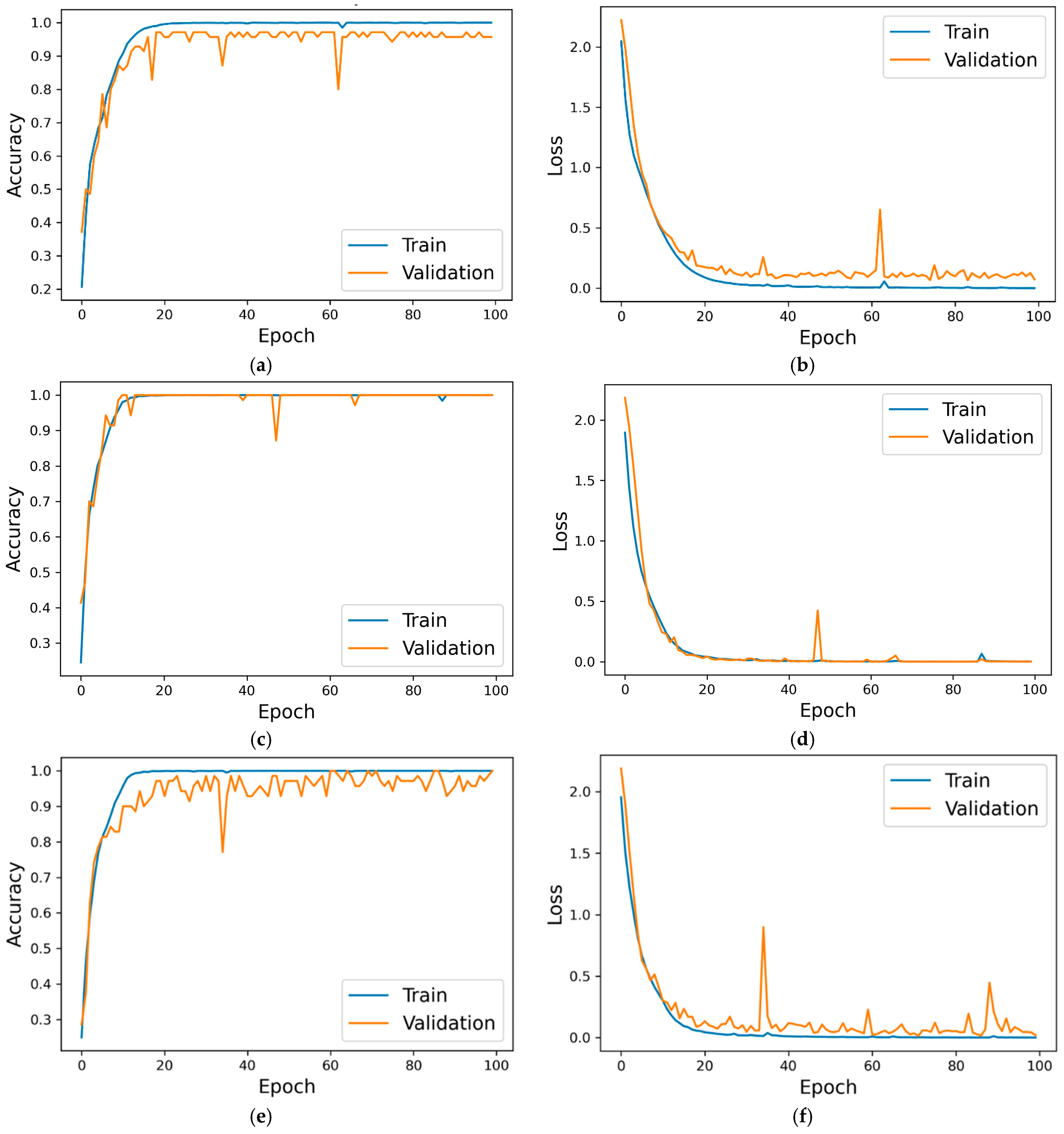
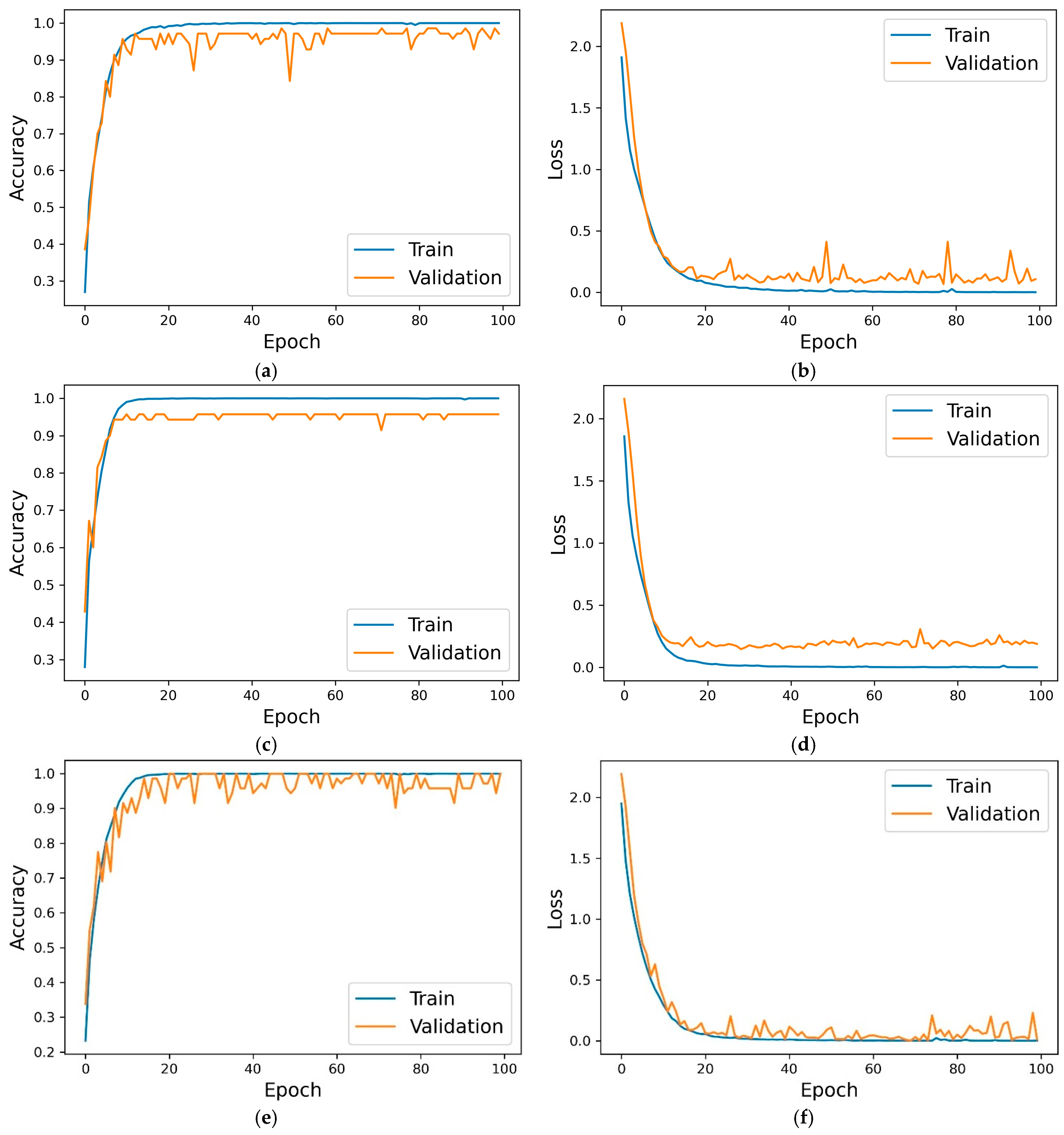
The mixed data are then split into three sets: training, validation, and testing. The 1-D CNN is trained on the training set, and a separate validation set is used to determine if overfitting occurs. The network architecture of the 1-D CNN is shown in
Figure 2. Details regarding each layer type in the architecture can be found in our previously published work [
34], which this study further extends.
The network parameters and training hyperparameters of the 1-D CNN are detailed in
Table 1 and
Table 2, respectively. These parameters and hyperparameters were determined through a series of experiments.
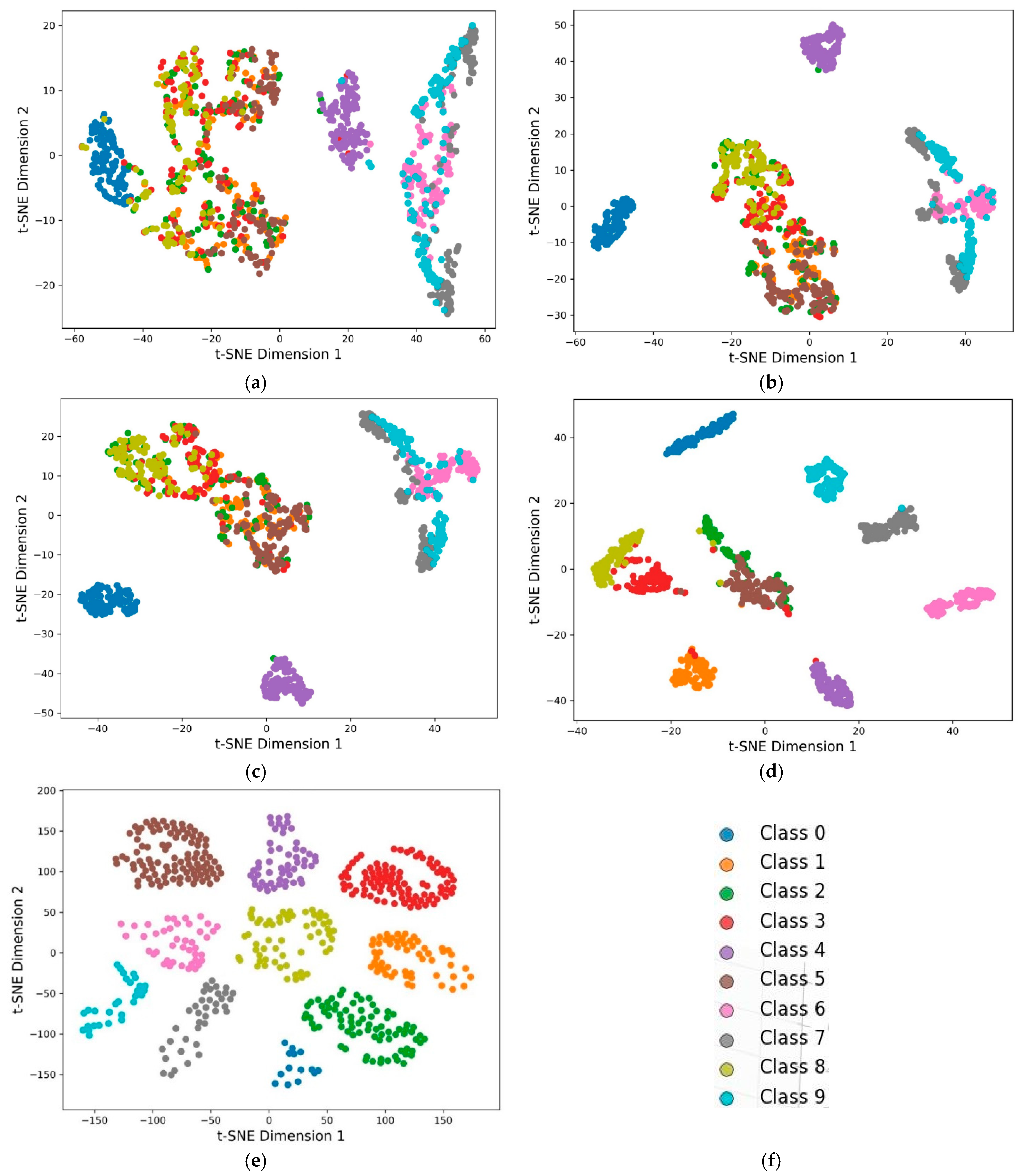
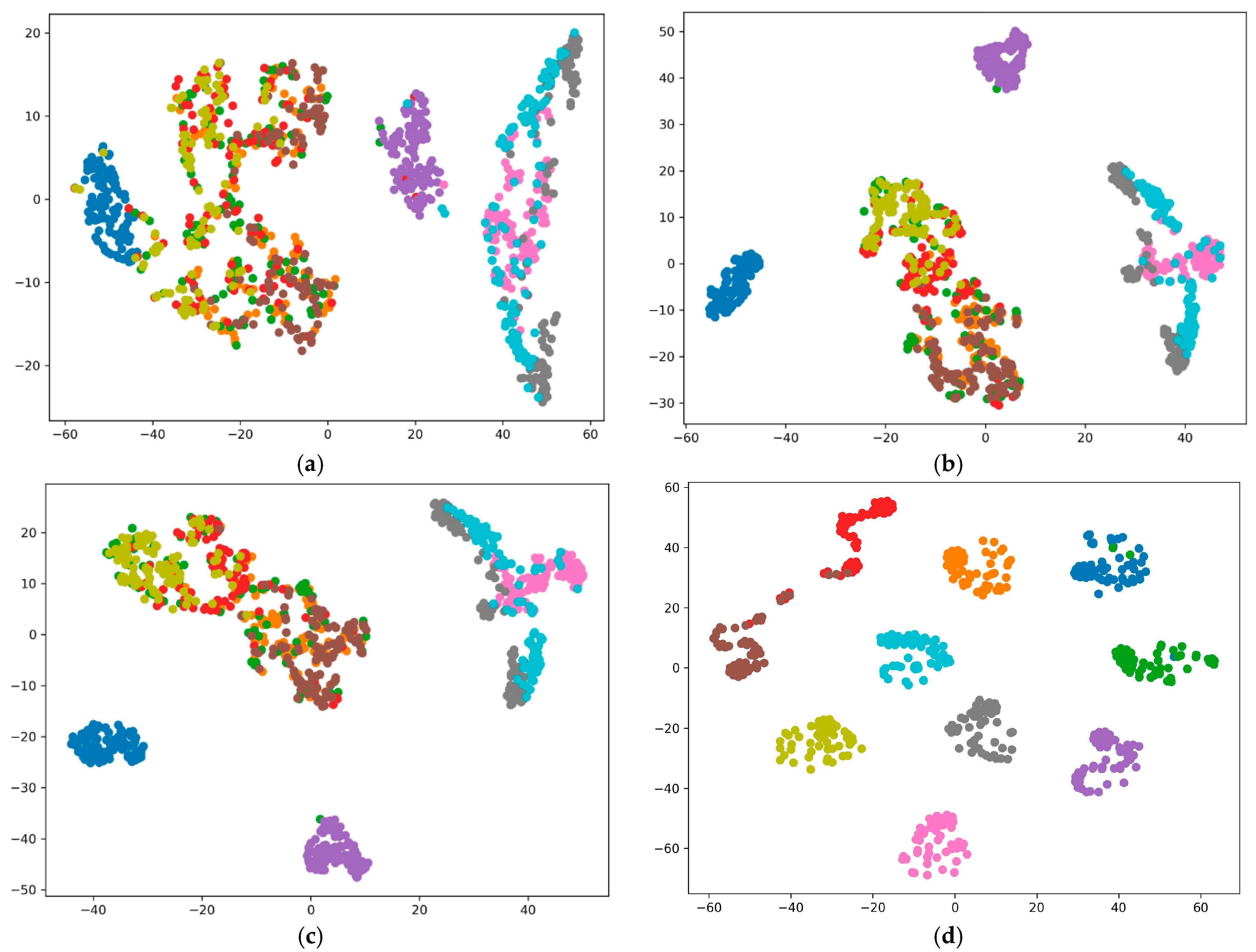
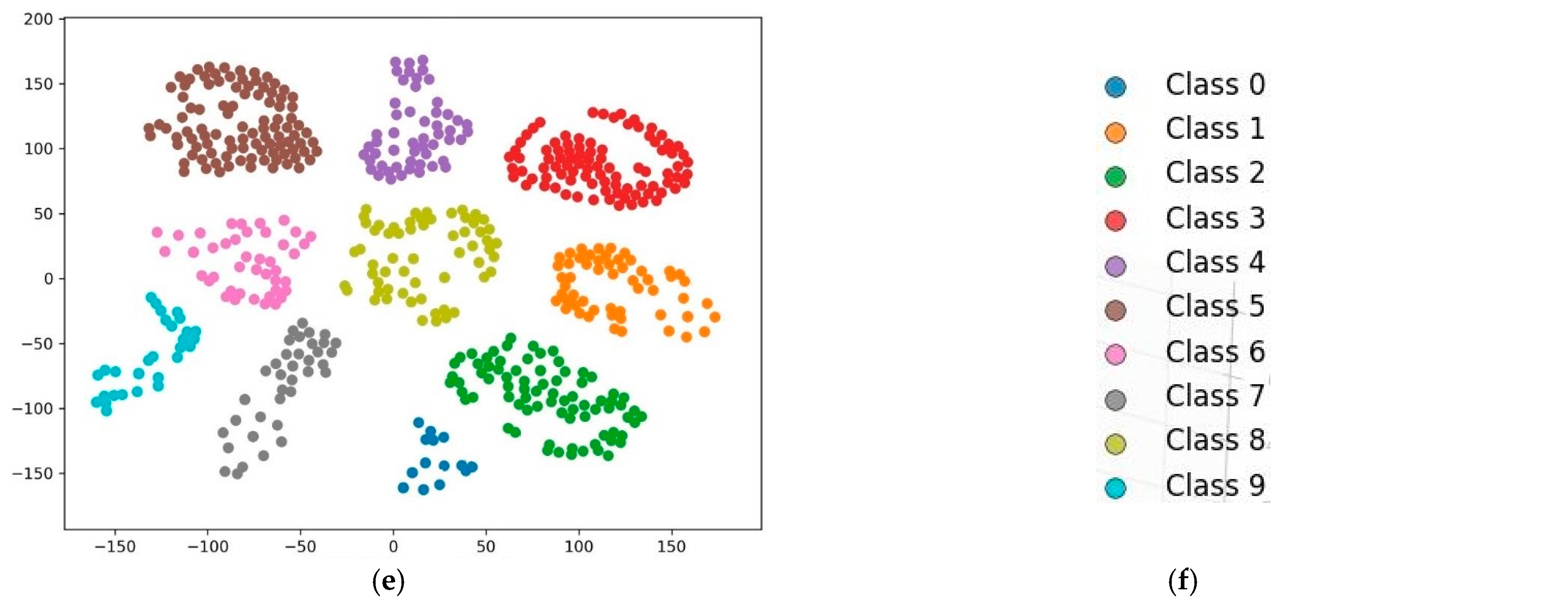
Once the training process is complete, the diagnostic capability of the 1-D CNN is rigorously evaluated via a separate test set. This evaluation is essential for determining the ability of the model to generalize to unseen data.
The overall flowchart in
Figure 3 shows the proposed methodology for data generation and fault diagnosis in the rotating machines used in this study. This flowchart details steps such as data imbalance evaluation, synthetic data generation, synthetic data quality assessment, integration of the synthetic data with the real data, and partitioning of the mixed data for fault diagnosis.
4. Conclusions
In this paper, a new hierarchical adaptive wavelet-guided adversarial network with a physics-informed regularization (HAWAN-PIR) framework is proposed to overcome the issue of imbalanced fault data and enhance the diagnostic accuracy of rotating machines, particularly for components such as bearings and gearboxes. The framework generates high-quality artificial fault data in the time domain through multiscale wavelet decomposition and is the first to incorporate relevant fault knowledge or physical principles.
Initially, the hierarchical wavelet-based imbalance severity score (HWISS) was employed to evaluate the level of data imbalance. Next, the HAWAN-PIR framework was employed to generate high-quality data at different scales, which were then evaluated via a comprehensive multiscale synthesis quality index (CMSQI). Furthermore, a scale-aware dynamic mixing algorithm was introduced to effectively combine synthetic and real data, thereby increasing the training dataset for the 1-D CNN. Finally, two experimental studies—rolling bearings and planetary gearboxes—were conducted to validate the effectiveness of the HAWAN-PIR framework and its fault diagnosis process. From the analysis of these cases, the following conclusions can be drawn:
The HWISS values indicate varying levels of data imbalance, with rolling bearings scoring from 0.68 to 0.82 and planetary gearboxes scoring from 0.68 to 0.75. These results underscore the significant imbalances present and prove the need for a data generation model (i.e., HAWAN-PIR in this case) to improve the diagnostic accuracy of deep learning models.
The CMSQI scores exceeded 0.80 in both case studies. This proves that the data generated by HAWAN-PIR have high fidelity and realism.
The mixing ratios for the bearing datasets range from 0.65 to 0.80, whereas those for the gearbox datasets range from 0.75 to 0.80. These ratios reflect a balance between synthetic and real data.
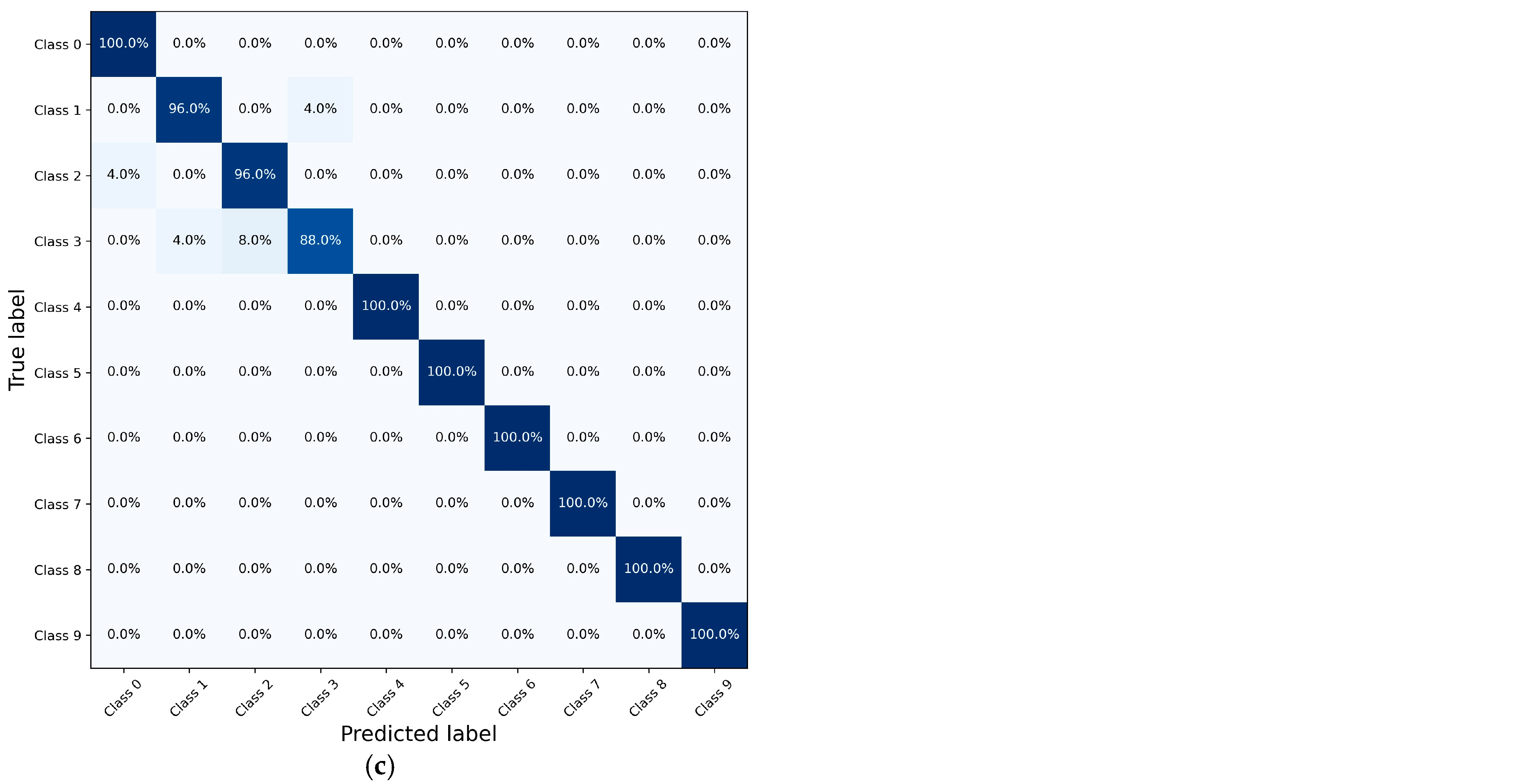
The diagnosis accuracy of the fault diagnosis model based on the 1-D CNN shows significant improvements, with a 17% increase for the bearing datasets and a 15% increase for the gearbox datasets. This advance is attributed to the high quality of the data generated via HAWAN-PIR.
Finally, the ablation study evaluated the contributions of each component of HAWAN-PIR—wavelet decomposition, physics-informed regularization, and hierarchical structure—to the 1-D CNN model. The integration of these components significantly improved the accuracy from 80.94% to 94.85% for the CWRU bearing dataset and from 79.77% to 96.73% for the SEU gearbox dataset, even under varying load conditions.
In the two case studies, the effectiveness of the HAWAN-PIR framework was validated solely through the 1-D CNN. However, other deep learning models remain unexamined. Therefore, for future work, the authors plan to investigate the applicability of the HAWAN-PIR framework to increase the diagnostic accuracy of these other models. Additionally, this study considers limited physics principles for the rolling bearing and gearbox cases, specifically focusing on fault characteristic frequencies for the rolling bearing case and gear mesh frequencies for the gearbox case. In the future, the authors intend to explore the integration of additional physical principles, such as material properties, thermal effects, and dynamic behavior, to further improve the diagnostic performance of deep learning models in real-world applications.