Optimization of 3D Tolerance Design Based on Cost–Quality–Sensitivity Analysis to the Deviation Domain
Abstract
1. Introduction
2. Parametric Modeling and Representation of 3D Tolerance Zone Based on New GPS
2.1. Small Displacement Torsor Theory and Homogeneous Transformation Matrix (HTM) Principle
2.2. 3D Tolerance Modeling
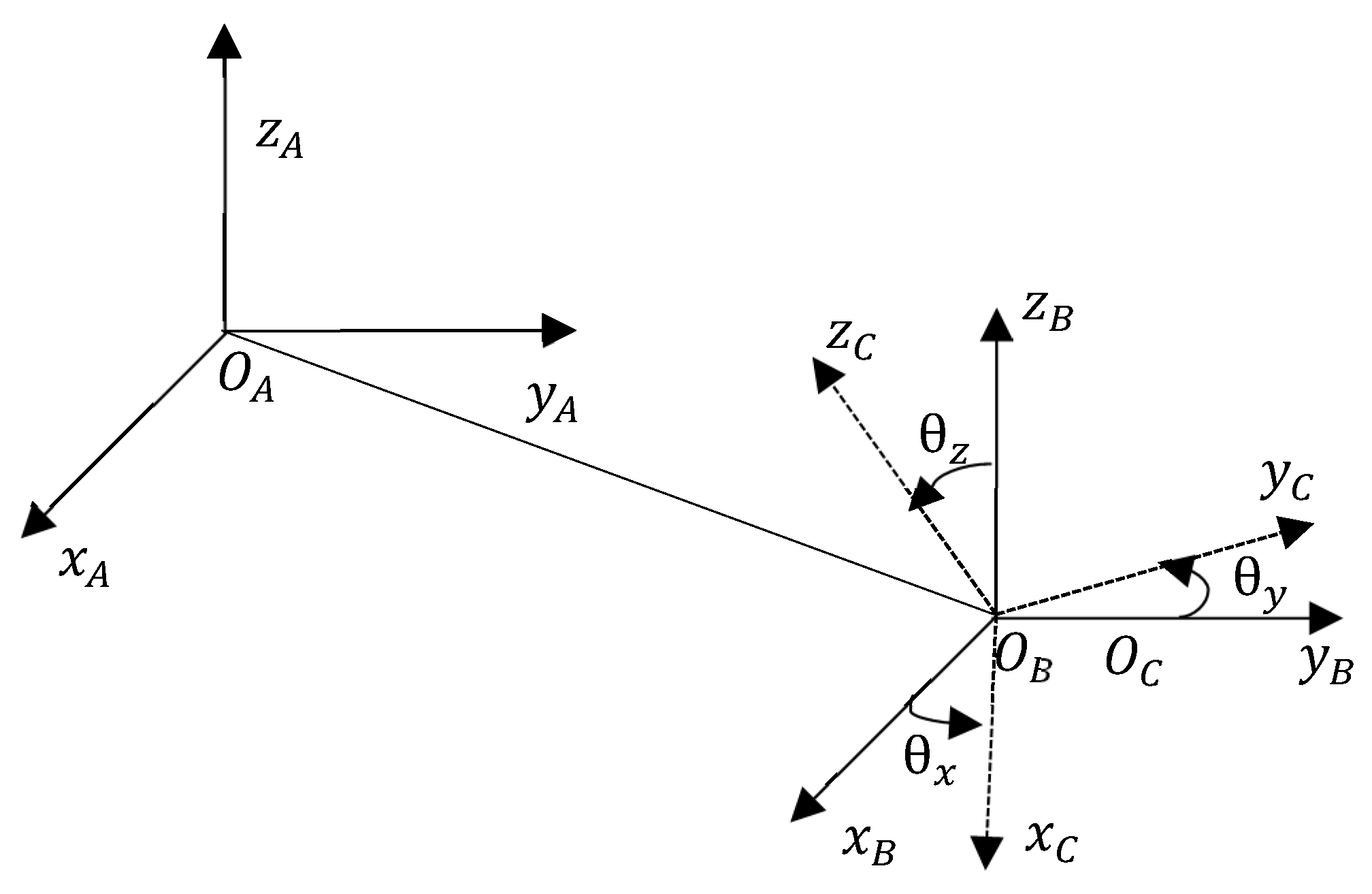
2.2.1. Create a Coordinate System
2.2.2. Kinematic Model of Three-Dimensional Tolerance Accumulation Based on HTM
2.2.3. The Basic Properties of the Tolerance Zone and Its Torsor Interval Description
3. Mathematical Modeling of 3D Tolerance Allocation
3.1. Establishment of 3D Tolerance Mathematical Model
- By studying the SDT torsor constraint relationship of different functional feature surfaces, the tolerance zone and clearance domain between parts are mapped to the deviation domain, and the geometric variation is represented in six directions.
- Based on the mathematical model of cost-tolerance in the classic two-dimensional dimensional chain, the single independent variable is replaced with six deviation components through torsor parameters of the deviation domain. Because the deviations in the six directions are orthogonal and linearly independent, the deviation cost can be represented by the product of each direction.
- Next, we establish the relationship between the deviation domain and the cost function. According to Table 1, it can be found that each torsor has a constraint boundary. After combining the objective function and constraint conditions, a three-dimensional tolerance mathematical model is established.
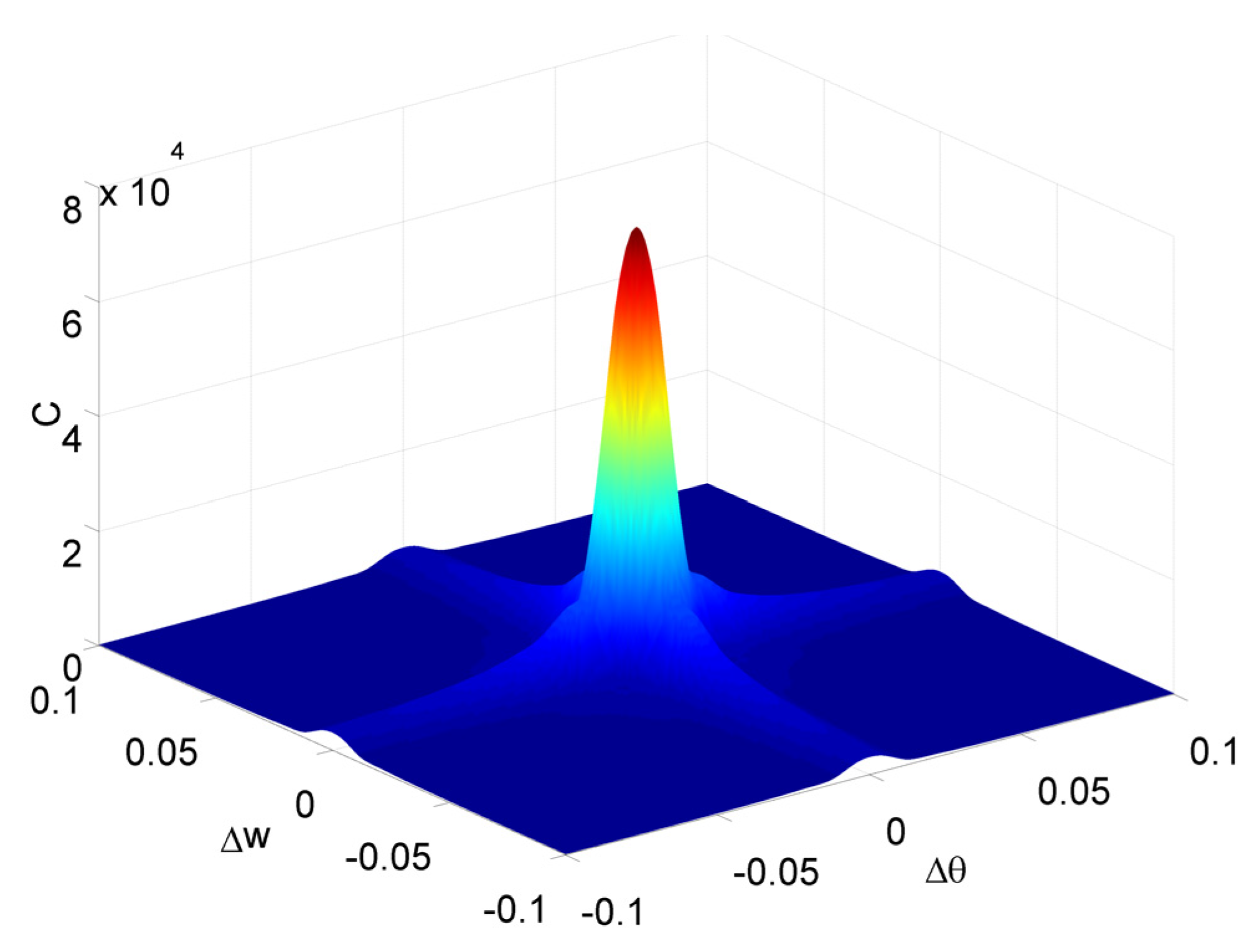
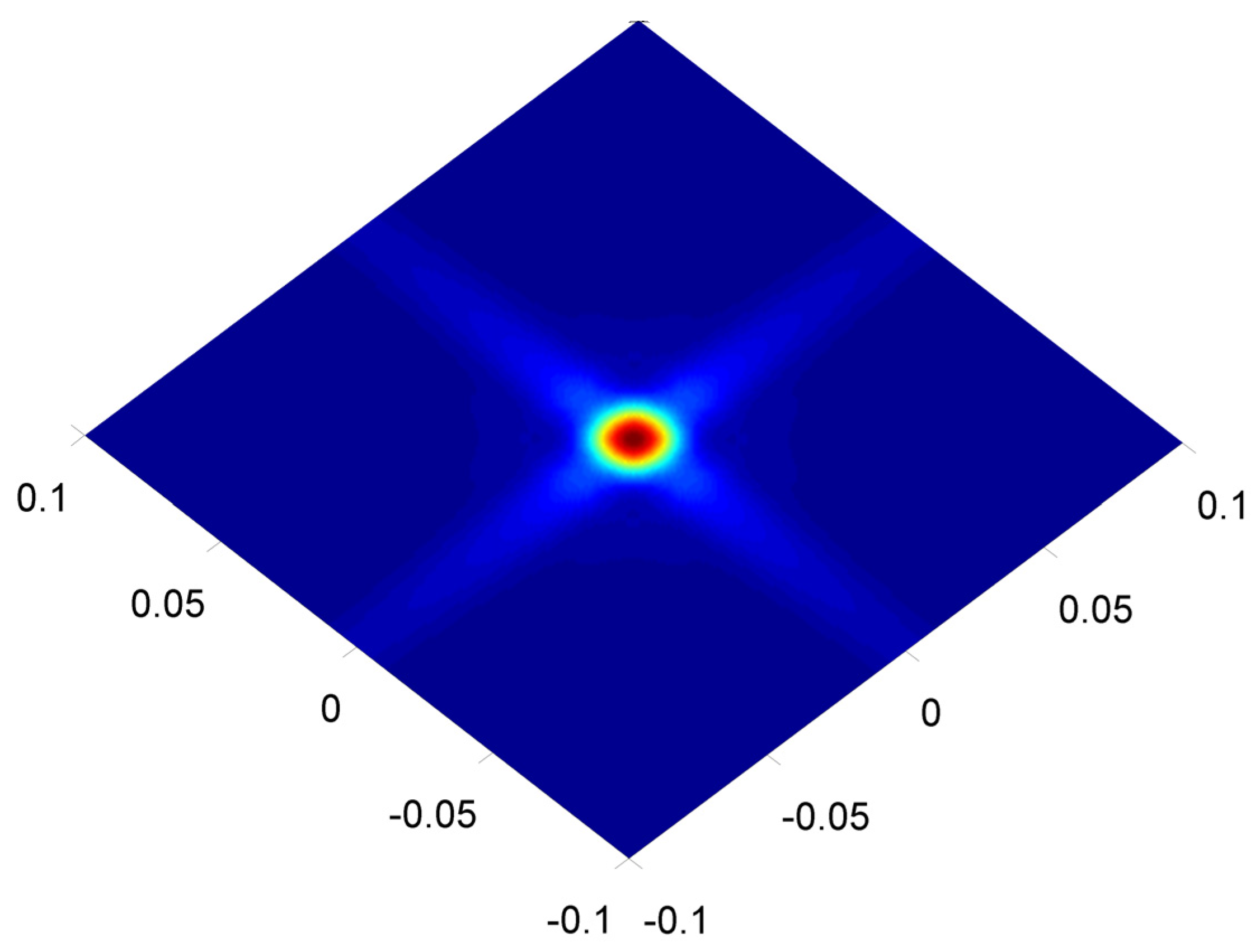
- In order to verify the validity and correctness of the mathematical model, a three-dimensional function graph is made under the given correlation coefficient to judge whether the model is in line with actual production and use.
- In addition to the geometric variation constraints of the SDT torsor, it is also necessary to consider the functional requirements constraints and assembly tolerance constraints, and they should be expressed in the deviation domain.
- Combining the objective function and constraint conditions based on the deviation domain, the three-dimensional tolerance mathematical model is built.
3.2. Processing Cost–Tolerance Model Based on HTM-SDT
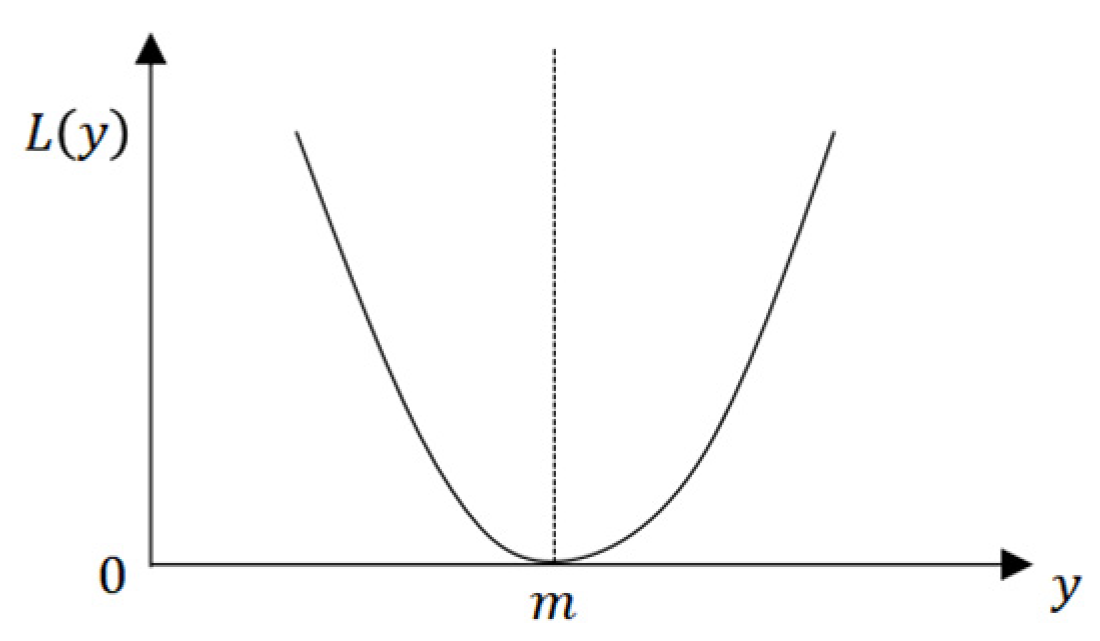
3.3. Quality Loss–Tolerance Model Based on HTM-SDT
3.4. Sensitivity–Tolerance Model Based on HTM-SDT
3.5. Constraints
3.5.1. Constraints of Machining Capacity and Geometric Function
3.5.2. Constraints of Assembly Tolerance
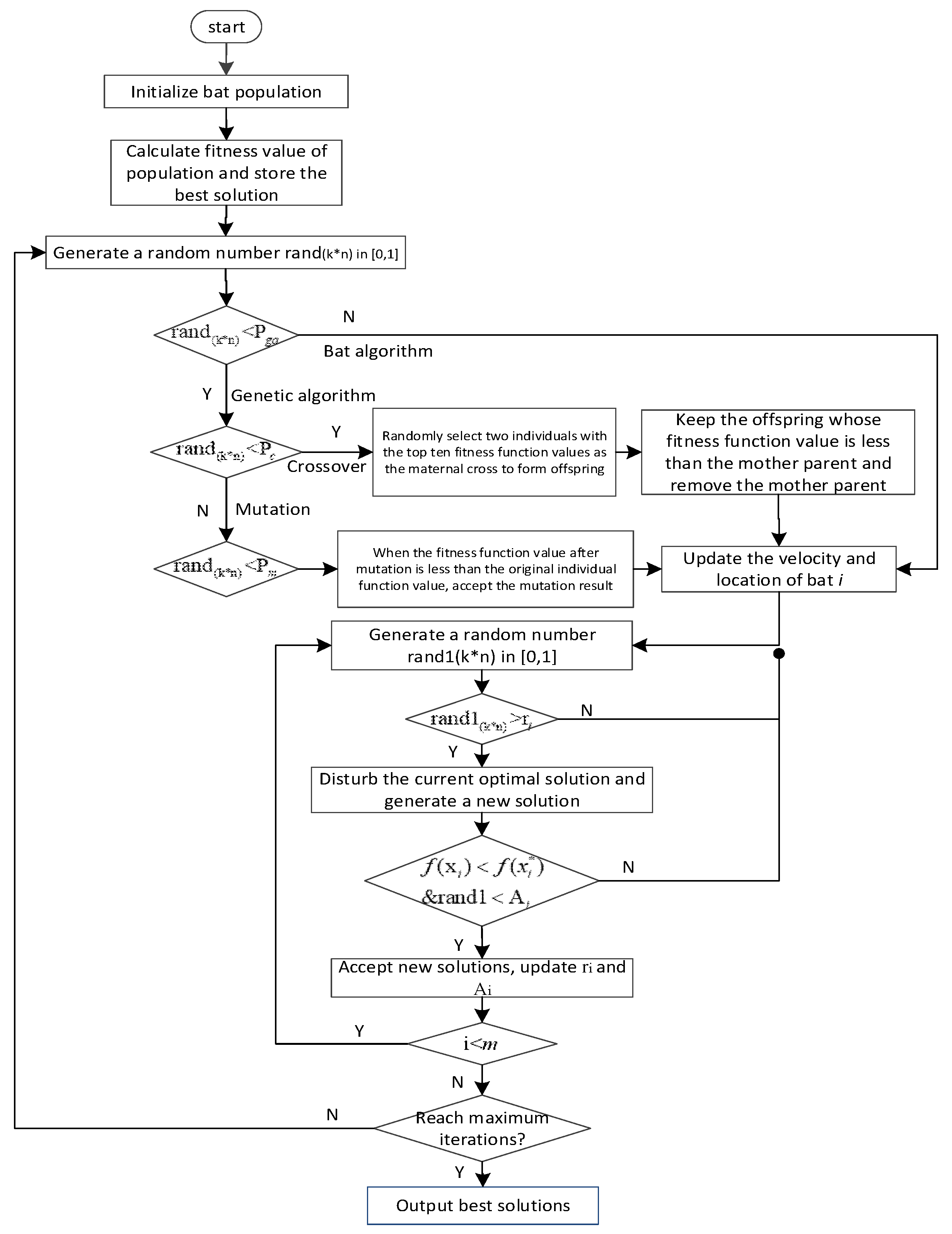
4. Steps of Optimal Allocation for 3D Tolerance Based on Modified Bat Algorithm
4.1. Basic Concepts of Functional Structural Tolerance
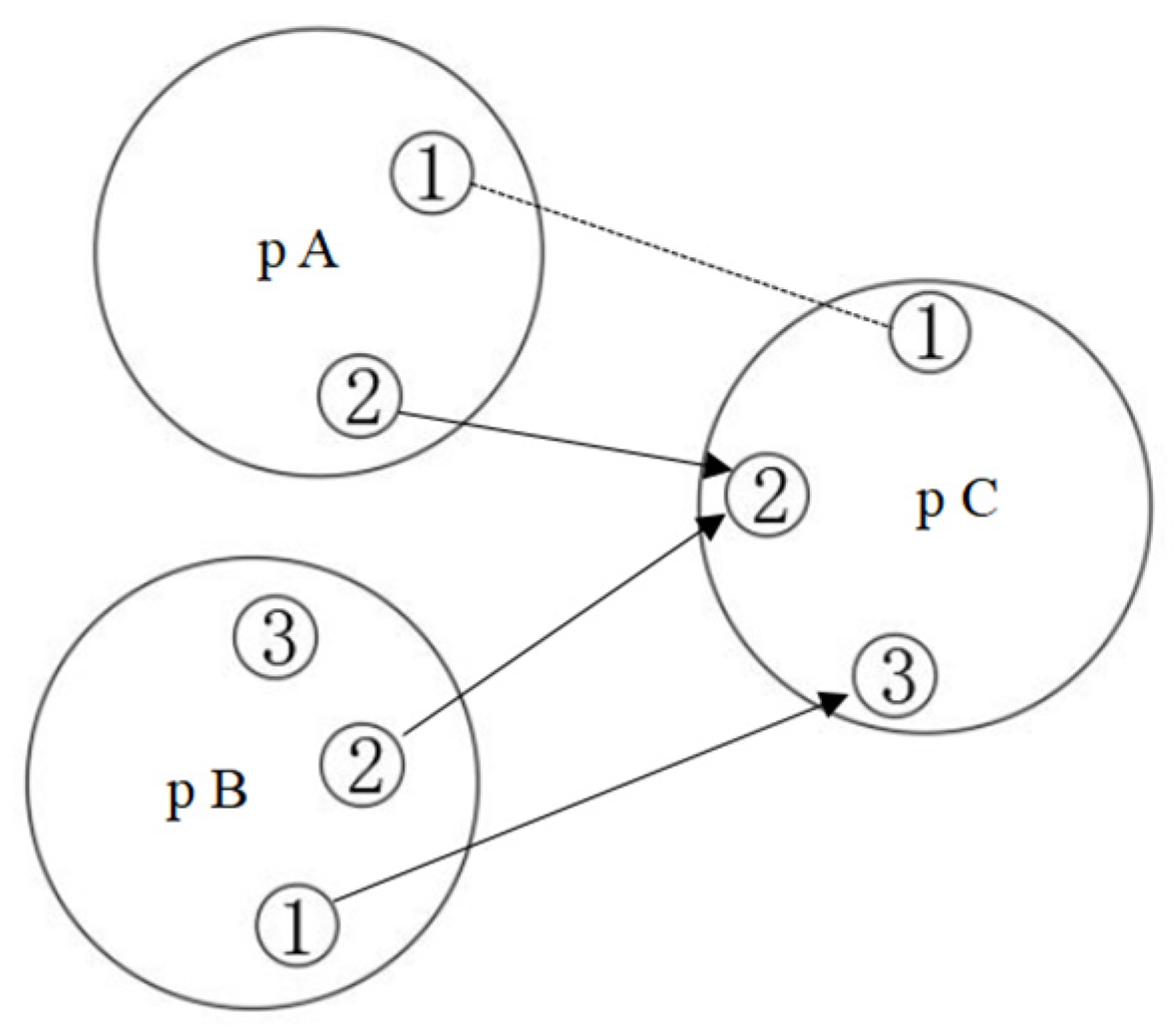
4.2. Construction of Assembly Tolerance Loop Based on Functional Surface
- Determine the geometric constraints and degrees of freedom of the two functional surfaces for functional requirements.
- Select the part where one of the functional surfaces is located, and filter out the surface of the part that participates in the constraint degree of freedom.
- Remove irrelevant part feature surfaces.
- Continue the above steps to find the next part and its surface that has geometric constraints with the functional surface of the part until it returns to the original functional surface.
4.3. Optimal Allocation for 3D Tolerance Based on Modified Bat Algorithm
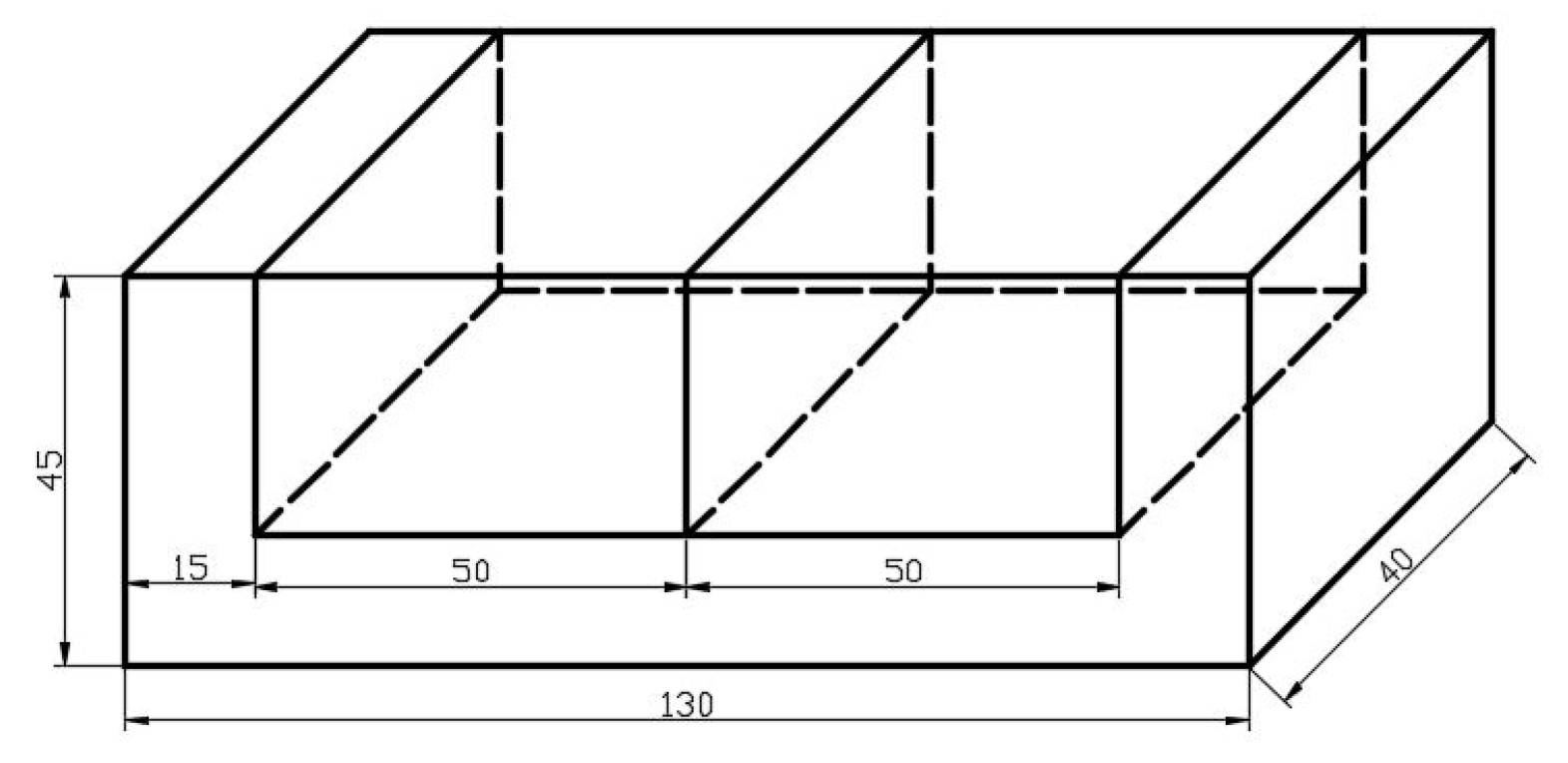
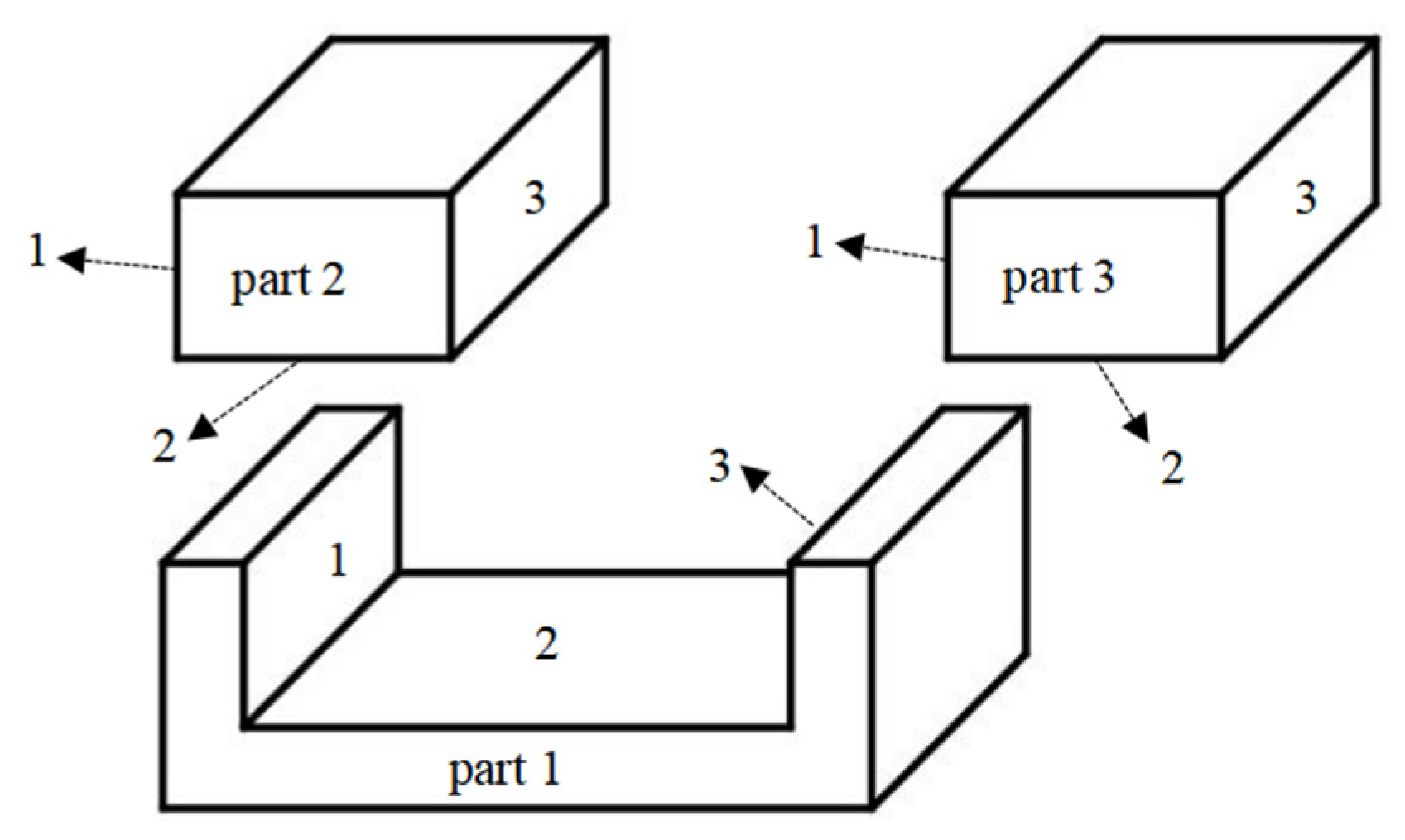
5. Case Study
5.1. Set up a Coordinate System
5.2. Generation of Assembly Tolerance Loop
5.3. Establish a Mathematical Model of Deviation Optimization
5.3.1. Objective Function
5.3.2. Constraints
5.3.3. Mathematical Model of Optimal Deviation Allocation
5.4. Solve the Model with Genetic Bat Algorithm
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hongfang, F.; Zhaotong, W. A Research of Concurrent Design in Computer-Aided Design Tolerance and Process Tolerance. China Mech. Eng. 1995, 6, 25–27. [Google Scholar]
- Cao, Y.L.; Mathieu, L.; Jiang, J. Key research on computer aided tolerancing. J. Zhejiang Univ. Sci. 2015, 16, 335–340. [Google Scholar] [CrossRef]
- Narahari, Y.; Sudarsan, R.; Lyons, K.; Duffey, M.; Sriram, R. Design for tolerance of electro-mechanical assemblies: An integrated approach. Robot. Autom. IEEE Trans. 1999, 15, 1062–1079. [Google Scholar] [CrossRef]
- Dantan, J.Y.; Anwer, N.; Mathieu, L. Integrated toleranclng process forconceptual deslgn. CIRP Ann. Manuf. Technol. 2003, 52, 135–138. [Google Scholar] [CrossRef]
- Yifei, H.E.; Davidson, J.K.; Jami, J. Tolerance-Maps for line-profiles constructed from Boolean intersection of T-Map primitives for arc-segments. J. Zhejiang Univ. Sci. 2015, 5, 341–352. [Google Scholar]
- Mantripragada, R.; Whitney, D.D.E. The datum flow chain: A systematic approach to assembly design and modeling. Res. Eng. Des. 1998, 10, 150–165. [Google Scholar] [CrossRef]
- Huang, W.; Lin, J.; Bezdecny, M.; Kong, Z.; Ceglarek, D. Stream-of-variation modeling—Part I: A generic three-dimensional variation model for rigid-body assembly in single station assembly processes. J. Manuf. Sci. Eng. 2007, 129, 821–831. [Google Scholar] [CrossRef]
- Zhao, C.; Lv, J.; Du, S. Geometrical deviation modeling and monitoring of 3D surface based on multi-output Gaussian process. Measurement 2022, 199, 111569. [Google Scholar] [CrossRef]
- Ghaderi, A.; Hassani, H.; Khodaygan, S. A Bayesian-reliability based multi-objective optimization for tolerance design of mechanical assemblies. Reliab. Eng. Syst. Saf. 2021, 213, 107748. [Google Scholar] [CrossRef]
- Balamurugan, C.; Saravanan, A.; Dinesh Babu, P.; Jagan, S.; Ranga Narasimman, S. Concurrent optimal allocation of geometric and process tolerances based on the present worth of quality loss using evolutionary optimisation techniques. Res. Eng. Des. 2017, 28, 185–202. [Google Scholar] [CrossRef]
- Feng, Z.; Wang, J.; Ma, Y.; Ma, Y. Integrated parameter and tolerance design based on a multivariate Gaussian process model. Eng. Optim. 2021, 53, 1349–1368. [Google Scholar] [CrossRef]
- Goetz, S.; Schleich, B.; Wartzack, S. Integration of robust and tolerance design in early stages of the product development process. Res. Eng. Des. 2020, 31, 157–173. [Google Scholar] [CrossRef]
- Ahmad, M.T.; Firouz, M.; Mondal, S. Robust supplier-selection and order-allocation in two-echelon supply networks: A parametric tolerance design approach. Comput. Ind. Eng. 2022, 171, 108394. [Google Scholar] [CrossRef]
- ISO/TC213. ISO 17450-2:2012; Geometrical Product Specifications (GPS)—General Concepts—Part 2: Basic Tenets, Specifications, Operators, Uncertainties and Ambiguities. International Organization for Standardization: Geneva, Switzerland, 2012.
- Bourdet, P.; Clement, A. A study of optimal-criteria identification based on the small-displacement screw model. CIRP Ann. 1988, 37, 503–506. [Google Scholar] [CrossRef]
- Bourdet, P. The concept of small displacement torsor in metrology. Ser. Adv. Math. Appl. Sci. 1996, 40, 110–122. [Google Scholar]
- Tang, X.; Davies, B.J. Computer aided dimensional planning. Int. J. Prod. Res. 1998, 26, 283–297. [Google Scholar]
- Fainguelernt, D.; Weill, R.; Bourdet, P. Computer Aided Tolerancing and Dimensioning in Process Planning. CIRP Ann. 1986, 35, 381–386. [Google Scholar] [CrossRef]
- Speckhart, F.H. Calculation of Tolerance Based on a Minimum Cost Approach. ASME J. Eng. Ind. 1972, 94, 447–453. [Google Scholar] [CrossRef]
- Hofmann, R.; Gröger, S. Closed loop geometrical tolerance engineering with measuring data for reverse information processing. Procedia CIRP 2019, 84, 311–315. [Google Scholar] [CrossRef]
- Michael, W.; Siddall, J.N. The optimization problem with optimal tolerance assignment and full acceptance. ASME. J. Mech. Des. 1981, 103, 842–848. [Google Scholar] [CrossRef]
- Taguchi, G. Introduction to Off-Line Quality Control; Central Japan Quality Control Assoc: Tokyo, Japan, 1985. [Google Scholar]
- Sun, L.; Liu, F.; Dance, B. Research on extended quality loss function model. Chin. J. Mech. Eng. 1998, 34, 26–32. [Google Scholar]
- Clement, A.; Riviere, A. Tolerancing versus nominal modeling in next generation CAD/CAM system. In Proceedings of the 3rd CIRP Seminar on Computer Aided Tolerancing, Cachan, France, 27 April 1993; pp. 98–113. [Google Scholar]
- Salomons, O.W.; Poerink, H.J.; Van Slooten, F.; Van Houten, F.J.; Kals, H.J. A tolerancing tool based on kinematic analogies. In Computer-Aided Tolerancing; Springer: Dordrecht, The Netherlands, 1996; pp. 47–70. [Google Scholar]
- Hu, J.; Wu, Z. Automatic generation of function-oriented geometric tolerance. China Mech. Eng. 2002, 13, 204–207. [Google Scholar]
- Wu, Z.; Liu, T.; Gao, Z.; Cao, Y.; Yang, J. Tolerance design with multiple resource suppliers on cloud-manufacturing platform. Int. J. Adv. Manuf. Technol. 2016, 84, 335–346. [Google Scholar] [CrossRef]
- Zhu, Z. Research on Product Disassembly Sequence Planing Based on Genetic Bat Algorithm; Shandong University: Jinan, China, 2018. [Google Scholar]
- Xu, X. Study on the Theories and Method of Functional Tolerancing Based on New GPS; Zhejiang University: Hangzhou, China, 2008. [Google Scholar]













| Tolerance Zone | Describe the Area | Homogeneous Transformation Matrix | Constraint Inequality |
|---|---|---|---|
| Between two parallel lines |  | ||
| Between two parallel curves |  | ||
| Between two parallel planes |  | ||
| Between two parallel surfaces | 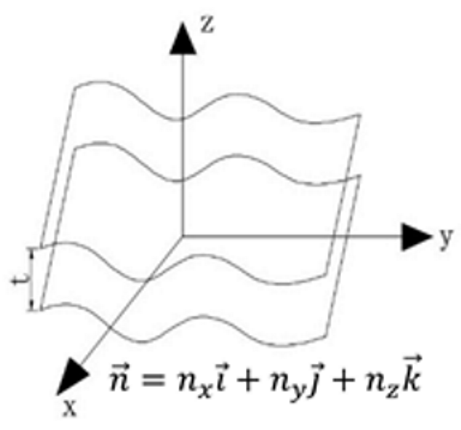 | ||
| Ring | 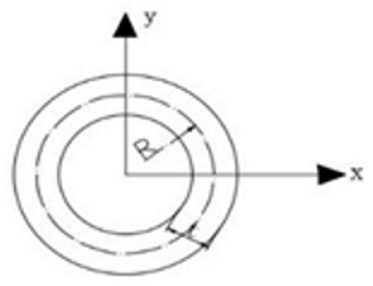 | ||
| Circle |  | ||
| Sphere | 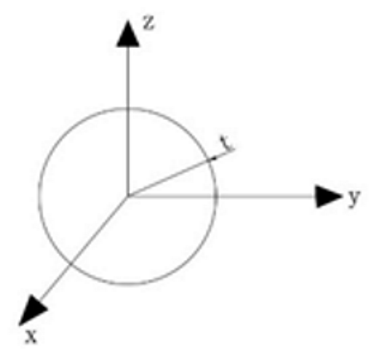 | ||
| Cylinder | 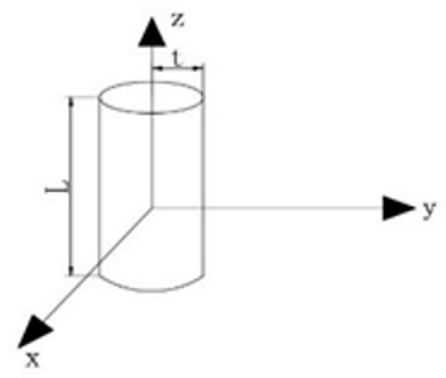 | ||
| Between two concentric cylindrical surfaces | 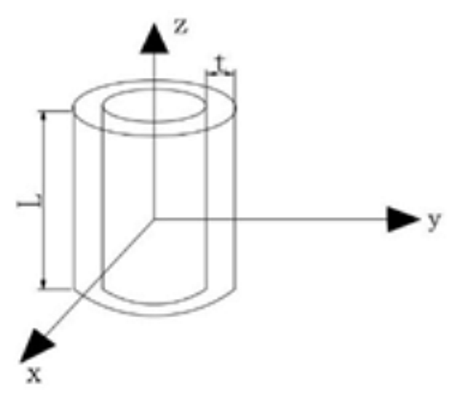 |
| Tolerance Types | Function Expression |
|---|---|
| Reciprocal model | |
| Exponential model | |
| Power-exponential model | |
| Negative square model | |
| Composite power-exponential and exponential model | |
| Composite linear and exponential model | |
| Cubic model | |
| Polynomial model |
| Functional Surfaces | Sphere | Plane | Cylinder | Helical | Rotational | Prismatic | General |
|---|---|---|---|---|---|---|---|
| MGDE | point | plane | line | Point and line | Point and line | Line and plane | Point and line and plane |
| Degrees of invariances | 3 rotations | 1 rotation 2 translation | 1 rotation 1 translation | 1 helical displacement | 1 rotation | 1 translation | None |
| Reference element | sphere center | plane | cylinder axis | Rotation axis and points on the surface | Rotation axis and points on the surface | Straight line in translation direction and plane in determined direction | Any combinations of surface elements |
| Type | p1,1 | p1,1/2,1 | p2,1 | p2,3 | p2,3/3,1 | p3,1 | p3,3 | p3,3/1,3 | p1,3 |
|---|---|---|---|---|---|---|---|---|---|
| ∆α1 | −0.0626 | 0.0686 | 0.1339 | 0.0666 | 0.0750 | −0.0711 | 0.2132 | −0.2062 | 0.3365 |
| ∆α2 | −0.1070 | −0.1661 | 0.0687 | 0.0328 | 0.0769 | 0.3695 | 0.0554 | −0.0226 | 0.0033 |
| ∆α3 | −0.0083 | 0.0885 | −0.0164 | 0.1955 | −0.0300 | 0.2892 | −0.2052 | −0.2146 | 0.0073 |
| ∆α4 | −0.0598 | −0.0036 | 0.2237 | 0.1418 | 0.3842 | 0.0350 | 0.2310 | −0.1199 | 0.3371 |
| ∆β1 | 0.2322 | −0.0184 | 0.2598 | −0.2113 | 0.3229 | −0.0298 | −0.0993 | −0.0328 | −0.0641 |
| ∆β2 | −0.1472 | 0.3395 | −0.1493 | −0.1989 | 0.2057 | −0.1731 | −0.0340 | −0.1542 | 0.1300 |
| ∆β3 | −0.1926 | 0.0816 | 0.1306 | 0.2561 | −0.0248 | 0.1936 | 0.3226 | −0.0024 | 0.3058 |
| ∆β4 | −0.0019 | 0.3776 | −0.1030 | 0.1998 | 0.2418 | 0.13816 | 0.1633 | −0.1097 | 0.1772 |
| ∆w1 | 0.0558 | −0.1005 | 0.0327 | 0.1723 | 0.1229 | 0.1767 | −0.1343 | −0.1327 | 0.0079 |
| ∆w2 | 0.3817 | 0.0896 | 0.1699 | −0.1589 | 0.3161 | −0.1238 | −0.1077 | −0.1144 | 0.3893 |
| ∆w3 | 0.0312 | 0.0115 | −0.1237 | 0.1247 | 0.3588 | −0.2559 | 0.1361 | −0.0632 | 0.0810 |
| ∆w4 | −0.0037 | −0.0810 | 0.2691 | 0.3744 | −0.1031 | 0.1071 | −0.0366 | −0.0150 | −0.0700 |
| Functional Surface | Tmin | Tmax |
|---|---|---|
| p1,1 | −0.0037 | 0.3817 |
| p1,1/2,1 | −0.1005 | 0.0896 |
| p2,1 | −0.1237 | 0.2691 |
| p2,3 | −0.1589 | 0.3744 |
| p2,3/3,1 | −0.1031 | 0.3588 |
| p3,1 | −0.2559 | 0.1767 |
| p3,3 | −0.1343 | 0.1361 |
| p3,3/1,3 | −0.1327 | −0.0150 |
| p1,3 | −0.0700 | 0.3893 |
| Functional Surface | Tmin | Tmax |
|---|---|---|
| p1,1 | −0.3724 | 0.3378 |
| p1,1/2,1 | −0.3043 | 0.2805 |
| p2,1 | −0.3889 | 0.2604 |
| p2,3 | −0.2918 | 0.1297 |
| p2,3/3,1 | −0.2882 | 0.2972 |
| p3,1 | −0.2517 | 0.3030 |
| p3,3 | −0.1318 | 0.3349 |
| p3,3/1,3 | −0.3451 | −0.1162 |
| p1,3 | −0.3870 | 0.2681 |
| p1,1 | p1,1/2,1 | C(T) | L(T) | ∆C(T) | Total Cost | |
|---|---|---|---|---|---|---|
| Result of the single objective function | T1,2 | 1.3653 | 1.8829 | 111.8426 | 56.6813 | 493.6342 |
| T2,2 | 1.0708 | 2.6002 | 68.7968 | 92.6071 | ||
| T3,2 | 1.0214 | 2.7176 | 62.5955 | 93.9102 | ||
| Result of the multi objective function | T1,2 | 1.0096 | 2.7503 | 61.1575 | 94.5597 | 477.9916 |
| T2,2 | 1.2587 | 2.0571 | 95.0595 | 58.1012 | ||
| T3,2 | 0.7582 | 3.2887 | 34.4920 | 126.5256 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Gan, Y.; Cao, Y.; Yang, J.; Wu, Z. Optimization of 3D Tolerance Design Based on Cost–Quality–Sensitivity Analysis to the Deviation Domain. Automation 2023, 4, 123-150. https://doi.org/10.3390/automation4020009
Yang K, Gan Y, Cao Y, Yang J, Wu Z. Optimization of 3D Tolerance Design Based on Cost–Quality–Sensitivity Analysis to the Deviation Domain. Automation. 2023; 4(2):123-150. https://doi.org/10.3390/automation4020009
Chicago/Turabian StyleYang, Kaili, Yi Gan, Yanlong Cao, Jiangxin Yang, and Zijian Wu. 2023. "Optimization of 3D Tolerance Design Based on Cost–Quality–Sensitivity Analysis to the Deviation Domain" Automation 4, no. 2: 123-150. https://doi.org/10.3390/automation4020009
APA StyleYang, K., Gan, Y., Cao, Y., Yang, J., & Wu, Z. (2023). Optimization of 3D Tolerance Design Based on Cost–Quality–Sensitivity Analysis to the Deviation Domain. Automation, 4(2), 123-150. https://doi.org/10.3390/automation4020009











