Development and Performance Measurement of an Affordable Unmanned Surface Vehicle (USV)
Abstract
:1. Introduction
2. Equation of Motion of the Proposed USV
2.1. Kinematics of USV
2.2. Dynamics of USV
3. Materials and Design Methods
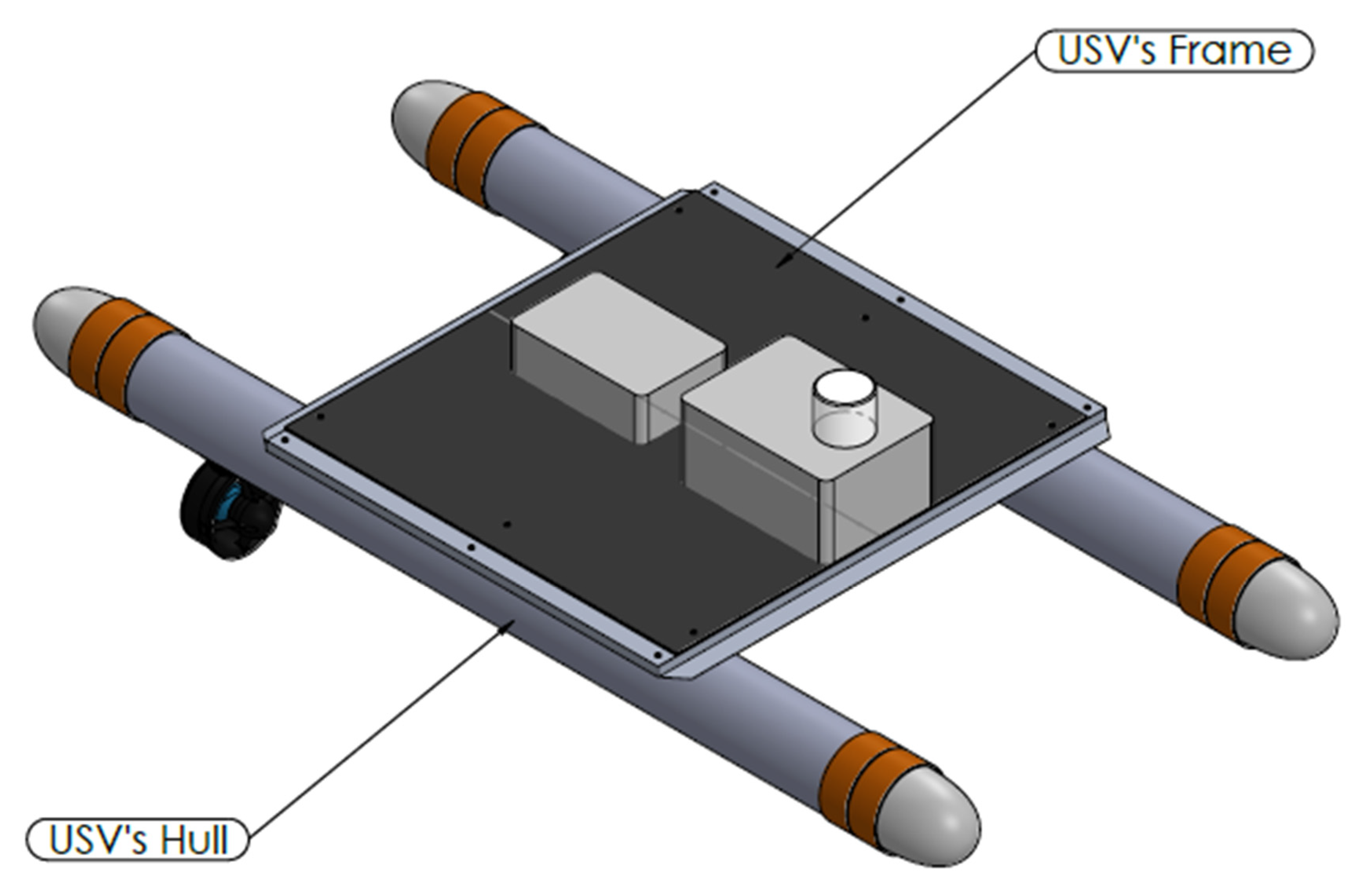
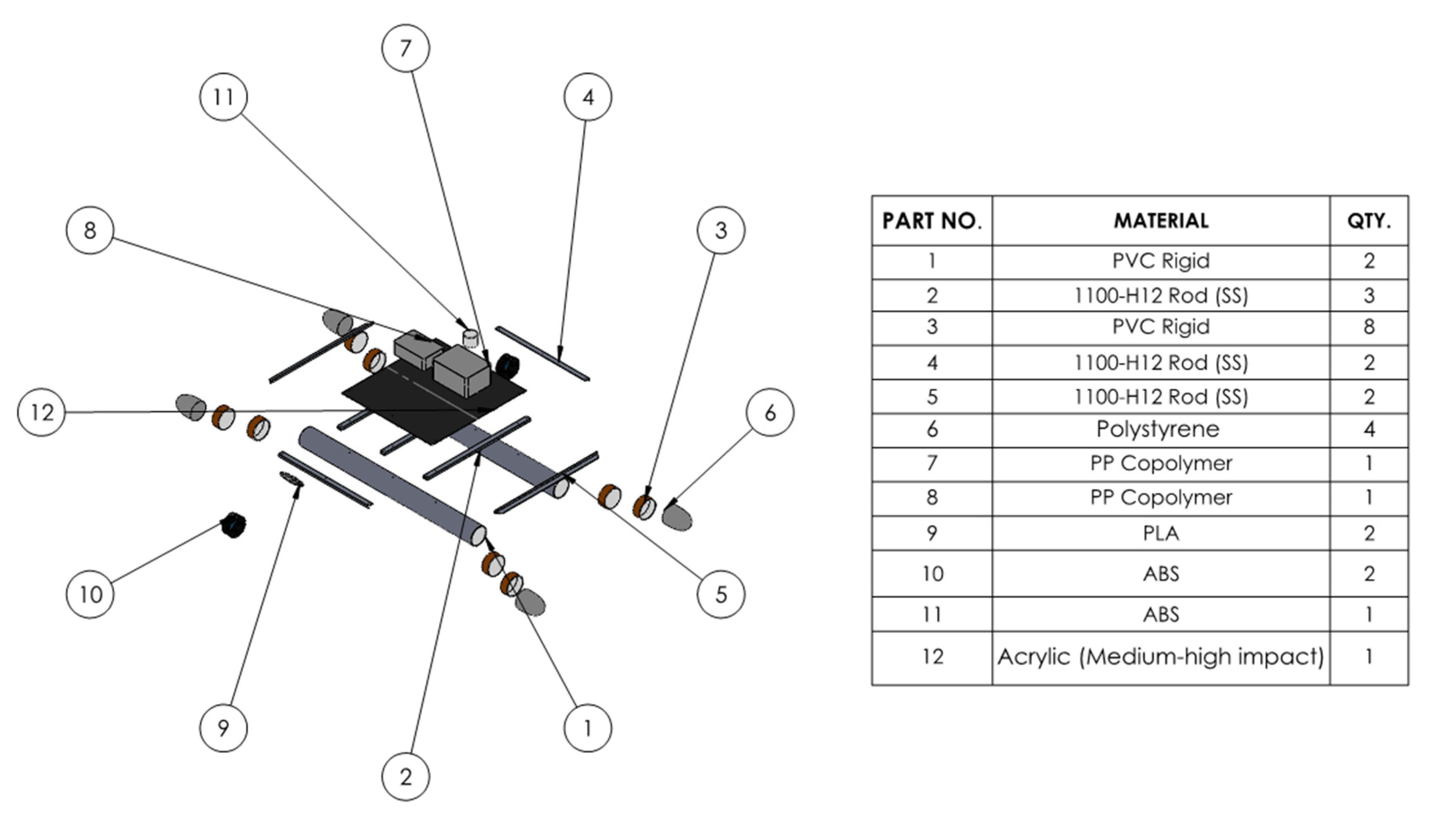
3.1. Mechanical Design
3.2. Electrical Wiring
4. Design Analysis
4.1. Buoyancy
4.2. Required Thruster
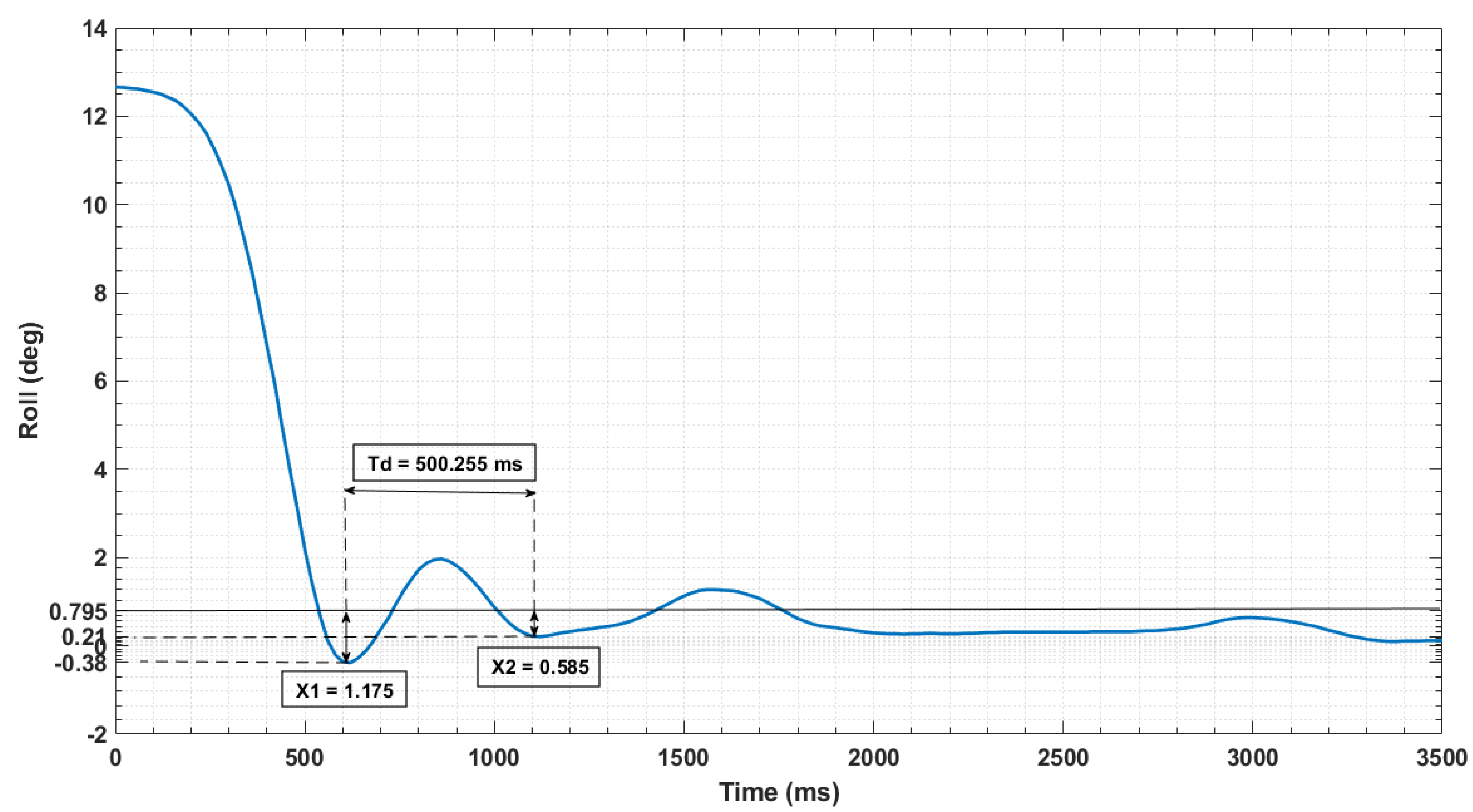
4.3. Stability Analysis
5. Design Implementation
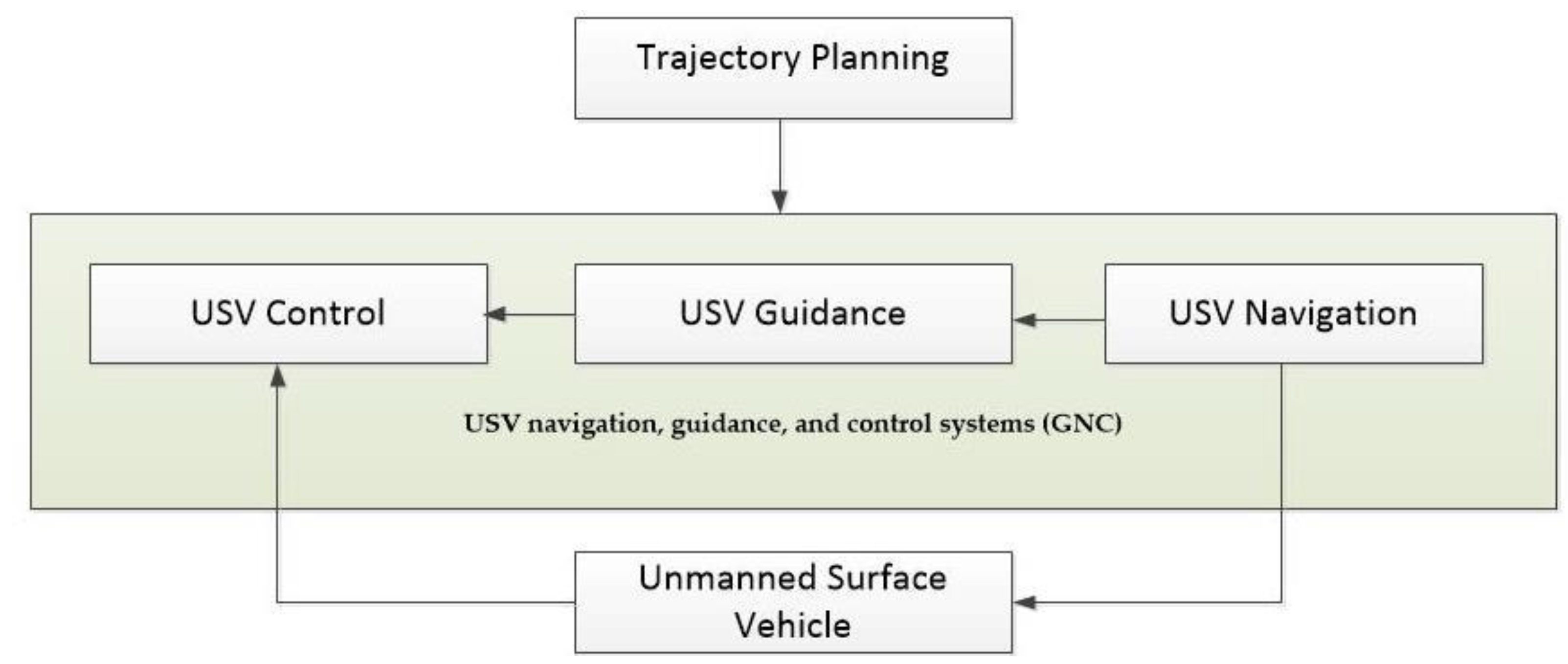
6. Guidance Navigation and Control (GNC)
6.1. Guidance
6.2. Navigation
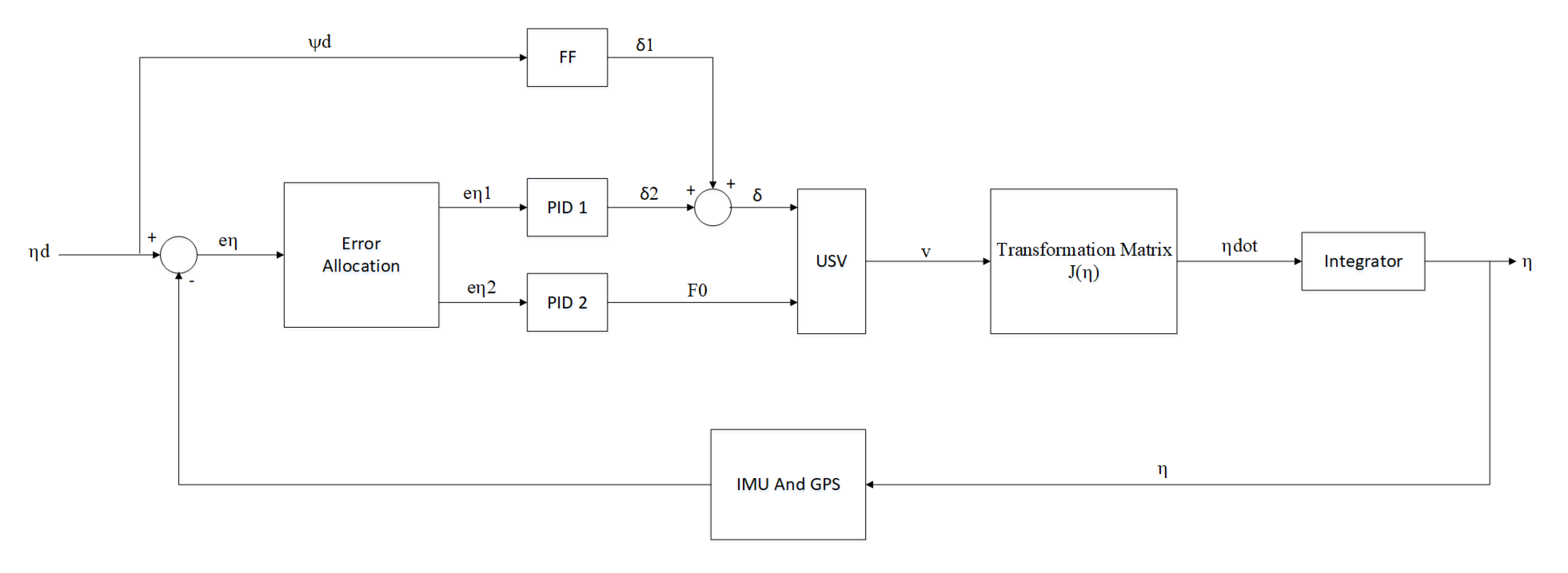
6.3. Control
7. Experimental Results
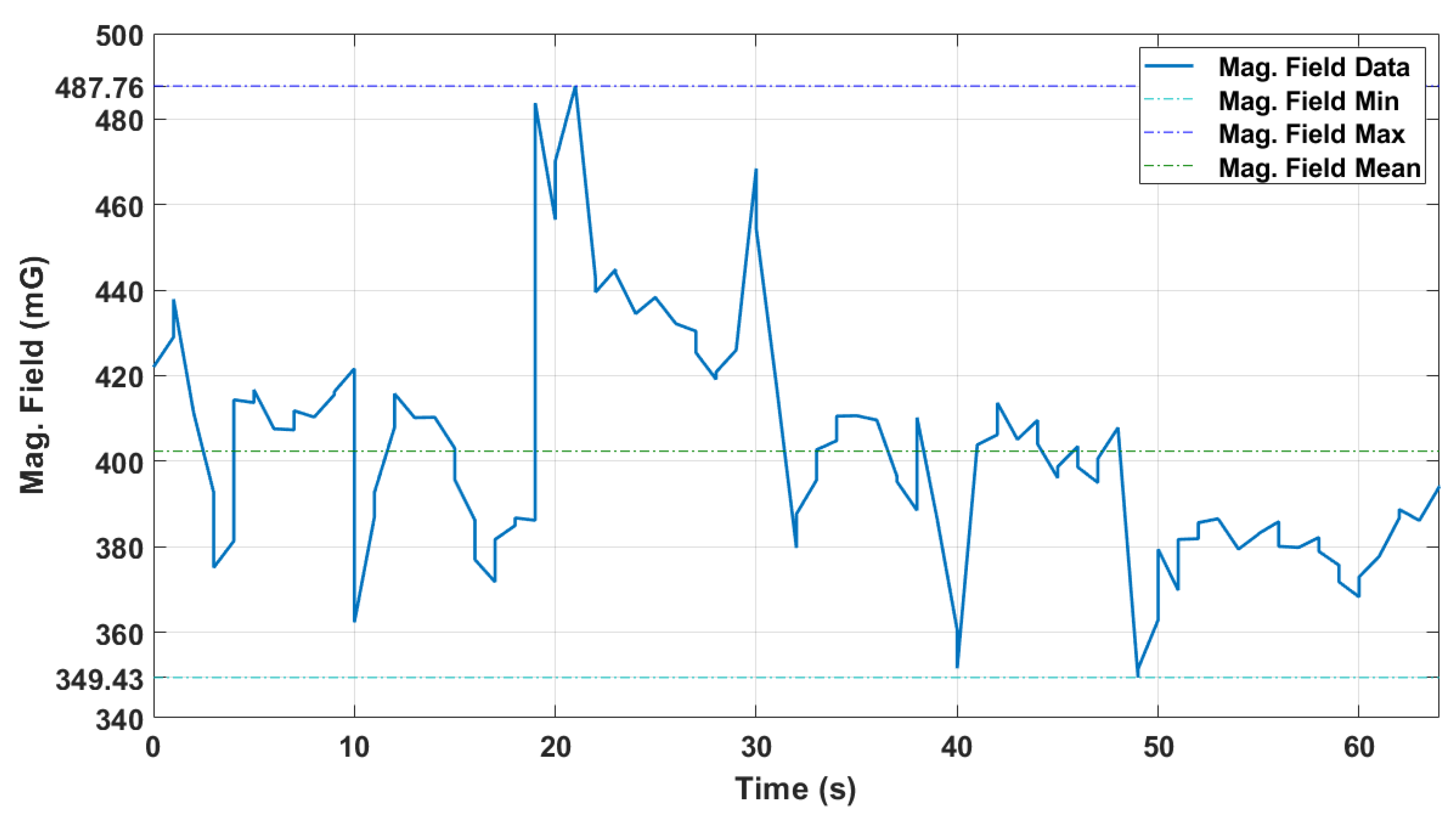
7.1. Compass Accuracy Measurement
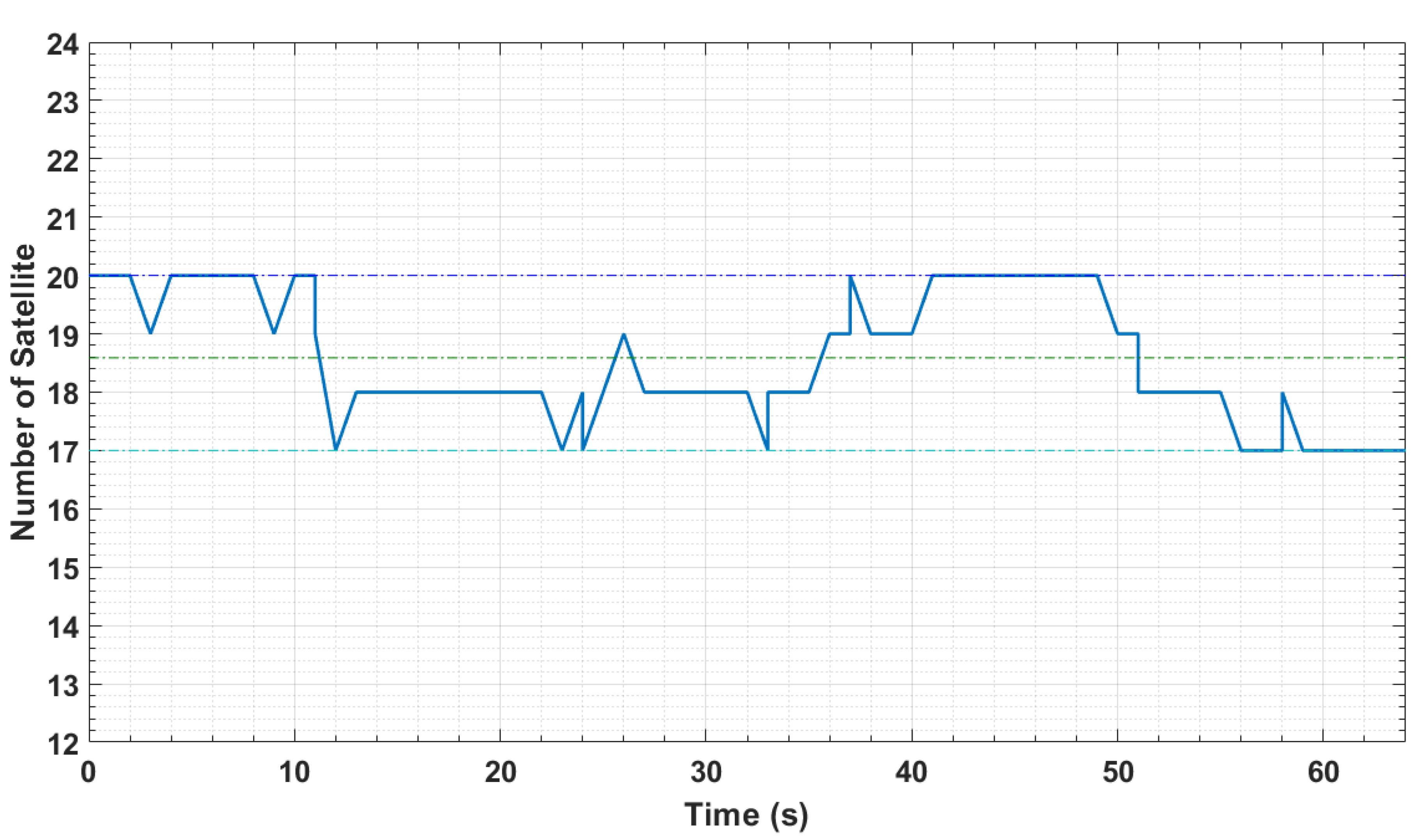
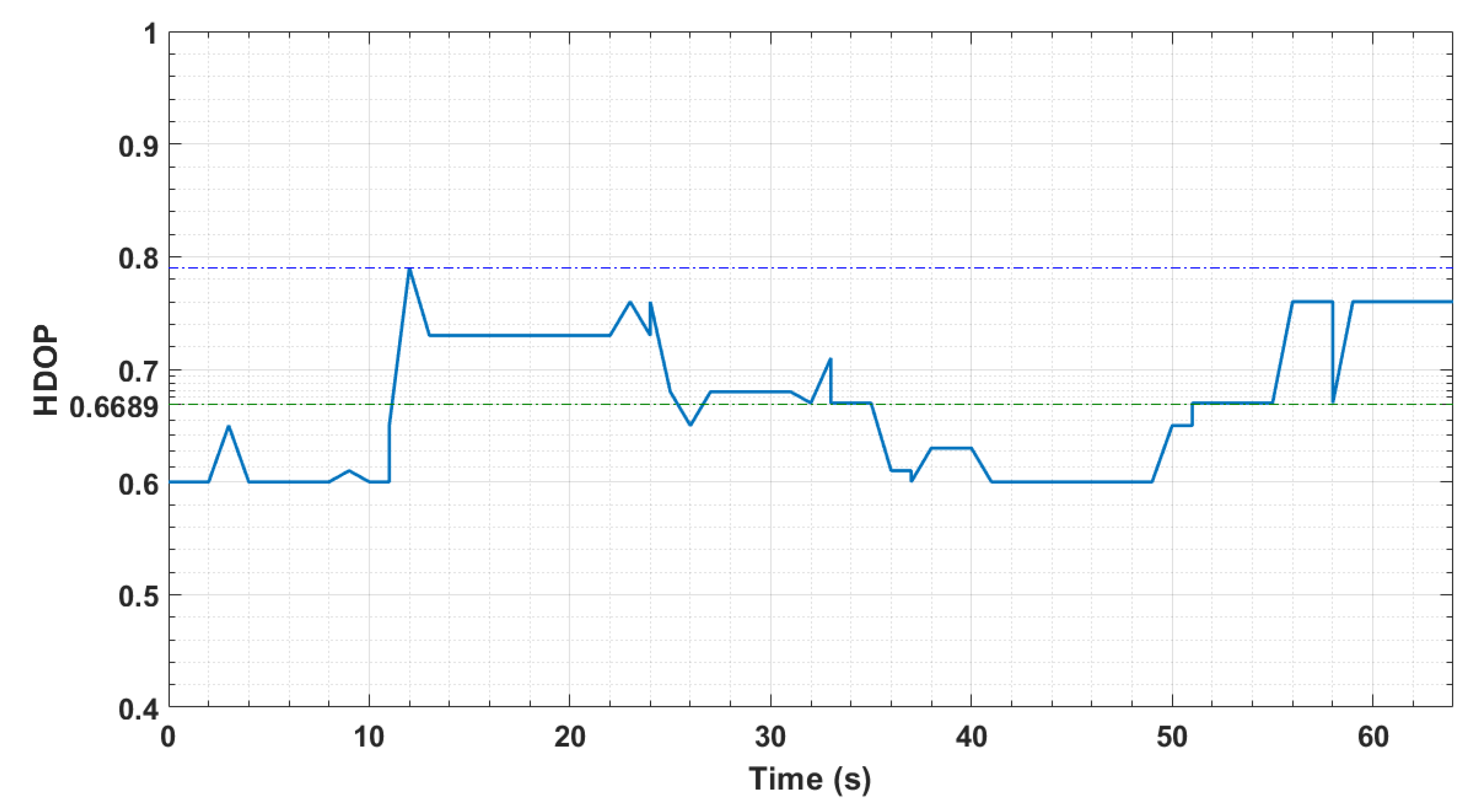
7.2. GPS Accuracy Measurement
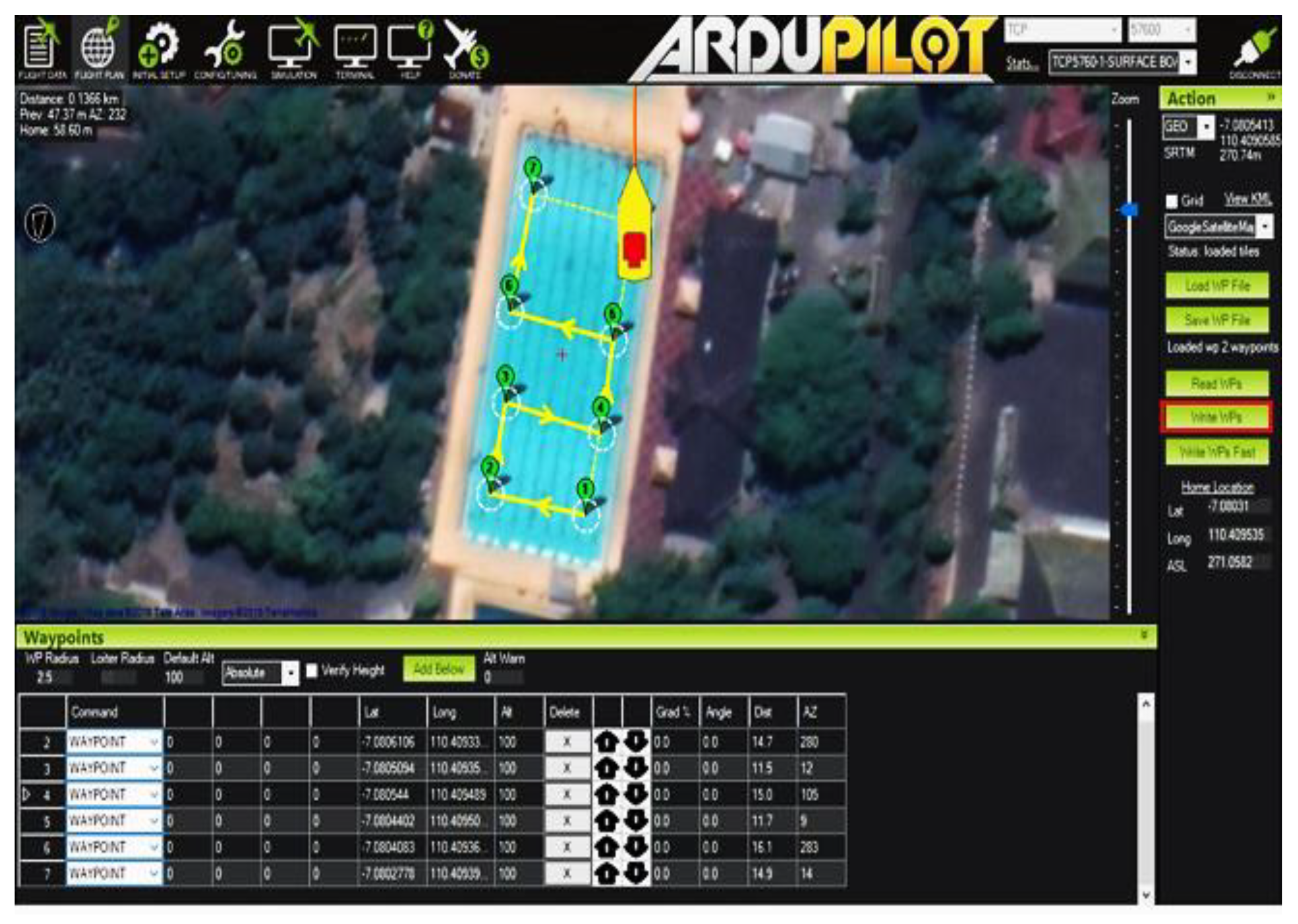
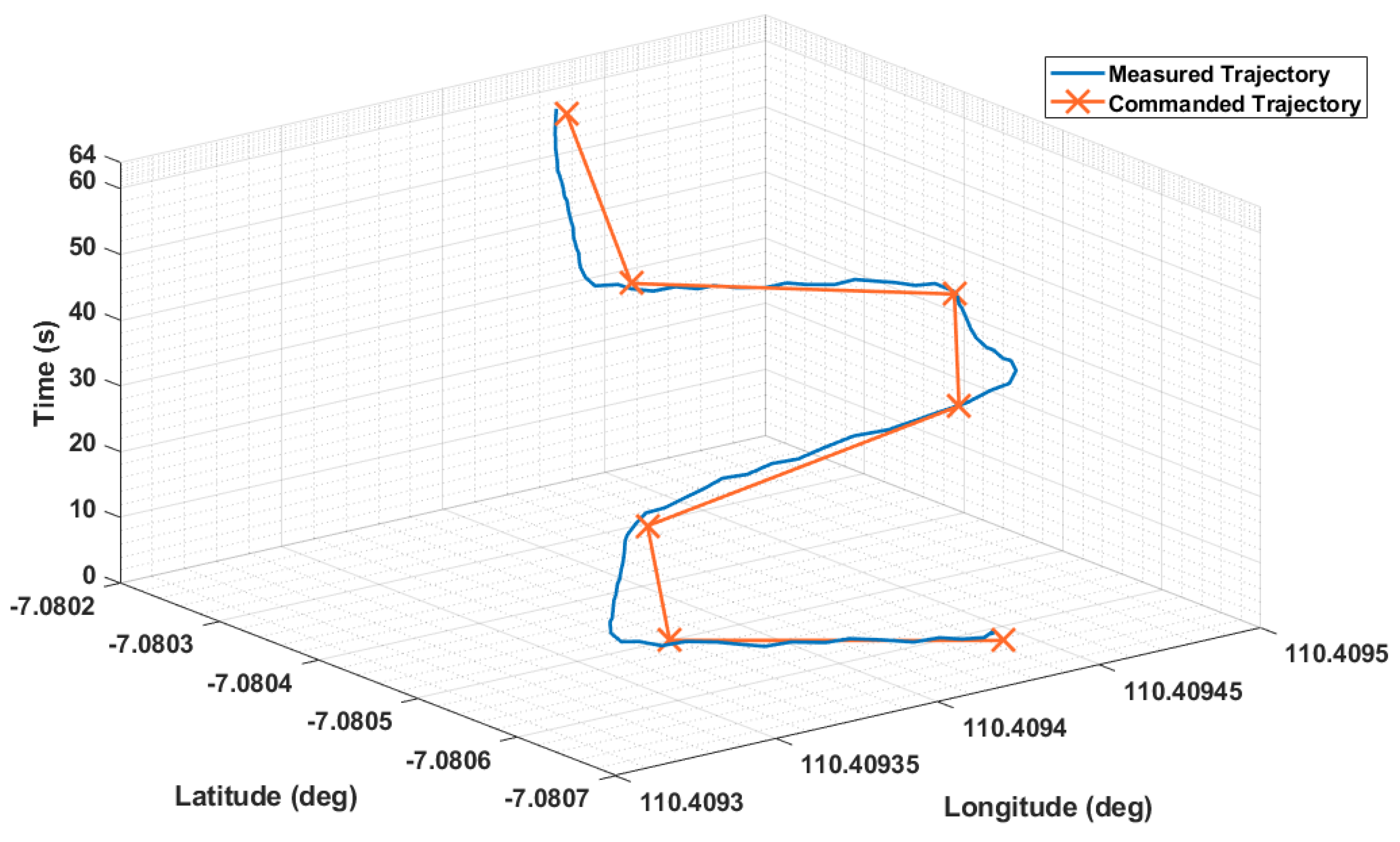
7.3. Trajectory Measurement
7.4. Energy Consumption Measurement
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Putri, F.T.; Ariyanto, M.; Haryanto, I.; Arozi, M.; Caesarendra, W.; Hanan, M.R.I. Development of Unmanned Aerial Vehicle (UAV) ornithopter with wireless radio control. In Proceedings of the 2016 3rd International Conference on Information Technology, Computer, and Electrical Engineering (ICITACEE), Semarang, Indonesia, 19–21 October 2017; pp. 79–84. [Google Scholar]
- Harfina, D.M.; Zaini, Z.; Wulung, W.J. Disinfectant spraying system with quadcopter type unmanned aerial vehicle technology as an effort to break the chain of the covid-19 virus. J. Robot. Control 2021, 2, 502–507. [Google Scholar]
- Alshorman, A.M.; Alshorman, O.; Irfan, M.; Glowacz, A.; Muhammad, F.; Caesarendra, W. Fuzzy-based fault-tolerant control for omnidirectional mobile robot. Machines 2020, 8, 55. [Google Scholar] [CrossRef]
- Balestrieri, E.; Daponte, P.; De Vito, L.; Lamonaca, F. Sensors and measurements for unmanned systems: An overview. Sensors 2021, 21, 1518. [Google Scholar] [CrossRef] [PubMed]
- Ball, M. USV Performs Offshore Data Harvesting in North Sea 2019. Available online: https://www.unmannedsystemstechnology.com/2019/09/usv-performs-offshore-data-harvesting-in-north-sea/ (accessed on 19 January 2020).
- Stenersen, H.S. Construction and Control of an Autonomous Sail Boat; Norwegian University of Science and Technology: Trondheim, Norway, 2015. [Google Scholar]
- Setiawan, J.D.; Chrismianto, D.; Ariyanto, M.; Sportyawan, C.W.; Widyantara, R.D.; Alimi, S. Development of Dynamic Model of Autonomous Sailboat for Simulation and Control. In Proceedings of the 2020 7th International Conference on Information Technology, Computer, and Electrical Engineering (ICITACEE), Dubai, United Arab Emirates, 18–19 December 2020; pp. 52–57. [Google Scholar]
- Setiawan, J.D.; Arief Budiman, B.; Ariyanto, M.; Andromeda, T.; Chrismianto, D.; Aziz, M.A. Experimental Study on the Aerodynamic Performance of Autonomous Boat with Wind Propulsion and Solar Power. In Proceedings of the 2019 6th International Conference on Electric Vehicular Technology (ICEVT), Ungasan, Bali, 18–21 November 2019; pp. 213–219. [Google Scholar]
- Barrera, C.; Padron, I.; Luis, F.S.; Llinas, O.; Marichal, G.N. Trends and challenges in unmanned surface vehicles (Usv): From survey to shipping. TransNav 2021, 15, 135–142. [Google Scholar] [CrossRef]
- Manley, J.E. Unmanned Surface Vehicles, 15 Years of Development. In Proceedings of the OCEANS 2008, Quebec City, QC, Canada, 15–18 September 2008; pp. 1–4. [Google Scholar]
- Zhou, M.; Shi, J. The Design and Development of an Affordable Unmanned Surface Vehicle for Estuary Research and STEM Education. In Proceedings of the Global Oceans 2020: Singapore–US Gulf Coast, Biloxi, MS, USA, 5–30 October 2020. [Google Scholar]
- Bae, J.H.; Min, B.C.; Luo, S.; Kannan, S.S.; Singh, Y.; Lee, B.; Voyles, R.M.; Postigo-Malaga, M.; Zenteno, E.G.; Aguilar, L.P. Development of an unmanned surface vehicle for remote sediment sampling with a van veen grab sampler. In Proceedings of the OCEANS 2019 MTS/IEEE SEATTLE, Seattle, WA, USA, 27–31 October 2019. [Google Scholar]
- Iovino, S.; Savvaris, A.; Tsourdos, A. Experimental Testing of a Path Manager for Unmanned Surface Vehicles in Survey Missions. IFAC-PapersOnLine 2018, 51, 226–231. [Google Scholar] [CrossRef]
- Mou, J.; He, Y.; Zhang, B.; Li, S.; Xiong, Y. Path following of a water-jetted USV based on maneuverability tests. J. Mar. Sci. Eng. 2020, 8, 354. [Google Scholar] [CrossRef]
- Sutton, R.; Sharma, S.; Xao, T. Adaptive navigation systems for an unmanned surface vehicle. J. Mar. Eng. Technol. 2011, 10, 3–20. [Google Scholar] [CrossRef] [Green Version]
- Huayna-Aguilar, M.M.; Cutipa-Luque, J.C.; Yanyachi, P.R. Robust control and fuzzy logic guidance for an unmanned surface vehicle. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 766–772. [Google Scholar] [CrossRef]
- Marchel, L.; Specht, C.; Specht, M. Assessment of the steering precision of a hydrographic usv along sounding profiles using a high-precision gnss rtk receiver supported autopilot. Energies 2020, 13, 5637. [Google Scholar] [CrossRef]
- Zhao, D.; Yang, T.; Ou, W.; Zhou, H. Autopilot design for unmanned surface vehicle based on CNN and ACO. Int. J. Comput. Commun. Control 2018, 13, 429–439. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Jiang, J.; Duan, F.; Liu, W.; Wang, X.; Bu, L.; Sun, Z.; Yang, G. Modeling and experimental testing of an unmanned surface vehicle with rudderless double thrusters. Sensors 2019, 19, 2051. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fahimi, F. Autonomous Robots Modeling, Path Planning, and Control, 1st ed.; Springer: Edmonton, AB, Canada, 2009. [Google Scholar]
- SNAME. Nomenclature for Treating the Motion of a Submerged Body Through a Fluid; The Society of Naval Architects and Marine Engineers: New York, NY, USA, 1950. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; ISBN 9781119991496. [Google Scholar]
- Mancini, A.; Frontoni, E.; Zingaretti, P. Development of a low-cost Unmanned Surface Vehicle for digital survey. In Proceedings of the 2015 European Conference on Mobile Robots (ECMR), Lincoln, UK, 2–4 September 2015. [Google Scholar]
- Mitchell, J.W. Fox and McDonald’s Introduction to Fluids Mechanics, 10th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2020; ISBN 9781119616566. [Google Scholar]
- Villa, J.L.; Paez, J.; Quintero, C.; Yime, E.; Cabrera, J. Design and Control of an Unmanned Surface Vehicle for Environmental Monitoring Applications. In Proceedings of the 2016 IEEE Colombian Conference on Robotics and Automation (CCRA), Bogota, Colombia, 29–30 September 2016. [Google Scholar]
- Lekkas, A.M. Guidance and Path-Planning Systems for Autonomous Vehicles; Norwegian University of Science and Technology: Trondheim, Norway, 2014. [Google Scholar]
- Sun, C.; Liu, M.; Liu, C.; Feng, X.; Wu, H. An industrial quadrotor uav control method based on fuzzy adaptive linear active disturbance rejection control. Electronics 2021, 10, 376. [Google Scholar] [CrossRef]
- Xiong, S.; Xie, H.; Song, K.; Zhang, G. A speed tracking method for autonomous driving via ADRC with extended state observer. Appl. Sci. 2019, 9, 3339. [Google Scholar] [CrossRef] [Green Version]
- Wurzburg, H.; Willee, H.; Mackay, R.; Kancir, P.; Barker, P.; Grahamjamesaddis; Tridgell, A. Diagnosing Problems Using Logs. 2019. Available online: https://ardupilot.org/copter/docs/common-diagnosing-problems-using-logs.html (accessed on 9 December 2019).
- Gisgeography Latitude, Longitude and Coordinate System Grids. 2019. Available online: https://gisgeography.com/latitude-longitude-coordinates/ (accessed on 8 December 2019).








| DOF | Motions | Forces and Moments | Linear and Angular Velocities | Position and Euler Angle |
|---|---|---|---|---|
| 1 | Surge | X | u | x |
| 2 | Sway | Y | v | y |
| 3 | Yaw | N | r | ψ |
| Waypoint | Latitude | Longitude |
|---|---|---|
| 1 | 110.4094434 | −7.0806239 |
| 2 | 110.4093455 | −7.0806066 |
| 3 | 110.4093656 | −7.0805187 |
| 4 | 110.4094568 | −7.080536 |
| 5 | 110.4094823 | −7.0804482 |
| 6 | 110.4093884 | −7.0804282 |
| 7 | 110.4094112 | −7.0802885 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Setiawan, J.D.; Septiawan, M.A.; Ariyanto, M.; Caesarendra, W.; Munadi, M.; Alimi, S.; Sulowicz, M. Development and Performance Measurement of an Affordable Unmanned Surface Vehicle (USV). Automation 2022, 3, 27-46. https://doi.org/10.3390/automation3010002
Setiawan JD, Septiawan MA, Ariyanto M, Caesarendra W, Munadi M, Alimi S, Sulowicz M. Development and Performance Measurement of an Affordable Unmanned Surface Vehicle (USV). Automation. 2022; 3(1):27-46. https://doi.org/10.3390/automation3010002
Chicago/Turabian StyleSetiawan, Joga Dharma, Muhammad Aldi Septiawan, Mochammad Ariyanto, Wahyu Caesarendra, M. Munadi, Sabri Alimi, and Maciej Sulowicz. 2022. "Development and Performance Measurement of an Affordable Unmanned Surface Vehicle (USV)" Automation 3, no. 1: 27-46. https://doi.org/10.3390/automation3010002
APA StyleSetiawan, J. D., Septiawan, M. A., Ariyanto, M., Caesarendra, W., Munadi, M., Alimi, S., & Sulowicz, M. (2022). Development and Performance Measurement of an Affordable Unmanned Surface Vehicle (USV). Automation, 3(1), 27-46. https://doi.org/10.3390/automation3010002









