Stator-Rotor Contact Force Estimation of Rotating Machine
Abstract
:1. Introduction
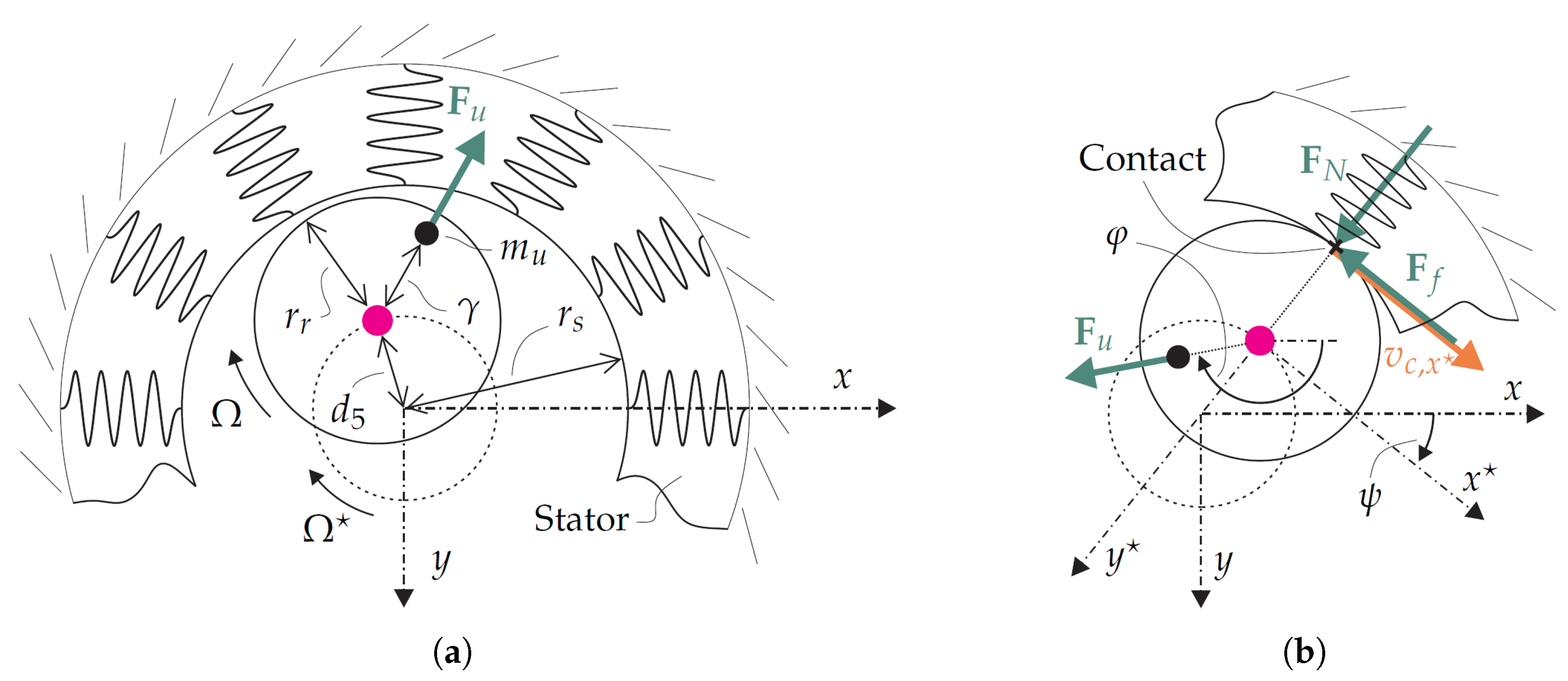
2. Stator–Rotor Contact Force Modeling
2.1. Modeling of Rotating Shaft
2.2. Modeling of Stator–Rotor Contact
3. State and Contact Force Estimation
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Finite Element Modeling
References
- Jacquet-Richardet, G.; Torkhani, M.; Cartraud, P.; Thouverez, F.; Baranger, T.N.; Herran, M.; Gibert, C.; Baguet, S.; Almeida, P.; Peletan, L. Rotor to stator contacts in turbomachines. Review and application. Mech. Syst. Signal Process. 2013, 40, 401–420. [Google Scholar] [CrossRef] [Green Version]
- Ma, H.; Zhao, Q.; Zhao, X.; Han, Q.; Wen, B. Dynamic characteristics analysis of a rotor–stator system under different rubbing forms. Appl. Math. Model. 2015, 39, 2392–2408. [Google Scholar] [CrossRef]
- Chamroon, C.; Cole, M.O.; Wongratanaphisan, T. An active vibration control strategy to prevent nonlinearly coupled rotor–stator whirl responses in multimode rotor-dynamic systems. IEEE Trans. Control Syst. Technol. 2013, 22, 1122–1129. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; Shang, Z.; Hong, L. Characteristics of dry friction backward whirl—A self-excited oscillation in rotor-to-stator contact systems. Sci. China Technol. Sci. 2010, 53, 674–683. [Google Scholar] [CrossRef]
- Jiang, J. Determination of the global responses characteristics of a piecewise smooth dynamical system with contact. Nonlinear Dyn. 2009, 57, 351–361. [Google Scholar] [CrossRef] [Green Version]
- Varney, P.; Green, I. Nonlinear phenomena, bifurcations, and routes to chaos in an asymmetrically supported rotor–stator contact system. J. Sound Vib. 2015, 336, 207–226. [Google Scholar] [CrossRef]
- Prabith, K.; Krishna, I.P. The numerical modeling of rotor–stator rubbing in rotating machinery: A comprehensive review. Nonlinear Dyn. 2020, 101, 1317–1363. [Google Scholar] [CrossRef]
- Ehehalt, U.; Alber, O.; Markert, R.; Wegener, G. Experimental observations on rotor-to-stator contact. J. Sound Vib. 2019, 446, 453–467. [Google Scholar] [CrossRef]
- Chipato, E.T.; Shaw, A.D.; Friswell, M.I. Nonlinear rotordynamics of a MDOF rotor–stator contact system subjected to frictional and gravitational effects. Mech. Syst. Signal Process. 2021, 159, 107776. [Google Scholar] [CrossRef]
- von Groll, G.T.; Ewins, D.J. A mechanism of low subharmonic response in rotor/stator contact—Measurements and simulations. J. Vib. Acoust. 2002, 124, 350–358. [Google Scholar] [CrossRef]
- Varney, P.; Green, I. Rotordynamic analysis of rotor–stator rub using rough surface contact. J. Vib. Acoust. 2016, 138. [Google Scholar] [CrossRef]
- Kuseyri, İ.S. Robust control and unbalance compensation of rotor/active magnetic bearing systems. J. Vib. Control 2012, 18, 817–832. [Google Scholar] [CrossRef]
- Kitanidis, P.K. Unbiased minimum-variance linear state estimation. Automatica 1987, 23, 775–778. [Google Scholar] [CrossRef]
- Gillijns, S.; De Moor, B. Unbiased minimum-variance input and state estimation for linear discrete-time systems. Automatica 2007, 43, 111–116. [Google Scholar] [CrossRef]
- Friedland, B. Treatment of bias in recursive filtering. IEEE Trans. Autom. Control 1969, 14, 359–367. [Google Scholar] [CrossRef]
- Hmida, F.B.; Khémiri, K.; Ragot, J.; Gossa, M. Three-stage Kalman filter for state and fault estimation of linear stochastic systems with unknown inputs. J. Frankl. Inst. 2012, 349, 2369–2388. [Google Scholar] [CrossRef]
- Ding, B.; Zhang, T.; Fang, H. On the equivalence between the unbiased minimum-variance estimation and the infinity augmented kalman filter. Int. J. Control 2020, 93, 2995–3002. [Google Scholar] [CrossRef]
- Klein, B. Grundlagen und Anwendungen der Finite-Element-Methode im Maschinen-und Fahrzeugbau; Springer Vieweg: Wiesbaden, Germany, 2012. [Google Scholar]
- Yu, J.; Goldman, P.; Bently, D.; Muzynska, A. Rotor/seal experimental and analytical study on full annular rub. J. Eng. Gas Turbines Power 2002, 124, 340–350. [Google Scholar] [CrossRef]
- Kim, Y.B.; Noah, S. Quasi-periodic response and stability analysis for a non-linear Jeffcott rotor. J. Sound Vib. 1996, 190, 239–253. [Google Scholar] [CrossRef]
- Kwakernaak, H.; Sivan, R. Linear Optimal Control Systems; John Wiley & Sons: Hoboken, NJ, USA, 1972; Volume 1. [Google Scholar]





| Description | Parameter | Unit | Value |
|---|---|---|---|
| Length of beam elements | m | 437.5 | |
| Cross section area | 159,043 | ||
| 31,416 | |||
| Material density | 7850 | ||
| Shaft mass | m | kg | 863 |
| Unbalance mass | kg | 20 | |
| Displacement of unbalance mass | mm | 35 | |
| Young modulus | E | ||
| Second moment of area | |||
| Spring coefficient (bearing) | |||
| Damper coefficient (bearing) | 1000 | ||
| Damping coefficients (shaft) | - | 0.002 | |
| - | 0.002 | ||
| Clearance | mm | 1.55 |
| Mean | Mean | Median | Median | |
|---|---|---|---|---|
| Forward whirl | 219.54 | 257.34 | 21.03 | 21.01 |
| Backward whirl | 78.89 | 80.51 | 15.89 | 16.36 |
| Forward whirl * | 24.30 | 24.21 | 16.90 | 17.09 |
| Backward whirl * | 22.44 | 23.05 | 12.26 | 13.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spiller, M.; Söffker, D. Stator-Rotor Contact Force Estimation of Rotating Machine. Automation 2021, 2, 83-97. https://doi.org/10.3390/automation2030005
Spiller M, Söffker D. Stator-Rotor Contact Force Estimation of Rotating Machine. Automation. 2021; 2(3):83-97. https://doi.org/10.3390/automation2030005
Chicago/Turabian StyleSpiller, Mark, and Dirk Söffker. 2021. "Stator-Rotor Contact Force Estimation of Rotating Machine" Automation 2, no. 3: 83-97. https://doi.org/10.3390/automation2030005
APA StyleSpiller, M., & Söffker, D. (2021). Stator-Rotor Contact Force Estimation of Rotating Machine. Automation, 2(3), 83-97. https://doi.org/10.3390/automation2030005







