Dispersive Optical Gap Soliton Perturbation with Multiplicative White Noise
Abstract
1. Introduction
Governing Model
2. Mathematical Preliminaries
3. Enhanced Direct Algebraic Method
- Case-1: If we set , using the Maple and the algebraic system Equation (25), we obtain the following results:with constraint conditions:In this regime, the auxiliary profile reduces to the elementary hyperbolic families, and the cubic balance fixes the effective coefficients through and . Depending on the sign pattern of , one obtains either localized (bell-shaped) or singular envelopes, as detailed below.
- (I) When and , Equations (2) and (3) have bell-shaped soliton solutions:For all subsequent solutions, we impose the ansatz
- (II) When and , Equations (1) and (2) have singular soliton solutions:
- Case-2: If we set . Using the Maple and the algebraic system Equation (25), we obtain the following results:with constraint conditions:Here, the expansion collapses to the negative-power branch (since ), which selects another sector of the auxiliary phase portrait of . The condition is precisely the degeneracy that permits rational combinations of hyperbolic functions when (23) is integrated, yielding either singular or kink-type envelopes for .
- (I) When . Equations (2) and (3) have the kink-shaped soliton solutions:Also, Equations (2) and (3) have the singular soliton solutions:The solutions (32) and (33) exist under the constraint condition (31). From a qualitative viewpoint, (32) describes heteroclinic (kink/antikink) connections between asymptotic plateaus in the reduced phase space, whereas (33) represents profiles with pole-type singularities arising from the structure.
- Case-3: If we set , using the Maple and the algebraic system Equation (25), we obtain the following results:
- (I) When , we getwith constraint conditions:The Jacobi elliptic doubly periodic-type soliton solutions are now found for Equations (2) and (3):
- (II) When , we getwith constraint conditions:Now, Equations (2) and (3) have the Jacobi elliptic doubly periodic type soliton solutions:
- (III) When , we getwith constraint conditions:The Jacobi elliptic doubly periodic-type soliton solutions have been obtained for Equations (2) and (3):
- Case-4: If we set , using the Maple and the algebraic system Equation (25), we obtain the following results:with constraint conditionsHere are the solutions of the Weierstrass elliptic doubly periodic-type for Equations (2) and (3):where Also, Equations (2) and (3) havewhere and . The invariants and of the Weierstrass elliptic function solutions (47) and (48) are given by the following:
- Case-5: If we set using the Maple and the algebraic system Equation (25), we obtain the following results:with constraint conditionsNow, the straddled soliton solutions have been identified for Equations (2) and (3), when , and ,also,
4. Modified Sub-ODE Approach
- Set-1: By substituting the specific values into the framework, and subsequently applying Maple together with the algebraic relations in Equation (59), we arrive at the following results:accompanied by the corresponding constraint condition:Under the assumptions that and , the system admits a bright soliton-type solution, which can be expressed as follows:
- Set-2: In the second configuration, we impose and assign . By employing Maple alongside the algebraic formulation in Equation (59), the solutions simplify to the following:together with the following constraint:Under these conditions, one obtains the dark soliton class of solutions, which can be written in the following explicit form:
- Set-3: By considering the substitutions and , and by applying Maple together with the system of algebraic equations given in (59), we are led to the following relations:with the associated constraint condition expressed asHere, represents an arbitrary constant. Based on particular selections of , one can derive a variety of families of solutions.
- (I) In the case when , then it follows that . Assuming the modulus parameter satisfies , the system admits Jacobi elliptic function type solutions of the form:which are consistent when and .
- (II) For the alternative case where , it follows that , with the range . Under these conditions, the Jacobi elliptic solutions take the following form:valid under and . Furthermore, in the limiting case when in (68) and (69), the elliptic solutions degenerate to the well-known bright soliton structures:
- (III) Finally, when , then , for . In this situation, the Jacobi elliptic solutions are obtained as follows:These remain consistent when and . Furthermore, in the limit , Expression (71) reduces to the standard dark soliton solutions:
- Set-4: Taking now the case where , and once again employing Maple in conjunction with the algebraic system (59), we distinguish two subcases as follows:
- (I) If and , the obtained relations arewith the constraintFor this case, the corresponding bright soliton solutions are as follows:
- (II) In the second case, where and , the results simplify to the following:with the constraint conditionThis scenario leads to the following form of dark soliton solutions:
- Set-5: Proceeding with the choice together with , and invoking Maple in concert with the algebraic system (59), we obtain the relations below. In this setting, the analysis naturally splits into several subclasses:subject to the constraintwhere the parameter regime is specified by , , and . Under these prerequisites, multiple soliton forms emerge as described below.
- (I) Singular soliton solutions: In this subcase, the solutions can be represented compactly as
- (II) Combo-bright-dark soliton solutions: A mixed-profile family also arises, taking the explicit form
- (III) Combo-singular soliton solutions: In addition, a combined singular-type behavior is captured by
- Set-6: We now consider the alternative reduction . Employing Maple again and applying the algebraic relations encoded in (59) leads directly totogether with the constraintwith the sign condition . Within this framework, four distinct Weierstrass elliptic families can be written as follows.
- (I) The first representation iswhere .
- (II) A second, equivalent parametrization can be expressed asunder the common sign requirement . The Weierstrass invariants are given succinctly by
- (III) A third form involves the derivative of the Weierstrass function:with as before.
- (IV) Finally, an alternative reciprocal representation is available:again with , and in this variant the invariants are specified byCollectively, the Weierstrass-based families in (86) and (90) remain valid, provided that constraint (85) is enforced, thereby completing the characterization of this set.
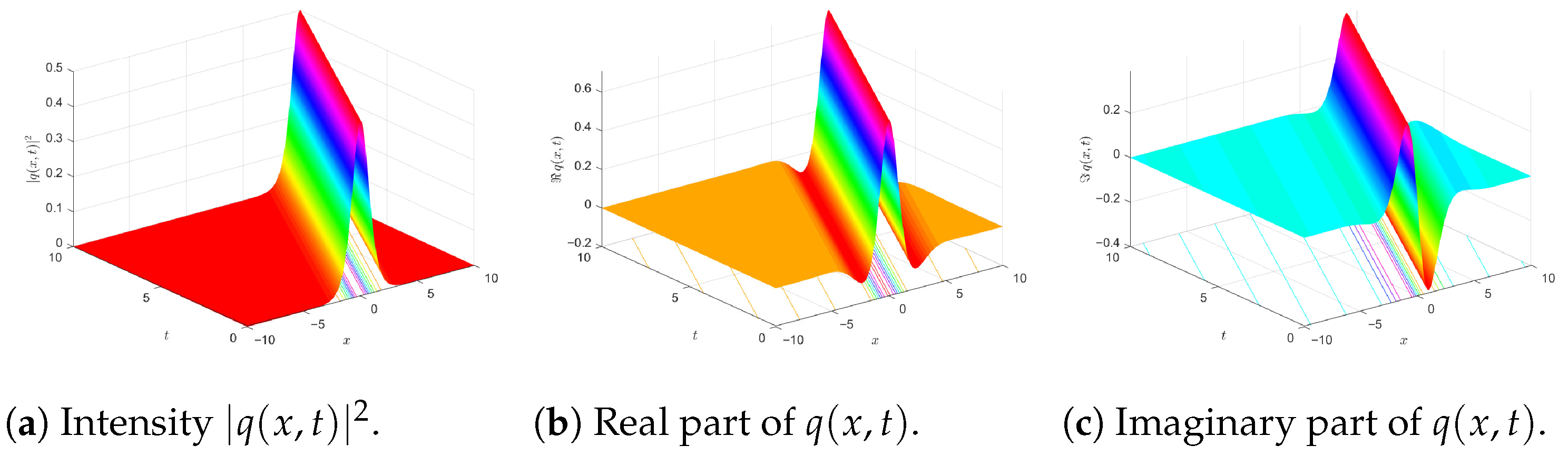
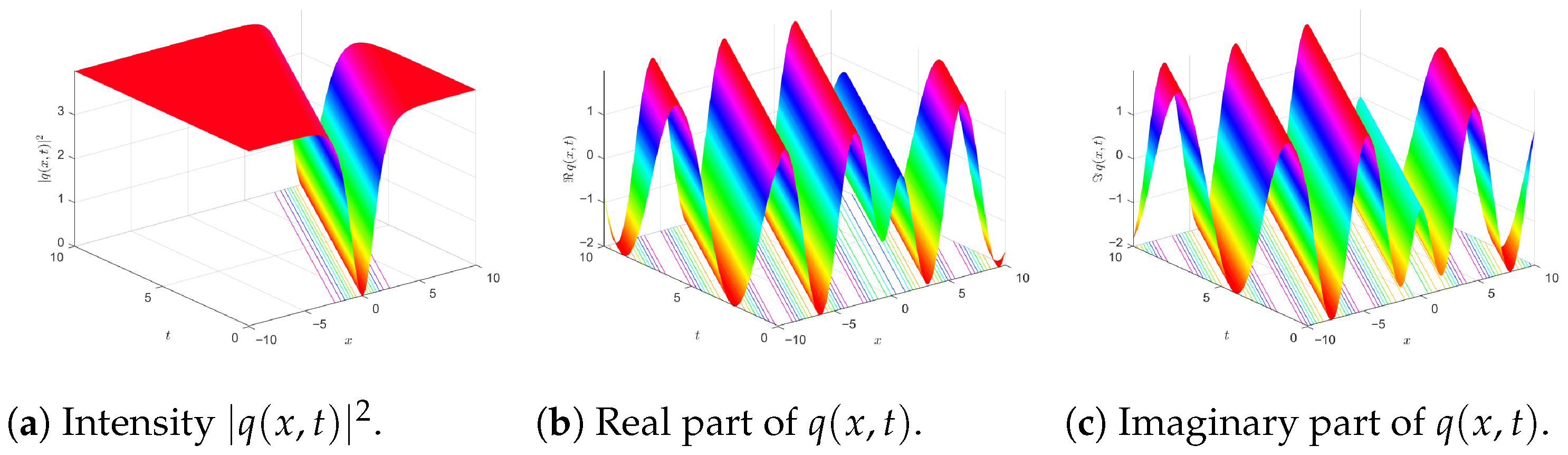
5. Results and Discussion
5.1. Physical Interpretation and System Relevance
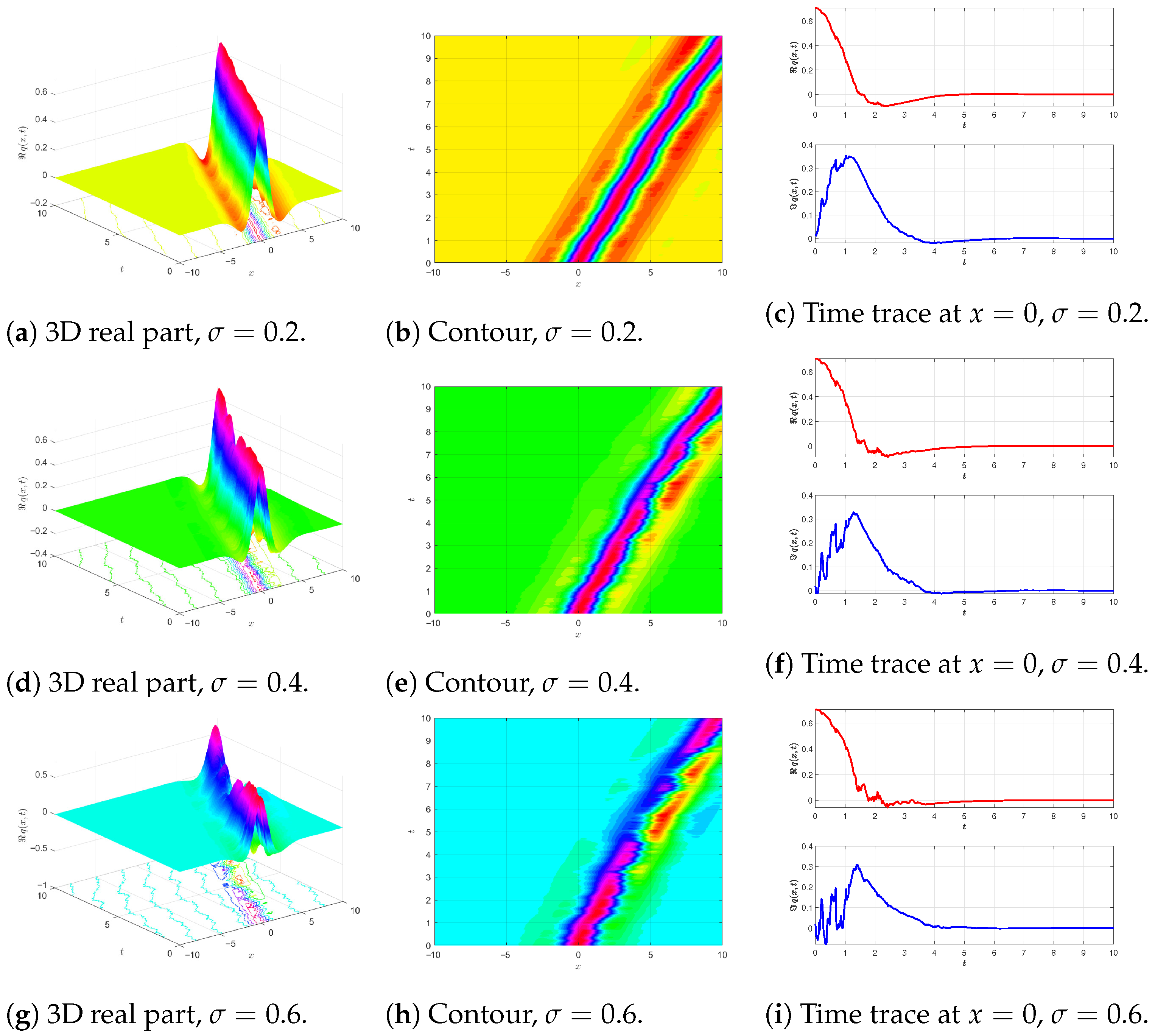
5.2. Quantitative Effect of Multiplicative Noise
6. Validation
6.1. Single-Field Model in Equation (1)
6.2. Bragg-Coupled Model in Equations (2) and (3)
6.3. Diagnostics and Tolerances
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Malaguti, S.; Bellanca, G.; Combrie, S.; de Rossi, A.; Trillo, S. Temporal gap solitons and all-optical control of group delay in line-defect waveguides. Phys. Rev. Lett. 2012, 109, 163902. [Google Scholar] [CrossRef]
- Pan, S.; Weng, M.; Fleury, R.; Segev, M.; Li, H. Superluminal gap solitons in nonlinear photonic time crystals. Phys. Rev. Lett. 2023, 130, 233801. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Xu, T.-F. Gap solitons with quadratic and quartic dispersion competition in one-dimensional nonlinear periodic systems. Phys. Rev. A 2023, 108, 013509. [Google Scholar] [CrossRef]
- Shnaiderman, R.; Tasgal, R.S.; Band, Y.B. Creating very slow optical gap solitons with a grating-assisted coupler. Opt. Lett. 2011, 36, 2438–2440. [Google Scholar] [CrossRef]
- Baratali, B.H.; Atai, J. Dynamics of moving gap solitons in linearly coupled Bragg gratings with dispersive reflectivity. J. Opt. Soc. Am. B 2015, 32, 1309–1317. [Google Scholar] [CrossRef]
- Mohanraj, P.; Padhi, P.; Sivakumar, R. Enhanced higher-order modulational instability in a parity–time-symmetric fiber Bragg grating system with modified saturable nonlinearity. J. Opt. Soc. Am. B 2022, 39, 3263–3274. [Google Scholar] [CrossRef]
- Raja, R.A.; Shah, D.V. Multifaceted dynamics and gap solitons in parity–time-symmetric periodic structures. Phys. Rev. A 2019, 100, 033838. [Google Scholar] [CrossRef]
- Tao, Y.; He, J.S. Multisolitons, breathers, and rogue waves for the Hirota equation generated by Darboux transformation. Phys. Rev. E 2012, 85, 026601. [Google Scholar] [CrossRef]
- Zhang, G.-Q.; Chen, J.; Yan, Z.-Y. Focusing and defocusing Hirota equations with non-zero boundary conditions: Rogue waves, breathers and solitons. Commun. Nonlinear Sci. Numer. Simul. 2020, 80, 104927. [Google Scholar] [CrossRef]
- Chen, S.; Yan, Z. The Hirota equation: Darboux transform of the Riemann–Hilbert problem and higher-order rogue waves. Appl. Math. Lett. 2019, 95, 65–71. [Google Scholar] [CrossRef]
- Li, J.; Gai, X.; Gu, C.; Xu, R. Phase properties and intensity characteristics of rogue waves in the Hirota and Sasa–Satsuma equations. Phys. Rev. A 2023, 107, 013511. [Google Scholar] [CrossRef]
- Armaroli, A. Stochastic modulational instability in the nonlinear Schrödinger equation with random group-velocity dispersion. Phys. Rev. A 2022, 106, 063505. [Google Scholar]
- Armaroli, A. Modulational instability in randomly dispersion-managed fibers. Phys. Rev. A 2023, 107, 053519. [Google Scholar]
- de Bouard, A.; Debussche, A. The nonlinear Schrödinger equation with white noise dispersion. J. Differ. Equ. 2010, 249, 1300–1321. [Google Scholar] [CrossRef]
- Li, J.; Lord, G.J.; Wang, X.; Zhao, W. Exponential integrators for stochastic Schrödinger equations. Phys. Rev. E 2020, 102, 033301. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.J.; Atai, J. Stability of moving gap solitons in linearly coupled Bragg gratings with cubic–quintic nonlinearity. Nonlinear Dyn. 2018, 92, 2725–2733. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Ahmad, H.; Boulares, H.; Khelifi, F. Exact solutions of Hirota–Maccari system forced by multiplicative noise in the Itô sense. J. Low Freq. Noise Vib. Act. Control 2022, 41, 74–84. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Mohammed, W.W.; Cesarano, C.; El-Morshedy, M. The influence of multiplicative noise and fractional derivative on the solutions of the stochastic fractional Hirota–Maccari system. Axioms 2022, 11, 357. [Google Scholar] [CrossRef]
- Fan, W.; Liang, Y.; Han, T. Novel insights into high–order dispersion and soliton dynamics in optical fibers via the perturbed Schrödinger–Hirota equation. Sci. Rep. 2024, 14, 31055. [Google Scholar] [CrossRef]
- Mohamed, E.M.; El-Kalla, I.L.; Tarabia, A.M.K.; Kader, A.H.A. New optical solitons for perturbed stochastic nonlinear Schrödinger equation by functional variable method. Opt. Quantum Electron. 2023, 55, 603. [Google Scholar] [CrossRef]
- Triki, H.; Kruglov, V.I. Generation of solitons and periodic wave trains in birefringent optical fibers. Chaos Solitons Fractals 2024, 186, 115300. [Google Scholar] [CrossRef]
- Cui, J.; Hong, J.; Liu, Z.; Zhou, W. Stochastic symplectic and multi-symplectic methods for nonlinear Schrödinger equation with white noise dispersion. J. Comput. Phys. 2017, 342, 267–285. [Google Scholar] [CrossRef]
- Arnous, A.H.; Hashemi, M.S.; Nisar, K.S.; Shakeel, M.; Ahmad, J.; Ahmad, I.; Jan, R.; Ali, A.; Kapoor, M.; Shah, N.A. Investigating solitary wave solutions with enhanced algebraic method for new extended Sakovich equations in fluid dynamics. Results Phys. 2024, 57, 107369. [Google Scholar] [CrossRef]
- Sirendaoreji. Auxiliary equation method and new solutions of Klein–Gordon equations. Chaos Solitons Fractals 2007, 31, 943–950. [Google Scholar] [CrossRef]
- Yang, Z.; Hon, B.Y. An improved modified extended tanh-function method. Z. Naturforschung A 2007, 61, 103–115. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alngar, M.E.M. Application of newly proposed sub-ODE method to locate chirped optical solitons to Triki–Biswas equation. Optik 2020, 207, 164360. [Google Scholar] [CrossRef]
- Li, Z.L. Periodic wave solutions of a generalized KdV–mKdV equation with higher-order nonlinear terms. Z. Naturforschung A 2010, 65, 649–657. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Gepreel, K.A.; Alngar, M.E.M.; Biswas, A.; Dakova, A.; Ekici, M.; Alshehri, H.M.; Belic, M.R. Cubic–quartic solitons for twin-core couplers in optical metamaterials. Optik 2021, 245, 167632. [Google Scholar] [CrossRef]
- Jawad, A.J.M.; Abu-AlShaeer, M.J. Highly dispersive optical solitons with cubic law and cubic–quintic–septic law nonlinearities by two methods. Al–Rafidain J. Eng. Sci. 2023, 1, 1–8. [Google Scholar] [CrossRef]
- Jawad, A.J.M.; Biswas, A. Solutions of resonant nonlinear Schrödinger’s equation with exotic non–Kerr law nonlinearities. Al–Rafidain J. Eng. Sci. 2024, 2, 43–50. [Google Scholar]
- Jihad, N.; Almuhsan, M.A.A. Evaluation of impairment mitigations for optical fiber communications using dispersion compensation techniques. Al–Rafidain J. Eng. Sci. 2023, 1, 81–92. [Google Scholar]
- Mendez-Zuniga, I.M.; Belyaeva, T.L.; Agüero, M.A.; Serkin, V.N. Multisoliton bound states in the fourth–order concatenation model of the nonlinear Schrödinger equation hierarchy. Trans. Opt. Photonics 2025, 1, 22–33. [Google Scholar]
- Kasapeteva, Z. Energy exchange between the polarization components of an optical pulse under the influence of degenerate four–photon parametric processes. Trans. Opt. Photonics 2025, 1, 58–66. [Google Scholar]

| Family | Envelope Form | Typical Regime Selector | Carrier and Drift | Role of Noise |
|---|---|---|---|---|
| Bright gap soliton | Localized hump, sech limit of an elliptic cn or dn branch | Effective dispersion and Kerr nonlinearity balance in the focusing sense near a band-gap operating point. Bragg detuning places the carrier inside the gap so that the effective mass is negative and the envelope is trapped. Existence is guaranteed when the reduced parameters satisfy the bright-branch inequalities for and from Section 4, with a positive amplitude parameter. Third-order dispersion adjusts asymmetry and walk-off but does not change the sign of the existence conditions. | and chosen by detuning set the carrier placement inside the gap. The drift follows from the travelling-wave phase matching and is used to position the pulse in the moving frame. | Multiplicative term adds a common stochastic phase. The intensity stays invariant to leading order while phase observables decorrelate at a rate proportional to . |
| Dark and gray gap soliton | Localized notch on a finite pedestal, tanh limit of an elliptic sn branch | Effective dispersion and Kerr nonlinearity balance in the defocusing sense or in the negative-mass portion of the gap. Detuning near a band edge fixes the pedestal. Existence follows from the dark-branch inequalities for and in Section 5, which set pedestal level, notch depth, and healing length. Third-order dispersion primarily skews the kink phase and modifies the recovery length. | Carrier pair and detuning control the phase jump across the notch. The drift transports the kink without altering the pedestal. | Same multiplicative-phase mechanism. The notch geometry and pedestal remain stable, while the field phase undergoes diffusion that increases with . |
| Elliptic periodic states | Doubly periodic wave with Jacobi or Weierstrass profile, modulus | Parameters in the compatibility set where and permit bounded periodic solutions. The limit connects continuously to the bright or dark soliton branches depending on the sign pattern of the reduced coefficients. | select the lattice speed and the carrier within the periodic envelope. | Noise causes loss of temporal coherence while preserving the average lattice intensity. |
| Singular and break-type solutions | Peaked, cusp, or gradient-catastrophe-like profiles | Outside the bounded-solution sets for and , or when amplitude or denominator conditions in the closed-form expressions fail. Often associated with parameter choices that violate the balance between dispersive terms and Kerr terms, or operate far from the gap. | Carrier and drift are defined, but the profile is non-localized or develops a singularity. | Noise accelerates phase wandering and may trigger earlier loss of smoothness, while not setting the onset by itself. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zayed, E.M.E.; El-Shater, M.; Arnous, A.H.; Moshokoa, S.P.; Biswas, A. Dispersive Optical Gap Soliton Perturbation with Multiplicative White Noise. Telecom 2025, 6, 90. https://doi.org/10.3390/telecom6040090
Zayed EME, El-Shater M, Arnous AH, Moshokoa SP, Biswas A. Dispersive Optical Gap Soliton Perturbation with Multiplicative White Noise. Telecom. 2025; 6(4):90. https://doi.org/10.3390/telecom6040090
Chicago/Turabian StyleZayed, Elsayed M. E., Mona El-Shater, Ahmed H. Arnous, Seithuti P. Moshokoa, and Anjan Biswas. 2025. "Dispersive Optical Gap Soliton Perturbation with Multiplicative White Noise" Telecom 6, no. 4: 90. https://doi.org/10.3390/telecom6040090
APA StyleZayed, E. M. E., El-Shater, M., Arnous, A. H., Moshokoa, S. P., & Biswas, A. (2025). Dispersive Optical Gap Soliton Perturbation with Multiplicative White Noise. Telecom, 6(4), 90. https://doi.org/10.3390/telecom6040090







