Highly Dispersive Optical Soliton Perturbation for Complex Ginzburg–Landau Equation, Implementing Three Forms of Self-Phase Modulation Structures with Power Law via Semi-Inverse Variation

Abstract

This paper provides highly dispersive optical soliton solutions to the perturbed complex Ginzburg–Landau equation. The self-phase modulation structures are maintained in three forms, which are derived from the power law of nonlinearity with arbitrary intensity. The paper employs the semi-inverse variational principle as its integration scheme, as conventional methods are incapable for it. The amplitude–width relation of the solitons is reconstructed by employing Cardano’s method to solve a cubic polynomial equation. Also presented are the necessary parameter constraints that naturally arise from the scheme. These findings enhance our understanding of soliton dynamics and pave the way for further research into more complex nonlinear systems. Future studies may explore the implications of these results in various physical contexts, potentially leading to novel applications in fields such as fiber optics and quantum fluid dynamics.

1. Introduction

The telecommunication industry has been profoundly influenced by the propagation dynamics of optical solitons. Many unknown aspects of this dynamic have yet to be explored, although several features have already been investigated [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. One such feature is the integrability of models, which allows the recovery of an exact mathematical expression for a bright one-soliton solution in the presence of perturbation terms, even when the light intensity is arbitrary. This is the subject of this paper. This paper considers the complex Ginzburg–Landau equation (CGLE), which involves three forms of self-phase modulation (SPM) structures derived from a power law format. The perturbation terms in the CGLE are all of the Hamiltonian type and occur with arbitrary intensity. The solitons considered here are highly dispersive (HD). Intermodal dispersion and chromatic dispersion (CD) are among the dispersion terms, which extend to sixth-order dispersion (6OD). This implies that dispersion-compensating fibers (DCF) are normally considered when propagating such solitons [23].

The integrability of the perturbed CGLE applies to retrieving HD bright one-soliton solutions when the nonlinearity parameters of the SPM terms and the perturbation terms are inconsistent. The research encompasses three types of SPM structures: the power law, dual-power law, and triple-power law. Thus, this paper continues the study of similar models in which the SPM structures originate from the Kerr law, parabolic law, and polynomial law [1]. In the current paper, the previously studied SPM structures are formulated when the nonlinearity parameter in the SPM structures is relaxed to unity [1]. The usual methods for solving such problems, such as the classical inverse scattering transform, cannot be used to find a bright one-soliton solution for the model because the nonlinearity parameters of the SPM structures do not align with the disturbance terms. This situation necessitates the application of the semi-inverse variational principle (SVP) to retrieve it. Additionally, the SVP has been successfully applied to obtain bright one-soliton solutions for various models in optical fibers. These include the Fokas–Lennels equation, the concatenation model, Kudryashov’s model, the Lakshmanan–Porsezian–Daniel model, and numerous others [1,2,3,4,5,6]. In addition, this principle encompasses the examination of cubic–quartic optical solitons, in which third-order and fourth-order dispersion replace CD collectively [4,5].

It is important to note that the SVP does not yield an exact bright one-soliton solution. Instead, it facilitates the derivation of an approximate analytical bright one-soliton solution. The structure of this soliton is similar to that of the unperturbed version of the CGLE [20]. The remainder of this paper examines the specifics of the derivation of an analytical one-soliton solution using the SVP for the three forms of SPM structures, following a brief presentation of the model. The corresponding parameter constraints that naturally arise during the derivation of the soliton solution are also provided.

The current paper recovers the bright one-soliton solution to the perturbed CGLE using the SVP when the standard integration methodologies fail in this regard. This includes the inverse scattering transform (IST) as well as other visible algorithms such as Hirota’s bilinear approach, the trial function method, the sub-ODE approach, the $G’/G$-expansion method, and several others, as reported [26,27,28,29,30]. The primary cause for the failure of integrability is that the power law nonlinearity parameter n is not the same as, nor related to, the arbitrary intensity parameter m of the perturbation terms. Another reason for the failure of integrability using the schemes known thus far is that the Painleve test of integrability will not pass for the model. Therefore the SVP plays a vital role in this work for the retrieval of the bright one-soliton solutions. It is noteworthy to mention that the soliton solutions are not exact; however, they are analytical. The results are therefore supplemented with numerical simulations to paint a complete picture of the analytical scheme, namely the SVP. This scheme, therefore, when applied to the model makes this paper truly novel.

The manuscript is organized as indicated here. After a brief introduction to the model with a general form of SPM structure, in the subsequent subsection, including the perturbation terms, a preliminary mathematical analysis is presented where the velocity of the perturbed soliton is computed and displayed. Additional parameter constraints that emerge from this preliminary analysis are also enumerated. The variational principle is next introduced. The SVP is subsequently applied to the model with three forms of SPM structures, namely the power law, dual-power law, and the triple-power law. The application of the SVP leads to the bright one-soliton solutions for the three forms of SPM structures. The soliton amplitude–width relation is recovered after solving an algebraic equation, for all three forms of SPM structure, by the well-known Cardano method. Finally, the numerical simulations for the three SPM structures are presented that support the analytical scheme.

The Structure of the Complex Ginzburg–Landau Equation

The fundamental model studied in this paper is the HD-CGLE, which is given by

$$\begin{array}{ccc}\hfill & & i{\varphi }_t+i{a}_1{\varphi }_x+a_2{\varphi }_{xx}+i{a}_3{\varphi }_{xxx}+a_4{\varphi }_{xxxx}+i{a}_5{\varphi }_{xxxxx}+a_6{\varphi }_{xxxxxx}\hfill \\ & +& {\displaystyle \frac{1}{{\left|\varphi \right|}^2{\varphi }^{*}}}\left[\alpha {\left|\varphi \right|}^2{\left({\left|\varphi \right|}^2\right)}_{xx}-\beta {\left\{{\left({\left|\varphi \right|}^2\right)}_x\right\}}^2\right]+F\left({\left|\varphi \right|}^2\right)\varphi \hfill \\ & =& i\left[\lambda {\left({\left|\varphi \right|}^{2m}\varphi \right)}_x+\theta {\left({\left|\varphi \right|}^{2m}\right)}_x\varphi +\sigma {\left|\varphi \right|}^{2m}{\varphi }_x\right]\hfill \end{array}$$

(1)

The wave profile transmitted along the optical fiber is denoted by $\varphi (x,t)$, a complex-valued function. The first term represents linear temporal evolution, with $i=\sqrt{-1}$. The six dispersion terms are represented by the coefficients of $a_j$ for $1\le j\le 6$. Here, $a_1$ represents intermodal dispersion, $a_2$ represents chromatic dispersion, and $a_3$ through $a_6$ represent third-order, fourth-order, fifth-order, and sixth-order dispersion effects, respectively. Next, the nonlinear effects that are taken into account in the CGLE [19] are responsible for $\alpha$ and $\beta$. Lastly, the perturbation terms on the right-hand side are derived from self-steepening effects, self-frequency shift, and soliton self-frequency shift, as denoted by the coefficients of $\lambda$, $\theta$, and $\sigma$, respectively. An arbitrary intensity may be utilized to determine the parameter m. The intensity-dependent nonlinear refractive index of the fiber is regulated by the functional F. This paper investigates three distinct forms of nonlinearities: the power law, dual-power law, and triple-power law. These laws are generalized versions of the Kerr law, parabolic law, and polynomial law, respectively, in nonlinear SPM structures. Each of these nonlinearities plays a crucial role in understanding the behavior of light propagation in optical fibers. By analyzing their effects, we can gain deeper insights into the performance and efficiency of fiber optic communication systems [1].

2. Basic Mathematical Preliminaries

This section will separate Equation (1) into its real and imaginary components based on the traveling wave hypothesis, which is essential for using the semi-inverse variations principle.

The initial assumption for treating Equation (1) is the following substitution:

$$\begin{array}{c}\hfill \varphi (x,t)=\zeta (x-vt)e^{i\left(-\mu x+\omega t+{\theta }_0\right)}.\end{array}$$

(2)

In Equation (2), the function $\zeta (x,t)$ reflects the traveling wave hypothesis, where $\mu$ signifies the frequency, $\omega$ represents the wave number, and ${\theta }_0$ indicates the phase constant. Substituting Equation (2) into Equation (1) and then separating into real and imaginary components produces the following pair of relations. The real component results in

$$\begin{array}{ccc}\hfill & & \left(-\omega +a_1\mu -a_2{\mu }^2-a_3{\mu }^3+a_4{\mu }^4+a_5{\mu }^5-a_6{\mu }^6\right)\zeta \hfill \\ & +& \left(a_2+2\alpha +3a_3\mu -6a_4{\mu }^2-10a_5{\mu }^3+15a_6{\mu }^4\right){\zeta }^{\prime \prime }\hfill \\ & +& \left(a_4+5a_5\mu -15a_6{\mu }^2\right){\zeta }^{\left(iv\right)}+a_6{\zeta }^{\left(vi\right)}+2\left(\alpha -2\beta \right){\displaystyle \frac{{\left({\zeta }^{\prime }\right)}^2}{\zeta }}+F\left({\zeta }^2\right)\zeta \hfill \\ & =& \mu \left(\lambda +\sigma \right){\zeta }^{2m+1}.\hfill \end{array}$$

(3)

Furthermore, the imaginary component results in

$$\begin{array}{ccc}\hfill & & \left\{(2m+1)\lambda +2m\theta +\sigma \right\}{\zeta }^{2m}{g}^{\prime }+\left(v-a_1+2a_2\mu +3a_3{\mu }^2-4a_4{\mu }^3-5a_5{\mu }^4+6a_6{\mu }^5\right){\zeta }^{\prime }\hfill \\ & -& \left(a_3-4a_4\mu -10a_5{\mu }^2+20a_6{\mu }^3\right){\zeta }^{\prime \prime \prime }-\left(a_5-6a_6\mu \right){\zeta }^{\left(v\right)}=0.\hfill \end{array}$$

(4)

In Equation (3), introducing the notations

$$\begin{array}{c}\hfill P_1=-\omega +a_1\mu -a_2{\mu }^2-a_3{\mu }^3+a_4{\mu }^4+a_5{\mu }^5-a_6{\mu }^6,\end{array}$$

(5)

$$\begin{array}{c}\hfill P_2=a_2+2\alpha +3a_3\mu -6a_4{\mu }^2-10a_5{\mu }^3+15a_6{\mu }^4,\end{array}$$

(6)

$$\begin{array}{c}\hfill P_3=a_4+5a_5\mu -15a_6{\mu }^2,\end{array}$$

(7)

and setting

$$\begin{array}{c}\hfill \alpha =2\beta ,\end{array}$$

(8)

transforms it to

$$\begin{array}{c}\hfill P_1\zeta +P_2{\zeta }^{\prime \prime }+P_3{\zeta }^{\left(iv\right)}+a_6{\zeta }^{\left(vi\right)}+F\left({\zeta }^2\right)\zeta =\mu \left(\lambda +\sigma \right){\zeta }^{2m+1},\end{array}$$

(9)

where ${\zeta }^{\prime }=d\zeta /ds$, ${\zeta }^{\prime \prime }=d^2\zeta /d{s}^2$, ${\zeta }^{\prime \prime \prime }=d^3\zeta /d{s}^3$, ${\zeta }^{\left(iv\right)}=d^4\zeta /d{s}^4$, ${\zeta }^{\left(v\right)}=d^5\zeta /d{s}^5$ and ${\zeta }^{\left(vi\right)}=d^6\zeta /d{s}^6$ with $s=x-vt$. Thus, with (8), the governing Equation (1) modifies to

$$\begin{array}{ccc}\hfill & & i{\varphi }_t+i{a}_1{\varphi }_x+a_2{\varphi }_{xx}+i{a}_3{\varphi }_{xxx}+a_4{\varphi }_{xxxx}+i{a}_5{\varphi }_{xxxxx}+a_6{\varphi }_{xxxxxx}\hfill \\ & +& {\displaystyle \frac{\beta }{{\left|\varphi \right|}^2{\varphi }^{*}}}\left[2{\left|\varphi \right|}^2{\left({\left|\varphi \right|}^2\right)}_{xx}-{\left\{{\left({\left|\varphi \right|}^2\right)}_x\right\}}^2\right]+F\left({\left|\varphi \right|}^2\right)\varphi \hfill \\ & =& i\left[\lambda {\left({\left|\varphi \right|}^{2m}\varphi \right)}_x+\theta {\left({\left|\varphi \right|}^{2m}\right)}_x\varphi +\sigma {\left|\varphi \right|}^{2m}{\varphi }_x\right].\hfill \end{array}$$

(10)

The following parameter constraints are calculated when the coefficients of the linearly independent functions are made null in the imaginary portion of Equation (4):

$$\begin{array}{c}\hfill (2m+1)\lambda +2m\theta +\sigma =0,\end{array}$$

(11)

$$\begin{array}{c}\hfill v=a_1-2a_2\mu -3a_3{\mu }^2+4a_4{\mu }^3+5a_5{\mu }^4-6a_6{\mu }^5,\end{array}$$

(12)

$$\begin{array}{c}\hfill a_3-4a_4\mu -10a_5{\mu }^2+20a_6{\mu }^3=0,\end{array}$$

(13)

and

$$\begin{array}{c}\hfill a_5=6\mu a_6.\end{array}$$

(14)

Equation (12) gives the velocity of the soliton. It must be noted that the relations of (11)–(14) stay the same irrespective of the SPM structure.

3. Application of the Semi-Inverse Variational Principle

The SVP will be applied to Equation (1) in this section, taking into account the treatment presented in the previous section. The equation will be solved using Cardano’s formula to identify brilliant single solitons. The calculation will be performed for various forms of nonlinearities. This methodology is not frequently employed in nonlinear optics, as far as we are aware.

Multiplying by ${\zeta }^{\prime }$ and integrating from Equation (9), we obtain

$$\begin{array}{c}\hfill P_1{\zeta }^2+P_2{\left({\zeta }^{\prime }\right)}^2-P_3{\left({\zeta }^{\prime \prime }\right)}^2+a_6{\left({\zeta }^{\prime \prime \prime }\right)}^2+2\int F\left({\zeta }^2\right)\zeta {\zeta }^{\prime }d\zeta -{\displaystyle \frac{\mu \left(\lambda +\sigma \right)}{m+1}}{\zeta }^{2m+2}=K,\end{array}$$

(15)

where K is an integration constant. The stationary integral is described as

$$\begin{array}{c}\hfill J={\int }_{-\infty }^{\infty }\left[P_1{\zeta }^2+P_2{\left({\zeta }^{\prime }\right)}^2-P_3{\left({\zeta }^{\prime \prime }\right)}^2+a_6{\left({\zeta }^{\prime \prime \prime }\right)}^2+2\int F\left({\zeta }^2\right)\zeta {\zeta }^{\prime }d\zeta -{\displaystyle \frac{\mu \left(\lambda +\sigma \right)}{m+1}}{\zeta }^{2m+2}\right]dx.\end{array}$$

(16)

In Equation (16), the coefficients of $P_3$ and $a_6$ are recovered and simplified with the application of the integration by parts and subsequently implementing the asymptotic conditions at the two wings of the bright solitons since these are assumed to be radiation-free.

The SVP suggests that the bright one-soliton solution to Equation (10) is identical to that of the homogeneous counterpart, which is with $\lambda =\theta =\sigma =0$, characterized by the following structure:

$$\begin{array}{c}\hfill \zeta \left(s\right)=Af\left(\mathrm{sech}\left(B(x-vt)\right)\right),\end{array}$$

(17)

The functional form of the bright soliton, denoted as f, is established based on the SPM structure. The amplitude A and inverse width B of the soliton are deduced from the coupled system of Equations [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]:

$$\begin{array}{c}\hfill {\displaystyle \frac{\mathsf{\partial }J}{\mathsf{\partial }A}}=0,\end{array}$$

(18)

and

$$\begin{array}{c}\hfill {\displaystyle \frac{\mathsf{\partial }J}{\mathsf{\partial }B}}=0.\end{array}$$

(19)

The above procedure will be used to analyze the HD bright one-soliton solution to Equation (10) for three nonlinear versions, as detailed in the subsequent subsections. Each version will highlight distinct characteristics and behaviors of the soliton, which will reveal the underlying physics.

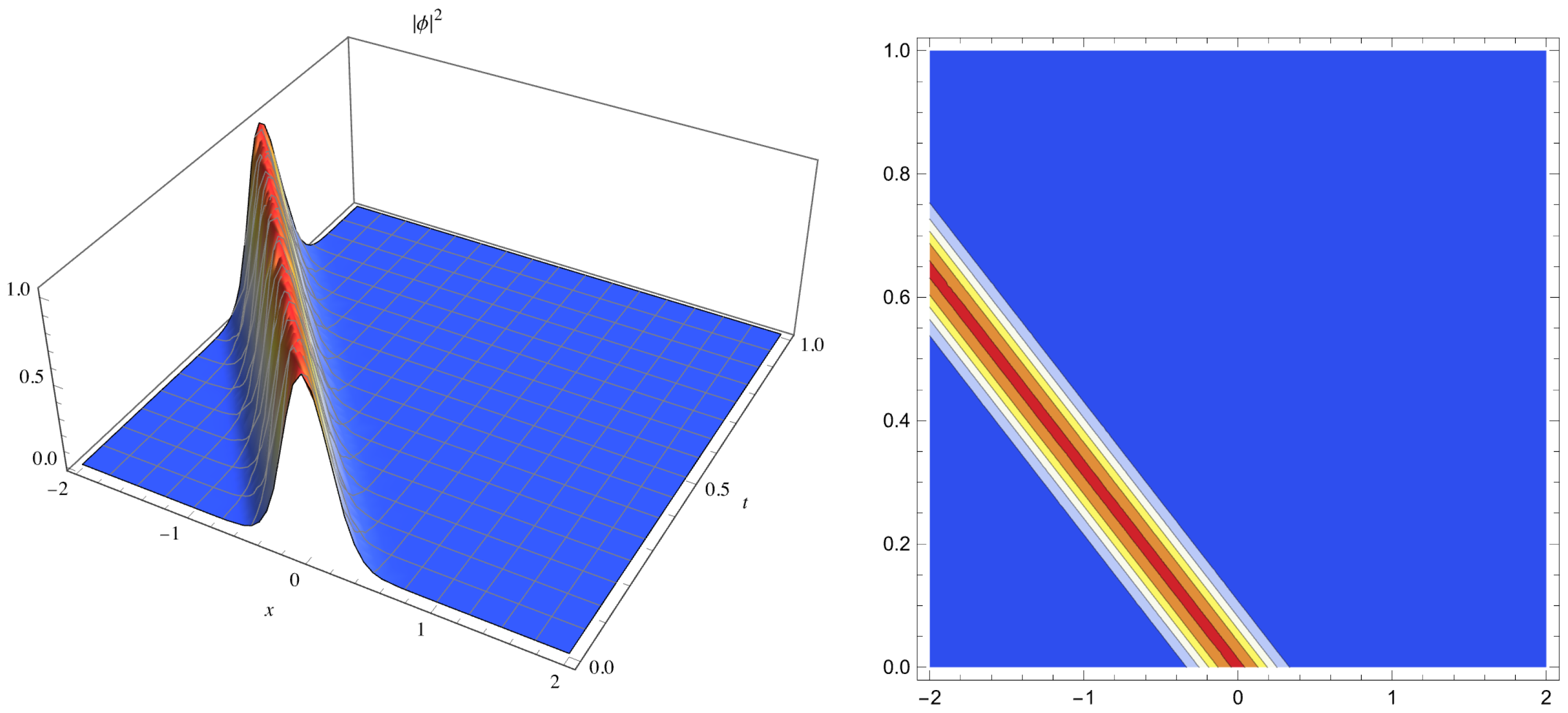
3.1. Considering Power Law

The Kerr law of nonlinearity, also referred to as the Kerr effect or cubic nonlinearity, is a fundamental phenomenon in nonlinear optics that explains how the refractive index of a material varies in proportion to the intensity of the light that passes through it.

The refractive index structure for Kerr or cubic nonlinearity is expressed as

$$\begin{array}{c}\hfill F\left(s\right)=b_0{s}^n,\end{array}$$

(20)

where $b_0$ is a real-valued constant while n is the power law nonlinearity parameter. Thus, Equation (10) transforms to

$$\begin{array}{ccc}\hfill & & i{\varphi }_t+i{a}_1{\varphi }_x+a_2{\varphi }_{xx}+i{a}_3{\varphi }_{xxx}+a_4{\varphi }_{xxxx}+i{a}_5{\varphi }_{xxxxx}+a_6{\varphi }_{xxxxxx}\hfill \\ & +& {\displaystyle \frac{\beta }{{\left|\varphi \right|}^2{\varphi }^{*}}}\left[2{\left|\varphi \right|}^2{\left({\left|\varphi \right|}^2\right)}_{xx}-{\left\{{\left({\left|\varphi \right|}^2\right)}_x\right\}}^2\right]+b_0{\left|\varphi \right|}^{2n}\varphi \hfill \\ & =& i\left[\lambda {\left({\left|\varphi \right|}^{2m}\varphi \right)}_x+\theta {\left({\left|\varphi \right|}^{2m}\right)}_x\varphi +\sigma {\left|\varphi \right|}^{2m}{\varphi }_x\right],\hfill \end{array}$$

(21)

so that Equation (15) modifies to

$$\begin{array}{c}\hfill P_1{\zeta }^2+P_2{\left({\zeta }^{\prime }\right)}^2-P_3{\left({\zeta }^{\prime \prime }\right)}^2+a_6{\left({\zeta }^{\prime \prime \prime }\right)}^2+b_0{\displaystyle \frac{{\zeta }^{2n+2}}{2n+2}}-{\displaystyle \frac{\mu \left(\lambda +\sigma \right)}{m+1}}{\zeta }^{2m+2}=K.\end{array}$$

(22)

The stationary integral, in this instance, is given as

$$\begin{array}{c}\hfill J={\int }_{-\infty }^{\infty }\left[P_1{\zeta }^2+P_2{\left({\zeta }^{\prime }\right)}^2-P_3{\left({\zeta }^{\prime \prime }\right)}^2+a_6{\left({\zeta }^{\prime \prime \prime }\right)}^2+b_0{\displaystyle \frac{{\zeta }^{2n+2}}{n+1}}-{\displaystyle \frac{\mu \left(\lambda +\sigma \right)}{m+1}}{\zeta }^{2m+2}\right]dx.\end{array}$$

(23)

The solution to Equation (21), for $\lambda =\theta =\sigma =0$, is expressed as [1,20]

$$\begin{array}{c}\hfill \zeta (x-vt)=A{\mathrm{sech}}^{{\displaystyle \frac{3}{n}}}\left[B(x-vt)\right].\end{array}$$

(24)

Substituting this form of the one-soliton solution into Equation (23), the stationary integral reduces to

$$\begin{array}{ccc}\hfill J& =& \left[{\displaystyle \frac{P_1{A}^2}{B}}+{\displaystyle \frac{9P_2{A}^{2}B}{n(n+6)}}-{\displaystyle \frac{9(4n+9)P_3{A}^2{B}^3}{n^2(n+2)(n+6)}}+{\displaystyle \frac{9\left(16n^3+192n^2+540n+405\right)a_6{A}^2{B}^5}{n^3(n+2)(n+6)(5n+6)}}\right.\hfill \\ & +& \left.{\displaystyle \frac{8(n+3)(2n+3)b_0{A}^{2n+2}}{(n+1)(n+2)(n+6)(5n+6)B}}\right]{\displaystyle \frac{\Gamma \left(\frac{3}{n}\right)\Gamma \left(\frac{1}{2}\right)}{\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)}}\hfill \\ & -& {\displaystyle \frac{\mu (\lambda +\sigma )A^{2m+2}}{(m+1)B}}{\displaystyle \frac{\Gamma \left(\frac{3m}{n}+\frac{3}{n}\right)\Gamma \left(\frac{1}{2}\right)}{\Gamma \left(\frac{3m}{n}+\frac{3}{n}+\frac{1}{2}\right)}}.\hfill \end{array}$$

(25)

The interconnected Equations (18) and (19) for the Kerr law are presented as follows:

$$\begin{array}{ccc}\hfill & & P_1+{\displaystyle \frac{9P_2{B}^2}{n(n+6)}}-{\displaystyle \frac{9(4n+9)P_3{B}^4}{n^2(n+2)(n+6)}}+{\displaystyle \frac{9\left(16n^3+192n^2+540n+405\right)a_6{B}^6}{n^3(n+2)(n+6)(5n+6)}}\hfill \\ & +& {\displaystyle \frac{8(n+3)(2n+3)b_0{A}^{2n}}{(n+2)(n+6)(5n+6)B}}-\mu (\lambda +\sigma )A^{2m}{\displaystyle \frac{\Gamma \left(\frac{3m}{n}+\frac{3}{n}\right)\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3m}{n}+\frac{3}{n}+\frac{1}{2}\right)\Gamma \left(\frac{3}{n}\right)}}=0,\hfill \end{array}$$

(26)

and

$$\begin{array}{ccc}\hfill & -& P_1+{\displaystyle \frac{9P_2{B}^2}{n(n+6)}}-{\displaystyle \frac{27(4n+9)P_3{B}^4}{n^2(n+2)(n+6)}}+{\displaystyle \frac{45\left(16n^3+192n^2+540n+405\right)a_6{B}^6}{n^3(n+2)(n+6)(5n+6)}}\hfill \\ & -& {\displaystyle \frac{8(n+3)(2n+3)b_0{A}^{2n}}{(n+1)(n+2)(n+6)(5n+6)}}+{\displaystyle \frac{\mu (\lambda +\sigma )A^{2m}}{m+1}}{\displaystyle \frac{\Gamma \left(\frac{3m}{n}+\frac{3}{n}\right)\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3m}{n}+\frac{3}{n}+\frac{1}{2}\right)\Gamma \left(\frac{3}{n}\right)}}=0.\hfill \end{array}$$

(27)

Adding Equations (26) and (27) leaves us with

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{18P_2{B}^2}{n(n+6)}}-{\displaystyle \frac{36(4n+9)P_3{B}^4}{n^2(n+2)(n+6)}}+{\displaystyle \frac{54\left(16n^3+192n^2+540n+405\right)a_6{B}^6}{n^3(n+2)(n+6)(5n+6)}}\hfill \\ & +& {\displaystyle \frac{8n(n+3)(2n+3)b_0{A}^{2n}}{(n+1)(n+2)(n+6)(5n+6)}}-{\displaystyle \frac{m\mu (\lambda +\sigma )A^{2m}}{m+1}}{\displaystyle \frac{\Gamma \left(\frac{3m}{n}+\frac{3}{n}\right)\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3m}{n}+\frac{3}{n}+\frac{1}{2}\right)\Gamma \left(\frac{3}{n}\right)}}=0.\hfill \end{array}$$

(28)

Equation (28) is a cubic polynomial in the variable u, which guarantees that it can be reformulated as

$$\begin{array}{c}\hfill a{u}^3+b{u}^2+cu+d=0,\end{array}$$

(29)

with the following notations:

$$\begin{array}{c}\hfill B^2=u,\end{array}$$

(30)

$$\begin{array}{c}\hfill a={\displaystyle \frac{54\left(16n^3+192n^2+540n+405\right)a_6}{n^3(n+2)(n+6)(5n+6)}}\end{array}$$

(31)

$$\begin{array}{c}\hfill b=-{\displaystyle \frac{36(4n+9)P_3}{n^2(n+2)(n+6)}}\end{array}$$

(32)

$$\begin{array}{c}\hfill c={\displaystyle \frac{18P_2}{n(n+6)}}\end{array}$$

(33)

and the independent term is

$$\begin{array}{c}\hfill d={\displaystyle \frac{8n(n+3)(2n+3)b_0{A}^{2n}}{(n+1)(n+2)(n+6)(5n+6)}}-{\displaystyle \frac{m\mu (\lambda +\sigma )A^{2m}}{m+1}}{\displaystyle \frac{\Gamma \left(\frac{3m}{n}+\frac{3}{n}\right)\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3m}{n}+\frac{3}{n}+\frac{1}{2}\right)\Gamma \left(\frac{3}{n}\right)}}\end{array}$$

(34)

We solve Equation (29) by considering (30) using the widely used Cardano method to solve the cubic equation. Consequently, we obtain

$$\begin{array}{c}\hfill B=\left[{\left\{\left(-{\displaystyle \frac{b^3}{27a^3}}+{\displaystyle \frac{bc}{6a^2}}-{\displaystyle \frac{d}{2a}}\right)-\sqrt{{\left(-{\displaystyle \frac{b^3}{27a^3}}+{\displaystyle \frac{bc}{6a^2}}-{\displaystyle \frac{d}{2a}}\right)}^2+{\left({\displaystyle \frac{c}{3a}}-{\displaystyle \frac{b^2}{9a^2}}\right)}^3}\right\}}^{{\displaystyle \frac{1}{3}}}\right.\\ \hfill +{\left.{\left\{\left(-{\displaystyle \frac{b^3}{27a^3}}+{\displaystyle \frac{bc}{6a^2}}-{\displaystyle \frac{d}{2a}}\right)+\sqrt{{\left(-{\displaystyle \frac{b^3}{27a^3}}+{\displaystyle \frac{bc}{6a^2}}-{\displaystyle \frac{d}{2a}}\right)}^2+{\left({\displaystyle \frac{c}{3a}}-{\displaystyle \frac{b^2}{9a^2}}\right)}^3}\right\}}^{{\displaystyle \frac{1}{3}}}-{\displaystyle \frac{b}{3a}}\right]}^{{\displaystyle \frac{1}{2}}}.\end{array}$$

(35)

For this solution to exist, the following constraint must be accomplished:

$$\begin{array}{c}\hfill a_6\ne 0,\end{array}$$

(36)

In addition, the discriminant must satisfy $D>0$, being

$$\begin{array}{c}\hfill D={\left(-{\displaystyle \frac{b^3}{27a^3}}+{\displaystyle \frac{bc}{6a^2}}-{\displaystyle \frac{d}{2a}}\right)}^2+{\left({\displaystyle \frac{c}{3a}}-{\displaystyle \frac{b^2}{9a^2}}\right)}^3.\end{array}$$

(37)

Moreover,

$$\begin{array}{c}\hfill {\left\{\left(-{\displaystyle \frac{b^3}{27a^3}}+{\displaystyle \frac{bc}{6a^2}}-{\displaystyle \frac{d}{2a}}\right)-\sqrt{{\left(-{\displaystyle \frac{b^3}{27a^3}}+{\displaystyle \frac{bc}{6a^2}}-{\displaystyle \frac{d}{2a}}\right)}^2+{\left({\displaystyle \frac{c}{3a}}-{\displaystyle \frac{b^2}{9a^2}}\right)}^3}\right\}}^{{\displaystyle \frac{1}{3}}}\\ \hfill +{\left\{\left(-{\displaystyle \frac{b^3}{27a^3}}+{\displaystyle \frac{bc}{6a^2}}-{\displaystyle \frac{d}{2a}}\right)+\sqrt{{\left(-{\displaystyle \frac{b^3}{27a^3}}+{\displaystyle \frac{bc}{6a^2}}-{\displaystyle \frac{d}{2a}}\right)}^2+{\left({\displaystyle \frac{c}{3a}}-{\displaystyle \frac{b^2}{9a^2}}\right)}^3}\right\}}^{{\displaystyle \frac{1}{3}}}>{\displaystyle \frac{b}{3a}}.\end{array}$$

(38)

Consequently, the analytical HD bright one-soliton solution to Equation (21) is the following:

$$\begin{array}{c}\hfill \varphi (x,t)=A{\mathrm{sech}}^{{\displaystyle \frac{3}{n}}}\left[B(x-vt)\right]e^{i\left(-\mu x+\omega t+{\theta }_0\right)},\end{array}$$

(39)

where the inverse width of the soliton is directly expressed in terms of the amplitude as specified in Equation (35) under the assumption that the constraint conditions described in Equations (36)–(38) are fulfilled.

To observe the dynamic behavior of HD bright one-optical-soliton propagation, as described by Equation (39) and illustrated in Figure 1, various values of the pertinent parameters are chosen.

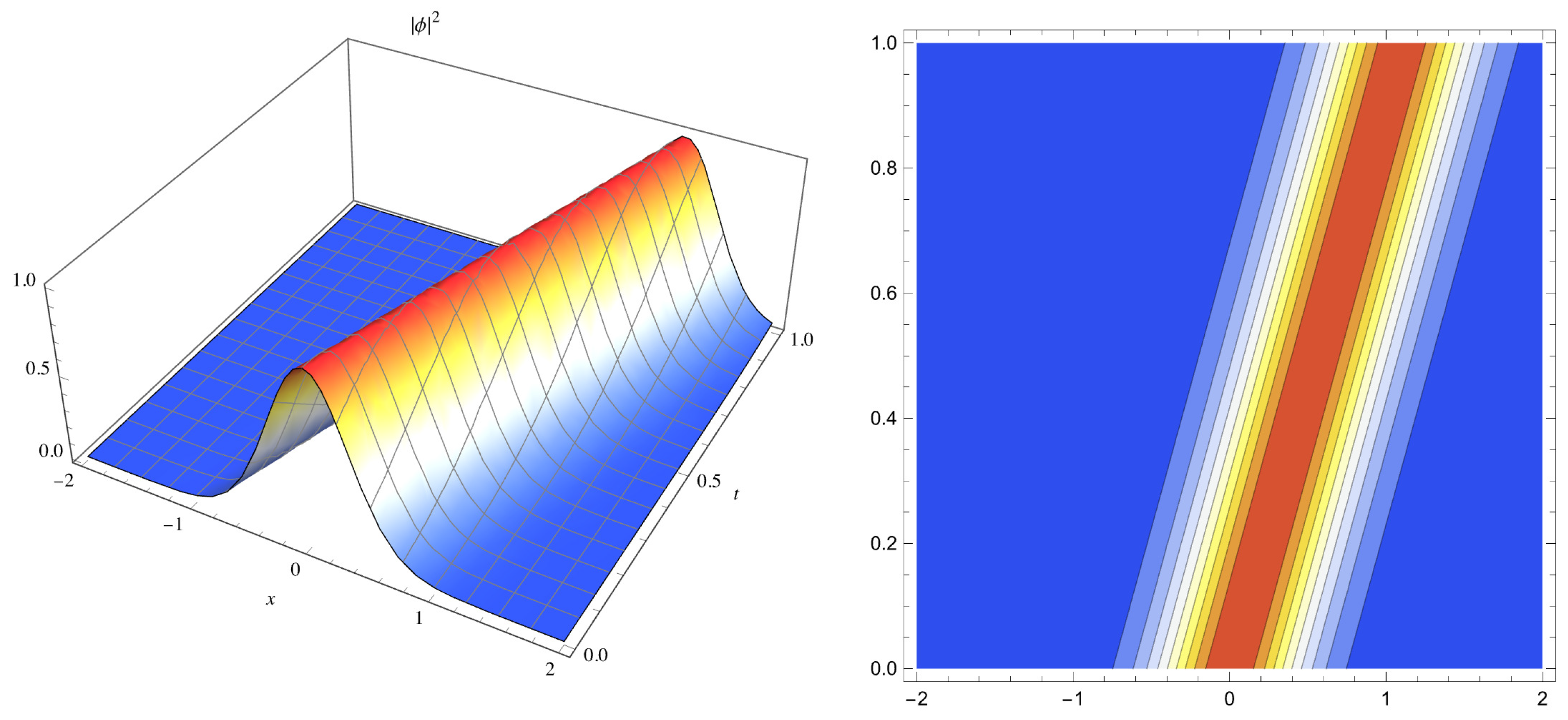
3.2. Considering Dual-Power Law

The dual-power law of nonlinearity is a model used to describe how the refractive index of an optical medium changes when light intensity changes. The dual-power law differs from simpler models such as the Kerr nonlinearity, which implies a linear relationship between the change in refractive index and light intensity. It includes two distinct power elements.

For the parabolic law of nonlinearity, the refractive index structure can be described as

$$\begin{array}{c}\hfill F\left(s\right)=b_1{s}^n+b_2{s}^{n+1},\end{array}$$

(40)

where $b_1$ and $b_2$ are real-valued constants. Then, Equation (10) transforms to

$$\begin{array}{ccc}\hfill & & i{\varphi }_t+i{a}_1{\varphi }_x+a_2{\varphi }_{xx}+i{a}_3{\varphi }_{xxx}+a_4{\varphi }_{xxxx}+i{a}_5{\varphi }_{xxxxx}+a_6{\varphi }_{xxxxxx}\hfill \\ & +& {\displaystyle \frac{\beta }{{\left|\varphi \right|}^2{\varphi }^{*}}}\left[2{\left|\varphi \right|}^2{\left({\left|\varphi \right|}^2\right)}_{xx}-{\left\{{\left({\left|\varphi \right|}^2\right)}_x\right\}}^2\right]+\left(b_1{\left|\varphi \right|}^{2n}+b_2{\left|\varphi \right|}^{2n+2}\right)\varphi \hfill \\ & =& i\left[\lambda {\left({\left|\varphi \right|}^{2m}\varphi \right)}_x+\theta {\left({\left|\varphi \right|}^{2m}\right)}_x\varphi +\sigma {\left|\varphi \right|}^{2m}{\varphi }_x\right],\hfill \end{array}$$

(41)

so that Equation (15) modifies to

$$\begin{array}{c}\hfill P_1{\zeta }^2+P_2{\left({\zeta }^{\prime }\right)}^2-P_3{\left({\zeta }^{\prime \prime }\right)}^2+a_6{\left({\zeta }^{\prime \prime \prime }\right)}^2+{\displaystyle \frac{b_1{\zeta }^{2n+2}}{2n+2}}+{\displaystyle \frac{b_2{\zeta }^{2n+4}}{2n+4}}-{\displaystyle \frac{\mu \left(\lambda +\sigma \right)}{m+1}}{\zeta }^{2m+2}=K.\end{array}$$

(42)

The stationary integral, in this instance, is given as

$$\begin{array}{c}\hfill J={\int }_{-\infty }^{\infty }\left[P_1{\zeta }^2+P_2{\left({\zeta }^{\prime }\right)}^2-P_3{\left({\zeta }^{\prime \prime }\right)}^2+a_6{\left({\zeta }^{\prime \prime \prime }\right)}^2+{\displaystyle \frac{b_1{\zeta }^{2n+2}}{n+1}}+{\displaystyle \frac{b_2{\zeta }^{2n+4}}{n+2}}-{\displaystyle \frac{\mu \left(\lambda +\sigma \right)}{m+1}}{\zeta }^{2m+2}\right]dx.\end{array}$$

(43)

The solution to Equation (42), for $\lambda =\theta =\sigma =0$, is expressed as [1,20]

$$\begin{array}{c}\hfill \zeta (x-vt)=A{\mathrm{sech}}^{{\displaystyle \frac{3}{2n}}}\left[B(x-vt)\right].\end{array}$$

(44)

Substituting this form of the one-soliton solution into Equation (43), the stationary integral reduces to

$$\begin{array}{c}\hfill J=\left[{\displaystyle \frac{P_1{A}^2}{B}}+{\displaystyle \frac{9P_2{A}^{2}B}{n(n+3)}}-{\displaystyle \frac{9(8n+9)P_3{A}^2{B}^3}{16n^2(n+1)(n+3)}}+{\displaystyle \frac{9\left(128n^3+768n^2+1080n+405\right)a_6{A}^2{B}^5}{64n^3(n+1)(n+3)(5n+3)}}\right]\\ \hfill \times {\displaystyle \frac{\Gamma \left(\frac{3}{n}\right)\Gamma \left(\frac{1}{2}\right)}{\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)}}+{\displaystyle \frac{2n(n+3)b_1{A}^{2n+2}}{3(n+1)(2n+3)B}}{\displaystyle \frac{\Gamma \left(\frac{3}{2n}+\frac{1}{2}\right)\Gamma \left(\frac{1}{2}\right)}{\Gamma \left(\frac{3}{2n}\right)}}+{\displaystyle \frac{n(n+6)b_2{A}^{2n+4}}{6(n+2)(n+3)B}}{\displaystyle \frac{\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)\Gamma \left(\frac{1}{2}\right)}{\Gamma \left(\frac{3}{n}\right)}}\\ \hfill -{\displaystyle \frac{\mu (\lambda +\sigma )A^{2m+2}}{(m+1)B}}{\displaystyle \frac{\Gamma \left(\frac{3m}{2n}+\frac{3}{2n}\right)\Gamma \left(\frac{1}{2}\right)}{\Gamma \left(\frac{3m}{2n}+\frac{3}{2n}+\frac{1}{2}\right)}}.\end{array}$$

(45)

The interconnected Equations (18) and (19) for the parabolic law are presented as follows:

$$\begin{array}{ccc}\hfill & & P_1+{\displaystyle \frac{9P_2{B}^2}{n(n+3)}}-{\displaystyle \frac{9(8n+9)P_3{B}^4}{16n^2(n+1)(n+3)}}+{\displaystyle \frac{9\left(128n^3+768n^2+1080n+405\right)a_{6}A{B}^6}{64n^3(n+1)(n+3)(5n+3)}}\hfill \\ & +& {\displaystyle \frac{2n(n+3)b_1{A}^{2n}}{3(2n+3)}}{\displaystyle \frac{{\left\{\Gamma \left(\frac{3}{2n}+\frac{1}{2}\right)\right\}}^2}{{\left\{\Gamma \left(\frac{3}{2n}\right)\right\}}^2}}+{\displaystyle \frac{n(n+6)b_2{A}^{2n+2}}{6(n+3)}}{\displaystyle \frac{\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)\Gamma \left(\frac{3}{2n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3}{n}\right)\Gamma \left(\frac{3}{2n}\right)}}\hfill \\ & -& \mu (\lambda +\sigma )A^{2m}{\displaystyle \frac{\Gamma \left(\frac{3m}{2n}+\frac{3}{2n}\right)\Gamma \left(\frac{3}{2n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3m}{2n}+\frac{3}{2n}+\frac{1}{2}\right)\Gamma \left(\frac{3}{2n}\right)}}=0,\hfill \end{array}$$

(46)

and

$$\begin{array}{ccc}\hfill & -& P_1+{\displaystyle \frac{9P_2{B}^2}{n(n+3)}}-{\displaystyle \frac{27(8n+9)P_3{B}^4}{16n^2(n+1)(n+3)}}+{\displaystyle \frac{45\left(128n^3+768n^2+1080n+405\right)a_6{B}^6}{64n^3(n+1)(n+3)(5n+3)}}\hfill \\ & -& {\displaystyle \frac{2n(n+3)b_1{A}^{2n}}{3(n+1)(2n+3)}}{\displaystyle \frac{{\left\{\Gamma \left(\frac{3}{2n}+\frac{1}{2}\right)\right\}}^2}{{\left\{\Gamma \left(\frac{3}{2n}\right)\right\}}^2}}-{\displaystyle \frac{n(n+6)b_2{A}^{2n+2}}{6(n+2)(n+3)}}{\displaystyle \frac{\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)\Gamma \left(\frac{3}{2n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3}{n}\right)\Gamma \left(\frac{3}{2n}\right)}}\hfill \\ & -& {\displaystyle \frac{\mu (\lambda +\sigma )A^{2m}}{m+1}}{\displaystyle \frac{\Gamma \left(\frac{3m}{2n}+\frac{3}{2n}\right)\Gamma \left(\frac{3}{2n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3m}{2n}+\frac{3}{2n}+\frac{1}{2}\right)\Gamma \left(\frac{3}{2n}\right)}}=0,\hfill \end{array}$$

(47)

Adding Equations (46) and (47) yields

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{18P_2{B}^2}{n(n+3)}}-{\displaystyle \frac{9(8n+9)P_3{B}^4}{4n^2(n+1)(n+3)}}+{\displaystyle \frac{27\left(128n^3+768n^2+1080n+405\right)a_6{B}^6}{32n^3(n+1)(n+3)(5n+3)}}\hfill \\ & +& {\displaystyle \frac{2n^2(n+3)b_1{A}^{2n}}{3(n+1)(2n+3)}}{\displaystyle \frac{{\left\{\Gamma \left(\frac{3}{2n}+\frac{1}{2}\right)\right\}}^2}{{\left\{\Gamma \left(\frac{3}{2n}\right)\right\}}^2}}+{\displaystyle \frac{n(n+1)(n+6)b_2{A}^{2n+2}}{6(n+2)(n+3)}}{\displaystyle \frac{\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)\Gamma \left(\frac{3}{2n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3}{n}\right)\Gamma \left(\frac{3}{2n}\right)}}\hfill \\ & -& {\displaystyle \frac{m\mu (\lambda +\sigma )A^{2m}}{m+1}}{\displaystyle \frac{\Gamma \left(\frac{3m}{2n}+\frac{3}{2n}\right)\Gamma \left(\frac{3}{2n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3m}{2n}+\frac{3}{2n}+\frac{1}{2}\right)\Gamma \left(\frac{3}{2n}\right)}}=0,\hfill \end{array}$$

(48)

Equation (48) is reducible to (29) with

$$\begin{array}{c}\hfill a={\displaystyle \frac{27\left(128n^3+768n^2+1080n+405\right)a_6}{32n^3(n+1)(n+3)(5n+3)}}\end{array}$$

(49)

$$\begin{array}{c}\hfill b=-{\displaystyle \frac{9(8n+9)P_3}{4n^2(n+1)(n+3)}}\end{array}$$

(50)

$$\begin{array}{c}\hfill c={\displaystyle \frac{18P_2}{n(n+3)}}\end{array}$$

(51)

and the independent term is

$$\begin{array}{ccc}\hfill d& =& {\displaystyle \frac{2n^2(n+3)b_1{A}^{2n}}{3(n+1)(2n+3)}}{\displaystyle \frac{{\left\{\Gamma \left(\frac{3}{2n}+\frac{1}{2}\right)\right\}}^2}{{\left\{\Gamma \left(\frac{3}{2n}\right)\right\}}^2}}+{\displaystyle \frac{n(n+1)(n+6)b_2{A}^{2n+2}}{6(n+2)(n+3)}}{\displaystyle \frac{\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)\Gamma \left(\frac{3}{2n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3}{n}\right)\Gamma \left(\frac{3}{2n}\right)}}\hfill \\ & -& {\displaystyle \frac{m\mu (\lambda +\sigma )A^{2m}}{m+1}}{\displaystyle \frac{\Gamma \left(\frac{3m}{2n}+\frac{3}{2n}\right)\Gamma \left(\frac{3}{2n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3m}{2n}+\frac{3}{2n}+\frac{1}{2}\right)\Gamma \left(\frac{3}{2n}\right)}}\hfill \end{array}$$

(52)

Finally, the analytical HD bright one-soliton solution to Equation (41) is given as

$$\begin{array}{c}\hfill \varphi (x,t)=A{\mathrm{sech}}^{{\displaystyle \frac{3}{2n}}}\left[B(x-vt)\right]e^{i\left(-\mu x+\omega t+{\theta }_0\right)},\end{array}$$

(53)

where the inverse width of the soliton is directly expressed in terms of the amplitude as specified in Equation (35) under the assumption that the constraint conditions described in Equations (36)–(38) are fulfilled.

To observe the dynamic behavior of HD bright one-optical-soliton propagation, as described by Equation (53) and illustrated in Figure 2, various values of the pertinent parameters are chosen.

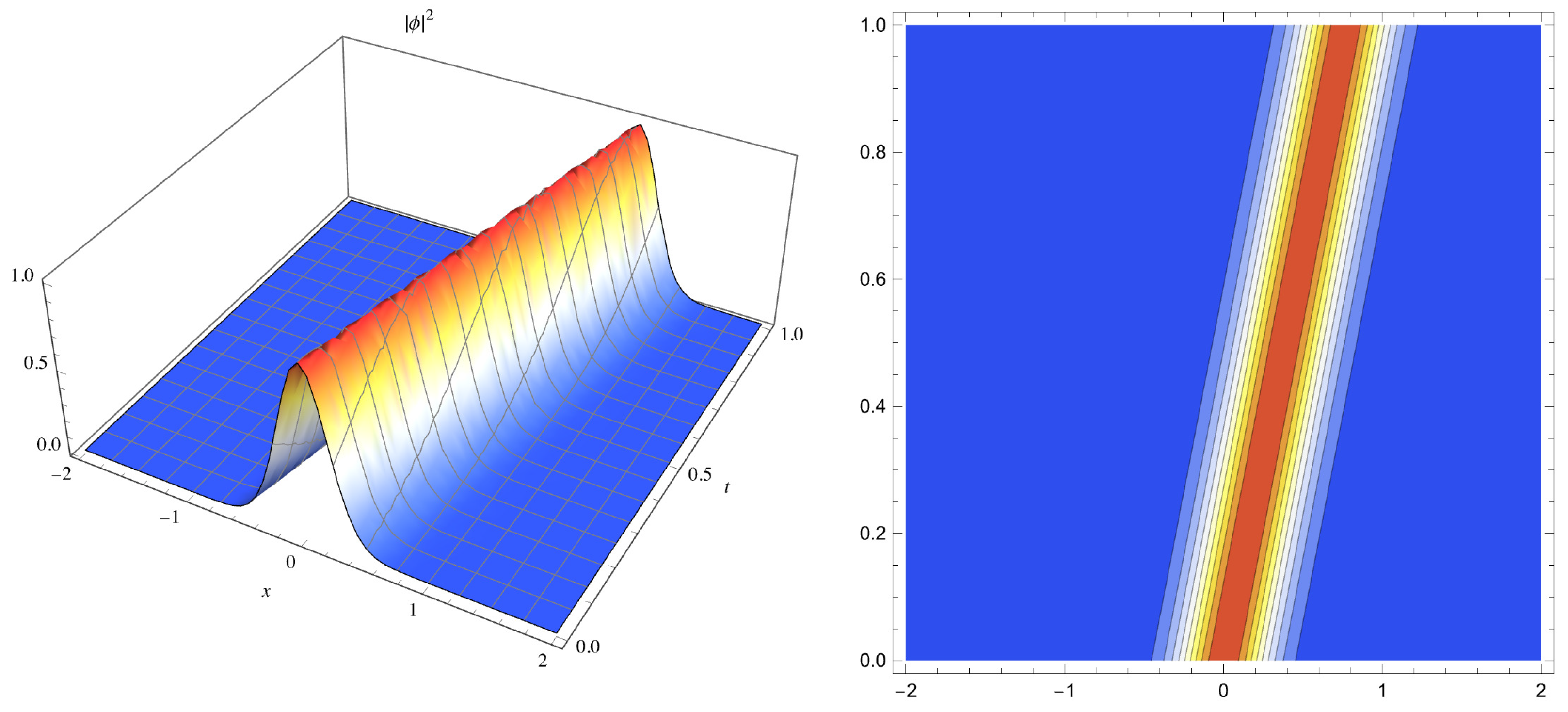
3.3. Considering Triple-Power Law

In nonlinear optics, the triple-power law is a non-Kerr law nonlinearity that is characterized by a nonlinear term in the governing equation that adopts a more intricate, multi-term power law form. Basically, the exact mathematical expression can change based on the specific model and situation; it typically includes the intensity (or amplitude squared) of the optical field raised to several different powers.

For the triple-power law of nonlinearity, the refractive index structure can be described as

$$\begin{array}{c}\hfill F\left(s\right)=b_1{s}^n+b_2{s}^{n+1}+b_3{s}^{n+2},\end{array}$$

(54)

where $b_j$, for $j=1,2$ and 3, are real-valued constants. Therefore, Equation (10) modifies to

$$\begin{array}{ccc}\hfill & & i{\varphi }_t+i{a}_1{\varphi }_x+a_2{\varphi }_{xx}+i{a}_3{\varphi }_{xxx}+a_4{\varphi }_{xxxx}+i{a}_5{\varphi }_{xxxxx}+a_6{\varphi }_{xxxxxx}\hfill \\ & +& {\displaystyle \frac{\beta }{{\left|\varphi \right|}^2{\varphi }^{*}}}\left[2{\left|\varphi \right|}^2{\left({\left|\varphi \right|}^2\right)}_{xx}-{\left\{{\left({\left|\varphi \right|}^2\right)}_x\right\}}^2\right]+\left(b_1{\left|\varphi \right|}^{2n}+b_2{\left|\varphi \right|}^{2n+2}+b_3{\left|\varphi \right|}^{2n+4}\right)\varphi \hfill \\ & =& i\left[\lambda {\left({\left|\varphi \right|}^{2m}\varphi \right)}_x+\theta {\left({\left|\varphi \right|}^{2m}\right)}_x\varphi +\sigma {\left|\varphi \right|}^{2m}{\varphi }_x\right],\hfill \end{array}$$

(55)

so that (15) now is

$$\begin{array}{c}\hfill P_1{\zeta }^2+P_2{\left({\zeta }^{\prime }\right)}^2-P_3{\left({\zeta }^{\prime \prime }\right)}^2+a_6{\left({\zeta }^{\prime \prime \prime }\right)}^2+{\displaystyle \frac{b_1{\zeta }^{2n+2}}{2n+2}}+{\displaystyle \frac{b_2{\zeta }^{2n+4}}{2n+4}}+{\displaystyle \frac{b_3{\zeta }^{2n+6}}{2n+6}}-{\displaystyle \frac{\mu \left(\lambda +\sigma \right)}{m+1}}{\zeta }^{2m+2}=K.\end{array}$$

(56)

The stationary integral, in this instance, is given as

$$\begin{array}{c}\hfill J={\int }_{-\infty }^{\infty }\left[P_1{\zeta }^2+P_2{\left({\zeta }^{\prime }\right)}^2-P_3{\left({\zeta }^{\prime \prime }\right)}^2+a_6{\left({\zeta }^{\prime \prime \prime }\right)}^2+{\displaystyle \frac{b_1{\zeta }^{2n+2}}{2n+2}}+{\displaystyle \frac{b_2{\zeta }^{2n+4}}{2n+4}}+{\displaystyle \frac{b_3{\zeta }^{2n+6}}{2n+6}}-{\displaystyle \frac{\mu \left(\lambda +\sigma \right)}{m+1}}{\zeta }^{2m+2}\right]dx.\end{array}$$

(57)

The solution to Equation (57), for $\lambda =\theta =\sigma =0$, is expressed as [1,20]

$$\begin{array}{c}\hfill \zeta (x-vt)=A{\mathrm{sech}}^{{\displaystyle \frac{1}{n}}}\left[B(x-vt)\right].\end{array}$$

(58)

Substituting this form of the one-soliton solution into (57), the stationary integral comes out as

$$\begin{array}{ccc}\hfill J& =& \left[{\displaystyle \frac{P_1{A}^2}{B}}+{\displaystyle \frac{P_2{A}^{2}B}{n(n+2)}}-{\displaystyle \frac{\left(2n^3-3n^2-6n-2\right)P_3{A}^2{B}^3}{n^4(n+2)(3n+2)}}+{\displaystyle \frac{\left(16n^3+64n^2+60n+15\right)a_6{A}^2{B}^5}{n^3(n+2)(3n+2)(5n+2)}}\right.\hfill \\ & +& \left.{\displaystyle \frac{2b_1{A}^{2n+2}}{(n+1)(n+2)B}}\right]{\displaystyle \frac{\Gamma \left(\frac{1}{n}\right)\Gamma \left(\frac{1}{2}\right)}{\Gamma \left(\frac{1}{n}+\frac{1}{2}\right)}}+{\displaystyle \frac{2b_2{A}^{2n+4}}{{(n+2)}^{2}B}}{\displaystyle \frac{\Gamma \left(\frac{2}{n}\right)\Gamma \left(\frac{1}{2}\right)}{\Gamma \left(\frac{2}{n}+\frac{1}{2}\right)}}+{\displaystyle \frac{2b_3{A}^{2n+6}}{(n+2)(n+3)B}}{\displaystyle \frac{\Gamma \left(\frac{3}{n}\right)\Gamma \left(\frac{1}{2}\right)}{\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)}}\hfill \\ & -& {\displaystyle \frac{\mu (\lambda +\sigma )A^{2m+2}}{(m+1)B}}{\displaystyle \frac{\Gamma \left(\frac{m}{n}+\frac{1}{n}\right)\Gamma \left(\frac{1}{2}\right)}{\Gamma \left(\frac{m}{n}+\frac{1}{n}+\frac{1}{2}\right)}}.\hfill \end{array}$$

(59)

The interconnected Equations (18) and (19) for the triple-power law are presented as follows:

$$\begin{array}{c}\hfill P_1+{\displaystyle \frac{P_2{B}^2}{n(n+2)}}-{\displaystyle \frac{\left(2n^3-3n^2-6n-2\right)P_3{B}^4}{n^4(n+2)(3n+2)}}+{\displaystyle \frac{\left(16n^3+64n^2+60n+15\right)a_6{B}^6}{n^3(n+2)(3n+2)(5n+2)}}\\ \hfill +{\displaystyle \frac{2b_1{A}^{2n}}{n+2}}+{\displaystyle \frac{2b_2{A}^{2n+2}}{n+2}}{\displaystyle \frac{\Gamma \left(\frac{2}{n}\right)\Gamma \left(\frac{1}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{2}{n}+\frac{1}{2}\right)\Gamma \left(\frac{1}{n}\right)}}+{\displaystyle \frac{2b_3{A}^{2n+4}}{n+2}}{\displaystyle \frac{\Gamma \left(\frac{3}{n}\right)\Gamma \left(\frac{1}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)\Gamma \left(\frac{1}{n}\right)}}\\ \hfill -\mu (\lambda +\sigma )A^{2m}{\displaystyle \frac{\Gamma \left(\frac{m}{n}+\frac{1}{n}\right)\Gamma \left(\frac{1}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{m}{n}+\frac{1}{n}+\frac{1}{2}\right)\Gamma \left(\frac{1}{n}\right)}}=0,\end{array}$$

(60)

and

$$\begin{array}{c}\hfill -P_1+{\displaystyle \frac{P_2{B}^2}{n(n+2)}}-{\displaystyle \frac{3\left(2n^3-3n^2-6n-2\right)P_3{B}^4}{n^4(n+2)(3n+2)}}+{\displaystyle \frac{5\left(16n^3+64n^2+60n+15\right)a_6{B}^6}{n^3(n+2)(3n+2)(5n+2)}}\\ \hfill -{\displaystyle \frac{2b_1{A}^{2n}}{(n+1)(n+2)}}-{\displaystyle \frac{2b_2{A}^{2n+2}}{{(n+2)}^2}}{\displaystyle \frac{\Gamma \left(\frac{2}{n}\right)\Gamma \left(\frac{1}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{2}{n}+\frac{1}{2}\right)\Gamma \left(\frac{1}{n}\right)}}-{\displaystyle \frac{2b_3{A}^{2n+4}}{(n+2)(n+3)}}{\displaystyle \frac{\Gamma \left(\frac{3}{n}\right)\Gamma \left(\frac{1}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)\Gamma \left(\frac{1}{n}\right)}}\\ \hfill +{\displaystyle \frac{\mu (\lambda +\sigma )A^{2m}}{m+1}}{\displaystyle \frac{\Gamma \left(\frac{m}{n}+\frac{1}{n}\right)\Gamma \left(\frac{1}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{m}{n}+\frac{1}{n}+\frac{1}{2}\right)\Gamma \left(\frac{1}{n}\right)}}=0.\end{array}$$

(61)

Adding Equations (60) and (61) implies that

$$\begin{array}{c}\hfill {\displaystyle \frac{2P_2{B}^2}{n(n+2)}}-{\displaystyle \frac{4\left(2n^3-3n^2-6n-2\right)P_3{B}^4}{n^4(n+2)(3n+2)}}+{\displaystyle \frac{6\left(16n^3+64n^2+60n+15\right)a_6{B}^6}{n^3(n+2)(3n+2)(5n+2)}}\\ \hfill +{\displaystyle \frac{2n{b}_1{A}^{2n}}{(n+1)(n+2)}}+{\displaystyle \frac{2(n+1)b_2{A}^{2n+2}}{{(n+2)}^2}}{\displaystyle \frac{\Gamma \left(\frac{2}{n}\right)\Gamma \left(\frac{1}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{2}{n}+\frac{1}{2}\right)\Gamma \left(\frac{1}{n}\right)}}-{\displaystyle \frac{2b_3{A}^{2n+4}}{n+3}}{\displaystyle \frac{\Gamma \left(\frac{3}{n}\right)\Gamma \left(\frac{1}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)\Gamma \left(\frac{1}{n}\right)}}\\ \hfill -{\displaystyle \frac{m\mu (\lambda +\sigma )A^{2m}}{m+1}}{\displaystyle \frac{\Gamma \left(\frac{m}{n}+\frac{1}{n}\right)\Gamma \left(\frac{1}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{m}{n}+\frac{1}{n}+\frac{1}{2}\right)\Gamma \left(\frac{1}{n}\right)}}=0.\end{array}$$

(62)

Equation (62) is reducible to (29) with

$$\begin{array}{c}\hfill a={\displaystyle \frac{6\left(16n^3+64n^2+60n+15\right)a_6}{n^3(n+2)(3n+2)(5n+2)}}\end{array}$$

(63)

$$\begin{array}{c}\hfill b=-{\displaystyle \frac{4\left(2n^3-3n^2-6n-2\right)P_3}{n^4(n+2)(3n+2)}}\end{array}$$

(64)

$$\begin{array}{c}\hfill c={\displaystyle \frac{2P_2}{n(n+2)}}\end{array}$$

(65)

and the independent term is

$$\begin{array}{ccc}\hfill d& =& {\displaystyle \frac{2n{b}_1{A}^{2n}}{(n+1)(n+2)}}+{\displaystyle \frac{2(n+1)b_2{A}^{2n+2}}{{(n+2)}^2}}{\displaystyle \frac{\Gamma \left(\frac{2}{n}\right)\Gamma \left(\frac{1}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{2}{n}+\frac{1}{2}\right)\Gamma \left(\frac{1}{n}\right)}}-{\displaystyle \frac{2b_3{A}^{2n+4}}{n+3}}{\displaystyle \frac{\Gamma \left(\frac{3}{n}\right)\Gamma \left(\frac{1}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{3}{n}+\frac{1}{2}\right)\Gamma \left(\frac{1}{n}\right)}}\hfill \\ & -& {\displaystyle \frac{m\mu (\lambda +\sigma )A^{2m}}{m+1}}{\displaystyle \frac{\Gamma \left(\frac{m}{n}+\frac{1}{n}\right)\Gamma \left(\frac{1}{n}+\frac{1}{2}\right)}{\Gamma \left(\frac{m}{n}+\frac{1}{n}+\frac{1}{2}\right)\Gamma \left(\frac{1}{n}\right)}}\hfill \end{array}$$

(66)

Hence, the analytical HD bright one-soliton solution to Equation (55) is given as

$$\begin{array}{c}\hfill \varphi (x,t)=A{\mathrm{sech}}^{{\displaystyle \frac{1}{n}}}\left[B(x-vt)\right]e^{i\left(-\mu x+\omega t+{\theta }_0\right)},\end{array}$$

(67)

where the inverse width of the soliton is directly expressed in terms of the amplitude as specified in Equation (35) under the assumption that the constraint conditions described in Equations (36)–(38) are fulfilled.

To observe the dynamic behavior of HD bright one-optical-soliton propagation, as described by Equation (67) and illustrated in Figure 3, various values of the pertinent parameters are chosen.

4. Conclusions and Future Perspectives

The current paper, using the SVP, effectively retrieved the perturbed, highly dispersive, bright one-soliton solution to the CGLE, taking into account Hamiltonian perturbation terms. The intensity of the perturbation terms was arbitrary. Three forms of SPM structures that originated from the power law platform were considered. These were the power law, dual-power law, and triple-power law. Each of these structures exhibited distinct behaviors under varying conditions, highlighting the complicated relationship between nonlinearity and dispersive effects. The implications of these findings could pave the way for further advancements in the understanding of soliton dynamics in nonlinear systems. The analytical form of the wave was retrieved by solving a cubic polynomial equation, which was facilitated by Cardano’s solution retrieval algorithm. The analytical findings were visually enhanced by the numerical simulations that were outlined. Also, the parameter constraints that automatically emerged from the analysis in each phase of the procedure were enumerated and listed. The existence of such solitons is guaranteed by these constraints. It is important to recognize that the perturbed CGLE cannot be used to retrieve dark and singular optical solitons using the SVP approach. The stationary integral for the model with such solitons would be divergent. Consequently, the SVP approach also has its own limitations. These limitations necessitate the exploration of alternative methods that could potentially yield more accurate representations of dark and singular solitons. Future research may focus on developing new theoretical frameworks or computational techniques to overcome the challenges presented by the perturbed CGLE.

The results of this paper are thus interesting and promising. The SVP algorithm can be applied to address this model, with additional forms of SPM structures, or additional models in a wide range of optoelectronic devices such as fibers with Bragg gratings to retrieve gap solitons, magneto-optic waveguides, optical couplers, optical metamaterials, and several others. Such studies are all under way and their results will be disseminated upon availability.