Design Procedure of a Frequency Reconfigurable Metasurface Antenna at mmWave Band
Abstract
:1. Introduction
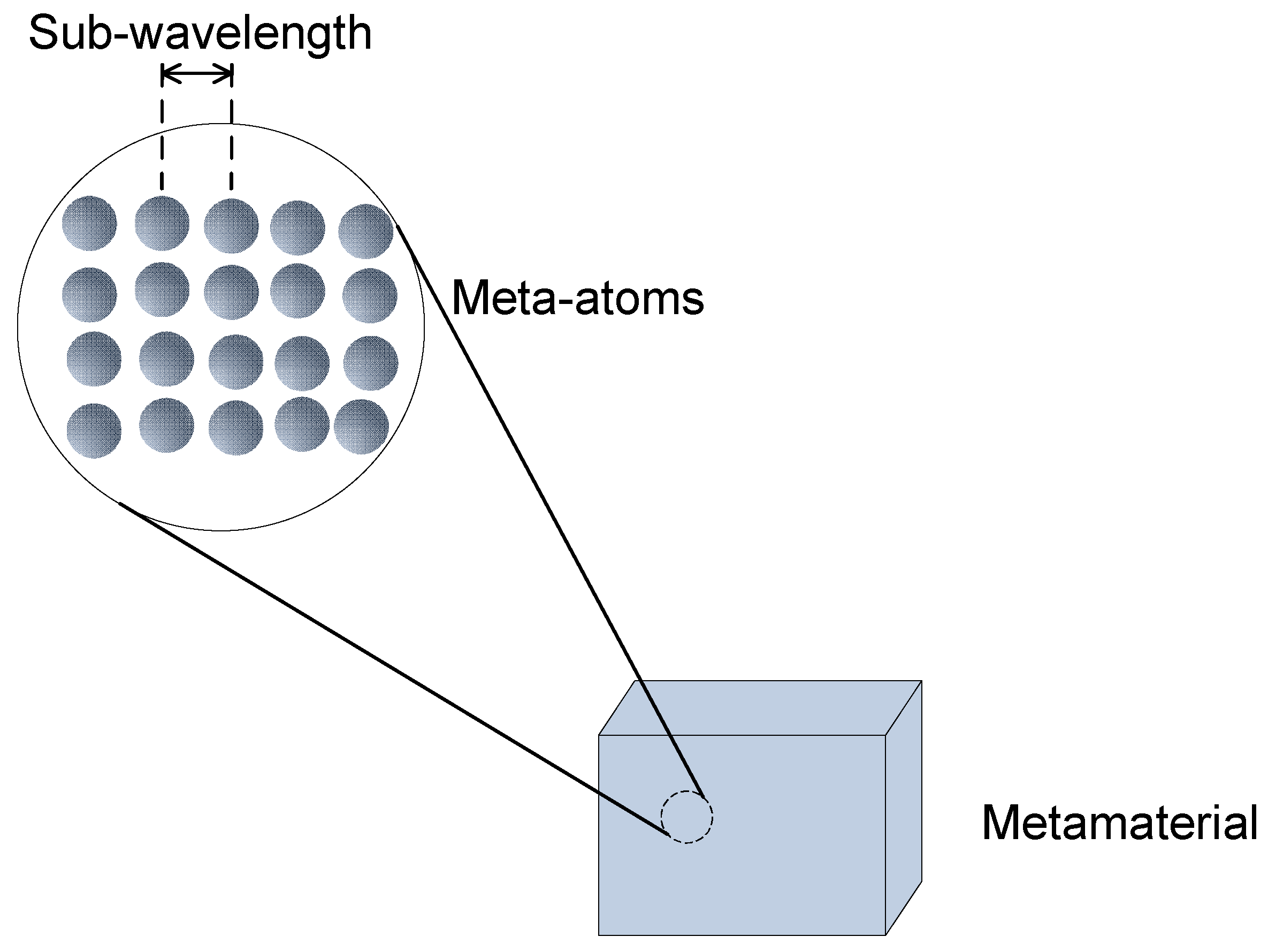
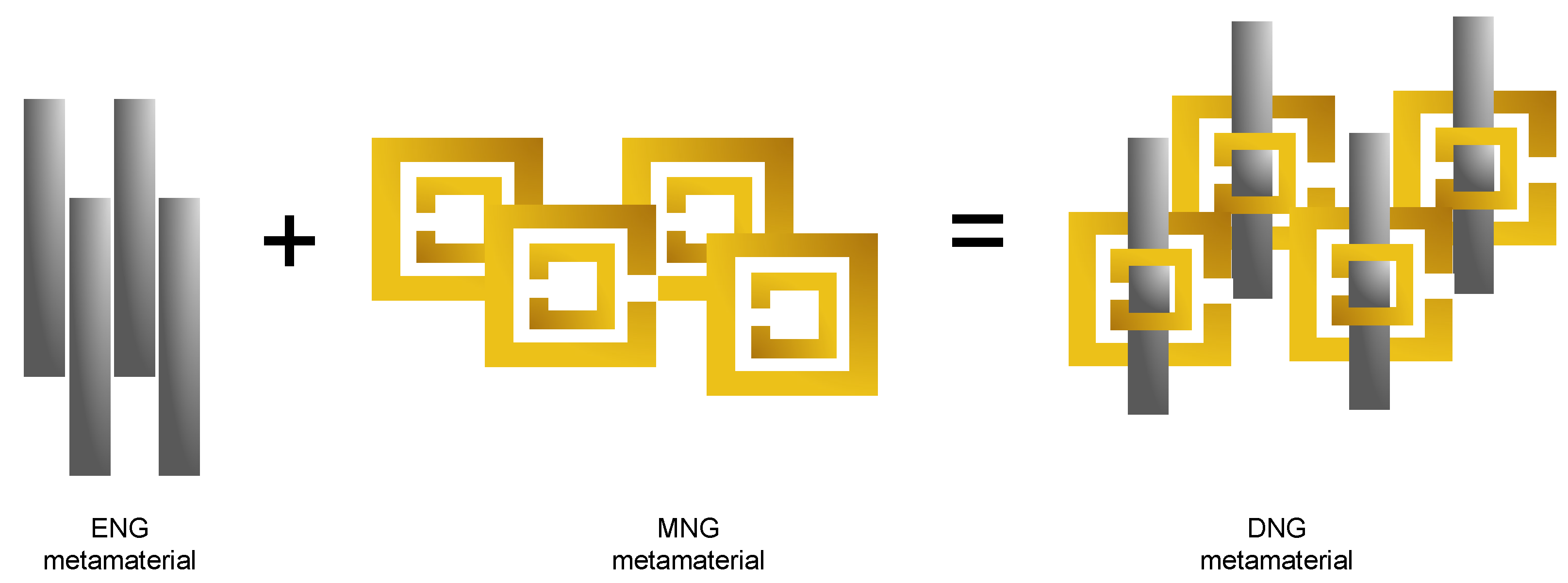
Metamaterials and Metasurface Structures
2. Related Works
Contribution
- Firstly, a demonstration of a step-by-step procedure on how to achieve SRR geometrical parameters at dual frequency of operation is provided;
- Secondly, the proposed unit cell was used to design a 16 element frequency RMS;
- Finally, the characteristics of the proposed frequency RMS were analyzed and compared with previous works.
3. Design Procedure
4. Simulation Processes
5. Results and Analysis
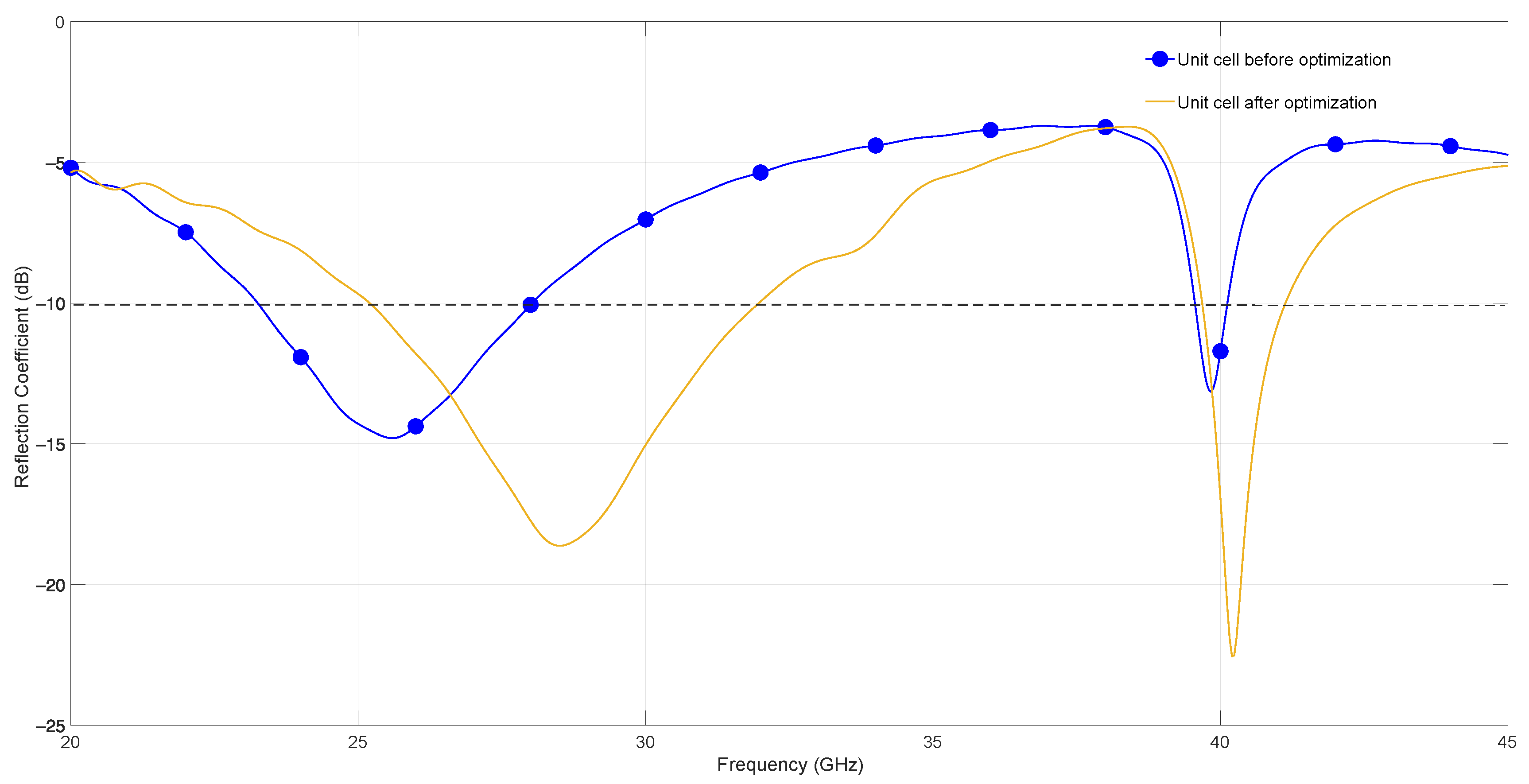
5.1. Reflection Coefficient
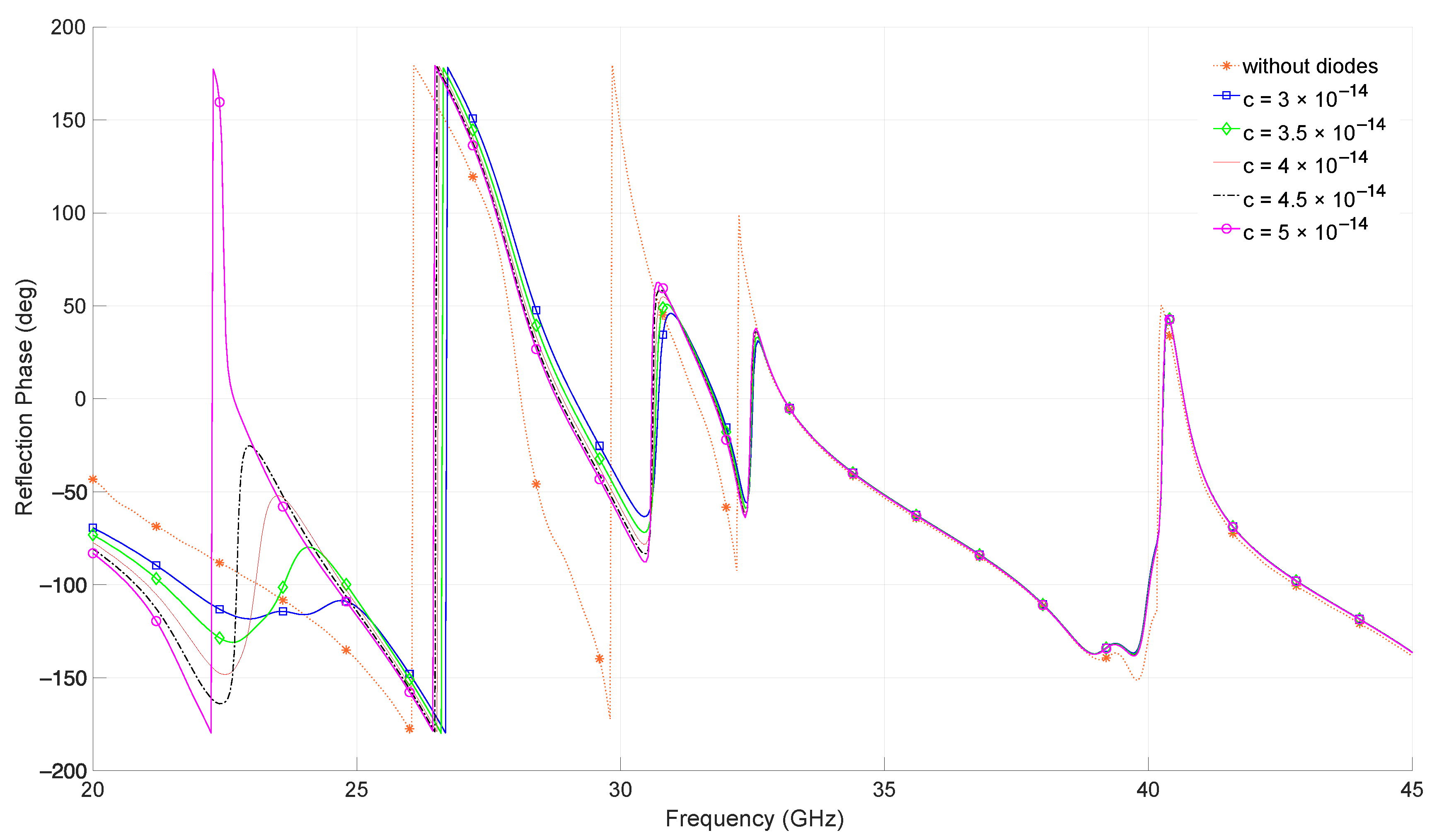
5.2. Reflection Phase
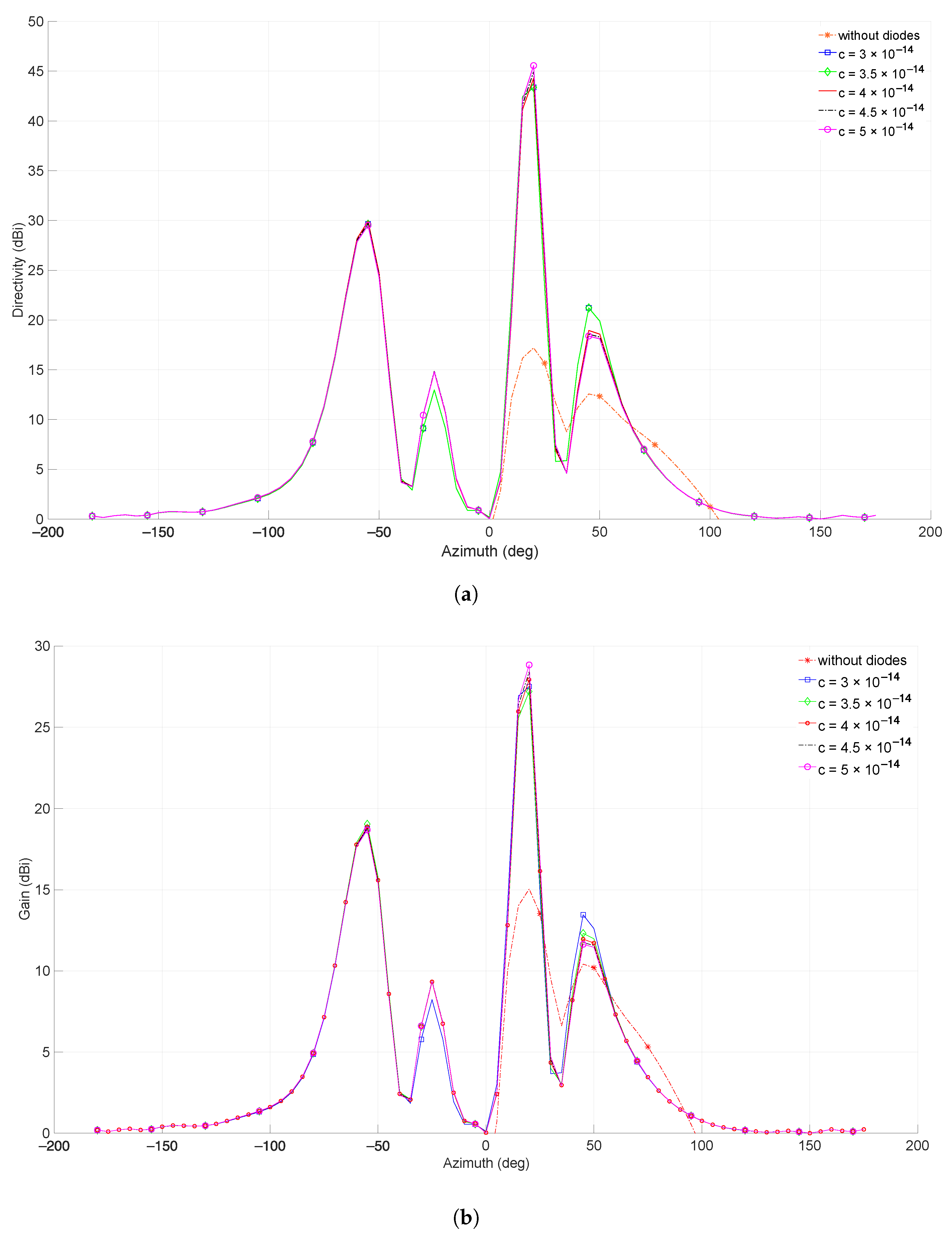
5.3. Gain and Directivity
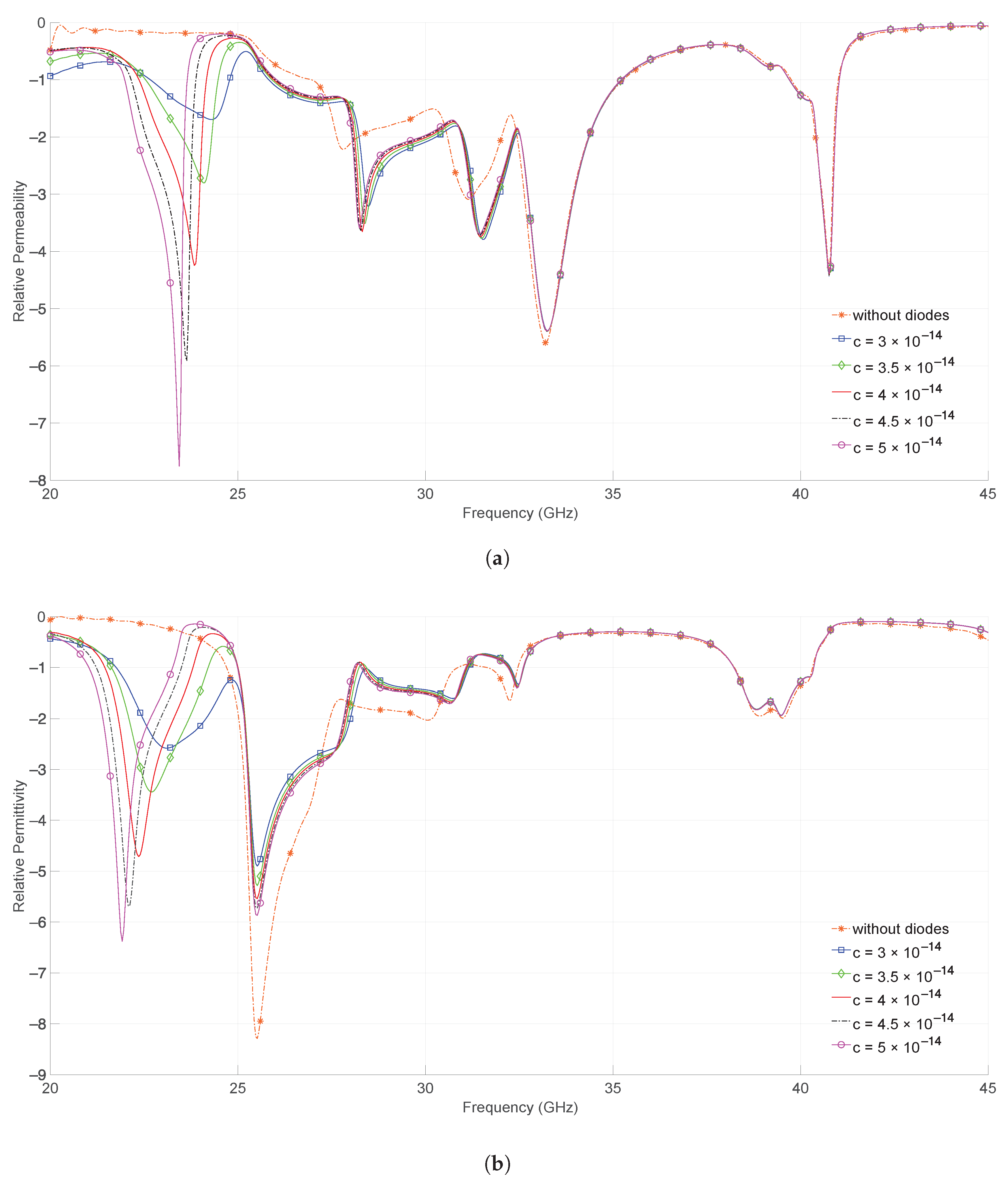
5.4. Effective Permittivity, and Permeability
5.5. Comparison with Previous Work
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Masoudi, M.; Khafagy, M.G.; Conte, A.; El-Amine, A.; Françoise, B.; Nadjahi, C.; Salem, F.E.; Labidi, W.; Süral, A.; Gati, A.; et al. Green Mobile Networks for 5G and Beyond. IEEE Access 2019, 7, 107270–107299. [Google Scholar] [CrossRef]
- Meng, X.; Nekovee, M.; Wu, D. Reconfigurable liquid crystal reflectarray metasurface for THz communications. In Proceedings of the Antennas and Propagation Conference 2019 (APC-2019), Birmingham, UK, 11–12 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, P.; Xiao, Y.; Xiao, M.; Li, S. 6G Wireless Communications: Vision and Potential Techniques. IEEE Netw. 2019, 33, 70–75. [Google Scholar] [CrossRef]
- Awan, W.A.; Alibakhshikenari, M.; Limiti, E. Design and Analysis of a Simple Miniaturized Fractal Antenna for 5G Ka-Band Applications. In Proceedings of the 2021 IEEE Asia-Pacific Microwave Conference (APMC), Brisbane, Australia, 28 November–1 December 2021; pp. 22–24. [Google Scholar] [CrossRef]
- Naqvi, S.A.; Awan, W.A.; Alibakhshikenari, M.; Falcone, F.; Limiti, E. Design and Characterization of a Simple and Wideband Antenna for 5G mm-wave Applications. In Proceedings of the 2020 IEEE MTT-S Latin America Microwave Conference (LAMC 2020), Cali, Colombia, 26–28 May 2021; pp. 1–3. [Google Scholar] [CrossRef]
- Rusek, F.; Persson, D.; Lau, B.K.; Larsson, E.G.; Marzetta, T.L.; Edfors, O.; Tufvesson, F. Scaling up MIMO: Opportunities and challenges with very large arrays. IEEE Signal Process. Mag. 2012, 30, 40–60. [Google Scholar] [CrossRef] [Green Version]
- Chataut, R.; Akl, R. Massive MIMO Systems for 5G and beyond Networks—Overview, Recent Trends, Challenges, and Future Research Direction. Sensors 2020, 20, 2753. [Google Scholar] [CrossRef]
- Shlezinger, N.; Dicker, O.; Eldar, Y.C.; Yoo, I.; Imani, M.F.; Smith, D.R. Dynamic Metasurface Antennas for Uplink Massive MIMO Systems. IEEE Trans. Commun. 2019, 67, 6829–6843. [Google Scholar] [CrossRef] [Green Version]
- Alkhateeb, A.; Mo, J.; González-Prelcic, N.; Heath, R. MIMO precoding and combining solutions for millimeter-wave systems. IEEE Commun. Soc. Mag. 2014, 52, 122–131. [Google Scholar] [CrossRef]
- Mo, J.; Alkhateeb, A.; Abu-Surra, S.; Heath, R.W. Hybrid Architectures with Few-Bit ADC Receivers: Achievable Rates and Energy-Rate Tradeoffs. IEEE Trans. Wirel. Commun. 2017, 16, 2274–2287. [Google Scholar] [CrossRef]
- Sleasman, T.; Boyarsky, M.; Pulido-Mancera, L.; Fromenteze, T.; Imani, M.F.; Reynolds, M.S.; Smith, D.R. Experimental Synthetic Aperture Radar with Dynamic Metasurfaces. IEEE Trans. Antennas Propag. 2017, 65, 6864–6877. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Chen, S.; Che, W.; Xue, Q.; Meng, Q. Compact High-Gain Metasurface Antenna Arrays Based on Higher-Mode SIW Cavities. IEEE Trans. Antennas Propag. 2018, 66, 4918–4923. [Google Scholar] [CrossRef]
- Smith, D.R.; Yurduseven, O.; Mancera, L.P.; Bowen, P.; Kundtz, N.B. Analysis of a Waveguide-Fed Metasurface Antenna. Phys. Rev. Appl. 2017, 8, 054048. [Google Scholar] [CrossRef] [Green Version]
- Yoo, I.; Imani, M.F.; Sleasman, T.; Pfister, H.D.; Smith, D.R. Enhancing Capacity of Spatial Multiplexing Systems Using Reconfigurable Cavity-Backed Metasurface Antennas in Clustered MIMO Channels. IEEE Trans. Commun. 2019, 67, 1070–1084. [Google Scholar] [CrossRef]
- Rotshild, D.; Rahamim, E.; Abramovich, A. Innovative Reconfigurable Metasurface 2-D Beam-Steerable Reflector for 5G Wireless Communication. Electronics 2020, 9, 1191. [Google Scholar] [CrossRef]
- Achouri, K.; Salem, M.A.; Caloz, C. General Metasurface Synthesis Based on Susceptibility Tensors. IEEE Trans. Antennas Propag. 2015, 63, 2977–2991. [Google Scholar] [CrossRef] [Green Version]
- Vahabzadeh, Y.; Chamanara, N.; Achouri, K.; Caloz, C. Computational analysis of metasurfaces. IEEE J. Multiscale Multiphys. Comput. Tech. 2018, 3, 37–49. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.T.; Taylor, A.J.; Yu, N. A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 2016, 79, 76401. [Google Scholar] [CrossRef] [Green Version]
- Bukhari, S.S.; Vardaxoglou, J.; Whittow, W. A Metasurfaces Review: Definitions and Applications. Appl. Sci. 2019, 9, 2727. [Google Scholar] [CrossRef] [Green Version]
- Choudhury, P.; El-Nasr, M.A. Waves in resonant metasurfaces. J. Electromagn. Waves Appl. 2020, 34, 1309–1313. [Google Scholar] [CrossRef]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef]
- He, Q.; Sun, S.; Zhou, L. Tunable/Reconfigurable Metasurfaces: Physics and Applications. Research 2019, 2019, 1849272. [Google Scholar] [CrossRef] [Green Version]
- Zheludev, N.; Kivshar, Y. From metamaterials to metadevices. Nat. Mater. 2012, 11, 917–924. [Google Scholar] [CrossRef]
- Veselago, V.G. The Electrodynamicsof substances with simultaneously negative values of ϵ and μ. Usp. Fiz. Nauk 1967, 92, 517. [Google Scholar] [CrossRef]
- Krzysztofik, W.J.; Cao, T.N. Metamaterials in application to improve antenna parameters. Metamater. Metasurf. 2018, 12, 63–85. [Google Scholar]
- Antipov, S.; Liu, W.; Power, J.; Spentzouris, L. Left-Handed Metamaterials Studies and their Application to Accelerator Physics. In Proceedings of the 2005 Particle Accelerator Conference, Knoxville, TN, USA, 16–20 May 2005; pp. 458–460. [Google Scholar] [CrossRef]
- Tong, X.C. Functional Metamaterials and Metadevices; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Alici, K.B.; Ozbay, E. Radiation properties of a split ring resonator and monopole composite. Phys. Status Solidi B Basic Solid State Phys. 2007, 244, 1192–1196. [Google Scholar] [CrossRef]
- Sliusar, I.; Slyusar, V.; Utkin, Y.; Kopishynska, O. Parametric synthesis of 3D structure of SRR element of the metamaterial. In Proceedings of the 2020 IEEE International Conference on Problems of Infocommunications. Science and Technology (PIC S&T), Kharkiv, Ukraine, 6–9 October 2020; pp. 577–582. [Google Scholar]
- Aydin, K.; Guven, K.; Kafesaki, M.; Soukoulis, C.; Ozbay, E. Experimental observation of true left-handed transmission peak in metamaterials. Opt. Lett. 2004, 29, 2623–2625. [Google Scholar] [CrossRef] [Green Version]
- Shaltout, A.; Kinsey, N.; Kim, J.; Chandrasekar, R.; Ndukaife, J.; Boltasseva, A.; Shalaev, V. Development of Optical Metasurfaces: Emerging Concepts and New Materials. Proc. IEEE 2016, 104, 1–18. [Google Scholar] [CrossRef]
- Basar, E. Transmission through Large Intelligent Surfaces: A New Frontier in Wireless Communications. In Proceedings of the 2019 European Conference on Networks and Communications (EuCNC), Valencia, Spain, 18–21 June 2019; pp. 112–117. [Google Scholar] [CrossRef] [Green Version]
- Lv, L.; Wu, Q.; Li, Z.; Al-Dhahir, N.; Chen, J. Secure Two-Way Communications via Intelligent Reflecting Surfaces. IEEE Commun. Lett. 2021, 25, 744–748. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef] [Green Version]
- Feng, K.; Li, X.; Han, Y.; Jin, S.; Chen, Y. Physical Layer Security Enhancement Exploiting Intelligent Reflecting Surface. IEEE Commun. Lett. 2021, 25, 734–738. [Google Scholar] [CrossRef]
- Shlezinger, N.; Alexandropoulos, G.C.; Imani, M.F.; Eldar, Y.C.; Smith, D.R. Dynamic metasurface antennas for 6G extreme massive MIMO communications. IEEE Wirel. Commun. 2021, 28, 106–113. [Google Scholar] [CrossRef]
- Guanxing, Z.; Liu, Z.; Deng, W.; Zhu, W. Reconfigurable metasurfaces with mechanical actuations: Towards flexible and tunable photonic devices. J. Opt. 2020, 23, 013001. [Google Scholar] [CrossRef]
- Tang, W.; Dai, J.Y.; Chen, M.; Li, X.; Cheng, Q.; Jin, S.; Wong, K.K.; Cui, T.J. Programmable metasurface-based RF chain-free 8PSK wireless transmitter. Electron. Lett. 2019, 55, 417–420. [Google Scholar] [CrossRef] [Green Version]
- Tsilipakos, O.; Tasolamprou, A.; Pitilakis, A.; Liu, F.; Wang, X.; Mirmoosa, M.; Tzarouchis, D.; Abadal, S.; Taghvaee, H.; Liaskos, C.; et al. Toward intelligent metasurfaces: The progress from globally tunable metasurfaces to software-defined metasurfaces with an embedded network of controllers. Adv. Opt. Mater. 2020, 8, 2000783. [Google Scholar] [CrossRef]
- Liu, F.; Tsilipakos, O.; Pitilakis, A.; Tasolamprou, A.; Mirmoosa, M.; Kantartzis, N.; Kwon, D.; Kafesaki, M.; Soukoulis, C.; Tretyakov, S. Intelligent Metasurfaces with Continuously Tunable Local Surface Impedance for Multiple Reconfigurable Functions. Phys. Rev. Appl. 2019, 11, 044024. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Zhang, C.; Yang, J.; Sun, B.; Zhao, B.; Luo, X. Reconfigurable Metasurface for Multifunctional Control of Electromagnetic Waves. Adv. Opt. Mater. 2017, 5, 1700485. [Google Scholar] [CrossRef]
- Chaimool, S.; Hongnara, T.; Rakluea, C.; Akkaraekthalin, P.; Zhao, Y. Design of a PIN Diode-Based Reconfigurable Metasurface Antenna for Beam Switching Applications. Int. J. Antennas Propag. 2019, 2019, 7216324. [Google Scholar] [CrossRef] [Green Version]
- Qian, T. Reconfigurable Metasurface Antenna Based on the Liquid Metal for Flexible Scattering Fields Manipulation. Micromachines 2021, 12, 243. [Google Scholar] [CrossRef]
- Li, W.; Wang, Y.M.; Hei, Y.; Li, B.; Shi, X. A Compact Low-Profile Reconfigurable Metasurface Antenna with Polarization and Pattern Diversities. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 1170–1174. [Google Scholar] [CrossRef]
- Nemati, A.; Wang, Q.; Hong, M.; Teng, J. Tunable and reconfigurable metasurfaces and metadevices. Opto-Electron. Adv. 2018, 1, 180009. [Google Scholar] [CrossRef] [Green Version]
- Yurduseven, O.; Smith, D.R.; Fromenteze, T. Design of a Reconfigurable Metasurface Antenna for Dynamic Near-Field Focusing. In Proceedings of the 2018 IEEE International Symposium on Antennas and Propagation USNC/URSI National Radio Science Meeting, Boston, MA, USA, 8–13 July 2018; pp. 1707–1708. [Google Scholar] [CrossRef]
- Chen, L.; Ruan, Y.; Cui, H.Y. Liquid metal metasurface for flexible beam-steering. Opt. Express 2019, 27, 23282–23292. [Google Scholar] [CrossRef]
- Abdalrazik, A.; Abdel-Rahman, A.B.; Allam, A.; Abo-Zahhad, M.; Yoshitomi, K.; Pokharel, R.K. Frequency-reconfigurable dielectric resonator antenna using metasurface. Int. J. Microw. Wirel. Technol. 2021, 1–7. [Google Scholar] [CrossRef]
- Xavier, G.; Serres, A.; Costa, E.; Oliveira, A.; Nobrega, L.; Souza, V. Design and Application of a Metamaterial Superstrate on a Bio-Inspired Antenna for Partial Discharge Detection through Dielectric Windows. Sensors 2019, 19, 4255. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, K.; Hsieh, L.H. Microwave Ring Circuits and Related Structures; Wiley Online Library: Hoboken, NJ, USA, 2004; Volume 156. [Google Scholar]
- Balanis, C.A. Antenna Theory: Analysis and Design, 4th ed.; Wiley: Hoboken, NJ, USA, 2015; p. 1104. [Google Scholar]
- Kumar, M.S.; Basarkod, P.I. A Study of the Effect of Dielectric Composition on Metamaterial Performance in a Multilayer Environment. In Proceedings of the 2019 International Conference on Data Science and Communication (IconDSC), Bangalore, India, 1–2 March 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Smith, D.R.; Schultz, S.; Marko, P.; Soukoulis, C. Determination of effective permittivity and permeability of metamaterials from reflection and transmission coefficients. Phys. Rev. B 2002, 65, 195104. [Google Scholar] [CrossRef] [Green Version]
- Pujari, P.; Vyras, K.; Sharma, B.K. Design & Simulation of Circular Patch Antenna for Multiband application of X Band Using Varactor Diodes. In Proceedings of the Conference on Advances in Communication and Control Systems (CAC2S 2013), Dehradun, India, 6–8 April 2013; Atlantis Press: Paris, France, April 2013; pp. 140–144. [Google Scholar]
- Barrowes, B.; Prishvin, M.; Jutras, G.; Shubitidze, F. High-Frequency Electromagnetic Induction (HFEMI) Sensor Results from IED Constituent Parts. Remote Sens. 2019, 11, 2355. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Cao, X.; Yang, F.; Gao, J.; Xu, S.; Li, M.; Chen, X.; Zhao, Y.; Zheng, Y.; Li, S. A programmable metasurface with dynamic polarization, scattering and focusing control. Sci. Rep. 2016, 6, 35692. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feth, N.; König, M.; Husnik, M.; Stannigel, K.; Niegemann, J.; Busch, K.; Wegener, M.; Linden, S. Electromagnetic interaction of split-ring resonators: The role of separation and relative orientation. Opt. Express 2010, 18, 6545–6554. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Penciu, R.S.; Aydin, K.; Kafesaki, M.; Koschny, T.; Ozbay, E.; Economou, E.N.; Soukoulis, C.M. Multi-gap individual and coupled split-ring resonator structures. Opt. Express 2008, 16, 18131–18144. [Google Scholar] [CrossRef] [PubMed]
- Seetharaman, S.S.; King, C.; Hooper, I.R.; Barnes, W.L. Electromagnetic interactions in a pair of coupled split-ring resonators. Phys. Rev. B 2017, 96, 085426. [Google Scholar] [CrossRef] [Green Version]
- Tatartschuk, E.; Gneiding, N.; Hesmer, F.; Radkovskaya, A.A.; Shamonina, E. Mapping inter-element coupling in metamaterials: Scaling down to infrared. J. Appl. Phys. 2012, 111, 094904. [Google Scholar] [CrossRef] [Green Version]
- Radkovskaya, A.; Kiriushechkina, S.; Vakulenko, A.; Petrov, P.; Solymar, L.; Li, L.; Vallecchi, A.; Stevens, C.; Shamonina, E. Superdirectivity from arrays of strongly coupled meta-atoms. J. Appl. Phys. 2018, 124, 104901. [Google Scholar] [CrossRef] [Green Version]
- Sydoruk, O.; Tatartschuk, E.; Shamonina, E.; Solymar, L. Analytical formulation for the resonant frequency of split rings. J. Appl. Phys. 2009, 105, 014903. [Google Scholar] [CrossRef]
- Ashoor, A.; Gupta, S. Metasurface Reflector with Real-Time Independent Magnitude and Phase Control. arXiv 2020, arXiv:2009.13369. [Google Scholar]
- Poisel, R. Antenna Systems and Electronic Warfare Applications; Artech House: Sydney, Australia, 2012. [Google Scholar]
- Nassar, I.T.; Weller, T.M. An electrically small meandered line antenna with truncated ground plane. In Proceedings of the 2011 IEEE Radio and Wireless Symposium, Phoenix, AZ, USA, 16–19 January 2011; pp. 94–97. [Google Scholar]
- Shirazi, M.; Li, T.; Gong, X. Effects of PIN diode switches on the performance of reconfigurable slot-ring antenna. In Proceedings of the 2015 IEEE 16th Annual Wireless and Microwave Technology Conference (WAMICON), Cocoa Beach, FL, USA, 13–15 April 2015; pp. 1–3. [Google Scholar]
- Chen, X.; Grzegorczyk, T.; Wu, B.I.; Pacheco, J.; Kong, J. Robust method to retrieve the constitutive effective parameters of metamaterials. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2004, 70 Pt 2, 016608. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vassos, E.; Churm, J.; Powell, J.; Viegas, C.; Alderman, B.; Feresidis, A. Air-bridged Schottky diodes for dynamically tunable millimeter-wave metamaterial phase shifters. Sci. Rep. 2021, 11, 5988. [Google Scholar] [CrossRef] [PubMed]

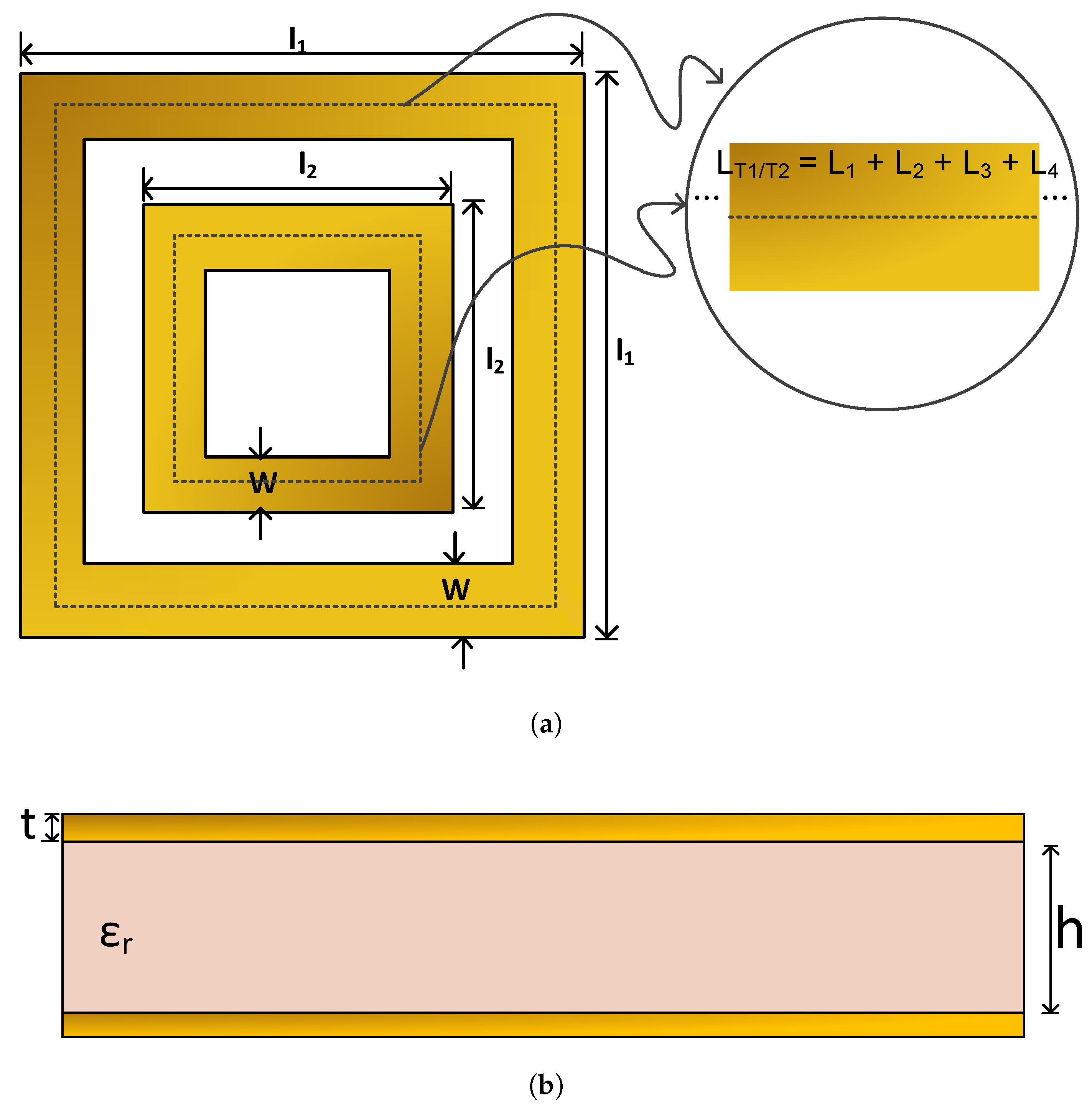


| Step | Equation | Purpose |
|---|---|---|
| 1 | Equation (6) | Calculate the width of a characteristic impedance |
| 2 | Equations (5) and (14) | Calculate the dielectric constant and use it to find the internal and external average lengths & for each frequency |
| 3 | Equation (9) | Calculate the internal and external side lengths of each outer ring using the calculated average lengths in Step 2 |
| Dimensions | Before Optimization (mm) | After Optimization (mm) |
|---|---|---|
| h | 0.5 | 0.56 |
| W | 1.54 | 1.54 |
| 3.51 | 3.47 | |
| 4.68 | 4.4 |
| Capacitance (pF) | Resonating Frequency (GHz) | Bandwidth (GHz) |
|---|---|---|
| Without diodes | 26.90–31.39, 32.26, and 40.20 | 4.46, 0.66, and 1.36 |
| 0.03 | 26.61–31.49, 32.49, and 40.28 | 4.88, 0.42, and 1.41 |
| 0.035 | 23.60, 26.72–31.47, 32.48, and 40.28 | 1.17, 4.73, 0.43, and 1.41 |
| 0.04 | 23.08, 26.79–31.46, 32.48, and 40.24 | 1.17, 4.68, 0.44, and 1.39 |
| 0.045 | 22.72, 26.81–31.44, 32.48, and 40.24 | 1.05, 4.63, 0.45, and 1.38 |
| 0.05 | 22.48, 26.89–31.43, 32.44, and 40.24 | 0.98, 4.58, 0.46, and 1.38 |
| Capacitance | Angular | Gain | Directivity | Radiation |
|---|---|---|---|---|
| (pF) | Beamwidth (°) | (dBi) | (dBi) | Efficiency (%) |
| Without diodes | 16.5 | 15 | 17.2 | 87.2 |
| 0.03 | 15.3 | 27.23 | 43.37 | 62.79 |
| 0.035 | 15.0 | 27.50 | 43.06 | 63.86 |
| 0.04 | 14.5 | 27.93 | 44.28 | 63.08 |
| 0.045 | 14.31 | 28.42 | 44.93 | 63.25 |
| 0.05 | 13.9 | 28.8 | 45.6 | 63.31 |
| Ref | Size | Reconfiguration | Actuators | Frequency | Detailed Design |
|---|---|---|---|---|---|
| (mm) | Band | Procedure | |||
| [68] | 2 × 4 | Frequency | GaAs air-bridged Schottky diode | mmWave | Not specified |
| [42] | 80 × 80 | Pattern | 12 PIN diodes | Sub-mmWave | Not specified |
| [43] | 180 × 180 | Frequency | Liquid metal | Sub-mmWave | Not specified |
| [44] | 117 × 117 | Frequency and Pattern | 16 PIN diodes | mmWave | Not specified |
| This work | 17.6 × 17.6 | Frequency | 16 PIN diodes | mmWave | Specified |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ledimo, B.K.; Moaro, P.; Ramogomana, R.; Mosalaosi, M.; Basutli, B. Design Procedure of a Frequency Reconfigurable Metasurface Antenna at mmWave Band. Telecom 2022, 3, 379-395. https://doi.org/10.3390/telecom3020020
Ledimo BK, Moaro P, Ramogomana R, Mosalaosi M, Basutli B. Design Procedure of a Frequency Reconfigurable Metasurface Antenna at mmWave Band. Telecom. 2022; 3(2):379-395. https://doi.org/10.3390/telecom3020020
Chicago/Turabian StyleLedimo, Bokamoso Kebatho, Pako Moaro, Reuben Ramogomana, Modisa Mosalaosi, and Bokamoso Basutli. 2022. "Design Procedure of a Frequency Reconfigurable Metasurface Antenna at mmWave Band" Telecom 3, no. 2: 379-395. https://doi.org/10.3390/telecom3020020
APA StyleLedimo, B. K., Moaro, P., Ramogomana, R., Mosalaosi, M., & Basutli, B. (2022). Design Procedure of a Frequency Reconfigurable Metasurface Antenna at mmWave Band. Telecom, 3(2), 379-395. https://doi.org/10.3390/telecom3020020








