Improved Networks Routing Using an Arrow-Based Description
Abstract
1. Introduction
- Section 2 introduces the basic notations used in the paper;
- Section 3 describes an arrow-description of the graph;
- Section 4 describes the use of the arrow algebra;
- Section 5 describes the routing algorithm using arrows;
- Section 6 is dedicated to a more detailed description of the algorithm;
- Section 7 is dedicated to conclusions and future work.
2. Basic Definitions and Notations
2.1. Background
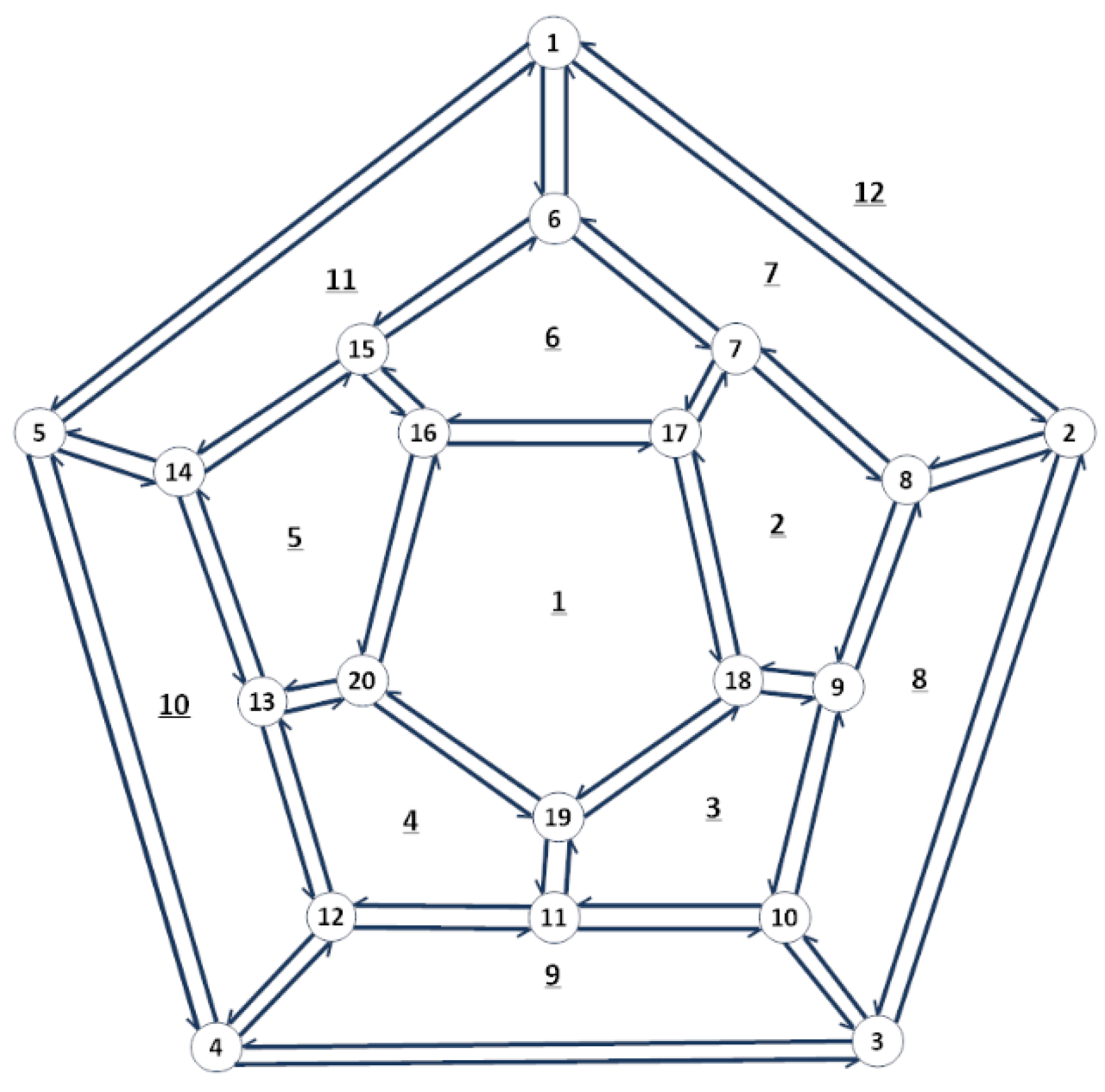
2.2. Adjacency and Cycles Merger
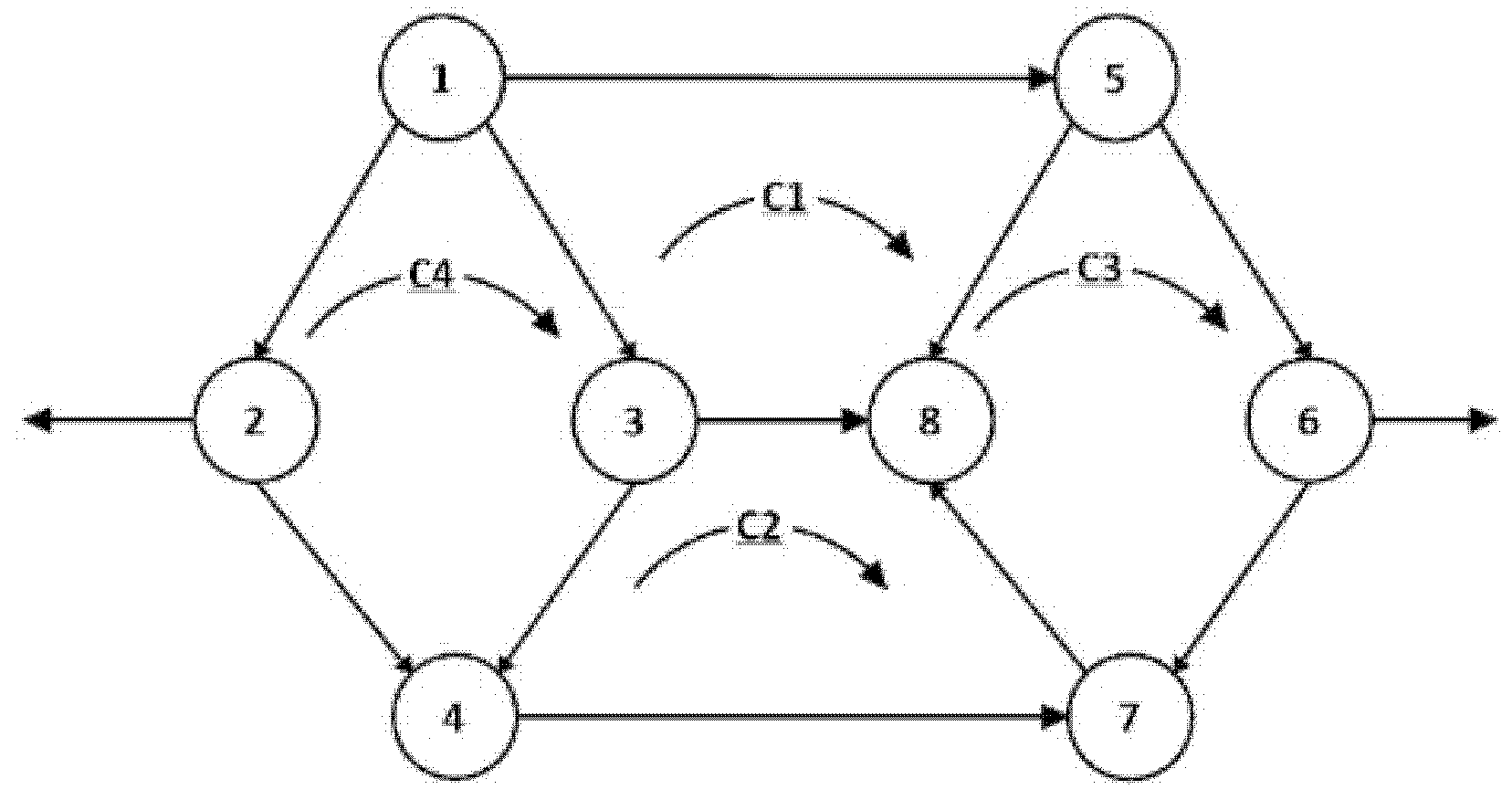
3. An Arrow-Based Description and Its Algebra
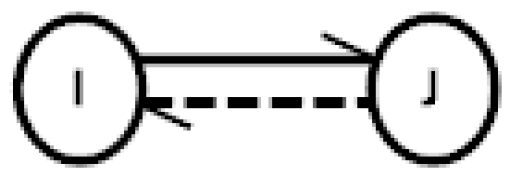
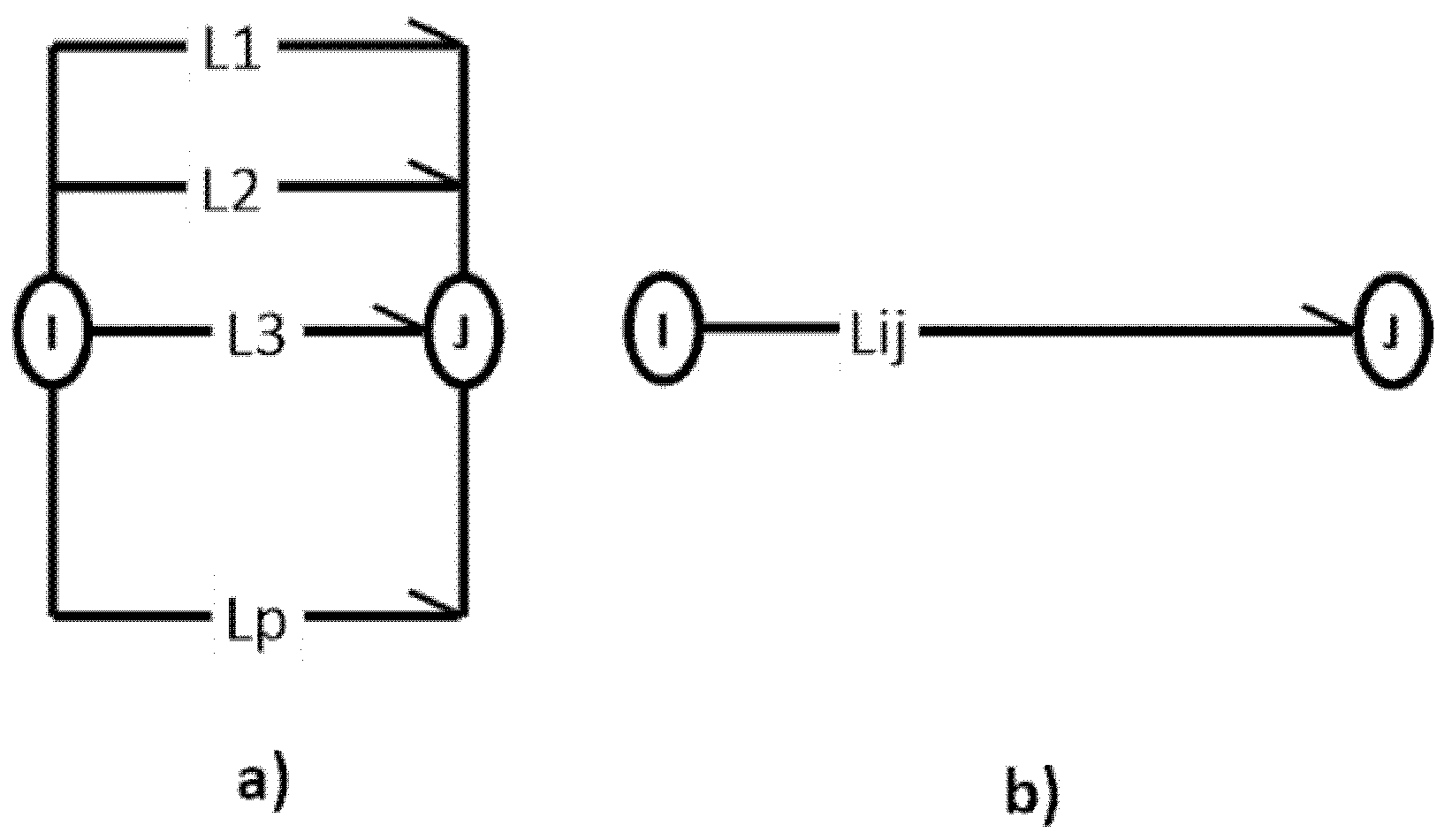
3.1. Graph Arrows
- ;
- ;
- ; if and ;
- ;
- ;
- .
3.2. Basic Graph Operations with Arrows
4. Using Graph Arrows
5. Routing Algorithm Using Arrows
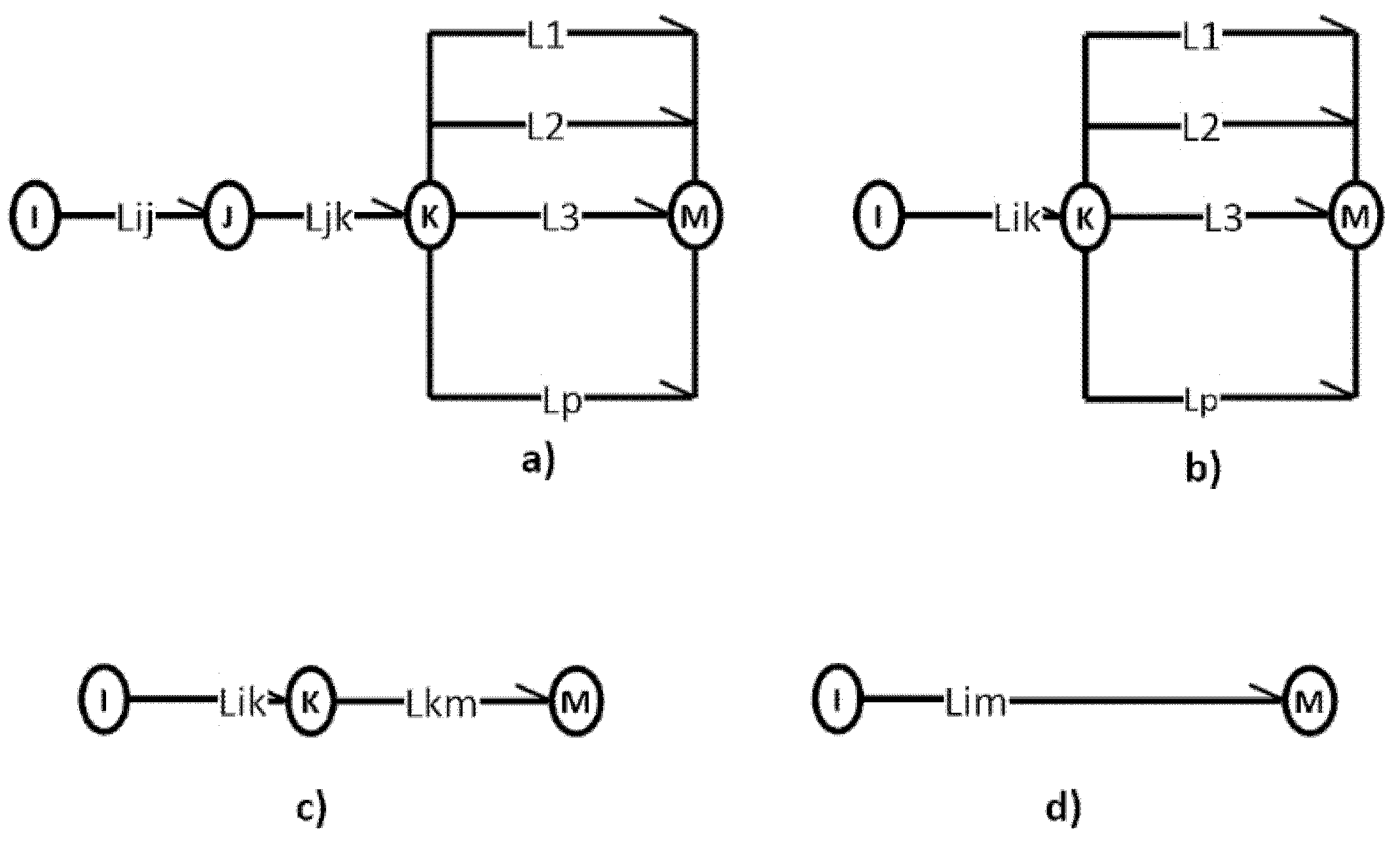
5.1. Serial Addition
5.2. Parallel Composition of Graph Arrows
5.3. Series-Parallel Composition of Graph Arrows
| Algorithm 1: The path finding using graph arrows. |
| Input: the starting node nsand the end node ne; Determine the cycles containing nsand ne; Determine the cycles paths comprising both nsand ne using cycles mergers; If there is no path, then STOP and print “No path found”; Once a path is found, translate the list of graph arrows to sets T and H as discussed. By successive applications of the KMP algorithm as described above, find a direct and a return path between the nodes; Output: the path discovered. |
- Each time, the number of cycles limits the iterations to less than C.
- The end criteria of the program can be flexible such that it can be stopped whenever a first path is found or alternatively it can be run until a path with a specific length is obtained.
6. The Algorithm in More Detail
7. Conclusions and Further Work
Author Contributions
Funding
Conflicts of Interest
References
- Onete, C.E.; Onete, M.C.C. Improved networks routing using link addition. In Proceedings of the MOCAST 2020, Bremen, Germany, 7–9 September 2020. [Google Scholar]
- Bhondekar, A.P.; Kaur, H. Routing Protocols in Zigbee Based Networks: A Survey. Available online: https://www.researchgate.net/publication/275637579 (accessed on 10 November 2019).
- Narmada, A.; Rao, P.S. Performance comparison of routing protocols for zigbee wpan. Int. J. Comput. Sci. Issues (IJCSI) 2011, 8, 394–402. [Google Scholar]
- Prativa, P.; Saraswala, A. Survey on routing protocols in zigbee network. Int. J. Eng. Sci. Innov. Technol. IJESIT 2013, 2, 471–476. [Google Scholar]
- Kumar, P.S.S.; Babu, A.R. A survey on routing techniques in zigbee wireless networks in contrast with other wireless networks. Indian J. Sci. Technol. 2017, 10, 1–8. [Google Scholar] [CrossRef]
- Onete, C.E.; Onete, M.C.C. An alternative to zigbee routing using a cycles description of a planar graph. In Proceedings of the 2019 8th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 13–15 May 2019; pp. 29–32. [Google Scholar]
- Bondy, A.; Murty, U.S.R. Graph Theory, Springer Graduate Texts in Mathematics; Springer: Berlin, Germany, 2008. [Google Scholar] [CrossRef]
- Balabanian, N.; Bickart, T.A. Electrical Network Theory; John Wiley and Sons Inc.: New York, NY, USA, 1969. [Google Scholar]
- Onete, C.E.; Onete, M.C.C. Building hamiltonian networks using the laplacian of the underlying graph. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; pp. 145–148. [Google Scholar]
- Onete, C.E.; Onete, M.C.C. Finding the Hamiltonian circuits in an undirected graph using the mesh-links incidence. In Proceedings of the 19th IEEE International Conference Electronica, Circuits and Systems (ICECS), Seville, Spain, 9–12 December 2012; pp. 472–475. [Google Scholar]
- Kavitha, T.; Liebchen, C.; Mehlhorn, K.; Michail, D.; Rizzi, R.; Ueckerdt, T.; Zweig, K. Cycle bases in graphs characterization, algorithms, complexity, and applications. Comput. Sci. Rev. 2009, 3, 199–243. [Google Scholar] [CrossRef]
- ICS 161: Design and Analysis of Algorithms. Available online: https://www.ics.uci.edu/~eppstein/161/960227.html (accessed on 10 November 2019).
- Algorithm, D. Dijkstra’s Algorithm. Available online: https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm (accessed on 22 August 2020).
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar]


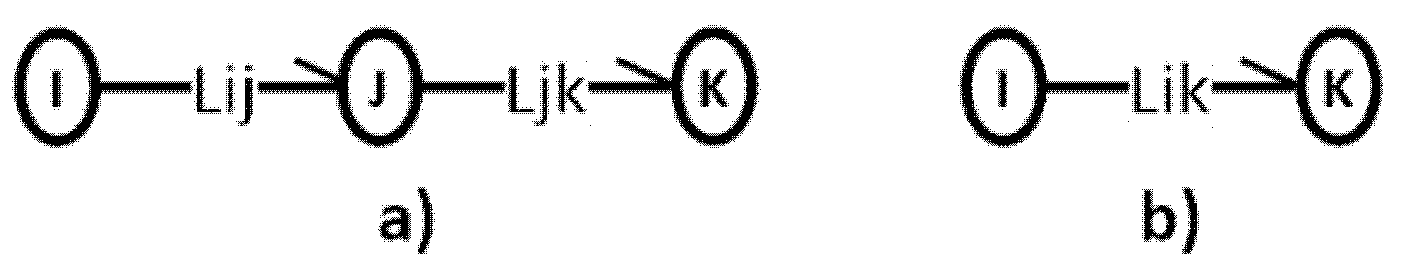
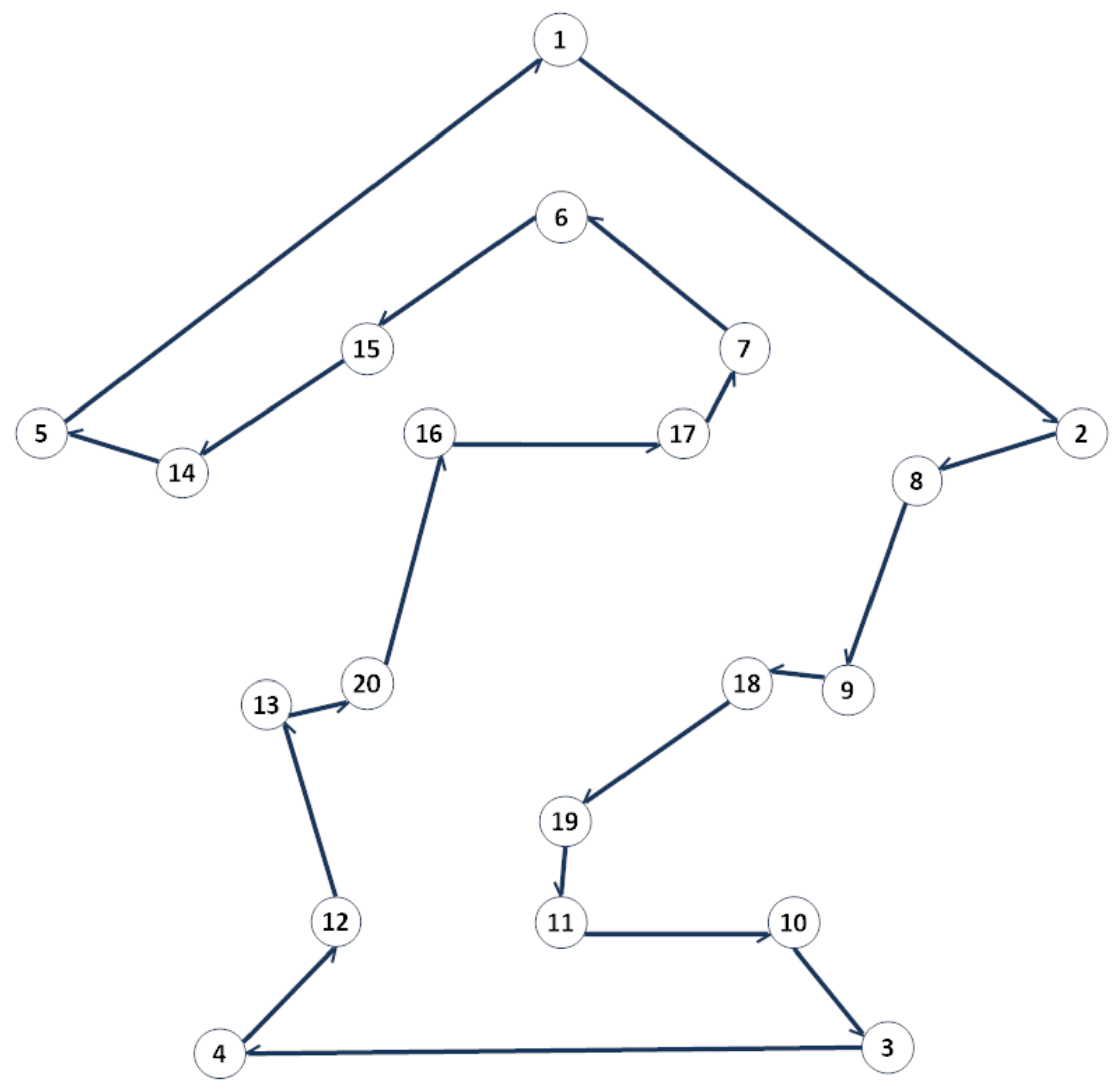
| Cycle | Arrows |
|---|---|
| 1 | ,,,, |
| 2 | ,,,, |
| 3 | ,,,, |
| 4 | ,,,, |
| 5 | ,,,, |
| 6 | ,,,, |
| 7 | ,,,, |
| 8 | ,,,, |
| 9 | ,,,, |
| 10 | ,,,, |
| 11 | ,,,, |
| 12 | ,,,, |
| 26 | 27 | 28 | 29 | 30 |
|---|---|---|---|---|
| Arrow | Source | End |
|---|---|---|
| 19 | 20 | |
| 20 | 16 | |
| 16 | 17 | |
| 17 | 7 | |
| 7 | 8 | |
| 8 | 9 | |
| 9 | 18 | |
| 18 | 19 |
| Source | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| End | 2 | 8 | 4 | 12 | 1 | 15 | 6 | 9 | 18 | 3 | 10 | 13 | 20 | 5 | 14 | 17 | 7 | 19 | 11 | 16 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onete, C.E.; Onete, M.-C.C. Improved Networks Routing Using an Arrow-Based Description. Telecom 2020, 1, 150-160. https://doi.org/10.3390/telecom1030011
Onete CE, Onete M-CC. Improved Networks Routing Using an Arrow-Based Description. Telecom. 2020; 1(3):150-160. https://doi.org/10.3390/telecom1030011
Chicago/Turabian StyleOnete, Cristian E., and Maria-Cristina C. Onete. 2020. "Improved Networks Routing Using an Arrow-Based Description" Telecom 1, no. 3: 150-160. https://doi.org/10.3390/telecom1030011
APA StyleOnete, C. E., & Onete, M.-C. C. (2020). Improved Networks Routing Using an Arrow-Based Description. Telecom, 1(3), 150-160. https://doi.org/10.3390/telecom1030011





