Abstract
In this study, a novel two-parameter, three-dimensional chaotic system is constructed. The system has no linear terms and its equilibrium is a line, so it is a system with hidden attractors. The system is first studied by computation of its bifurcation diagrams and diagram of Lyapunov exponents. Then, the system is applied to two encryption related problems. First, the problem of secure communications is considered, using the symmetric chaos shift keying modulation method. Here, the states of the chaotic system are combined with a binary information signal in order to mask it, safely transmit it through a communication channel, and successfully reconstruct the information at the receiver end. In the second problem, the states of the system are utilized to design a simple rule to generate a bit sequence that possesses random properties, and is thus suitable for encryption related applications. For both applications, simulations are performed through Matlab to verify the soundness of the designs.
1. Introduction
Since its first emergence in the 1960s [1], chaos theory has emerged in multiple scientific fields, ranging from physics to biology, medicine, engineering, communications and economics. Chaotic systems are deterministic dynamical systems, modelled by a set of differential or difference equations. Their unique feature is that their solution can be extremely prone to changes in the initial conditions of the system, or to parameter changes. This means that solution trajectories starting from almost identical initial key values will diverge over time, giving rise to completely different behaviors.
The above-mentioned feature makes chaotic systems hard to predict. This property, combined with their deterministic nature, makes chaotic systems suitable in security applications that require the use of complex dynamics, like encryption [2,3,4], communications [5,6,7,8,9], random number generators [10] and more [11].
Thus, there is an ongoing interest in creating novel chaotic systems, since their demand in applications is continuous. To design a chaotic system, researchers developed several different approaches. One way is to consider an existing chaotic system, and modify it by adding more terms to the differential/difference equations describing the system, or modifying an existing term, or even adding a new state to the system and changing its order [12,13,14]. In such cases, the new system should preferably have a more complex behavior compared to the original one, which is usually indicated by the highest value that the Lyapunov exponent can achieve.
Another approach, which is the method used here, is to design a new system by utilizing nonlinear functions that are documented to yield chaotic behavior, like the hyperbolic sine function, the exponential function, the cubic power, or the absolute value; see, for example [15,16,17,18,19,20] and the references found therein.
Interestingly, when considering chaotic systems, it is preferable if the resulting system has hidden attractors [21]. An attractor is called hidden if its basin of attraction does not intersect with any open neighbourhood of an equilibrium. Systems with hidden attractors have gained attention due to their complex behavior, which makes them suitable for applications. Examples of recent works on such systems are [7,18,21,22,23,24,25,26].
Based on the above, this work considers a chaotic system with a hidden attractor, having a line equilibrium. The system has two parameters, and is purely nonlinear, having no linear terms. A dynamical analysis on the system is performed by studying its bifurcation diagrams, the Poincaré map, and the Lyapunov exponents diagram.
Moreover, to showcase the applicability of the system to chaos based encryption applications, the system is applied to two problems. First, the problem of secure communications is considered. Here, the aim is to find a method to combine an information signal, with the values of the states of the chaotic system, resulting in a scrambled signal that carries the masked information in it. Then, this signal can be safely transmitted through a communication channel, and after appropriate signal processing, the original information can be unmasked and safely retrieved at the receiver end [6,27]. The method used here is the symmetric chaos shift keying (SCSK) modulation, applied in [7,28]. The present work extends the work of [29] by including an extensive bit-error-rate (BER) performance analysis of the proposed communication scheme. The simulation results show that a combination of the states of the chaotic system with a sine function can yield better performance under a noisy transmission channel.
In addition to the above application, the design of a pseudo-random bit generator (PRBG) is considered. In this application, the states of the chaotic system are used to generate a sequence of bits, that possesses properties similar to those of a random sequence. Such bit generators are highly useful, since they can be used to encrypt binary information signals. The proposed PRBG generates three bits per iteration, and the generated sequence passes all statistical tests of the NIST test suite.
The rest of the paper is structured as follows: In Section 2, the proposed chaotic system is presented and studied. In Section 3, the problem of secure communications is considered, followed by the problem of random bit generation in Section 4. Section 5 concludes the paper with a discussion on future topics of interest.
2. The Proposed Chaotic System
In this section, the 3-D chaotic system is proposed and studied. The system is given by the following differential equations:
where x, y, z are the state variables and a, b are positive parameters. System (1) is chaotic for a wide range of parameter values. For example, when parameters a and b take the values , , the chaotic behavior of the system is presented in the phase portraits of Figure 1 and Figure 2. Moreover, the state trajectories are shown in Figure 3, and in Figure 4—the phase portraits of each state with respect to its derivative are depicted.
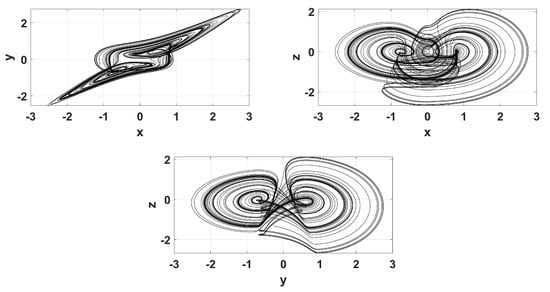
Figure 1.
Phase portraits of system (1), for and and , for 1500 s.
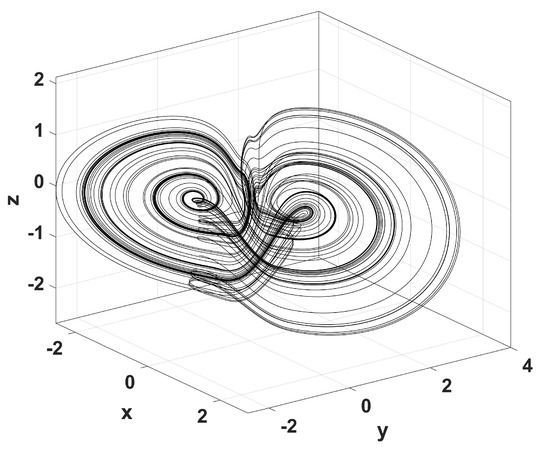
Figure 2.
3D chaotic attractor of system (1), for and and , for 1500 s.
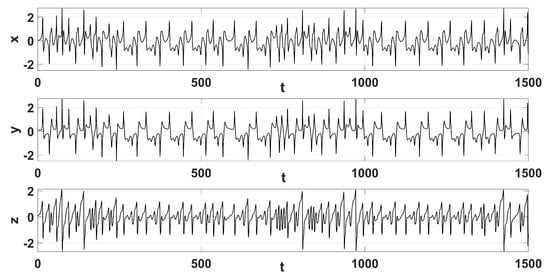
Figure 3.
State trajectories of system (1), for and and , for 1500 s.
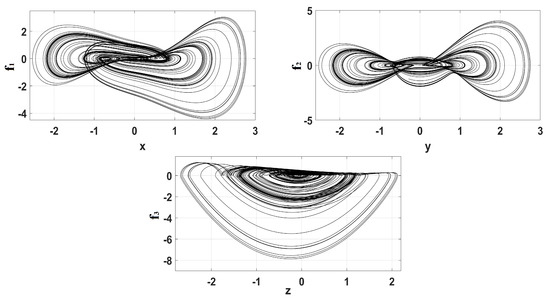
Figure 4.
Phase portraits of system (1) for each state versus its derivative, for and and , for 1500 s.
Moreover, although the system (1) is structurally simple, it is purely nonlinear, having no linear terms, and two independent parameters . In addition, the equilibria of system (1) lie in the line . So, it belongs to the recently discovered dynamical systems with hidden attractors [7,21,23,30,31].
For a detailed analysis of system’s (1) dynamical behavior, the system is investigated numerically by using the fourth order Runge–Kutta algorithm. The bifurcation diagram is first computed. This diagram depicts the points of intersection where the trajectory cuts the plane with . In this way, the bifurcation diagram of variable x versus the parameter a, for reveals the richness of system’s dynamical behavior (Figure 5). It can be seen that the system enters chaos following a period doubling route, as the parameter a increases. The system remains chaotic for a wide range of parameter values, which is interrupted by small periodic windows. As an additional simulation, the bifurcation diagram of variable z versus the parameter a, for is shown in Figure 6, from which the same dynamical behavior can be observed. Also, Figure 7 depicts the Poincaré map of the system, as the trajectory cuts the plane with , for , . The subfigure also depicts clearly the plane that cuts the attractor, with respect to which the Poincaré map is taken.
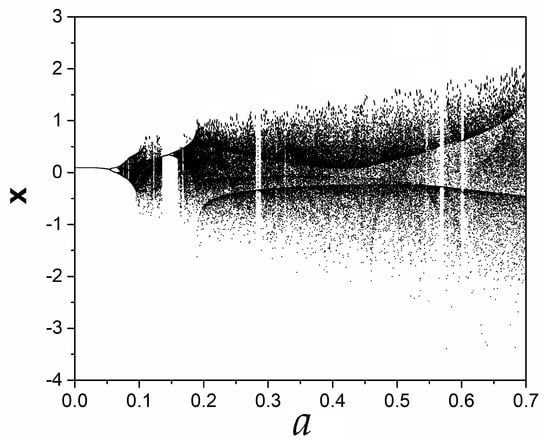
Figure 5.
Bifurcation diagram of x versus a for .
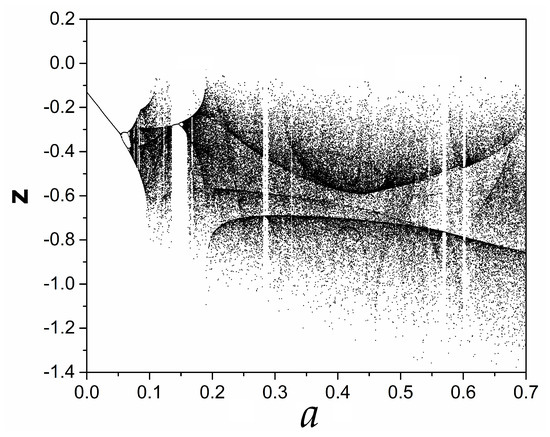
Figure 6.
Bifurcation diagram of z versus a for .
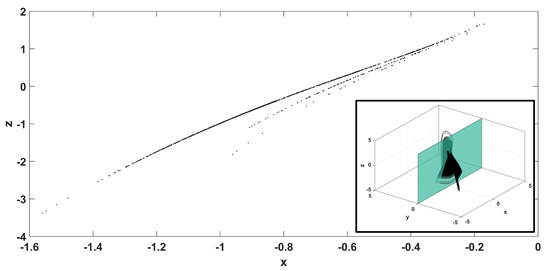
Figure 7.
Poincaré map of x versus z for , .
Figure 8 depicts the diagram of the two largest Lyapunov exponents with respect to bifurcation parameter a, which are computed using the well-known Wolf et al. [32] algorithm. The third exponent is discarded from the graph, since its values are negative and too low to depict. As can be seen, when the system is periodic, the maximal Lyapunov exponent (MLE) is equal to zero, while when it is chaotic, the system has a positive MLE, as it is expected according to the theory. So, from Figure 8, the system’s (1) chaotic behavior is found for a wide range of parameter values, confirming the bifurcation diagram of Figure 5. Moreover, as parameter a increases, the value of the MLE also increases, and the behaviour of the system becomes more complex.
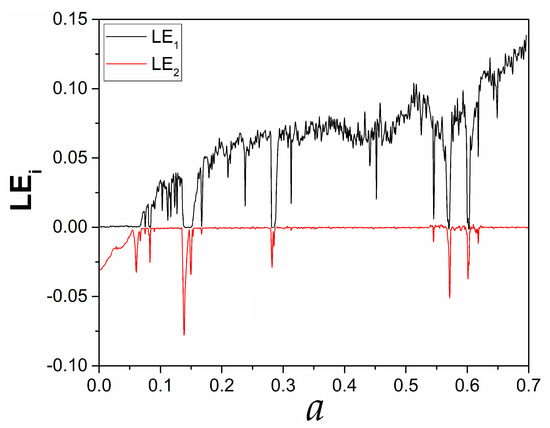
Figure 8.
Diagram of the two largest Lyapunov exponents with respect to parameter a, for .
3. Application to Secure Communications
3.1. Symmetric Chaos Shift Keying Modulation
In this section, the proposed chaotic system is applied to the problem of secure communications. The methodology considered is the symmetric chaos shift keying (SCSK) modulation, which was applied in [7,28]; see also [27,33,34,35,36,37,38,39] for similar approaches. The system design is shown in Figure 9. The system is comprised of two units, a transmitter and a receiver, connected through a noisy communication channel.
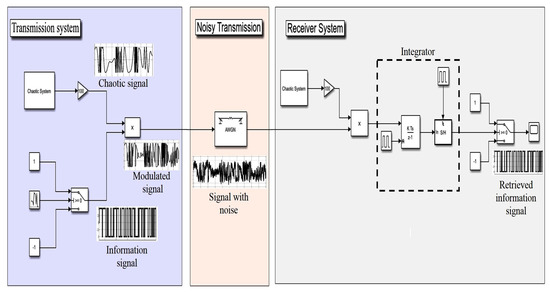
Figure 9.
SCSK secure communications design.
In the transmitter unit, the information signal is multiplied (modulated) with a chaotic signal generated by the chaotic system, resulting in a masked signal. The generated masked signal is then transmitted to the receiver. In the simulations, the information signal is taken as a binary signal with a period of 1 s. For the chaotic signal used, different options were considered, as will be seen in the following subsection, generated from (1), with , . During transmission, it is also assumed that the channel is disturbed by an additive white Gaussian noise (AWGN). In the receiver end, the received masked signal is multiplied by the chaotic signal generated by the same chaotic system as in the receiver, and the resulting signal is integrated in the correlator. This way, the bit energy of the signal is calculated and the binary information signal is reconstructed by passing the resulting signal through a threshold detector, with threshold set to 0. So, this threshold detector generates a ”1” if its input is positive, and a ”−1” if its input is negative.
Note that in this design, the same chaotic signal is used in the transmitter and receiver ends; hence, the term symmetric is used in its description. So in the receiver end, in order to replicate the chaotic signal, knowledge of the systems initial conditions and parameter values is required. These five parameters are called the key space of the design. So assuming a 16-digit accuracy, an upper bound of the key space is . This is higher than the upper bound of that is generally required to resist brute force attacks [40].
The SCSK communication system was studied under the presence of AWGN in the communications channel. The retrieved signal is delayed by s, due to the sample/hold block on the receiving unit. Therefore, there is a s delay between the transmitted information signal and the retrieved information signal on the receiving unit.
3.2. Bit Error Rate Performance
To study the bit-error-rate (BER) performance of the system under different noise intensities, we considered several cases of chaotic signals S used in the transmission. The signals considered were , , , . For each case, the simulation results for 100 s are shown in Figure 10, Figure 11, Figure 12 and Figure 13 for dB. From the simulations, it can be seen that the combination of all the states with a sine function yields a more complex signal, especially when the gain term inside the sine function increases. In addition, it is seen that, in all cases, the information signal is successfully retrieved at the receiver end.
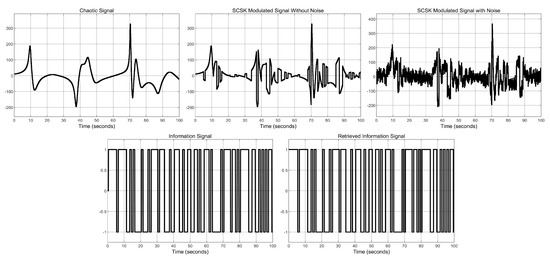
Figure 10.
Simulation results of the SCSK secure communications design, for chaotic signal .
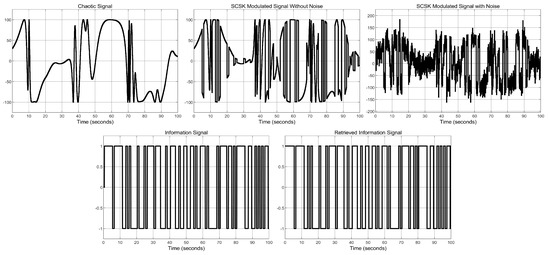
Figure 11.
Simulation results of the SCSK secure communications design, for chaotic signal .
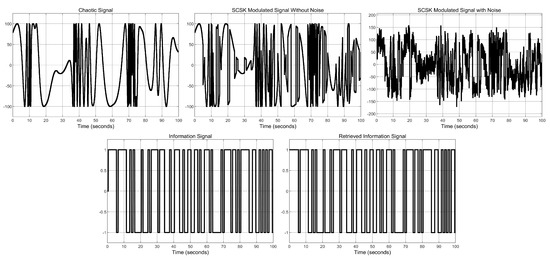
Figure 12.
Simulation results of the SCSK secure communications design, for chaotic signal .
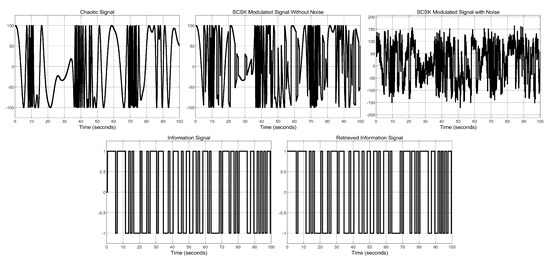
Figure 13.
Simulation results of the SCSK secure communications design, for chaotic signal .
The BER performance results are shown in Figure 14. The noise intensity is considered in the range of −10 dB to 3 dB, and the simulation time is 40,000 s. It is verified that more complex chaotic signals yield a consistently better BER performance compared to simply using a state of the chaotic system.
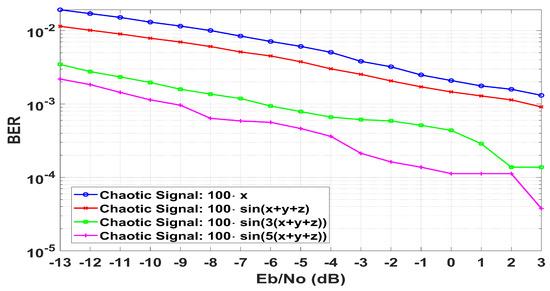
Figure 14.
BER simulation results.
4. Application to Random Bit Generation
As an additional application of the proposed system, we will consider the design of a random bit generator (PRBG). The problem consists of designing a simple rule to generate a bit sequence, using the values of the states of a chaotic system [10,41,42,43,44,45,46,47]. The resulting bit sequence, also called bitstream, should have the statistical properties of a random sequence. This can be tested through a series of statistical tests, provided by the National Institute of Standards and Technology (NIST) [48]. The test suite consists of 15 statistical tests. Each test returns a p-value, and if it is higher than a chosen significance level, the test is considered successful and the bitstream is considered random. The significance level here is taken as the default .
The PRBG generates bits using the following simple rule. The system (1) is simulated using ode45 in Matlab, with a simulation step of . Then, in each discrete time instance i, the following rule is applied to generate the bitstream:
where are the values of the states at the discrete time instance i, and denotes the integer part of the argument. The coefficients were chosen after some trial and error, until the obtained sequence was indeed random, as will be seen next. The complete bit sequence is obtained as
In addition, to reduce cross-correlation in the generated bitstreams, the first 200 s of the system simulation are discarded. It is clear that with the above rule, 3 bits can be generated in each discrete time. So, for example, given the time step , to generate bits, the system (1) needs to be simulated for s. Similar approaches were used in [42,46,49], using different operators to generate the bits.
To test the algorithm, a sequence of bits is generated and tested. The sequence was generated using parameter values , and initial conditions . The NIST test results are shown in Table 1. It can be seen that all tests are successful, so the resulting sequence is indeed random.

Table 1.
NIST statistical test results, if , the test is successful.
In addition, Figure 15 depicts the autocorrelation and cross-correlation for a bit sequence of length . For a random bit sequence, the auto-correlation should have a delta form, while the cross-correlation should be close to zero [41]. This is indeed verified from the diagrams. For the cross-correlation, the initial conditions for the two bitstreams were chosen as and .
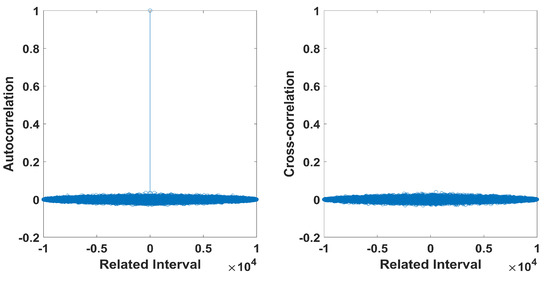
Figure 15.
Autocorrelation and cross-correlation for a bit sequence of length .
Finally, Table 2 shows a comparison between the key space of different generators.

Table 2.
Key space of different techniques.
5. Conclusions
In this work, a 3D chaotic system with a line equilibrium was proposed. The system was studied through the computation of its bifurcation diagrams and Lyapunov exponents diagram. To study the applicability of the system to encryption and security related applications, the system was applied to a secure communications scheme using the SCSK modulation method, yielding satisfactory BER performance. Moreover, the problem of random bit generation was considered. The proposed design can generate three bits per iteration, with statistical randomness for the generated sequence.
It is worth noting here that as far as the numerical evaluation of the chaotic system in the transmitter and receiver ends is concerned, there are instances where errors can arise, that may lead to degradation of the design. Examples can include round-off errors that arise when a different error tolerance is chosen between transmitter and receiver, or errors that arise when a different integration step is chosen or different numerical methods are used to solve the system; see for example, discussions in the recent works [52,53,54]. This is one of the main obstacles that have so far held up the possible commercialization of chaos-based secure communications.
Here, since no implementation of the design is performed, we assumed, as many works do, that the receiver and transmitter systems are simulated in devices with the same configuration settings. Yet, it is within our scope of research interest to physically implement such a design, to see when and how such erros arise and how thay can be tackled. Thus, future aspects of this work would be the experimental implementation of the communications design [55], and the further application of the proposed PRBG to image encryption.
Author Contributions
Conceptualization, C.V., S.Ç., V.-T.P., L.M.; Formal analysis, L.M., C.V., S.Ç., V.-T.P., V.K.M.; Software, L.M., C.V., S.Ç.; Supervision, C.V., I.S., S.G., S.Ç., V.-T.P.; Validation, C.V., S.Ç., I.S., S.G., V.K.M.; Visualization, C.V., L.M., S.Ç.; Writing, L.M., C.V., S.Ç. All authors have read and agreed to the published version of the manuscript.
Funding
This research is co-financed by Greece and the European Union (European Social Fund- ESF) through the Operational Programme «Human Resources Development, Education and Lifelong Learning» in the context of the project “Reinforcement of Postdoctoral Researchers—2nd Cycle” (MIS-5033021), implemented by the State Scholarships Foundation (IKY). This research is funded by PHENIKAA University under grant number 03.2019.02. The research leading to these results has received funding from the Fond for Scientific Research Vlaanderen (FWO) projects G028015N and G090117N and the FNRS-FWO under Excellence of Science (EOS) Project no 30468160 “Structured low-rank matrix/tensor approximation: numerical optimization-based algorithms and applications”.
Acknowledgments
The authors would like to thank the anonymous reviewers for their valuable comments that have improved the quality of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Guan, Z.H.; Huang, F.; Guan, W. Chaos-based image encryption algorithm. Phys. Lett. A 2005, 346, 153–157. [Google Scholar] [CrossRef]
- Karmakar, J.; Nandi, D.; Mandal, M. A novel hyper-chaotic image encryption with sparse-representation based compression. Multimed. Tools Appl. 2020, 79, 28277–28300. [Google Scholar] [CrossRef]
- Jithin, K.; Sankar, S. Colour image encryption algorithm combining Arnold map, DNA sequence operation, and a Mandelbrot set. J. Inf. Secur. Appl. 2020, 50, 102428. [Google Scholar] [CrossRef]
- Zaher, A.A.; Abu-Rezq, A. On the design of chaos-based secure communication systems. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 3721–3737. [Google Scholar] [CrossRef]
- Dedieu, H.; Kennedy, M.P.; Hasler, M. Chaos shift keying: Modulation and demodulation of a chaotic carrier using self-synchronizing Chua’s circuits. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1993, 40, 634–642. [Google Scholar] [CrossRef]
- Rajagopal, K.; Cicek, S.; Akgul, A.; Jafari, S.; Karthikeyan, A. Chaotic cuttlesh: King of camouage with self-excited and hidden flows, its fractional-order form and communication designs with fractional form. Discret. Contin. Dyn. Syst.-B 2019, 25, 1001. [Google Scholar] [CrossRef]
- Stavroulakis, P. Chaos Applications in Telecommunications; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Souza, C.E.; Chaves, D.P.; Pimentel, C. Digital communication systems based on three-dimensional chaotic attractors. IEEE Access 2019, 7, 10523–10532. [Google Scholar] [CrossRef]
- Patidar, V.; Sud, K.K.; Pareek, N.K. A pseudo random bit generator based on chaotic logistic map and its statistical testing. Informatica 2009, 33, 441–452. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Phys. Today 2015, 68, 54. [Google Scholar]
- Hassan, S.S.; Reddy, M.P.; Rout, R.K. Dynamics of the modified n-degree Lorenz system. Appl. Math. Nonlinear Sci. 2019, 4, 315–330. [Google Scholar] [CrossRef]
- Wang, X.; Wang, M. A hyperchaos generated from Lorenz system. Phys. A Stat. Mech. Its Appl. 2008, 387, 3751–3758. [Google Scholar] [CrossRef]
- Han, C. An image encryption algorithm based on modified logistic chaotic map. Optik 2019, 181, 779–785. [Google Scholar] [CrossRef]
- Xiong, L.; Zhang, S.; Zeng, Y.; Liu, B. Dynamics of a new composite four–Scroll chaotic system. Chin. J. Phys. 2018, 56, 2381–2394. [Google Scholar] [CrossRef]
- Wang, Z.; Volos, C.; Kingni, S.T.; Azar, A.T.; Pham, V.T. Four-wing attractors in a novel chaotic system with hyperbolic sine nonlinearity. Optik 2017, 131, 1071–1078. [Google Scholar] [CrossRef]
- Pham, V.T.; Vaidyanathan, S.; Volos, C.; Jafari, S. Hidden attractors in a chaotic system with an exponential nonlinear term. Eur. Phys. J. Spec. Top. 2015, 224, 1507–1517. [Google Scholar] [CrossRef]
- Pham, V.T.; Volos, C.; Kingni, S.T.; Kapitaniak, T.; Jafari, S. Bistable hidden attractors in a novel chaotic system with hyperbolic sine equilibrium. Circuits Syst. Signal Process. 2018, 37, 1028–1043. [Google Scholar] [CrossRef]
- Dalkiran, F.Y.; Sprott, J.C. Simple chaotic hyperjerk system. Int. J. Bifurc. Chaos 2016, 26, 1650189. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, C.; Xu, D.; Chen, C. Dynamic analysis and synchronisation control of a novel chaotic system with coexisting attractors. Pramana 2020, 94, 19. [Google Scholar] [CrossRef]
- Dudkowski, D.; Jafari, S.; Kapitaniak, T.; Kuznetsov, N.V.; Leonov, G.A.; Prasad, A. Hidden attractors in dynamical systems. Phys. Rep. 2016, 637, 1–50. [Google Scholar] [CrossRef]
- Pham, V.T.; Volos, C.; Jafari, S.; Kapitaniak, T. A novel cubic–equilibrium chaotic system with coexisting hidden attractors: Analysis, and circuit implementation. J. Circuits Syst. Comput. 2018, 27, 1850066. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J. Simple chaotic flows with a line equilibrium. Chaos Solitons Fractals 2013, 57, 79–84. [Google Scholar] [CrossRef]
- Gotthans, T.; Sprott, J.C.; Petrzela, J. Simple chaotic flow with circle and square equilibrium. Int. J. Bifurc. Chaos 2016, 26, 1650137. [Google Scholar] [CrossRef]
- Azar, A.T.; Serrano, F.E. Stabilization of port Hamiltonian chaotic systems with hidden attractors by adaptive terminal sliding mode control. Entropy 2020, 22, 122. [Google Scholar] [CrossRef] [PubMed]
- Nag Chowdhury, S.; Ghosh, D. Hidden attractors: A new chaotic system without equilibria. Eur. Phys. J. Spec. Top. 2020, 229, 1299–1308. [Google Scholar] [CrossRef]
- Sushchik, M.; Tsimring, L.S.; Volkovskii, A.R. Performance analysis of correlation-based communication schemes utilizing chaos. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 1684–1691. [Google Scholar] [CrossRef]
- Wang, X.; Akgul, A.; Cicek, S.; Pham, V.T.; Hoang, D.V. A chaotic system with two stable equilibrium points: Dynamics, circuit realization and communication application. Int. J. Bifurc. Chaos 2017, 27, 1750130. [Google Scholar] [CrossRef]
- Moysis, L.; Volos, C.; Stouboulos, I.; Goudos, S.; Ciçek, S.; Pham, V.T.; Mishra, V.K. A Novel Chaotic System with Application to Secure Communications. In Proceedings of the 2020 9th International Conference on Modern Circuits and Systems Technologies (MOCAST), Bremen, Germany, 7–9 September 2020; pp. 1–4. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert–Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bifurc. Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef]
- Singh, J.P.; Roy, B. Coexistence of asymmetric hidden chaotic attractors in a new simple 4-D chaotic system with curve of equilibria. Optik 2017, 145, 209–217. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Çiçek, S.; Kocamaz, U.E.; Uyaroğlu, Y. Secure communication with a chaotic system owning logic element. AEU-Int. J. Electron. Commun. 2018, 88, 52–62. [Google Scholar] [CrossRef]
- Çiçek, S.; Ferikoğlu, A.; Pehlivan, I. A new 3D chaotic system: Dynamical analysis, electronic circuit design, active control synchronization and chaotic masking communication application. Optik 2016, 127, 4024–4030. [Google Scholar] [CrossRef]
- Kocamaz, U.E.; Çiçek, S.; Uyaroğlu, Y. Secure communication with chaos and electronic circuit design using passivity-based synchronization. J. Circuits, Syst. Comput. 2018, 27, 1850057. [Google Scholar] [CrossRef]
- Pone, J.R.M.; Çiçek, S.; Kingni, S.T.; Tiedeu, A.; Kom, M. Passive–active integrators chaotic oscillator with anti-parallel diodes: Analysis and its chaos-based encryption application to protect electrocardiogram signals. Analog. Integr. Circuits Signal Process. 2019, 1–15. [Google Scholar] [CrossRef]
- Kingni, S.T.; Rajagopal, K.; Çiçek, S.; Srinivasan, A.; Karthikeyan, A. Dynamic analysis, FPGA implementation, and cryptographic application of an autonomous 5D chaotic system with offset boosting. Front. Inf. Technol. Electron. Eng. 2020, 21, 950–961. [Google Scholar] [CrossRef]
- Rajagopal, K.; Çiçek, S.; Khalaf, A.J.M.; Pham, V.T.; Jafari, S.; Karthikeyan, A.; Duraisamy, P. A novel class of chaotic flows with infinite equilibriums and their application in chaos-based communication design using DCSK. Z. Für Naturforschung A 2018, 73, 609–617. [Google Scholar] [CrossRef]
- Rajagopal, K.; Pham, V.T.; Çiçek, S.; Jafari, S.; Karthikeyan, A.; Arun, S. A chaotic jerk system with different types of Equilibria and its application in communication system. Teh. Vjesn. 2020, 27, 681–686. [Google Scholar]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Huang, X.; Liu, L.; Li, X.; Yu, M.; Wu, Z. A New Pseudorandom Bit Generator Based on Mixing Three-Dimensional Chen Chaotic System with a Chaotic Tactics. Complexity 2019, 2019, 1–9. [Google Scholar] [CrossRef]
- Hu, H.; Liu, L.; Ding, N. Pseudorandom sequence generator based on the Chen chaotic system. Comput. Phys. Commun. 2013, 184, 765–768. [Google Scholar] [CrossRef]
- Tuna, M. A novel secure chaos-based pseudo random number generator based on ANN-based chaotic and ring oscillator: Design and its FPGA implementation. Analog Integr. Circuits Signal Process. 2020, 105, 167–181. [Google Scholar] [CrossRef]
- Moysis, L.; Volos, C.; Jafari, S.; Munoz-Pacheco, J.M.; Kengne, J.; Rajagopal, K.; Stouboulos, I. Modification of the Logistic Map Using Fuzzy Numbers with Application to Pseudorandom Number Generation and Image Encryption. Entropy 2020, 22, 474. [Google Scholar] [CrossRef] [PubMed]
- Demir, K.; Ergün, S. An analysis of deterministic chaos as an entropy source for random number generators. Entropy 2018, 20, 957. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Gao, C.; Liu, J.; Dong, S. A self-perturbed pseudo-random sequence generator based on hyperchaos. Chaos Solitons Fractals X 2019, 4, 100023. [Google Scholar] [CrossRef]
- Datcu, O.; Macovei, C.; Hobincu, R. Chaos Based Cryptographic Pseudo-Random Number Generator Template with Dynamic State Change. Appl. Sci. 2020, 10, 451. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Technical Report; Booz-Allen and Hamilton Inc.: Mclean, VA, USA, 2001. [Google Scholar]
- Lynnyk, V.; Sakamoto, N.; Čelikovskỳ, S. Pseudo random number generator based on the generalized Lorenz chaotic system. IFAC-PapersOnLine 2015, 48, 257–261. [Google Scholar] [CrossRef]
- Hamza, R. A novel pseudo random sequence generator for image-cryptographic applications. J. Inf. Secur. Appl. 2017, 35, 119–127. [Google Scholar] [CrossRef]
- Moysis, L.; Tutueva, A.; Volos, C.; Butusov, D.; Munoz-Pacheco, J.M.; Nistazakis, H. A Two-Parameter Modified Logistic Map and Its Application to Random Bit Generation. Symmetry 2020, 12, 829. [Google Scholar] [CrossRef]
- Nazaré, T.E.; Nepomuceno, E.G.; Martins, S.A.; Butusov, D.N. A Note on the Reproducibility of Chaos Simulation. Entropy 2020, 22, 953. [Google Scholar] [CrossRef]
- Sayed, W.S.; Radwan, A.G.; Fahmy, H.A.; El-Sedeek, A. Software and Hardware Implementation Sensitivity of Chaotic Systems and Impact on Encryption Applications. Circuits Syst. Signal Process. 2020, 39, 5638–5655. [Google Scholar] [CrossRef]
- Liu, B.; Xiang, H.; Liu, L. Reducing the Dynamical Degradation of Digital Chaotic Maps with Time-Delay Linear Feedback and Parameter Perturbation. Math. Probl. Eng. 2020, 2020, 4926937. [Google Scholar] [CrossRef]
- Kaddoum, G. Wireless chaos-based communication systems: A comprehensive survey. IEEE Access 2016, 4, 2621–2648. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).