Abstract
A large database of nuclear magnetic resonance (NMR) logging data from clastic rocks of offshore oil and gas fields of Western Australia was used to assess the performance of multi regression analysis (MRA) to calculate NMR log outputs from conventional well logs. This short paper introduces a set of MRA equations for the calculation of the NMR log outputs using conventional well logs as inputs. This study shows that unlike machine learning methods the MRA approach fails to predict most of the NMR log outputs with acceptable accuracy but can provide Coates and SDR permeabilities with R2 of more than 0.75.
1. Introduction
The nuclear magnetic resonance (NMR) logging tool uses the response of hydrogen to a magnetic field through T2 relaxation, which is the process by which the transverse components of hydrogen magnetisation decay [1]. In saturated porous media, the NMR T2 relaxation rate is governed by the following equation which is a function of individual intrinsic (or bulk), surface, and diffusion relaxation processes [2]:
where T2B, T2S, and T2D, are the bulk, surface, and diffusion transversal relaxation time in ms, respectively.
Since in geological porous media transversal relaxation is chiefly controlled by surface relaxation, the T2 relaxation time is related to surface to volume ratio (S/V) [3]:
where ρ is the transversal surface relaxivity (um/s).
As can be seen in Equation (2), the transverse relaxation rate, 1/T2, is proportional to the surface-to-volume ratio (S/V). As a result, the relaxation of hydrogen close to the solid surface is faster than that of those in the free-flowing fluid. Thus, the smaller pores where hydrogens are closer to solid surfaces have a faster relaxation rate than the larger pore spaces. This approach enables the NMR tool to provide some of the rock characteristics such as porosity, pore size distribution, and permeability that are explained in detail in many publications [1,4,5,6,7,8,9,10,11,12].
The T2 distribution is generally represented by a set of eight bins porosities (BP1 to BP8) determined by a set of T2 cutoffs. For clastic rocks, the cutoffs shown in Figure 1 are generally used to differentiate the bin porosities and therefore to present several types of pore systems as below:
where BP = bin porosity; CBW = clay bound water; BVI = bulk volume irreducible; FFI = free fluid index; = effective porosity; = total porosity; and = irreducible water saturation.
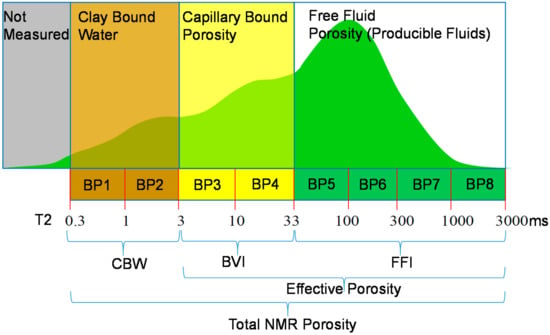
Figure 1.
The T2 distribution shows clay-bound water (CBW), capillary bound fluid (BVI), and free fluid (FFI). These properties are shown in relation to the T2 signal. From [13].
The pore size distribution of the NMR logging tool has been used to calculate the rock’s matrix absolute permeability. The two most applied equations are Coates (Equation (9)) and the SDR (Schlumberger-Doll Research, Equation (10)) models [10,14,15,16].
where k = matrix permeability (mD); φe = NMR effective porosity (%); C = a constant specific to the formation that reflects the correlation between the rock’s pore throat and pore size, and in fact, it is a function of pore geometry and is generally considered 10 as a default value for clastic rocks; T2LM = the logarithmic mean of the T2 distribution, milliseconds; and “a” = a coefficient that depends on formation type and has to be determined through calibration with core porosity. “a” is generally close to four for sandstone.
This study is an attempt to assess the ability of the multi regression analysis (MRA) method to generate NMR log outputs using conventional well logs as inputs for clastic rocks.
2. Materials and Methods
More than 16,000 data points from 16 formations of WA offshore basins were used to evaluate the performance of linear multi regression analysis (MRA) to calculate NMR logging tool outputs. The data were collected from formations with the age range of Permian to Tertiary from 14 wells with a complete set of CMR and conventional well logs. Wells are located within 3 main offshore basins of WA with a depth range of from 1188 to 4138 m (Table 1).

Table 1.
The list of the basins, number of data points for each formation, age, depth interval, and type of lithology used in this study.
The well logs used in this study as MRA inputs are density (RHOB, g/cc), Neutron (NPHI, v/v), Photoelectric (PEF, b/e), resistivity (deep, shallow, and very shallow, ohm-m), and sonic (DT, us/ft). Instead of gamma-ray (GR), the volume of shale (Vsh, v/v) was used since GR may vary from well to well for the same formation. Effective porosity calculated from the density tool (PHIDe, v/v) was also included to increase MRA accuracy. Table 2 provides a brief explanation for each well log used for this study. Figure 2 shows the variation of well logs inputs.

Table 2.
A list of typical well logs and their general applications.
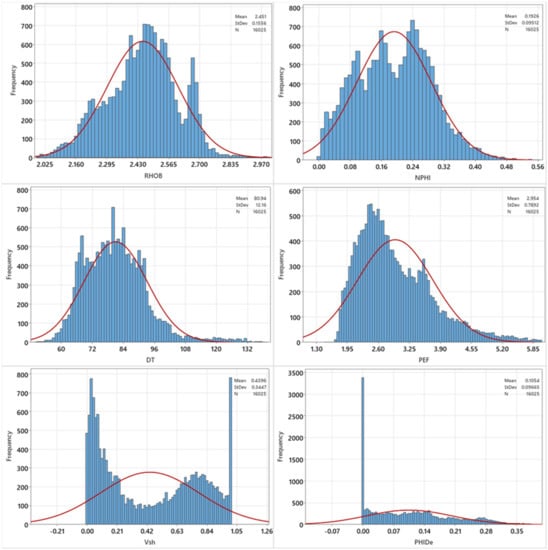
Figure 2.
Variations of the major MRA inputs.
The volume of shale was calculated for all formations with the following general equation to normalise the GR values:
The GRmin and GRmax values are the values of the sand and shale intervals, respectively, taken from the GR reading for each well.
The effective porosity was calculated by including a correction for the contribution of shale to the log measurements. The density log was used to calculate effective porosity for shaly formations using the following equation:
where φDshc = shale corrected density porosity; φe = effective porosity; ρb = bulk density (g/cc); ρf = fluid density (g/cc); ρma = matrix density (g/cc); Vsh = volumetric fraction of shale; ρsh = shale bulk density (g/cc) that was identified for each well separately.
MRA outputs are BP1 to BP8, CBW, BVI, FFI, Swirr, T2LM, Coates permeability (kCoates), SDR permeability (kSDR). To increase the performance of MRA, instead of using permeability values the logarithm of permeabilities (LogkCoates and LogkSDR) were used as outputs. Figure 3 shows the variation of major MRA outputs.
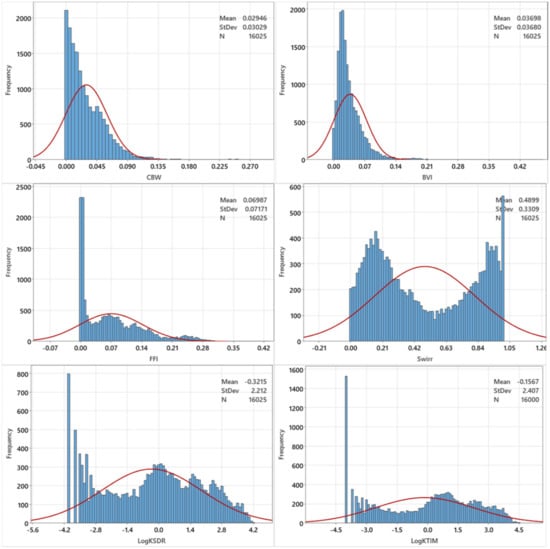
Figure 3.
Variations of the major MRA outputs.
Before running the MRA, all well logs were quality controlled and checked for any possible errors. A careful depth match was conducted between NMR and other logs using GR that was available for both NMR and conventional well logs.
3. Multi Regression Analysis Results
At first, all available conventional well logs were used as MRA inputs to predict NMR log outputs separately. This needs to be noted that all bin porosities were also considered as NMR outputs although they were also used in the form of CBW, BVI, and FFI too (see Equations (3)–(5)).
Table 3 shows the generated equations and their corresponding R2 for each output. To optimise the equations by using fewer log inputs with nearly the same accuracy in terms of R2, inputs with less influence were removed and new equations were generated for each output. Table 4 shows the optimised equations for each output with their R2.

Table 3.
MRA equations for the calculation of NMR log outputs. Variables with ignorable influence are removed from the equations.

Table 4.
Optimised MRA equations for the calculation of NMR log outputs.
To assess the performance of the MRA method for clay-rich and clay-poor lithologies, well logs were separated based on clay content. The dataset was classified based on Vsh (Vsh < 50% and Vsh > 50%), to separate shale from shaly sand. A comparison of the results showed that generally there were no improvements in the MRA performance, and even, the performance was reduced for all of the outputs. Perhaps the performance deterioration could be due to the reduction of the number of data points.
4. Discussion and Conclusions
In this study, the MRA method was used to generate the NMR tool’s outputs using a large database of conventional well logs. Figure 4 shows the success of linear MRA in providing NMR log outputs based on data in Table 4. As it can be seen from the figure, based on the coefficient of determination (R2), the SDR and Coates permeabilities are successfully calculated followed by FFI and Swirr. The prediction of the remaining parameters with R2 less than 0.6 is statistically unreliable.
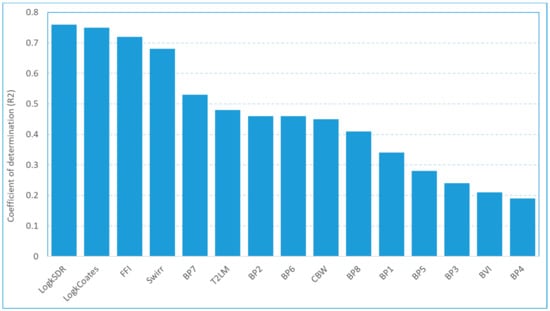
Figure 4.
The coefficient of determination (R2) or the success of MRA in predicting NMR log outputs.
The nature of the conventional logging tools is a way that each tool targets a specific property of rock and its pore fluid. GR detects natural emission of gamma radiation that in sedimentary rocks is mostly sourced from clays and therefore the tool is generally used for Vsh calculation. The density tool, RHOB, provides the bulk density of the rock based on the GR Compton scattering process and it is used to calculate total porosity. Neutron tool, NPHI, provides total porosity based on the hydrogen content that is believed to mostly reside in pore filling fluids. Sonic tool, DT, measures sound waves velocity that can be used to calculate porosity. Photoelectric tool, PEF, uses cross-sectional capture of low energy GR and thus can provide lithology. Resistivity tools measure the electrical resistivity of the rock which is the function of several parameters including pore water resistivity, formation factor, and fluid saturation. Therefore, the major application of resistivity data is to calculate fluid saturation. In shaly formations where clay is present the interpretation of well logs becomes complex. For example, in shaly formations all porosity tools (neutron, density, and sonic tools) overestimate porosity. In addition, clays create excessive conductivity due to their cation exchange capacity (CEC) and therefore result in reducing resistivity logs readings. This makes the relation between conventional logs and NMR more intricate.
On the other hand, the NMR logging tool uses hydrogen T2 relaxation time and provides pore size distribution based on some empirical T2 cutoffs. BP1 and BP2 make up a part of pore space that is occupied by CBW. BP3 and BP4 provide capillary pore spaces where immobile fluids exist and are named BVI. BP5 to BP8 provide large pore spaces where mobile pore fluid resides and is called FFI. This ability of the NMR tool to differentiate different pore spaces is out of reach of conventional logging tools where porosity tools such as RHOB, NPHI, and Sonic can just provide mostly total porosity regardless of their sizes. Such a difference between NMR and conventional logging tools could be the reason that they fail to predict bin porosities (BPs) accurately. On the other hand, it can be seen in Table 3 and Table 4 that permeability, FFI, and Swirr are the only NMR outputs that are calculated with relatively high accuracy. The key point here is that conventional logging tools provide total porosity which is naturally close to FFI which is the dominant porosity in sandstone reservoirs (see Figure 3), the major rock type in this study. Consequently, conventional logging tools fail to differentiate and predict CBW and BVI. Since for NMR’s permeability and Swirr, FFI plays an important controlling factor consequently conventional logging data can predict them with higher accuracy.
The same data set used in this study was used by the author to assess machine learning methods for generating NMR log outputs [13]. The study showed that Adaptive Boosting can predict CBW, FFI, permeability, T2LM, and SWirr with an R2 of more than 0.9. This indicates that, unlike machine learning models that can solve complex relations between inputs and output, linear MRA fails to perform well where the relation between inputs and outputs are complex.
In conclusion, this study indicates that the MRA can be utilised to generate NMR permeability with relatively high accuracy from conventional logging tools for clastic rocks.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Coates, G.R.; Xiao, L.; Prammer, M.G. NMR Logging: Principles and Applications; Haliburton Energy Services: Houston, TX, USA, 1999; Volume 234. [Google Scholar]
- Bloembergen, N.; Purcell, E.M.; Pound, R.V. Relaxation effects in nuclear magnetic resonance absorption. Phys. Rev. 1948, 73, 679. [Google Scholar] [CrossRef]
- Kleinberg, R.; Kenyon, W.; Mitra, P. Mechanism of NMR relaxation of fluids in rock. J. Magn. Reson. Ser. A 1994, 108, 206–214. [Google Scholar] [CrossRef]
- Freedman, R. Advances in NMR logging. J. Pet. Technol. 2006, 58, 60–66. [Google Scholar] [CrossRef]
- Dunn, K.-J.; Bergman, D.J.; LaTorraca, G.A. Nuclear Magnetic Resonance: Petrophysical and Logging Applications; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Kenyon, W. Petrophysical principles of applications of NMR logging. Log. Anal. 1997, 38. [Google Scholar]
- Prammer, M.G.; Drack, E.D.; Bouton, J.C.; Gardner, J.S. Measurements of Clay-Bound Water and Total Porosity by Magnetic Resonance Logging: SPE-36522. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 6–9 October 1996. [Google Scholar]
- Kleinberg, R.L. Utility of NMR T2 distributions, connection with capillary pressure, clay effect, and determination of the surface relaxivity parameter ρ2. Magn. Reson. Imaging 1996, 14, 761–767. [Google Scholar] [CrossRef]
- Timur, A. Producible porosity and permeability of sandstones investigated through nuclear magnetic resonance principles. Log. Anal. 1969, 3, 1–15. [Google Scholar]
- Kenyon, W.E.; Day, P.I.; Straley, C.; Willemsen, J.F. A three-part study of NMR longitudinal relaxation properties of water-saturated sandstones. SPE Form. Eval. 1988, 3, 622–636. [Google Scholar] [CrossRef]
- Prammer, M. NMR pore size distributions and permeability at the well site. In SPE Annual Technical Conference and Exhibition; OnePetro: New Orleans, LA, USA, 1994. [Google Scholar]
- Dunn, K.J.; LaTorraca, G.A.; Warner, J.L.; Bergman, D.J. On the calculation and interpretation of NMR relaxation time distributions. In SPE Annual Technical Conference and Exhibition; OnePetrol: New Orleans, LA, USA, 1994. [Google Scholar]
- Rezaee, R. Synthesizing Nuclear Magnetic Resonance (NMR) Outputs for Clastic Rocks Using Machine Learning Methods, Examples from North West Shelf and Perth Basin, Western Australia. Energies 2022, 15, 518. [Google Scholar] [CrossRef]
- Kenyon, W.E.; Day, P.I.; Straley, C.; Willemsen, J.F. NMR in partially saturated rocks: Laboratory insights on free fluid index and comparison with borehole logs. Log. Anal. 1995, 36, 40–56. [Google Scholar]
- Coates, G.R.; Galford, J.; Mardon, D.; Marschall, D. A new characterization of bulk-volume irreducible using magnetic resonance. Log. Anal. 1998, 39. [Google Scholar]
- Kleinberg, R.L. Nuclear Magnetic Resonance. In Experimental Methods in the Physical Sciences; Elsevier: Amsterdam, The Netherlands, 1999; pp. 337–385. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).