Evaluation of Chemical Kinetic Mechanisms for Methane Combustion: A Review from a CFD Perspective
Abstract
:1. Introduction
2. An Overview of Kinetic Mechanism Development
2.1. Concepts and Definitions
2.2. Target Combustion Characteristics for Mechanism Development
2.2.1. Premixed Auto-Ignition
2.2.2. Flame Propagation
2.2.3. Flame Extinction
3. Selected Kinetic Mechanisms
3.1. Detailed Mechanisms
3.2. Global Mechanisms
3.3. Reduced Mechanisms
4. Modeling Details
5. Mechanism Evaluation
5.1. CH4/Air Combustion
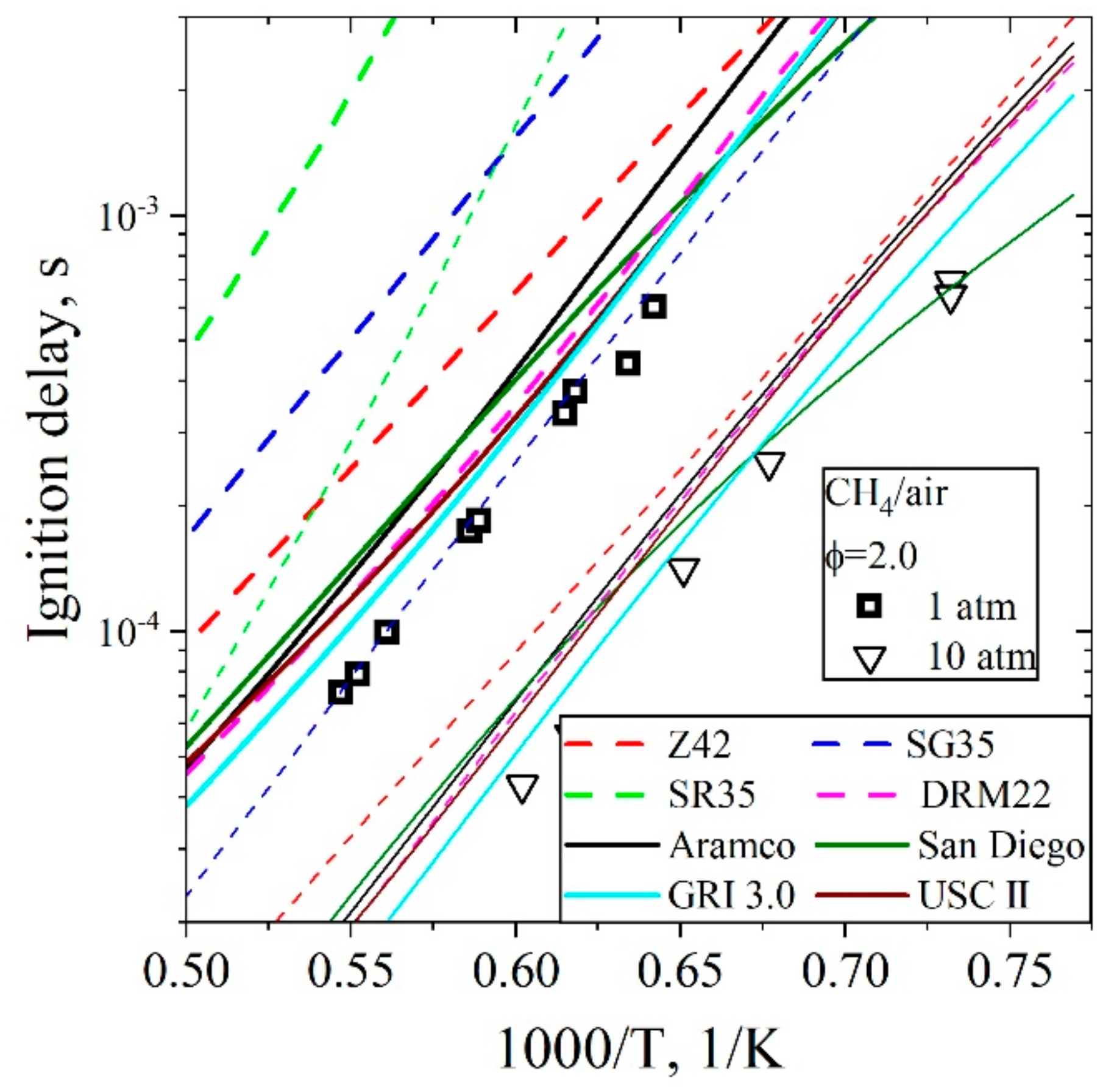
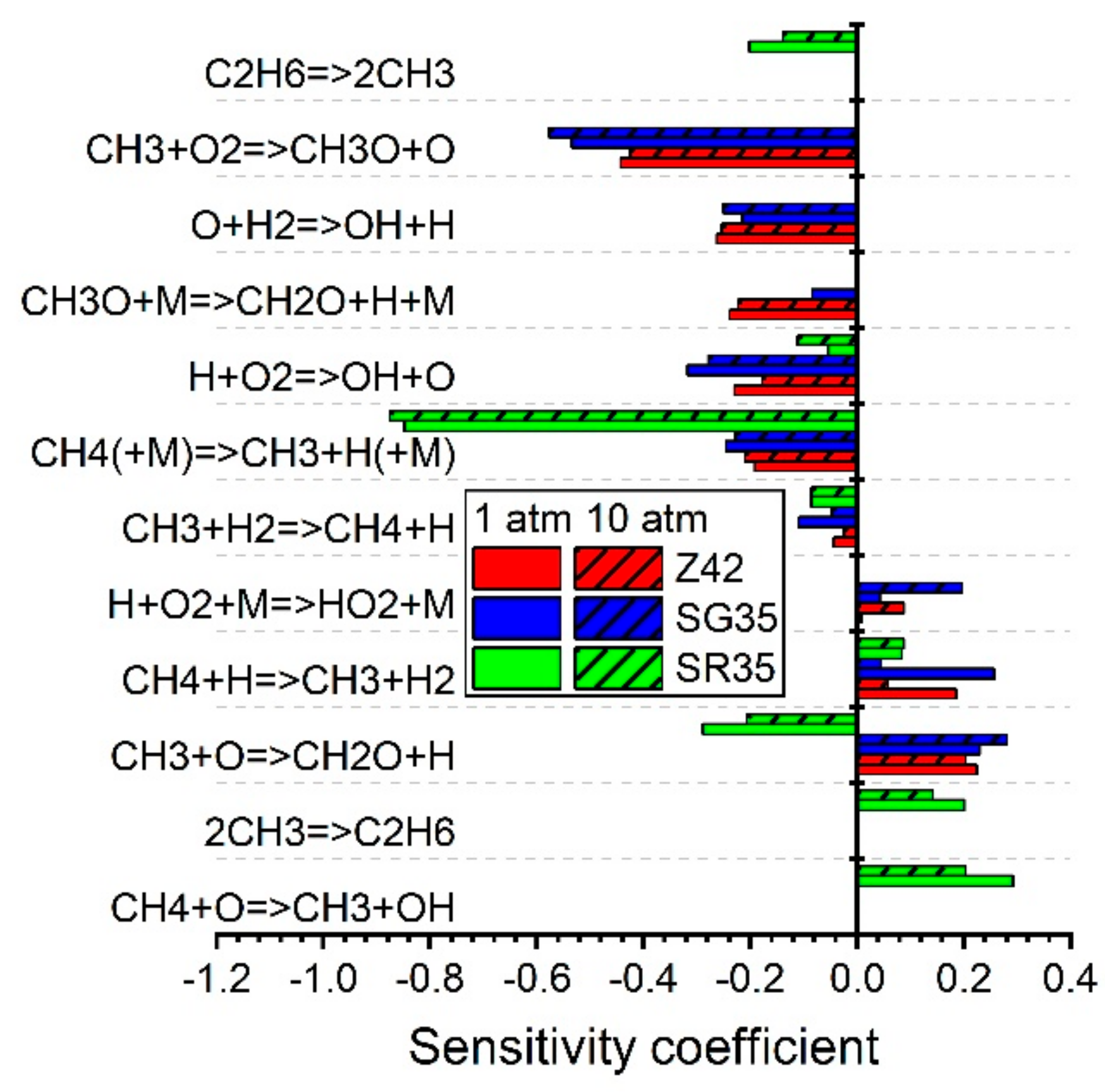
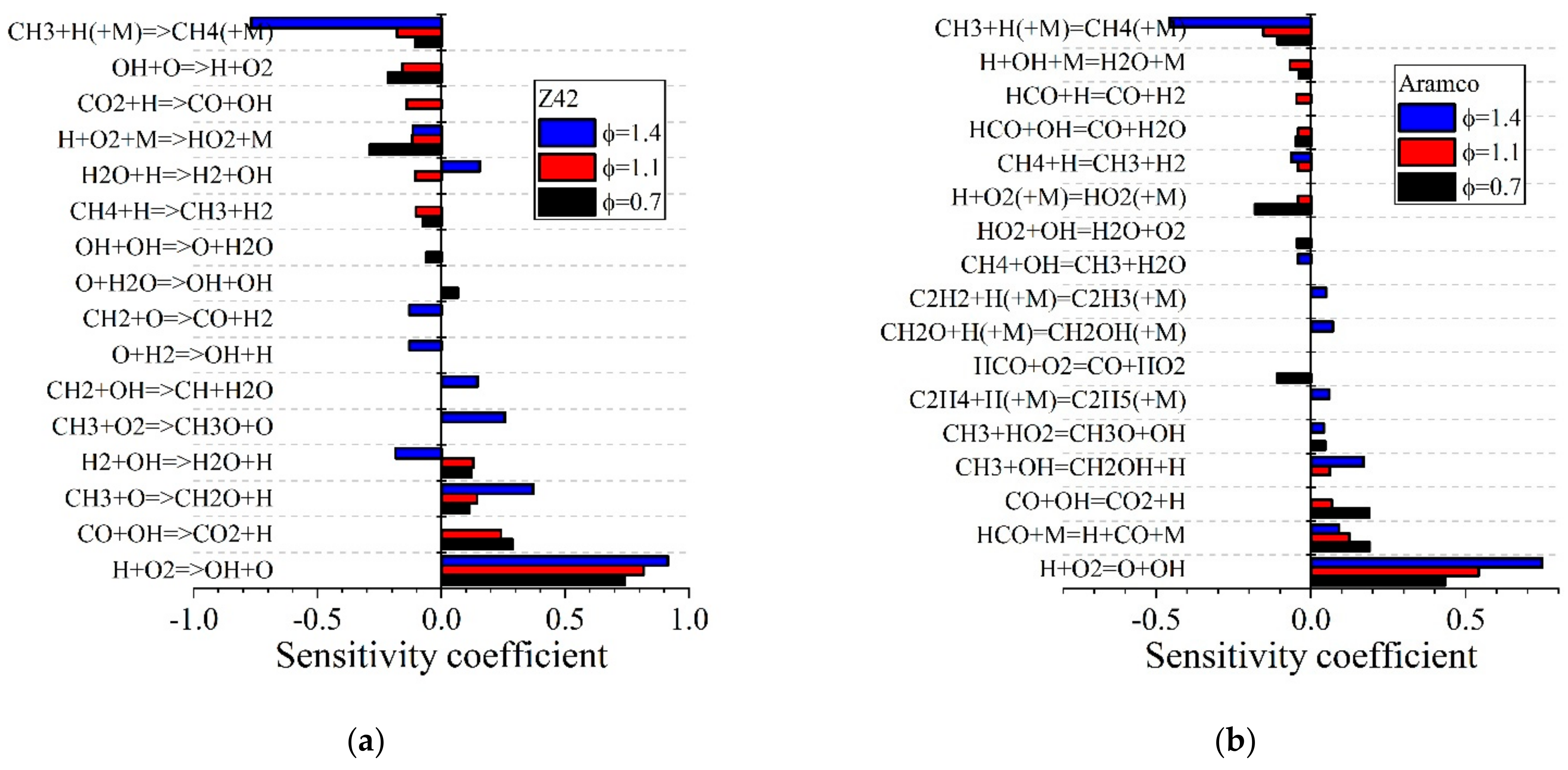
5.1.1. Ignition Delay Time CH4/Air
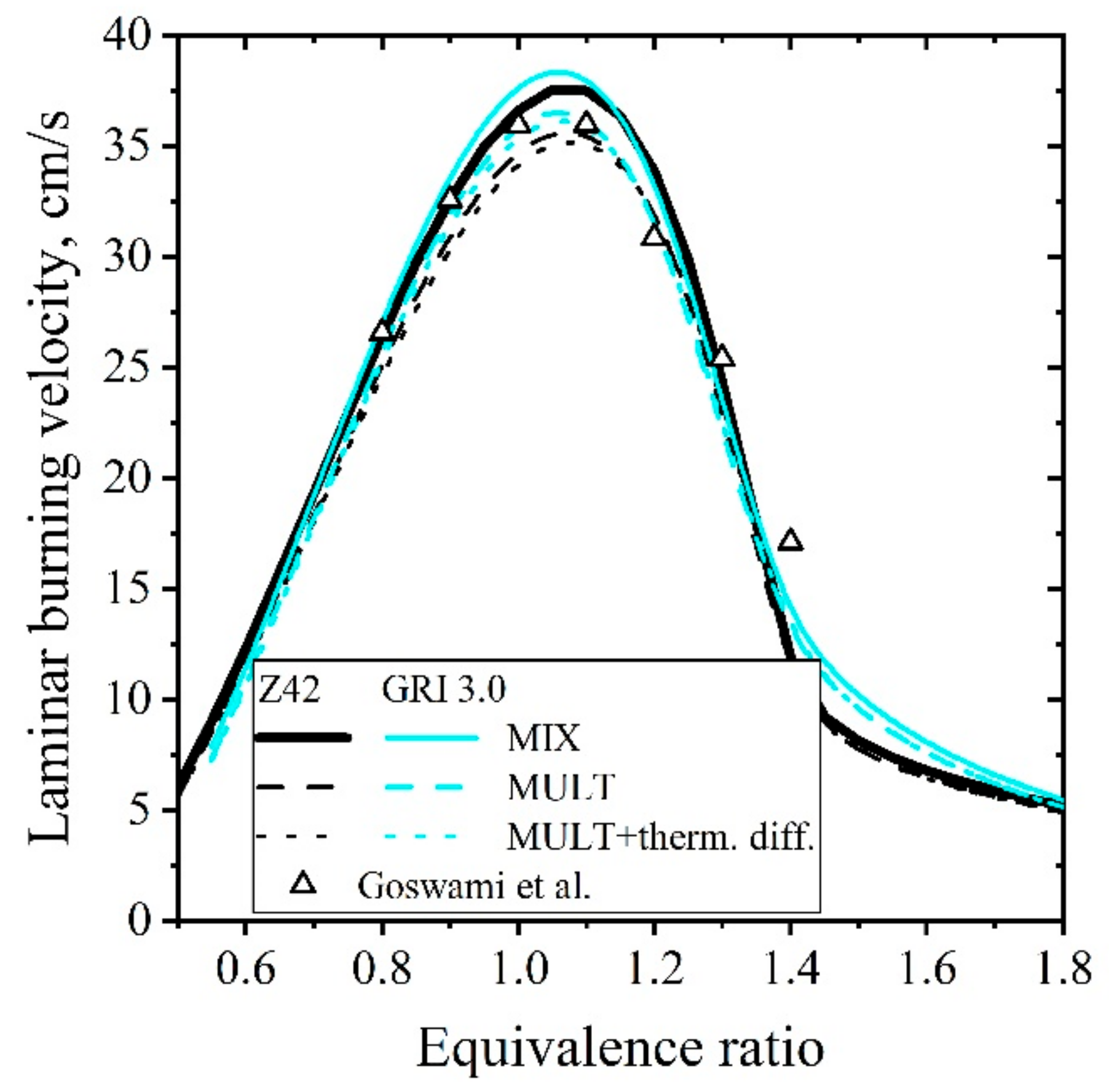
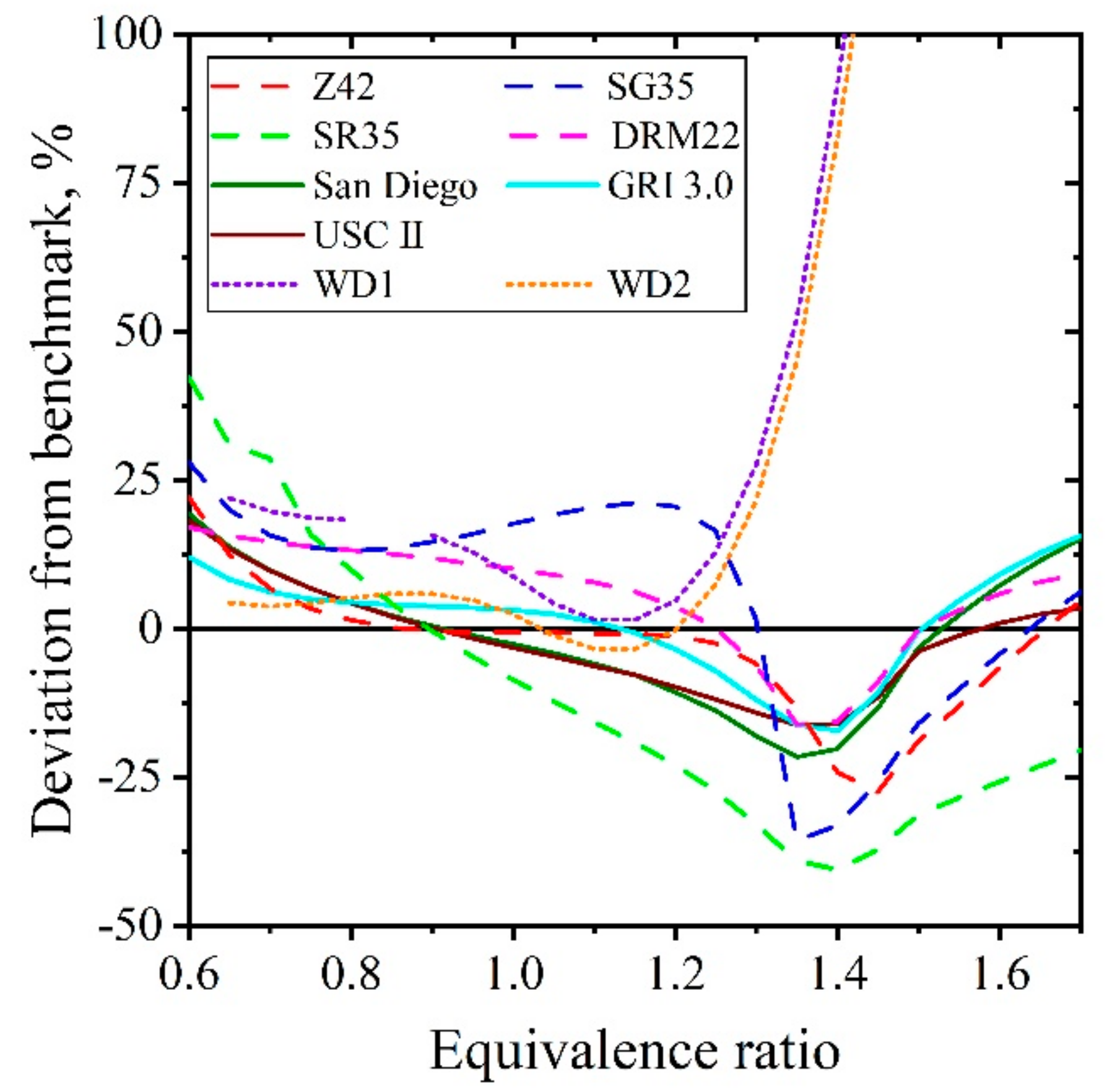
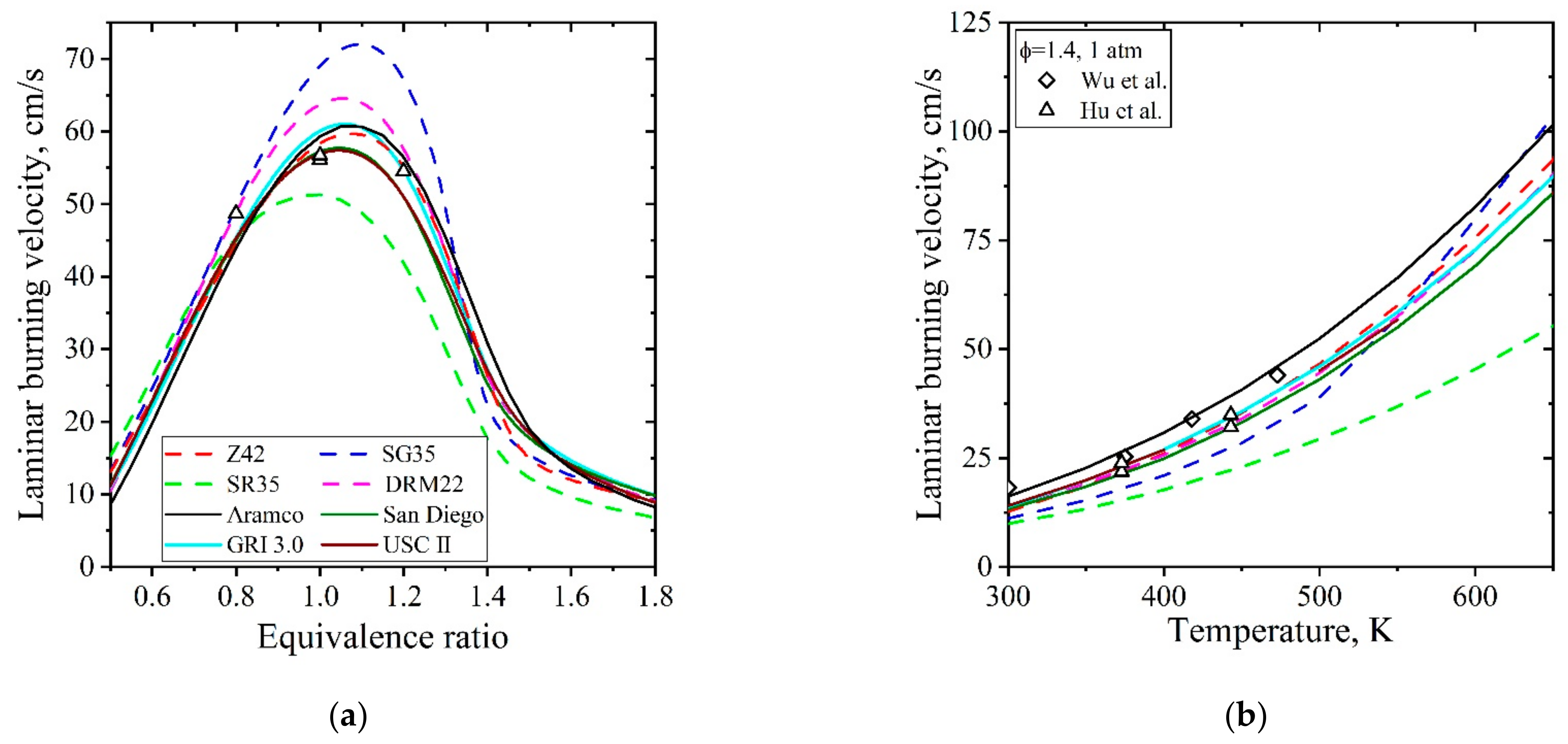
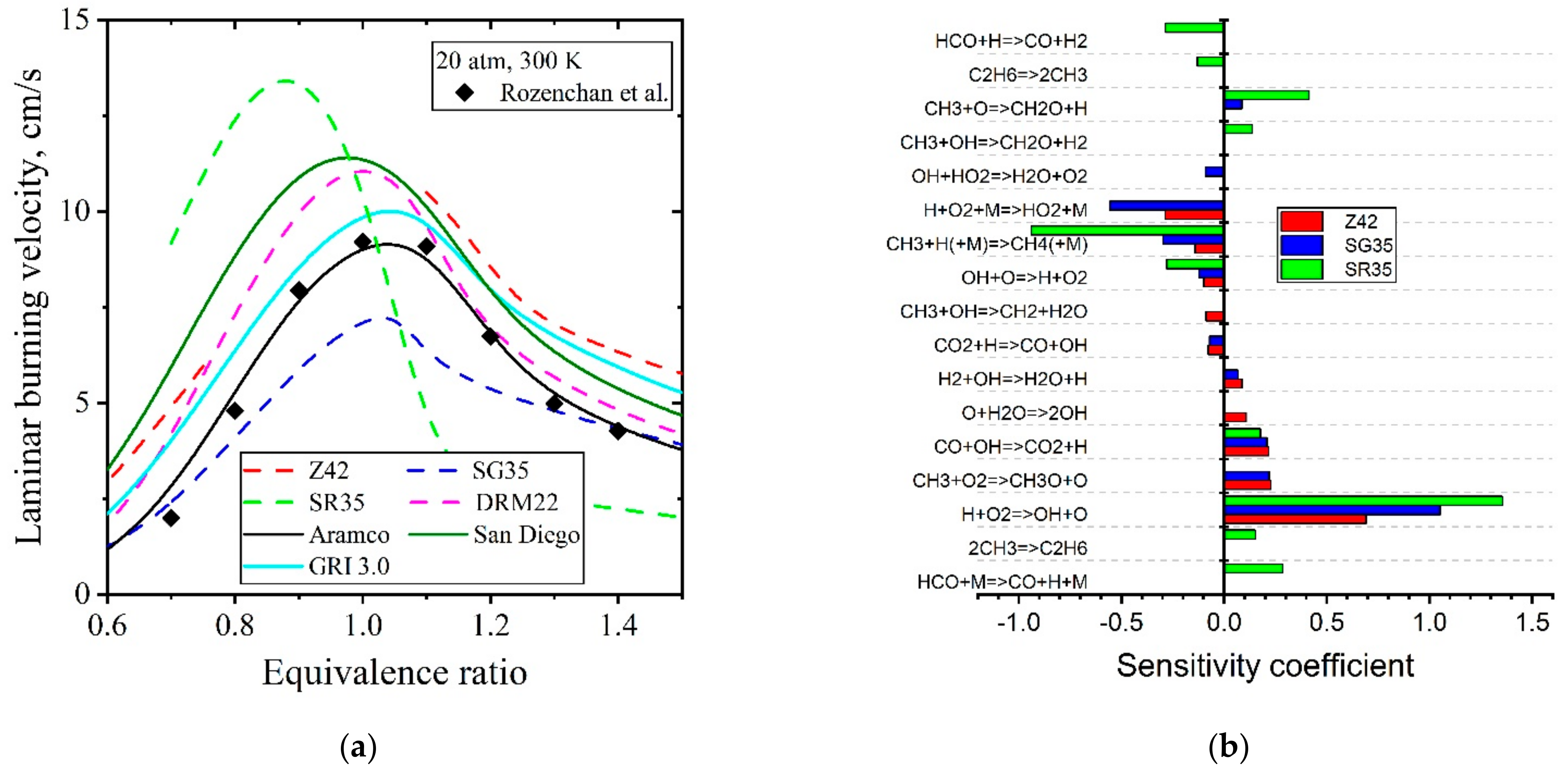
5.1.2. Laminar Flames of CH4/Air
5.1.3. Extinction Strain Rate of Premixed CH4/Air Flames
5.2. Flames at CO2 Enriched Conditions
5.3. CH4/H2/Air Combustion
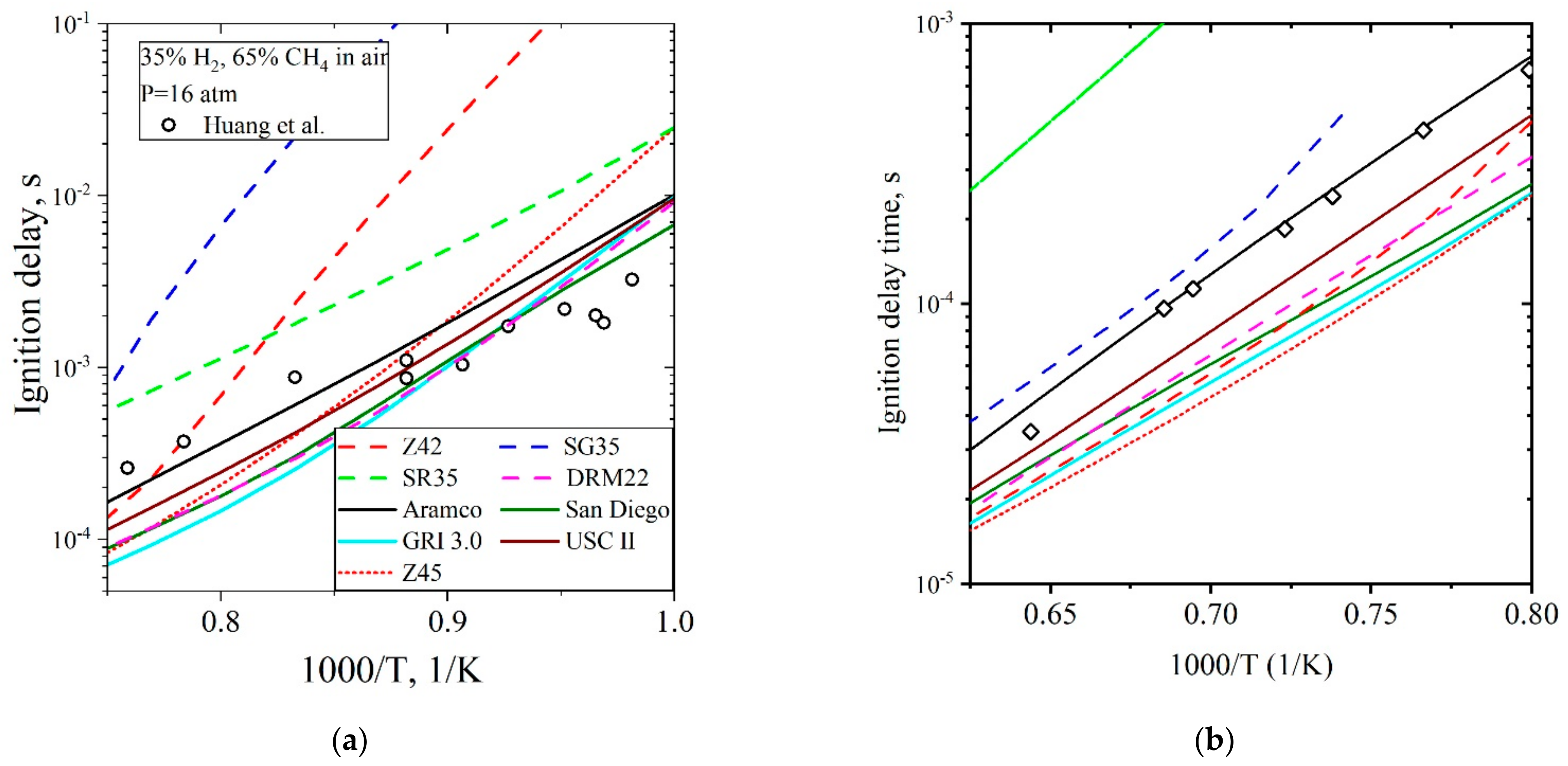
5.3.1. Ignition Delay Time CH4/H2/Air
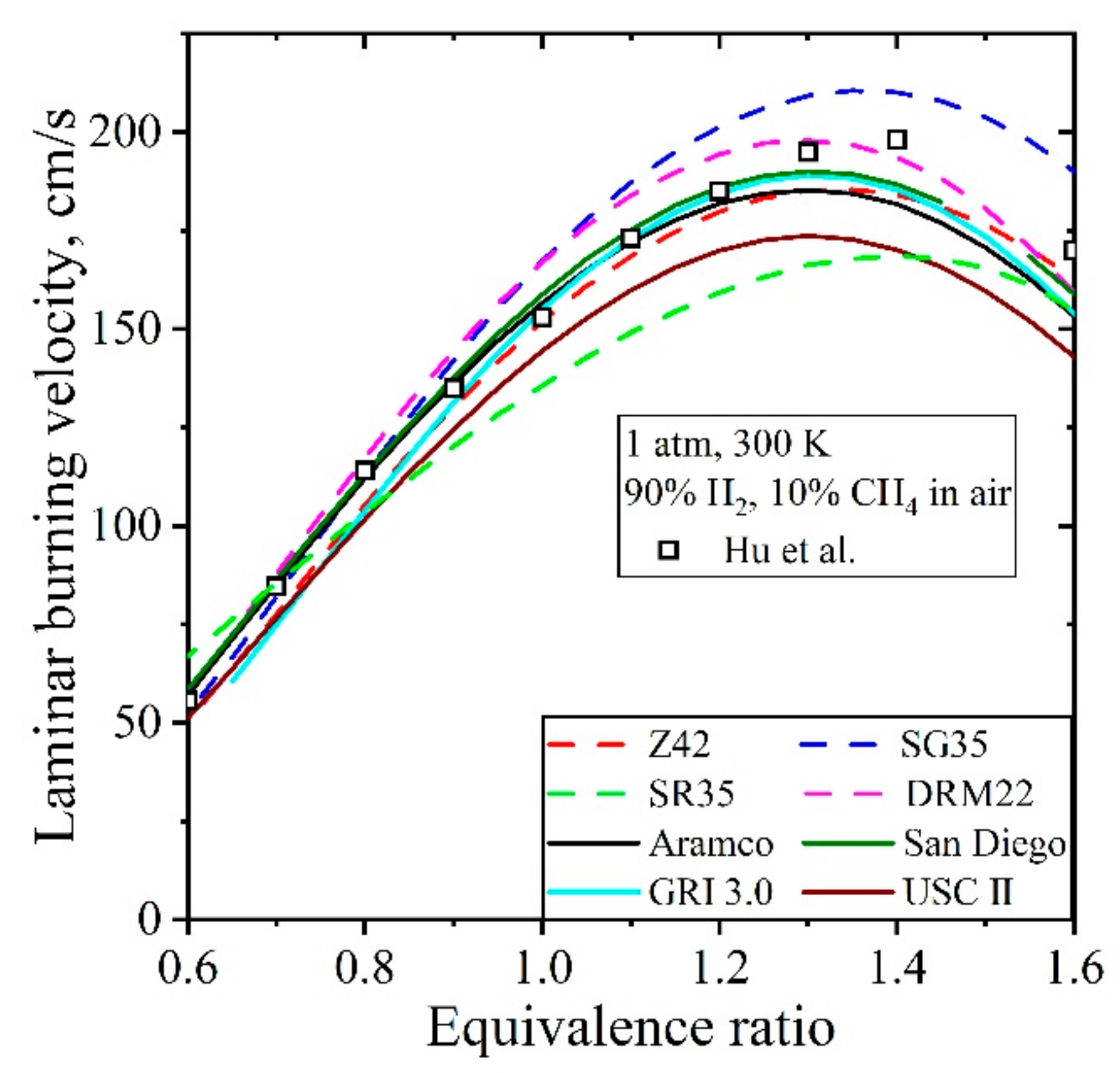
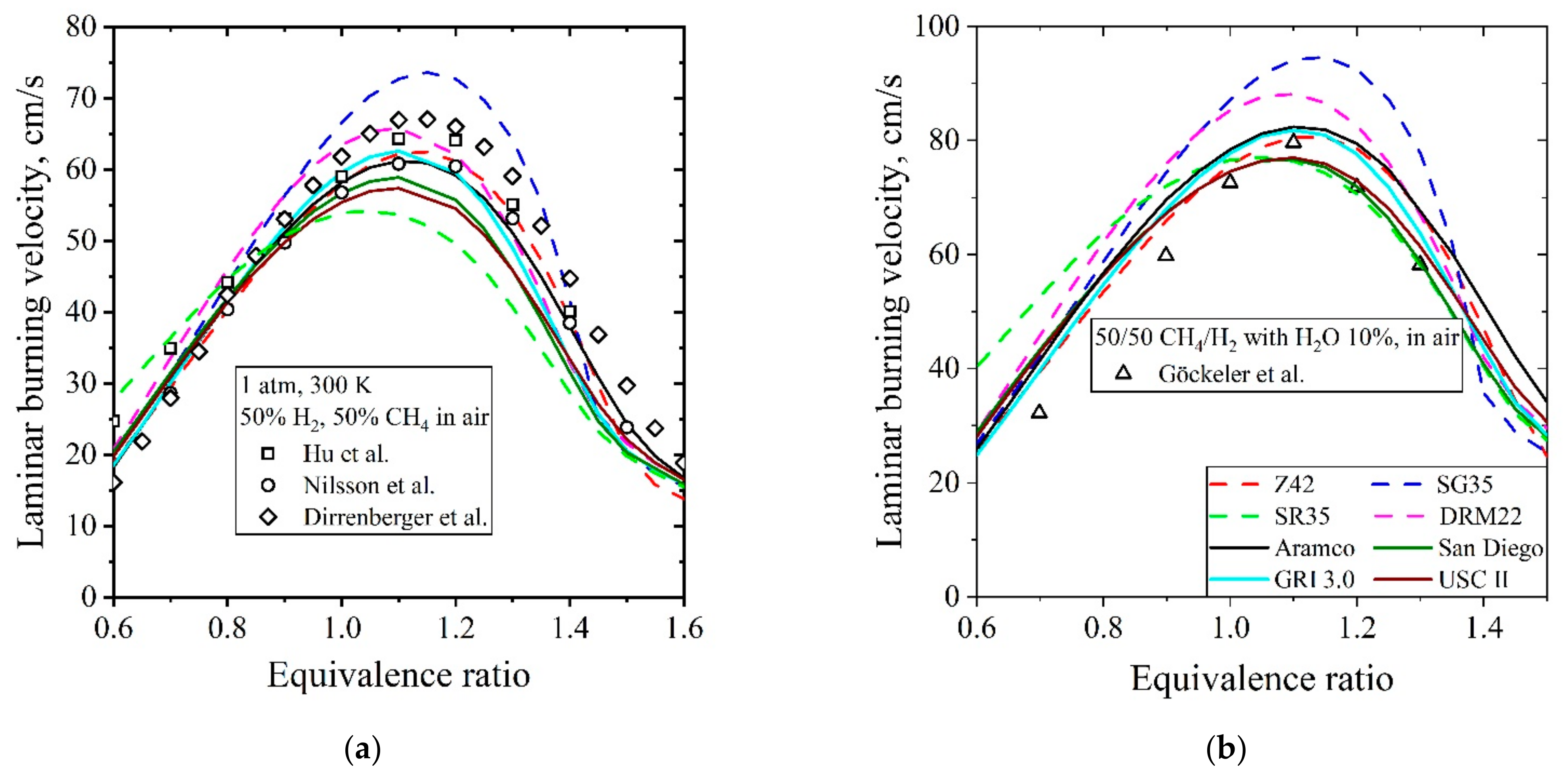
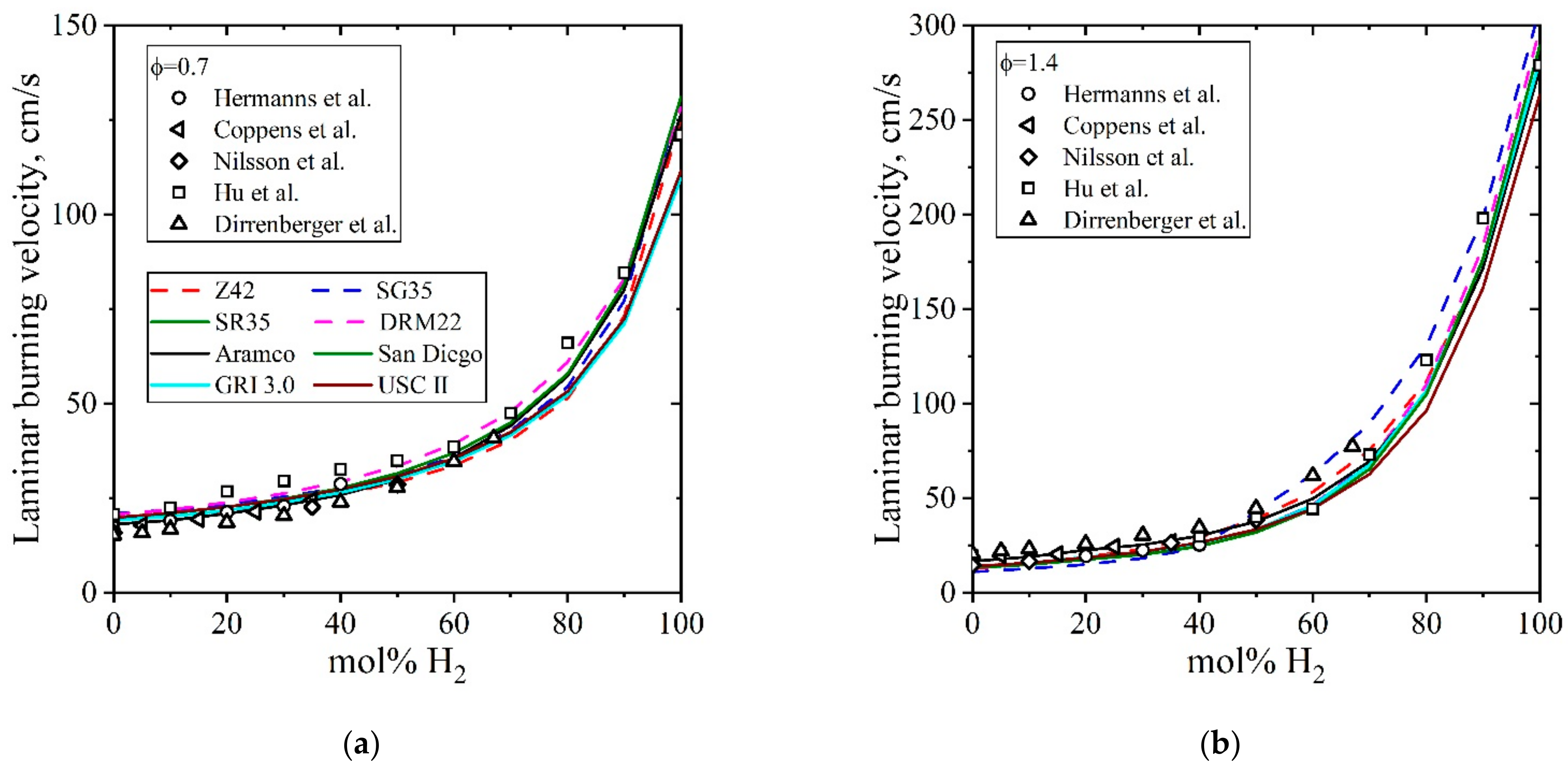
5.3.2. Laminar Burning Velocity CH4/H2/Air
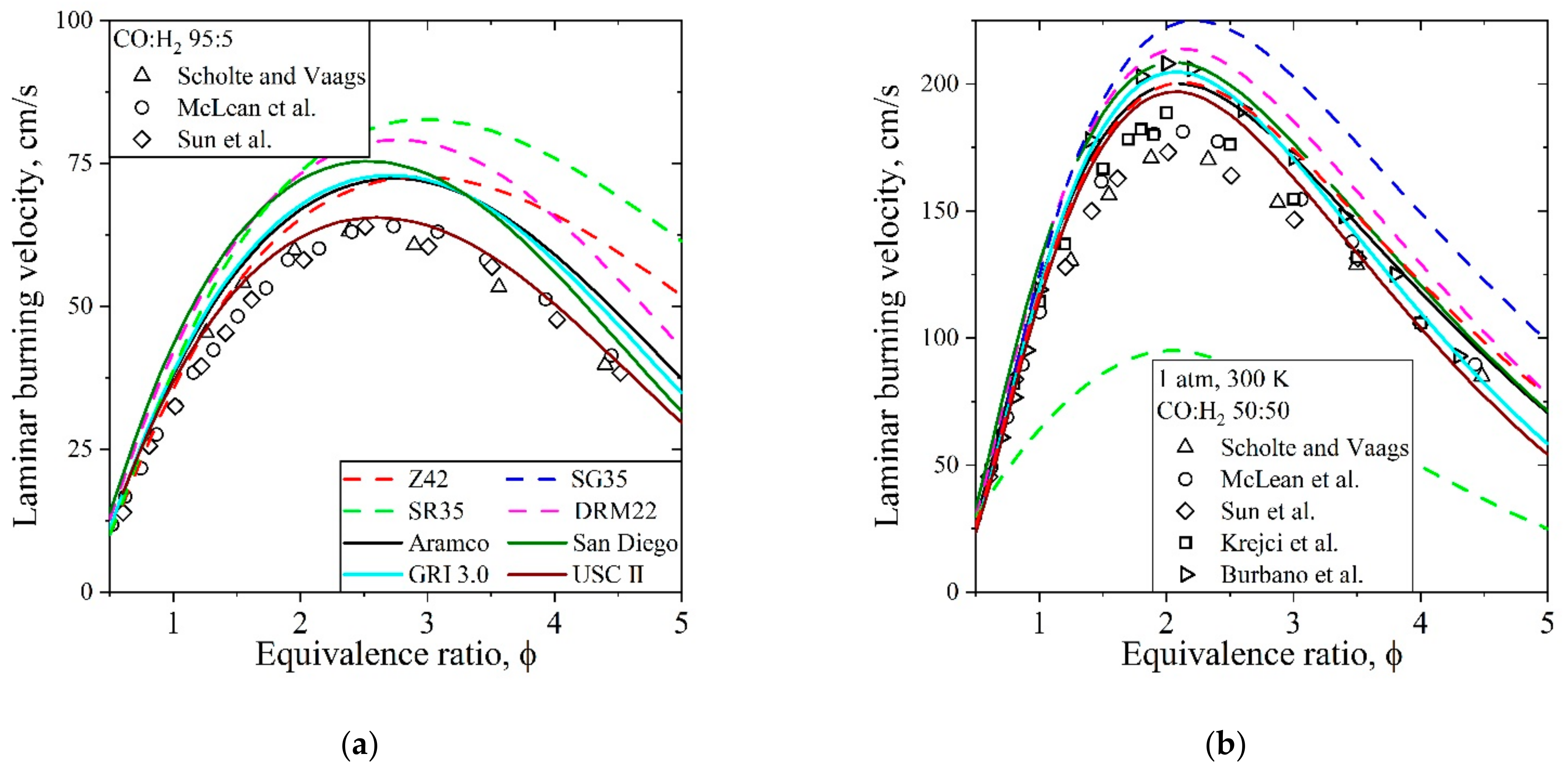
5.4. Syngas, CO/H2/Air, Flames
6. Discussion and Recommendations
6.1. Detailed Mechanisms
6.2. Reduced Mechanisms
6.3. Global Mechanisms
6.4. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
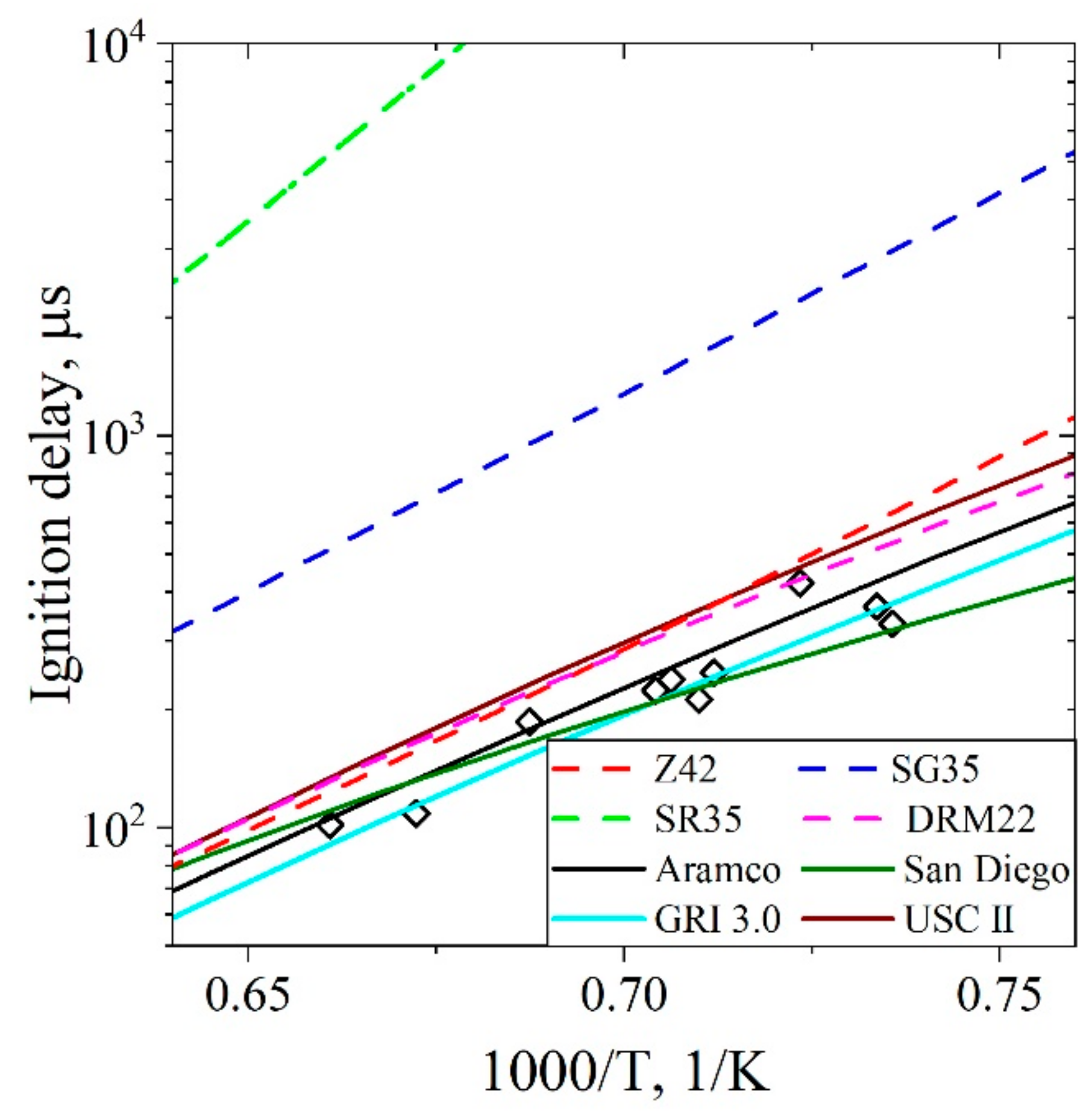
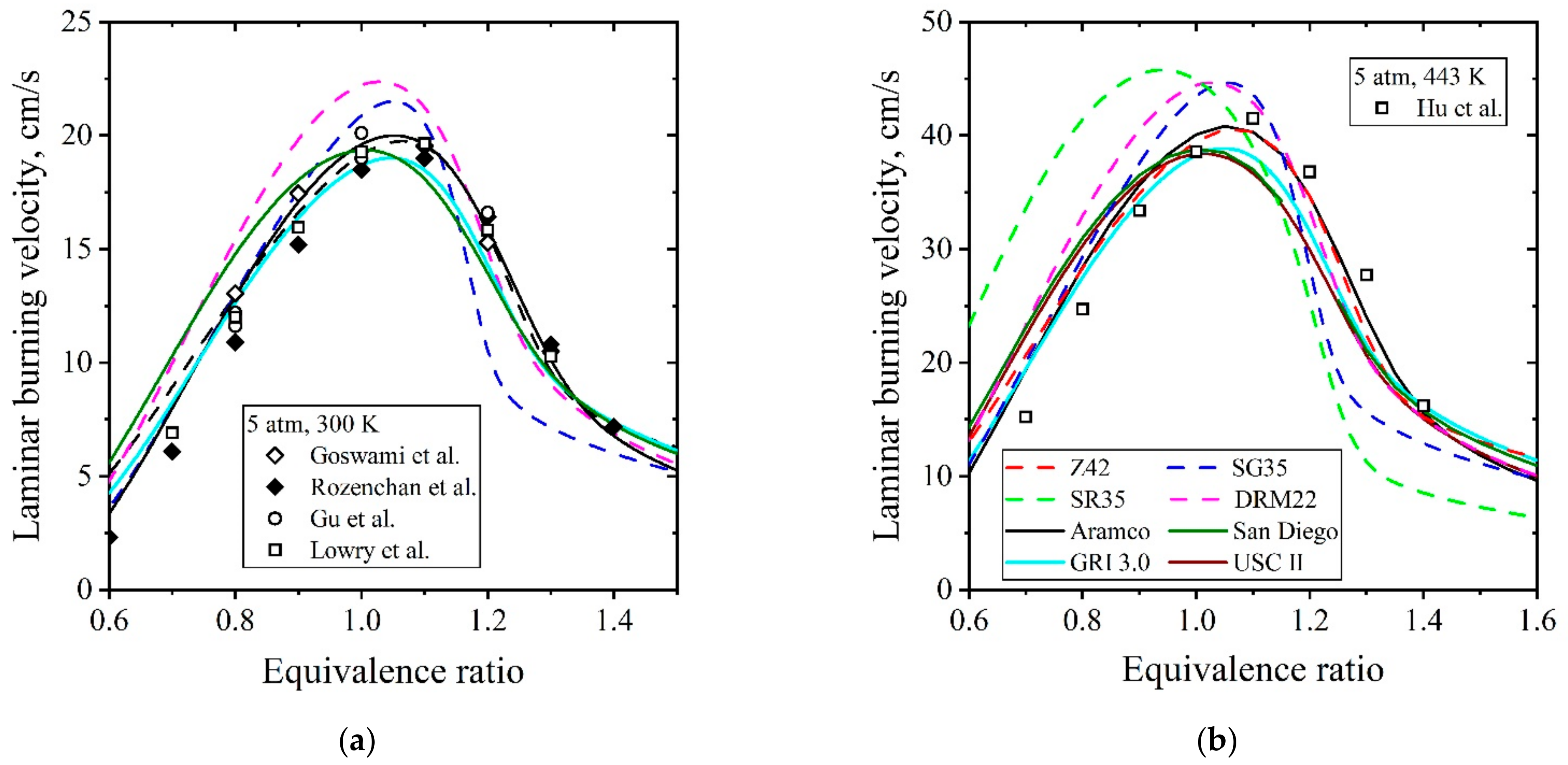
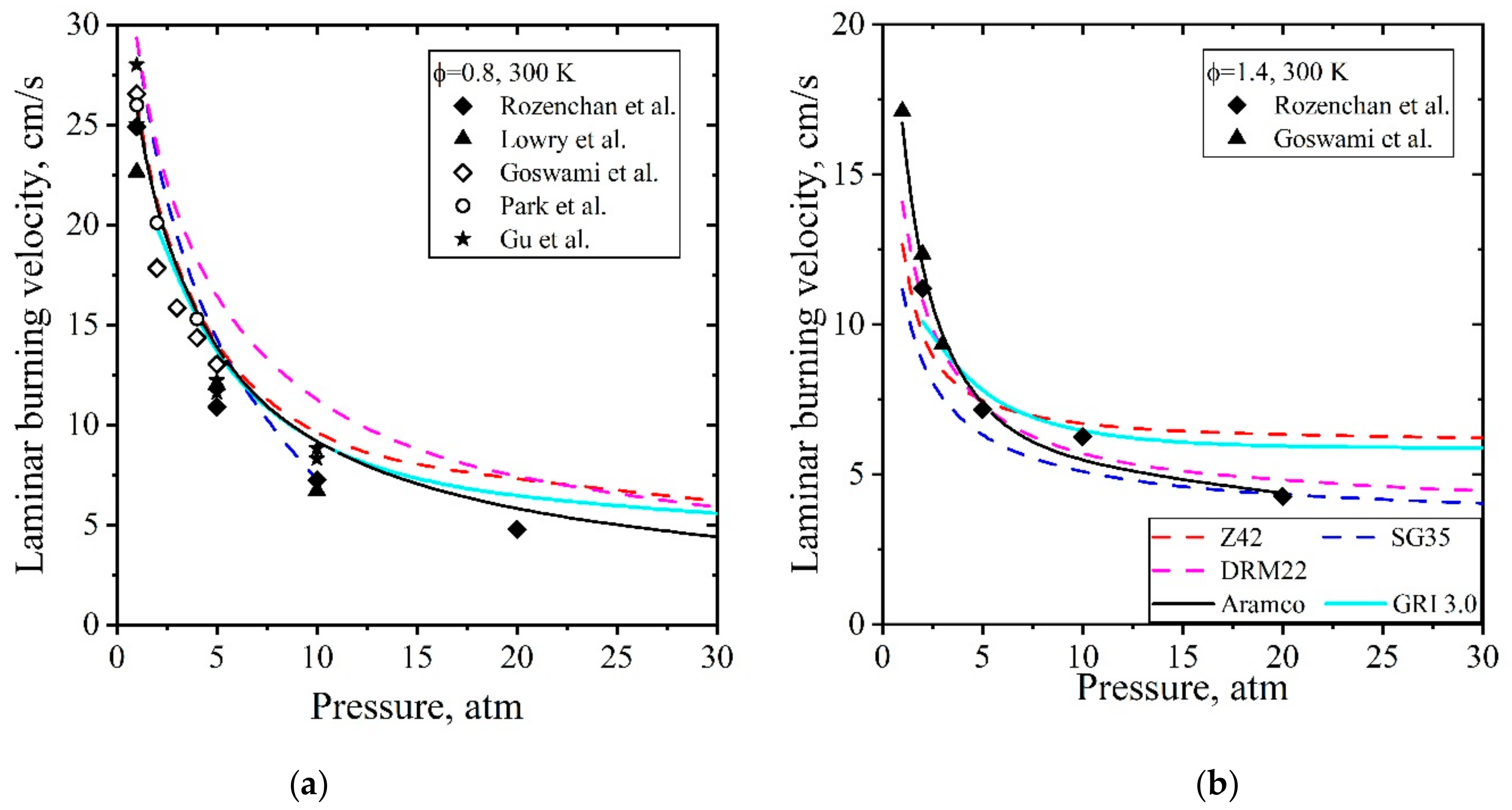
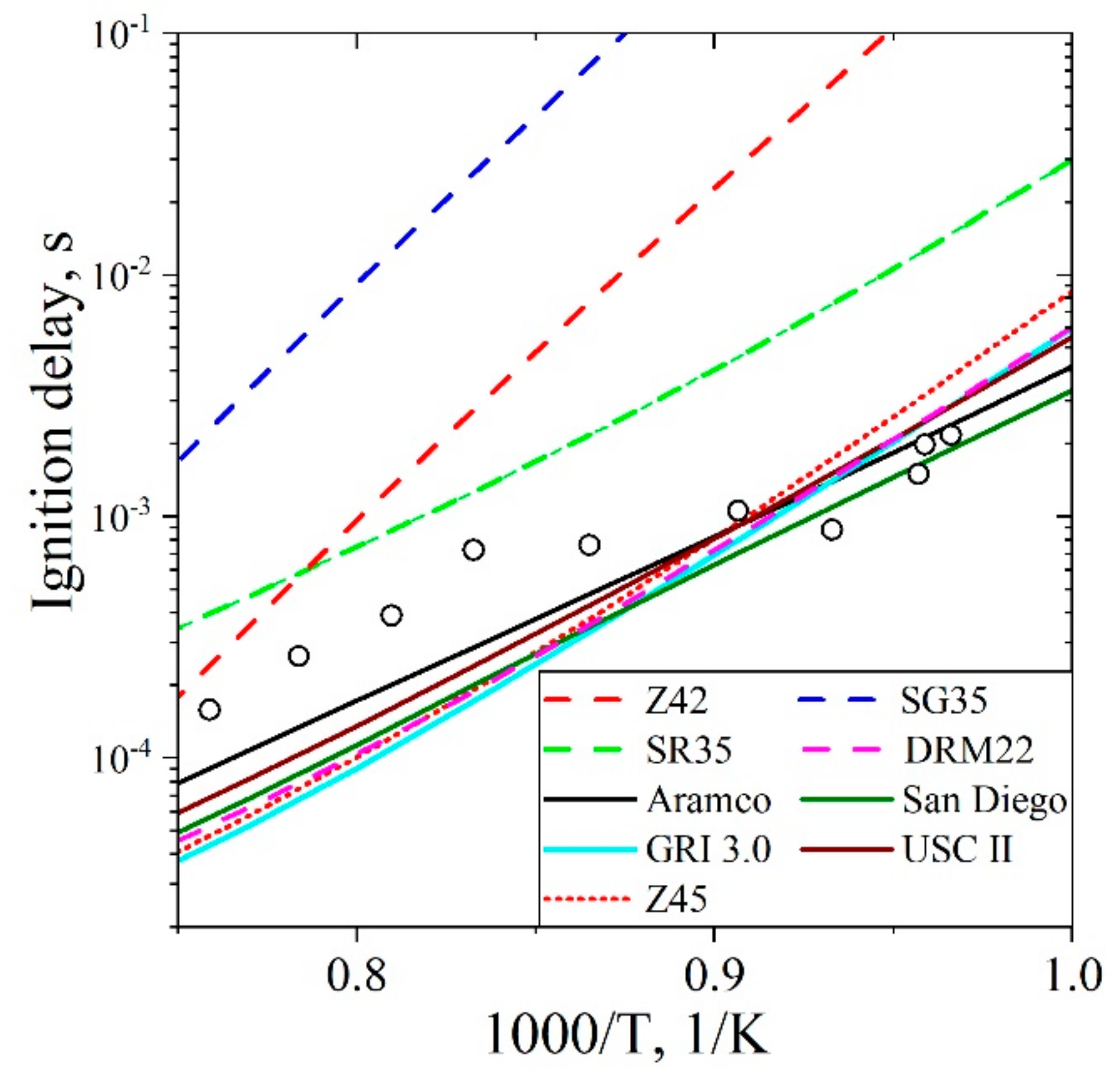
References
- Burnham, A.; Han, J.; Clark, C.E.; Wang, M.; Dunn, J.B.; Palou-Rivera, I. Life-cycle greenhouse gas emissions of shale gas, natural gas, coal, and petroleum. Environ. Sci. Technol. 2011, 46, 619–627. [Google Scholar] [CrossRef] [PubMed]
- Glassman, I.; Yetter, R.A. Combustion, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Lu, T.F.; Law, C.K. Toward accommodating realistic fuel chemistry in large-scale computations. Prog. Energy Combust. Sci. 2009, 35, 192–215. [Google Scholar] [CrossRef]
- Fiorina, B.; Veynante, D.; Candel, S. Modeling combustion chemistry in large eddy simulation of turbulent flames. Flow Turbul. Combust. 2015, 94, 3–42. [Google Scholar] [CrossRef]
- Pope, S.B. Small scales, many species and the manifold challenges of turbulent combustion. Proc. Combust. Inst. 2013, 34, 1–31. [Google Scholar] [CrossRef]
- Hilbert, R.; Tap, F.; El-Rabii, H.; Thevenin, D. Impact of detailed chemistry and transport models on turbulent combustion simulations. Prog. Energy Combust. Sci. 2004, 30, 61–117. [Google Scholar] [CrossRef]
- Fischer, M.; Jiang, X. A chemical kinetic modelling study of the combustion of CH4-CO-H-2-CO2 fuel mixtures. Combust. Flame 2016, 167, 274–293. [Google Scholar] [CrossRef] [Green Version]
- Fischer, M.; Jiang, X. An investigation of the chemical kinetics of biogas combustion. Fuel 2015, 150, 711–720. [Google Scholar] [CrossRef]
- Fischer, M.; Jiang, X. An assessment of chemical kinetics for bio-syngas combustion. Fuel 2014, 137, 293–305. [Google Scholar] [CrossRef]
- Dirrenberger, P.; Gall, H.L.; Bounaceur, R.; Herbinet, O.; Glaude, P.A.; Konnov, A.; Battin-Leclerc, F. Measurements of Laminar Flame Velocity for Components of Natural Gas. Energy Fuels 2011, 25, 3875–3884. [Google Scholar] [CrossRef] [Green Version]
- Rashwan, S.S.; Nemitallah, M.A.; Habib, M.A. Review on premixed combustion technology: Stability, emission control, applications, and numerical case study. Energy Fuels 2016. [Google Scholar] [CrossRef]
- Tang, C.L.; Zhang, Y.J.; Huang, Z.H. Progress in combustion investigations of hydrogen enriched hydrocarbons. Renew. Sustain. Energy Rev. 2014, 30, 195–216. [Google Scholar] [CrossRef]
- Taamallah, S.; Vogiatzaki, K.; Alzahrani, F.M.; Mokheimer, E.M.A.; Habib, M.A.; Ghoniem, A.F. Fuel flexibility, stability and emissions in premixed hydrogen-rich gas turbine combustion: Technology, fundamentals, and numerical simulations. Appl. Energy 2015, 154, 1020–1047. [Google Scholar] [CrossRef]
- Ayed, A.H.; Kusterer, K.; Funke, H.W.; Keinz, J.; Striegan, C.; Bohn, D. Experimental and numerical investigations of the dry-low-NOx hydrogen micromix combustion chamber of an industrial gas turbine. Prop. Power Res. 2015, 4, 123–131. [Google Scholar] [CrossRef] [Green Version]
- Brand, J.; Sampath, S.; Shum, F.; Bayt, R.; Cohen, J. Potential use of hydrogen in air propulsion. In Proceedings of the AIAA International Air and Space Symposium and Exposition: The Next 100 Years, Dayton, OH, USA, 14–17 July 2003; p. 2879. [Google Scholar]
- Tang, C.L.; Huang, Z.H.; Law, C.K. Determination, correlation, and mechanistic interpretation of effects of hydrogen addition on laminar flame speeds of hydrocarbon-air mixtures. Proc. Combust. Inst. 2011, 33, 921–928. [Google Scholar] [CrossRef]
- Eder, L.; Ban, M.; Pirker, G.; Vujanovic, M.; Priesching, P.; Wimmer, A. Development and Validation of 3D-CFD Injection and Combustion Models for Dual Fuel Combustion in Diesel Ignited Large Gas Engines. Energies 2018, 11, 643. [Google Scholar] [CrossRef] [Green Version]
- Monsalve-Serrano, J.; Belgiorno, G.; Di Blasio, G.; Guzmán-Mendoza, M. 1D Simulation and Experimental Analysis on the Effects of the Injection Parameters in Methane–Diesel Dual-Fuel Combustion. Energies 2020, 13, 3734. [Google Scholar] [CrossRef]
- Fraioli, V.; Beatrice, C.; Di Blasio, G.; Belgiorno, G.; Magliaccio, M. Multidimensional Simulations of Combustion in Methane-Diesel Dual-Fuel Light-Duty Engines; SAE Technical Paper 2017-01-0568; SAE: Warrendale, PA, USA, 2017. [Google Scholar]
- Konnov, A.A.; Mohammad, A.; Kishore, V.R.; Kim, N.I.; Prathap, C.; Kumar, S. A comprehensive review of measurements and data analysis of laminar burning velocities for various fuel+air mixtures. Prog. Energy Combust. Sci. 2018, 68, 197–267. [Google Scholar] [CrossRef]
- Ranzi, E.; Frassoldati, A.; Grana, R.; Cuoci, A.; Faravelli, T.; Kelley, A.P.; Law, C.K. Hierarchical and comparative kinetic modeling of laminar flame speeds of hydrocarbon and oxygenated fuels. Prog. Energy Combust. Sci. 2012, 38, 468–501. [Google Scholar] [CrossRef]
- Metcalfe, W.K.; Burke, S.M.; Ahmed, S.S.; Curran, H.J. A hierarchical and comparative kinetic modeling study of C1-C2 hydrocarbon and oxygenated fuels. Int. J. Chem. Kinet. 2013, 45, 638–675. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, C.-W.; Somers, K.P.; Zhang, K.; Curran, H.J. The oxidation of 2-butene: A high pressure ignition delay, kinetic modeling study and reactivity comparison with isobutene and 1-butene. Proc. Combust. Inst. 2017, 36, 403–411. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.-W.; Li, Y.; Burke, U.; Banyon, C.; Somers, K.P.; Ding, S.; Khan, S.; Hargis, J.W.; Sikes, T.; Mathieu, O.; et al. An experimental and chemical kinetic modeling study of 1,3-butadiene combustion: Ignition delay time and laminar flame speed measurements. Combust. Flame 2018, 197, 423–438. [Google Scholar] [CrossRef]
- Group, T.C.M. C1-C3 Mechanism Version 1412. Available online: http://creckmodeling.chem.polimi.it/menu-kinetics/menu-kinetics-detailed-mechanisms/menu-kinetics-c1-c3-mechanism (accessed on 29 August 2018).
- Curran, H.J. Developing detailed chemical kinetic mechanisms for fuel combustion. Proc. Combust. Inst. 2019, 37, 57–81. [Google Scholar] [CrossRef]
- Turanyi, T.; Tomlin, A.S. Analysis of Kinetic Reaction Mechanisms; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Zettervall, N.; Fureby, C.; Nilsson, E.J.K. Small skeletal kinetic mechanism for kerosene combustion. Energy Fuels 2016, 30, 9801–9813. [Google Scholar] [CrossRef]
- Zettervall, N.; Fureby, C.; Nilsson, E.J.K. A reduced chemical kinetic reaction mechanism for kerosene-air combustion. Fuel 2020, 269, 117446. [Google Scholar] [CrossRef]
- Davidson, D.F.; Hanson, R.K. Interpreting shock tube ignition data. Int. J. Chem. Kinet. 2004, 36, 510–523. [Google Scholar] [CrossRef]
- Goldsborough, S.S.; Hochgreb, S.; Vanhove, G.; Wooldridge, M.S.; Curran, H.J.; Sung, C.J. Advances in rapid compression machine studies of low- and intermediate-temperature autoignition phenomena. Prog. Energy Combust. Sci. 2017, 63, 1–78. [Google Scholar] [CrossRef] [Green Version]
- Sung, C.-J.; Curran, H.J. Using rapid compression machines for chemical kinetics studies. Prog. Energy Combust. Sci. 2014, 44, 1–18. [Google Scholar] [CrossRef]
- Ansari, A.; Egolfopoulos, F.N. Flame ignition in the counterflow configuration: Reassessing the experimental assumptions. Combust. Flame 2016, 174, 37–49. [Google Scholar] [CrossRef] [Green Version]
- Law, C.K. Comprehensive description of chemistry in combustion modeling. Combust. Sci. Technol. 2005, 177, 845–870. [Google Scholar] [CrossRef]
- Egolfopoulos, F.N.; Hansen, N.; Ju, Y.; Kohse-Hoinghaus, K.; Law, C.K.; Qi, F. Advances and challenges in laminar flame experiments and implications for combustion chemistry. Prog. Energy Combust. Sci. 2014, 43, 36–67. [Google Scholar] [CrossRef]
- Goswami, M.; Derks, S.C.R.; Coumans, K.; Slikker, W.J.; O’liveira, M.H.D.; Bastiaans, R.J.M.; Luijten, C.C.M.; de Goey, L.P.H.; Konnov, A.A. The effect of elevated pressures on the laminar burning velocity of methane plus air mixtures. Combust. Flame 2013, 160, 1627–1635. [Google Scholar] [CrossRef]
- Alekseev, V.A.; Naucler, J.D.; Christensen, M.; Nilsson, E.J.K.; Volkov, E.N.; de Goey, L.P.H.; Konnov, A.A. Experimental uncertainties of the heat flux method for measuring burning velocities. Combust. Sci. Technol. 2016, 188, 853–894. [Google Scholar] [CrossRef]
- Chen, Z. On the accuracy of laminar flame speeds measured from outwardly propagating spherical flames: Methane/air at normal temperature and pressure. Combust. Flame 2015, 162, 2442–2453. [Google Scholar] [CrossRef]
- Ranzi, E. A wide-range kinetic modeling study of oxidation and combustion of transportation fuels and surrogate mixtures. Energy Fuels 2006, 20, 1024–1032. [Google Scholar] [CrossRef]
- Holley, A.T.; Dong, Y.; Andac, M.G.; Egolfopoulos, F.N. Extinction of premixed flames of practical liquid fuels: Experiments and simulations. Combust. Flame 2006, 144, 448–460. [Google Scholar] [CrossRef]
- Holley, A.T.; You, X.Q.; Dames, E.; Wang, H.; Egolfopoulos, F.N. Sensitivity of propagation and extinction of large hydrocarbon flames to fuel diffusion. Proc. Combust. Inst. 2009, 32, 1157–1163. [Google Scholar] [CrossRef]
- Franzelli, B.; Riber, E.; Cuenot, B. Impact of the chemical description on a Large Eddy Simulation of a lean partially premixed swirled flame. Comptes Rendus Mécanique 2013, 341, 247–256. [Google Scholar] [CrossRef] [Green Version]
- Gu, X.J.; Haq, M.Z.; Lawes, M.; Woolley, R. Laminar burning velocity and Markstein lengths of methane-air mixtures. Combust. Flame 2000, 121, 41–58. [Google Scholar] [CrossRef]
- Rozenchan, G.; Zhu, D.L.; Law, C.K.; Tse, S.D. Outward propagation, burning velocities, and chemical effects of methane flames up to 60 ATM. Proc. Combust. Inst. 2002, 29, 1461–1470. [Google Scholar] [CrossRef]
- Lowry, W.; de Vries, J.; Krejci, M.; Petersen, E.; Serinyel, Z.; Metcalfe, W.; Curran, H.; Bourque, G. Laminar Flame Speed Measurements and Modeling of Pure Alkanes and Alkane Blends at Elevated Pressures. J. Eng. Gas. Turbines Power 2011, 133, 91501. [Google Scholar] [CrossRef]
- Bosschaart, K.J.; de Goey, L.P.H. The laminar burning velocity of flames propagating in mixtures of hydrocarbons and air measured with the heat flux method. Combust. Flame 2004, 136, 261–269. [Google Scholar] [CrossRef]
- Hu, E.J.; Li, X.T.; Meng, X.; Chen, Y.Z.; Cheng, Y.; Xie, Y.L.; Huang, Z.H. Laminar flame speeds and ignition delay times of methane-air mixtures at elevated temperatures and pressures. Fuel 2015, 158, 1–10. [Google Scholar] [CrossRef]
- Frenklach, F.; Wang, H.; Yu, C.L.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Davidson, D.F.; Chang, E.J.; Smith, G.P.; Golden, D.M.; et al. GRI Mech 1.2. Available online: http://www.me.berkeley.edu/gri_mech (accessed on 1 August 2018).
- Wang, H.; You, X.; Joshi, A.V.; Davis, S.G.; Laskin, A.; Egolfopoulos, F.; Law, C.K. USC Mech Version II. High-Temperature Combustion Reaction Model of H2/CO/C1-C4 Compounds. Available online: http://ignis.usc.edu/USC_Mech_II.htm (accessed on 1 May 2007).
- Chemical-Kinetic Mechanisms for Combustion Applications. Available online: http://combustion.ucsd.edu (accessed on 29 August 2018).
- Kazakov, A.; Frenklach, F. DRM22. Available online: http://combustion.berkeley.edu/drm/ (accessed on 10 October 2018).
- Smith, G.P.; Golden, D.M.; Frenklach, F.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C.; et al. GRI-Mech 3.0. Available online: http://combustion.berkeley.edu/gri_mech/ (accessed on 29 October 2018).
- Westbrook, C.K.; Dryer, F.L. Chemical kinetic modeling of hydrocarbon combustion. Prog. Energy Combust. Sci. 1984, 10, 1–57. [Google Scholar] [CrossRef]
- Westbrook, C.K.; Dryer, F.L. Simplified reaction-mechanisms for the oxidation of hydrocarbon fuels in flames. Combust. Sci. Technol. 1981, 27, 31–43. [Google Scholar] [CrossRef]
- Jones, W.P.; Lindstedt, R.P. Global reaction schemes for hydrocarbon combustion. Combust. Flame 1988, 73, 233–249. [Google Scholar] [CrossRef]
- Seshadri, K.; Bai, X.S.; Pitsch, H.; Peters, N. Asymptotic analysis of the structure of moderately rich methane-air flames. Combust. Flame 1998, 113, 589–602. [Google Scholar] [CrossRef] [Green Version]
- Fernandez-Tarrazo, E.; Sanchez, A.L.; Linan, A.; Williams, F.A. A simple one-step chemistry model for partially premixed hydrocarbon combustion. Combust. Flame 2006, 147, 32–38. [Google Scholar] [CrossRef] [Green Version]
- Nikolaou, Z.M.; Chen, J.Y.; Swaminathan, N. A 5-step reduced mechanism for combustion of CO/H-2/H2O/CH4/CO2 mixtures with low hydrogen/methane and high H2O content. Combust. Flame 2013, 160, 56–75. [Google Scholar] [CrossRef] [Green Version]
- Nikolaou, Z.M.; Swaminathan, N.; Chen, J.Y. Evaluation of a reduced mechanism for turbulent premixed combustion. Combust. Flame 2014, 161, 3085–3099. [Google Scholar] [CrossRef] [Green Version]
- Abou-Taouk, A.; Sadasivuni, S.; Lorstad, D.; Eriksson, L.-E. Evaluation of global mechanisms for les analysis of sgt-100 dle combustion system. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, 3–7 June 2013. Number V002t04a036. [Google Scholar]
- Smooke, M.D.; Giovangigli, V. Formulation of the premixed and nonpremixed test problems. In Reduced Chemical Mechansims and Asymptotic Approximations for Methane-Air Flames; Springer: New York, NY, USA, 1991; p. 384. [Google Scholar]
- Bulat, G.; Fedina, E.; Fureby, C.; Meier, W.; Stopper, U. Reacting flow in an industrial gas turbine combustor: LES and experimental analysis. Proc. Combust. Inst. 2015, 35, 3175–3183. [Google Scholar] [CrossRef]
- Ehn, A.; Petersson, P.; Zhu, J.J.; Li, Z.S.; Alden, M.; Nilsson, E.J.K.; Larfeldt, J.; Larsson, A.; Hurtig, T.; Zettervall, N.; et al. Investigations of microwave stimulation of a turbulent low-swirl flame. Proc. Combust. Inst. 2017, 36, 4121–4128. [Google Scholar] [CrossRef] [Green Version]
- Larsson, A.; Zettervall, N.; Hurtig, T.; Nilsson, E.J.K.; Ehn, A.; Petersson, P.; Alden, M.; Larfeldt, J.; Fureby, C. Skeletal methane–air reaction mechanism for large eddy simulation of turbulent microwave-assisted combustion. Energy Fuels 2017, 31, 1904–1926. [Google Scholar] [CrossRef]
- Zettervall, N.; Fureby, C. A computational study of ramjet, scramjet and dual-mode ramjet/scramjet combustion in a combustor with a cavity flameholder. In Proceedings of the AIAA 2018: 8th International Conference on Artificial Intelligence, Soft Computing and Applications, Melbourne, Australia, 24–25 November 2018. [Google Scholar]
- Zettervall, N.; Nordin-Bates, K.; Nilsson, E.J.K.; Fureby, C. Large Eddy Simulation of a premixed bluff body stabilized flame using global and skeletal reaction mechanisms. Combust. Flame 2017, 179, 1–22. [Google Scholar] [CrossRef]
- Niklas, Z.; Ekaterina, F.; Kevin, N.-B.; Heimdal, N.E.; Christer, F. Combustion LES of a multi-burner annular aeroengine combustor using a skeletal reaction mechanism for Jet-A air mixtures. In Proceedings of the 51st AIAA/SAE/ASEE Joint Propulsion Conference, American Institute of Aeronautics and Astronautics, Orlando, FL, USA, 27–29 July 2015. [Google Scholar] [CrossRef]
- Zettervall, N.; Fureby, C.; Nilsson, E.J.K. Small skeletal kinetic reaction mechanism for ethylene-air combustion. Energy Fuels 2017. [Google Scholar] [CrossRef]
- Sher, E.; Refael, S. A simplified reaction scheme for the combustion of hydrogen enriched methane air flame. Combust. Sci. Technol. 1988, 59, 371–389. [Google Scholar] [CrossRef]
- Refael, S.; Sher, E. Reaction-kinetics of hydrogen-enriched methane air and propane air flames. Combust. Flame 1989, 78, 326–338. [Google Scholar] [CrossRef]
- Pitz, W.J.; Westbrook, C.K. Chemical-kinetics of the high-pressure oxidation of normal-butane and its relation to engine knock. Combust. Flame 1986, 63, 113–133. [Google Scholar] [CrossRef]
- Frenklach, F.; Wang, H.; Yu, C.L.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Davidson, D.F.; Chang, E.J.; Smith, G.P.; Golden, D.M.; et al. GRI-Mech 1.2. Available online: http://combustion.berkeley.edu/gri_mech/new21/version12/text12.html (accessed on 29 August 2018).
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C.; et al. GRI 1.2; GRI: Berkeley, CA, USA, 1999. [Google Scholar]
- Wang, H.; Frenklach, F. Detailed reduction of reaction mechanisms for flame modeling. Combust. Flame 1991, 87, 365–370. [Google Scholar] [CrossRef]
- Kazakov, A.; Frenklach, F. DRM19. Available online: http://combustion.berkeley.edu/drm/ (accessed on 29 August 2018).
- Jaravel, T.; Riber, E.; Cuenot, B.; Bulat, G. Large Eddy Simulation of an industrial gas turbine combustor using reduced chemistry with accurate pollutant prediction. Proc. Combust. Inst. 2017, 36, 3817–3825. [Google Scholar] [CrossRef]
- Chen, Y.L.; Chen, J.Y. Towards improved automatic chemical kinetic model reduction regarding ignition delays and flame speeds. Combust. Flame 2018, 190, 293–301. [Google Scholar] [CrossRef]
- Goos, E.; Burcat, A.; Ruscic, B. Extended Third Millenium Ideal Gas and Condensed Phase Thermochemical Database for Combustion with Updates from Active Thermochemical Tables; Elke Goos: Remchingen, Germany, 2016. [Google Scholar]
- ANSYS. CHEMKIN-PRO 15151; ANSYS: Canonsburg, PA, USA, 2016. [Google Scholar]
- Goodwin, D.G.; Speth, R.L.; Moffat, H.K.; Weber, B.W. Cantera: An Object-Oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes, 2.4.0. Available online: https://cantera.org/community.html#citing-cantera (accessed on 1 August 2018).
- Kazakov, A. Igdelay v1.0; Princeton University: Princeton, NJ, USA, 2004. [Google Scholar]
- Nilsson, E.J.K.; van Sprang, A.; Larfeldt, J.; Konnov, A.A. The comparative and combined effects of hydrogen addition on the laminar burning velocities of methane and its blends with ethane and propane. Fuel 2017, 189, 369–376. [Google Scholar] [CrossRef]
- Park, O.; Veloo, P.S.; Liu, N.; Egolfopoulos, F.N. Combustion characteristics of alternative gaseous fuels. Proc. Combust. Inst. 2011, 33, 887–894. [Google Scholar] [CrossRef]
- Wu, Y.; Modica, V.; Rossow, B.; Grisch, F. Effects of pressure and preheating temperature on the laminar flame speed of methane/air and acetone/air mixtures. Fuel 2016, 185, 577–588. [Google Scholar] [CrossRef]
- Petersen, E.L.; Davidson, D.F.; Hanson, R.K. Ignition delay times of ram accelerator CH/O/Diluent mixtures. J. Propuls. Power 1999, 15, 82–91. [Google Scholar] [CrossRef]
- Eubank, C.S.; Rabinowitz, M.J.; Gardiner, W.C.; Zellner, R. Shock-initiated ignition of natural gas-air mixtures. Symp. (Int.) Combust. 1981, 17, 1767–1773. [Google Scholar] [CrossRef]
- Petersen, E.L.; Hall, J.M.; Smith, S.D.; de Vries, J.; Amadio, A.R.; Crofton, M.W. Ignition of lean methane-based fuel blends at gas turbine pressures. J. Eng. Gas. Turbines Power Trans. ASME 2007, 129, 937–944. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Bushe, W.K.; Hill, P.G.; Munshi, S.R. Experimental and kinetic study of shock initiated ignition in homogeneous methane-hydrogen-air mixtures at engine-relevant conditions. Int. J. Chem. Kinet. 2006, 38, 221–233. [Google Scholar] [CrossRef]
- Versailles, P.; Watson, G.M.G.; Lipardi, A.C.A.; Bergthorson, J.M. Quantitative CH measurements in atmospheric-pressure, premixed flames of C1-C4 alkanes. Combust. Flame 2016, 165, 109–124. [Google Scholar] [CrossRef]
- Le Cong, T.; Dagaut, P.; Dayma, G. Oxidation of natural gas, natural gas/syngas mixtures, and effect of burnt gas recirculation: Experimental and detailed kinetic modeling. J. Eng. Gas. Turbines Power Trans. ASME 2008, 130. [Google Scholar] [CrossRef]
- Goeckeler, K.; Krueger, O.; Paschereit, C.O. Laminar burning velocities and emissions of hydrogen-methane-air-steam mixtures. J. Eng. Gas. Turb Power 2015, 137. [Google Scholar] [CrossRef]
- Scholte, T.G.; Vaags, P.B. Burning Velocities of Mixtures of Hydrogen, Carbon Monoxide and Methane with Air. Combust. Flame 1959, 3, 511. [Google Scholar] [CrossRef]
- McLean, I.C.; Smith, D.B.; Taylor, S.C. The use of carbon monoxide/hydrogen burning velocities to examine the rate of the CO + OH reaction. Symp. Combust. Proc. 1994, 25, 749. [Google Scholar] [CrossRef]
- Krejci, M.C.; Mathieu, O.; Vissotski, A.J.; Ravi, S.; Sikes, T.G.; Petersen, E.L.; Kermones, A.; Metcalfe, W.; Curran, H.J. Laminar flame speed and ignition delay time data for the kinetic modeling of hydrogen and syngas fuel blends. J. Eng. Gas. Turbines Power Trans. ASME 2013, 135. [Google Scholar] [CrossRef]
- Burbano, H.J.; Pareja, J.; Amell, A.A. Laminar burning velocities and flame stability analysis of H2/CO/air mixtures with dilution of N2 and CO2. Int. J. Hydrogen Energy 2011, 36, 3232. [Google Scholar] [CrossRef]
- Sun, H.; Yang, S.I.; Jomaas, G.; Law, C.K. High-pressure laminar flame speeds and kinetic modeling of carbon monoxide/hydrogen combustion. Proc. Combust. Inst. 2007, 31, 439. [Google Scholar] [CrossRef]
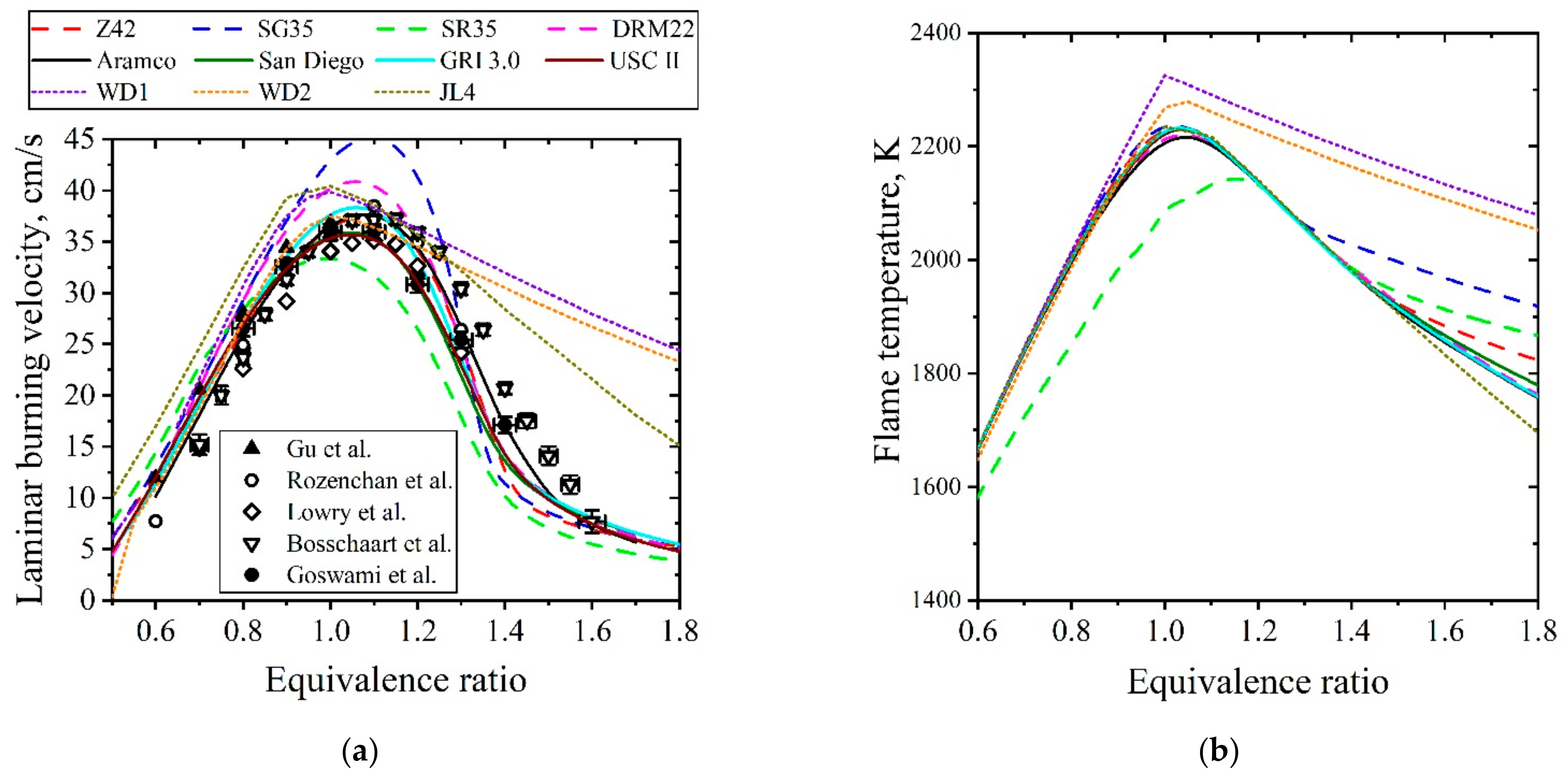
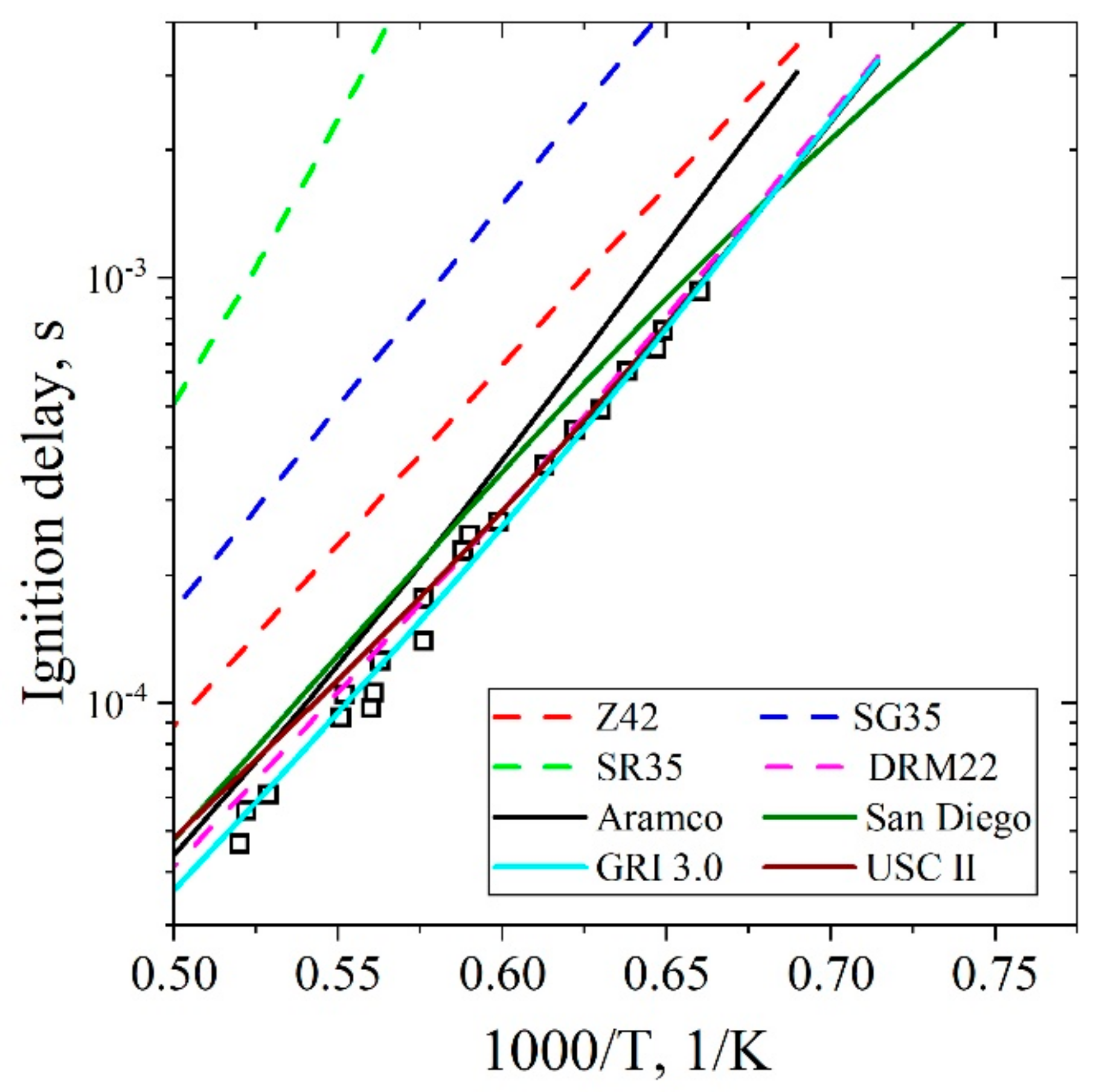
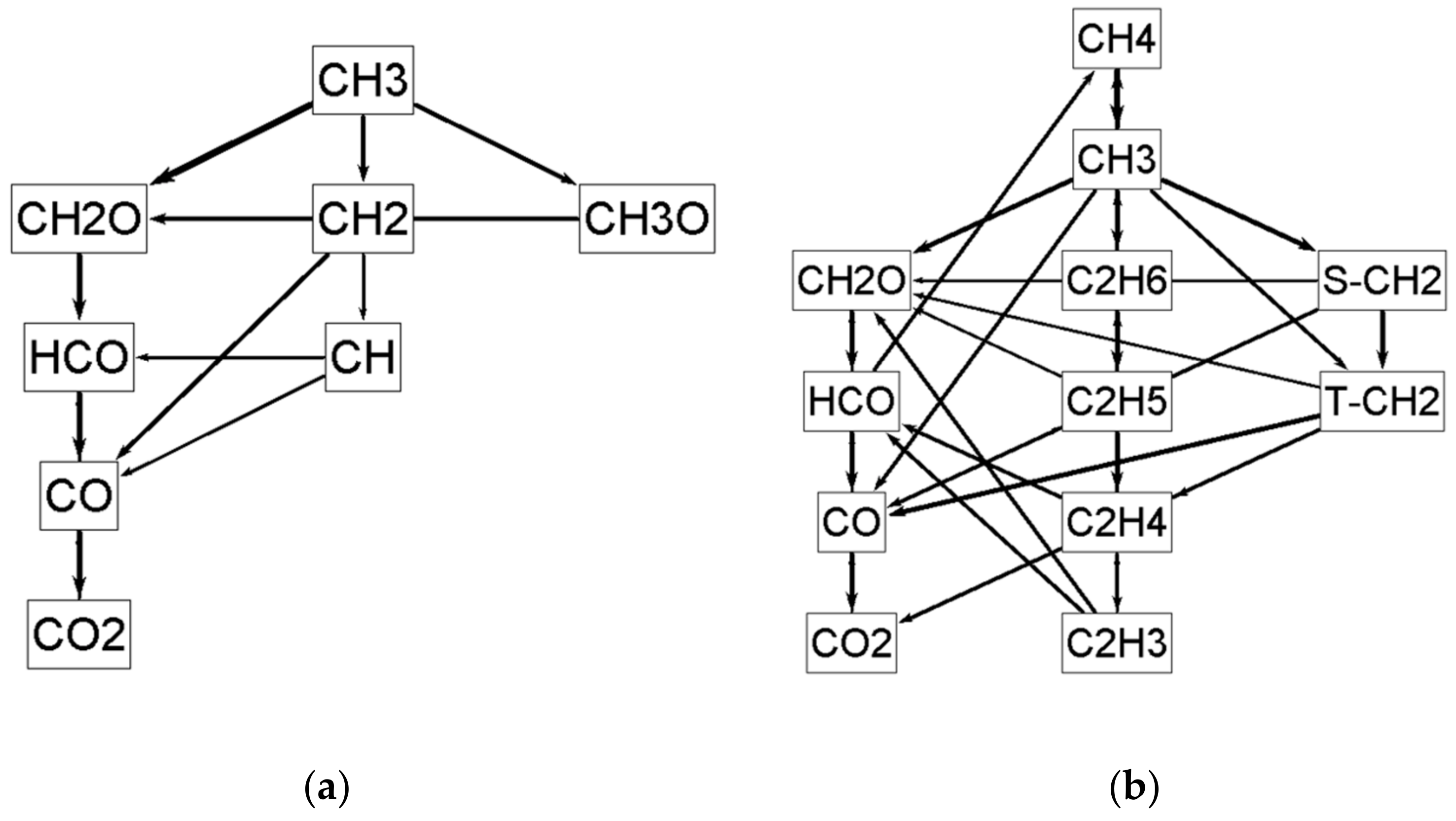
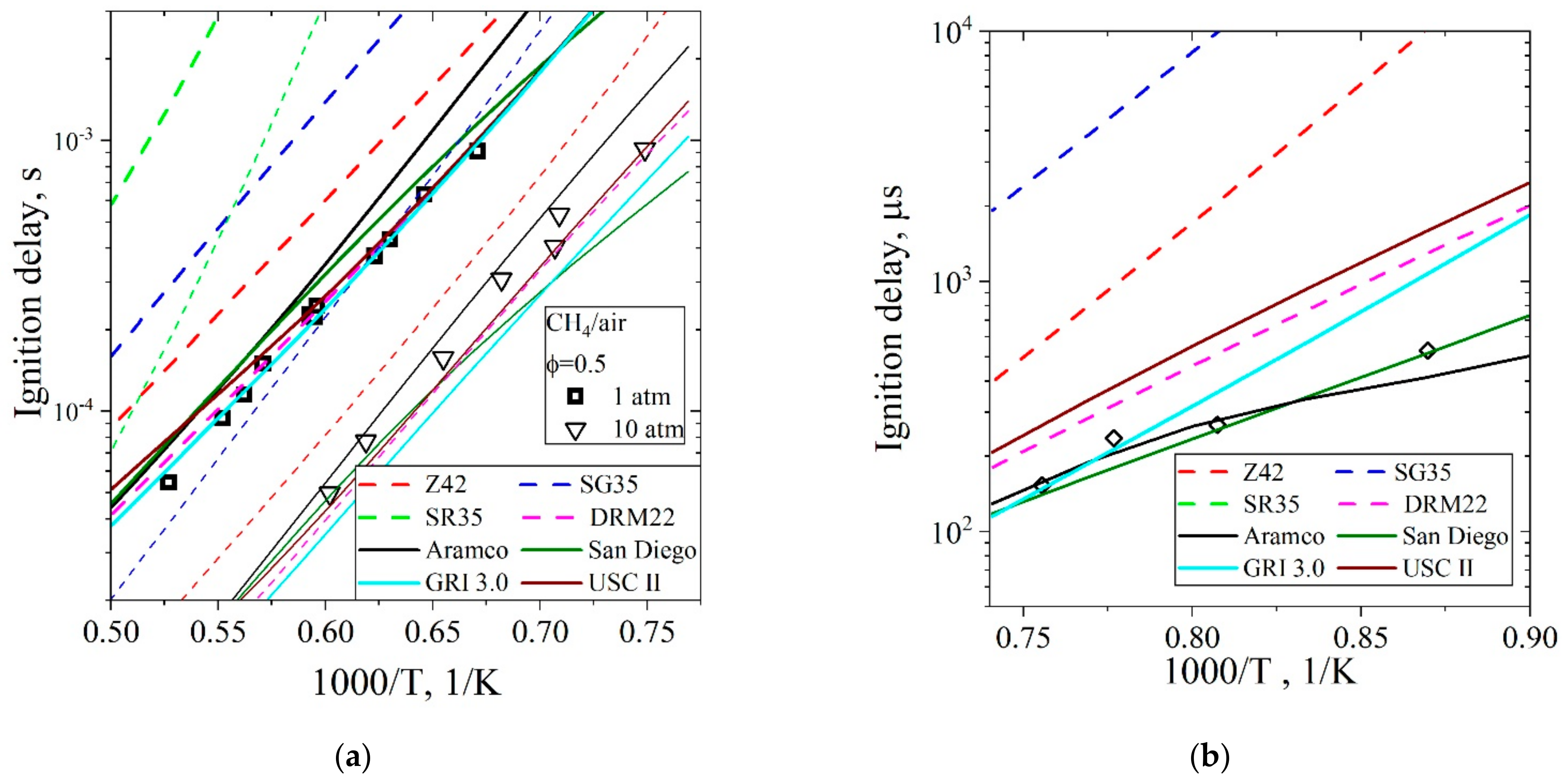
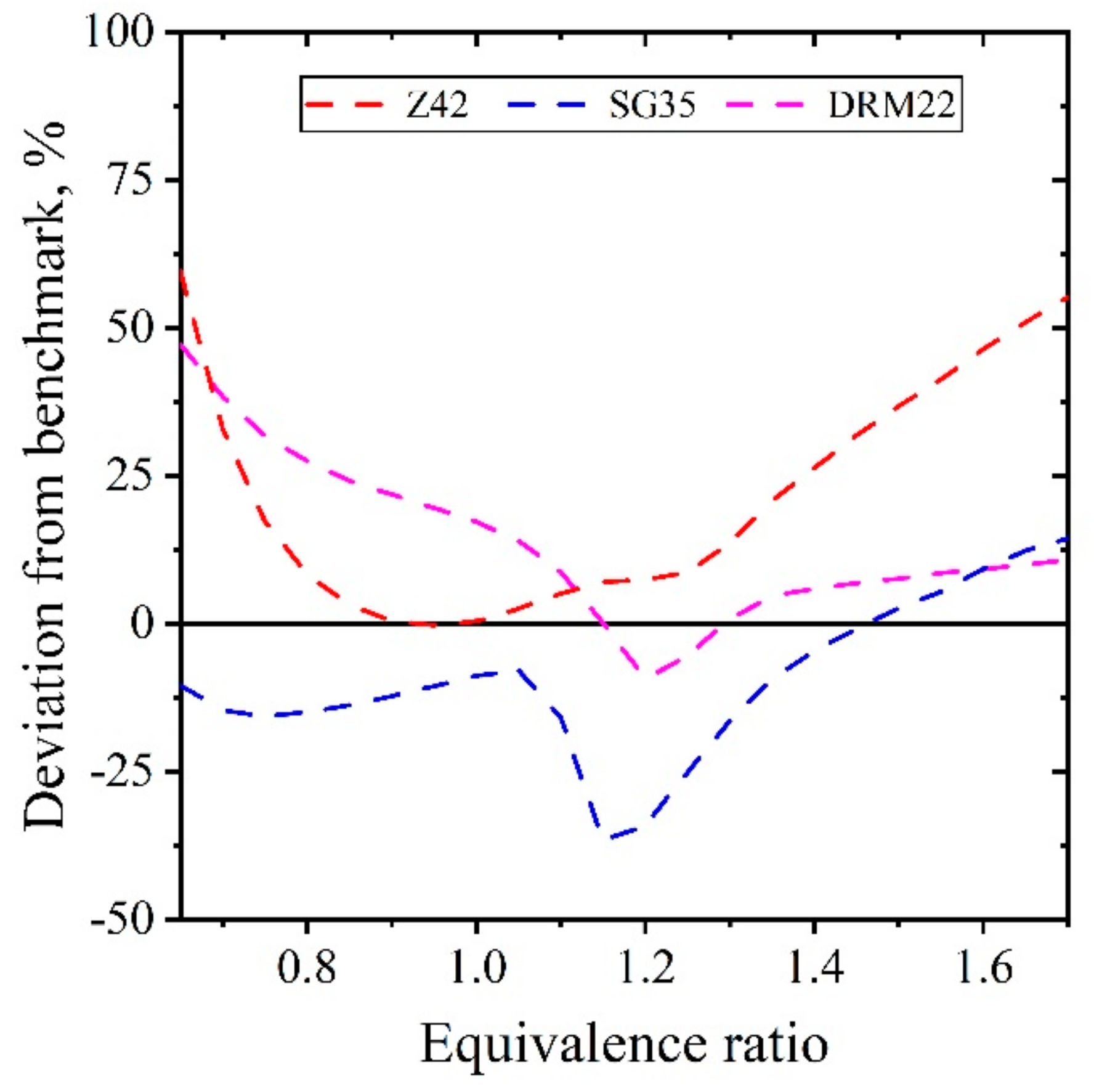
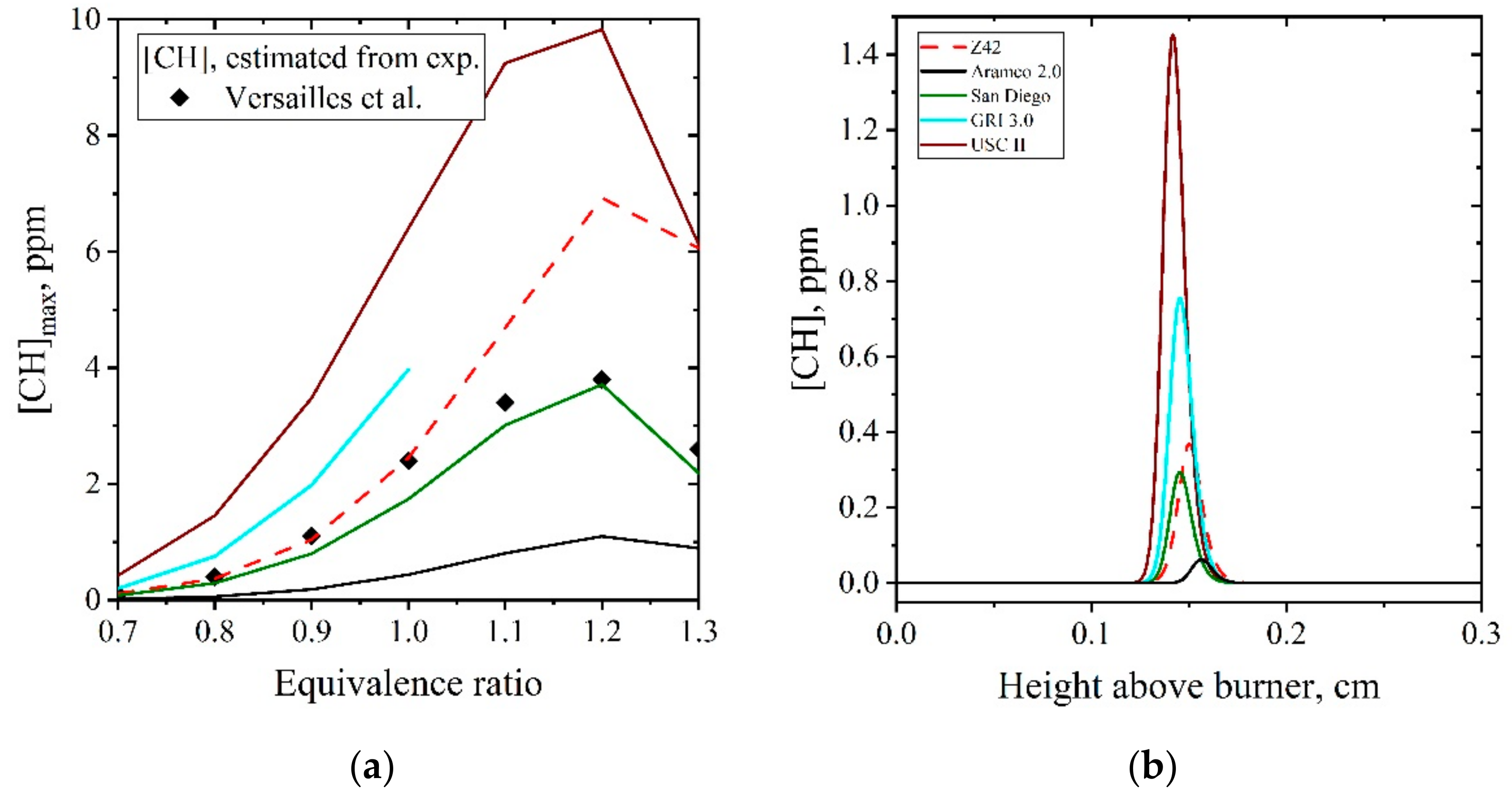
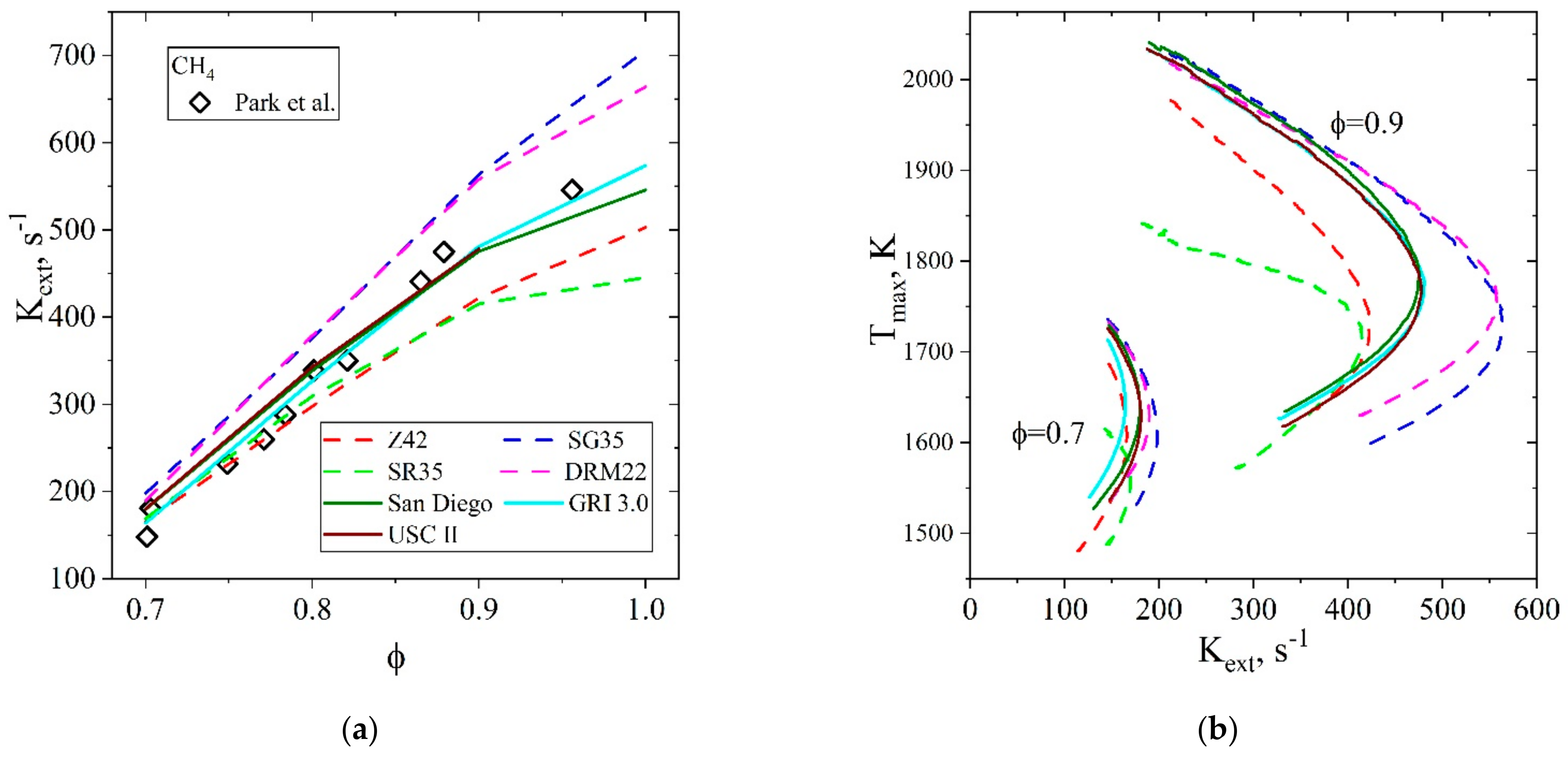
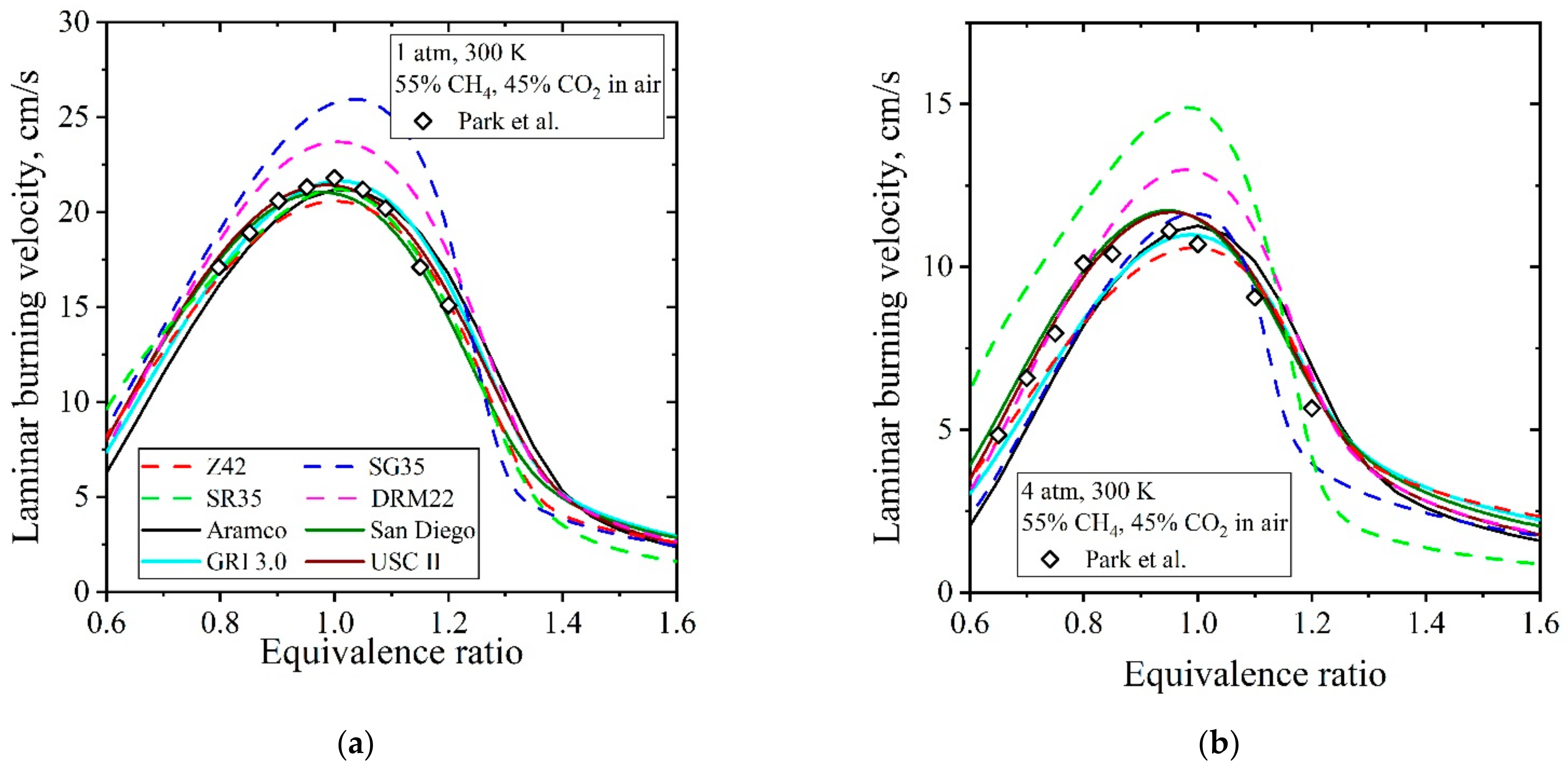
| Natural Gas | Biogas [7,8] | Bio-Syngas [7,9] | |||
|---|---|---|---|---|---|
| Fuel Components | Typical Range a | Frigg (North Sea) [10] | Lacq (France) [10] | ||
| CH4 | 87–97 | 95.7 | 69.2 | 50–75 | 8–11 |
| H2 | Trace | - | - | 0–1 | 22–32 |
| CO2 | 0.05–1 | 0.3 | 9.3 | 25–50 | 21–30 |
| CO | - | - | - | - | 28–36 |
| High HC | 1.5–10 | 3.6 | 5.2 | - | - |
| Name | Ref | Fuel | No. of Species | No. of Reactions |
|---|---|---|---|---|
| Aramco | [22,23,24] | C0-C4, including oxygenates (2.0) | 493 | 5131 |
| GRI 3.0 | [52] | CH4, Natural gas | 53 | 325 |
| San Diego | [50] | CH4, Natural gas | 56 | 235 |
| USCII | [49] | H2/CO/C1-C4 | 111 | 784 |
| Name | Ref | No. of Species | No. of Reactions | Development Conditions | Validation Targets |
|---|---|---|---|---|---|
| WD1 | [53,54] | 4 | 1 irrev | 1 bar, 300 K, ϕ = 0.5–1.5 | Tad, SL |
| WD2 | [53,54] | 5 | 3 irrev | 1 bar, 300 K, ϕ = 0.5–1.5 | Tad, SL |
| JL4 | [55] | 6 | 2 irrev + 2 rev | Species profiles, premixed and diffusion flames | |
| Seshadri | [56] | 7 | 4 rev | 1 bar, 300 K, ϕ = 1–1.4 | Flame structure |
| Williams | [57] | 4 | 1 irrev | 1 bar, 300 K, ϕ = 0.5–1.5 | Tad, SL, σext (ϕ < 1) |
| Nikolaou | [58,59] | 9 | 5 irrev | SL, τig, flame structure |
| Name | Ref | Fuel | No. of Species | No. of Reactions | Development Conditions | Validation Targets |
|---|---|---|---|---|---|---|
| SG35 | [61] | CH4 | 16 | 35 irrev | SL, | |
| Z42/45 | [63,64] | CH4, CH4 + H2 | 18 | 42 + 3 irrev | SL: 0.5–40 atm; 300–750 K; ϕ = 0.5–1.8 τig: 1 atm; 300 K; ϕ = 1.0 | SL, Flame structure, τig, σext |
| SR35/39 | [69,70] | CH4, CH4 + H2 | 17 | 35 + 4 irrev | SL: 0.8–20 atm; 280–650 K; ϕ = 0.4–1.5; 0–25 mass% H2 | SL, Flame structure |
| DRM19 | [75] | CH4 | 19 | 84 | SL: 1, 20 atm; 300, 400 K; ϕ = 0.6–1.5 τig: 0.1–50 atm; 1300–2500 K; ϕ = 0.2–2.0 | SL, τig, |
| DRM22 | [51] | CH4 | 22 | 104 | SL: 1, 20 atm; 300, 400 K; ϕ = 0.6–1.5 τig: 0.1–50 atm; 1300–2500 K; ϕ = 0.2–2.0 | SL, τig, |
| Property | Type | Fuel | P (atm) | T (K) | ϕ | Ref |
|---|---|---|---|---|---|---|
| SL | Heat flux method | CH4 CH4/H2 | 1–5 | 298 | 0.8–1.4 | [10,36,46,82] |
| SL | Counter flow | 1, 5, 10 | 298, 360, 400 | [83] | ||
| SL | Spherical flame | CH4 CH4/H2 | 1, 5, 10 | 298, 443 | 0.7–1.3 | [43,44,45,47] |
| SL | Bunsen flame | 343–523 | 0.6–1.3 | [84] | ||
| tig | Shock tube | CH4 | 1–115 | 1100–2000 | 0.1–3.0 | [47,85,86] |
| tig | Shock tube | CH4/H2 | 16–40 | 1000–1550 | 0.5–1.0 | [87,88] |
| [CH] | Stagnation flame | CH4 | 1 | 296 | 0.7–1.3 | [89] |
| σext | Counter flow flame | CH4 | 1 | 298 | 0.7–1.0 | [83] |
| Species profiles | Perfectly stirred reactor | CH4 CH4/H2 | 10 | 0.3 | [90] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zettervall, N.; Fureby, C.; Nilsson, E.J.K. Evaluation of Chemical Kinetic Mechanisms for Methane Combustion: A Review from a CFD Perspective. Fuels 2021, 2, 210-240. https://doi.org/10.3390/fuels2020013
Zettervall N, Fureby C, Nilsson EJK. Evaluation of Chemical Kinetic Mechanisms for Methane Combustion: A Review from a CFD Perspective. Fuels. 2021; 2(2):210-240. https://doi.org/10.3390/fuels2020013
Chicago/Turabian StyleZettervall, Niklas, Christer Fureby, and Elna J. K. Nilsson. 2021. "Evaluation of Chemical Kinetic Mechanisms for Methane Combustion: A Review from a CFD Perspective" Fuels 2, no. 2: 210-240. https://doi.org/10.3390/fuels2020013
APA StyleZettervall, N., Fureby, C., & Nilsson, E. J. K. (2021). Evaluation of Chemical Kinetic Mechanisms for Methane Combustion: A Review from a CFD Perspective. Fuels, 2(2), 210-240. https://doi.org/10.3390/fuels2020013