C60/CZTS Junction Combination to Improve the Efficiency of CZTS-Based Heterostructure Solar Cells: A Numerical Approach
Abstract
1. Introduction
2. Device Modeling and Simulation Parameters
3. Simulation Results and Discussion
- Structure—Al/ITO/C60/CZTS/SnS/Pt
3.1. Band Diagram
3.2. Effect of Absorber Layer Thickness and Acceptor Concentration on PV Performance
3.2.1. Effect of Defect Density
3.2.2. Effect of Series and Shunt Resistance
3.2.3. Effect of Temperature
3.2.4. Effect of Capacitance and Mott–Schottky
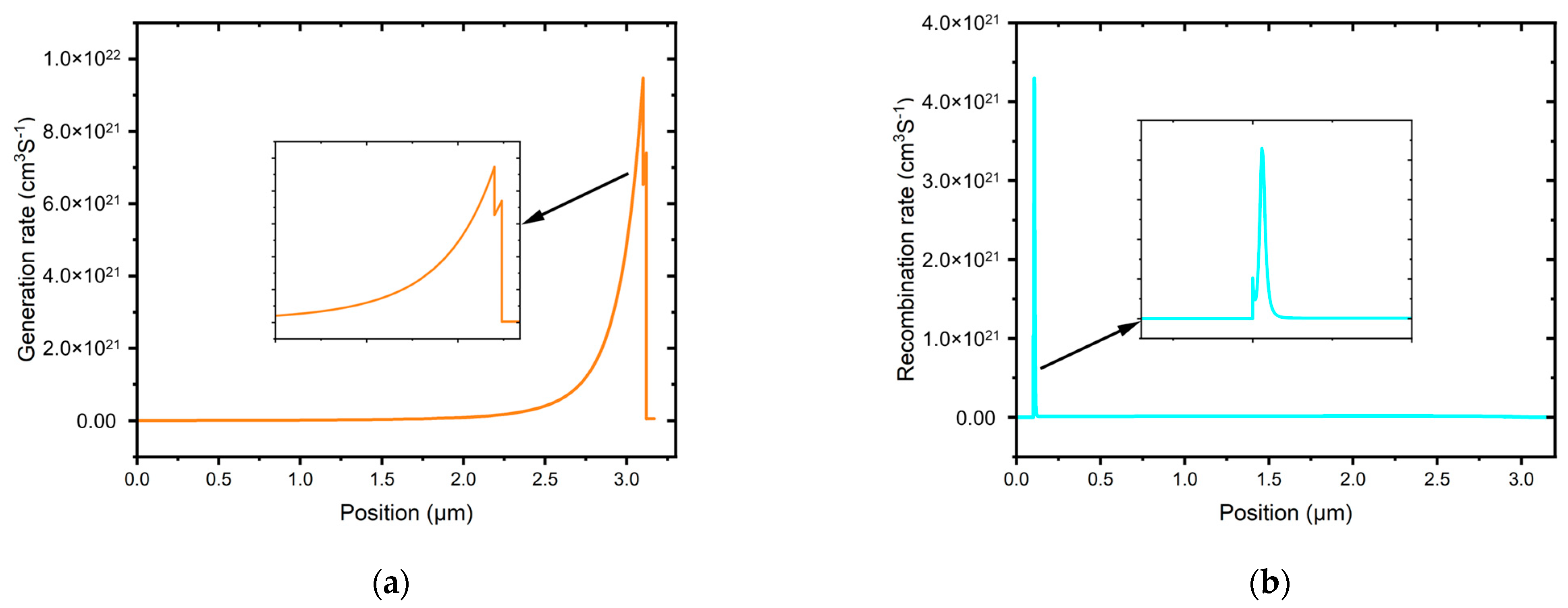
3.2.5. Effect of Generation and Recombination Rate
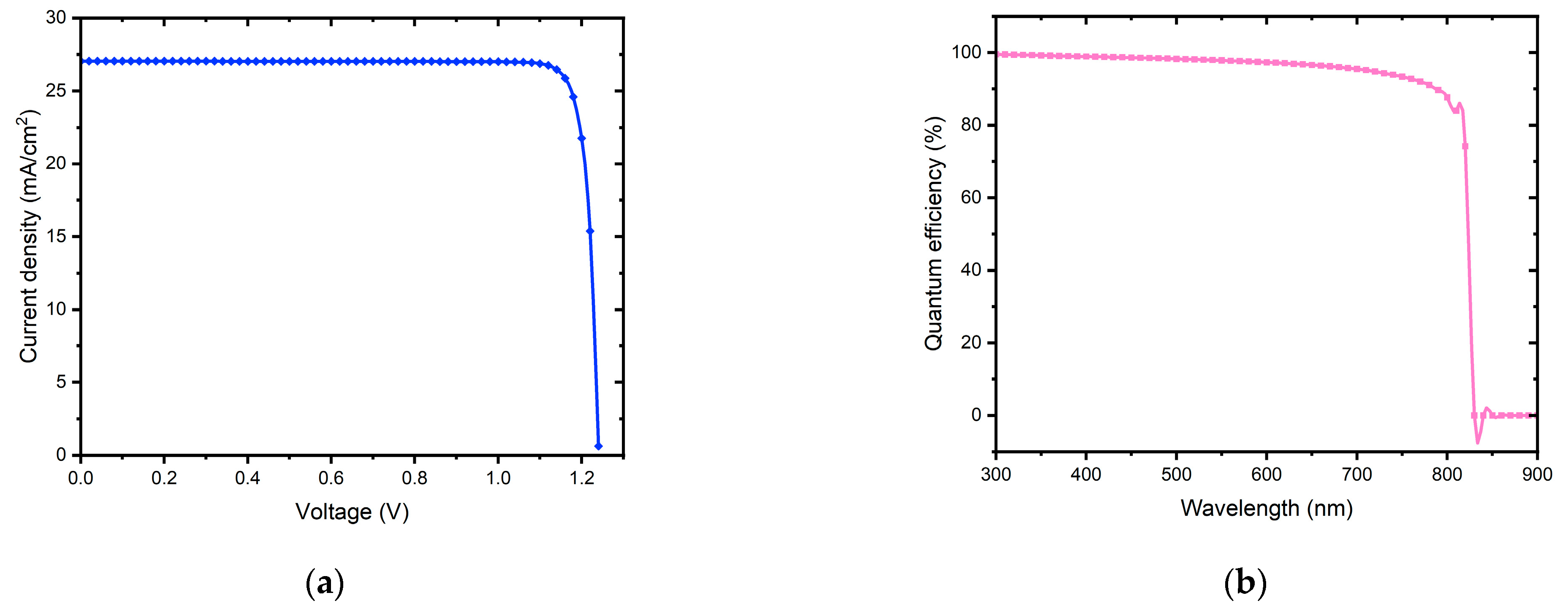
3.2.6. J–V and QE Characteristics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Suryawanshi, M.P.; Agawane, G.L.; Bhosale, S.M.; Shin, S.W.; Patil, P.S.; Kim, J.H.; Moholkar, A.V. CZTS Based Thin Film Solar Cells: A Status Review. Mater. Technol. 2013, 28, 98–109. [Google Scholar] [CrossRef]
- Vallisree, S.; Thangavel, R.; Lenka, T.R. Theoretical Investigations on Enhancement of Photovoltaic Efficiency of Nanostructured CZTS/ZnS/ZnO Based Solar Cell Device. J. Mater. Sci. Mater. Electron. 2018, 29, 7262–7272. [Google Scholar] [CrossRef]
- Reshak, A.H.; Nouneh, K.; Kityk, I.V.; Bila, J.; Auluck, S.; Kamarudin, H.; Sekkat, Z. Structural, Electronic and Optical Properties in Earth- Abundant Photovoltaic Absorber of Cu2ZnSnS4 and Cu2ZnSnSe4 from DFT Calculations. Int. J. Electrochem. Sci. 2014, 9, 955–974. [Google Scholar] [CrossRef]
- Mekhilef, S.; Saidur, R.; Safari, A. A Review on Solar Energy Use in Industries. Renew. Sustain. Energy Rev. 2011, 15, 1777–1790. [Google Scholar] [CrossRef]
- Hosenuzzaman, M.; Rahim, N.A.; Selvaraj, J.; Hasanuzzaman, M.; Malek, A.B.M.A.; Nahar, A. Global Prospects, Progress, Policies, and Environmental Impact of Solar Photovoltaic Power Generation. Renew. Sustain. Energy Rev. 2015, 41, 284–297. [Google Scholar] [CrossRef]
- Graetzel, M.; Janssen, R.A.J.; Mitzi, D.B.; Sargent, E.H. Materials Interface Engineering for Solution-Processed Photovoltaics. Nature 2012, 488, 304–312. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S. An Evolution Review in Solar Photovoltaic Materials. J. Commun. Technol. Electron. Comput. Sci. 2018, 20, 7–15. [Google Scholar]
- Jaiswal, D.; Mittal, M.; Mittal, V. A Review on Solar PV Cell and Its Evolution. In Proceedings of the Latest Trends in Renewable Energy Technologies; Vadhera, S., Umre, B.S., Kalam, A., Eds.; Springer: Singapore, 2021; pp. 303–313. [Google Scholar]
- Mitzi, D.B.; Gunawan, O.; Todorov, T.K.; Wang, K.; Guha, S. The Path towards a High-Performance Solution-Processed Kesterite Solar Cell. Sol. Energy Mater. Sol. Cells 2011, 95, 1421–1436. [Google Scholar] [CrossRef]
- ur Rehman, A.; Iqbal, M.Z.; Bhopal, M.F.; Khan, M.F.; Hussain, F.; Iqbal, J.; Khan, M.; Lee, S.H. Development and Prospects of Surface Passivation Schemes for High-Efficiency c-Si Solar Cells. Sol. Energy 2018, 166, 90–97. [Google Scholar] [CrossRef]
- Irvine, S. Solar Cells and Photovoltaics. In Springer Handbook of Electronic and Photonic Materials; Kasap, S., Capper, P., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 1097–1109. ISBN 978-3-319-48933-9. [Google Scholar]
- Gunaicha, P.P.; Gangam, S.; Roehl, J.L.; Khare, S.V. Structural, Energetic and Elastic Properties of Cu2ZnSn(SxSe1−x)4 (x = 1, 0.75, 0.5, 0.25, 0) Alloys from First-Principles Computations. Sol. Energy 2014, 102, 276–281. [Google Scholar] [CrossRef]
- Simya, O.K.; Mahaboobbatcha, A.; Balachander, K. A Comparative Study on the Performance of Kesterite Based Thin Film Solar Cells Using SCAPS Simulation Program. Superlattices Microstruct. 2015, 82, 248–261. [Google Scholar] [CrossRef]
- Atwater, H.A.; Polman, A. Plasmonics for Improved Photovoltaic Devices. Nat. Mater 2010, 9, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Green, M.; Dunlop, E.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Hao, X. Solar Cell Efficiency Tables (Version 57). Prog. Photovolt. Res. Appl. 2021, 29, 3–15. [Google Scholar] [CrossRef]
- Green, M.A.; Emery, K.; Hishikawa, Y.; Warta, W. Solar Cell Efficiency Tables (Version 37). Prog. Photovolt. Res. Appl. 2011, 19, 84–92. [Google Scholar] [CrossRef]
- Kayes, B.M.; Nie, H.; Twist, R.; Spruytte, S.G.; Reinhardt, F.; Kizilyalli, I.C.; Higashi, G.S. 27.6% Conversion Efficiency, a New Record for Single-Junction Solar Cells under 1 Sun Illumination. In Proceedings of the 2011 37th IEEE Photovoltaic Specialists Conference, Seattle, WA, USA, 19–24 June 2011; pp. 000004–000008. [Google Scholar]
- Green, M.A.; Emery, K.; Hishikawa, Y.; Warta, W.; Dunlop, E.D. Solar Cell Efficiency Tables (Version 43). Prog. Photovolt. Res. Appl. 2014, 22, 1–9. [Google Scholar] [CrossRef]
- Mitzi, D.B.; Yuan, M.; Liu, W.; Kellock, A.J.; Chey, S.J.; Deline, V.; Schrott, A.G. A High-Efficiency Solution-Deposited Thin-Film Photovoltaic Device. Adv. Mater. 2008, 20, 3657–3662. [Google Scholar] [CrossRef]
- Fthenakis, V.M.; Moskowitz, P.D. Photovoltaics: Environmental, Health and Safety Issues and Perspectives. Prog. Photovolt. Res. Appl. 2000, 8, 27–38. [Google Scholar] [CrossRef]
- Tanaka, A. Toxicity of Indium Arsenide, Gallium Arsenide, and Aluminium Gallium Arsenide. Toxicol. Appl. Pharmacol. 2004, 198, 405–411. [Google Scholar] [CrossRef]
- Phipps, G.; Mikolajczak, C.; Guckes, T. Indium and Gallium: Long-Term Supply. Renew. Energy Focus 2008, 9, 56–59. [Google Scholar] [CrossRef]
- Patel, M.; Ray, A. Enhancement of Output Performance of Cu2ZnSnS4 Thin Film Solar Cells—A Numerical Simulation Approach and Comparison to Experiments. Phys. B Condens. Matter 2012, 407, 4391–4397. [Google Scholar] [CrossRef]
- Nitsche, R.; Sargent, D.F.; Wild, P. Crystal Growth of Quaternary 122464 Chalcogenides by Iodine Vapor Transport. J. Cryst. Growth 1967, 1, 52–53. [Google Scholar] [CrossRef]
- Lahoual, M.; Bourennane, M.; Aidaoui, L. Numerical Investigation of Copper Zinc Tin Sulphide Based Solar Cell with Non-Toxic Zn (O, S) Buffer Layer. Phys. Status Solidi 2024, 221, 2300732. [Google Scholar] [CrossRef]
- Mansouri, S.; Dehimi, L.; Bencherif, H.; Pezzimenti, F.; Zulfiqar, M.; Alotaibi, N.H.; Mohammad, S.; Haldhar, R.; Darwish, M.A.; Hossain, M.K. Theoretical Simulation on Enhancing the Thin-Film Copper Zinc Tin Sulfide Solar Cell Performance Using MoS2, MoOx, and CuI as Efficient Hole Transport Layers. Energy Fuels 2024, 38, 8187–8198. [Google Scholar] [CrossRef]
- Dakua, P.K.; Dash, R.K.; Laidouci, A.; Bhattarai, S.; Dudekula, U.; Kashyap, S.; Agarwal, V.; Rashed, A.N.Z. Evaluating CZTS Solar Cell Performance Based on Generation and Recombination Models for Possible ETLs Through Numerical Analysis. J. Electron. Mater. 2024, 53, 2015–2025. [Google Scholar] [CrossRef]
- Sawa, H.B.; Babucci, M.; Keller, J.; Björkman, C.P.; Samiji, M.E.; Mlyuka, N.R. Toward Improving the Performance of Cu2ZnSnS4-Based Solar Cells with Zr, W or Sulfurized Layers at the SnO2:F/Cu2ZnSnS4 Rear Interface. Thin Solid Film. 2024, 793, 140276. [Google Scholar] [CrossRef]
- Kissin, S.A.; Owens, D.A.R. The Relatives of Stannite in the Light of New Data. Can. Mineral. 1989, 27, 673–688. [Google Scholar]
- Nakazawa, K.I. Electrical and Optical Properties of Stannite-Type Quaternary Semiconductor Thin Films. Jpn. J. Appl. Phys. 1988, 27, 2094. [Google Scholar] [CrossRef]
- Cherouana, A.; Labbani, R. Study of CZTS and CZTSSe Solar Cells for Buffer Layers Selection. Appl. Surf. Sci. 2017, 424, 251–255. [Google Scholar] [CrossRef]
- Niki, S.; Contreras, M.; Repins, I.; Powalla, M.; Kushiya, K.; Ishizuka, S.; Matsubara, K. CIGS Absorbers and Processes. Prog. Photovolt. Res. Appl. 2010, 18, 453–466. [Google Scholar] [CrossRef]
- Amin, N.; Hossain, M.I.; Chelvanathan, P.; Mukter Uzzaman, A.S.M.; Sopian, K. Prospects of Cu2ZnSnS4 (CZTS) Solar Cells from Numerical Analysis. In Proceedings of the International Conference on Electrical & Computer Engineering (ICECE 2010), Dhaka, Bangladesh, 18–20 December 2010; pp. 730–733. [Google Scholar]
- Shin, B.; Gunawan, O.; Zhu, Y.; Bojarczuk, N.A.; Chey, S.J.; Guha, S. Thin Film Solar Cell with 8.4% Power Conversion Efficiency Using an Earth-Abundant Cu2ZnSnS4 Absorber. Prog. Photovolt. Res. Appl. 2013, 21, 72–76. [Google Scholar] [CrossRef]
- Adewoyin, A.D.; Olopade, M.A.; Chendo, M. Enhancement of the Conversion Efficiency of Cu2ZnSnS4 Thin Film Solar Cell through the Optimization of Some Device Parameters. Optik 2017, 133, 122–131. [Google Scholar] [CrossRef]
- Siebentritt, S. Why Are Kesterite Solar Cells Not 20% Efficient? Thin Solid Film. 2013, 535, 1–4. [Google Scholar] [CrossRef]
- Zanatta, A.R. The Shockley–Queisser Limit and the Conversion Efficiency of Silicon-Based Solar Cells. Results Opt. 2022, 9, 100320. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H. Detailed Balance Limit of Efficiency of p–n Junction Solar Cells. In Renewable Energy; Routledge: London, UK, 2011; ISBN 978-1-315-79324-5. [Google Scholar]
- Lv, Z.; Deng, Z.; Xu, D.; Li, X.; Jia, Y. Efficient Organic Light-Emitting Diodes with C60 Buffer Layer. Displays 2009, 30, 23–26. [Google Scholar] [CrossRef]
- Ferhati, H.; Djeffal, F.; AbdelMalek, F. Towards Improved Efficiency of SnS Solar Cells Using Back Grooves and Strained-SnO2 Buffer Layer: FDTD and DFT Calculations. J. Phys. Chem. Solids 2023, 178, 111353. [Google Scholar] [CrossRef]
- Isha, A.; Kowsar, A.; Kuddus, A.; Hossain, M.K.; Ali, M.H.; Haque, M.D.; Rahman, M.F. High Efficiency Cu2MnSnS4 Thin Film Solar Cells with SnS BSF and CdS ETL Layers: A Numerical Simulation. Heliyon 2023, 9, e15716. [Google Scholar] [CrossRef]
- Gohri, S.; Sharma, S.; Pandey, R.; Madan, J.; Sharma, R. Influence of SnS and Sn2S3 Based BSF Layers on the Performance of CZTSSe Solar Cell. In Proceedings of the 2020 47th IEEE Photovoltaic Specialists Conference (PVSC), Calgary, AB, Canada, 15 June–21 August 2020; pp. 2300–2303. [Google Scholar]
- Srivastava, A.; Dua, P.; Lenka, T.R.; Tripathy, S.K. Numerical Simulations on CZTS/CZTSe Based Solar Cell with ZnSe as an Alternative Buffer Layer Using SCAPS-1D. Mater. Today Proc. 2021, 43, 3735–3739. [Google Scholar] [CrossRef]
- Burgelman, M.; Nollet, P.; Degrave, S. Modelling Polycrystalline Semiconductor Solar Cells. Thin Solid Film. 2000, 361–362, 527–532. [Google Scholar] [CrossRef]
- Oublal, E.; Ait Abdelkadir, A.; Sahal, M. High Performance of a New Solar Cell Based on Carbon Nanotubes with CBTS Compound as BSF Using SCAPS-1D Software. J. Nanopart. Res. 2022, 24, 202. [Google Scholar] [CrossRef]
- Rahman, M.A. Design and Simulation of a High-Performance Cd-Free Cu2SnSe3 Solar Cells with SnS Electron-Blocking Hole Transport Layer and TiO2 Electron Transport Layer by SCAPS-1D. SN Appl. Sci. 2021, 3, 253. [Google Scholar] [CrossRef]
- Mohandes, A.; Moradi, M.; Kanani, M. Numerical Analysis of High Performance Perovskite Solar Cells with Stacked ETLs/C60 Using SCAPS-1D Device Simulator. Opt. Quant. Electron. 2023, 55, 533. [Google Scholar] [CrossRef]
- Atowar Rahman, M. Enhancing the Photovoltaic Performance of Cd-Free Cu2ZnSnS4 Heterojunction Solar Cells Using SnS HTL and TiO2 ETL. Sol. Energy 2021, 215, 64–76. [Google Scholar] [CrossRef]
- Islam, M.A.; Al Rafi, J.; Uddin, M.A. Modeling and Formation of a Single-Walled Carbon Nanotube (SWCNT) Based Heterostructure for Efficient Solar Energy: Performance and Defect Analysis by Numerical Simulation. AIP Adv. 2023, 13, 115201. [Google Scholar] [CrossRef]
- Uddin, M.A.; Rafi, J.A.; Islam, M.A.; Mominuzzaman, S.M.; Nath, I.D. Modeling and Numerical Analysis of Heterostructure Single-Walled Carbon Nanotube (SWCNT) Solar Cell. In Proceedings of the 2022 12th International Conference on Electrical and Computer Engineering (ICECE), Dhaka, Bangladesh, 21–23 December 2022; pp. 388–391. [Google Scholar]

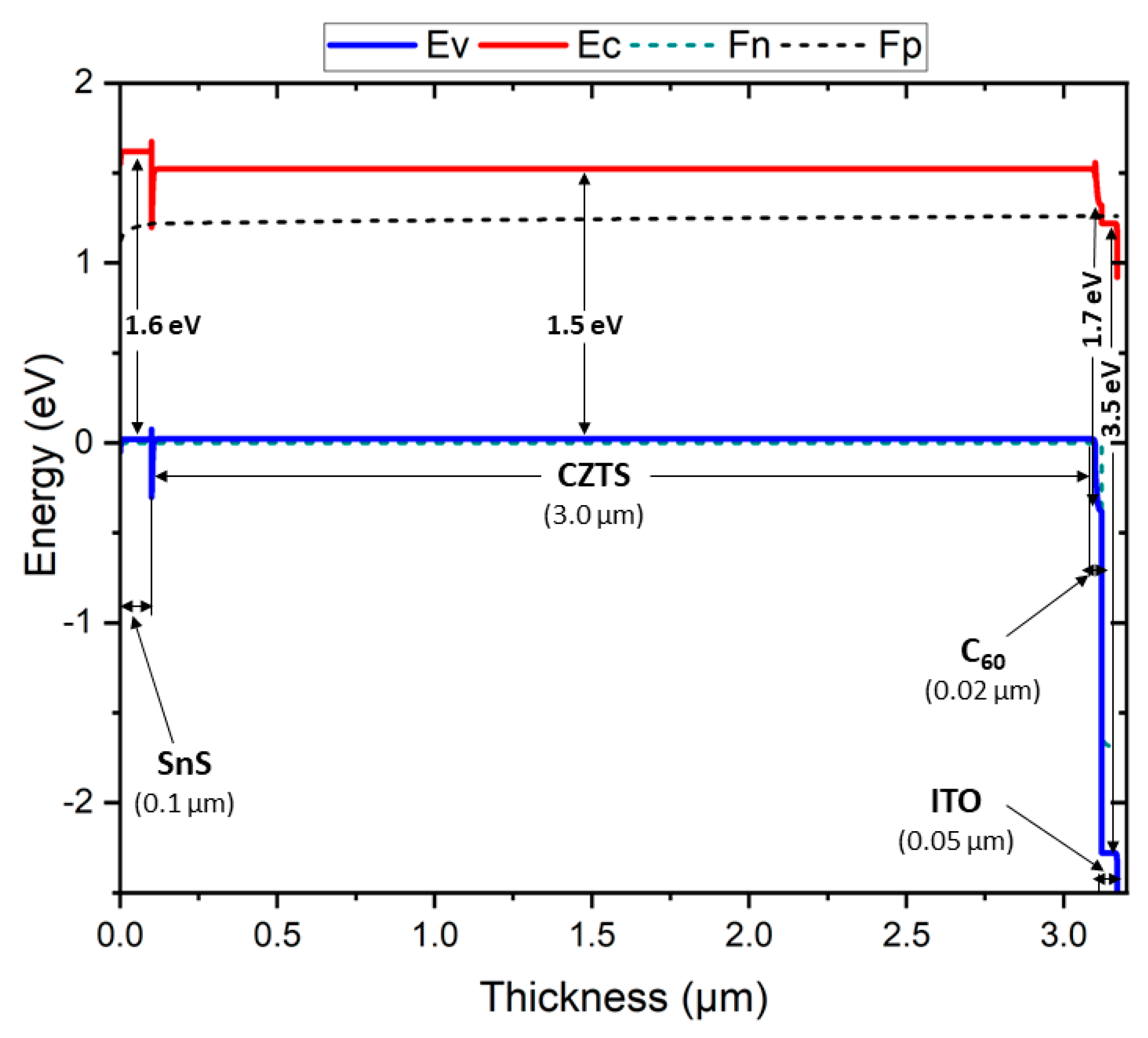



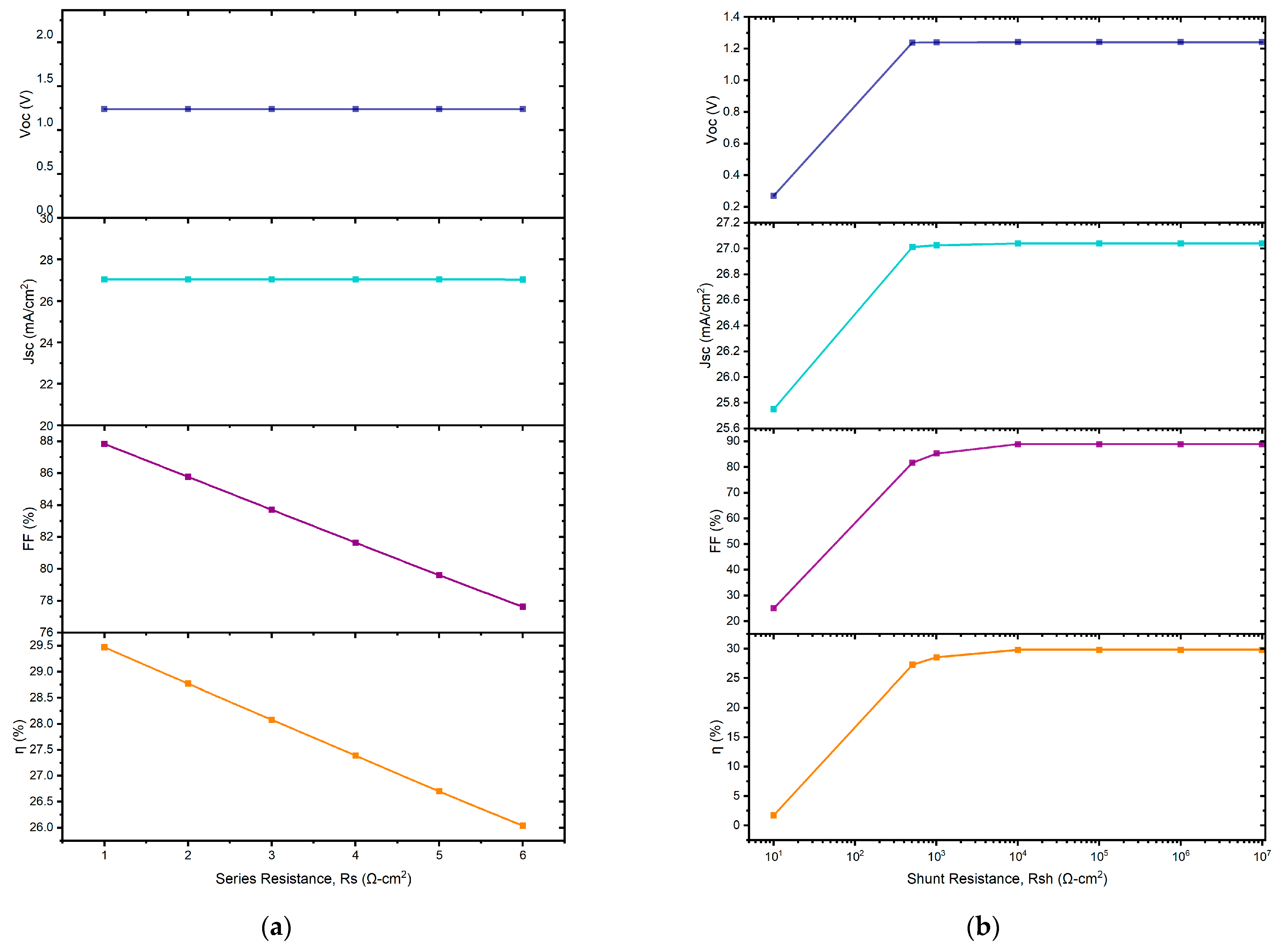
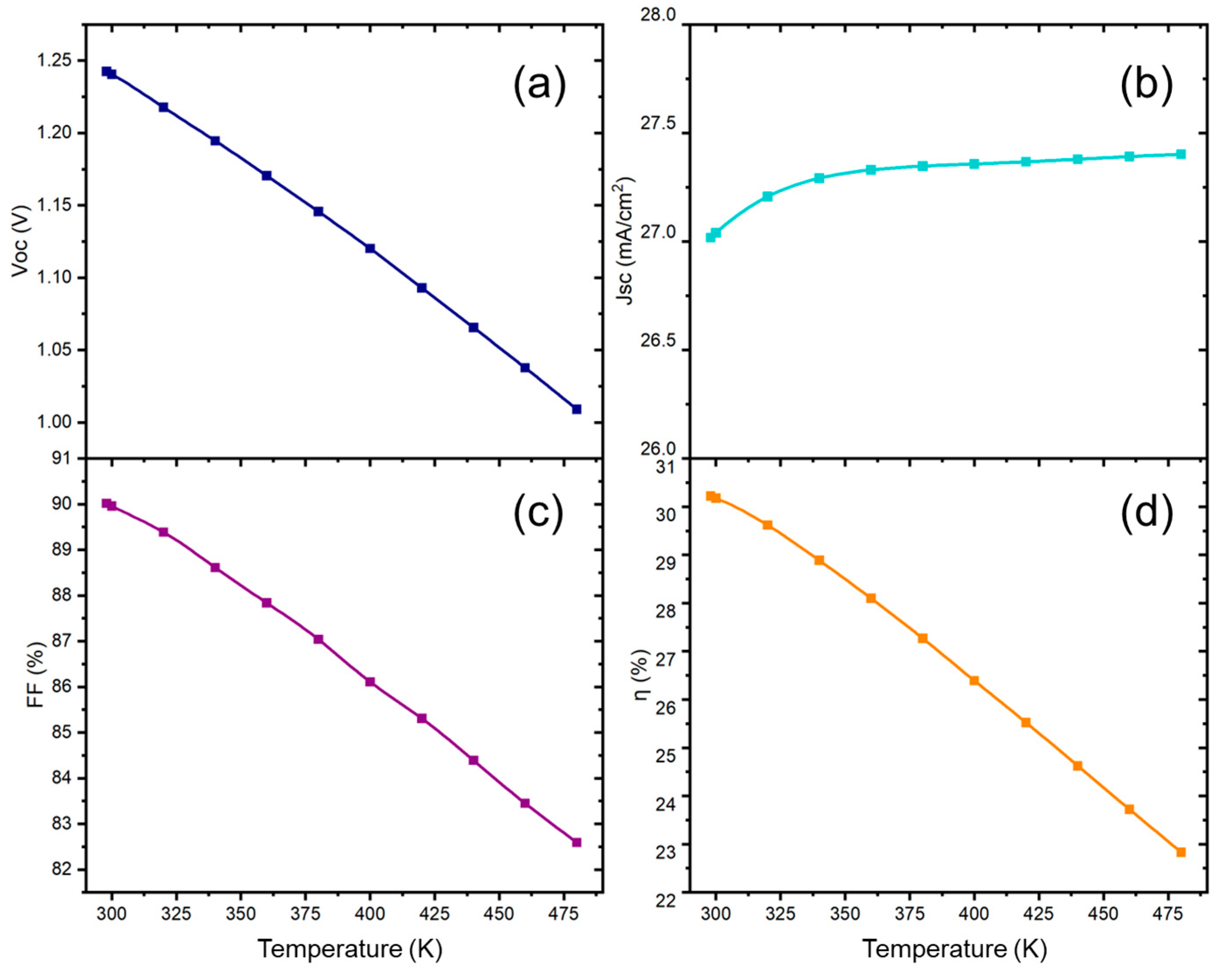
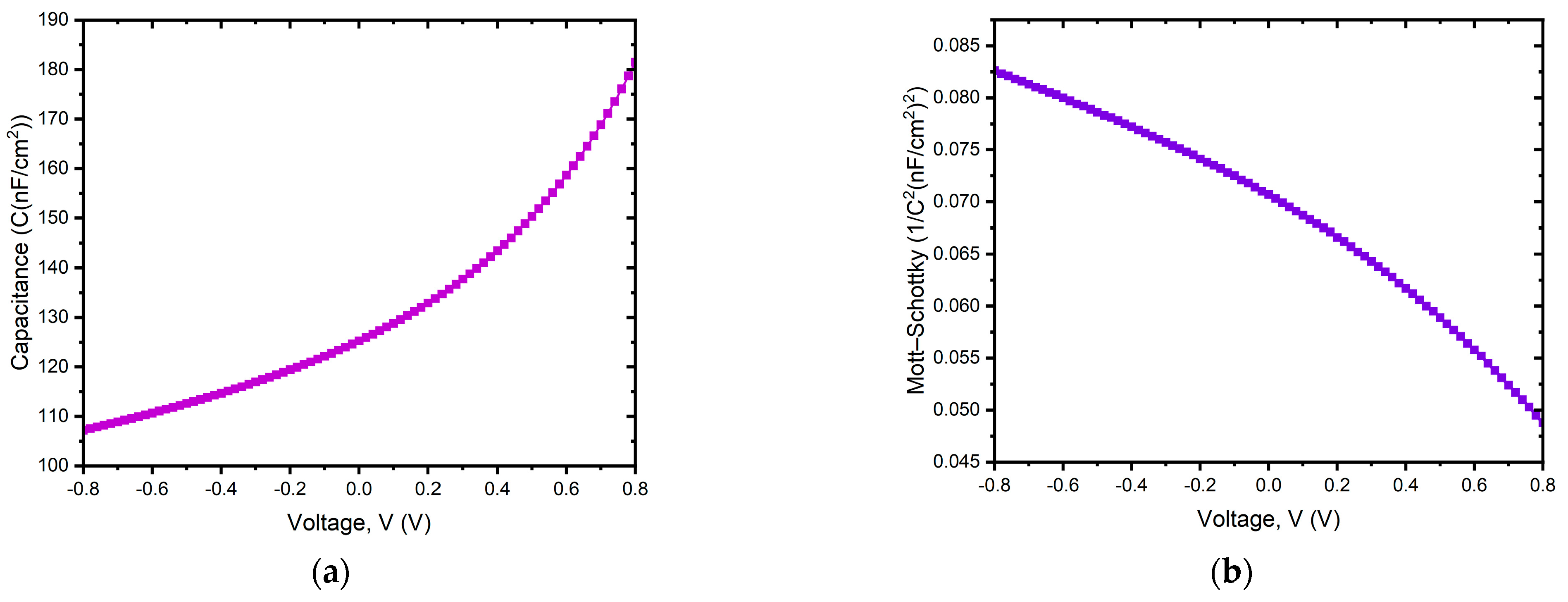
| Parameter | ITO [46] | C60 [47] | CZTS [43] | SnS [46] |
|---|---|---|---|---|
| Thickness (nm) | 50 | 20 | 1500–3000 | 100 |
| Bandgap Eg (eV) | 3.5 | 1.7 | 1.5 | 1.6 |
| Electron affinity, χ (eV) | 4.6 | 4.5 | 4.58 | 4.1 |
| Dielectric permittivity | 8.9 | 6.0 | 9.5 | 13.0 |
| CB effective density of states (cm−3) | 2.2 × 1018 | 1.0 × 1019 | 1.91 × 1018 | 2.18 × 1018 |
| VB effective density of states (cm−3) | 1.8 × 1019 | 1.0 × 1019 | 2.58 × 1018 | 4.46 × 1018 |
| Electron thermal velocity (cm s−1) | 1.0 × 107 | 1.0 × 107 | 1.0 × 107 | 1.0 × 107 |
| Hole thermal velocity (cm s−1) | 1.0 × 107 | 1.0 × 107 | 1.0 × 107 | 1.0 × 107 |
| Electron mobility, μn (cm2 V−1 s−1) | 10 | 50 | 50 | 15 |
| Hole mobility, μp (cm2 V−1 s−1) | 10 | 50 | 10 | 100 |
| Donor concentration, ND (cm−3) | 1.0 × 1019 | 1.0 × 1018 | 0.0 | 0.0 |
| Acceptor concentration, NA (cm−3) | 0.0 | 0.0 | 6.0 × 1015–6.0 × 1018 | 1.0 × 1019 |
| Parameter | Front Contact Electrical Properties | Back Contact Electrical Properties |
|---|---|---|
| [Al] | [Pt] | |
| Surface recombination velocity of electrons (cm s−1) | 1.0 × 107 | 1.0 × 105 |
| Surface recombination velocity of holes (cm s−1) | 1.0 × 105 | 1.0 × 107 |
| Work function (eV) | 4.26 | 5.65 |
| Parameter | ITO/C60 | C60/CZTS | CZTS/SnS |
|---|---|---|---|
| Defect type | Neutral | Neutral | Neutral |
| Capture cross-section of electrons (cm2) | 1.0 × 10–19 | 1.0 × 10–19 | 1.0 × 10–19 |
| Capture cross-section of holes (cm2) | 1.0 × 10–19 | 1.0 × 10–19 | 1.0 × 10–19 |
| Energetic distribution | Single | Gaussian | Single |
| Total defect density (cm−2) | 1.0 × 1010 | 1.0 × 1010 | 1.0 × 1010 |
| Parameter | At Each Layer (ITO, C60, CZTS, SnS) |
|---|---|
| Defect type | Neutral |
| Capture cross-section of electrons (cm2) | 1.0 × 10−15 |
| Capture cross-section of holes (cm2) | 1.0 × 10−15 |
| Energetic distribution | Single |
| Reference for defect energy level Et | Above EV (SCAPS < 2.7) |
| Total density (cm−3): uniform | 1.0 × 1014–1.0 × 1017 |
| Auger hole/electron capture coefficient (cm6 s−1) | 1.0 × 10−26 |
| Optimum Input Conditions | Output Parameters at Optimized Input Conditions | ||||
|---|---|---|---|---|---|
| W (μm) | NA (cm−3) | VOC (V) | JSC (mA/cm2) | FF (%) | η (%) |
| 3.0 | 6 × 1018 | 1.2405 | 27.039539 | 89.96 | 30.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafi, J.A.; Islam, M.A.; Mahmud, S.; Honda, M.; Ichikawa, Y.; Athar Uddin, M. C60/CZTS Junction Combination to Improve the Efficiency of CZTS-Based Heterostructure Solar Cells: A Numerical Approach. Electron. Mater. 2024, 5, 145-159. https://doi.org/10.3390/electronicmat5030010
Rafi JA, Islam MA, Mahmud S, Honda M, Ichikawa Y, Athar Uddin M. C60/CZTS Junction Combination to Improve the Efficiency of CZTS-Based Heterostructure Solar Cells: A Numerical Approach. Electronic Materials. 2024; 5(3):145-159. https://doi.org/10.3390/electronicmat5030010
Chicago/Turabian StyleRafi, Jobair Al, Md. Ariful Islam, Sayed Mahmud, Mitsuhiro Honda, Yo Ichikawa, and Muhammad Athar Uddin. 2024. "C60/CZTS Junction Combination to Improve the Efficiency of CZTS-Based Heterostructure Solar Cells: A Numerical Approach" Electronic Materials 5, no. 3: 145-159. https://doi.org/10.3390/electronicmat5030010
APA StyleRafi, J. A., Islam, M. A., Mahmud, S., Honda, M., Ichikawa, Y., & Athar Uddin, M. (2024). C60/CZTS Junction Combination to Improve the Efficiency of CZTS-Based Heterostructure Solar Cells: A Numerical Approach. Electronic Materials, 5(3), 145-159. https://doi.org/10.3390/electronicmat5030010








