Magnetization of Magnetically Inhomogeneous Sr₂FeMoO_6-δ Nanoparticles

Abstract

In this work, we describe the magnetization of nanosized SFMO particles with a narrow size distribution around ca. 70 nm fabricated by the citrate-gel technique. The single-phase composition and superstructure ordering degree were proved by X-ray diffraction, the superparamagnetic behavior by magnetization measurements using zero-field cooled and field-cooled protocols, as well as by electron magnetic resonance. Different contributions to the magnetic anisotropy constant and the temperature dependence of the magnetocrystalline anisotropy are discussed.

1. Introduction

Strontium ferromolybdate (Sr₂FeMoO_6-δ, SFMO) is a widely studied ferrimagnetic double perovskite. SFMO is a promising candidate for magnetic electrode materials for room-temperature spintronic applications, because they present a half-metallic character (with theoretically 100% polarization), a high Curie temperature (T_C) of about 415 K (ferromagnets should be operated in their ordered magnetic state below T_C), and a low-field magnetoresistance [1]. The same is valid for its derivatives such as (SrBa)FeMoO_6-δ or (SrLa)FeMoO_6-δ. However, wide application of SFMO is still missing, because of the low reproducibility of its magnetic properties originating in ceramic processing issues and its ageing upon contact with air and moisture. SFMO is a material which properties are very sensitive to disordering at the B-site, i.e., Fe_Mo and Mo_Fe antisite defect formation, nonstoichiometry of the magnetic Fe ions, and, with a lesser extent, to oxygen- and Sr-deficit [2].

Recently, an inhomogeneous magnetic state was obtained in SFMO nanoparticles fabricated by solid-state reactions from partially reduced SrFeO_3−x and SrMoO₄ precursors by studying the temperature dependences of the magnetization measured in the field-cooling (FC) and zero-field-cooling (ZFC) modes and small-angle neutron scattering [3]. This state was attributed to the frustration of the exchange bonds and simultaneous occurrence of various magnetic states: antiferromagnetic, ferrimagnetic, and superparamagnetic when the spin inversion does not change the energy of the system in a wide range of temperatures. In another report [4], the Mössbauer spectrum of SFMO fine particles of about 30 nm size, consisting of small traces of SrMoO₄, revealed a paramagnetic doublet above a blocking temperature T_B = 45 K, while the spectrum of a similar sample with a size of 197 nm taken at 77 K included superparamagnetic, ferromagnetic and surface contributions. Diverse magnetic behavior - superparamagnetic, ferromagnetic and paramagnetic–was detected in single-phase Mg_xZn_1−xFe₂O₄ nanoparticles by Mössbauer spectroscopy and curve fitting of the magnetic-field dependence of the magnetization [5]. This was attributed to the distribution of particle sizes in the samples.

In this work, we determine the magnetization behavior of nanosized magnetically inhomogeneous SFMO particles by means of ZFC-FC magnetization and electron magnetic resonance measurements. Furthermore, we discuss different contributions to magnetic anisotropy and evaluate the temperature dependence of the uniaxial magnetocrystalline anisotropy constant.

2. Materials and Methods

The citrate-gel technique was used for the synthesis of SFMO nanoparticles using ultra-high purity Sr(NO₃)₂, Fe(NO₃)₃⋅9H₂O, (NH₄)₆Mo₇O₂₄ and citric acid monohydrate C₆H₈O₇H₂O as initial reagents. The solid foam resulting from the synthesis was crushed and annealed at T = 770 K and p_O2 = 2.1×10⁴ Pa for 10 h. After that, the powders were annealed in a 5% H₂/Ar gas mixture flow at 1170 K for 5 h, followed by quenching at room temperature. Synthesis details are described in Ref. [6] (cf. Supplemental Materials, Figure S1). Since the SFMO powders were agglomerated, ultrasonic dispersion as used to obtain highly dispersed particles with an average size smaller than 100 nm. Ethyl alcohol was chosen as a liquid medium since there is neither chemical interaction with SFMO nor SFMO decomposition.

To optimize the process of SFMO dispersion, the effects of time and radiation power of the ultrasonic homogenizer on the dispersion of the particles were studied in a suspension of 0.1 g of powder per 25 mL of C₂H₅OH. The power of ultrasonic exposure was varied from 1% to 100% of the nominal power (P_n) with a step of 25% at a frequency of 22 kHz and an exposure time ranging from 15 to 60 min with a step of 15 min. To prevent the process of coagulation of SFMO grains, different surfactants were used. The surfactant was selected to achieve a high Z-potential. Cationic hexadecyltrimethylammonium bromide, anionic sodium tripolyphosphate, nonionic polyoxyethylene (20) sorbitan monolaurate Tween20^TM, and nonionic polycarboxylate/sodium salt Dolapix PC 67 were tested. The most suitable was the nonionic Tween20^TM surfactant providing the main results described in this work. In this case, the Zeta potential of SFMO nanopowder has negative values. The highest values of the Zeta potential (Z = −63.2 mV) in 25 mL (C₂H₅OH) + 0.01 g SFMO + x g Tween 20^TM subjected to dispersion for 45 min was achieved at x = 0.05 g Tween20^TM.

X-ray diffraction (XRD) patterns of samples with a weight of ca. 60 mg were recorded at room temperature at a rate of 60°/h in the range of angles Θ = 10–90° using a DRON-3 diffractometer (Bourevestnik, Saint Petersburg, Russia) in CuK_α radiation and analyzed by means of the ICSD-PDF2 database (Release 2000) and PowderCell software. The microstructure, morphology, and elemental composition of grains of annealed SFMO powders were investigated by field-emission scanning electron microscope JEOL JSM-7000F (JEOL Ltd., Tokyo, Japan). The grain sizes were estimated by an NT-206 atomic force microscope (Microtestmachines, Gomel, Belarus). The particle size distribution was obtained by dynamic light scattering (DLS) analysis using a Zetasizer Nanoparticles analyzer (Malvern Nano ZS90, Malvern, UK).

Magnetization measurements of the samples were performed at magnetic fields up to 4 T in a temperature range from 4.2 K to 320 K using a Liquid Helium-Free High-Field Measurement System vibrating sample magnetometer (Cryogenic Ltd., London, UK). ZFC-FC curves were acquired in a magnetic field of 0.01 T.

The electron magnetic resonance (EMR) measurements of samples with a weight of ca. 20 mg were performed in the X-band (9.45 GHz) at a field modulation frequency of 100 kHz using an EleXsys E-500 electron paramagnetic resonance spectrometer (Bruker, Billerica, MA, USA) equipped with a nitrogen-flow cryostat. The first field derivative of the microwave absorption, dP_mw/dB ∝ dχ″/dB, with P_mw the microwave power and χ″ the imaginary part of the magnetic AC susceptibility, was registered. The magnetic field was swept from high to low values.

3. Results

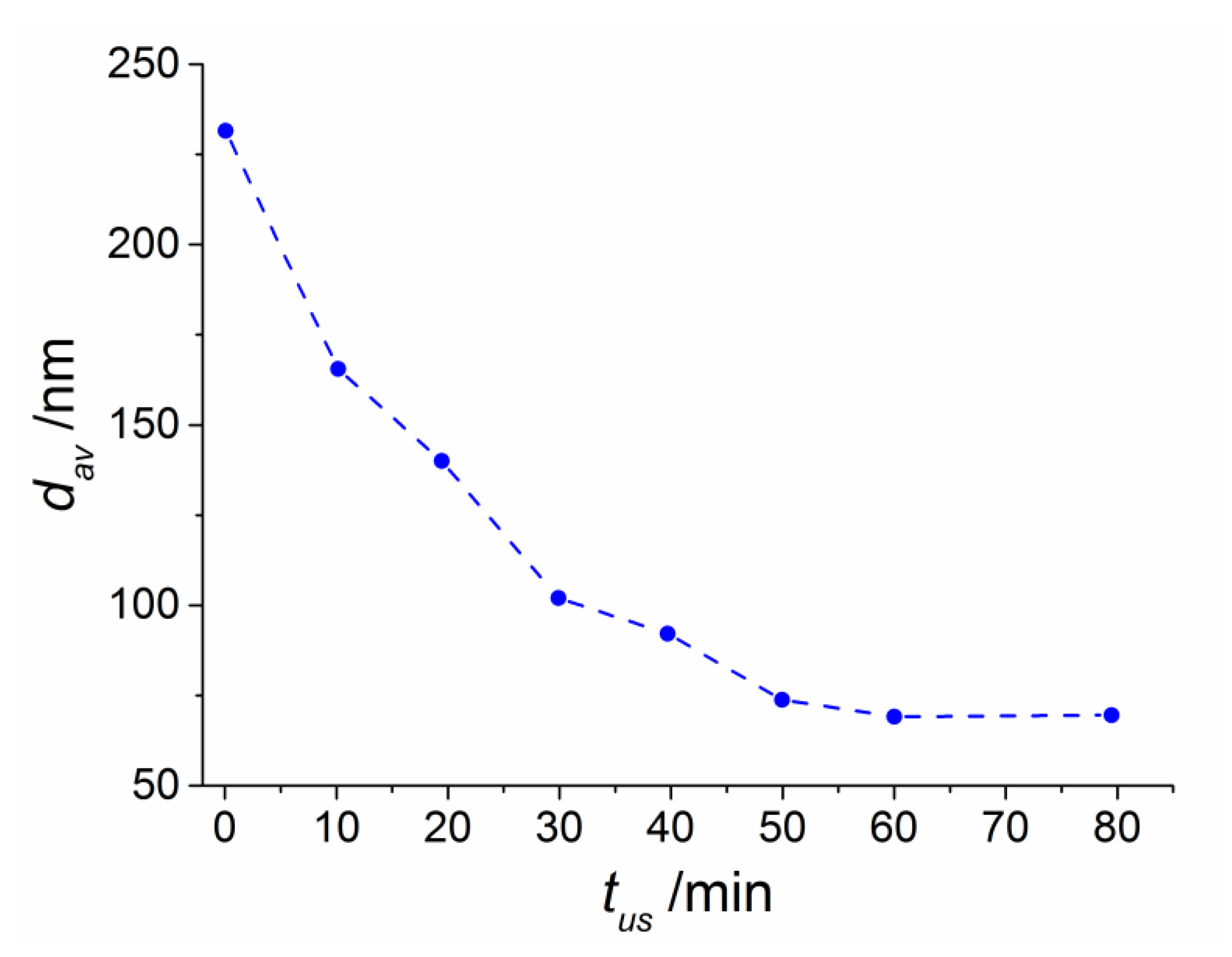
Single-phase SFMO powders were obtained with crystal lattice parameters a = b = 0.55629 nm, c = 0.78936 nm and with a B-site superstructural ordering degree of 88% (cf. Supplemental Materials, Figures S2 and S3). After ultrasonic treatment, the sizes of agglomerates in a suspension of 25 mL (C₂H₅OH) + 0.01 g (SFMO) + 0.05 g (Tween 20), subjected to sonication for 60 min, smoothly decrease from 230 nm to about 70 nm (Figure 1). At an ultrasonic power of P = 25% P_n, a release of dissolved gases begins in the rarefaction regions being at low pressure, which is accompanied by the formation of a durable bubble. The latter is stabilized by a monolayer of SFMO particles and oscillates linearly with the frequency of the ultrasonic wave relatively to its equilibrium position. Here, dispersion is less effective. A further increase of the power up to P = 75% P_n leads to a violation of linearity of oscillations of the bubble walls. The stage of stable cavitation begins. The bubble itself becomes a source of ultrasonic higher-harmonic vibrations. Waves, microcurrents and electric discharges appear on its surface [7,8]. This increases the dispersion of SFMO particles. Thus, at sonication times up to 45 min, particles are effectively dispersed in the entire suspension volume, and processes of coagulation and sedimentation of particles are prevented. The ultrasonic wave passing through the liquid creates zones of compression and depression, which alternate in each half-period of the wave. For this reason, the particles of the medium vibrate with small amplitudes (in the sub-µm range) and huge accelerations [7,8]. A further increase of p beyond 75% P_n leads to unstable cavitation and the formation of a cavitation cloud on the surface of the alcohol solution, which hinders the transmission of ultrasonic vibrations into the volume [7,8]. This state of the alcohol suspension is characterized by the formation of rapidly growing vapor-gas bubbles, which instantly contract in volume during the compression phase and collapse. Because of this, the average particle size increases again up to 450 nm as a result of ultrasonic treatment with P = P_n for times up to 60 min. This indicates intensive coagulation prevailing over the dispersion process, which can be explained by the formation of a cavitation cloud (a large number of air bubbles) on the surface of the working tool hindering the transmission of ultrasonic vibrations into the volume and, thus, reducing the grinding efficiency. Saturation of particle size was reached after 80 min ultrasonic treatment. Figure 2 illustrates the increase of the volume fraction of fine SFMO particles with sonication time.

The nanoparticle size distribution was analyzed by means of DLS. It is most widely represented by the lognormal distribution:

$$f(d)=\frac{1}{\sqrt{2\pi }d\sigma }\exp \left\{-\frac{{[\ln (d)-\ln (d_{av})]}^2}{2{\sigma }^2}\right\}$$

(1)

where d_av and σ are the average diameter and dispersion of the particle size distribution, respectively [9]. The calculated average particle diameter for the powder subjected to sonication for 60 min amounts to d_av = 67.8 nm and the dispersion to σ = 0.214 nm (Figure 3).

Figure 4 shows a scanning electron microscopy image of the as-fabricated, agglomerated SFMO nanoparticles (Figure 4a) and an atomic force microscopy (AFM) scan of the nanoparticles on a substrate (Figure 4b). The figures demonstrate a narrow size distribution of particles with a size in the order of 70 nm and the de-agglomeration after ultrasonic treatment. The height of the AFM features corresponds approximately to the average particle size obtained by DLS. Note that features with a size of about 10 nm could not be resolved by AFM.

Measurements of the temperature dependence of the magnetization following the ZFC-FC protocol revealed the presence of at least superparamagnetic and metastable blocked behavior (Figure 5) (cf. [4]). The maximum of the ZFC curve is located at a maximum temperature T_max of ca. 20 K. The low blocking temperature, as well as a large increment of magnetization with decreasing temperature in the FC data, reveal that the magnetic interaction between the nanoparticles is quite weak. With regard to the lognormal size distribution, the position of T_max is not the same as the average blocking temperature T_B. The latter is shifted down to smaller values by a correction factor of 1.5 [10] giving rise to T_B ≈ 13 K. The corresponding K₁V value amounts to 5.25 × 10⁻²¹ J. Note that the difference between the maximum position of the ZFC curve at 20 K and the bifurcation point between the ZFC and FC curves at ca. 170 K is another measure of the dispersion of grain sizes [11]: the biggest particles are deblocked at the latter temperature. Also, we have to take into account that the value of T_B depends on the applied magnetic field. Following a model proposed in [12], we found that in our case T_B is underestimated by about 7%.

In Figure 6a, EMR spectra of a similar SFMO sample with a B-site superstructure ordering degree of 81% are plotted for measurement temperatures ranging from 120 K to 480 K. Figure 6b shows the corresponding resonant magnetic field B_r, defined as the field for which the derivative dP_mw/dB goes through zero, and the linewidth ΔB_pp defined as the field interval between the positive and negative peaks of the resonance curve. The signal reduces rapidly at temperatures above 400 K, however, the line is still observable at 440 K and completely disappears at 460 K. Thus, the Curie temperature T_C is slightly above 400 K (the FMR is usually observed even at the paramagnetic side of T_C [13]). The resonance field B_r is always below that of the paramagnetic resonance value corresponding to g = 2 and approaches the latter with increasing temperature. As the temperature decreases below T_C, the spectra are broadened and shift towards lower magnetic fields. The latter effect is typical of predominantly cubic magnetic anisotropy.

Since in magnetic resonance measurements in the X-band the characteristic measurement time τ_m amounts to 10⁻¹⁰ s, the characteristic blocking temperature is roughly given by kT_B ≈ K₁V [14]. Considering ZFC magnetization measurements, this yields T_B^EMR ≈ 330 K. Unfortunately, passing through 330 K produces no clear effect on the curves in Figure 6b. In [14], the T_B value has been obtained by plotting the total intensity (second integral) of the experimental EMR absorption band versus temperature. However, this method is rather imprecise when a part of the resonance band is not recorded as is the case at low temperatures.

The linewidth is determined by the spread of the resonance fields of the individual nanoparticles caused by the random distribution of their easy magnetization axes and by the precession damping of the magnetic moments. The spontaneous magnetization can contribute to the linewidth of individual grains via its site-to-site distributions concerning both the Zeeman and the magnetostatic energy terms [14]. With lowering temperature, the thermal fluctuation energy becomes smaller than the anisotropy energy. Here, the random thermal fluctuation field B_f ~ kT/µ_eff (with µ_eff being the effective magnetic moment of the superparamagnetic particle) diminishes [15], thus broadening the linewidth. Another reason for the temperature-dependent broadening is the variation of the anisotropy energy with temperature.

At very low temperatures, the spin-wave spectrum of nanoparticles is quantized with a dominating uniform mode n = 0 [16]. This results in a linear temperature dependence of magnetization:

$$M(T)\approx M(0)\left(1-\frac{kT}{2K_{1}V}\right)$$

(2)

Fitting the asymptote of the low-temperature part of M(T) to Equation (2), we obtain K₁V ≈ 5.0 × 10⁻²¹ J in good agreement with the value derived above from the blocking temperature. Divided by the superparamagnetic particle volume this yields K₁’≈ 5.0 × 10³ J/m³.

In our case, we have to take into account that the size of our particles is above the superparamagnetic limit of about 10.5 nm, Equation (6). Here, a correction factor (1 − H/H_c)² appears for the K₁V value [17]. For K₁ ≈ 1.7 × 10⁵ J/m³ (cf. Section 4), we find µ₀H_c ≈ 12 mT (the measuring field was µ₀H = 10 mT) in accordance with the experimental value of µ₀H_c ≈ 12–14 mT at 4.2 K of similar samples, but pressed into pellets and long-term annealed at 1420 K in a flux of a gas mixture of 5% H₂/Ar [18].

4. Discussion

The remanent magnetization of uniaxial, single-domain nanoparticles which are fully magnetized along the easy axis vanishes after removing the magnetic field as:

$$M=M_s\exp \left(-\frac{t}{\tau }\right)$$

(3)

where M_s is the saturation magnetization, t the time after removal of the field. The value τ denotes the Néel-Brown relaxation time for an energy barrier ΔE = K₁V [19,20]:

$$\tau ={\tau }_0\exp \left(\frac{K_{1}V}{kT}\right)$$

(4)

with τ₀ a time constant in the order of 10⁻⁹ s [21], K₁ the uniaxial anisotropy constant, V the particle volume, k the Boltzmann constant and T the temperature. Note that K₁ is also temperature dependent [22]. Superparamagnetic behavior is obtained using an instrument with a characteristic measuring time τ_m ≥ τ. For τ_m < τ, the magnetic moments remain in a fixed direction during the measurement. This leads to a remanent magnetization and appearance of a coercive field, thus, a metastable ferromagnetic (ferrimagnetic) state is detected. The condition τ = τ_m defines the so-called blocking temperature [23]:

$$T_B=\frac{K_{1}V}{k\cdot \ln ({\tau }_m/{\tau }_0)}$$

(5)

Here, τ_m amounts to ca. 100 s in static magnetometry [24], and to τ_m ≈ 10⁻⁸ s in Mössbauer spectrometry [23]. Simultaneous ferromagnetic and SPM behavior is obtained when τ is of the order of τ_m. Thus, particles at a temperature T > T_B reveal a dominating SPM behavior, while particles at T < T_B show a predominant ferromagnetic behavior. In the latter case thermal excitations are not sufficient to overcome the barrier K₁V. The easiest way to implement such conditions is to use a mixture of particles of different sizes slightly below and slightly above a critical size, which for spherical particles amounts to:

$$d_{cr}^{spm}={\left(\frac{q\cdot kT}{K_1(T)}\right)}^{1/3}$$

(6)

where the parameter q = π/6⋅ln(τ_m/τ₀) amounts in magnetometry to ca. 48 and in Mössbauer spectrometry to ca. 4.4.

In the simplest form of uniaxial anisotropy, the total free energy U of a particle is given by [24]:

$$U=K_{1}V{\sin }^2\phi -\mu H\cos \phi$$

(7)

where φ is the angle between µ and the symmetry axis of the particle. Experimental values of K₁ for SFMO are scarce. EMR measurements on SFMO thin films grown by pulsed laser deposition onto (100) SrTiO₃ substrates with a thickness of 400 nm revealed for M_s = 3.8 µ_B an in-plane uniaxial magnetocrystalline anisotropy constant of ca. 3 × 10⁴ J/m³ at room temperature [25]. On the other hand, the estimated zero-temperature value of K₁ is much higher and amounts to 1.7 × 10⁵ J/m³ [26]. This is the low-temperature value used in the present work.

The shape-anisotropy constant calculated employing demagnetization factors γ in the c and a directions [27] is given by:

$$K_{sh}=\frac{1}{2}({\gamma }_c-{\gamma }_a){\mu }_0{M}_s^2$$

(8)

Here, µ₀ is the vacuum permeability. Optical inspection of the particle shape revealed that the latter is well approximated by oblate spheroids with a c/a ratio in the range from 0.85 to 1.0. With M_s = 282 kA/m (50 Am²/kg), this results in a negligible value of K_sh ≤ 3.3 × 10³ J/m³.

Inhomogeneous surface conditions during synthesis yield an effective anisotropy constant of [28,29]:

$$K_{eff}=K_V+\frac{S}{V}{K}_S(d)$$

(9)

where K_V is the anisotropy constant per unit volume, K_S the surface anisotropy constant per unit of surface area S, and d the particle size. For a sphere or cube, the total surface-area-to-volume ratio amounts to 6/d. Surface anisotropy arises due to symmetry breaking and reduction in the nearest-neighbor coordination at the surface. It can significantly enhance the total magnetic anisotropy of nanoparticles. For instance, K_eff of γ-Fe₂O₃ nanoparticles with a mean size of about 8.6 nm dispersed in a polymer exceeds K_V by about two orders of magnitude [30]. However, in our case, the surface conditions after a long-time ultrasonic treatment are mostly balanced. On the other hand, strains relax in homogeneous, twin-free nanoparticles, that have no shell or grain boundary. Therefore, only the particle size needs to be considered as the origin of the simultaneous observation of ferromagnetic and superparamagnetic behavior. As a result, we have only to account for the magnetocrystalline anisotropy constant.

Replotting B_r in Figure 6b using a reduced temperature ϑ = (1 − T/T_C), we obtain a slope of dB_r/dϑ = −1.825 T (cf. Supplemental Materials, Figure S4). The shift of B_r is determined by the temperature dependence of the magnetic anisotropy field:

$$H_a(T)=\frac{2\alpha K_1(T)}{{\mu }_{0}M(T)}$$

(10)

where α is an averaged factor, which depends only on the angles between the applied field and the magnetic axes of the particles. A satisfactory approximation of the temperature dependence of the magnetization derived from Monte-Carlo and Landau–Lifshitz–Gilbert simulations is M(T) = M(0)⋅ϑ ^1/3 [31]. With regard to the linear temperature dependence of B_r, we conclude

$$K_1(T)=K_1(0)\cdot {(1-T/T_C)}^{4/3}$$

(11)

Taking into account dB_r/dϑ = −1.825 T, for M_s = 3.8 µ_B/f.u. we arrive at 2αK₁(0) = 5.2 × 10⁵ J/m³, which is of the order of the values considered above. For K₁(0 K) = 1.7 × 10⁵ J/m³ [26], Equation (11) yields a room-temperature value of K₁(300 K) = 2.35 × 10⁴ J/m³ comparable to the in-plane uniaxial anisotropy constant of SFMO thin films amounting to ~3 × 10⁴ J/m³ at room temperature [25].

A lower limit of the critical diameter of a single-domain particle amounts to [32]:

$$d_{cr}^{sd}\ge \frac{36\sqrt{A(T)\cdot K_1(T)}}{{\mu }_0{M}_s^2}$$

(12)

where A(T) is the (temperature-dependent) exchange constant. An estimation of the A value using the spin-wave stiffness D(T) [33], yields a low-temperature value A(0) = 1.85 × 10⁻¹² J/m assuming M_s(0) = 3.8 µ_B/f.u. [26].

$$A(T)=\frac{D(T)M_s(T)}{2g{\mu }_{\mathrm{B}}}$$

(13)

The temperature dependencies of D(T) and M_s(T) then determine A(T). On the other hand, the reduced magnetization m(T) = M(T)/M(0) of SFMO measured in the FC mode decreases from liquid helium temperatures to 120 K just by 12% (cf. Figure 5). Consequently, the temperature dependence of A can be neglected when calculating the size of superparamagnetic particles in the low-temperature range. The A value at room temperature was recently estimated to be A(300 K) = 9.2 × 10⁻¹³ J/m [26].

As a result, the lower limit of the critical diameter d_cr^sd of a single-domain particle according to Equation (12) was calculated to be 41 nm at low temperatures and ca. 68 nm near room temperature, that is, of the order of the nanoparticle size. The critical size of a spherical superparamagnetic particle d_cr^spm (cf. Equation (6)) at room temperature amounts to 10.5 nm corresponding to a volume of 605 nm³ and about 4900 spins. Obviously, particles with a size around d_cr^sd determine the DLS while larger particles, though less numerous, dominate the magnetic response at high temperatures.

Alternatively, the magnetization behavior could be analyzed solely as a superposition of Langevin functions of various magnetic moments [29]. This would result in a broad distribution of µ in order to reproduce the steep slope of the M(B) dependence (cf. Supplemental Materials, Figure S5).

5. Conclusions

Nanosized SFMO particles with a narrow size distribution around ca. 70 nm were fabricated by the citrate-gel technique. Single-phase composition and superstructure ordering degree were proved by X-ray diffraction. Superparamagnetic behavior was demonstrated by magnetization measurements using zero-field cooled and field-cooled protocols as well as by electron magnetic resonance. The linear slope of the shift of the resonance field B_r versus reduced temperature served as the basis for the derivation of an approximate 4/3 power dependency of the magnetocrystalline anisotropy constant on the reduced temperature ϑ = (1 − T/T_C). The origin of the simultaneous superparamagnetic and blocked behavior was attributed to a nanoparticle size distribution around a value in the order of the critical diameter of single-domain particles.