Abstract
Polymer matrix composites (PMCs) are crucial for their applications in aerospace, electronics, defense, and structural materials. PMCs reinforced with nanofillers offer substantial potential for enhanced thermal and mechanical performance. Although there have been significant developments in nanofiller-based high-performance composites involving graphene, carbon nanotubes, and metal oxides, the smallest of all the fillers, the graphene quantum dot (GQD), has not been explored thoroughly. The objective of this study is to investigate the effects of GQDs on the thermal properties of epoxy nanocomposites using all-atom molecular dynamics (MD) simulations. Specifically, the influence of GQDs on the glass transition temperature (Tg) and coefficient of linear thermal expansion (CTE) of the bisphenol F epoxy is evaluated. Further, the effects of surface functionalization and edge functionalization of GQDs are analyzed. Results demonstrate that the inclusion of functionalized GQDs leads to a 16% improvement in Tg, attributed to enhanced interfacial interactions and restricted molecular mobility in the epoxy network. MD simulations reveal that functional groups on GQDs form strong physical and chemical interactions with the polymer matrix, effectively altering its dynamics at the Tg. These results provide key molecular-level insights into the design of the next generation of thermally stable epoxy nanocomposites for high-performance applications in aerospace and defense.
1. Introduction
Polymer matrix composites (PMCs) are crucial in a wide range of engineering applications due to their excellent strength-to-weight ratios, processability, and chemical resistance. A variety of polymers that include both thermosets and thermoplastics such as epoxy, PEEK, polyimides, and cyanate esters are commonly used as matrix materials in PMCs [1,2,3,4]. Among them, epoxy resins are widely used as thermosetting matrices due to their outstanding mechanical properties, adhesion, and ease of processability. However, their inherent brittleness and relatively low glass transition temperature (Tg) limit their performance as structural materials in high-temperature conditions.
Polymers such as polyimides and bismaleimides (BMIs) are well known for their excellent thermal stability [5,6,7,8]. BMI has been reported to be stable at 230–300 °C [9,10]. The previous studies show that the Tg ranges between 280–360 °C for BMI [8,11,12] and 320 °C for polyimides [13]; showing that polyimides and BMI are suitable candidates as structural materials in aerospace for high-temperature applications. However, both BMI and polyimides are expensive compared to epoxy [5]. Iredale et al. [5] discussed how epoxy is a cost-effective polymer compared to BMI and polyimides in terms of specific strength per cost. Although the mechanical properties of epoxy and BMI are comparable, the thermal stability of epoxy is relatively inferior to that of BMI and polyimides due to the relatively lower Tg of 156 °C. Therefore, to develop a cost-effective and efficient alternative to BMI and polyimides as matrix material, there is a need to improve the thermal stability of the epoxy.
Thus far, there have been significant efforts towards the enhancement of the thermal properties of epoxy matrix through nanofiller infiltration [14,15]. Hu et al. [16] reported the increase in Tg of epoxy by nearly 12 °C by the addition of amine-functionalized graphene with epoxy. Further, the effect of mass fraction was observed on the Tg of epoxy, where a 0.5 volume% graphene sample demonstrated the highest increases in the Tg [16]. Ribeiro et al. [17] reported the increase in the Tg of bisphenol A epoxy by 20 °C with graphene oxide (GO) nanoplatelets. Li et al. [18] also reported the increases in the Tg of epoxy in GO sheets due to hindrance in the polymer chain movements via hydrogen bonding with oxygen functional groups on the surface. Moreover, Park et al. [19] reported a 14 °C increase in the Tg of epoxy–graphene nanocomposite. These increases in the Tg are observed due to increased resistance to the chain or network mobility during the transition of epoxy from the rubbery state to the glassy state. Conversely, some studies have also reported the negative impact on the Tg after the inclusion of graphene, carbon nanofibers, and carbon nanotubes (CNTs) in the epoxy due to interphase [20,21]. The effect on the Tg of epoxy is observed due to factors such as network mobility, functionalization, and quantity of the nanofillers.
Similar to graphene and CNTs, a novel nanofiller material, graphene quantum dot (GQD), is predicted to improve the thermo-mechanical properties of the thermoset polymers. GQDs are a zero-dimensional form of graphene and are of a size ranging from 0.5–20 nm [22]. The nanoscale size of the GQDs offers a larger area of interaction with the polymers, allowing for further improvement of the network immobility in the thermoset polymers. Moreover, GQDs provide the highest ratio of surface and edge functional groups to the volume compared to graphene [23], thus promoting the interfacial bonding and impacting the composite’s performance. Several efforts indicate that the inclusion of GQDs improves the mechanical properties of the polymer [22,23,24,25].
Seibert et al. [24] demonstrated that the inclusion of GQDs improved the Tg of bisphenol A epoxy by 10 °C. Schneider et al. [26] studied the effect of GQDs on the thermal properties of bisphenol A epoxy and demonstrated a significant increase in Tg of 40 °C with 5 wt.% GQD with epoxy. Schneider et al. [26] further demonstrated the effect of wt.% on the thermal properties of the nanocomposites. These studies provide a baseline to explore the influence of GQDs on the thermal properties of epoxy. To explore the full potential of GQDs, there is a need to investigate the effect of various functional groups on the thermal properties of epoxy efficiently.
Experiments involving functionalization of GQDs, materials characterization of nanocomposites, and materials testing are critical and costly. Fortunately, computational approaches provide a reliable alternative to predict the materials properties efficiently. Specifically, molecular dynamics (MD) simulations offer a platform to investigate the polymer chemistry, interfacial interactions, and materials properties [27,28,29,30,31]. Additionally, MD simulations offer nanoscale insights into the interfacial interactions that dictate the material performance at a higher length scale in PMCs. Therefore, to fully unravel the potential of GQD–epoxy nanocomposites and the effects of GQDs on the thermal properties of epoxy, a comprehensive MD study is needed.
The objective of this study is to investigate the thermal properties of epoxy–GQD nanocomposites. All-atom simulations are used to predict the Tg and coefficient of linear thermal expansion (CTE) of the epoxy nanocomposites. The effects of various functional groups on the Tg and CTE are investigated. The results of the MD simulations advance the understanding of GQD–epoxy interactions and offer insights for the development of high-performance polymer composites with improved thermal stability.
2. MD Modeling
MD simulations were performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) [32] software package. MD models were created using the forcefield parameters developed by Heinz et al. [33] for the class 2 interface forcefield (IFF). IFF has previously been used to predict the thermo-mechanical properties of neat polymers such as epoxy [34,35], PEEK [36], Elium [28], and benzoxazine [37], and polymer nanocomposites [4,30,38]. The MD modeling and simulation details are outlined below.
2.1. MD Modeling of GQDs
The MD model of pristine GQD was developed using Avogadro. As the hexagonal shape is the most energetically stable shape of the GQD, a hexagonal GQD model was developed with an approximate size of 9 Å as a radius. Figure 1a shows the molecular structure of the pristine GQD. The valency of the edge carbon atoms was terminated with the hydrogen atoms.

Figure 1.
Molecular structures of (a) pristine GQD, (b) diglycidyl ether of bisphenol F (DGEBF), and (c) diethyl toluene diamine (DETDA).
A total of seven such GQD models with different functional groups were generated. Figure 2 shows the types of functional groups attached to the GQD models. Amine and carboxyl groups were attached as edge functional groups, whereas hydroxyl and epoxide functional groups were attached as surface functional groups. The functional group sites were selected randomly. The GQD model with functional groups on the edge of the GQD is referred to with the “e” prefix, whereas the surface functional group models are referred to with the “s” prefix. This prefix is followed by a quantity of functional groups and the type of functional group attached to GQD. For example, in the name “e4N-GQD”, “e” stands for edge functional groups, and “4N” stands for four amine functional groups. For other models, O represents an epoxide group, OH represents a hydroxyl group, and COOH represents a carboxyl group.
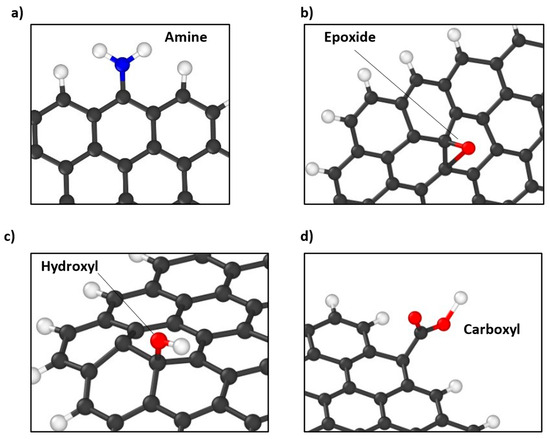
Figure 2.
Snapshots of MD models of functionalized GQDs showing (a) amine functional group in 4N-GQD and 6N-GQD, (b) epoxide functional group in s4O-GQD and s4O-e4COOH-GQD, (c) hydroxyl functional group in s4OH-GQD, and (d) carboxyl functional group in e4COOH-GQD and s4O-e4COOH-GQD. Black colored atoms represent carbon, white colored atoms represent hydrogen, red colored atoms represent oxygen, and blue atom represent nitrogen.
Figure 2a shows the snapshot of the MD model of e4N-GQD and represents the attached of amine functional groups in e4N-GQD and e6N-GQD models. The snapshot of s4O-GQD is shown in Figure 2b, which represents the attached epoxide functional groups in s4O-GQD and s4O-e4COOH-GQD. Figure 2c shows a snapshot of the s4OH-GQD model representing the hydroxyl functional groups in the s4OH-GQD model, and Figure 2d shows a snapshot of the e4COOH-GQD model representing the carboxyl functional group attached to the edge of GQD in the e4COOH-GQD and s4O-e4COOH-GQD models.
GQD models were imported into LAMMPS for energy-minimization simulation to obtain an energy-equilibrated GQD structure. This was performed using the “minimize” command in LAMMPS. Table 1 lists the details of the GQD models generated. The molecular structures of all the functionalized GQDs are shown in the supporting information (SI) in Section S1 as Figures S1–S6. Figure 3b shows a snapshot of the MD model of the pristine GQD.

Table 1.
Details of the GQD MD models.
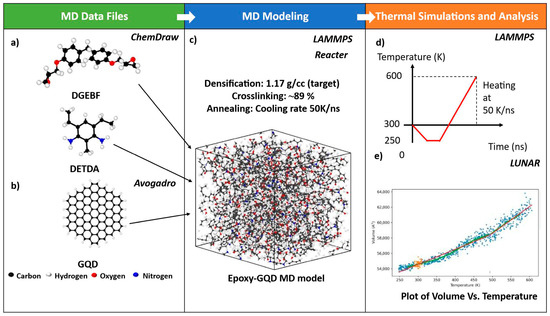
Figure 3.
MD framework illustrating (a) snapshots of epoxy monomers, (b) snapshot of a pristine GQD model (b), (c) snapshot of the epoxy–GQD nanocomposite MD model, (d) thermal simulation setup, and (e) plot of a representative epoxy–GQD nanocomposite showing analysis of the volume data as a function of temperature performed using LUNAR. Blue datapoints represents the raw volume data, green curve represents the moving average in the data, orange datapoints are used to calculate the average volume at 300 K (room temperature), and red line represents the slope in the data below and above the Tg.
2.2. MD Modeling of Epoxy
The epoxy system was modeled by mixing a diglycidyl ether of bisphenol F (DGEBF) epoxy resin and diethyl toluene diamine (DETDA) hardener molecules in the stoichiometric ratio of 2:1. This epoxy system was modeled after EPON 862-EPIKURE-W epoxy. The molecular structures of the DGEBF and DETDA molecules are shown in Figure 1b and Figure 1c, respectively. To create the monomer structures, the initial atomic positions were generated using ChemDraw [39]. The MD data files for monomers were created using the IFF parameters, as shown in Figure 3a. The monomer data files were then imported into LAMMPS and minimized using the “minimize” command to obtain an energetically stable monomer structure. Further, monomers were replicated to create the bulk model in LAMMPS, containing a total of 96 resin molecules and 48 hardener molecules. The total number of atoms in the epoxy model was 5616. The simulation box boundaries were set to periodic in x-, y-, and z-directions.
2.3. Mixing of Epoxy and GQD
The bulk epoxy models and the GQD models were then mixed to create the epoxy nanocomposite models. The GQD models were inserted into the bulk epoxy models at a low-density stage to avoid the overlapping of atoms upon the GQD model insertion. For each GQD model, five replicate models were created to account for the statistical variation in the MD simulations. The mass fraction of GQD in the epoxy for the pristine GQD–epoxy nanocomposite was 3.05%.
The mixing of epoxy and GQD was followed by a densification simulation, where the simulation box was densified using the “fix deform” command in LAMMPS from initial densities of ~0.09 g/cc to the target density of 1.17 g/cc at 300 K in controlled volume and temperature (NVT) conditions. For densification, the simulation box was deformed at a rate of 5 Å/ns in all x-, y-, and z-directions. Next, annealing simulations were performed, where the temperature of the simulation box was ramped up to 500 K and subsequently cooled to 300 K at a cooling rate of 50 K/ns in controlled pressure and temperature (NPT) conditions. Annealing was performed to eliminate any unfavorable configurations of the monomers or GQD during the densification step. For mixing, densification, and annealing simulations, the timestep was set to 1 fs.
2.4. Crosslinking of Epoxy
The REACTER [40,41] protocol in LAMMPS was implemented to simulate the crosslinking reaction of the epoxy. Gissinger et al. [40] developed the REACTER protocol to model the chemical reactions in MD simulations. REACTER uses the topology of the reaction site before and after the reaction to simulate the reaction mechanism. More information about the REACTER protocol can be found elsewhere [42]. The required pre-reaction template files, post-reaction template files, and mapping files, which map atoms from the pre-reaction template to the post-reaction template, were created for each reaction mechanism. More information on the epoxy crosslinking reaction and its 2-step mechanism can be found elsewhere [34,43].
Polymerization simulations were performed in an NVT ensemble with a timestep of 1 fs. The temperature of the simulation box was raised to 500 K for both reacting and non-reacting atoms. Crosslinking was simulated using the “fix bond/react” command in LAMMPS, where maximum cutoff distance for bond formation was set to 6 Å, and reaction probability was set to 0.00001 and 0.001 for 2-step amine–epoxide reactions. The reaction site was stabilized every 500 steps. The higher temperature increases the mobility of the monomers to achieve a higher degree of crosslinking. The % crosslinking density was calculated by
where is the number of bonds formed during the crosslinking simulation, and is the number of maximum bonds that can be formed during the crosslinking simulation.
Functional groups attached to GQDs were allowed to crosslink with the epoxy molecules using REACTER. Amine and carboxyl groups attached to GQD edges were included to react with the epoxide groups of the epoxy molecules to create a covalent bond between GQD and epoxy for increased interaction [25]. Similarly, surface epoxide functional groups attached to GQDs were included to react with the amine groups of the hardener molecules for increased epoxy–GQD interaction [25]. Figure 4 shows the cluster analysis of the nanocomposite models performed using the OVITO visualization tool. Figure 4d–h clearly show that the functionalized GQD is part of the epoxy cluster formed during the crosslinking simulation. Pristine GQD and s4OH-GQD nanocomposite models did not include the covalent bonding between epoxy and the GQD, as shown in Figure 4b,c. It is important to note that for s4O-eCOOH-GQD–epoxy models, the simulation box contained two networks of epoxy. This is observed due to the increased steric hindrance caused by the highly functionalized GQD cluster.
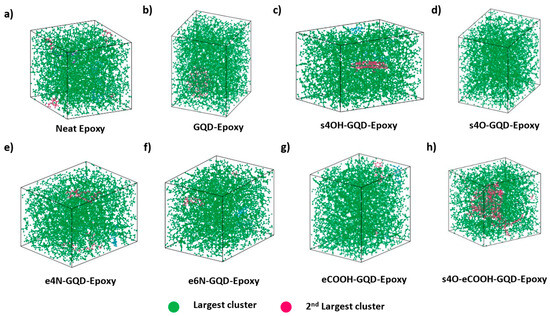
Figure 4.
Visualization of epoxy network in the epoxy nanocomposite MD models created by the cluster analysis algorithm in OVITO. Snapshots of MD models after crosslinking for (a) neat epoxy, (b) GQD–epoxy, (c) s4OH-GQD–epoxy, (d) s4O-GQD–epoxy, (e) e4N-GQD–epoxy, (f) e6N-GQD–epoxy, (g) eCOOH-GQD–epoxy, and (h) s4O-eCOOH-GQD–epoxy.
Next, annealing simulations were performed, where the temperature of the simulation box was decreased from 500 K to 300 K at a constant cooling rate of 50 K/ns in the NPT ensemble. Annealing simulation was performed to eliminate any residual stress formed in the materials during the crosslinking simulation. The annealing step was followed by a relaxation simulation at 300 K in the NPT ensemble for a 1 ns simulation time. Relaxation simulation was performed to equilibrate the MD models further and obtain energetically stable configurations. For annealing and relaxation, the timestep of 1 fs was used. Figure 3c shows a snapshot of the representative GQD–epoxy MD model observed after the relaxation. The average volume fraction of the GQD in the relaxed GQD–epoxy model was ~1.13%.
2.5. Thermal Simulations
Odegard et al. [35] demonstrated that MD models of epoxy that are crosslinked at temperatures higher than Tg (rubbery build) show no statistical difference in Tg predicted by heating and cooling simulations. Therefore, the heating simulations were performed to predict the Tg of the epoxy nanocomposites. The temperature of the simulation box was ramped down from 300 K to 250 K in an NPT ensemble. Further, a quick energy stabilization simulation was performed at 250 K for 100 ps using a timestep of 1 fs in an NPT ensemble. Further, MD models were heated to 600 K at a heating rate of 50 K/ns in an NPT ensemble using a timestep of 1 fs. The temperature of 250 K was selected as a starting temperature for thermal simulations to generate a wide range of volume data as a function of temperature below Tg to accurately predict the Tg. Figure 3d illustrates the heating profile of the MD thermal simulations.
Even though MD simulations employ significantly higher heating and cooling rates compared to experiments, the heating rate/cooling rate corrections are not applied to the MD-predicted Tg values herein. Amorphous polymers typically experience the cooling rate effect on Tg measurements in experiments due to a non-equilibrium locking of the polymer chains. Higher cooling rates provide less time for polymer chains to attain its equilibrium state causing apparent higher values of Tg. But MD models are built at room temperature, and the polymer chains are already in the glassy equilibrium state before the thermal simulations. Hence, the cooling rate effects are not observed for these specific models. More discussion about cooling rate effects on Tg can be found elsewhere [34].
2.6. Thermal Property Calculations
The Tg and the CTE were calculated by using LUNAR “log analysis” tools. The volume of the simulation box as a function of temperature over the range of thermal simulations was plotted for each MD model, as shown in Figure 5. Using LUNAR, MD data were analyzed by hyperbola fit. The hyperbola center was identified as a point of glass transition for the material. Further, the linear slopes of the volume data below and above the Tg were calculated. CTE above and below were calculated by using
where is the initial volume at room temperature, and is the rate of change of volume with respect to the temperature. Further, the % thermal shrinkage from Tg to the room temperature is calculated using
where is the initial volume at room temperature, and is the volume of the system at Tg.
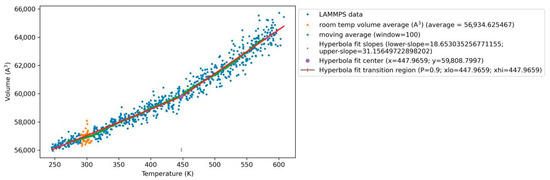
Figure 5.
Plot of volume as a function of temperature during the thermal simulations for a representative s4OH-GQD–epoxy MD model. The hyperbola curve is fitted through the MD-predicted volume data. Red lines represent the linear slopes of the volume data below and above the predicted hyperbola fit center. The hyperbola fit center is identified as a glass transition point represented in violet color. The MD-predicted Tg in this plot is given as 447.9 K (174.75 °C).
In addition to the hyperbola fit, LUNAR provides the option of using a bilinear fit for the volume data analysis as a function of temperature. Analysis of a representative s4O-GQD–epoxy MD model using the bilinear regression was performed and is discussed the Section S2 of the SI. Additionally, the density of the same representative model was plotted as a function of temperature to calculate the Tg, as discussed in Section S3 of the SI. Table S1 from the SI shows that the predicted Tg values based on all three methods are consistent with each other.
3. Results and Discussion
Table 2 shows the comparison of the density predicted in this work using IFF with previously predicted density values with the ReaxFF forcefield by Keles et al. [23]. The predicted density values of neat epoxy are in agreement with the previously reported IFF values. Further, the predicted density values of functionalized GQD models are consistent with the neat epoxy density, showing that the inclusion of GQDs does not affect the density of the epoxy at this nanoscale and for this specific mixture of GQD and epoxy. Functionalized GQD models demonstrated a discrepancy in the density predictions, with IFF predicting a lower density than ReaxFF. The predicted density value of neat epoxy was compared with the experimentally measured density value by Littell et al. [44] and Gilat et al. [45], demonstrating that the IFF value closely aligns with the experimentally measured density of epoxy compared to the ReaxFF value.

Table 2.
MD predicted density values of epoxy-GQD nanocomposites.
Figure 6 shows the MD-predicted Tg of the neat epoxy and epoxy–GQD nanocomposites. The MD-predicted Tg of 159 ± 7 °C for the neat epoxy accurately matches the experimentally measured Tg of 156 °C by Odegard et al. [35]. MD models predicted a lower Tg for epoxy nanocomposites with the inclusion of pristine GQD. Note that the pristine GQD is not crosslinked with the epoxy network, nor does it have any surface or edge functional groups. The interactions of pristine GQD with epoxy are purely non-bonded, which creates additional free volume in the system. The MD-predicted average free volume is 2.98 ± 0.16 for the neat epoxy and 3.34 ± 0.1 for the epoxy–GQD nanocomposite. This additional free volume in the epoxy–GQD nanocomposite facilitates the increased mobility of the epoxy network around GQD. This results in improved relaxation of the epoxy network during cooling in the vicinity of GQD compared to neat epoxy, causing a lower Tg.
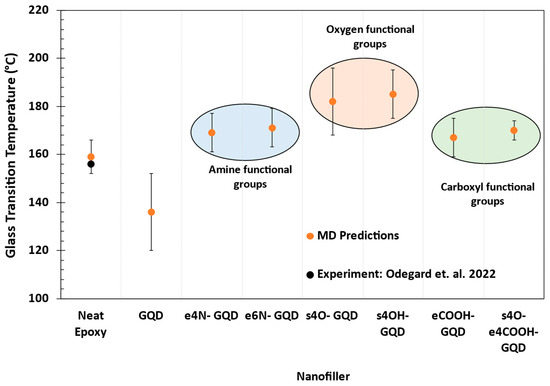
Figure 6.
MD predictions of Tg of the neat epoxy and epoxy–GQD nanocomposites. Experimental value is reported by Odegard et al. [35].
The epoxy nanocomposites with amine functional groups on GQD show improvement in Tg compared to neat epoxy, as shown in Figure 6. The predicted Tg of e4N-GQD–epoxy is 169 ± 8 °C, and for e6N-GQD–epoxy, it is 171 ± 8 °C. There is no statistical difference between the predicted Tg of the two amine-functionalized GQD–epoxy nanocomposites. The lack of statistical differences in the Tg as an effect of the quantity of amine functionalization is due to the wide scatter typically observed in the MD-predicted Tg. The functionalized amine groups are covalently bonded with epoxide groups in the epoxy, thus providing restricted mobility compared to pristine GQD. Hence, a significant average improvement in the Tg of 34 °C is predicted compared to pristine GQD epoxy, and of 11 °C compared to neat epoxy. This improvement in the Tg observed due to amine-functionalized GQD agrees with the 12 °C increase in the Tg with amine-functionalized graphene measured by Hu et al. [16].
The epoxy nanocomposites with oxygen functional groups show average increases in the Tg of 25 °C compared to the neat epoxy models. The predicted Tg for s4O-GQD–epoxy is 182 ± 14 °C, and for s4OH-GQD, it is 85 ± 10 °C. This increase in the Tg is consistent with the experimentally observed increase in the Tg of epoxy by 20 °C with GO by Ribeiro et al. [17]. It has been previously reported that the oxygen atoms on the surface of graphene increased the hydrogen bonding interactions in the GO–epoxy nanocomposites [18]. Similarly, the surface-functionalized oxygen atoms in s4O-GQD and s4OH-GQD offer steric hindrances to the epoxy network mobility due to hydrogen bonding. The predicted Tg for oxygen-functionalized GQD systems is higher than that of amine-functionalized GQD systems. It is important to note that the amine groups are edge functional groups, and the oxygen groups are surface functional groups, indicating that surface functional groups offer restricted mobility compared to edge functional groups due to a larger surface area and increased interactions with epoxy.
Figure 6 also shows that epoxy nanocomposites with carboxyl functional groups show improved Tg compared to neat epoxy. However, the predicted Tg values are lower compared to epoxy nanocomposites with oxygen functional groups. The predicted Tg for eCOOH-GQD–epoxy is 167 ± 8 °C, and for s4O-e4COOH-GQD–epoxy, it is 170 ± 4 °C. There is no statistical difference between any of the amine-functionalized and carboxyl-functionalized epoxy nanocomposites. Table S2 in the SI enlists the MD-predicted Tg values for all materials.
Overall, the improvements predicted in the Tg are consistent with the Tg improvements that are measured experimentally in the literature with GQDs [24,26]. Note that these improvements cannot be compared quantitatively to the literature values due to differences in the epoxy materials, but they can be compared with the trends in the improvement.
Figure 7 shows the thermal shrinkage that the different materials experience below Tg. For amorphous polymers below Tg, the polymer conformation is locked in a glassy state, and materials undergo pure thermal shrinkage. The s4O-GQD–epoxy and s4OH-GQD–epoxy show the highest thermal shrinkage amongst the materials modeled in this study. Higher thermal shrinkage in the materials may indicate that the polymer network may have transitioned into a glassy state at a non-equilibrium state. For all other models, there is no statistical difference in predicted thermal shrinkage, demonstrating minimal effect on the thermal shrinkage of the epoxy. Lower thermal shrinkages are desired for lower process-induced residual stresses in the composite materials in high-performance applications.
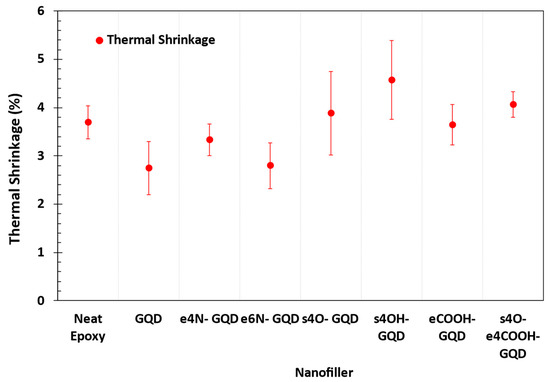
Figure 7.
Thermal shrinkage of the neat epoxy and epoxy–GQD nanocomposites from Tg to room temperature.
Figure 8 shows the MD predictions of the CTE of the epoxy nanocomposites below and above Tg. MD predictions of CTE for neat epoxy agree well with the experimentally measured CTE values of epoxy by Wang et al. [46]. It is clear that there is no statistical difference between the CTE values of the epoxy nanocomposites with various GQDs above Tg. The CTE of s4OH-GQD–epoxy is predicted to be higher than the other epoxy nanocomposites, which show no statistical difference. The predicted CTE of s4OH-GQD–epoxy is 1.01 ± 0.2 × 10−4 per °C compared to neat epoxy, with a CTE of 0.97 ± 0.1 × 10−4 per °C, i.e., 4% increases in CTE.
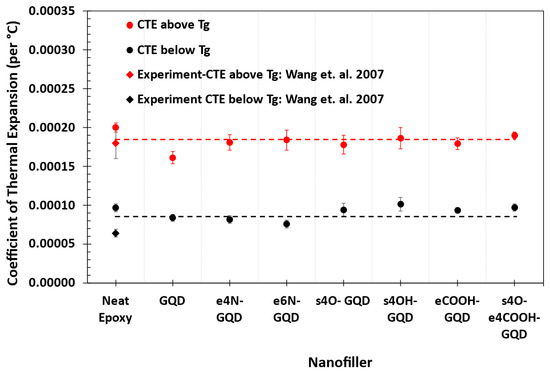
Figure 8.
CTE of the neat epoxy and epoxy–GQD nanocomposites above and below Tg. Experimental values are reported by Wang et al. [46].
4. Conclusions
This work provides MD predictions about the thermal behavior of epoxy nanocomposites with various GQD nanofillers. The MD-predicted density and thermal properties of neat epoxy resin agree well with the experiments. MD predictions demonstrate that functionalization groups on the surface and edge of the GQD influence thermal properties. The following important conclusions can be drawn from this study:
- 1.
- Functionalized GQDs increase the Tg of the epoxy nanocomposite due to restricted network mobility and relaxation at the glass transition.
- 2.
- The oxygen-based functionalization groups on GQD demonstrate the highest increases of 16% in the Tg, whereas amine- and carboxyl-functionalized GQDs are predicted to increase the epoxy Tg by approximately 7%.
- 3.
- The GQDs demonstrate that the effect of GQDs on the CTE of the epoxy both below and above Tg is statistically insignificant, except for s4OH-GQD, which is predicted to increase the CTE of the epoxy below Tg by 4%.
Based on these conclusions, it is evident that the thermal properties can be tailored significantly for improved performance of the bisphenol F epoxy. The outcomes of this effort provide an understanding of the influence of GQDs on the thermal performance of epoxy and advance the design and development of the next generation of high-performance PMCs with improved thermal stability.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/applnano6030015/s1, Figure S1: Molecular structure of e4N-GQD; Figure S2: Molecular structure of e6N-GQD; Figure S3: Molecular structure of s4O-GQD; Figure S4: Molecular structure of s4OH-GQD; Figure S5: Molecular structure of e4COOH-GQD; Figure S6: Molecular structure of s4O-e4COOH-GQD; Figure S7: Plot of volume as a function of temperature during the thermal simulations for a representative s4OH-GQD–epoxy molecular dynamics (MD) model. Red lines represent the linear slopes of the volume data below and above the predicted bilinear point. The bilinear point is identified as a glass transition point and is shown in violet; Figure S8: Plot of density as a function of temperature during the thermal simulations for a representative s4OH-GQD–epoxy MD model. Orange lines represent the linear slopes of the density data. The bilinear point is identified as a glass transition point and is shown in green; Table S1: Comparison of Tg values calculated by different methods. Table S2: MD-predicted Tg values of epoxy nanocomposites [47].
Author Contributions
Conceptualization, S.S.B. and O.K.; methodology, S.S.B.; software, S.S.B.; validation, S.S.B.; formal analysis, S.S.B.; investigation, S.S.B.; resources, S.S.B., O.K.; data curation, S.S.B.; writing—original draft preparation, S.S.B.; writing—review and editing, S.S.B., O.K.; visualization, S.S.B.; supervision, O.K.; project administration, O.K.; funding acquisition, O.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by U.S. National Science Foundation CAREER award, grant #2450841.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Acknowledgments
ORION, a high-performance computing cluster at the University of North Carolina at Charlotte, was used to perform the simulations presented in this publication. The authors would like to thank Prathamesh Deshpande for their insightful conversations.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kessler, M.R. Polymer Matrix Composites: A Perspective for a Special Issue of Polymer Reviews. Polym. Rev. 2012, 52, 229–233. [Google Scholar] [CrossRef]
- Bamane, S.S.; Gaikwad, P.S.; Radue, M.S.; Gowtham, S.; Odegard, G.M. Wetting Simulations of High-Performance Polymer Resins on Carbon Surfaces as a Function of Temperature Using Molecular Dynamics. Polymers 2021, 13, 2162. [Google Scholar] [CrossRef]
- Patil, S.U.; Radue, M.S.; Pisani, W.A.; Deshpande, P.; Xu, H.; Al Mahmud, H.; Dumitrică, T.; Odegard, G.M. Interfacial characteristics between flattened CNT stacks and polyimides: A molecular dynamics study. Comput. Mater. Sci. 2020, 185, 109970. [Google Scholar] [CrossRef]
- Deshpande, P.P.; Radue, M.S.; Gaikwad, P.; Bamane, S.; Patil, S.U.; Pisani, W.A.; Odegard, G.M. Prediction of the Interfacial Properties of High-Performance Polymers and Flattened CNT-Reinforced Composites Using Molecular Dynamics. Langmuir 2021, 37, 11526–11534. [Google Scholar] [CrossRef]
- Iredale, R.J.; Ward, C.; Hamerton, I. Modern advances in bismaleimide resin technology: A 21st century perspective on the chemistry of addition polyimides. Prog. Polym. Sci. 2017, 69, 1–21. [Google Scholar] [CrossRef]
- Ma, X.; Zheng, F.; van Sittert, C.G.C.E.; Lu, Q. Role of Intrinsic Factors of Polyimides in Glass Transition Temperature: An Atomistic Investigation. J. Phys. Chem. B 2019, 123, 8569–8579. [Google Scholar] [CrossRef]
- Liaw, D.-J.; Wang, K.-L.; Huang, Y.-C.; Lee, K.-R.; Lai, J.-Y.; Ha, C.-S. Advanced polyimide materials: Syntheses, physical properties and applications. Prog. Polym. Sci. 2012, 37, 907–974. [Google Scholar] [CrossRef]
- Tungare, A.V.; Martin, G.C. Glass transition temperatures in bismaleimide-based resin systems. Polym. Eng. Sci. 1993, 33, 614–621. [Google Scholar] [CrossRef]
- Loos, M. Chapter 2—Composites. In Carbon Nanotube Reinforced Composites; Loos, M., Ed.; William Andrew Publishing: Oxford, UK, 2015; pp. 37–72. [Google Scholar]
- McKeen, L. 6—Polyimides. In The Effect of Sterilization on Plastics and Elastomers, 3rd ed.; McKeen, L., Ed.; William Andrew Publishing: Boston, MA, USA, 2012; pp. 169–182. [Google Scholar]
- Wang, D.; Zhao, L.; Yang, H.; Yue, C.E.; Li, H.; Xiao, W.; Liu, C.; Qu, C. High temperature and toughened bismaleimide structural film adhesive for high performance CFRP bonding over 300 °C. Polym. Degrad. Stab. 2022, 204, 110125. [Google Scholar] [CrossRef]
- Kirmani, M.H.; Ramachandran, J.; Arias-Monje, P.J.; Gulgunje, P.; Kumar, S. The effects of processing and carbon nanotube type on the impact strength of aerospace-grade bismaleimide based nanocomposites. Polym. Eng. Sci. 2022, 62, 1187–1196. [Google Scholar] [CrossRef]
- Wang, Y.; Goh, S.H.; Chung, T.-S. Miscibility study of Torlon® polyamide-imide with Matrimid® 5218 polyimide and polybenzimidazole. Polymer 2007, 48, 2901–2909. [Google Scholar] [CrossRef]
- Szeluga, U.; Pusz, S.; Kumanek, B.; Olszowska, K.; Kobyliukh, A.; Trzebicka, B. Effect of graphene filler structure on electrical, thermal, mechanical, and fire retardant properties of epoxy-graphene nanocomposites—A review. Crit. Rev. Solid State Mater. Sci. 2021, 46, 152–187. [Google Scholar] [CrossRef]
- Wei, J.; Vo, T.; Inam, F. Epoxy/graphene nanocomposites—Processing and properties: A review. RSC Adv. 2015, 5, 73510–73524. [Google Scholar] [CrossRef]
- Hu, Y.; Shen, J.; Li, N.; Ma, H.; Shi, M.; Yan, B.; Huang, W.; Wang, W.; Ye, M. Comparison of the thermal properties between composites reinforced by raw and amino-functionalized carbon materials. Compos. Sci. Technol. 2010, 70, 2176–2182. [Google Scholar] [CrossRef]
- Ribeiro, H.; Silva, W.M.; Rodrigues, M.-T.F.; Neves, J.C.; Paniago, R.; Fantini, C.; Calado, H.D.R.; Seara, L.M.; Silva, G.G. Glass transition improvement in epoxy/graphene composites. J. Mater. Sci. 2013, 48, 7883–7892. [Google Scholar] [CrossRef]
- Chen, L.; Chai, S.; Liu, K.; Ning, N.; Gao, J.; Liu, Q.; Chen, F.; Fu, Q. Enhanced Epoxy/Silica Composites Mechanical Properties by Introducing Graphene Oxide to the Interface. ACS Appl. Mater. Interfaces 2012, 4, 4398–4404. [Google Scholar] [CrossRef]
- Park, J.K.; Kim, D.S. Effects of an aminosilane and a tetra-functional epoxy on the physical properties of di-functional epoxy/graphene nanoplatelets nanocomposites. Polym. Eng. Sci. 2014, 54, 969–976. [Google Scholar] [CrossRef]
- Putz, K.W.; Palmeri, M.J.; Cohn, R.B.; Andrews, R.; Brinson, L.C. Effect of Cross-Link Density on Interphase Creation in Polymer Nanocomposites. Macromolecules 2008, 41, 6752–6756. [Google Scholar] [CrossRef]
- Yang, Z.; McElrath, K.; Bahr, J.; D’Souza, N.A. Effect of matrix glass transition on reinforcement efficiency of epoxy-matrix composites with single walled carbon nanotubes, multi-walled carbon nanotubes, carbon nanofibers and graphite. Compos. Part B Eng. 2012, 43, 2079–2086. [Google Scholar] [CrossRef]
- Gobi, N.; Vijayakumar, D.; Keles, O.; Erogbogbo, F. Infusion of Graphene Quantum Dots to Create Stronger, Tougher, and Brighter Polymer Composites. ACS Omega 2017, 2, 4356–4362. [Google Scholar] [CrossRef]
- Keleş, Ö.; Deshpande, P.P. Mechanical behavior of graphene quantum dot epoxy nanocomposites: A molecular dynamics study. Mater. Lett. 2024, 362, 136206. [Google Scholar] [CrossRef]
- Seibert, J.R.; Keleş, Ö.; Wang, J.; Erogbogbo, F. Infusion of graphene quantum dots to modulate thermal conductivity and dynamic mechanical properties of polymers. Polymer 2019, 185, 121988. [Google Scholar] [CrossRef]
- Deshpande, P.P.; Chan-Jobe, R.; Kemppainen, J.; Odegard, G.M.; Keles, O. Optimizing Epoxy Nanocomposites with Oxidized Graphene Quantum Dots for Superior Mechanical Performance: A Molecular Dynamics Approach. ACS Omega 2025, 10, 14209–14220. [Google Scholar] [CrossRef] [PubMed]
- Schneider, B.; Ornaghi, H.L., Jr.; Monticeli, F.M.; Romanzini, D. Effect of the Graphene Quantum Dot Content on the Thermal, Dynamic-Mechanical, and Morphological Properties of Epoxy Resin. Polymers 2023, 15, 4531. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Strachan, A. Molecular scale simulations on thermoset polymers: A review. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 103–122. [Google Scholar] [CrossRef]
- Bamane, S.S.; Deshpande, P.P.; Patil, S.U.; Maiaru, M.; Odegard, G.M. Evolution of Physical, Thermal, and Mechanical Properties of Poly(methyl Methacrylate)-Based Elium Thermoplastic Polymer During Polymerization. J. Phys. Chem. C 2024, 128, 15639–15648. [Google Scholar] [CrossRef]
- Bamane, S.S.; Jakubinek, M.B.; Kanhaiya, K.; Ashrafi, B.; Heinz, H.; Odegard, G.M. Boron Nitride Nanotubes: Force Field Parameterization, Epoxy Interactions, and Comparison with Carbon Nanotubes for High-Performance Composite Materials. ACS Appl. Nano Mater. 2023, 6, 3513–3524. [Google Scholar] [CrossRef]
- Sachdeva, G.; Patil, S.U.; Bamane, S.S.; Deshpande, P.P.; Pisani, W.A.; Odegard, G.M.; Pandey, R. Mechanical response of polymer/BN composites investigated by molecular dynamics method. J. Mater. Res. 2022, 37, 4533–4543. [Google Scholar] [CrossRef]
- Al Mahmud, H.; Radue, M.S.; Pisani, W.A.; Odegard, G.M. Computational Modeling of Hybrid Carbon Fiber/Epoxy Composites Reinforced with Functionalized and Non-Functionalized Graphene Nanoplatelets. Nanomaterials 2021, 11, 2919. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ‘t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Heinz, H.; Lin, T.-J.; Kishore Mishra, R.; Emami, F.S. Thermodynamically Consistent Force Fields for the Assembly of Inorganic, Organic, and Biological Nanostructures: The INTERFACE Force Field. Langmuir 2013, 29, 1754–1765. [Google Scholar] [CrossRef]
- Odegard, G.M.; Patil, S.U.; Deshpande, P.P.; Kanhaiya, K.; Winetrout, J.J.; Heinz, H.; Shah, S.P.; Maiaru, M. Molecular Dynamics Modeling of Epoxy Resins Using the Reactive Interface Force Field. Macromolecules 2021, 54, 9815–9824. [Google Scholar] [CrossRef]
- Odegard, G.M.; Patil, S.U.; Gaikwad, P.S.; Deshpande, P.; Krieg, A.S.; Shah, S.P.; Reyes, A.; Dickens, T.; King, J.A.; Maiaru, M. Accurate predictions of thermoset resin glass transition temperatures from all-atom molecular dynamics simulation. Soft Matter 2022, 18, 7550–7558. [Google Scholar] [CrossRef]
- Kashmari, K.; Al Mahmud, H.; Patil, S.U.; Pisani, W.A.; Deshpande, P.; Maiaru, M.; Odegard, G.M. Multiscale Process Modeling of Semicrystalline PEEK for Tailored Thermomechanical Properties. ACS Appl. Eng. Mater. 2023, 1, 3167–3177. [Google Scholar] [CrossRef]
- Gaikwad, P.; Krieg, A.; Deshpande, P.; Patil, S.; King, J.; Maiaru, M.; Odegard, G. Understanding the Origin of the Low Cure Shrinkage of Polybenzoxazine Resin by Computational Simulation. ACS Appl. Polym. Mater. 2021, 3, 6407–6415. [Google Scholar] [CrossRef]
- Pisani, W.A.; Radue, M.S.; Patil, S.U.; Odegard, G.M. Interfacial modeling of flattened CNT composites with cyanate ester and PEEK polymers. Compos. Part B Eng. 2021, 211, 108672. [Google Scholar] [CrossRef]
- Evans, D.A. History of the Harvard ChemDraw Project. Angew. Chem. Int. Ed. 2014, 53, 11140–11145. [Google Scholar] [CrossRef] [PubMed]
- Gissinger, J.R.; Jensen, B.D.; Wise, K.E. REACTER: A Heuristic Method for Reactive Molecular Dynamics. Macromolecules 2020, 53, 9953–9961. [Google Scholar] [CrossRef]
- Gissinger, J.R.; Jensen, B.D.; Wise, K.E. Modeling chemical reactions in classical molecular dynamics simulations. Polymer 2017, 128, 211–217. [Google Scholar] [CrossRef]
- Gissinger, J.R.; Jensen, B.D.; Wise, K.E. Molecular modeling of reactive systems with REACTER. Comput. Phys. Commun. 2024, 304, 109287. [Google Scholar] [CrossRef]
- Patil, S.U.; Shah, S.P.; Olaya, M.; Deshpande, P.P.; Maiaru, M.; Odegard, G.M. Reactive Molecular Dynamics Simulation of Epoxy for the Full Cross-Linking Process. ACS Appl. Polym. Mater. 2021, 3, 5788–5797. [Google Scholar] [CrossRef]
- Littell Justin, D.; Ruggeri Charles, R.; Goldberg Robert, K.; Roberts Gary, D.; Arnold William, A.; Binienda Wieslaw, K. Measurement of Epoxy Resin Tension, Compression, and Shear Stress–Strain Curves over a Wide Range of Strain Rates Using Small Test Specimens. J. Aerosp. Eng. 2008, 21, 162–173. [Google Scholar] [CrossRef]
- Gilat, A.; Goldberg Robert, K.; Roberts Gary, D. Strain Rate Sensitivity of Epoxy Resin in Tensile and Shear Loading. J. Aerosp. Eng. 2007, 20, 75–89. [Google Scholar] [CrossRef]
- Wang, S.; Liang, Z.; Gonnet, P.; Liao, Y.H.; Wang, B.; Zhang, C. Effect of Nanotube Functionalization on the Coefficient of Thermal Expansion of Nanocomposites. Adv. Funct. Mater. 2007, 17, 87–92. [Google Scholar] [CrossRef]
- Kemppainen, J.; Gissinger, J.R.; Gowtham, S.; Gowtham, G.M. LUNAR: Automated Input Generation and Analysis for Reactive LAMMPS Simulations. J. Chem. Inf. Model. 2024, 64, 5108–5126. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).