A Novel Online State of Health Estimation Method for Electric Vehicle Pouch Cells Using Magnetic Field Imaging and Convolution Neural Networks
Abstract
1. Introduction
- A novel SoH estimation approach based on current density images (CDIs) is proposed. This method uses the convolutional neural network (CNN) algorithm to classify and characterise a collection of captured CDIs, from a highly accurate Newman model of the NMC graphite cells of the battery pack and calculates the accurate SoH based on the cell parameters.
- Fast, online readings using an Arduino board connected to a 4 × 8 array of magnetic sensors were carried out for capturing the current density distributions across the positive electrode of a Li-ion pouch cell.
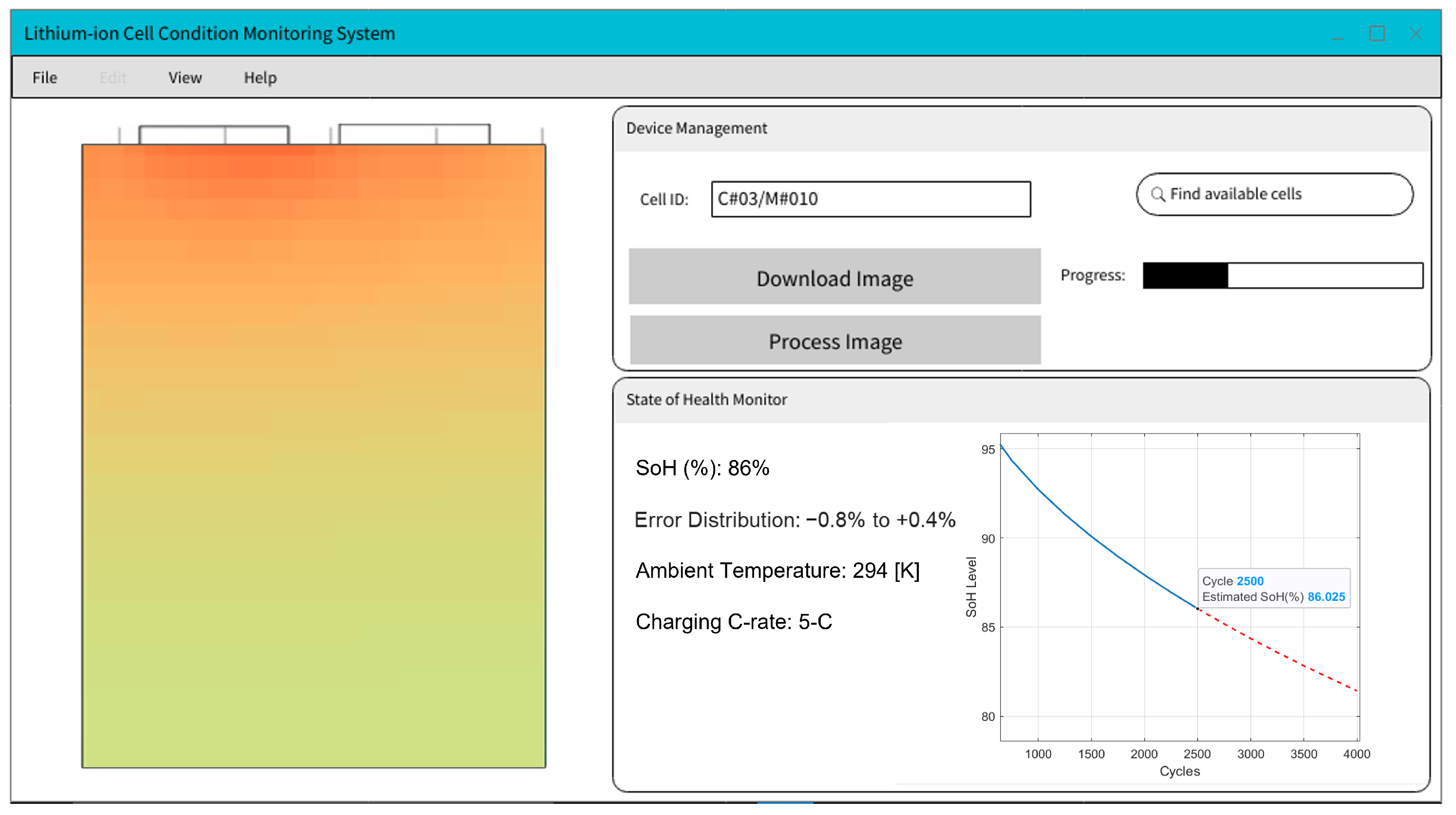
- As a part of a condition monitoring system (CMS), a Python-based user interface with an embedded inference model was designed to monitor the remaining SoH of the selected cells, based on the recorded current density images.
2. Magnetic Field Monitoring in LiBs
2.1. Preliminaries of the DFN Model
2.2. Sources of Magnetic Fields Produced by a LiB Cell
3. Characterisation of Current Density Images Using Deep Learning
4. Experimental Validation and Discussion of Results
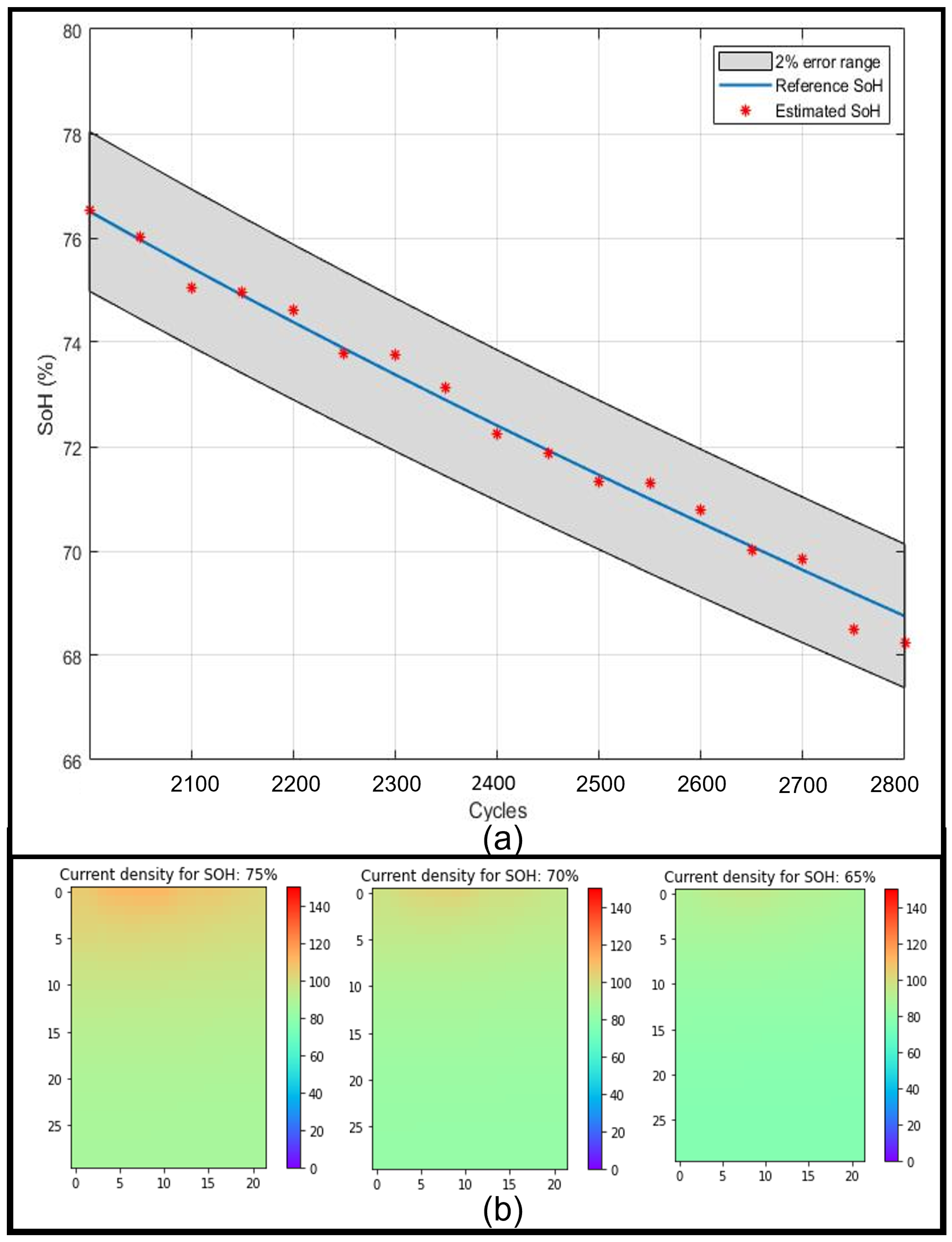
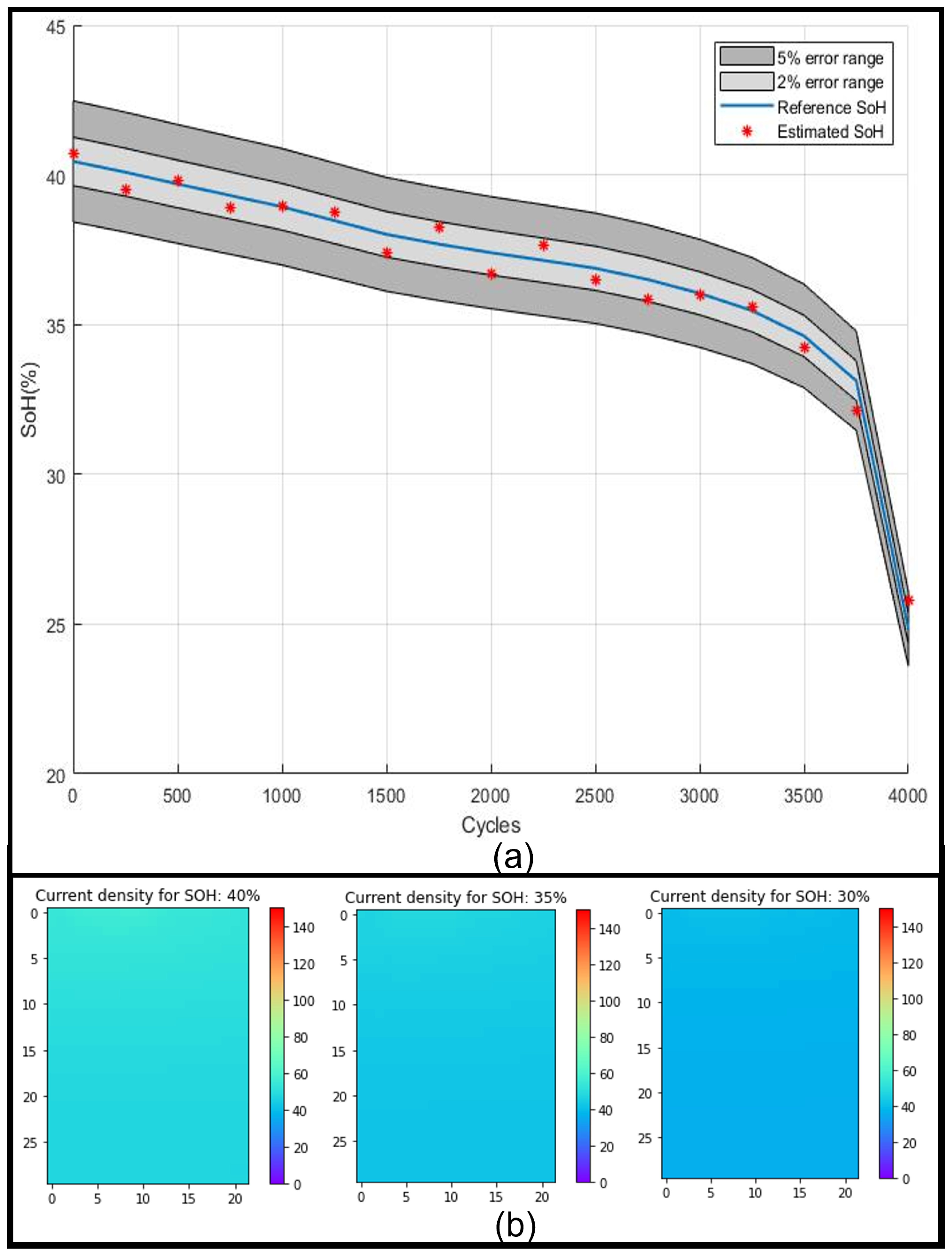
4.1. Experimental Test-Bench and Model Validation
4.2. The Effect of Fast-Charging and High Ambient Temperature on CDIs
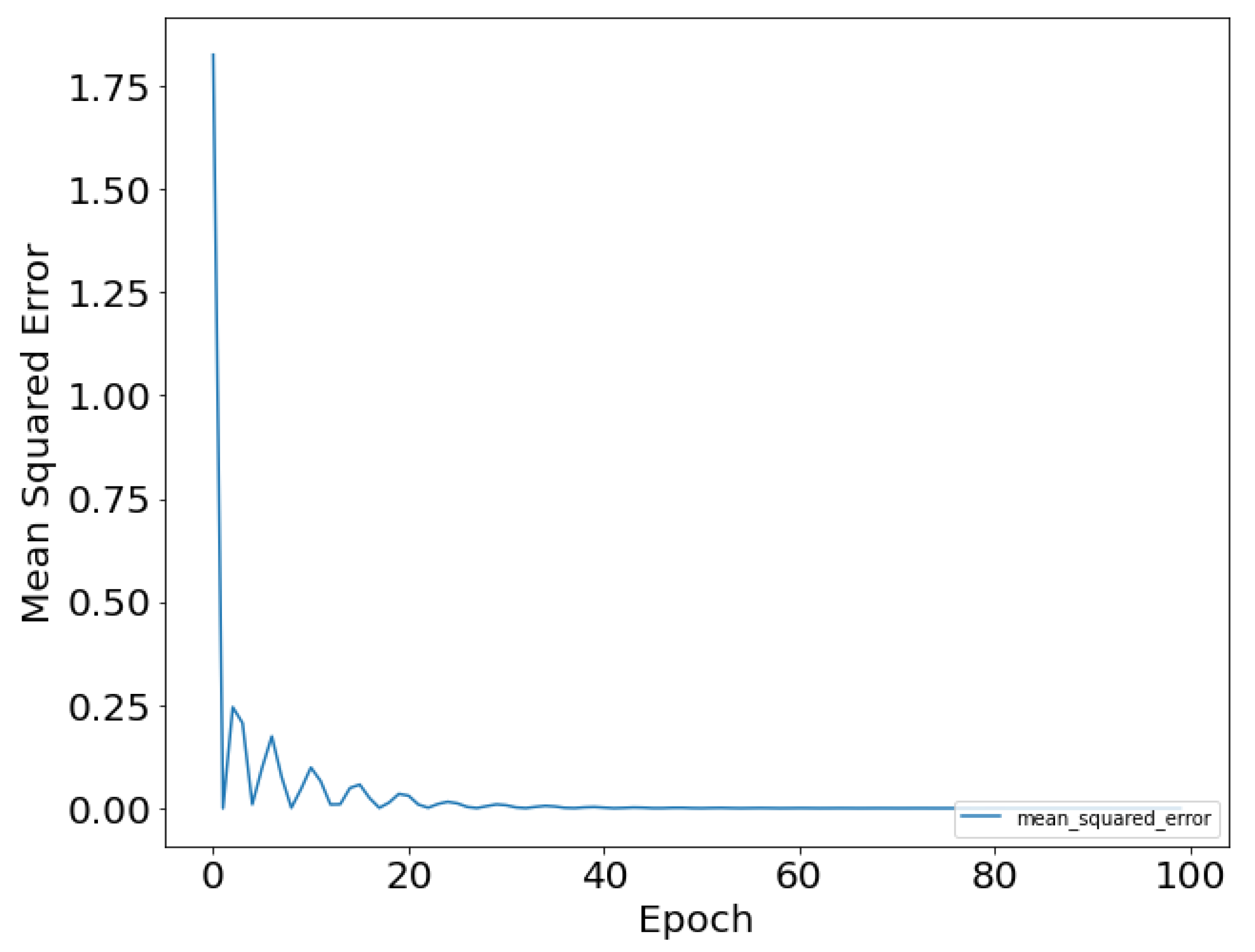
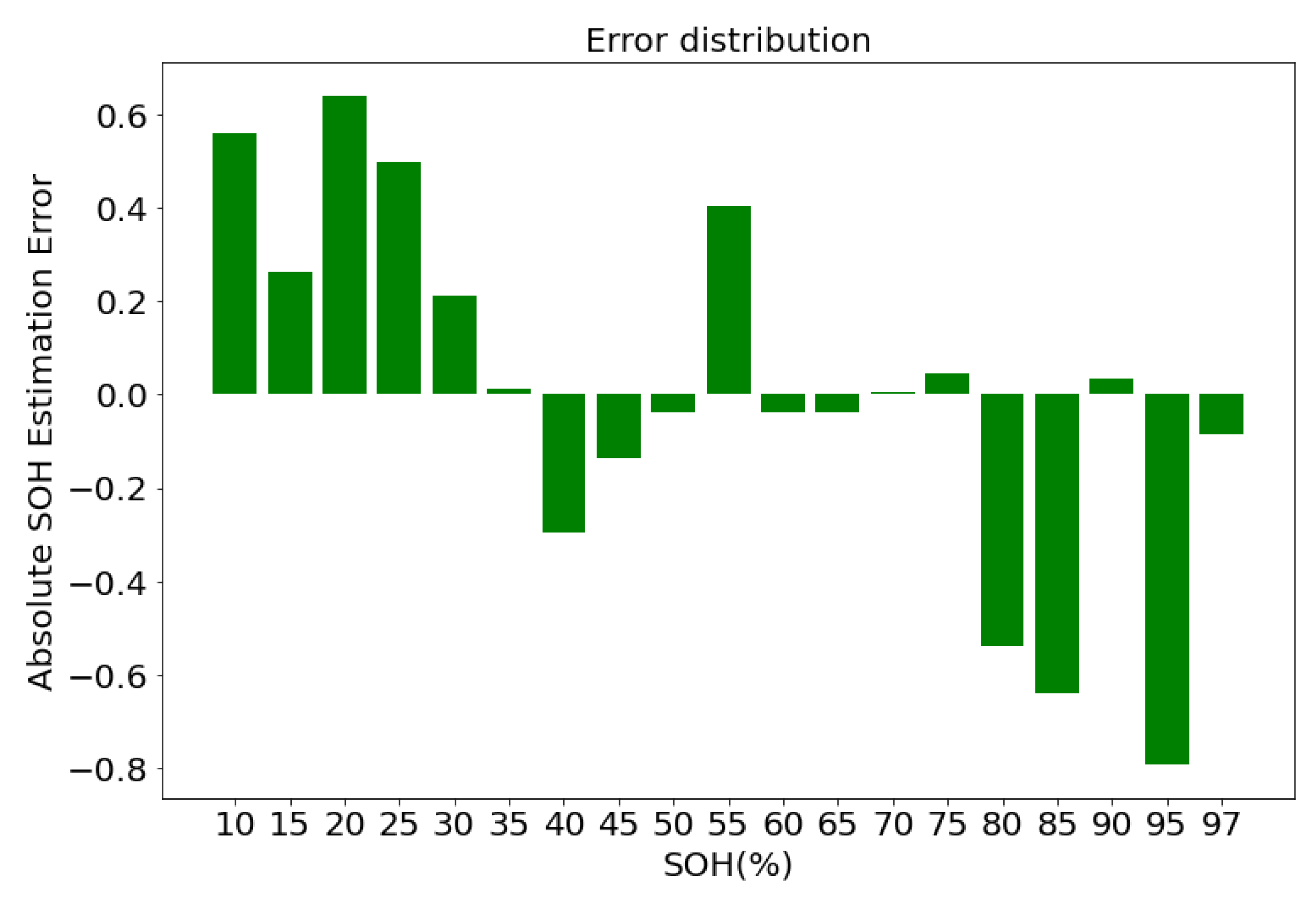
4.3. Classification of CDIs and CNN Training Accuracy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thies, C.; Kieckhäfer, K.; Spengler, T.S.; Sodhi, M.S. Assessment of social sustainability hotspots in the supply chain of lithium-ion batteries. Procedia CIRP 2019, 80, 292–297. [Google Scholar] [CrossRef]
- Liu, K.; Hu, X.; Yang, Z.; Xie, Y.; Feng, S. Lithium-ion battery charging management considering economic costs of electrical energy loss and battery degradation. Energy Convers. Manag. 2019, 195, 167–179. [Google Scholar] [CrossRef]
- Atalay, S.; Sheikh, M.; Mariani, A.; Merla, Y.; Bower, E.; Widanage, W.D. Theory of battery ageing in a lithium-ion battery: Capacity fade, nonlinear ageing and lifetime prediction. J. Power Sources 2020, 478, 229026. [Google Scholar] [CrossRef]
- Hemavathi, S. Overview of cell balancing methods for Li-ion battery technology. Energy Storage 2021, 3, e203. [Google Scholar] [CrossRef]
- Palacín, M.R. Understanding ageing in Li-ion batteries: A chemical issue. Chem. Soc. Rev. 2018, 47, 4924–4933. [Google Scholar] [CrossRef] [PubMed]
- Probstl, A.; Park, S.; Narayanaswamy, S.; Steinhorst, S.; Chakraborty, S. Soh-Aware active cell balancing strategy for high power battery packs. In Proceedings of the 2018 Design, Automation and Test in Europe Conference and Exhibition, DATE 2018, Dresden, Germany, 19–23 March 2018; pp. 431–436. [Google Scholar] [CrossRef]
- Thiruvonasundari, D.; Deepa, K. Evaluation and Comparative Study of Cell Balancing Methods for Lithium-Ion Batteries Used in Electric Vehicles. Int. J. Renew. Energy Dev. 2021, 10, 471–479. [Google Scholar] [CrossRef]
- Venugopal, P.; Vigneswaran, T. State-of-Health Estimation of Li-ion Batteries in Electric Vehicle Using IndRNN under Variable Load Condition. Energies 2019, 12, 4338. [Google Scholar] [CrossRef]
- Hu, X.; Zheng, Y.; Lin, X.; Xie, Y. Optimal Multistage Charging of NCA/Graphite Lithium-Ion Batteries Based on Electrothermal-Aging Dynamics. IEEE Trans. Transp. Electrif. 2020, 6, 427–438. [Google Scholar] [CrossRef]
- Noura, N.; Boulon, L.; Jemeï, S. A Review of Battery State of Health Estimation Methods: Hybrid Electric Vehicle Challenges. World Electr. Veh. J. 2020, 11, 66. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, G.; Zhen, D.; Gu, F.; Ball, A. A review on online state of charge and state of health estimation for lithium-ion batteries in electric vehicles. Energy Rep. 2021, 7, 5141–5161. [Google Scholar] [CrossRef]
- Wang, K.; Gao, F.; Zhu, Y.; Liu, H.; Qi, C.; Yang, K.; Jiao, Q. Internal resistance and heat generation of soft package Li4Ti5O12 battery during charge and discharge. Energy 2018, 149, 364–374. [Google Scholar] [CrossRef]
- Messing, M.; Shoa, T.; Habibi, S. Estimating battery state of health using electrochemical impedance spectroscopy and the relaxation effect. J. Energy Storage 2021, 43, 103210. [Google Scholar] [CrossRef]
- Huang, H.; Meng, J.; Wang, Y.; Feng, F.; Cai, L.; Peng, J.; Liu, T. A comprehensively optimized lithium-ion battery state-of-health estimator based on Local Coulomb Counting Curve. Appl. Energy 2022, 322, 119469. [Google Scholar] [CrossRef]
- Flaherty, N. GlobalFoundries Teams for Wireless Battery Management Chip-eeNews Europe. Technical Report. Available online: https://www.eenewseurope.com/ (accessed on 16 January 2022).
- Zhu, Q.; Xu, M.; Liu, W.; Zheng, M. A state of charge estimation method for lithium-ion batteries based on fractional order adaptive extended kalman filter. Energy 2019, 187, 115880. [Google Scholar] [CrossRef]
- Omariba, Z.B.; Zhang, L.; Kang, H.; Sun, D. Parameter Identification and State Estimation of Lithium-Ion Batteries for Electric Vehicles with Vibration and Temperature Dynamics. World Electr. Veh. J. 2020, 11, 50. [Google Scholar] [CrossRef]
- Azis, N.A.; Joelianto, E.; Widyotriatmo, A. State of Charge (SoC) and State of Health (SoH) Estimation of Lithium-Ion Battery Using Dual Extended Kalman Filter Based on Polynomial Battery Model. In Proceedings of the 2019 6th International Conference on Instrumentation, Control, and Automation, ICA 2019, Bandung, Indonesia, 31 July–2 August 2019; pp. 88–93. [Google Scholar] [CrossRef]
- Xiao, B.; Xiao, B.; Liu, L. Rapid measurement method for lithium-ion battery state of health estimation based on least squares support vector regression. Int. J. Energy Res. 2021, 45, 5695–5709. [Google Scholar] [CrossRef]
- Qiao, J.; Wang, S.; Yu, C.; Shi, W.; Fernandez, C. A novel bias compensation recursive least square-multiple weighted dual extended Kalman filtering method for accurate state-of-charge and state-of-health co-estimation of lithium-ion batteries. Int. J. Circuit Theory Appl. 2021, 49, 3879–3893. [Google Scholar] [CrossRef]
- Guida, G.; Faverato, D.; Colabella, M.; Buonomo, G. Robust state of charge and state of health estimation for batteries using a novel multi model approach. Control Theory Technol. 2022, 20, 418–438. [Google Scholar] [CrossRef]
- Yang, N.; Song, Z.; Hofmann, H.; Sun, J. Robust State of Health estimation of lithium-ion batteries using convolutional neural network and random forest. J. Energy Storage 2022, 48, 103857. [Google Scholar] [CrossRef]
- Pan, H.; Lü, Z.; Wang, H.; Wei, H.; Chen, L. Novel battery state-of-health online estimation method using multiple health indicators and an extreme learning machine. Energy 2018, 160, 466–477. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Z.; Xiong, Q.; Ding, B.; Hou, J.; Luo, D.; Rong, Y.; Li, S. State-of-health estimation and remaining useful life prediction for the lithium-ion battery based on a variant long short term memory neural network. J. Power Sources 2020, 459, 228069. [Google Scholar] [CrossRef]
- Rastegarpanah, A.; Hathaway, J.; Ahmeid, M.; Lambert, S.; Walton, A.; Stolkin, R. A rapid neural network—Based state of health estimation scheme for screening of end of life electric vehicle batteries. J. Syst. Control Eng. 2020, 235, 330–346. [Google Scholar] [CrossRef]
- Kim, J.; Yu, J.; Kim, M.; Kim, K.; Han, S. Estimation of Li-ion Battery State of Health based on Multilayer Perceptron: As an EV Application. IFAC-Papersonline 2018, 51, 392–397. [Google Scholar] [CrossRef]
- Roman, D.; Saxena, S.; Robu, V.; Pecht, M.; Flynn, D. Machine learning pipeline for battery state-of-health estimation. Nat. Mach. Intell. 2021, 3, 447–456. [Google Scholar] [CrossRef]
- Li, Y.; Li, K.; Liu, X.; Zhang, L. Fast battery capacity estimation using convolutional neural networks. Trans. Inst. Meas. Control 2020, 0142331220966425. [Google Scholar] [CrossRef]
- Li, Y.; Tao, J. CNN and transfer learning based online SOH estimation for lithium-ion battery. In Proceedings of the 32nd Chinese Control and Decision Conference, CCDC 2020, Hefei, China, 22–24 August 2020; Institute of Electrical and Electronics Engineers Inc.: Interlaken, Switzerland, 2020; pp. 5489–5494. [Google Scholar] [CrossRef]
- Shen, S.; Chen, X.; Hu, C.; Sadoughi, M.K.; Hong, M. Online Estimation of Lithium-Ion Battery Capacity Using Deep Convolutional Neural Networks. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 2A-2018. [Google Scholar] [CrossRef]
- Javadipour, M.; Mehran, K. Analysis of current density in the electrode and electrolyte of lithium-ion cells for ageing estimation applications. IET Smart Grid 2021, 4, 176–189. [Google Scholar] [CrossRef]
- Bason, M.G.; Coussens, T.; Withers, M.; Abel, C.; Kendall, G.; Krüger, P. Non-invasive current density imaging of lithium-ion batteries. J. Power Sources 2022, 533, 231312. [Google Scholar] [CrossRef]
- Tsai, P.C.; Wen, B.; Wolfman, M.; Choe, M.J.; Pan, M.S.; Su, L.; Thornton, K.; Cabana, J.; Chiang, Y.M. Single-particle measurements of electrochemical kinetics in NMC and NCA cathodes for Li-ion batteries. Energy Environ. Sci. 2018, 11, 860–871. [Google Scholar] [CrossRef]
- Ilott, A.J.; Mohammadi, M.; Schauerman, C.M.; Ganter, M.J.; Jerschow, A. Rechargeable lithium-ion cell state of charge and defect detection by in-situ inside-out magnetic resonance imaging. Nat. Commun. 2018, 9, 1776. [Google Scholar] [CrossRef]
- Zou, D.; Li, M.; Wang, D.; Li, N.; Su, R.; Zhang, P.; Gan, Y.; Cheng, J. Temperature Estimation of Lithium-Ion Battery Based on an Improved Magnetic Nanoparticle Thermometer. IEEE Access 2020, 8, 135491–135498. [Google Scholar] [CrossRef]
- Khalik, Z.; Donkers, M.C.; Bergveld, H.J. Model simplifications and their impact on computational complexity for an electrochemistry-based battery modeling toolbox. J. Power Sources 2021, 488, 229427. [Google Scholar] [CrossRef]
- Xia, L.; Najafi, E.; Li, Z.; Bergveld, H.J.; Donkers, M.C. A computationally efficient implementation of a full and reduced-order electrochemistry-based model for Li-ion batteries. Appl. Energy 2017, 208, 1285–1296. [Google Scholar] [CrossRef]
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J.; Wang, J.; Deng, T.; Shang, W. Temperature effect and thermal impact in lithium-ion batteries: A review. Prog. Nat. Sci. Mater. Int. 2018, 28, 653–666. [Google Scholar] [CrossRef]
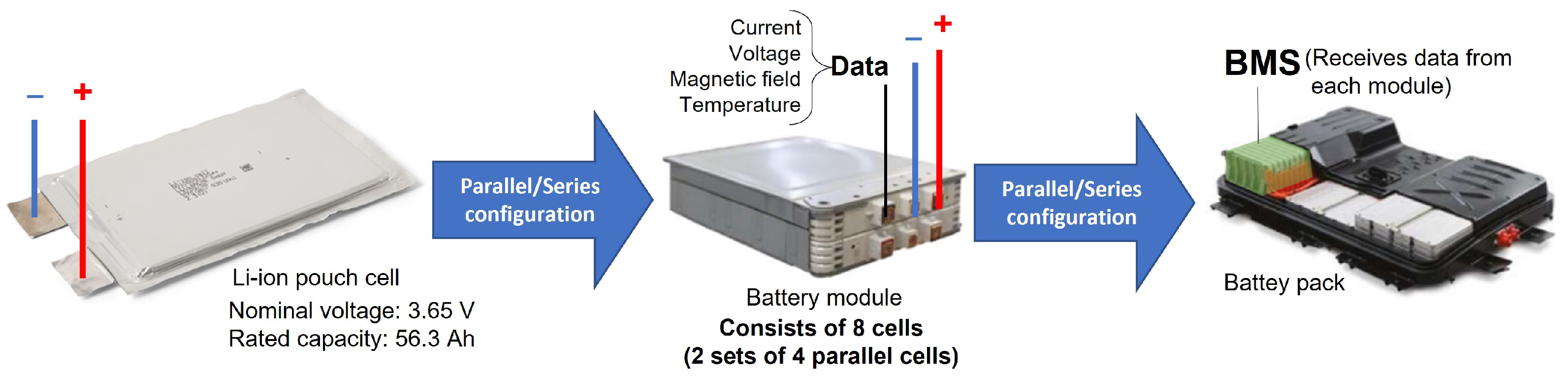




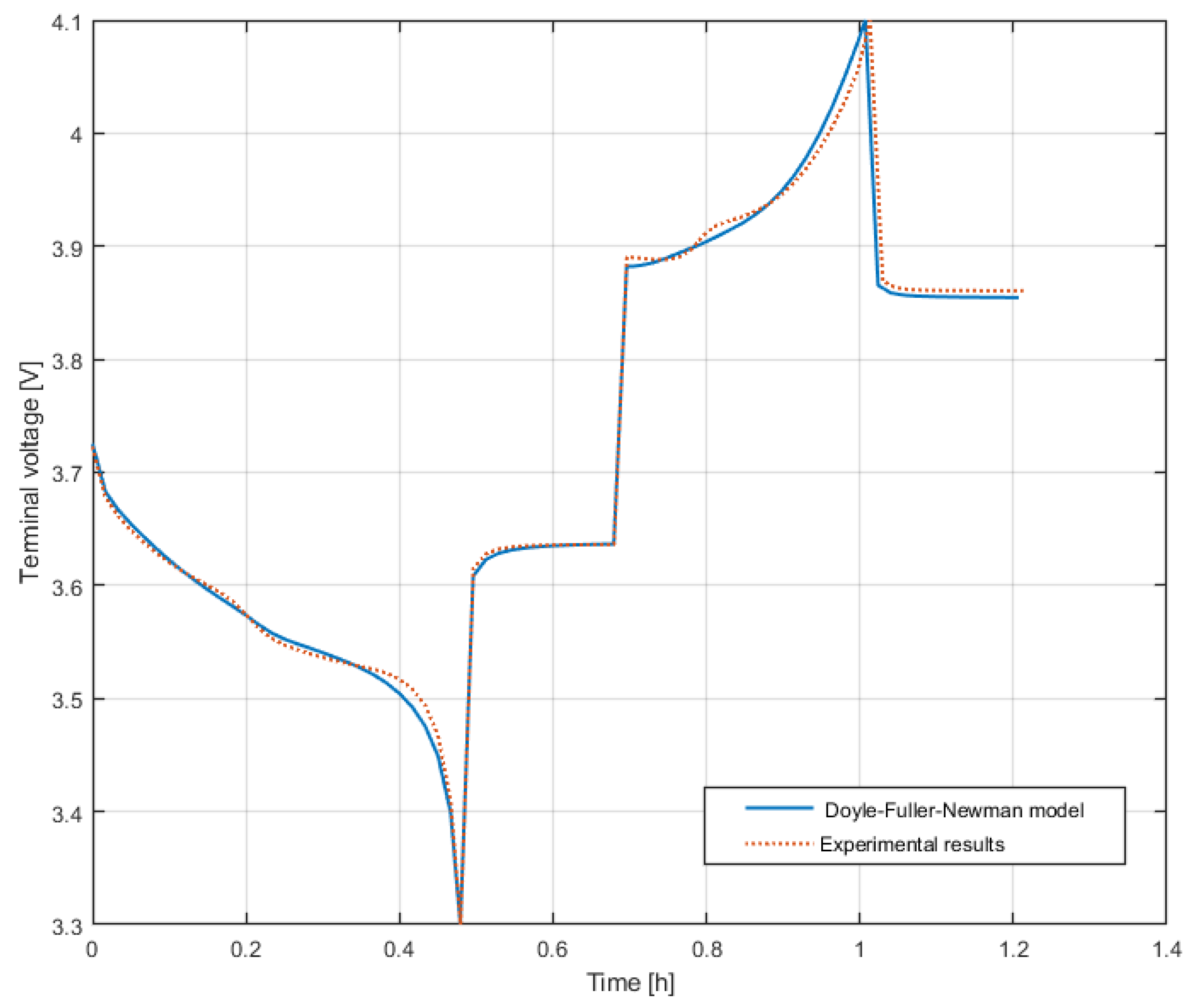
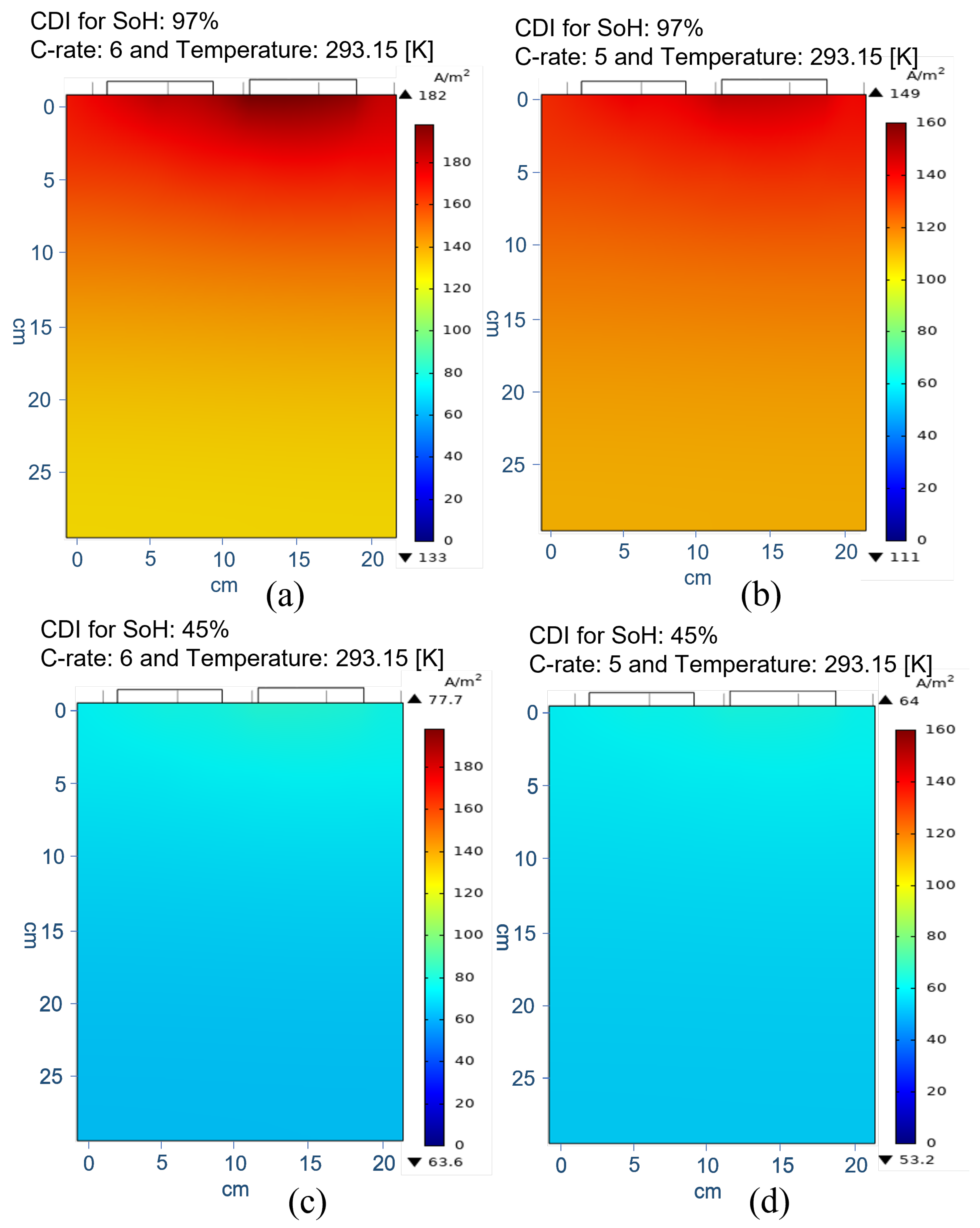
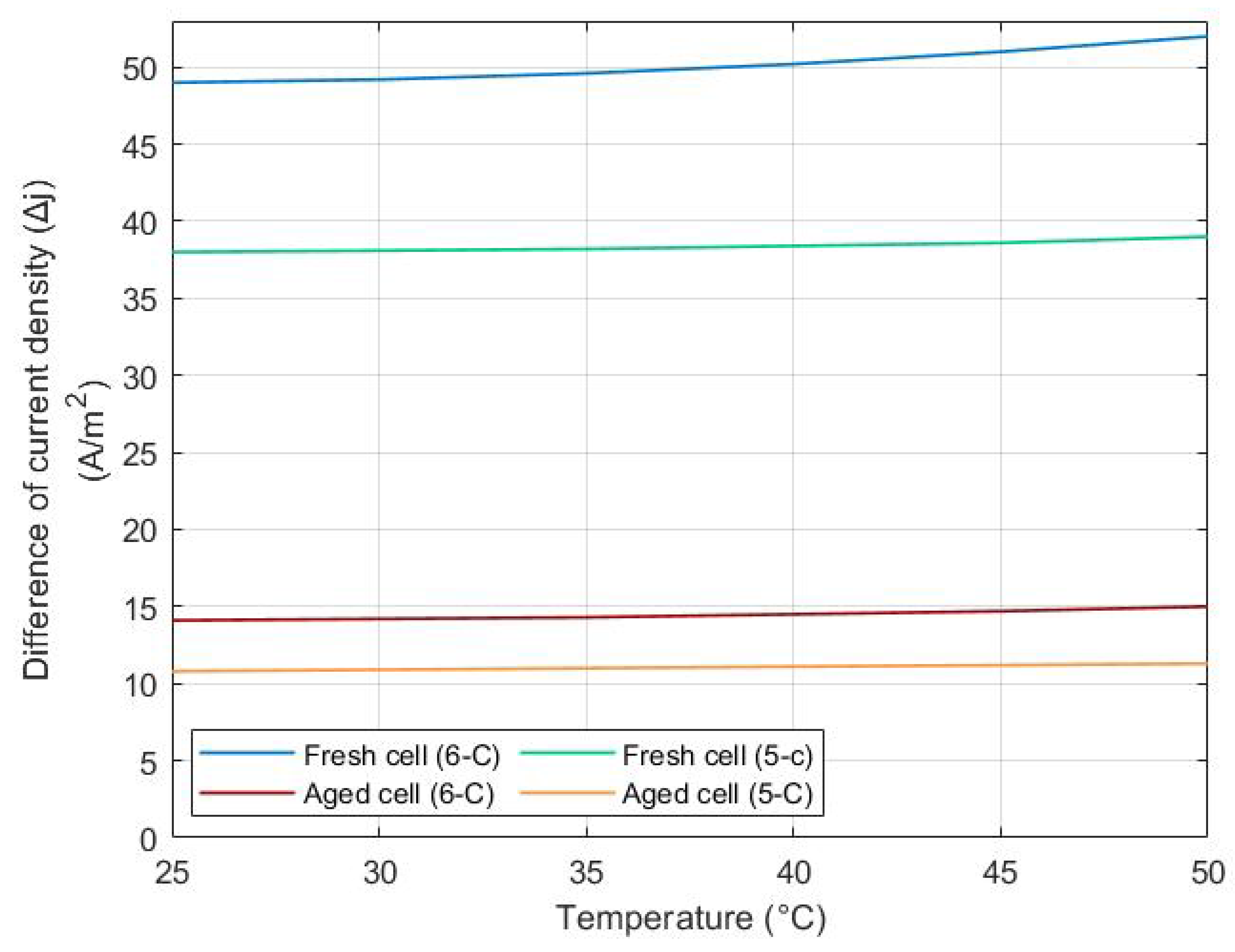

| Estimation Category | Approach | Benefits | Drawbacks | SoH Error% |
|---|---|---|---|---|
| Experimental methods | Measuring internal resistance and internal impedance [10,12] | + Easy implementation + Widely used in automotive profiles | - Operating off-line - Possibility of error accumulation - High time consumption | <3% |
| Experimental methods | Electrochemical Impedance Spectroscopy (EIS) [13] | + Low time consumption + Very good accuracy | - Required hardware is complex and costly | <2% |
| Model-based methods (Adaptive filtering) [16,17] | Kalman filter-based method [18] Robust estimation method [21,22] | + Operating onboard + Low time consumption + High accuracy | - Accuracy depends on parameters of battery - High computational cost | <2% |
| Model-based methods | Least square-based method [19] | + Operating onboard + Widely used in automotive profiles | - High computational complexity | <5% |
| Machine Learning methods [23,24] | Convolutional Neural Network(CNN) method [22,28,29] | + Operating Online + Effectively capturing LiB’s non-linear characteristics | - Requires large dataset to train the network - The precision of the method is conditional * | <1.5% |
| Li-ion concentration | Solid phase () | (1a) | |
| Electrolyte phase () | (1b) | ||
| Boundary condition for Li-ion concentration | Solid phase | (2a) | |
| Electrolyte phase | (2b) | ||
| Exchange current density | (3a) | ||
| Measurable terminal voltage | (3b) |
| Symbol | Description | Value |
|---|---|---|
| Area of electrode plate | 6.264 [cm] | |
| Anodic transfer coefficient | 0.5 [1] | |
| Anodic transfer coefficient | 0.5 [1] | |
| The specific inter-facial surface area | ||
| Maximum solid-phase concentration in positive electrode | 49,000 [mol/m] | |
| Maximum solid-phase concentration in negative electrode | 31,507 [mol/m] | |
| Solid-phase concentration at the solid–electrolyte interface | ||
| Positive electrode thickness | 60 [m] | |
| Separator thickness | 30 [m] | |
| Negative electrode thickness | 60 [m] | |
| Li-ion diffusion coefficient in the solid phase | [m/s] | |
| Li-ion diffusion coefficient in the electrolyte | [m/s] | |
| Volume fraction of active particles in positive electrode | 0.35 | |
| Volume fraction of active particles in negative electrode | 0.68 | |
| Electrolyte volume fraction | 0.65 | |
| Applied current through the cell | (variable) | |
| Kinetic rate constant in positive electrode | ||
| F | Faraday’s constant | [C/mol] |
| Kinetic rate constant in negative electrode | ||
| L | Cell thickness | 160 [m] |
| p | Bruggeman porosity exponent | 1.5 |
| Film resistance | [] | |
| Transport number | 0.363 | |
| x | Position across the cell | (variable) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javadipour, M.; Wickramanayake, T.; Alavi, S.A.; Mehran, K. A Novel Online State of Health Estimation Method for Electric Vehicle Pouch Cells Using Magnetic Field Imaging and Convolution Neural Networks. Electrochem 2022, 3, 769-788. https://doi.org/10.3390/electrochem3040051
Javadipour M, Wickramanayake T, Alavi SA, Mehran K. A Novel Online State of Health Estimation Method for Electric Vehicle Pouch Cells Using Magnetic Field Imaging and Convolution Neural Networks. Electrochem. 2022; 3(4):769-788. https://doi.org/10.3390/electrochem3040051
Chicago/Turabian StyleJavadipour, Mehrnaz, Toshan Wickramanayake, Seyed Amir Alavi, and Kamyar Mehran. 2022. "A Novel Online State of Health Estimation Method for Electric Vehicle Pouch Cells Using Magnetic Field Imaging and Convolution Neural Networks" Electrochem 3, no. 4: 769-788. https://doi.org/10.3390/electrochem3040051
APA StyleJavadipour, M., Wickramanayake, T., Alavi, S. A., & Mehran, K. (2022). A Novel Online State of Health Estimation Method for Electric Vehicle Pouch Cells Using Magnetic Field Imaging and Convolution Neural Networks. Electrochem, 3(4), 769-788. https://doi.org/10.3390/electrochem3040051









