Battery Energy Consumption Analysis of Automated Vehicles Based on MPC Trajectory Tracking Control
Abstract
:1. Introduction
2. Materials and Methods
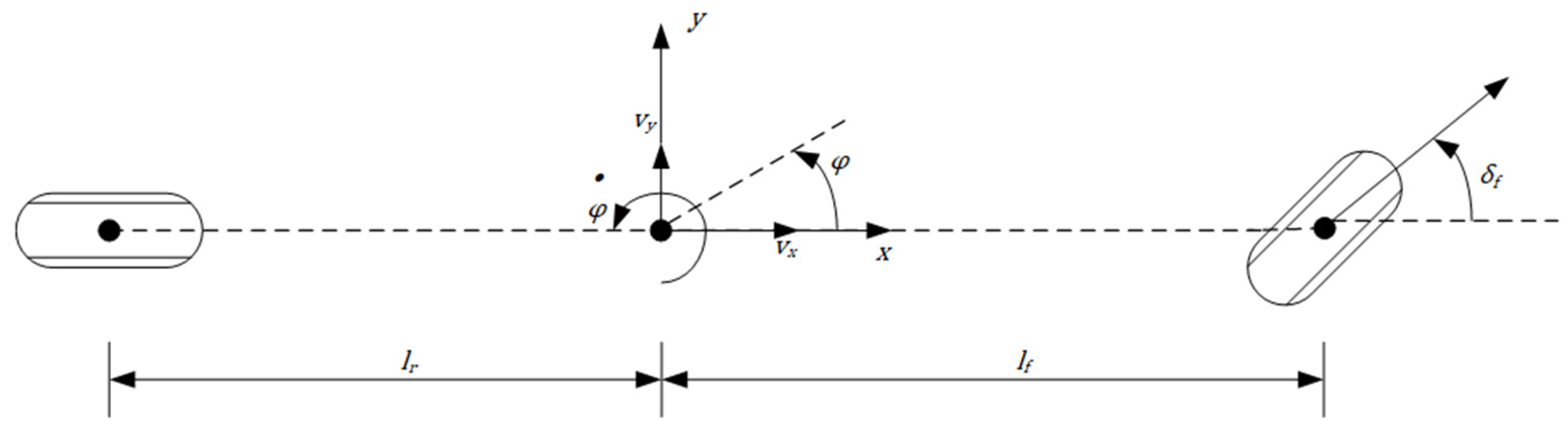
2.1. Vehicle Dynamics Model
2.2. Design Objective Function
2.3. Power Battery Energy Consumption
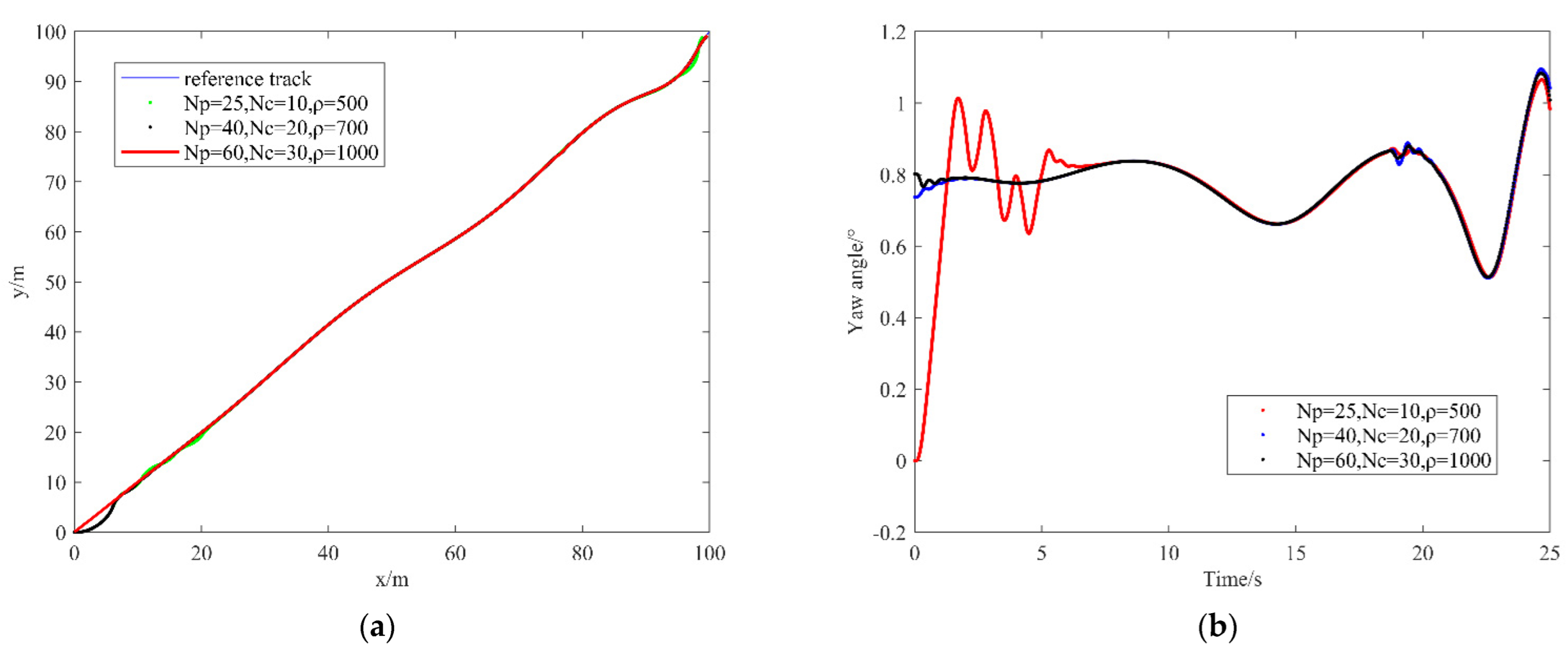
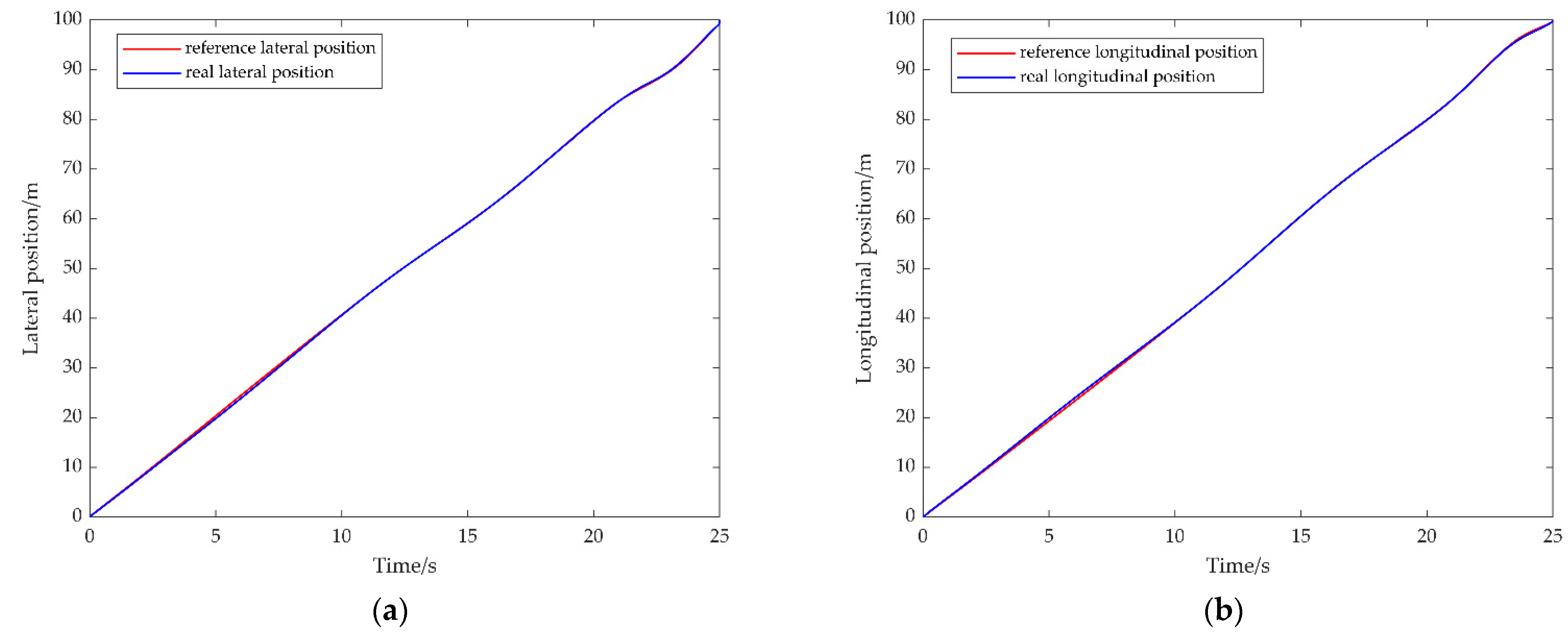
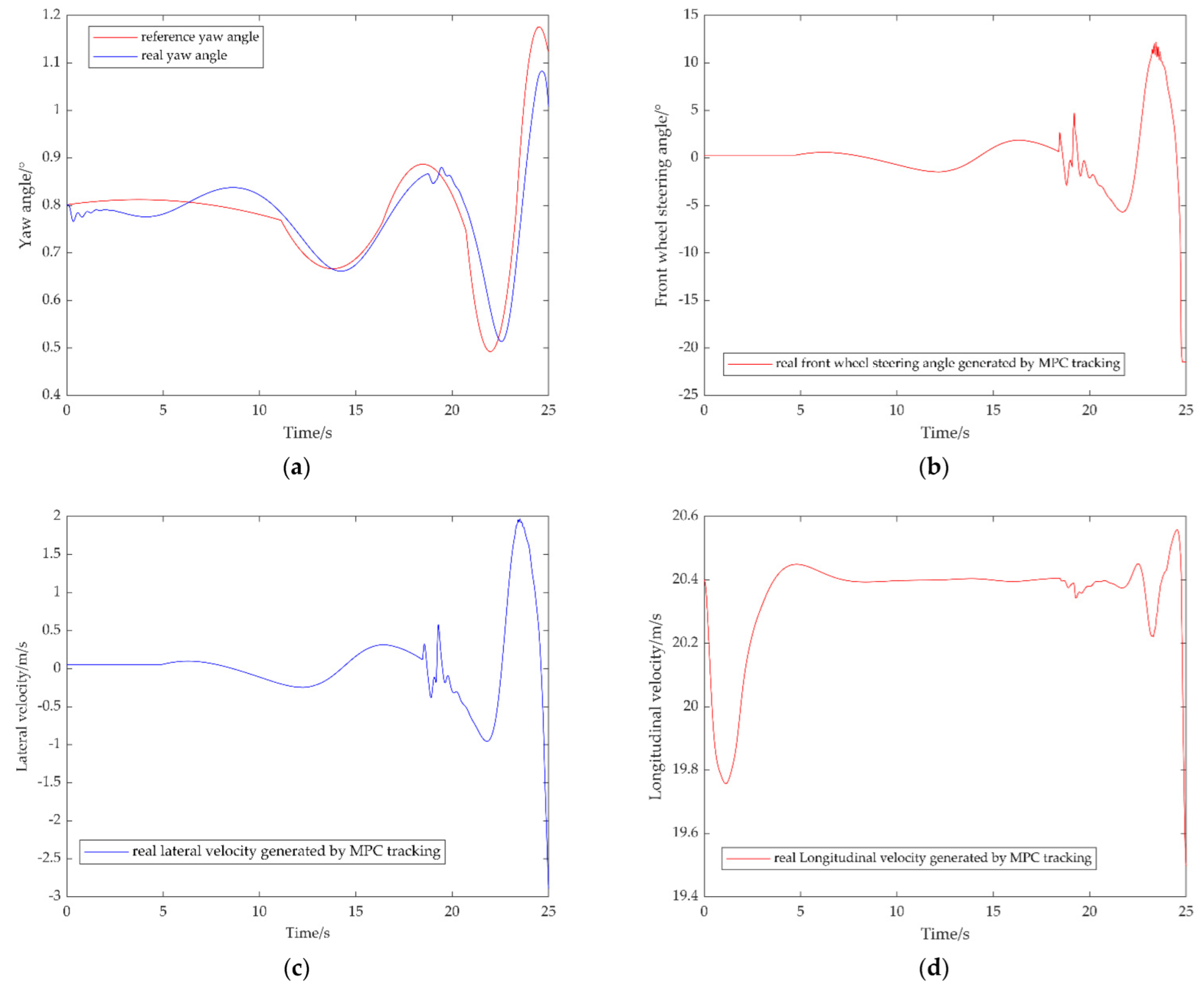
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hariharan, C.; Gunadevan, D.; Prakash, S.A. Simulation of battery energy consumption in an electric car with traction and HVAC model for a given source and destination for reducing the range anxiety of the driver. Energy 2022, 249, 123657. [Google Scholar] [CrossRef]
- Cetin, M.S.; Güler, H.; Gençoğlu, M.T. Fuzzy Logic Based Battery Control System Design for Electric Vehicles. In Proceedings of the Innovations in Intelligent Systems and Applications Conference (ASYU), Elazig, Turkey, 6–8 October 2021; pp. 1–4. [Google Scholar]
- Hoekstra, F.S.J.; Bergveld, H.J.; Donkers, M.C.F. Optimal Control of Active Cell Balancing: Extending the Range and Useful Lifetime of a Battery Pack. IEEE Trans. Control. Syst. Technol. 2022, 1–8. [Google Scholar] [CrossRef]
- He, C.; Li, M.; Wang, F. Simulation study of a cylindrical battery module. J. Energy Storage 2022, 48, 104000. [Google Scholar] [CrossRef]
- Ruhani, B.; Abidi, A.; Hussein, A.K. Numerical simulation of the effect of battery distance and inlet and outlet length on the cooling of cylindrical lithium-ion batteries and overall performance of thermal management system. J. Energy Storage 2022, 45, 103714. [Google Scholar] [CrossRef]
- Khiari, J.; Olaverri-Monreal, C. Uncertainty-Aware Prediction of Battery Energy Consumption for Hybrid Electric Vehicles. arXiv 2022, arXiv:2204.12825. [Google Scholar]
- Sagaria, S.; Neto, R.C.; Baptista, P. Modelling approach for assessing influential factors for EV energy performance. Sustain. Energy Technol. Assess. 2021, 44, 100984. [Google Scholar] [CrossRef]
- Babu, A.R.; Minovski, B.; Sebben, S. Thermal encapsulation of large battery packs for electric vehicles operating in cold climate. Appl. Therm. Eng. 2022, 212, 118548. [Google Scholar] [CrossRef]
- Ma, Y.; Ding, H.; Liu, Y. Battery thermal management of intelligent-connected electric vehicles at low temperature based on NMPC. Energy 2022, 244, 122571. [Google Scholar] [CrossRef]
- Singirikonda, S.; Obulesu, Y.P. Battery modelling and state of charge estimation methods for Energy Management in Electric Vehicle-A review. IOP Conf. Ser. Mater. Sci. Eng. 2020, 937, 012046. [Google Scholar] [CrossRef]
- Kebbati, Y.; Ait-Oufroukh, N.; Vigneron, V.; Ichalal, D. Optimized self-adaptive PID speed control for autonomous vehicles. In Proceedings of the International Conference on Automation and Computing, Portsmouth, UK, 2–4 September 2021; pp. 1–6. [Google Scholar]
- Tian, M.W.; Yan, S.R.; Mohammadzadeh, A. Stability of Interval Type-3 Fuzzy Controllers for Autonomous Vehicles. Mathematics 2021, 9, 2742. [Google Scholar] [CrossRef]
- Dong, X.P.; Pei, H.Y.; Gan, M. Autonomous Vehicle Lateral Control Based on Fractional-order PID. In Proceedings of the Information Technology, Networking, Electronic and Automation Control Conference, Xi’an, China, 15–17 October 2021; Volume 5, pp. 830–835. [Google Scholar]
- Zuñiga-Peña, S.; Hernández-Romero, N.; Seck-Tuoh-Mora, C. Improving 3D Path Tracking of Unmanned Aerial Vehicles through Optimization of Compensated PD and PID Controllers. Appl. Sci. 2021, 12, 99. [Google Scholar] [CrossRef]
- Mao, J.; Yang, L.; Hu, Y.B.; Liu, K.; Du, J.F. Research on Vehicle Adaptive Cruise Control Method Based on Fuzzy Model Predictive Control. Machines 2021, 9, 160. [Google Scholar] [CrossRef]
- Yang, J.R.; Peng, W.F.; Sun, C. A Learning Control Method of Automated Vehicle Platoon at Straight Path with DDPG-Based PID. Electronics 2021, 11, 617. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, W.Q.; Qureshi, W.S. Autonomous navigation for a wolfberry picking robot using visual cues and fuzzy control. Inf. Process. Agric. 2021, 8, 15–26. [Google Scholar] [CrossRef]
- Yatak, M.Ö.; Şahin, F. Ride Comfort-Road Holding Trade-off Improvement of Full Vehicle Active Suspension System by Interval Type-2 Fuzzy Control. Eng. Sci. Technol. Int. J. 2021, 24, 259–270. [Google Scholar] [CrossRef]
- Lei, Y.L.; Wen, G.; Fu, Y.; Li, X.; Hou, B.; Geng, X. Trajectory-following of a 4WID-4WIS vehicle via feedforward–backstepping sliding-mode control. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 322–333. [Google Scholar] [CrossRef]
- Subroto, R.K.; Wang, C.Z.; Lian, K.L. Four-wheel independent drive electric vehicle stability control using novel adaptive sliding mode control. IEEE Trans. Ind. Appl. 2020, 56, 5995–6006. [Google Scholar] [CrossRef]
- Peng, B.; Yu, D.; Zhou, H.; Xiao, X.; Fang, Y. A platoon control strategy for autonomous vehicles based on sliding-mode control theory. IEEE Access 2020, 8, 81776–81788. [Google Scholar] [CrossRef]
- Ao, D.; Huang, W.; Wong, P.K.; Li, J. Robust Backstepping Super-Twisting Sliding Mode Control for Autonomous Vehicle Path Following. IEEE Access 2021, 9, 123165–123177. [Google Scholar] [CrossRef]
- Abooee, A.; Hayeri Mehrizi, M.; Arefi, M.M.; Yin, S. Finite-time sliding mode control for a 3-DOF fully actuated autonomous surface vehicle. Trans. Inst. Meas. Control. 2021, 43, 371–389. [Google Scholar] [CrossRef]
- Lu, Z.; Shyrokau, B.; Boulkroune, B.; Van Aalst, S.; Happee, R. Performance benchmark of state-of-the-art lateral path-following controllers. In Proceedings of the 2018 IEEE 15th International Workshop on Advanced Motion Control (AMC), Tokyo, Japan, 9–11 March 2018; pp. 541–546. [Google Scholar]
- Nebeluk, R.; Ławryńczuk, M. Computationally Simple Nonlinear MPC Algorithm for Vehicle Obstacle Avoidance with Minimization of Fuel Utilization. IEEE Access 2021, 9, 17296–17311. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Chen, X.; Wu, J.; Wang, H.D. Model-Predictive-Control-Based Path Tracking Controller of Autonomous Vehicle Considering Parametric Uncertainties and Velocity-Varying. IEEE Trans. Ind. Electron. 2021, 68, 8698–8707. [Google Scholar] [CrossRef]
- Li, Z.H.; Wang, P.; Liu, H.H.; Hu, Y.F.; Chen, H. Coordinated longitudinal and lateral vehicle stability control based on the combined-slip tire model in the MPC framework. Mech. Syst. Signal Process. 2021, 161, 107947. [Google Scholar] [CrossRef]
- Ammour, M.; Orjuela, R.; Basset, M. Collision avoidance for autonomous vehicle using MPC and time varying Sigmoid safety constraints. IFAC-PapersOnLine 2021, 54, 39–44. [Google Scholar] [CrossRef]
- Pang, H.; Liu, N.; Hu, C.; Xu, Z.J. A practical trajectory tracking control of autonomous vehicles using linear time-varying MPC method. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 709–723. [Google Scholar] [CrossRef]
- Jeong, Y.h.; Yim, S.J. Model Predictive Control-Based Integrated Path Tracking and Velocity Control for Autonomous Vehicle with Four-Wheel Independent Steering and Driving. Electronics 2021, 10, 2812. [Google Scholar] [CrossRef]
- Chen, C.P.; Guo, J.H.; Guo, C.; Chen, C.Y.; Zhang, Y.; Wang, J.W. Adaptive Cruise Control for Cut-In Scenarios Based on Model Predictive Control Algorithm. Appl. Sci. 2021, 11, 5293. [Google Scholar] [CrossRef]
- Zhang, K.W.; Sun, Q.; Shi, Y. Trajectory tracking control of autonomous ground vehicles using adaptive learning MPC. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5554–5564. [Google Scholar] [CrossRef]
- Pae, D.S.; Kim, G.H.; Kang, T.K.; Lim, M.T. Path planning based on obstacle-dependent gaussian model predictive control for autonomous driving. Appl. Sci. 2021, 11, 3703. [Google Scholar] [CrossRef]
- Xu, Y.; Tang, W.T.; Chen, B.Y.; Qiu, L.; Yang, R. A model predictive control with preview-follower theory algorithm for trajectory tracking control in autonomous vehicles. Symmetry 2021, 13, 381. [Google Scholar] [CrossRef]
- Chen, S.; Chen, H.; Negrut, D. Implementation of MPC-Based Trajectory Tracking Considering Different Fidelity Vehicle Models. J. Beijing Inst. Technol. 2020, 29, 303–316. [Google Scholar]
- Lazcano, A.M.R.; Niu, T.; Akutain, X.C.; Cole, D.; Shyrokau, B. MPC-Based Haptic Shared Steering System: A Driver Modeling Approach for Symbiotic Driving. IEEE/ASME Trans. Mechatron. 2021, 26, 1201–1211. [Google Scholar] [CrossRef]
- Chen, S.; Chen, H. MPC-based path tracking with PID speed control for autonomous vehicles. IOP Conf. Ser. Mater. Sci. Eng. 2020, 892, 012034. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, B.; Zhu, X.; Su, Y. Linear Time-Varying MPC Vehicle Trajectory Tracking Controller Considering Driving Road Surface Factors. In Proceedings of the International Conference on Control Science and Electric Power Systems (CSEPS), Shanghai, China, 28–30 May 2021; pp. 83–88. [Google Scholar]
- Liang, Y.; Li, Y.; Khajepour, A.; Huang, Y.; Qin, Y.; Zheng, L. A Novel Combined Decision and Control Scheme for Autonomous Vehicle in Structured Road Based on Adaptive Model Predictive Control. IEEE Trans. Intell. Transp. Syst. 2022, 1–15. [Google Scholar] [CrossRef]
- Chowdhri, N.; Ferranti, L.; Iribarren, F.S.; Shyrokau, B. Integrated nonlinear model predictive control for automated driving. Control. Eng. Pract. 2021, 106, 104654. [Google Scholar] [CrossRef]
- Gong, J.W. Model Predictive Control of Unmanned Vehicles, 2nd ed.; Beijing Institute of Technology Press: Beijing, China, 2020; pp. 38–39. [Google Scholar]
- Liu, Q.; Liu, J.H.; Le, W.W.; Guo, Z.X.; He, Z.G. Data-driven intelligent location of public charging stations for electric vehicles. J. Clean. Prod. 2019, 232, 531–541. [Google Scholar] [CrossRef]
- Liu, B.Y.; Ye, X.B.; Wang, X.B. Path Avoidance Algorithm for Unmanned Ground Vehicles Based on Improved Artificial Potential Field. Chin. J. Inert. Technol. 2020, 28, 769–777. [Google Scholar]

| Variable | Name and Unit | Numerical Value |
|---|---|---|
| Prediction time domain | 60 | |
| Control time domain | 30 | |
| Sampling period/s | 0.02 | |
| Relaxation factor weight coefficient | 1000 | |
| Vehicle mass/kg | 1723 | |
| Front wheelbase/m | 1.232 | |
| Rear wheelbase/m | 1.468 | |
| 4175 | ||
| Front wheel lateral cornering stiffness | 66,900 | |
| Rear wheel lateral cornering stiffness | 62,700 | |
| Front wheel longitudinal cornering stiffness | 66,900 | |
| Rear wheel longitudinal cornering stiffness | 62,700 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, H.; Pei, W.; Zhang, Q. Battery Energy Consumption Analysis of Automated Vehicles Based on MPC Trajectory Tracking Control. Electrochem 2022, 3, 337-346. https://doi.org/10.3390/electrochem3030023
Ma H, Pei W, Zhang Q. Battery Energy Consumption Analysis of Automated Vehicles Based on MPC Trajectory Tracking Control. Electrochem. 2022; 3(3):337-346. https://doi.org/10.3390/electrochem3030023
Chicago/Turabian StyleMa, Hao, Wenhui Pei, and Qi Zhang. 2022. "Battery Energy Consumption Analysis of Automated Vehicles Based on MPC Trajectory Tracking Control" Electrochem 3, no. 3: 337-346. https://doi.org/10.3390/electrochem3030023
APA StyleMa, H., Pei, W., & Zhang, Q. (2022). Battery Energy Consumption Analysis of Automated Vehicles Based on MPC Trajectory Tracking Control. Electrochem, 3(3), 337-346. https://doi.org/10.3390/electrochem3030023








