Modelling the Current Response and Sensitivity of Oxidase Enzyme Electrodes, Monitored Amperometrically by the Consumption of Oxygen

Abstract

Biosensor behaviour is characterised by non-linear differential equations that describe well-defined physical, chemical, and biological processes. Mathematical modelling of these biosensors is highly desirable since they have many applications. These models enable the prediction of a variety of their properties. In this study, the cyclic conversion of the substrate in an amperometric biosensor with an oxidase enzyme membrane electrode is studied using a mathematical model. The governing parameters for the Michaelis–Menten kinetics of enzymatic reactions are the enzyme kinetic and diffusion rates across the enzymatic layer. In this paper, we solved the non-linear equations analytically and numerically for all experimental values of parameters. This problem is simulated in MATLAB^® v2016b software using the PDE solver. Our analytical solutions are compared to simulation results to validate the proposed model.

1. Introduction

Biosensors are analytic devices that detect biochemical and physiological changes. They are an emerging technology for low-cost, quick, and easy-to-use biomedical diagnostic instruments. Biosensor design and functionality are based on well-understood physical and chemical processes that can be easily converted into non-linear ODE or PDE equations mathematical models. As a result, mathematical and computational modelling approaches may be utilised to evaluate the biosensor response as a factor of its input variables in a wide range of physical situations, thus reducing development time and costs.

Biosensors, specifically enzyme-based amperometric sensors, have been extensively studied in academic and applied fields due to their scientific significance and commercial value [1,2]. Clark and Lyons [3] proposed the central concept of enzyme electrodes roughly three decades ago. Many biosensors based on electrochemical enzyme electrodes have been described since, most of which operate in an amperometric mode. The development of models for enzyme electrodes provides a better understanding of the individual processes influencing the device’s response, and this information may be used as a guide for directions for the improvement of the sensor design. Mathematical models can explain such regularities. For example, Mell and Maloy [4,5] analysed the general features of amperometric response. There have been many reports on models for enzyme electrodes.

Models for multilayer and multi-enzyme electrodes were described by Schulmeister [6,7], and these models assumed that the electrode operates under diffusion control, with enzyme kinetics that is linear with the substrate. This allows the reaction and diffusion system to be described by a parabolic differential equation with linear inhomogeneities. Leypoldt and Gough [8] proposed a two-substrate enzyme electrode model that considers the non-linear enzyme reaction. However, only a few enzyme electrode models have been described [9,10,11,12,13] that emphasise electrode design.

The transient behaviour of an amperometric enzyme sensor was calculated by Cambiaso et al. [14]. A theoretical model and numerical simulation of an electrochemical enzyme biosensor were compared by Dana Mackey et al. [15]. To simulate the steady-state and transient behaviour of multi-membrane multi-enzyme sensors, Jobst et al. [16] developed an implicit difference method. Many algebraic solutions and simulations have been published in the literature to characterise the coupling of reaction and mass transport as immensely useful [17,18,19]. The non-linear kinetics of cyclic substrate conversions in amperometric enzyme sensors was studied by Sorochinskii and Kurganov [20].

Kulys et al. [21] analysed the biosensors’ transient kinetics. Manimozhi et al. [22] proposed a rigorous analytical and numerical solution for a steady-state substrate concentration under mixed enzyme kinetics at the biosensor. The electrochemical responses of immobilised enzyme biosensors are calculated using relaxation and simplex mathematical techniques [23].

In a flow-injection system with a single line of chemistry, Kolev [24] developed mathematical models for analysing the concentration profile observed by a single-layer, single-enzyme electrode. Baronas et al. [25] investigated a plate-gap model of a porous enzyme doped electrode inert membrane using the finite-difference technique

Gooding and Hall [9] used a two-substrate model to predict the response of an amperometric oxidase enzyme electrode. However, no general and simple analytical results for the concentration mediator and substrate for all values of the reaction/diffusion parameters have been reported [9]. This paper seeks to apply the recently developed Akbari–Ganji method (AGM) to solve the pertinent reaction-diffusion equations for redox mediator (oxygen) and substrate in the modified electrode. In so doing, approximate analytical solutions for both the mediator and substrate concentrations in the film are derived, and a closed-form expression for the amperometric steady-state current response and sensor sensitivity is obtained. These closed-form expressions for current are valid for a wide range of substrate concentration values.

2. Mathematical Formulation and Analysis of the Problem

2.1. Mathematical Formulation

Amperometric enzyme electrodes have been a subject of study for many years. Early work on mediated enzyme electrodes was reported by Gooding and Hall [9], who presented a concise discussion and the derivation of the mass transport equation for an amperometric oxidase enzyme electrode. Martens and Hall subsequently [12] extended the analysis to consider a more detailed study of mediated amperometric sensors. The model presented in this article further extends and develops a model reported by Parker and Schwartz [26] for a potentiometric sensor.

The assumptions underpinning the mathematical model developed in this paper include the following. Steady-state diffusion of substrate and mediator in the matrix obeys the Fick diffusion equation. The enzyme matrix is homogeneous, and the reaction is isothermal. Finally, it is assumed that the Michaelis–Menten kinetic parameters for the immobilised glucose oxidase are the same as those for the soluble enzyme.

2.2. Schematic Representation

The model describes the mechanism by which an oxidase enzyme moves from the fully oxidised state to the fully reduced form and back to an oxidised state in a catalytic cycle, which may be written as follows:

$$\begin{array}{cc}E+S\stackrel{\stackrel{k_{-1}}{\leftarrow }}{\underset{k_1}{\to }}\mathrm{ES}\stackrel{\hspace{1em}{k}_2\hspace{1em}}{\to }{E}_{\mathrm{red}}+P& \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{E}_{\mathrm{red}}+O_2\stackrel{\hspace{1em}{k}_3\hspace{1em}}{\to }{E}_{\mathrm{OX}}+H_2{O}_2\end{array}$$

where $k_1$ and $k_{-1}$ is the rate constant for the forward and backward direction, respectively. The all-time total enzyme concentration is $\left[E_T]=[E_{\mathrm{OX}}]+[\mathrm{ES}]+[E_{\mathrm{red}}\right]$ where $\left[E_{\mathrm{OX}}\right]$, $\left[\mathrm{ES}\right]$ and $\left[E_{\mathrm{red}}\right]$ are the oxidased, substrate, and reduced mediator enzyme concentrations, respectively. The material balance of oxygen and substrate within the thickness of the matrix may be written as [9] follows:

$$D_O\frac{d^2[O_2]}{d{y}^2}=k_3\left[E_{\mathrm{red}}\right]\left[O_2\right]=\frac{k_2{k}_1}{k_{-1}+k_2}\left[E_{\mathrm{OX}}\right]\left[S\right]=\frac{k_2\left[E_T\right]}{\frac{{\beta }_S}{\left[S\right]}+\frac{{\beta }_O}{\left[O_2\right]}+1}$$

(1)

and

$$D_S\frac{d^2\left[S\right]}{\mathrm{d}{y}^2}=k_1\left[E_O\right]\left[S\right]-k_{-1}\left[\mathrm{ES}\right]=\left(k_1-\frac{k_{-1}{k}_1}{k_{-1}+k_2}\right)\left[E_{\mathrm{OX}}\right]\left[S\right]=\frac{k_2\left[E_T\right]}{\frac{{\beta }_S}{\left[S\right]}+\frac{{\beta }_O}{\left[O_2\right]}+1}$$

(2)

where $D_O$ and $D_S$ are the oxygen and substrate diffusion coefficients within the enzyme layer, respectively. $[O_2]$ and $\left[S\right]$ are the concentration of the mediator (oxygen) and substrate at any point in the enzyme layer. Following the nomenclature [27], we can write ${\beta }_S=\left(k_{-1}+k_2\right)/k_1$ and ${\beta }_O=k_2/k_3$. The following equation is obtained from Equations (1) and (2).

$$D_O\frac{d^2[O_2]}{d{y}^2}=D_S\frac{d^2\left[S\right]}{d{y}^2}$$

(3)

Boundary Conditions

At the polymer/solution interface, $y=d$:

$$\left[O_2]=[O_2{]}_b=K_O\right[O_2{]}_{\infty }, \left[S\right]=\left[S{]}_b=K_S\right[S{]}_{\infty }$$

(4)

and at the electrode, y = 0:

$$\left[O_2\right]=0,d\left[S\right]/\mathit{dy}=0$$

(5)

where ${[O_2]}_b$ and ${[S]}_b$ are the concentration of oxygen and substrate at the enzyme layer|electrode boundary, and ${[O_2]}_{\infty }$ and ${[S]}_{\infty }$ are the bulk solution concentrations. The equivalent subscripts have the same meanings for the subtract concentration.

2.3. Normalised Form

The process of non-dimensionalising Equations (1) and (2) and the boundary conditions that go with them reduce the number of effective parameters, resulting in the following equations.

$${\varphi }_O^2=\left(\frac{d^2{k}_2\left[E_T\right]}{D_O{[O_2]}_b}\right), {\varphi }_S^2=\left(\frac{d^2{k}_2\left[E_T\right]}{D_S{[S]}_b}\right)$$

(6)

where ${\varphi }_O^2$ and ${\varphi }_S^2$ are the Thiele modulus for the oxygen and substrate which governs reaction/diffusion. $B_O\left(={[O_2]}_b/{\beta }_O\right)$, $B_S\left(={[S]}_b/{\beta }_S\right)$ is the normalised surface concentration of oxygen and substrate, respectively. $F_O=\left[O_2\right]/{[O_2]}_b$, $F_S\left(=\left[S\right]/{[S]}_b\right)$ is the normalised oxygen concentration, substrate concentration in the matrix, respectively and $X\left(=y/d\right)$ is the normalised distance. Considering ${\varphi }_O={\varphi }_S=\varphi$, then the normalised Equations (1) and (2) are given by:

$$\frac{d^2{F}_O\left(X\right)}{d{X}^2}={\varphi }^2\left(\frac{B_O{B}_S{F}_O\left(X\right)F_S\left(X\right)}{B_O{F}_O\left(X\right)+B_S{F}_S\left(X\right)+B_O{B}_S{F}_O\left(X\right)F_S\left(X\right)}\right)$$

(7)

$$\frac{d^2{F}_S\left(X\right)}{d{X}^2}={\varphi }^2\left(\frac{B_O{B}_S{F}_O\left(X\right)F_S\left(X\right)}{B_O{F}_O\left(X\right)+B_S{F}_S\left(X\right)+B_O{B}_S{F}_O\left(X\right)F_S\left(X\right)}\right)$$

(8)

The boundary conditions become,

$$F_O\left(X\right)=1,F_S\left(X\right)=1 \mathrm{when} X=1$$

(9)

$$F_O\left(X\right)=0,d{F}_S\left(X\right)/dX=0 \mathrm{when} X=0$$

(10)

From the above equations, the following relation is obtained

$$\frac{d^2{F}_O\left(X\right)}{d{X}^2}=\frac{d^2{F}_S\left(X\right)}{d{X}^2}={\varphi }^2\left(\frac{B_O{B}_S{F}_O\left(X\right)F_S\left(X\right)}{B_O{F}_O\left(X\right)+B_S{F}_S\left(X\right)+B_O{B}_S{F}_O\left(X\right)F_S\left(X\right)}\right).$$

(11)

From Equation (14), we get,

$$\frac{d^2{F}_O\left(X\right)}{d{X}^2}=\frac{d^2{F}_S\left(X\right)}{d{X}^2}$$

(12)

Solving Equation (12) using boundary conditions, we can readily show that the relation between the concentrations is given as follows:

$$F_O\left(X\right)=F_s\left(X\right)-F_s\left(0\right)\left(1-\mathrm{X}\right)$$

(13)

3. Analytical Expression of Concentrations of Mediator and Substrate under Steady-State Condition Using the AGM

Akbari–Ganji’s method [28] is used to solve the boundary value problem and its associated boundary conditions represented by the Equations (7)–(10), which have a minimum number of unknowns. It is an appropriate and simple method to find the solution of the non-linear differential equations [29]. It is a particular case of the exponential function method and homotopy perturbation method, which is proposed by He [30]. Using this method, the general analytical expression for normalised concentrations can be obtained (Appendix A) as follows:

$$F_S\left(X\right)\approx \frac{cosh(bX)}{cosh(b)}$$

(14)

$$F_O\left(X\right)\approx \frac{cosh(bX)-\left(1-X\right)}{cosh(b)}$$

(15)

$$\mathrm{where} b=\varphi \sqrt{\frac{B_O{B}_S}{B_O+B_S+B_O{B}_S}}$$

(16)

The flux $J$ at the electrode surface is given by,

$$J={\left(\frac{d{F}_O}{dX}\right)}_{X=0}=\frac{1}{cosh(b)}$$

(17)

4. Discussion

For all parameters $\varphi , B_O \mathrm{and} B_S$, Equations (14) and (15) describe the closed and simple approximate analytical expressions of the normalised concentrations of the mediator (oxygen) and substrate. The closed and uncomplicated analytical expression of fluxes is Equation (17). The thickness of the enzyme layer or the amount of enzyme immobilised in the matrix affects the parameter Thiele modulus ${\varphi }^2$. This parameter describes the relative impact of diffusion and reaction in the enzyme layer. When ${\varphi }^2$ is low, the primary resistance is kinetics; the overall absorption of mediator and substrate in the enzyme matrix is kinetically controlled. Therefore, the substrate concentration profile across the membrane is nearly uniform under these conditions. The total amount of active enzyme determines the overall kinetics. When the Thiele module ${\varphi }^2$ is large, diffusion restrictions are the essential factor.

4.1. Previous Work

Recently, Loghambal et al. [31] obtained the analytical expression of concentrations of the mediator (oxygen) and substrate using the homotopy perturbation method [32,33,34,35] as follows:

$$F_O\left(X\right)=w_2\left[\begin{array}{c}2B_S^2\left[ln(B_S\right)-ln(w_{1}X+B_S)]\\ +\left\{\begin{array}{c}{w}_2{}^{-1}+2w_1{B}_S\left[ln(w_1+B_S\right)-ln(w_{1}X+B_S)]\\ +2B_S^2\left[ln(w_1+B_S\right)-ln(B_S)]-w_1^2\end{array}\right\}X+w_1^2{X}^2\end{array}\right]$$

(18)

$$F_S\left(X\right)=1-w_2\left[\begin{array}{c}{w}_1^2+2w_1{B}_S\left[1-ln(w_1+B_S\right)+ln(B_S)]\\ +2B_S^2\left[ln(w_{1}X+B_S\right)-ln(w_1+B_S)]\\ -2w_1{B}_S\left[1-ln(w_{1}X+B_S\right)+ln(B_S)]X-w_1^2{X}^2\end{array}\right]$$

(19)

$$\mathrm{where} w_1=B_O\left(1+B_S\right), w_2=\frac{{\varphi }^2{B}_S}{2B_O^2{(1+B_S)}^3}$$

(20)

The normalised flux is,

$$J=1-w_2\left[w_1\left(w_1+2B_S\right)+2B_S\left(w_1+B_S\right)\left(ln{B}_S-ln(w_1+B_S\right)\right]$$

(21)

Our result Equations (14)–(17) is very effective and easily simple compared to previous results.

4.2. Numerical Simulation

The function pdex4 in SCILAB software which is a function of solving the initial-boundary value problems for parabolic-elliptic partial differential equations, is used to solve the Equations (7) and (8). Upon comparison in Figure 1 and Figure 2, it is evident that both the results give satisfactory agreement.

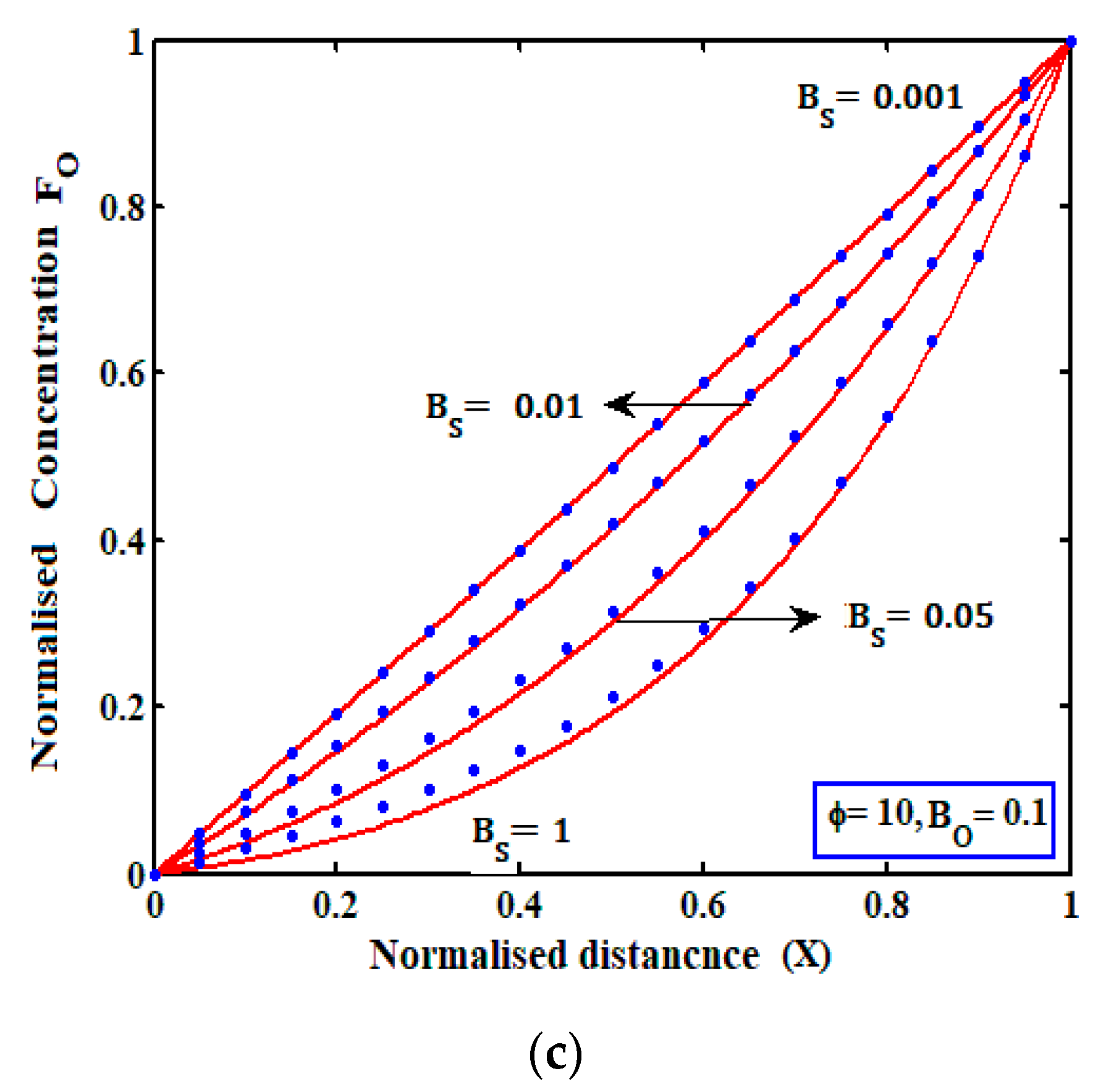
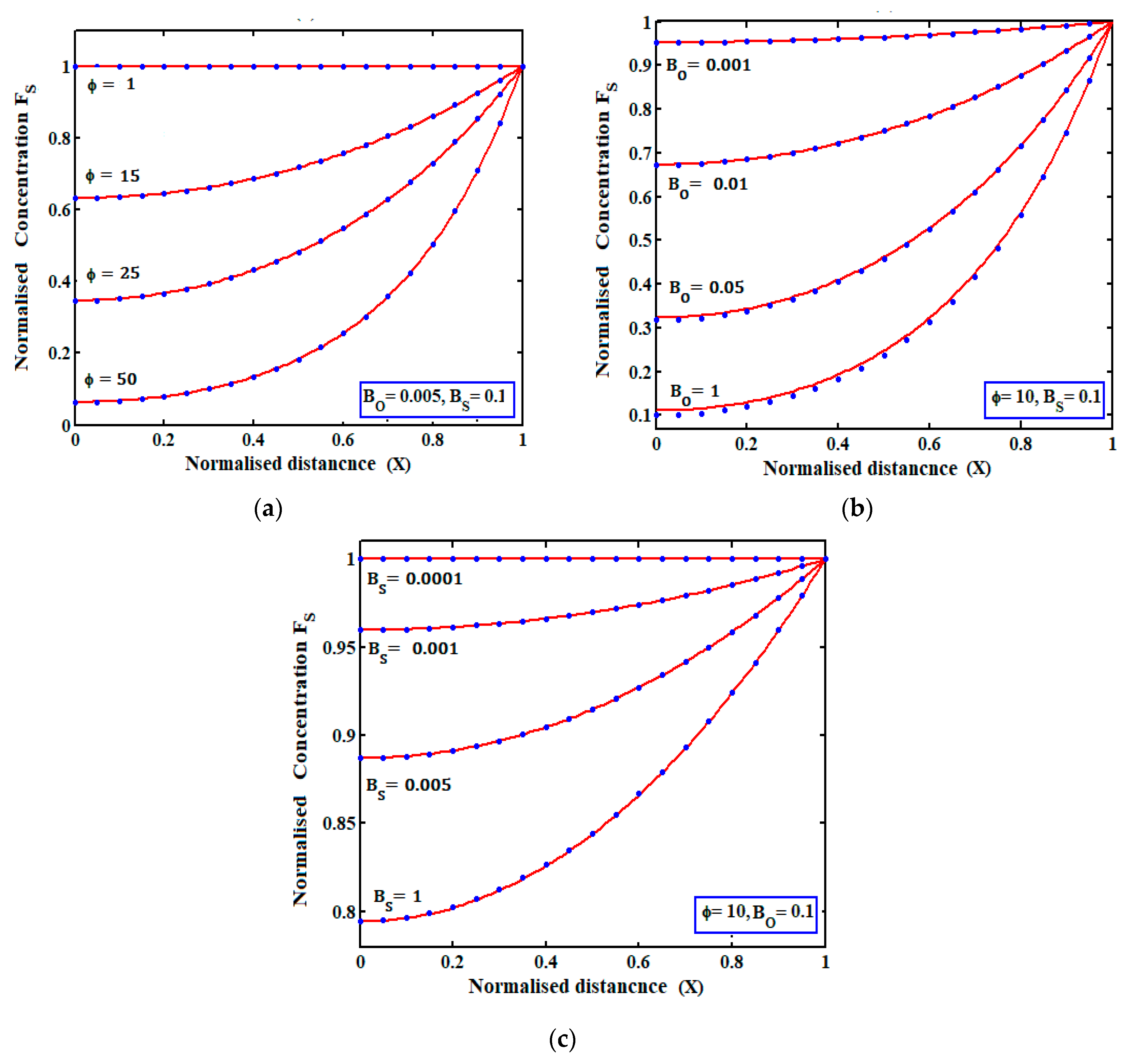
4.2.1. Concentrations of Mediator $F_O$ and Substrate $F_{\mathrm{S}}$

The normalised concentration profiles of oxidised mediator $F_O$ for various values parameters $\varphi , B_O \mathrm{and} B_S$ are shown in Figure 1. As oxygen is utilised in the enzyme reaction, the profile deviates more from the linear profile for rising values of all the parameters. The concentration of the mediator increases as all the parameters decrease, according to these figures. Equation (15) is used to plot normalised concentration profiles of substrate $F_S$ for various values of $\varphi$, $B_O$ and $B_S$ in Figure 2.

Figure 1 and Figure 2 represent the concentration profiles for the oxidised mediator and substrate for various values of $\varphi$. As the oxidised mediator flows inwards from the electrode interface, it is consumed by the enzyme process. The slight variation in substrate concentration across the matrix implies that the oxidised mediator is limited under these conditions rather than the substrate itself.

Additionally, from Figure 2, it is inferred that the small change in $\varphi$ produces significant change only in the concentration of substrate $F_S$. The concentration of mediator $F_O$ is linear where $\varphi \le 1 \mathrm{and} B_O \mathrm{and} B_S\le 0.001$. For the small values of all the parameters, it is clear from these figures that the concentration value is very near to the electrode surface ($F_S\approx 1$).

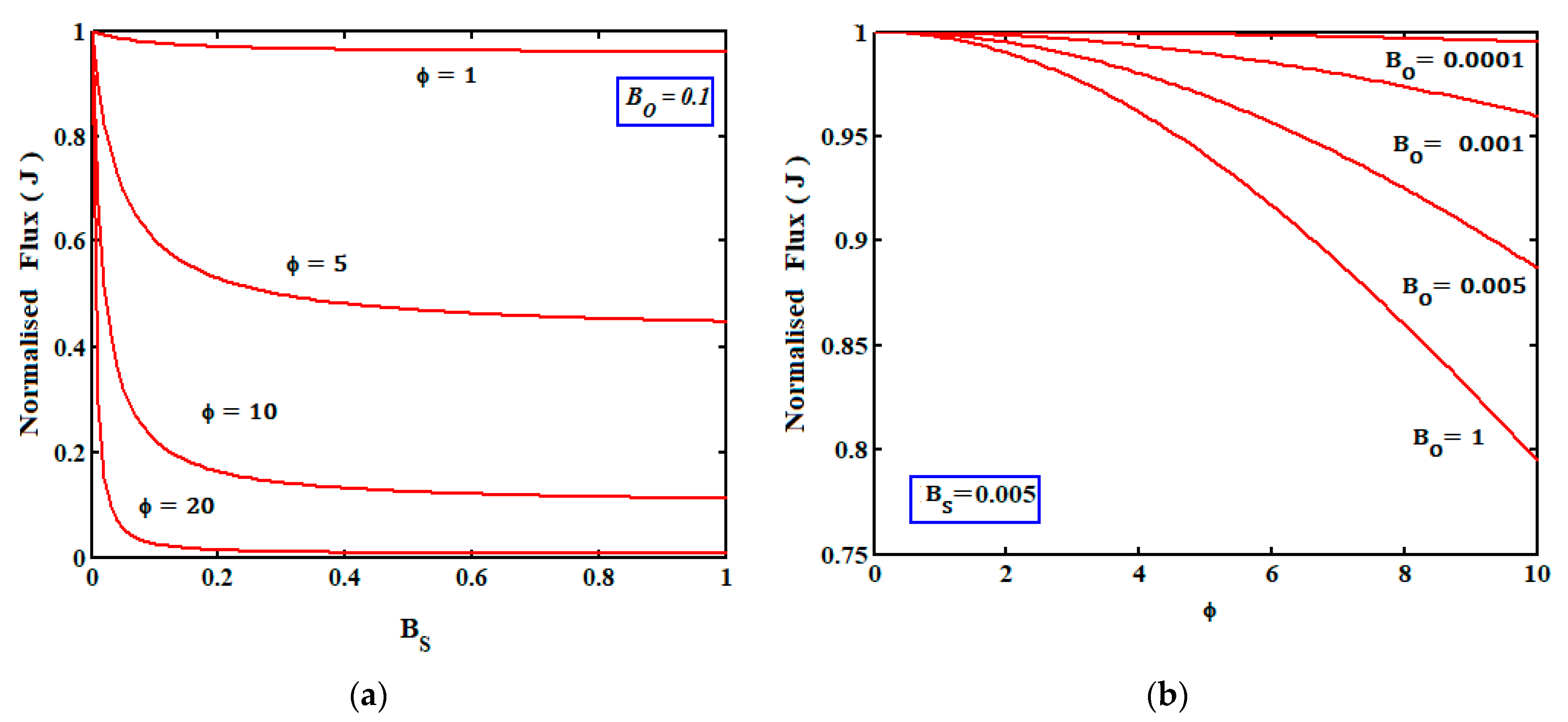
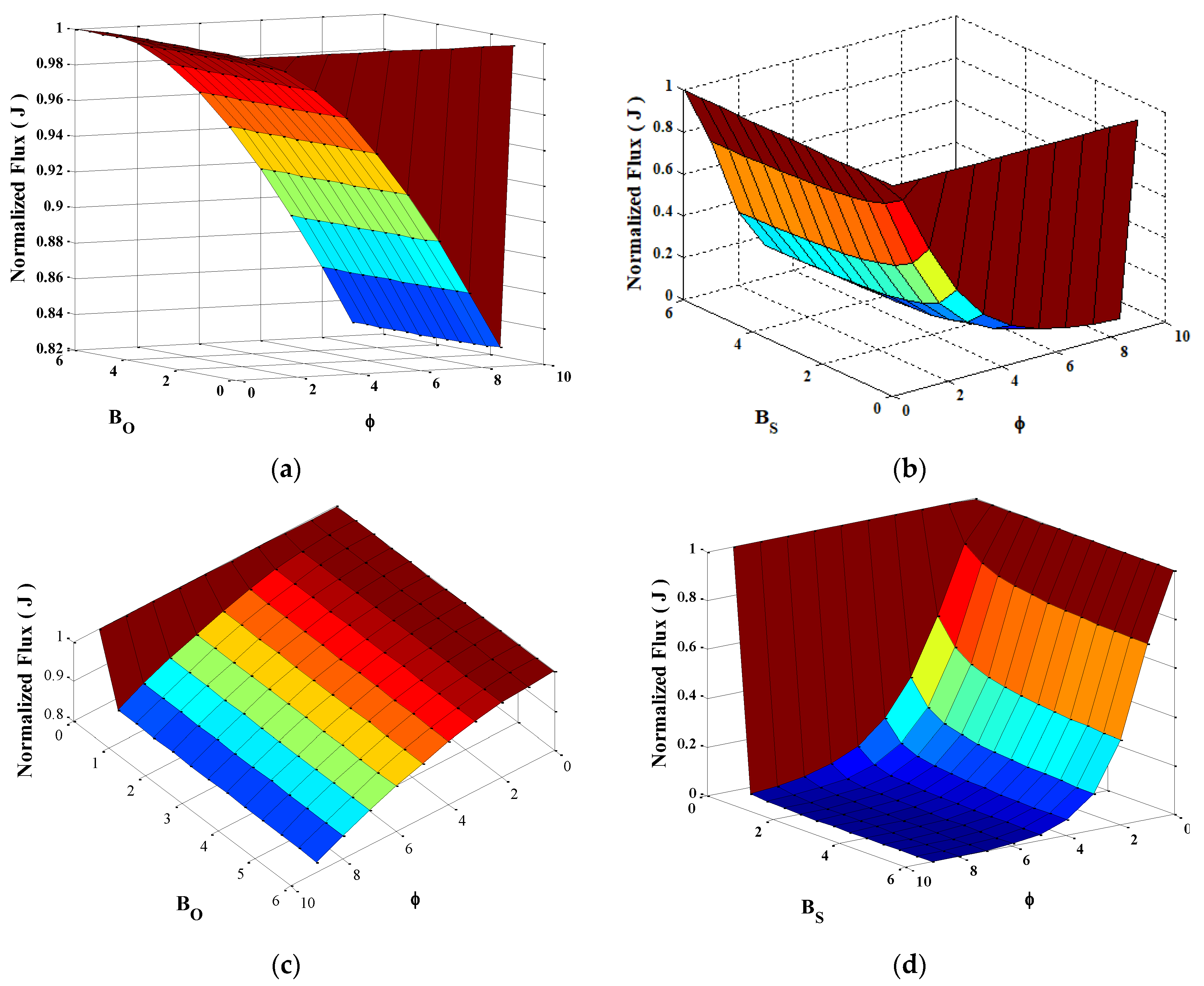
4.2.2. Effect of the Kinetic Parameters on the Current J

The current, related to the flux of electroactive material, is the most important parameter in an amperometric biosensor. Equation (17) is a simple closed-form expression of the flux. The variance of normalised flux response for various parameter values is depicted in Figure 3. It is evident from these graphs that as all parameters are increased, the flux value declines. In addition, when the thickness of the electrode decreases, the flux increases in value.

The three-dimensional steady-state flux response J is depicted in Figure 4. When the thickness of the membrane layer is less than or equal to one $\left(\varphi \le 1\right)$, the flux reaches its steady-state value. These figures confirm the observations in Figure 3.

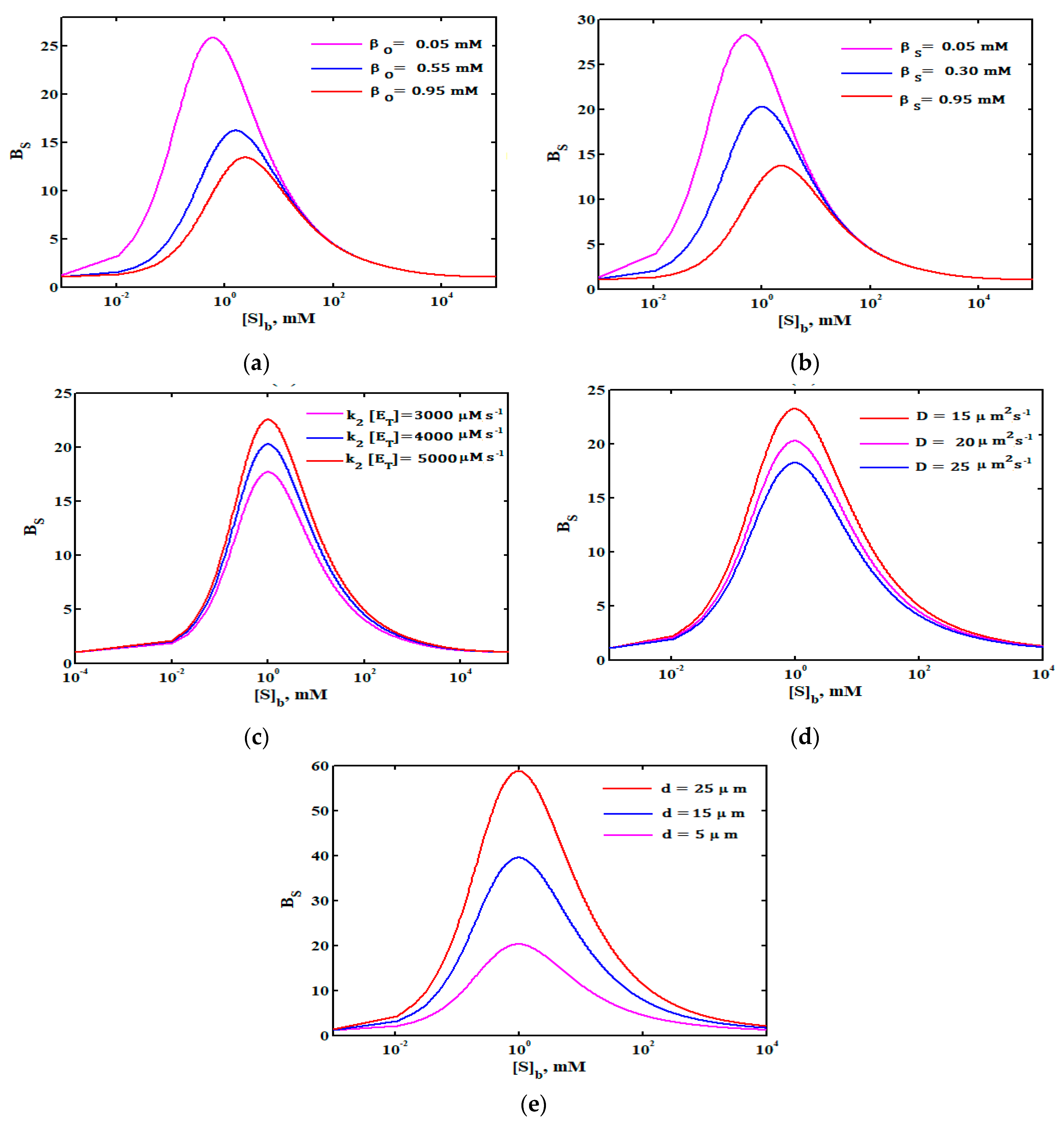
4.2.3. Sensitivity of Biosensor

One of the most important characteristics of biosensors is sensitivity. The sensitivity $B_S$ of a biosensor can be expressed as a gradient of the maximal biosensor current density concerning the substrate concentration ${[S]}_b$ [36]. The dimensionless sensitivity for the substrate concentration ${[S]}_b$ is given by

$$B_S\left({[S]}_b\right)=\frac{\partial I\left({[S]}_b\right)}{\partial {[S]}_b}\frac{{[S]}_b}{I\left({[S]}_b\right)}=\left|1+\frac{1}{2}b tanh\left(b\right)\frac{{[S]}_b}{\left({[S]}_b+{\beta }_O+{\beta }_S\right)} \right|$$

(22)

where $B_S$ stands for the dimensionless sensitivity of the amperometric biosensor and $I\left({[S]}_b\right)$ is the density of the steady-state biosensor current calculated at the substrate concentration ${[S]}_b$.

The biosensor sensitivity for different values of the parameter are displayed in Figure 5a–e. It is noticed that a decrease in ${\beta }_o,{\beta }_s,D$ and increase in d and $k_2\left[E_T\right]$ parameter leads to an increase in sensitivity up to the maximum value and then decreases gradually towards the bulk. When ${[S]}_b=1 \mathrm{mM},$ the sensitivity reaches its maximum value. Also, the sensitivity is minimum in the interval ${10}^2 \mathrm{mM}<{[S]}_b<{10}^{-2} \mathrm{mM}$ for all values of other parameters. Due to the substrate inhibition, the sensitivity differs notably (or sharp decrease or increases) only at intermediate concentrations of the substrate ${10}^{-2} \mathrm{mM}<{[S]}_b<{10}^2.$

5. Conclusions

A theoretical model for two substrates in the presence of oxygen has been described and applied to simulate a mediated enzyme electrode. This work analysed non-linear, coupled reaction-diffusion equations in a steady state. Under steady-state conditions, the AGM method approximates the concentrations and flux in an amperometric oxidase enzyme electrode with equal diffusion coefficients on a planar enzyme-membrane electrode. The primary outcome of this study is a straightforward approximation of concentration profiles and flux for small values and all values of $B_O$, $B_S$ and all values of $\varphi$. This method is a simple method for solving non-linear equations. This research method could easily be applied to find solutions for other enzymatic systems that use the homogeneous membrane media described here.