Theoretical and Numerical Analysis of Nonlinear Processes in Amperometric Enzyme Electrodes with Cyclic Substrate Conversion
Abstract
:1. Introduction
2. Mathematical Formulation of the Problem
Dimensionless Form of Problem
3. An Approximate Analytical Expression of Steady-State Concentrations Using AGM
3.1. Limiting Case: Unsaturated (First-Order) Catalytic Kinetics
3.2. Limiting Case: Saturated (Zero-Order) Catalytic Kinetics
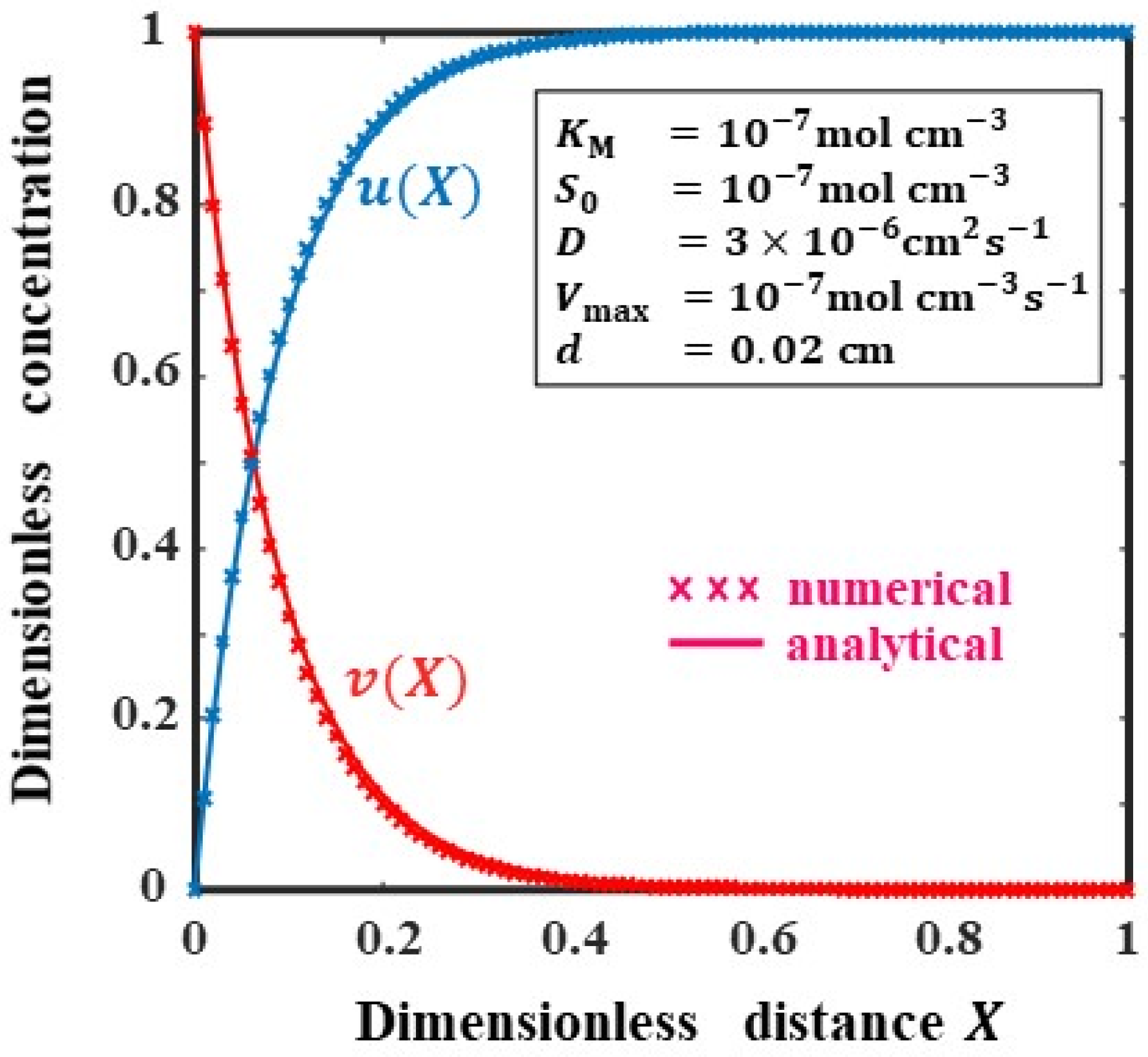
4. Validation of Analytical Results
5. Results and Discussion
5.1. Influence of Parameter on Concentration of Substrate and Product
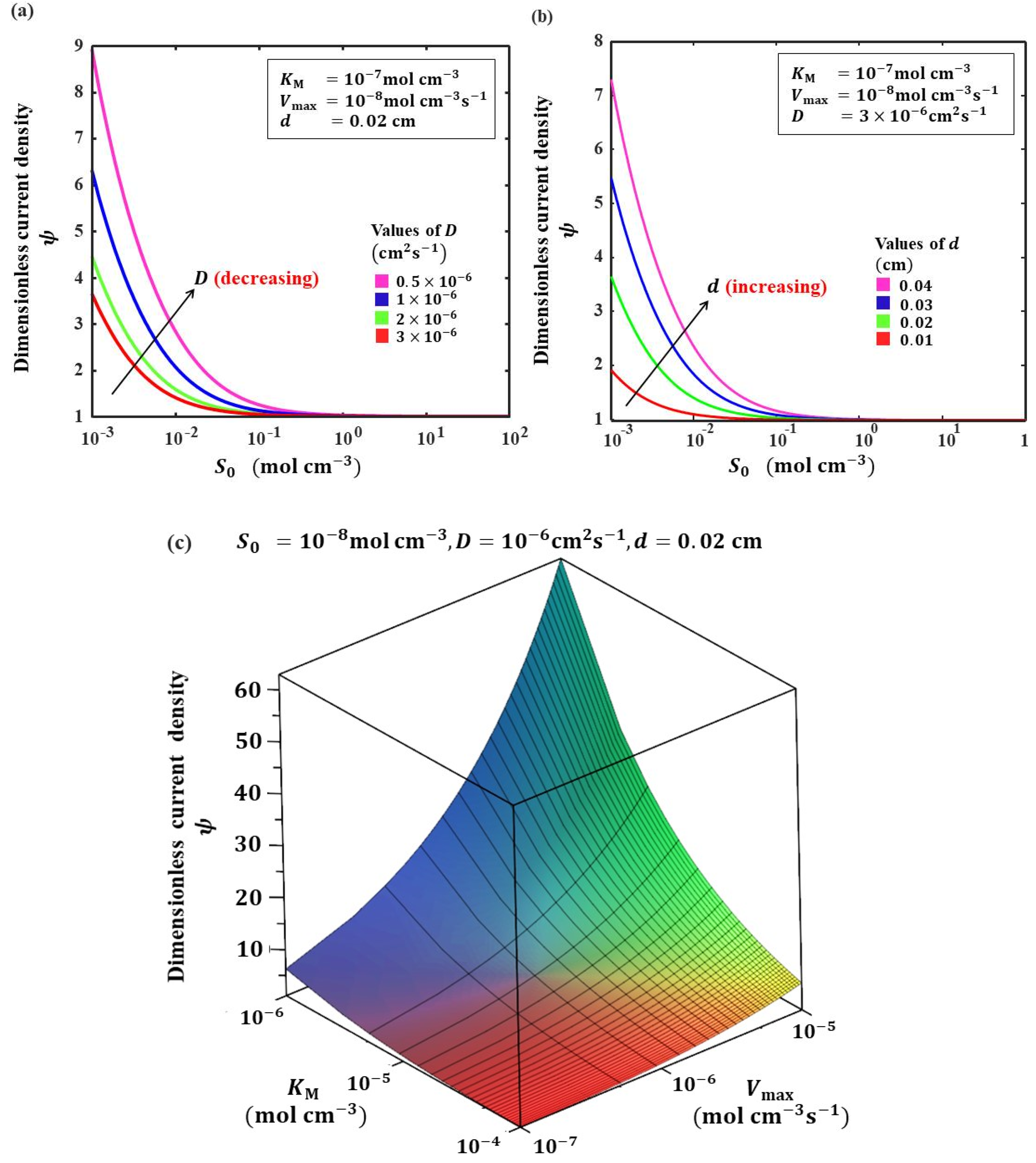
5.2. Influence of Transport and Reaction Parameters on the Current Response
5.3. Sensitivity of Biosensor

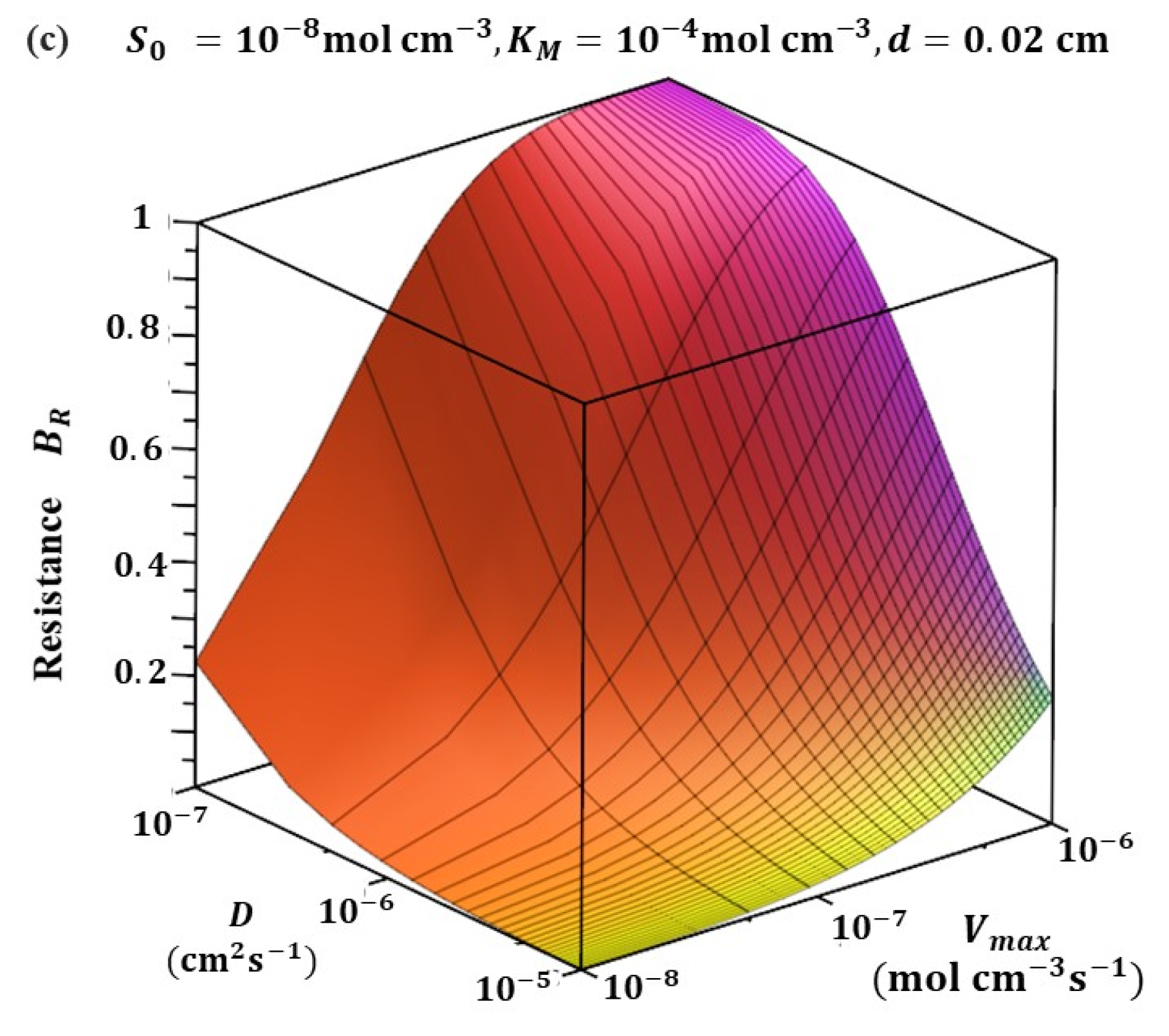
5.4. Resistance of Biosensor
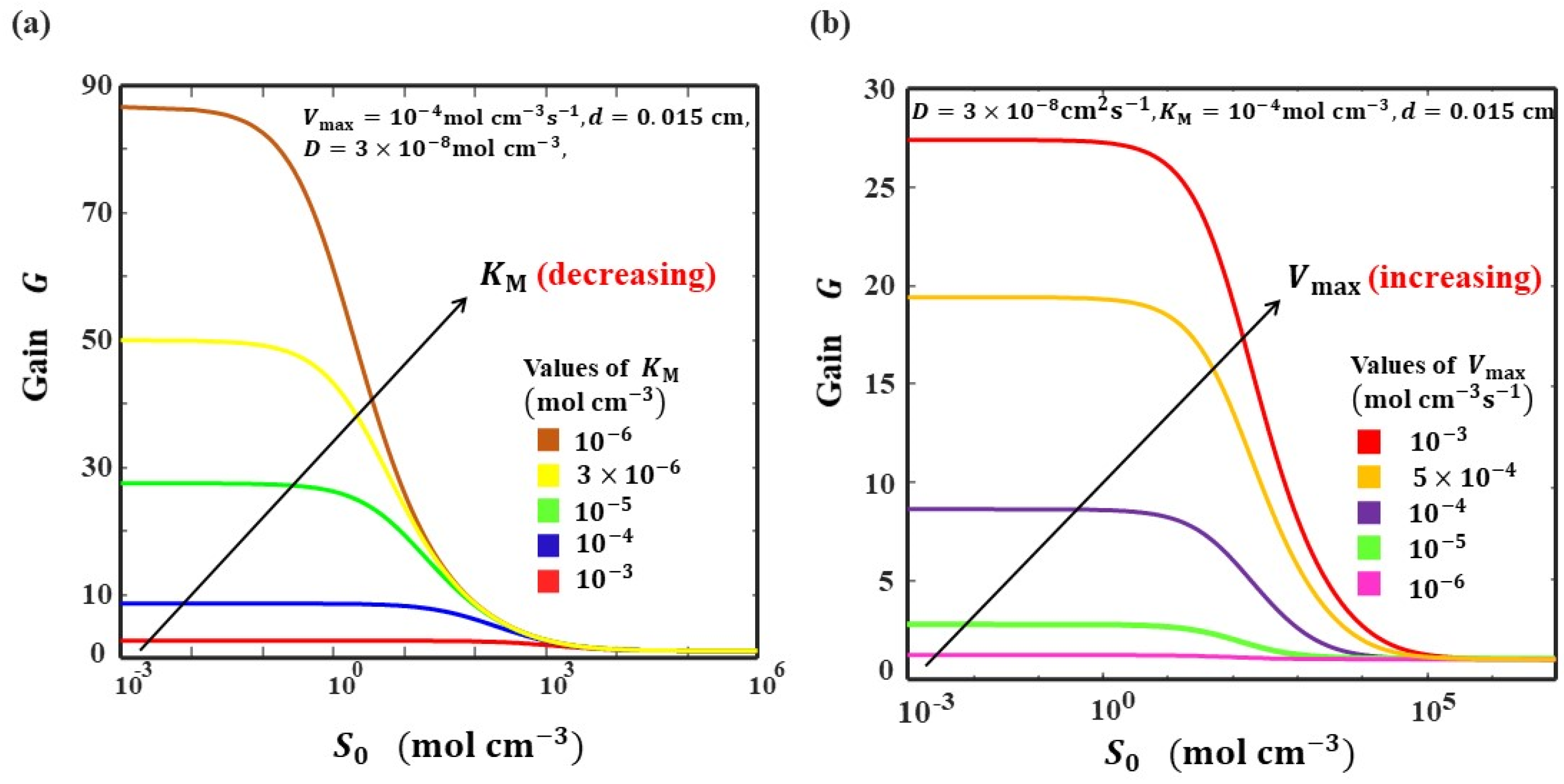
5.5. Gain of the Biosensor
6. Analysis of ‘Mixed Case’ Moving Boundary Scenario Corresponding to Varying Levels of Saturation across the Enzyme Membrane
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Notation Used
| Symbols | Description | Unit |
| Biosensor sensitivity | None | |
| Biosensor resistance | None | |
| Thickness of the enzyme membrane | ||
| Product diffusion coefficient | ||
| Substrate diffusion coefficient | ||
| Faraday’s constant | ||
| Sensitivity gain | None | |
| Current density | ||
| Michaelis constant | ||
| Number of electrons | None | |
| Concentration of product | ||
| Concentration of substrate | ||
| Bulk solution concentration of substrate | ||
| Normalised time | None | |
| Time | ||
| Normalised concentration of substrate at steady state | None | |
| Maximal enzymatic rates | ||
| Normalised concentration of product at steady state | None | |
| Normalised distance from electrode | None | |
| Moving normalised distance parameter | None | |
| Distance from electrode | ||
| Greek symbols | ||
| Saturation parameter | None | |
| Dimensionless parameter | None | |
| Damkohler number | None | |
| Normalised current density at steady state | None | |
Appendix A
Appendix B

References
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Clark, L.C.; Lyons, C. Electrode system for continuous monitoring in cardiovascular surgery. Ann. N. Y. Acad. Sci. 1962, 102, 29–45. [Google Scholar] [CrossRef]
- Turner, A.P.F.; Karube, I.; Wilson, G.S. Biosensors: Fundamentals and Applications; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Rogers, K.R. Biosensors for environmental applications. Biosens. Bioelectron 1995, 10, 533–541. [Google Scholar] [CrossRef]
- Wollenberger, U.; Lisdat, F.; Scheller, F.W. Frontiers in Biosensorics 2, Practical Applications; Birkhauser Verlag: Basel, Switzerland, 1997. [Google Scholar]
- Chaubey, A.; Malhotra, B.D. Mediated biosensors. Biosens. Bioelectron. 2002, 17, 441–456. [Google Scholar] [CrossRef]
- Blaedel, W.J.; Boguslaski, R.C. Chemical amplification in analysis: A review. Anal. Chem. 1978, 50, 1026–1032. [Google Scholar] [CrossRef]
- Fuhrmann, B.; Spohn, U. An enzymatic amplification flow injection analysis (FIA) system for the sensitive determination of phenol. Biosens. Bioelectron. 1998, 13, 895–902. [Google Scholar] [CrossRef]
- Korotcenkov, G. Chemical Sensors: Simulation and Modeling; Electrochemical Sensors; Momentum Press: New York, NY, USA, 2013; Volume 5. [Google Scholar]
- Swaminathan, R.; Devi, M.C.; Rajendran, L.; Venugopal, K. Sensitivity and resistance of amperometric biosensors in substrate inhibition processes. J. Electroanal. Chem. 2021, 895, 115527. [Google Scholar] [CrossRef]
- Rani, R.U.; Rajendran, L.; Lyons, M.E.G. Steady-state current in product inhibition kinetics in an amperometric biosensor: Adomian decomposition and Taylor series method. J. Electroanal. Chem. 2021, 886, 115103. [Google Scholar] [CrossRef]
- Devi, M.C.; Pirabaharan, P.; Rajendran, L.; Abukhaled, M. Amperometric biosensors in an uncompetitive inhibition processes: A complete theoretical and numerical analysis. React. Kinet. Mech. Catal. 2021, 133, 655–668. [Google Scholar] [CrossRef]
- Joy Salomi, R.; Vinolyn Sylvia, S.; Rajendran, L.; Lyons, M.E.G. Transient current, sensitivity and resistance of biosensors acting in a trigger mode: Theoretical study. J. Electroanal. Chem. 2021, 895, 115421. [Google Scholar] [CrossRef]
- Nirmala, K.; Manimegalai, B.; Rajendran, L. Steady-state substrate and product concentrations for non-Michaelis-Menten kinetics in an amperometric biosensor—Hyperbolic function and padéapproximants method. Int. J. Electrochem. Sci. 2020, 15, 5682–5697. [Google Scholar] [CrossRef]
- Swaminathan, R.; Narayanan, K.L.; Mohan, V.; Saranya, K.; Rajendran, L. Reaction/diffusion equation with Michaelis-Menten kinetics in microdisk biosensor: Homotopy perturbation method approach. Int. J. Electrochem. Sci. 2019, 14, 3777–3791. [Google Scholar] [CrossRef]
- Kirthiga, M.; Balamurugan, S.; Rajendran, L. Modelling of reaction-diffusion process at carbon, nanotube—Redox enzyme composite modified electrode biosensor. Chem. Phys. Lett. 2019, 715, 20–28. [Google Scholar]
- Kirthiga, O.M.; Rajendran, L. Approximate analytical solution for Non-linear Reaction diffusion equations in a mono-enzymatic biosensor involving Michaelis–Menten. J. Electroanal. Chem 2015, 751, 119–127. [Google Scholar] [CrossRef]
- Felicia Shirly, P.; Ananthaswamy, V.; Rajendran, L. Analytical expressions for an electrochemical biosensor employing the enzymes glucose oxidase & horseradish peroxidase using the homotopy perturbation method. Int. J. Sci. Eng. Res. 2014, 5, 1105–1116. [Google Scholar]
- Kulys, J. The development of new analytical systems based on biocatalysts. Anal. Lett. 1981, 14, 377–397. [Google Scholar] [CrossRef]
- Scheller, F.; Renneberg, R.; Schubert, F. Coupled enzyme reactions in enzyme electrodes using sequence, amplification, competition and anti-interference principles. In Methods in Enzymology; Academic Press: New York, NY, USA, 1988; Volume 137, pp. 29–43. [Google Scholar]
- Chulmeister, T.; Rose, J.; Scheller, F. Mathematical modelling of exponential amplification in membrane-based enzyme sensors. Biosens. Bioelectron 1997, 12, 1021–1030. [Google Scholar] [CrossRef]
- Kulys, J.J.; Sorochinski, V.V.; Vidziunaite, R.A. Transient response of bienzyme electrodes. Biosensors 1986, 2, 135–146. [Google Scholar] [CrossRef]
- Britz, D. Digital Simulation in Electrochemistry, 2nd ed.; Springer: Berlin/Heildeberg, Germany, 1988. [Google Scholar]
- Bartlett, P.N.; Pratt, K.F.E. Modelling of processes in enzyme electrodes. Biosens. Bioelectron. 1993, 8, 451–462. [Google Scholar] [CrossRef]
- Yokoyama, K.; Kayanuma, Y. Cyclic voltammetric simulation for electrochemically mediated enzyme reaction and determination of enzyme kinetic constants. Anal. Chem. 1998, 70, 3368–3376. [Google Scholar] [CrossRef]
- Baronas, R.; Kulys, J.; Ivanauskas, F. Modelling amperometric enzyme electrode with substrate cyclic conversion. Biosens. Bioelectron. 2004, 19, 915–922. [Google Scholar] [CrossRef]
- Saravanakumar, K.; Rajendran, L. Mathematical analysis of an enzyme-entrapped conducting polymer modified electrode. Appl. Math. Model 2015, 39, 7351–7363. [Google Scholar] [CrossRef]
- Rach, R.; Duan, J.S.; Wazwaz, A.M. Simulation of large deflections of a flexible cantilever beam fabricated from functionally graded materials by the Adomian decomposition method. Int. J. Dyn. Syst. Differ. Equ. 2020, 10, 287. [Google Scholar]
- Abukhaled, M. Variational iteration method for nonlinear singular two-point boundary value problems arising in human physiology. J. Math. 2013, 2013, 720134. [Google Scholar] [CrossRef] [Green Version]
- Abukhaled, M.; Khuri, S.A. A semi-analytical solution of amperometric enzymatic reactions based on Green’s functions and fixed point iterative schemes. J. Electroanal. Chem. 2017, 792, 66–71. [Google Scholar] [CrossRef]
- Abukhaled, M. Green’s function iterative approach for solving strongly nonlinear oscillators. J. Comput. Nonlinear Dyn. 2017, 12, 051021. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Salomi, R.J.; Vinolyn, S.S.; Rajendran, L. An approximate analytical solution of nonlinear equations in N-aminopiperidine synthesis: New approach of homotopy perturbation method. Turk. J. Comput. Math. Educ. 2021, 12, 595–605. [Google Scholar]
- Vinolyn Sylvia, S.; Joy Salomi, R.; Lyons, M.E.G.; Rajendran, L. Transient current of catalytic processes at chemically modified electrodes. Int. J. Electrochem. Sci. 2021, 16, 210452. [Google Scholar] [CrossRef]
- Lyons, M.E.G. Transport and kinetics in electrocatalytic thin film biosensors: Bounded diffusion with non-Michaelis-Menten reaction kinetics. J. Solid State Electrochem. 2020, 24, 2751–2761. [Google Scholar] [CrossRef]
- Akbari, M.R.; Ganji, D.D.; Majidian, A.; Ahmadi, A.R. Solving nonlinear differential equations of Vanderpol, Rayleigh and Duffing by AGM. Front. Mech. Eng. 2014, 9, 177–190. [Google Scholar] [CrossRef]
- Manimegalai, B.; Lyons, M.E.G.; Rajendran, L. A kinetic model for amperometricimmobilized enzymes at planar, cylindrical and spherical electrodes: The AkbariGanji method. J. Electroanal. Chem. 2021, 880, 114921. [Google Scholar] [CrossRef]
- Lilly Clarance Mary, M.; Chitra Devi, M.; Meena, A.; Rajendran, L.; Abukhaled, M. A Reliable Taylor series solution to the nonlinear reaction-diffusion model representing the steady-state behaviour of a cationic glucose-sensitive membrane. J. Math. Comput. Sci. 2021, 11, 8354–8381. [Google Scholar]
- Vinolyn Sylvia, S.; Joy Salomi, R.; Rajendran, L.; Abukhaled, M. Solving nonlinear reaction—diffusion problem in electrostatic interaction with reaction-generated pH change on the kinetics of immobilized enzyme systems using Taylor series method. J. Math. Chem. 2021, 59, 1332–1347. [Google Scholar] [CrossRef]
- Joy Salomi, R.; Vinolyn Sylvia, S.; Abukhaled, M.; Rajendran, L. Kinetics of the catalytic combustion of ethanol and ethyl acetate with estimation of activation energy and rate constants: An analytical study. Curr. Catal. 2021, 10, 108–118. [Google Scholar] [CrossRef]
- Vinolyn Sylvia, S.; Joy Salomi, R.; Rajendran, L.; Abukhaled, M. Poisson–Boltzmann equation and electrostatic potential around macroions in colloidal plasmas: Taylor series approach. Solid State Technol. 2020, 63, 10090–10106. [Google Scholar]
- Baronas, R.; Kulys, J.; Ivanauskas, F. Mathematical Modeling of Biosensors: An Introduction for Chemists and Mathematicians; Springer: Dordrecht, The Netherlands; Berlin/Heidelberg, Germany; London, UK; New York, NY, USA, 2010. [Google Scholar]
- Lyons, M.E.G. Mediated electron transfer at redox active monolayers. Part 4: Kinetics of redox enzymes coupled with redox mediators. Sensors 2003, 3, 19–42. [Google Scholar] [CrossRef]
- Lyons, M.E.G.; Greer, J.C.; Fitzgerald, C.A.; Bannon, T.; Bartlett, P.N. Reaction/diffusion with Michaelis Menten kinetics in electroactive polymer films. Part 1. The steady state amperometric response. Analyst 1996, 121, 715–731. [Google Scholar] [CrossRef]

| X | Concentration of the Substrate S | Concentration of the Product P | ||||
|---|---|---|---|---|---|---|
| Numerical | AGM Equation (16) | % of Deviation | Numerical | AGM Equation (17) | % of Deviation | |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0.1 | 0.1326 | 0.1317 | 0.68 | 0.8674 | 0.8683 | 0.10 |
| 0.2 | 0.2545 | 0.2528 | 0.67 | 0.7455 | 0.7472 | 0.23 |
| 0.3 | 0.3672 | 0.3649 | 0.63 | 0.6328 | 0.6351 | 0.36 |
| 0.4 | 0.4719 | 0.4693 | 0.55 | 0.5281 | 0.5307 | 0.49 |
| 0.5 | 0.5699 | 0.5672 | 0.47 | 0.4301 | 0.4328 | 0.63 |
| 0.6 | 0.6624 | 0.6599 | 0.38 | 0.3376 | 0.3401 | 0.74 |
| 0.7 | 0.7506 | 0.7485 | 0.28 | 0.2494 | 0.2515 | 0.84 |
| 0.8 | 0.8355 | 0.8340 | 0.18 | 0.1645 | 0.1660 | 0.91 |
| 0.9 | 0.9183 | 0.9175 | 0.09 | 0.0817 | 0.0825 | 0.98 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Average deviation | 0.36 | Average deviation | 0.02 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sylvia, V.; Salomi, R.J.; Rajendran, L.; Lyons, M.E.G. Theoretical and Numerical Analysis of Nonlinear Processes in Amperometric Enzyme Electrodes with Cyclic Substrate Conversion. Electrochem 2022, 3, 70-88. https://doi.org/10.3390/electrochem3010005
Sylvia V, Salomi RJ, Rajendran L, Lyons MEG. Theoretical and Numerical Analysis of Nonlinear Processes in Amperometric Enzyme Electrodes with Cyclic Substrate Conversion. Electrochem. 2022; 3(1):70-88. https://doi.org/10.3390/electrochem3010005
Chicago/Turabian StyleSylvia, Vinolyn, Rajendran Joy Salomi, Lakshmanan Rajendran, and Michael E. G. Lyons. 2022. "Theoretical and Numerical Analysis of Nonlinear Processes in Amperometric Enzyme Electrodes with Cyclic Substrate Conversion" Electrochem 3, no. 1: 70-88. https://doi.org/10.3390/electrochem3010005
APA StyleSylvia, V., Salomi, R. J., Rajendran, L., & Lyons, M. E. G. (2022). Theoretical and Numerical Analysis of Nonlinear Processes in Amperometric Enzyme Electrodes with Cyclic Substrate Conversion. Electrochem, 3(1), 70-88. https://doi.org/10.3390/electrochem3010005







