Effective Young’s Modulus of Complex Three Dimensional Multilayered Ti/Au Micro-Cantilevers Fabricated by Electrodeposition and the Temperature Dependency
Abstract
:1. Introduction
2. Experimental
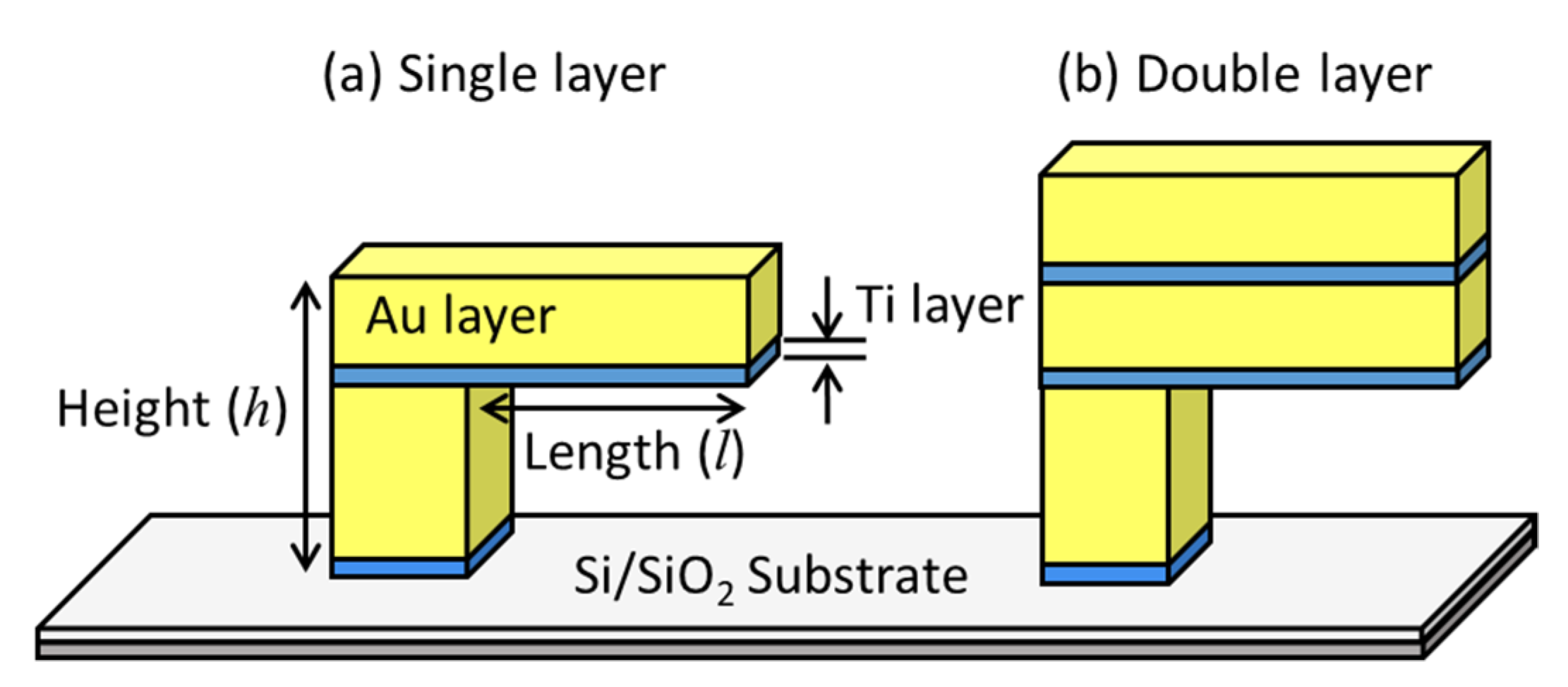
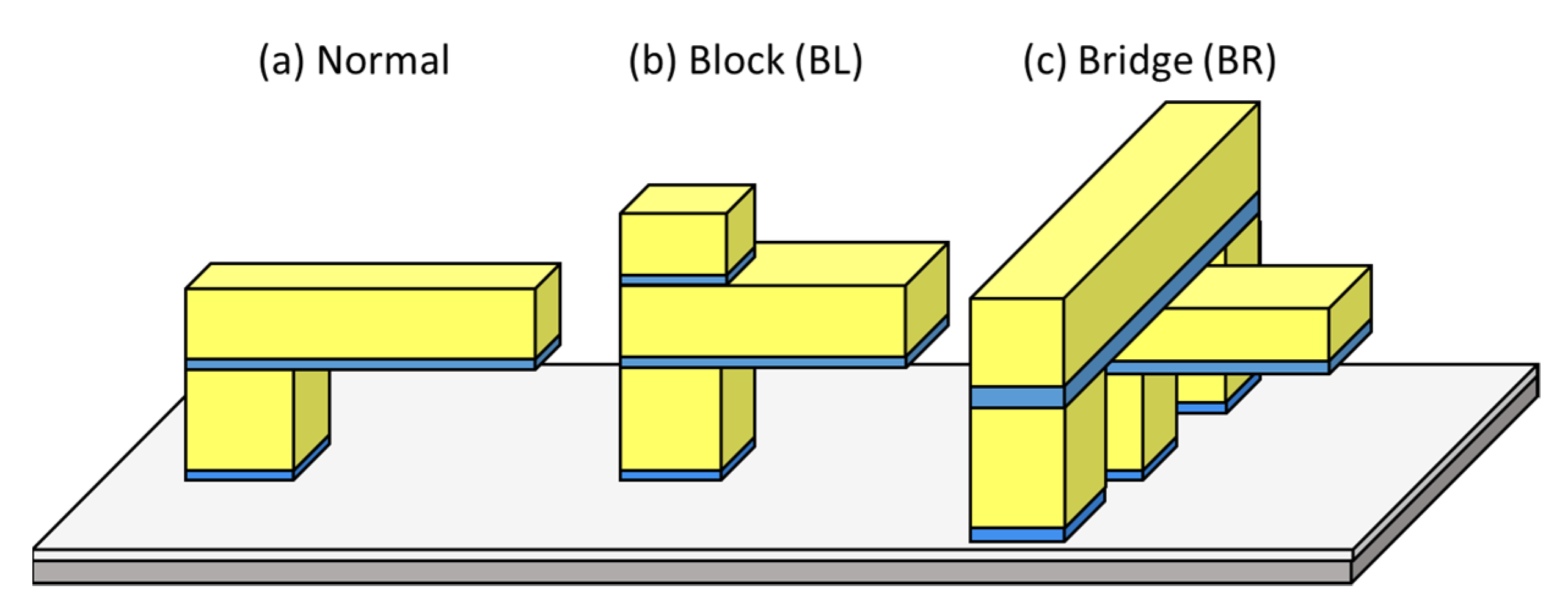
2.1. Structure Design and Fabrication Process of the Ti/Au Multilayered Micro-Cantilever
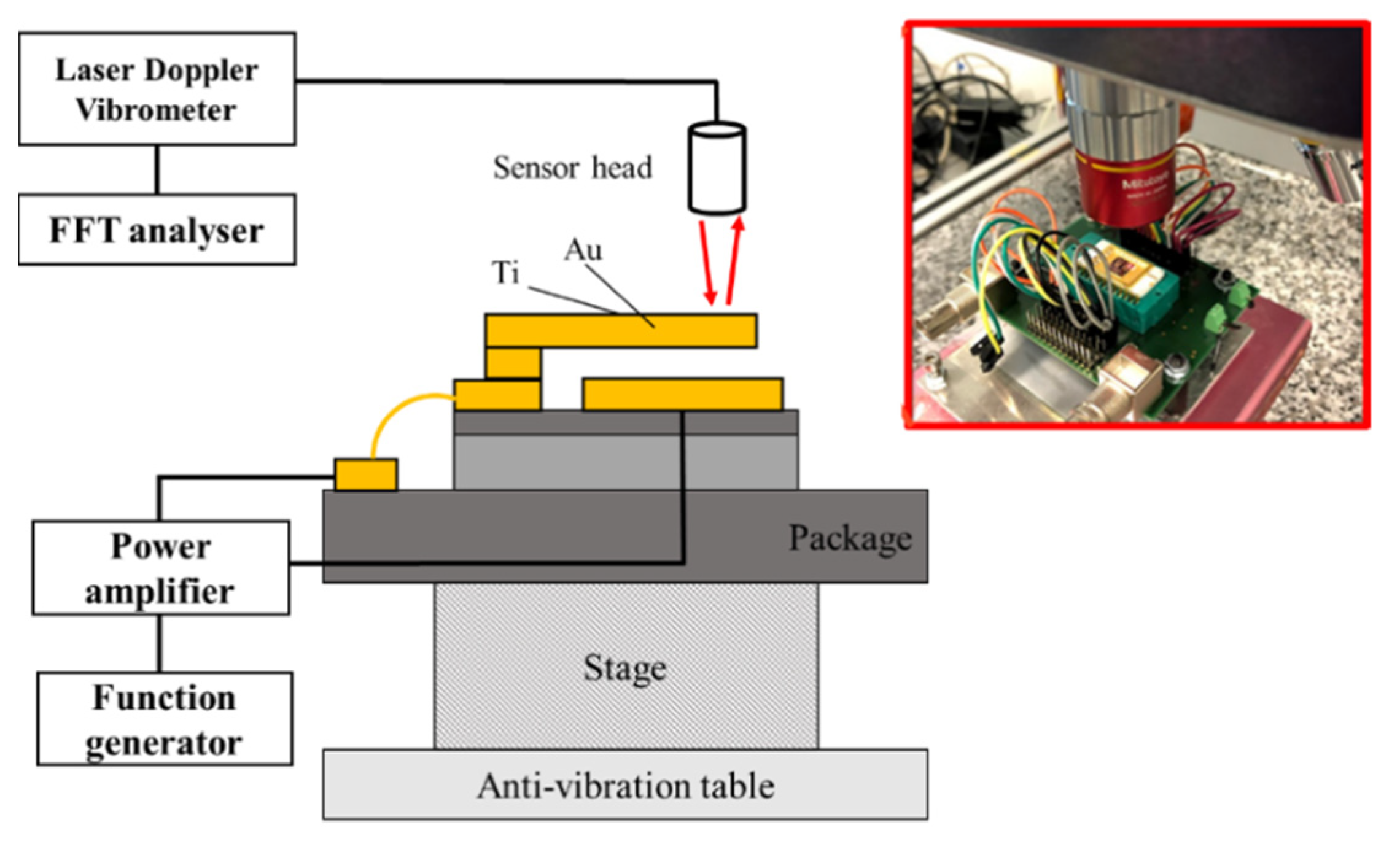
2.2. Temperature Dependency Test
2.3. Effective Young’s Modulus by Resonance Frequency Method
2.4. FEM Simulation of the Resonance Frequency
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weiss, A.; Herman, T.; Plotnik, M.; Brozgol, M.; Maidan, M.; Giladi, N.; Gurevich, T.; Hausdorff, J.M. Can an accelerometer enhance the utility of the timed up & go test when evaluating patients with Parkinson’s disease? Med. Eng. Phys. 2010, 32, 119–125. [Google Scholar]
- Yamane, D.; Konishi, T.; Matsushima, T.; Machida, K.; Toshiyoshi, H.; Masu, K. Design of sub-1g microelectromechanical systems accelerometers. Appl. Phys. Lett. 2014, 104, 074102. [Google Scholar] [CrossRef]
- Masu, K.; Machida, K.; Yamane, D.; Ito, H.; Ishihara, N.; Chang, T.F.M.; Sone, M.; Shigeyama, R.; Ogata, T.; Miyake, Y. CMOS-MEMS based microgravity sensor and its application. ECS Trans. 2020, 97, 91–108. [Google Scholar] [CrossRef]
- Koga, T.; Ichikawa, T.; Tanaka, N.; Ogata, T.; Ora, H.; Yamane, D.; Ishihara, N.; Ito, H.; Sone, M.; Machida, K.; et al. High-sensitivity inertial sensor module to measure hidden micro muscular sounds. In Proceedings of the 2019 IEEE Biomedical Circuits and Systems Conference (BioCAS), Nara, Japan, 17–19 October 2019; pp. 1–4. [Google Scholar]
- Niinomi, M. Metals for Biomedical Devices, 2nd ed.; Woodhead Publishing: Duxford, UK, 2019. [Google Scholar]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 75th ed.; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Chen, C.Y.; Yoshiba, M.; Nagoshi, T.; Chang, T.F.M.; Yamane, D.; Machida, K.; Masu, K.; Sone, M. Pulse electroplating of ultra-fine grained Au films with high compressive strength. Electrochem. Commun. 2016, 67, 51–54. [Google Scholar] [CrossRef] [Green Version]
- Tang, H.C.; Chen, C.Y.; Yoshiba, M.; Nagoshi, T.; Chang, T.F.M.; Yamane, D.; Machida, K.; Masu, K.; Sone, M. Enhancement of mechanical strength in Au films electroplated with supercritical carbon dioxide. Electrochem. Commun. 2016, 72, 126–130. [Google Scholar] [CrossRef] [Green Version]
- Tang, H.C.; Chen, C.Y.; Chang, T.F.M.; Nagoshi, T.; Yamane, D.; Konishi, T.D.; Machida, K.; Masu, K.; Sone, M. Au-Cu alloys prepared by pulse electrodeposition toward applications as movable micro-components in electronic devices. J. Electrochem. Soc. 2018, 165, D58–D63. [Google Scholar] [CrossRef]
- Wang, C.; Bhuiyan, M.E.H.; Moreno, S.; Minary-Jolandan, M. Direct-write printing copper-nickel (Cu/Ni) alloy with controlled composition from a single electrolyte using co-electrodeposition. ACS Appl. Mater. Interfaces 2020, 12, 18683–18691. [Google Scholar] [CrossRef]
- Bhuiyan, M.E.H.; Behroozfar, A.; Daryadel, S.; Moreno, S.; Morsali, S.; Minary-Jolandan, M. A hybrid process for printing pure and high conductivity nanocrystalline copper and nickel on flexible polymeric substrates. Sci. Rep. 2019, 9, 19032. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, H.C.; Chang, T.F.M.; Chai, Y.W.; Chen, C.Y.; Nagoshi, T.; Yamane, D.; Ito, H.; Machida, K.; Masu, K.; Sone, M. Nanoscale hierarchical structure of twins in nanograins embedded with twins and the strengthening Effect. Metals 2019, 9, 987. [Google Scholar] [CrossRef] [Green Version]
- Machida, K.; Yamane, D.; Konishi, T.; Iida, I.; Ishihara, N.; Chang, T.F.M.; Sone, M.; Ito, H.; Masu, K. MEMS Accelerometer Fabricated by Gold Multi-Layer Metal Technology. ECS Trans. 2019, 92, 169–184. [Google Scholar] [CrossRef]
- Tachibana, K.; Chang, T.F.M.; Chen, C.Y.; Yamane, K.D.; Konishi, T.; Ito, H.; Machida, K.; Masu, K.; Sone, M. Long-term structure stability of Ti/Au layered micro-cantilever evaluated by vibration test. Microelectron. Eng. 2019, 207, 33–36. [Google Scholar] [CrossRef]
- Teranishi, M.; Chen, C.Y.; Chang, T.F.M.; Konishi, T.; Yamane, D.; Machida, K.; Masu, K.; Sone, M. Enhancement in structure stability of gold micro-cantilever by constrained fixed-end in MEMS devices. Microelectron. Eng. 2018, 187–188, 105–109. [Google Scholar] [CrossRef]
- Gere, J.M.; Timoshenko, S.P. Mechanics of Materials; PWS Publishing Company: Boston, MA, USA, 1997. [Google Scholar]
- Kiener, D.; Motz, C.; Schöberl, T.; Jenko, M.; Dehm, G. Determination of mechanical properties of copper at the micron scale. Adv. Eng. Mater. 2006, 8, 1119–1125. [Google Scholar] [CrossRef]
- Suzuki, K.; Chang, T.F.M.; Hashigata, K.; Asano, K.; Chen, C.Y.; Nagoshi, T.; Yamane, D.; Ito, H.; Machida, K.; Masu, K.; et al. Sample geometry effect on mechanical property of gold micro-cantilevers by micro-bending test. MRS Commun. 2020, 10, 434–438. [Google Scholar] [CrossRef]
- Tang, H.C.; Hashigata, K.; Chang, T.F.M.; Chen, C.Y.; Nagoshi, T.; Konishi, T.; Yamane, D.; Ito, H.; Machida, K.; Masu, K.; et al. Sample size effect on micro-mechanical properties of gold electroplated with dense carbon dioxide. Surf. Coat. Technol. 2018, 350, 1065–1070. [Google Scholar] [CrossRef]
- Baek, C.W.; Kim, Y.K.; Ahn, Y.; Kim, Y.H. Measurement of the mechanical properties of electroplated gold thin films using micromachined beam structures. Sens. Actuators A 2005, 117, 17–27. [Google Scholar] [CrossRef]
- Kucera, M.; Wistrela, E.; Pfusterschmied, G.; Ruiz-Díez, V.; Manzaneque, T.; Hernando-García, J.; Sánchez-Rojas, J.L.; Jachimowicz, A.; Schalko, J.; Bittner, A.; et al. Design-dependent performance of self-actuated and self-sensing piezoelectric-AlN cantilevers in liquid media oscillating in the fundamental in-plane bending mode. Sens. Actuators B 2014, 200, 235–244. [Google Scholar] [CrossRef]
- Schmid, U. The impact of thermal annealing and adhesion film thickness on the resistivity and the agglomeration behavior of titanium/platinum thin films. J. Appl. Phys. 2008, 103, 054902. [Google Scholar] [CrossRef]
- Gillinger, M.; Schneider, M.; Bittner, A.; Nicolay, P.; Schmid, U. Impact of annealing temperature on the mechanical and electrical properties of sputtered aluminum nitride thin films. J. Appl. Phys. 2015, 117, 065303. [Google Scholar] [CrossRef]
- Machida, K.; Konishi, T.; Yamane, D.; Toshiyoshi, H.; Masu, K. Integrated CMOS-MEMS technology and its applications. ECS Trans. 2014, 61, 21–39. [Google Scholar] [CrossRef]
- COMSOL Multiphysics Reference Manual. Version 5.3, COMSOL, Inc. Available online: https://www.comsol.com (accessed on 19 July 2019).
- Teranishi, M.; Chang, T.F.M.; Chen, C.Y.; Konishi, T.; Machida, K.; Toshiyoshi, H.; Yamane, D.; Masu, K.; Sone, M. Structure stability of high aspect ratio Ti/Au two-layer cantilevers for applications in MEMS accelerometers. Microelectron. Eng. 2016, 159, 90–93. [Google Scholar] [CrossRef] [Green Version]
- Teranishi, M.; Chang, T.F.M.; Chen, C.Y.; Konishi, T.; Machida, K.; Toshiyoshi, H.; Yamane, D.; Masu, K.; Sone, M. Study on Ti/Au two-layered cantilevers with different aspect ratio for MEMS Devices. In Proceedings of the Extended Abstracts of the 2015 International Conference on Solid State Devices and Materials, Sapporo, Japan, 27–30 September 2015; pp. 52–53, Abstract Number: PS-2–3. [Google Scholar]

| Fixed-End | Single Layer | Double Layer | Triple Layer |
|---|---|---|---|
| Normal | 62.4 | 52.4 | 45.0 |
| Block | 62.7 | 57.4 | 48.0 |
| Bridge | 63.3 | 58.0 | 49.5 |
| Fixed-End | Single Layer |
|---|---|
| Normal | 68.1 GPa |
| Block | 69.4 GPa |
| Bridge | 69.4 GPa |
| Fixed-End | 150 °C | 200 °C | 250 °C | 300 °C |
|---|---|---|---|---|
| Normal | 62.3 | 62.3 | 62.3 | 62.5 |
| Block | 62.9 | 63.0 | 63.1 | 63.3 |
| Bridge | 65.1 | 65.1 | 65.3 | 65.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watanabe, H.; Chang, T.-F.M.; Schneider, M.; Schmid, U.; Chen, C.-Y.; Iida, S.; Yamane, D.; Ito, H.; Machida, K.; Masu, K.; et al. Effective Young’s Modulus of Complex Three Dimensional Multilayered Ti/Au Micro-Cantilevers Fabricated by Electrodeposition and the Temperature Dependency. Electrochem 2021, 2, 216-223. https://doi.org/10.3390/electrochem2020015
Watanabe H, Chang T-FM, Schneider M, Schmid U, Chen C-Y, Iida S, Yamane D, Ito H, Machida K, Masu K, et al. Effective Young’s Modulus of Complex Three Dimensional Multilayered Ti/Au Micro-Cantilevers Fabricated by Electrodeposition and the Temperature Dependency. Electrochem. 2021; 2(2):216-223. https://doi.org/10.3390/electrochem2020015
Chicago/Turabian StyleWatanabe, Hitomi, Tso-Fu Mark Chang, Michael Schneider, Ulrich Schmid, Chun-Yi Chen, Shinichi Iida, Daisuke Yamane, Hiroyuki Ito, Katsuyuki Machida, Kazuya Masu, and et al. 2021. "Effective Young’s Modulus of Complex Three Dimensional Multilayered Ti/Au Micro-Cantilevers Fabricated by Electrodeposition and the Temperature Dependency" Electrochem 2, no. 2: 216-223. https://doi.org/10.3390/electrochem2020015
APA StyleWatanabe, H., Chang, T.-F. M., Schneider, M., Schmid, U., Chen, C.-Y., Iida, S., Yamane, D., Ito, H., Machida, K., Masu, K., & Sone, M. (2021). Effective Young’s Modulus of Complex Three Dimensional Multilayered Ti/Au Micro-Cantilevers Fabricated by Electrodeposition and the Temperature Dependency. Electrochem, 2(2), 216-223. https://doi.org/10.3390/electrochem2020015









