Hybrid Routing and Spectrum Allocation in Elastic Optical Networks by Machine Learning and Topological Metrics

Abstract

To meet the increasing demands for data, elastic optical networks (EONs) require highly efficient resource management. While classical Routing and Spectrum Assignment (RSA) algorithms establish a path and allocate spectrum, advanced versions such as Routing, Modulation-format-selection, and Spectrum Assignment (RMSA) also optimize modulation format selection. However, these approaches often lack adaptability to diverse network aspects. The hybrid routing and spectrum assignment (HRSA) algorithm offers a more flexible and robust approach by providing multiple choices between route (resource savings) and spectrum prioritization (fragmentation mitigation and network load balancing) for each network node pair. Despite its potential, the adaptive nature of HRSA introduces complexity, and the influence of topological features on its decisions remains not fully understood. This knowledge gap hinders the ability to optimize network design and resource allocation fully. This paper examines how topological features influence HRSA’s adaptive decisions regarding routing and spectrum assignment prioritization for source-destination node pairs in EONs. By employing machine learning approaches—Decision Tree (DT), Random Forest (RF), Extreme Gradient Boosting (XGBoost), and Support Vector Machine (SVM)—we model and identify the key topological features that influence HRSA’s decision-making. Then, we compare the models generated by each approach and extract insights using an a posteriori analysis technique to evaluate feature importance. Our results show the algorithm’s behavior is highly predictable (over 91% accuracy), with decisions driven primarily by the network’s structure and node metrics. This work advances the understanding of how topological features influence the RSA problem.

1. Introduction

Data traffic in communication networks has been growing exponentially with the development of communication technologies such as 5G, the Internet of Things (IoT), cloud computing, and 4K video [1]. Data from the International Telecommunication Union (ITU) report shows that the number of Internet users jumped from 1.0 billion (16% of the world’s population) to 5.5 billion (68% of the world’s population) in 2024 [2]. In response to the exponential growth in network traffic and the increasing complexity of network operations, it is imperative to improve resource allocation and automation in communication networks [1].

Optical networks offer high transmission capacity, low transmission signal loss, and other key advantages. Therefore, this field presents significant development opportunities, since it constitutes the core network technology required to support high-capacity traffic demands [3]. In this scenario, elastic optical networks (EONs) stand out. In an EON operating under a dynamic traffic scenario, a connection between a pair of nodes requires a route and a spectrum slice to be established. This is known as the routing and spectrum assignment (RSA) problem. The spectrum slices assigned to these connections can vary in size to meet the requested transmission rate, promoting an efficient use of the spectrum [4].

Most works in the literature use solutions that follow the sequence of choosing a suitable route and then performing spectrum allocation on that route with the minimum number of necessary contiguous spectral resources, i.e., slots. This approach is called R-SA [5,6]. Some works propose the opposite order for solving the RSA problem, a solution that prioritizes the spectrum slice to be used and then finds a route in these available spectral bands, called the SA-R approach [7,8]. The R-SA strategy can be advantageous for providing the shortest routes (e.g., fewer hops) and saving network resources; whereas the SA-R technique, which prioritizes spectrum allocation, enables better spectrum compression and load distribution by selecting lower-index slots from an ordered frequency list [9].

A hybrid approach to RSA selection ordering, called hybrid RSA (HRSA) was proposed in [9] and uses a genetic algorithm (GA) to decide between spectrum assignment strategies based on routing or routing based on candidate spectrum bands precomputed by spectrum allocation algorithm criteria. HRSA selects the most appropriate strategy, R-SA or SA-R, for each source-destination pair in the network based on the established criteria. Yet, the influence of topological features on HRSA’s adaptive decisions remains not fully understood. This is important to explain how GA, a black box model, makes its decisions.

Recent RSA algorithms using ML include an agent to represent the network’s current state to compute the quality of the optical path [10,11]. In contrast, in [12], an agent decides on the route and spectrum to use based on the network information represented in the artificial neural network.

In this paper, we explore the influence of topological features on the HRSA algorithm in EONs. We propose using machine learning (ML) algorithms to extract information about how the HRSA algorithm decides between the R-SA and SA-R strategies. Our hypothesis is that it is possible to use network topology metrics to describe HRSA’s operation. This may provide insights for extracting simpler heuristic rules to perform the HRSA decision without requiring a costly computational training process, while still achieving satisfactory results. The HRSA algorithm was chosen as the performance benchmark because it outperformed classical RSA algorithms, as shown in [9]. We consider 15 topologies with varying characteristics (such as the number of nodes and links) to ensure a scenario with heterogeneous topology metric values.

The main contributions presented in this paper are as follows:

• Modeling HRSA’s decision-making process using ML techniques;
• Identifying influential topological features in HRSA’s decisions;
• Quantifying feature importance using explainable AI (XAI) techniques;
• Providing a foundation for extracting simpler heuristics in future work.

This paper is organized as follows. In Section 2, we establish the foundational concepts of the research. In Section 3, we outline the methodology used to analyze the HRSA algorithm. The goal is to create a model that can accurately predict HRSA’s decisions. In Section 4, we present the main findings of the experiments. The analysis identifies the key topological metrics for understanding HRSA’s decision-making process. In Section 5, we summarize the paper’s contributions and implications.

2. Theoretical Basis

This section describes important definitions about the ML techniques and network topological metrics used in this work.

Among the various applications of ML algorithms are their use in complex problems for which there is no good solution using a traditional approach and in obtaining insights into complex problems and large amounts of data. In this paper, we use ML in these situations.

The techniques used in this work are based on the supervised learning (SL) paradigm. In SL, the goal is to train a model that learns a mapping from inputs to their correct outputs, enabling it to predict or classify outputs for unseen data [1]. We employ several classification algorithms: Decision Tree (DT), Random Forest (RF), Support Vector Machine (SVM), and Extreme Gradient Boosting (XGBoost). We also utilize the All K-Nearest Neighbors (AllKNN) technique [13]. The four classification algorithms are used to model the HRSA decision as a function of topological metrics, while AllKNN is used to balance the dataset.

2.1. Machine Learning Models Used

DT was chosen because of its explainability. It is a class of versatile ML algorithms that can perform classification and regression tasks and even multi-output tasks, capable of fitting complex data sets [14]. DT uses a tree-like structure composed of internal (non-terminal) nodes that recursively partition the dataset based on input features and leaf (terminal) nodes that represent the final predicted classes or values [15].

The structure of a DT allows users to easily visualize and understand the decisions made by the model, which makes it easy to interpret. Building the model involves the following steps [15]:

• Attribute Selection: The tree starts with a root node that contains all the data. The algorithm selects the most informative attribute to divide the data into subgroups. The choice of attribute is usually based on measures of homogeneity, such as entropy or information gain;
• Data Splitting: Based on the selected attribute, the data is divided into subgroups, creating branches that lead to new nodes;
• Process Repetition: The process of attribute selection and splitting is recursively repeated for each subgroup until a stopping criterion is met, such as when all the data in a node belongs to the same class or when no information gain can be achieved with further splits;
• Final Nodes: The final nodes, or leaves, represent the predictive classes. Each leaf is labeled with the most common class among the data that arrived at that node.

Gini index is an impurity measure and can be interpreted as the expected training error rate in the node. It is calculated using [16]:

$$G=\sum _{i=1}^K{p}_{mk}(1-p_{mk}),$$

(1)

where K is the number of classes and $p_{mk}$ is the proportion of samples belonging to class k at node m.

Entropy measures the uncertainty or disorder in a dataset. It is calculated using [16]:

$$H=-\sum _{k=1}^K{p}_{mk}log{p}_{mk},$$

(2)

where K is the class number and $p_{mk}$ is the proportion of samples belonging to class k at node m.

Finally, the log loss measures the quality of a model considering the probability of the model predictions. It is calculated by [17]:

$$LL=-{\displaystyle \frac{1}{M}}\sum _{m=1}^M\sum _{k=1}^K{y}_{mk}log{p}_{mk},$$

(3)

where M is the number of samples, K is the number of classes, $y_{mk}$ is equal to 1 if the sample belongs to class k and is equal to 0 otherwise, and $p_{mk}$ is the proportion of samples belonging to class k at node m.

Random forest (RF) was chosen because it is more robust than DT and is capable of providing information on the relevance of independent variables. It uses the concept of ensemble learning, which consists of aggregating the integration of a group of predictors (such as classifiers or regressors) to obtain better results than an individual model would deliver [14].

RF is a class of ML algorithms that combines several DTs to form a decision-making architecture. Each DT in an RF is trained independently on a sample of the data set, and the final prediction is made based on the average or majority of the variations of individual trees. RFs are often used because they have the capabilities to handle large and complex data sets of categorical input variables, for classification, and numerical for regression [18].

SVM was selected for its robustness in dealing with regression and classification problems involving non-linear relationships among variables and for its ability to detect outliers [14]. It is designed to identify the optimal hyperplane that maximally separates classes in the feature space. The algorithm maximizes the margin, defined as the distance between the hyperplane and the nearest data points of each class—referred to as support vectors [15].

Linear classification is possible when two different classes can be separated by a straight line. For non-linear problems, SVM uses a technique called the kernel trick, which transforms the data into a higher-dimensional space, where it becomes possible to find a hyperplane that separates the classes [14].

XGBoost was chosen because it is more robust, in addition to having similar characteristics to the RF. The XGBoost algorithm, like RF, is an ensemble ML technique. Boosting involves building an ensemble learning model composed of multiple models, which for XGBoost are decision trees. In it, the final prediction for a given instance is obtained by summing the predictions of each individual tree [19].

Gradient boosting models are trained additively. In each iteration, a new tree is added to the ensemble to correct errors made by previous trees, using gradient descent to minimize the loss function. XGBoost introduces significant innovations in terms of regularization, sparse data handling, approximate learning, and system optimizations that have made it highly scalable and efficient, allowing it to achieve state-of-the-art results on a wide range of machine learning problems with fewer resources [19].

KNN was chosen because it is capable of handling an unbalanced data set in an intelligent manner. With this algorithm, it is possible to maintain representative instances and exclude those that are located closer to the boundaries between the groups formed by the clusters. KNN is an ML algorithm used for classification and regression. It is one of the simplest and most intuitive methods, based on the idea that similar objects are close to each other in a feature space [15,20].

KNN is considered a nonparametric method because it makes no assumptions about the distribution of the data. It simply stores the training data and performs distance calculations during prediction [15]. When applied to classification problems, it calculates the distance between the point to be classified and the existing data points in the training set. The closest prototypes are identified, and the most frequent class among these neighbors is assigned to the point to be classified.

The other pillar of this work is network science, specifically the analysis of topology metrics. Section 2.2 describes the specific metrics used in this paper.

2.2. Network Topological Metrics

A network is a structure composed of nodes and links that connect these nodes [21]. It can be represented as a graph $G(\mathcal{N},\mathcal{L})$, where $\mathcal{N}$ is the set of nodes and $\mathcal{L}$ is the set of links. The adjacency matrix $\mathcal{A}$ of this graph is defined as: $a_{ij}=1$ if nodes i and j are connected by a link and $a_{ij}=0$ if they are not.

Network metrics are quantitative mathematical tools that allow network scientists to describe, analyze, and predict the behavior of complex systems by focusing on interactions and their underlying structure [21,22]. They are relevant for developing solutions that impact the performance, resilience, and efficiency of an optical network [23]. In this context, previous work showed that some network topological features can provide important information regarding HRSA decisions in a single topology [24]. Our hypothesis is that this choice between R-SA and SA-R can be modeled based on network metrics.

In this paper we consider the following node’s metrics: degree, betweenness [25], degree centrality, closeness centrality, eigenvector centrality [26], PageRank [27], eccentricity [28] and clustering coefficient [25]. As link’s metrics, we consider betweenness and physical distance. The chosen metrics provide information such as the topology’s connectivity, centrality, and physical structure.

Degree $k_i$ of node i is the number of links it has with other nodes. In terms of the adjacency matrix $\mathcal{A}$, it is defined by Equation (4) as follows [25]:

$$k_i=\sum _{j\in \mathcal{N}}{a}_{ij}.$$

(4)

Degree of a node provides a local measure of its connectivity importance. The more connections a node has, the more important it is, in terms of how much this node shall be present in network routes. This metric is a simple measure that does not consider the overall structure of the network [22].

Degree centrality $D_c$ of a node i is calculated according to Equation (5) [26]:

$$D_c\left(i\right)={\displaystyle \frac{k_i}{n-1}},$$

(5)

where n is the number of nodes in the network.

Degree centrality uses degree as a basis for determining the importance of a node and is often a way to rank nodes [22].

Betweenness of a node, or link, is the number of all shortest paths running along the node, or link, between all pairs of nodes divided by the total number of shortest paths between all pairs of nodes, (j, k), in the network. The betweenness $b_i$ of a node i is defined by Equation (6) [21,25]:

$$b_i=\sum _{j,k\in \mathcal{N},j\ne k}{\displaystyle \frac{n_{jk}\left(i\right)}{n_{jk}}},$$

(6)

such that $n_{jk}$ is the number of shortest paths between nodes j and k, and $n_{jk}\left(i\right)$ is the number of those shortest paths that pass through node i. A node or link with high betweenness acts as a bridge that connects different parts of the network [22].

Closeness centrality measures the sum of the distances between a node and other nodes [29]. For a given node i, it is calculated according to the Equation (7) [30]:

$$C_c\left(i\right)={\displaystyle \frac{n-1}{{\sum }_{j\in \mathcal{N}}d(i,j)}},$$

(7)

$d(i,j)$ is the length of the shortest route between the pair of nodes i,j. A node with high closeness centrality is, on average, closer to all other nodes in the network [22].

Closeness centrality is a valuable measure to identify nodes that are central in terms of distance and can influence the network more quickly, offering a spatial perspective of the importance of nodes in the network [22].

Eigenvector centrality of a node is the largest eigenvalue ($\lambda$) of $\mathcal{A}$ that satisfies Equation (8) [31]:

$$\mathcal{A}x=\lambda x,\lambda x_i=\sum _{j=1}^n{a}_{ij}{x}_j,i=1,\dots ,n,$$

(8)

such that $x_j$ is the centrality of node j. This metric weights neighbors according to their respective centrality values, i.e., the centrality of node i is proportional to the sum of the centralities of the nodes to which it is connected [32].

Eigenvector centrality measures the influence of a node in a network, considering the influence of its neighbors. In this metric, a node is important if it is connected to other important nodes. Therefore, it is used to identify the hubs of a network, which are nodes with many connections that have a significant influence on the structure and functioning of the network [22].

PageRank has been proposed as a method for evaluating the importance rating of a web page [27]. This metric considers a web page to be important if many other pages link to it. However, the pages that make these links are not treated equally, since the algorithm also considers the importance (PageRank) of the pages that make the links and the number of outgoing links they have. Pages with higher PageRank are given more weight, while pages with many outgoing links are given less weight [16]. The pagerank of a node i, $PR\left(i\right)$, satisfies Equation (9) [33]:

$$PR\left(i\right)=\gamma \sum _{j\in \mathcal{N}}{\displaystyle \frac{a_{ij}}{k_j^{\left(out\right)}}}PR\left(j\right)+{\displaystyle \frac{1-\gamma }{n}},$$

(9)

where $\gamma \in [0,1)$ is a damping factor and $k_j^{\left(out\right)}$ is the number of links emanating out from j. PageRank is a type of eigenvector centrality. It provides a measure of the importance of a node in a directed network based on the structure of the links, considering both the quantity and quality of the connections. It is useful for networks where the influence and relevance of the nodes are important [22].

The eccentricity of a node is the greatest distance from it to any other node in the network. This can be useful for identifying nodes that are more isolated or have a more distant connection to other members of the network [22]. Eccentricity is used to calculate other network properties, such as diameter and radius. The diameter of a network is equal to the largest eccentricity among all nodes in the network, representing the greatest distance between any two nodes in the network. The radius of a network, on the other hand, is equal to the smallest eccentricity in the network [22]. The clustering coefficient of a node i with degree $k_i$ is defined as the ratio between the number of links existing between its neighbors ($l_i$) and the maximum possible number of links between these neighbors [25]. It is calculated according to Equation (10) is as follows:

$$c\left(i\right)={\displaystyle \frac{2l_i}{k_j(k_j-1)}}.$$

(10)

The clustering coefficient measures the density of links in the immediate neighborhood of a node [21].

In this paper, topological metrics are classified as structural, spatial, or spectral. Structural metrics depend exclusively on the connections and the organization of the network. Spatial metrics are quantitative measures that assess the distance or relationship between entities (e.g., nodes) in a space. Finally, a spectral metric refers to a quantitative measure that uses the spectrum of a graph, that is, the eigenvalues and eigenvectors of matrices that represent the network [22].

3. Materials and Methods

This section describes the materials used in the study and the adopted methodology in this work.

While typical RSA/RMSA algorithms are designed to solve the RSA problem with a single, predefined strategy, our work takes a different approach. Instead of simply prioritizing route over spectrum ordering, or vice versa, we conduct a descriptive and analytical study of the adaptive HRSA algorithm to understand which aspects impact its decision to choose one strategy over another for each particular source–destination pair.

The novelty lies in using ML not to replace the algorithm, but as an external analysis tool. We build a model that mimics HRSA’s behavior and then use explainable AI (XAI) to reveal which network features influence its decisions.

3.1. Materials

This work employs computational libraries in the Python 3.12.6 programming language, including scikit-learn [34], NetworkX [35] and Optuna [36]. Additionally, it makes use of SimEON (Simulator for Elastic Optical Networks) [37], an EON simulator. In SimEON, call requests follow a Poisson process. Therefore, the time between call requests follows an exponential distribution. The same occurs for the probability distribution of the duration of a call. The probability of choosing the source and destination node pair and the choice of the call bit rate follow a uniform distribution [38].

3.2. Methodology

The methodological steps undertaken in this study are outlined as follows:

• Execution of the HRSA in each network. Each selected network is subject to HRSA decision which provides the policy to be used (R-SA or SA-R) for each source-destination node pairs. This step is performed in SimEON;
• Calculation of topology metrics for each network. This step is performed using the Python library NetworkX. There are initially 46 features, i.e., independent variables as listed below:
  • Degree, betweenness, degree centrality, closeness centrality, eigenvector centrality, PageRank, eccentricity, and clustering coefficient for source and destination nodes. (This yields a total of 16 features, 8 for the source node and 8 for the destination node);
  • Average link betweenness, average node betweenness, distance, number of hops, average node degree centrality, average node closeness centrality, average node eigenvector centrality, average node pagerank, average node eccentricity, and average node clustering coefficient. Since each of these 10 metrics is calculated over each of the K routes in the RSA, a total of $10K$ features are obtained. In this paper, we have assumed $K=3$.
• Construction of a dataset containing the values found in the previous steps. It contains $10,214$ rows. We consider 15 topologies and each contributes $n(n-1)$ rows;
• Exclusion of missing network metric values when there are no possible alternative routes. This occurs, for example, when a given source-destination node pair does not have three available routes, but only two. In such cases, the corresponding row is excluded from the dataset, which resulted in $10,208$ rows, 1704 with the R-SA label, and 8504 with the SA-R label. If this is not carried out, the metrics associated with route k = 3 will be assigned as not a number (NaN);
• Standardization of dataset results to mean 0 and standard deviation 1. This preprocessing is done to avoid biases since ML models can be sensitive to the scales of the input variables;
• Balancing the dataset. We use the All KNN algorithm, considering four neighbors, to reduce the majority class so that bias towards it is avoided. At the end, the dataset contains 3984 rows, 1704 ($43\%$) with the label R-SA and 2280 ($57\%$) with the label SA-R;
• Selection of variables. Variance inflation factor (VIF) greater than 10 indicates high collinearity of a feature [39]. Thus, VIFs are computed, and the variable with the highest value is removed iteratively until all remaining variables present $VIF\le 10$. At the end of this step, the dataset contains 23 features;
• Run ML model tunning and fitting. This step is divided into two sub-steps. The first is the hyperparameter tuning of the models, and the second is the fitting of the data by the models. We use the Python libraries and Scikit-learn [34] (for DT, RF, SVM and All KNN) and XGBoost [19] (for itself).

  8.1

  Model tunning. A hyperparameter optimization process is conducted. 50 stratified folds are employed, and the weighted F1-score is used as the evaluation metric for selecting the best set of hyperparameters.

  8.2

  Model fitting. The importance of the model’s features corresponds to the mean values computed over 50 folds. Each model was trained independently, and the mean of the importances over 50 folds provides a more robust estimate.

The ML fitting discussed in this paper is an offline analysis tool used to model and interpret results after HRSA has already run, to understand its decisions. HRSA is trained using GA before the network starts operating. After the training phase is complete, the operational HRSA essentially functions as a fast lookup table. Therefore, its real-time speed for determining a solution for a given node pair is indeed comparable to the very low time cost of classical RSA and RMSA algorithms.

Partitioning a dataset into training, validation, and test subsets does not inherently increase the computational cost or algorithmic complexity of ML training. In a simple split configuration, where the model is trained once on a designated training subset and later evaluated on an independent test set, the partitioning cost is negligible compared to the learning process itself, and the algorithm’s complexity remains unchanged. Even with cross-validation, the increase in computational effort arises solely from the repeated execution of the same training procedure across multiple folds, not from any structural change in the algorithm. Thus, data division serves purely as an experimental design strategy to improve generalization assessment, without modifying the intrinsic complexity or efficiency of the learning algorithm.

3.3. Network Simulation Parameters

This subsection details Step 1 of the methodology described in Section 3.2. The HRSA construction was proposed using GA to determine the RSA policy to be used on path requests of each source-destination node pair in the network. At the end of the training process, a vector with binary numbers indicates which RSA procedure, i.e., if routing has preference over spectrum assignment or the opposite, shall be applied to each source-destination node pair in the network. Since this binary vector is the final solution for the RSA strategy, it is set as the dependent variable of the ML models. The independent variables are the network topology metrics.

The simulations were conducted using Yen’s K-shortest paths algorithm with $K=3$ for the fixed-alternative method, employing a unitary link cost metric. Traffic demands were set at 100, 200, and 400 Gbps, with physical layer impairments disabled. For each individual in the GA, a total of 500 blocked requests were processed to evaluate the algorithm’s performance in terms of blocking ratio, defined as the number of blocked requests divided by the total number of requests. The network topologies considered a single fiber for each direction of the link, with 128 available spectrum slots per fiber. Each slot represents the smallest unit of spectrum that can be allocated. The GA was configured with a population size of 50 individuals, evolving over 300 generations. Genetic operations were governed by a crossover probability ($p_c$) of 0.5 and a mutation probability ($p_m$) of 0.01. Each crossover operation generates two new individuals, and the mate parents are selected using the weighted roulette wheel strategy. Each gene of the new individual has a $P_c$ probability to inherit the contents of the same index gene from parent 1 and $1-P_c$ to inherit from parent 2 [40]. The mutation is applied in each individual gene with a ($p_m$) probability of the newly generated individuals in the crossover operation.

The topologies used for constructing the ML models are described in Table 1. The load values, in Erlangs, for the HRSA simulation were set following the criterion of blocking probabilities, the number of blocked requests to the total number of requests, close to $1\%$, considering the First-Fit as the spectrum assignment algorithm.

Table 1. Topologies considered.

Topology	Number of Nodes	Number of Links	Mean Degree	Load 1
ARPANET [41]	20	32	$3.2$	240
CHNNET [41]	15	27	$3.6$	320
Cost239 [42]	11	26	$4.73$	560
EON_RT [9]	25	34	$2.72$	180
European [43]	28	41	$2.93$	210
Finland [44]	12	19	$2.17$	270
Germany [45]	17	26	$3.06$	210
Italy [46]	14	29	$4.14$	360
JPN12 [47]	12	17	$2.83$	150
JPN25 [47]	25	43	$3.44$	170
JPN48 [47]	48	164	$6.83$	190
NOFN-India [20]	59	135	$4.58$	210
NSFNET [9]	14	21	$3.0$	290
PacificBell [44]	17	23	$2.71$	200
US Backbone [48]	24	42	$3.5$	330

¹ In Erlangs.

3.4. Machine Learning Models Tunning and Fitting

This subsection details Step 8 of the methodology described in Section 3.2. Besides fitting an ML model, hyperparameter tuning is necessary to obtain the best set of hyperparameter values. The values considered for the selected hyperparameters, the values obtained after tuning, and the optimization strategy are in Table 2.

Table 2. Tuning process details.

ML Model	Hyperparameters and Values Sets (Selected Values)	Framework
DT	Maximum tree depth: from 1 to 10 (10) Minimum number of samples per leaf: 2, 5, 10 (2) Split quality criterion: Gini, entropy, log loss (Gini)	Grid search
RF	Number of trees: 50, 75, 100, 125, 150, 175, 200 (175)	Grid search
XGBoost	Learning rate (log scale): from $0.01$ to $0.3$ ($0.0614$) 1 Maximum tree depth: from 3 to 10 (10) Minimum number of instances on a child node: from 1 to 10 (1) Minimum reduction in loss to allow for a split: from 0 to 5 ($0.0021$) 1 Fraction of training samples: from $0.5$ to $1.0$ ($0.6751$) 1 Fraction of features that used to build each tree: from $0.5$ to $1.0$ ($0.7472$) 1 L1 regularization term: from $0.0$ to $10.0$ ($0.1759$) 1 L2 regularization term: from $0.0$ to $10.0$ ($0.2709$) 1	Optuna
SVM	Regularization parameter (C): $0.001$ to 1000 (5) Kernel coefficient ($\gamma$): from $0.0001$ to 100 ($0.75$) Tolerance: from ${10}^{-4}$ to ${10}^{-1}$ (${10}^{-4}$)	Grid search

¹ Value rounded to four decimal places for ease of viewing.

The hyperparameter tuning considers the mean weighted F1-score as the scoring target in 50 stratified folds. For DT configuration, the metric is $0.7278$. The same set of hyperparameters used for the DT was applied to the RF, focusing on selecting the optimal number of trees. The best performance was achieved with a weighted F1-score of $0.7787$.

Regarding SVM, the Radial Basis Function (RBF) kernel was chosen, as it is capable of performing classification in scenarios in which the variables present non-linear relationships with each other. Hyperparameter selection involved a grid search over logarithmic scales. After the initial hyperparameter selection, a fine-tuning step was performed to refine the model’s performance. This refinement focused on a narrower search space: C ranged from 5 to 50 in increments of 5, and $\gamma$ ranged from $0.5$ to 5 in increments of $0.5$. The tolerance was fixed at ${10}^{-4}$. The best hyperparameter configuration obtained was $C=5$, $\gamma =0.75$ and $tol={10}^{-4}$. The mean weighted F1-score achieved with this configuration is $0.9023$.

The XGBoost classifier hyperparameter search was conducted using the Optuna [36]. The optimization targeted a binary classification task, employing the logistic objective function and the error evaluation metric, with trees constructed using the efficient histogram-based method. The model was configured with up to 1000 boosting rounds and early stopping after 100 rounds without improvement. A total of $10,000$ trials were performed, where Optuna explored the hyperparameter space using probabilistic sampling.

4. Results

This section presents the results and interpretations of HRSA models using ML and topological metrics. There are three focuses addressed: feature selection, interpretations of the decision processes of the HRSA algorithm, and the comparison between the results of each ML model. The preliminary results for the DT classifier are presented in [49].

4.1. Features Selection

In this subsection, we present the results obtained by ML models considered in this paper to list the necessary features to get insights into how HRSA makes its decision on RSA policy. Figure 1 shows the boxplots of the weighted F1-score as a function of the number of features for all ML models applied to this study. The black dots indicate values exceeding 1.5 times the interquartile range, defined as the difference between the third and first quartiles. In each iteration, the feature with the lowest value of importance is excluded. For DT and RF models, the importance of a feature is the normalized total reduction of the criterion brought by that feature. For the XGBoost model, feature importance is computed as the total gain across all splits in which the feature is used. Finally, the SVM model uses the permutation feature importance (PFI) technique to evaluate the importance of each feature. This technique evaluates how much model performance decreases when the values of a feature are shuffled randomly. A significant drop in performance indicates that the model relies heavily on that feature to make its predictions. The performance metric used is the weighted F1-score. For each feature, 30 iterations are used, each with random values, while the model performance drop is calculated. So, the importance of the feature is averaged from the results of the 30 iterations.

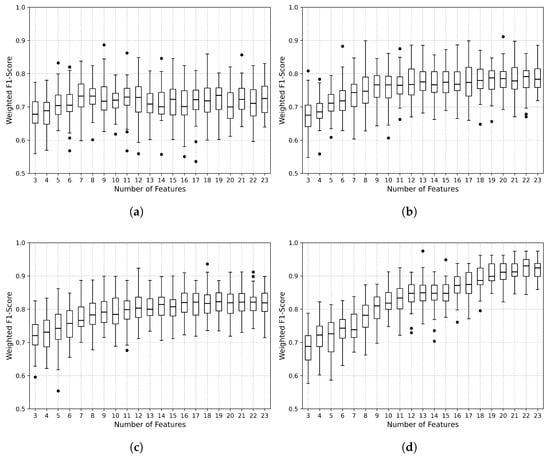
Figure 1. Boxplot of the weighted F1-score as a function of number of features for: (a) DT, (b) RF, (c) XGBoost, (d) SVM.

Since it is not visually clear from Figure 1 what the minimum number of features is that yields a statistically equivalent performance to that obtained with the 23 features, a hypothesis test is conducted to identify this value. A two-tailed Student’s t-test is performed at a $5\%$ significance level, starting by comparing the performance of the scenario with 3 features to that of the scenario with 23 features. The null hypothesis assumes that the mean F1-scores of the two scenarios are equal, while the alternative hypothesis posits that they are different. If the null hypothesis is rejected, the test is repeated by comparing the scenario with 4 features to the one with 23 features. This iterative procedure continues, increasing the number of features by one in each step until the null hypothesis is no longer rejected.

The hypothesis test verified that 5 features are enough for the DT model to obtain an equivalent performance to that obtained by 23 features. For the RF, SMV, and XGBoost models, the number of features is 12, 20, and 12, respectively. Table 3 shows the means and the standard deviations (SDs) of weighted F1-scores for 23 features and the minimum number of features found for each model.

Table 3. Mean and SDs of weigthed F1-scores for each ML model.

ML Model	Mean of Weighted F1-Scores (23 Features)	SD of Weighted F1-Scores (23 Features)	Mean of Weighted F1-Scores (Enough Features)	SD of Weighted F1-Scores (Enough Features)
DT	$0.7163$	$0.0461$	$0.7176$	$0.0504$
RF	$0.7864$	$0.0515$	$0.7714$	$0.0463$
XGBoost	$0.8179$	$0.0440$	$0.8069$	$0.0472$
SVM	$0.9216$	$0.0286$	$0.9115$	$0.0306$

According to Table 3, SVM performed best, followed by XGBoost, RF, and DT. Superiorities were verified after one-sided hypothesis tests with $95\%$ confidence performed on Student’s t considering the values of an adequate number of features. The results of the p-values are shown in Table 4.

Table 4. p-values of the hypothesis tests of the mean of weighted F1-scores of the classifiers.

${\mathit{H}}_0:{\mathit{\mu }}_{\mathit{RF}}\le {\mathit{\mu }}_{\mathit{DT}}$	${\mathit{H}}_0:{\mathit{\mu }}_{\mathit{XGBoost}}\le {\mathit{\mu }}_{\mathit{RF}}$	${\mathit{H}}_0:{\mathit{\mu }}_{\mathit{SVM}}\le {\mathit{\mu }}_{\mathit{XGBoost}}$
$0.0000$	$0.0001$	$0.0000$

The first test compared the means of the RF-weighted F1-scores with those of DT; the second test did the same, comparing XGBoost with RF; and the last one compared SVM with XGBoost. In Table 4, p-values confirm that the results of the means for enough features in Table 3 are statistically superior.

4.2. Interpretations on HRSA Decisions

This section presents insights into how HRSA makes its decisions on RSA policy. In this sense, we use a post-hoc approach named Shapley additive explanations (SHAP). Post-hoc explainability methods analyze and interpret the decision-making process of a trained ML model after it has made predictions, providing insights into how the model reached its outputs [50]. SHAP measures the importance of a feature as the average of the marginal contribution of this feature across all possible feature combinations [51]. Thus, understanding how an ML model makes its decision gives us insights into how HRSA does its decision-making process.

Table 5 shows the averages of the absolute SHAP values of the test set of the 20 features selected by the SVM model. Furthermore, the classification of the metric and the type of topological entity it refers to are reported. We verified that $52\%$ of the sum of the averages of the absolute SHAP values, the feature importance, corresponds to structural metrics. $27\%$ and $21\%$ are related to spatial and spectral metrics, respectively. Regarding network entities, $71\%$ of the sum of the averages of the absolute SHAP values refer to nodes and $29\%$ to links. The combination of the importance classified as structural and node represents $34\%$, being the most relevant pair.

Table 5. Mean absolute SHAP value for SVM model for the test set.

Feature	$\overline{\left|\mathbf{SHAP}\right|}$	Metric Classification	Network Element
Sou Eing Cent	$0.02496$	Spectral	Node
Dest Clus Coeff	$0.02438$	Structural	Node
Sou Ecc	$0.02381$	Space	Node
Dest Ecc	$0.02331$	Space	Node
Dist k = 1	$0.02269$	Space	Link
Dest Degree	$0.02221$	Structural	Node
Mean Clus Coeff k = 3	$0.02198$	Structural	Node
Dist k = 2	$0.02197$	Space	Link
Sou Clus Coeff	$0.02185$	Structural	Node
Dest Eing Cent	$0.02114$	Spectral	Node
Hops k = 3	$0.02087$	Structural	Link
Dist k = 3	$0.02075$	Space	Node
Mean Eing Cent k = 3	$0.02071$	Spectral	Node
Mean Link Bet k = 2	$0.02027$	Structural	Link
Sou Degree	$0.02011$	Structural	Node
Mean Eing Cent k = 2	$0.01992$	Spectral	Node
Mean Link Bet k = 3	$0.01857$	Structural	Link
Mean Link Bet k = 1	$0.01767$	Structural	Link
Dest Bet	$0.01656$	Structural	Node
Sou Bet	$0.01493$	Structural	Node

Figure 2a shows the SHAP values summary of the 20 selected features for the SVM model for policy SA-R, positive class, of the test set. Figure 2b is the Spearman correlation, in all datasets, of the five most relevant features according to the results in Table 5: eigenvector centrality, destination node clustering coefficient, source and destination node eccentricities, and distance of the route $k=1$.

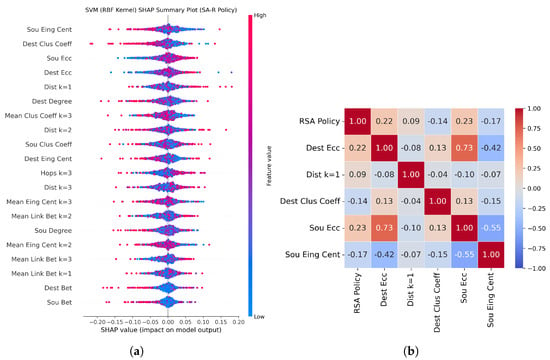
Figure 2. (a) SHAP values summary plot of the selected features for the SVM model and (b) Heatmap of the five most relevant features according to the SHAP values of the SVM model.

Positive SHAP values of a feature push the model to decide on class 1 (SA-R policy), while negative values push it towards class 0 (R-SA policy). In Figure 2a, we observe that low values of the features source node eigenvector centrality (Sou Eing Cent) and destination node clustering coefficient (Dest Clus Coeff) push the model to decide for the SA-R policy. In contrast, high feature values of source and destination node eccentricity and distance of the route $k=1$ push the model to decide on the SA-R policy. This is confirmed by the values of the correlations of the features with the RSA policy presented in the heatmap, Figure 2b, since a positive value of Spearman’s correlation indicates that the variables have an increasing monotonic relationship.

Since eigenvector centrality and clustering coefficient are metrics indicated to identify concentrating nodes in the network, HRSA prefers to use the SA-R policy for nodes with poorly physically connected neighborhoods, as these nodes tend to have the spectrum of the neighborhood with the lowest probability of availability, since there are few options for traffic to seek alternatives in cases of slot occupancy. It implies that the spectrum allocation problem is more critical to solve.

The eccentricity of a node identifies nodes that are more isolated or have a more distant connection to other members of the network. A node with high eccentricity is isolated from the others, so it is more difficult to find available spectrum since this node tends to be on the periphery, which limits the traffic flow options. This makes the most critical problem the choice of spectrum, so HRSA prioritizes the SA-R policy. The same understanding can be applied to the distance of the main route, since the eccentricity of a node is the maximum distance from all other nodes in the network.

4.3. Comparison Among the Four Most Relevant Feature Sets Derived from the Analysis

In this subsection, we compare the sets of the most relevant features obtained by the ML models employed in this paper. They are presented in Table 6, which also contains the relative importance of each of the features in the respective set.

Table 6. Importance of the most relevant features in each set derived.

Feature	SVM	XGBoost	RF	DT
Sou Eing Cent	$5.96\%$	$9.55\%$	$7.65\%$	$15.02\%$
Dest Clus Coeff	$5.82\%$	-	-	-
Sou Ecc	$5.69\%$	-	-	-
Dest Ecc	$5.57\%$	-	-	-
Dist k = 1	$5.42\%$	$10.28\%$	$9.31\%$	$16.76\%$
Dest Degree	$5.31\%$	-	-	-
Mean Clus Coeff k = 3	$5.25\%$	$10.22\%$	$14.71\%$	$22.92\%$
Dist k = 2	$5.25\%$	$6.74\%$	-	-
Sou Clus Coeff	$5.22\%$	-	-	-
Dest Eing Cent	$5.05\%$	-	-	-
Hops k = 3	$4.98\%$	-	-	-
Dist k = 3	$4.96\%$	-	-	-
Mean Eing Cent k = 3	$4.95\%$	$6.38\%$	$4.51\%$	-
Mean Link Bet k = 2	$4.84\%$	$6.39\%$	$6.52\%$	-
Sou Degre	$4.80\%$	-	-	-
Mean Eing Cent k = 2	$4.76\%$	-	-	-
Mean Link Bet k = 3	$4.44\%$	$10.23\%$	$10.59\%$	$30.74\%$
Mean Link Bet k = 1	$4.22\%$	$9.83\%$	$11.71\%$	-
Dest Bet	$3.96\%$	$8.75\%$	$5.60\%$	$33.01\%$
Sou Bet	$3.57\%$	$9.58\%$	$8.76\%$	-
Dest Page	-	$6.13\%$	$5.28\%$	-
Sou Page	-	$5.91\%$	$4.53\%$	-
Dest Degree Cent	-	-	$10.86\%$	-

Some observations can be obtained from Table 6. The first refers to the number of features in common with the set derived by the SVM model, which had the best result. All 5 features of the DT model set are in the SVM model, whereas for the RF and XGBoost model sets, the quantities are 9 out of 12 and 10 out of 12, respectively. Another highlight is that the sets of the RF and XGBoost models differ only in one feature. This similarity may occur because both models are DT-based ensemble models.

The standard deviations of the percentage values of the feature importances, shown in Table 6, within each set are as follows: $0.61\%$, $1.84\%$, $3.22\%$, and $8.07\%$ for SVM, XGBoost, RF, and DT, respectively. Since SVM models use a decision hyperplane to separate the classes, this makes the features tend to contribute in a more balanced way to the construction of these models. On the other hand, models based on DT split the dataset hierarchically and locally, so the features present in the initial nodes tend to have greater importance in the construction of these models.

Table 7 summarizes the distribution of the importance of the most relevant feature sets derived by the ML models for the classification of the metrics and the type of network element. Values are the percentage of the sum of the absolute SHAP values of features that have the specific classification or type, divided by the total of the absolute SHAP values of the model. The number in parentheses is the number of features.

Table 7. Summary of the importance of the most relevant feature sets derived in terms of metric classification and network type element.

Classification/Type	SVM	XGBoost	RF	DT
Structural	$52\%\left(11\right)$	$55\%\left(6\right)$	$69\%\left(7\right)$	$68\%\left(3\right)$
Space	$27\%\left(5\right)$	$17\%\left(2\right)$	$9\%\left(1\right)$	$17\%\left(1\right)$
Spectral	$21\%\left(4\right)$	$28\%\left(4\right)$	$22\%\left(4\right)$	$15\%\left(1\right)$
Node	$71\%\left(14\right)$	$57\%\left(7\right)$	$62\%\left(8\right)$	$52\%\left(3\right)$
Link	$29\%\left(6\right)$	$43\%\left(5\right)$	$38\%\left(4\right)$	$48\%\left(2\right)$

The results presented in Table 7 reveal that the structural features have the most significant influence on the four models analyzed, the lowest value being $52\%$ for the SVM and the highest value being $69\%$ for the RF. It is important to note that all models consider at least one aspect of the topological classification of the metric. With respect to the type of topological entity, metrics related to nodes are more influential than those related to links. In this regard, the lowest value is $52\%$ for the DT model and the highest value is $71\%$ for the SVM model.

5. Conclusions

Results demonstrated that the adaptive behavior of the HRSA algorithm can be accurately modeled. The SVM classifier was the most effective predictive model. A key insight from this analysis is understanding why HRSA makes its decisions: for nodes with poor connectivity or those on the network periphery, the algorithm is compelled to prioritize the spectrum-first, SA-R strategy, as spectrum alignment becomes the most critical constraint. Across all models, the analysis consistently confirmed that structural and node-related metrics were the most influential factors driving these algorithmic choices.

This more profound understanding of HRSA’s logic paves the way for significant future work, primarily focused on developing simpler, more efficient rule-based RSA policies. The ultimate goal is to leverage the insights gained from this study, particularly the knowledge of which topological features are most critical, to design new heuristic algorithms. Such algorithms could generalize their decision-making across different network topologies, achieving near-optimal performance without the high computational cost associated with complex intelligent algorithms, such as the GA, that currently power HRSA.