Abstract
To improve pulse contrast in chirped pulse amplification petawatt laser systems, the regenerative amplifier is substituted with a multipass amplifier at the Shanghai Superintense Ultrafast Laser Facility (SULF). To reduce the consequent angular dispersion of the broadband spectrum, a double-grating stretcher is established in the SULF front end. A grating compressor is set up for the 10-PW front end to obtain 20-TW output. An accurate adjustment method of grating attitude (angular position) is presented, which references the direction of gravity, improving dispersion management and focusing ability of the beam. After a pulse passes the front end compressor, its duration and phase in the frequency domain are measured, and the duration can be continuously compressed to <24 fs.
1. Introduction
Based on the chirped pulse amplification (CPA) [1] technique and its analogs, optical parametric chirped pulse amplification (OPCPA) [2] and non collinear optical parametric chirped pulse amplification (NOPCPA) [3,4,5], petawatt-class (PW) femtosecond laser systems have made notable progress over several decades [6]. To avoid the elongation of output pulse duration due to material dispersion in broadband CPA systems, high-order dispersion management is an essential part of the petawatt-class laser facility. Recent developments have significantly broadened the gain bandwidth, with future mainstream bandwidths of hundreds of nanometers [7,8,9], highlighting the importance of the design of an appropriate dispersion management system.
In broadband PW laser systems, spectral phase distortions should be eliminated to achieve a Fourier-transform-limited pulse. In addition to group-velocity dispersion (GVD) and third-order dispersion (TOD), the residual fourth-order dispersion over the required spectral range also needs to be compensated [10]. Since residual fourth-order dispersion compensation was proposed, it has been quite a difficult problem in large-scale laser facilities. Optical elements, such as the acousto-optic programmable dispersive filter (AOPDF) [11], grism pairs [12], and deformable mirrors [13], are widely used in CPA systems for high-order dispersion management. In 2015, we demonstrated a method for dispersion compensation by a grism pair [14], making further improvements in 2017 [15] to minimize the residual phase over the spectral bandwidth to 1.2 rad, presenting a final pulse duration of approximately 24 fs at a repetition frequency of 1 Hz. With an energy of 202.8 J, our prototype is able to produce 5.4-PW output [16], but the low optical transmittance of grism pair significantly degraded subsequent regenerative amplification.
High-order dispersion management is an important part of pulse compression. Several cases for high-order dispersion management have been made [17,18,19]. However, the most important optical elements are the stretcher and the compressor, together with the position of the gratings, which has a strong impact on the dispersion in the whole system [20]. In general, high-order dispersion results not only from a mismatch between the stretcher and compressor, but also from the misalignment of components, limited precision, chromatic aberration in optics, etc. An imperfect grating stretcher may produce residual angular dispersion, which leads to pulse-front tilt, yielding a pulse duration longer than allowable by the optical spectrum when integrated over the near-field or far-field [21,22,23,24,25]. As the element principally responsible for introduction of dispersion, it is important to carefully choose and precisely establish the grating stretcher and its corresponding compressor.
A novel double-grating stretcher was proposed this decade, due to the broad spectral width in actual applications [7,26], in which the spherical aberration of the standard spherical Offner stretcher cannot be neglected. Compared to the standard stretcher, the double-grating stretcher is absolutely aberration-free in both the near-field and far-field. However, the double-grating type is more complex. Minute differences between the angular alignment (attitude) of the two gratings placed in the same direction might cause not only residual spatial angular dispersion, but also mismatch between the compressor and the stretcher, resulting in additional high-order dispersion. Normally, for grating compressors, the grating positions are adjusted to make the compressor output spot a full circle, while the spot is monitored with a CCD camera. However, for a double-grating Offner stretcher, with multiple degrees of freedom of optical elements, such as gratings, the roof mirror, and prism, it cannot be determined whether the position of each element is correct by the focal spot alone; thus, it is not possible to eliminate high-order dispersion and residual angular dispersion. Moreover, the focusing ability of the laser facility is an important parameter determining the peak power density that can be attained. Since the intensity of 1023 W/cm2 was achieved in 2004 [27], researchers have been working to focus a laser beam with a radius of several hundred millimeters to a spot of 1-um2 area at the full width at half maximum (FWHM) for several years [28,29,30,31]. As the highest dispersion components in the whole facility, the grating pairs used in the stretcher and compressor are the key optical units that affect beam focusing capability. The pulse duration consistency of the different parts of a spot with the diameter of 500 mm is closely associated with grating position. The precise adjustment of gratings is difficult and has been the subject of much research [32,33,34]. However, a laboratory standard has not been proposed to facilitate the precise adjustment of every element.
In this paper, we present a 20-TW front end pre-compression system, emphasizing dispersion management. To reduce spherical aberration, a double-grating stretcher is introduced to the Shanghai Superintense Ultrafast Laser Facility (SULF). A novel method for grating position adjustment is described, in which gravity is the standard. This method is precise and establishes a standard for grating alignment. Using a broadband AOPDF, we achieved a pre-compression pulse of 22-fs in the SULF frond end, verifying effective dispersion management in 10-PW-class single shot experiment. Further, focusing ability can be increased predictably, and verification of this will be the subject of current research.
2. Chirped Pulse Amplification Front End
To improve contrast and to suppress amplified spontaneous emission, all multipass amplifications are employed throughout, rather than the regenerative amplifier first stage that was used in the SULF prototype [17]. An outline diagram of the SULF front end is shown in Figure 1. Four stages of laser amplifiers are employed, and each stage is followed optical beam expansion. The main energy of an amplified pulse is used for further amplification. About 0.8 J of the pulse energy is directed to a grating compressor by a beam splitter with a 1:7 splitting ratio. The compressor has an optical transmittance of approximately 65%; thus, a peak output power exceeding 20 TW can be obtained.
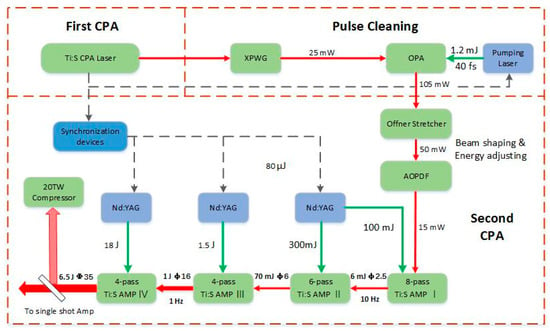
Figure 1.
High-contrast SULF front end.
The Ti:sapphire gain medium introduces material dispersion. As the first stage, a multipass amplifier (8 passes of a Ti:sapphire crystal) clearly has less material dispersion than that of a regenerative amplifier. There are >24 passes of a Ti:sapphire crystal and a KD*P Pockels cell in our prototype regenerative amplifier [14]. The new scheme increases the feasibility of compensating the high-order dispersion. The accurate design parameters and three orders of dispersion for each element are shown in Table 1, where the Sellmeier equation is used to calculate the dispersion introduced by Ti:S [35,36]. The residual fourth-order dispersion is greatly reduced so that it can be compensated by an AOPDF.

Table 1.
Results of dispersion calculation for the original design.
In the SULF prototype, the regenerative amplifier played a role in spectrum broadening and shaping. In the new scheme, an AOPDF is employed to meet these demands. However, the regenerative amplifier has an obvious advantage in terms of beam quality. The beam is regenerated so that the output beam can be isolated from the low beam quality initial seed. The all multipass amplifier scheme demands perfect beam quality from the grating stretcher.
It is difficult to obtain a high-quality beam from the traditional Offner grating stretcher [37] if the beam has a broadband spectrum exceeding 100 nm. We establish a raytracing model of the grating stretchers, and present the simulated far-field images in Figure 2. The focal length of the lens we used is 0.5 m, and the aperture value of the simulation is 5 mm. These results are for the same test environment, beam size, time-expansion ratio, and spacing of equivalent grating pairs, for a central wavelength of 800 nm. It is clear from Figure 2a that for a bandwidth of 100 nm, the spot of a single-grating type starts to degrade and shows spatial dispersion. In the raytracing model, the roof prism is located to retroreflect the light. In practice, the prism or roof mirror is usually off center, which aggravates the deterioration of the spot. Thus, the single-grating expander outputs a beam of poor quality.
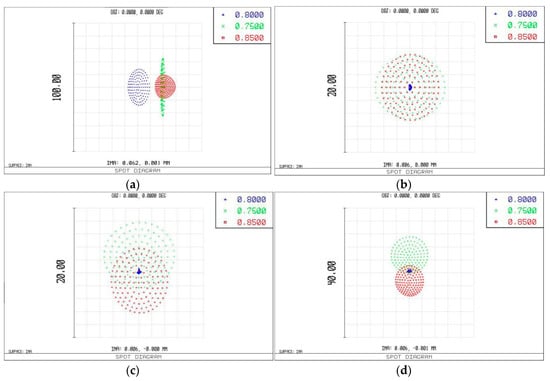
Figure 2.
Spot in the far-field of an Offner stretcher (all figures in micrometers). The residual angular dispersions are 0.66, 0, 0.125, and 0.24 μrad/nm, respectively. (a) The single-grating stretcher; (b) the double-grating stretcher, with Δθ = 0 μrad; (c) the double-grating stretcher, with Δθ = 174.4 μrad; (d) the double-grating stretcher, with Δθ = 348.9 μrad.
To eliminate spherical aberration and spatial dispersion resulting from aberration completely in the broadband, we adopt the double-grating Offner stretcher shown in Figure 3. The input pulse is diffracted by a grating at the spherical center, in contrast to a grating away from the spherical center of a traditional Offner stretcher. Such a double-grating Offner stretcher produces an output beam of high quality (shown in Figure 2b) and is a better choice. The pulse duration is stretched to 2.1 ns in our calculation.
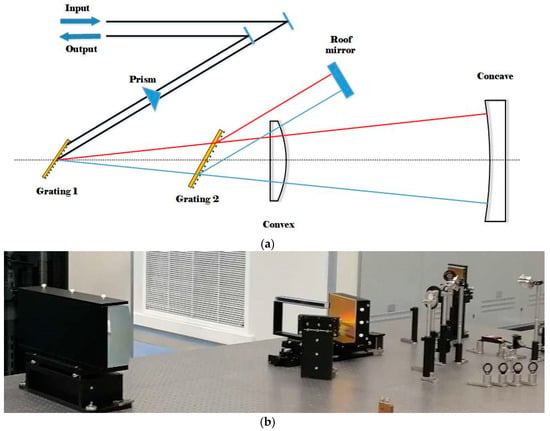
Figure 3.
Double-grating Offner stretcher at SULF. The grating groove is 1480/mm, the radii of the concave and convex mirrors are 2000 and 1000 mm, respectively, and the separation of the two gratings is 741.8 mm. (a) Aerial view sketch; (b) photograph.
The grating compressor structure employed in the SULF front end is shown in Figure 4a. The pulse compressor has a positive grating distance and, in contrast to the Offner stretcher, has a similar but negative grating distance. The mismatch between the stretcher and the compressor can compensate for the 2nd- and 3rd-order material dispersion of the system but results in high-order dispersion. In the double-grating stretcher, the two gratings must have the same attitude (parallel). With the interference amongst the spherical mirror, roof mirror, and prism, parallel misalignment becomes a significant problem, which increases the residual angular dispersion of the output spot and phase distortion of the pulse, making the amplified pulse difficult to compress. The focal spots of the far-field are shown in Figure 2c,d, where Δθ is the angle of deviation of the grating attitude.
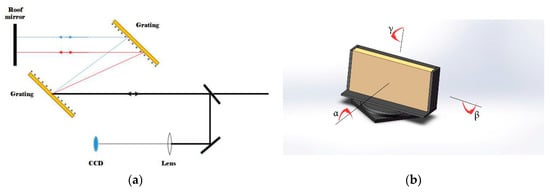
Figure 4.
(a) Sketch of the conventional method of grating calibration in a grating compressor, in which the only disturbance term is that of the roof mirror; (b) the three grating rotation angles α, β, and γ.
The angular dispersion is determined by the three rotation angles α, β, and γ of the grating as shown in Figure 4b, where, α regulates the grating ruling direction, β maintains the grating plane upright, and γ modifies the incident angle of the beam. According to the analyses and experimental results of Liu [32], these three-degrees-of-freedom affect the spatial chirp simultaneously, which makes grating adjustment challenging. For the above-mentioned reasons, we are motivated to not only ensure the accuracy of grating angles, but also to establish a standard for grating attitude.
Gravity is a stable vector in the laboratory, whose offset is negligible in an experimental station of hundreds or thousands of square meters, as is the pointing direction of the laser beam. They are good references for optical elements, especially gratings. The pointing direction of a laser is oriented by a self-leveling crossline laser referencing gravity, which provides horizontal, vertical, and crossline laser planes, as shown in the sketch of Figure 5. Plane A is the horizontal and plane B is perpendicular to plane A. Not only the grating attitude (angular orientation), but also the attitudes of all the optical elements in our system can be calibrated to a standard that is defined by gravity. In the SULF 10-PW frond end, the self-leveling crossline laser is firstly used for rapid calibration of the optical surfaces by measuring the autocorrelation. This operation greatly reduces the number of degrees of freedom in optical systems and the number of interference terms, especially in the double-grating Offner stretcher and grating compressor. As a result, the output beam quality is much higher, which greatly improves the focusing ability. The experimental results are shown in the next section.
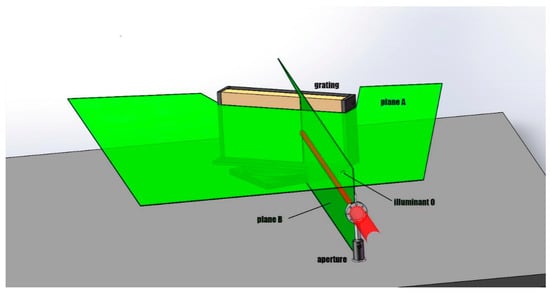
Figure 5.
Schematic of grating adjustment. Plane A and Plane B are orthogonal, and are formed by the illuminant O. The red cylinder represents the incident laser, apodized by the aperture and incident on the grating.
3. Results and Conclusions
We arranged our stretcher and compressor using the method of the previous section, and found strong evidence that the method is reliable. The spatial dispersion of the double-grating Offner stretcher is shown in Figure 6a, and the near-field and far-field spots are shown in Figure 6b,c, respectively. The far-field spots were focused by a f/800 lens, and were characterized with an offset from the focus ranging from −200 to 200 mm. The spatial dispersion and angular dispersion were well handled by our stretcher, which benefited from perfect optical element attitude. Additionally, wavefront aberrations of two spots between this double-grating Offner stretcher have been measured, as shown in Figure 7. Key Offner stretcher data are presented in Table 2. The increase of the Strehl ratio may be caused by instrument error, especially as the two spots are close to the diffraction limit. The Strehl ratio measured by the SID4 is 0.99, which indicates good focusability of the laser beam, although the ratio it is a little overestimated according to the actual measured focus [38].
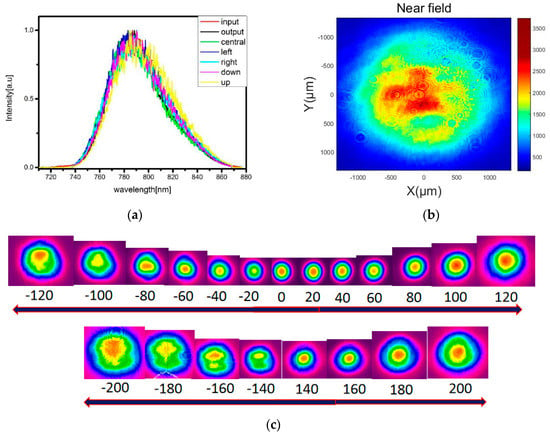
Figure 6.
Measurement results at the output of the Offner stretcher. (a) the spectrum of the output pulse; (b) the near-field spot; (c) the far-field spot. Offsets are in millimeters.
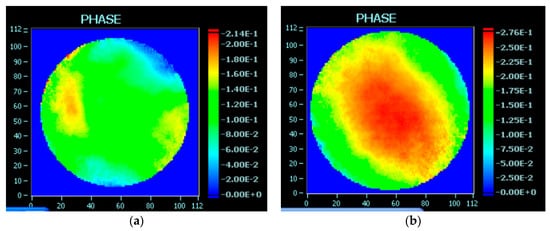
Figure 7.
Wavefront phase near the double-grating Offner stretcher, where the units are wavelength (800 nm). (a) Before stretcher; (b) after stretcher.

Table 2.
Key data for Offner stretcher wavefront.
Owing to the spectrum shaping of the AOPDF, spectral redshift during amplification is effectively suppressed. Meanwhile a Dazzler-Wizzler feedback system plays a critical role in dispersion management. We used a commercial measurement device (Fastlite, Wizzler) to measure the characteristics of the recompressed pulse. The final spectrum, spectral phase, pulse contrast, and far-field focused spot measurements after pre-compression are shown in Figure 8. The amplified pulse continuum can theoretically be compressed to <24 fs. It should be noted that the wavelength component from 800 to 850 nm is suppressed sufficiently for energy amplification to 10 PW. The maximum phase difference is less than 1.1 rad. It is expected that even with the redshift of PW-class amplification, a Fourier-transform-limited pulse, supported by the bandwidth of this system, can easily attain <24 fs. After passing through the compressor, the laser beam with a diameter of 35 mm is focused by an off-axis parabolic mirror with a focal length of 748 mm. The size of the focal spot obtained, as shown in Figure 8c, is very close to the diffraction limit. Benefiting from the all multipass amplifier design, the pulse contrast reaches 1011, which is a significant improvement compared to that of the prototype.
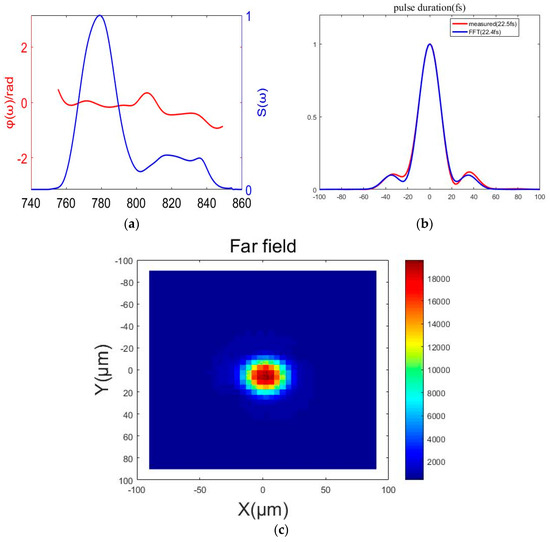
Figure 8.
Measurement results after the compressor. (a) Spectral intensity S(ω) and phase curve ϕ(ω); (b) pulse duration; (c) focused spot.
To conclude, this paper introduces the dispersion management system of the front end at SULF. In this system, a novel standard for grating adjustment is proposed, based on a self-leveling crossline laser that references the orientation of a high precision laser beam to gravity. The method can easily be applied to every optical element in the laboratory as needed. Once the standard is established, the pulse duration and size of the focal spot can be brought closer to their theoretical limits. We believe that the method will improve the focusing ability of the φ-500-mm spot at the back end. Benefiting from our standard, as well as the aberration-free double-grating Offner stretcher and auxiliary AOPDF, a near Fourier-transform-limited pulse with a suitable amplification spectrum outputs at an energy of 6.5 J and a repetition rate of 1 Hz. This experimental result is the basis for a great deal of of petawatt laser compression in the terminal output.
Author Contributions
Conceptualization, X.L. (Xingyan Liu) and C.W.; Data curation, X.L. (Xingyan Liu), X.W. and L.Y.; Formal analysis, X.L. (Xingyan Liu) and C.W.; Investigation, X.L. (Xingyan Liu), C.W., X.W., X.L. (Xiaoming Lu), P.B., Y.L. (Yanqi Liu), Y.L. (Yanyan Li), K.L. and L.Y.; Project administration, Y.L. (Yuxin Leng) and R.L.; Resources, Y.L. (Yanqi Liu), Y.L. (Yanyan Li), Y.L. (Yuxin Leng) and R.L.; Software, X.L. (Xingyan Liu); Supervision, C.W., X.L. (Xiaoming Lu), Y.L. (Yanqi Liu), L.Y., Y.L. (Yuxin Leng) and R.L.; Validation, Y.L. (Yuxin Leng) and R.L.; Visualization, X.L. (Xingyan Liu) and X.W.; Writing – original draft, X.L. (Xingyan Liu); Writing – review & editing, X.L. (Xingyan Liu), C.W., X.W. and L.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The Strategic Priority Research Program of the Chinese Academy of Sciences, (XDB16030100); International S&T Cooperation Program of China, (2016YFE0119300); Program of Shanghai Academic/Technology Research Leader, (18XD1404200); Shanghai Municipal Science and Technology Major Project, (2017SHZDZX02); Shanghai special science and technology innovation supported project, (2019-jmrh1-kj1).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 56, 219–221. [Google Scholar] [CrossRef]
- Dubietis, A.; Jonusauskas, G.; Piskarskas, A. Powerful femtosecond pulse generation by chirped and stretched pulse parametric amplification in BBO crystal. Opt. Commun. 1992, 88, 437–440. [Google Scholar] [CrossRef]
- Stepanenko, Y.; Radzewicz, C. High-gain multipass noncollinear optical parametric chirped pulse amplifier. Appl. Phys. Lett. 2005, 86, 211120. [Google Scholar] [CrossRef]
- Stepanenko, Y.; Radzewicz, C. Multipass non-collinear optical parametric amplifier for femtosecond pulses. Opt. Express 2006, 14, 779–785. [Google Scholar] [CrossRef] [PubMed]
- Li, X.L.; Liu, H.J.; Wang, H.Y.; Zhao, W.; Wang, Y.; Shi, S.X. Compact high gain double-pass optical parametric chirped pulse amplifier. Eur. Phys. J. D 2008, 47, 309–312. [Google Scholar] [CrossRef]
- Danson, C.N.; Haefner, C.; Bromage, J.; Butcher, T.; Chanteloup, J.-C.F.; Chowdhury, E.A.; Galvanauskas, A.; Gizzi, L.A.; Hein, J.; Hillier, D.I.; et al. Petawatt and exawatt class lasers worldwide. High Power Laser Sci. Eng. 2019, 7. [Google Scholar] [CrossRef]
- Chériaux, G.; Giambruno, F.; Fréneaux, A.; Leconte, F.; Ramirez, L.P.; Georges, P.; Druon, F.; Papadopoulos, D.N.; Pellegrina, A.; Le Blanc, C.; et al. Apollon-10P: Status and implementation. In Proceedings of the AIP Conference, Szeged, Hungary, 14–18 November 2011; AIP Publishing: Melville, NY, USA, 2012; Volume 1462, pp. 78–83. [Google Scholar]
- Hernandez-Gomez, C.; Blake, S.P.; Chekhlov, O.; Clarke, R.; Dunne, A.M.; Galimberti, M.; Hancock, S.; Heathcote, R.; Holligan, P.; Lyachev, A.; et al. The vulcan 10 PW project. J. Physics: Conf. Ser. 2010, 244, 032006. [Google Scholar] [CrossRef]
- Li, W.; Gan, Z.; Yu, L.; Wang, C.; Liu, Y.; Guo, Z.; Xu, L.; Xu, M.; Hang, Y.; Xu, Y.; et al. 339 J high-energy Ti:sapphire chirped-pulse amplifier for 10 PW laser facility. Opt. Lett. 2018, 43, 5681–5684. [Google Scholar] [CrossRef] [PubMed]
- Kane, S.; Squier, J. Fourth-order-dispersion limitations of aberration-free chirped-pulse amplification systems. J. Opt. Soc. Am. B 1997, 14, 1237. [Google Scholar] [CrossRef]
- Verluise, F.; Laude, V.; Cheng, Z.; Spielmann, C.; Tournois, P. Amplitude and phase control of ultrashort pulses by use of an acousto-optic programmable dispersive filter: Pulse compression and shaping. Opt. Lett. 2000, 25, 575–577. [Google Scholar] [CrossRef]
- Gibson, E.A.; Gaudiosi, D.M.; Kapteyn, H.; Jimenez, R.; Kane, S.; Huff, R.; Durfee, C.; Squier, J. Efficient reflection grisms for pulse compression and dispersion compensation of femtosecond pulses. Opt. Lett. 2006, 31, 3363–3365. [Google Scholar] [CrossRef]
- Zeek, E.; Maginnis, K.; Backus, S.; Russek, U.; Murnane, M.; Mourou, G.; Kapteyn, H.; Vdovin, G. Pulse compression by use of deformable mirrors. Opt. Lett. 1999, 24, 493–495. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Wang, C.; Liu, Y.; Xu, Y.; Liu, Z.; Lu, J.; Li, Y.; Liu, X.; Li, Z.; Leng, Y.; et al. Dispersion management of the SULF front end. Quantum Electron. 2017, 47, 179–183. [Google Scholar] [CrossRef]
- Li, S.; Wang, C.; Liu, Y.; Xu, Y.; Li, Y.; Liu, X.; Gan, Z.; Yu, L.; Liang, X.Y.; Leng, Y.; et al. High-order dispersion control of 10-petawatt Ti:sapphire laser facility. Opt. Express 2017, 25, 17488–17498. [Google Scholar] [CrossRef] [PubMed]
- Gan, Z.; Yu, L.; Li, S.; Wang, C.; Liang, X.; Liu, Y.; Li, W.; Guo, Z.; Fan, Z.; Yuan, X.; et al. 200 J high efficiency Ti:sapphire chirped pulse amplifier pumped by temporal dual-pulse. Opt. Express 2017, 25, 5169–5178. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wang, C.; Li, S.; Xu, Y.; Chen, L.; Dai, Y.; Leng, Y. Fourth-order dispersion compensation for ultra-high-power femtosecond lasers. Opt. Commun. 2015, 357, 71–77. [Google Scholar] [CrossRef]
- Oliver, J.B.; Bromage, J.; Smith, C.; Sadowski, D.; Dorrer, C.; Rigatti, A.L. Plasma-ion-assisted coatings for 15 femtosecond laser systems. Appl. Opt. 2014, 53, A221–A228. [Google Scholar] [CrossRef]
- Sun, Z.; Chai, L.; Zhang, Z.; Wang, C.; Zhang, W.; Xie, X.; Huang, X.; Yuan, X. Mutual compensation of higher-order dispersion in chirped pulse amplification system with regenerative amplifier. Opt. Laser Technol. 2007, 39, 29–33. [Google Scholar] [CrossRef]
- Yakovlev, I. Stretchers and compressors for ultra-high power laser systems. Quantum Electron. 2014, 44, 393–414. [Google Scholar] [CrossRef]
- Dorrer, C. Spatiotemporal metrology of broadband optical pulses. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–16. [Google Scholar] [CrossRef]
- Fiorini, C.; Sauteret, C.; Rouyer, C.; Blanchot, N.; Seznec, S.; Migus, A. Temporal aberrations due to misalignments of a stretcher-compressor system and compensation. IEEE J. Quantum Electron. 1994, 30, 1662–1670. [Google Scholar] [CrossRef]
- Osvay, K.; Ross, I.N. On a pulse compressor with gratings having arbitrary orientation. Opt. Commun. 1994, 105, 271–278. [Google Scholar] [CrossRef]
- Pretzler, G.; Kasper, A.; Witte, K. Angular chirp and tilted light pulses in CPA lasers. Appl. Phys. A 2000, 70, 1–9. [Google Scholar] [CrossRef]
- Osvay, K.; Kovacs, A.P.; Heiner, Z.; Kurdi, G.; Klebniczki, J.; Csatari, M. Angular dispersion and temporal change of femtosecond pulses from misaligned pulse compressors. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 213–220. [Google Scholar] [CrossRef]
- Bromage, J.; Dorrer, C.; Millecchia, M.; Bunkenburg, J.; Jungquist, R.; Zuegel, J.D. A front end for ultra-intense OPCPA. AIP Conf. Proc. 2012, 1462, 74–77. [Google Scholar]
- Bahk, S.-W.; Rousseau, P.; Planchon, T.A.; Chvykov, V.; Kalintchenko, G.; Maksimchuk, A.; Mourou, G.A.; Yanovsky, V. Generation and characterization of the highest laser intensities (10(22) W/cm2). Opt. Lett. 2004, 29, 2837–2839. [Google Scholar] [CrossRef]
- Yoon, J.W.; Jeon, C.; Shin, J.; Lee, S.K.; Lee, H.W.; Choi, I.W.; Kim, H.T.; Sung, J.H.; Nam, C.H. Achieving the laser intensity of 5.5x10(22) W/cm(2) with a wavefront-corrected multi-PW laser. Opt. Express. 2019, 27, 20412–20420. [Google Scholar] [CrossRef]
- Tiwari, G.; Gaul, E.; Martinez, M.; Dyer, G.; Gordon, J.; Spinks, M.; Toncian, T.; Bowers, B.; Jiao, X.; Kupfer, R.; et al. Beam distortion effects upon focusing an ultrashort petawatt laser pulse to greater than 1022 W/cm2. Opt. Lett. 2019, 44, 2764–2767. [Google Scholar] [CrossRef]
- Guo, Z.; Yu, L.; Wang, J.; Wang, C.; Liu, Y.; Gan, Z.; Li, W.; Leng, Y.; Liang, X.; Li, R. Improvement of the focusing ability by double deformable mirrors for 10-PW-level Ti: Sapphire chirped pulse amplification laser system. Opt. Express 2018, 26, 26776–26786. [Google Scholar] [CrossRef]
- Turcu, I.C.E.; Shen, B.; Neely, D.; Sarri, G.; Tanaka, K.A.; McKenna, P.; Mangles, S.P.D.; Yu, T.-P.; Luo, W.; Zhu, X.-L.; et al. Quantum electrodynamics experiments with colliding petawatt laser pulses. High Power Laser Sci. Eng. 2019, 7. [Google Scholar] [CrossRef]
- Liu, F.; Wang, Z.H.; Ma, J.L.; Zhang, L.; Wang, J.; Wang, S.; Lin, X.X.; Li, Y.T.; Chen, L.M.; Wei, Z.Y.; et al. Compression grating alignment by far-field monitoring. Appl. Phys. A 2010, 101, 587–591. [Google Scholar] [CrossRef]
- Li, S.; Li, Z.; Wang, C.; Xu, Y.; Li, Y.; Leng, Y.; Li, R. Broadband spectrographic method for precision alignment of compression gratings. Opt. Eng. 2016, 55, 086105. [Google Scholar] [CrossRef]
- Börzsönyi, A.; Mangin-Thro, L.; Cheriaux, G.; Osvay, K. Two-dimensional single-shot measurement of angular dispersion for compressor alignment. Opt. Lett. 2013, 38, 410–412. [Google Scholar] [CrossRef] [PubMed]
- Available online: http://www.unitedcrystals.com/KDPProp.html. (accessed on 15 July 2018).
- Ghosh, G. Sellmeier coefficients and dispersion of thermo-optic coefficients for some optical glasses. Appl. Opt. 1997, 36, 1540–1546. [Google Scholar] [CrossRef] [PubMed]
- Chériaux, G.; Walker, B.; DiMauro, L.F.; Rousseau, P.; Salin, F.; Chambaret, J.P. Aberration-free stretcher design for ultrashort-pulse amplification. Opt. Lett. 1996, 21, 414–416. [Google Scholar] [CrossRef] [PubMed]
- Pirozhkov, A.S.; Fukuda, Y.; Nishiuchi, M.; Kiriyama, H.; Sagisaka, A.; Ogura, K.; Mori, M.; Kishimoto, M.; Sakaki, H.; Dover, N.P.; et al. Approaching the diffraction-limited, bandwidth-limited Petawatt. Opt. Express 2017, 25, 20486. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).