Volumetric Calibration Refinement of a Multi-Camera System Based on Tomographic Reconstruction of Particle Images
Abstract
1. Introduction
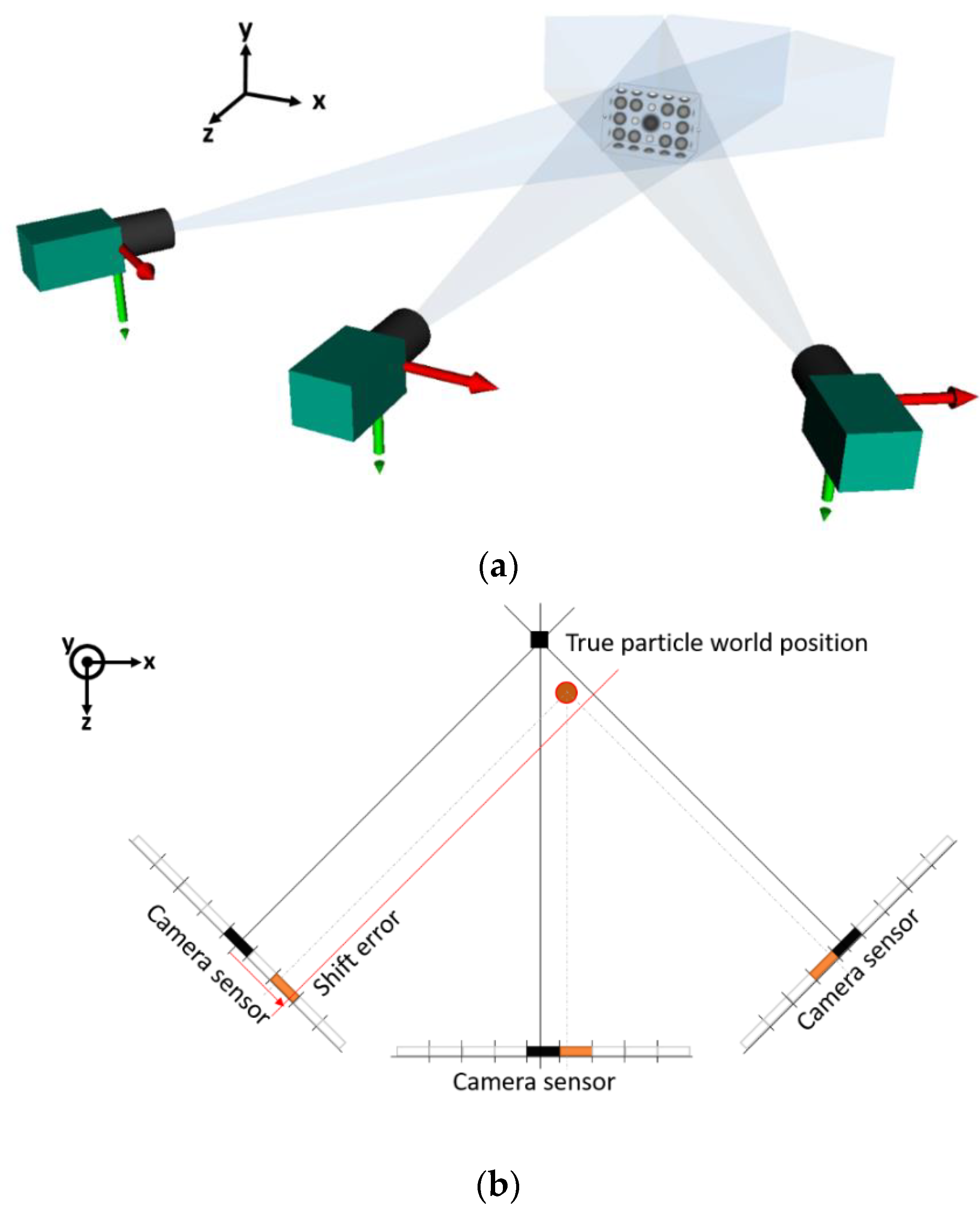
2. Methodology of Calibration Refinement
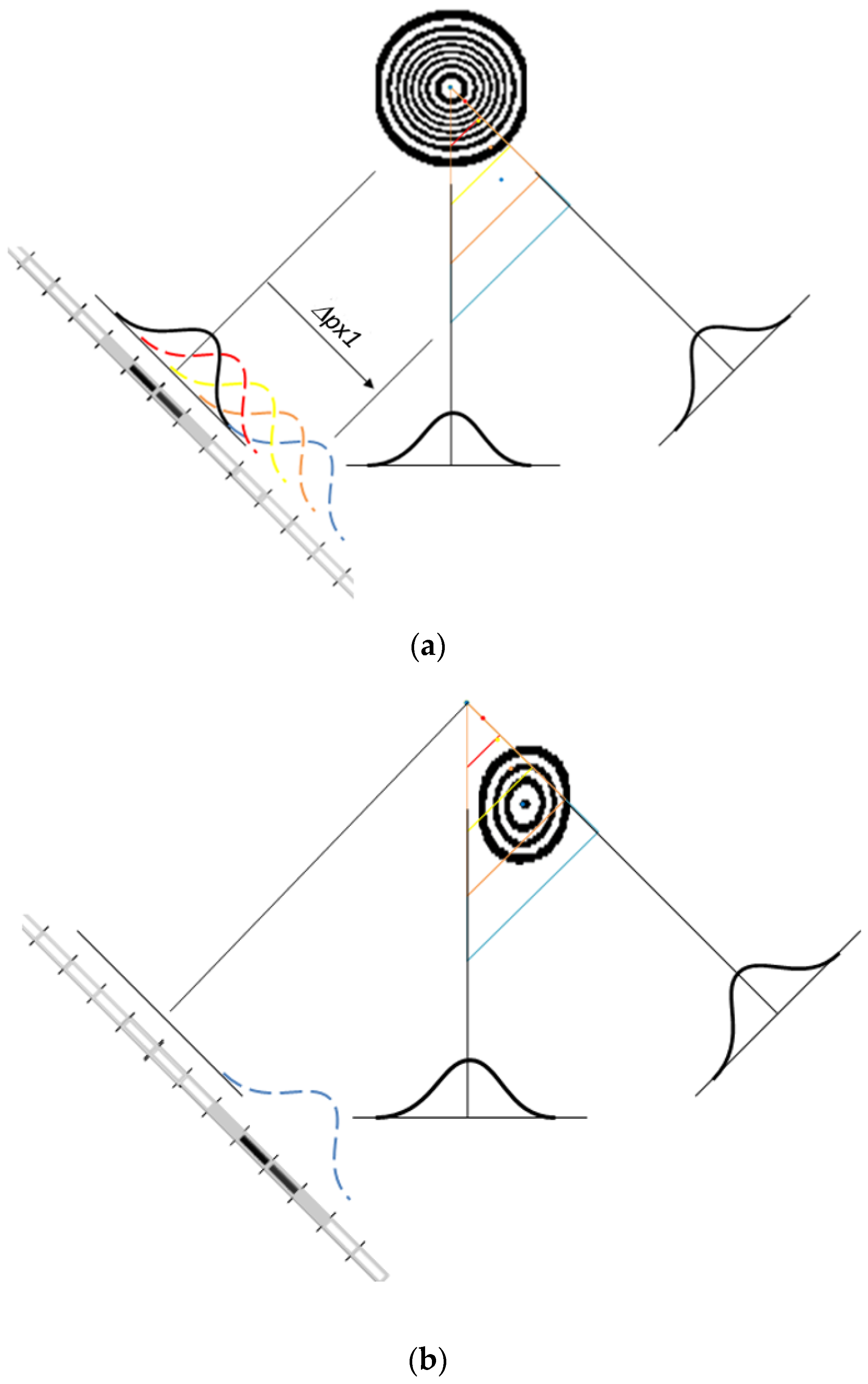
2.1. The Shape of a Particle Reconstruction with Camera Mismatch
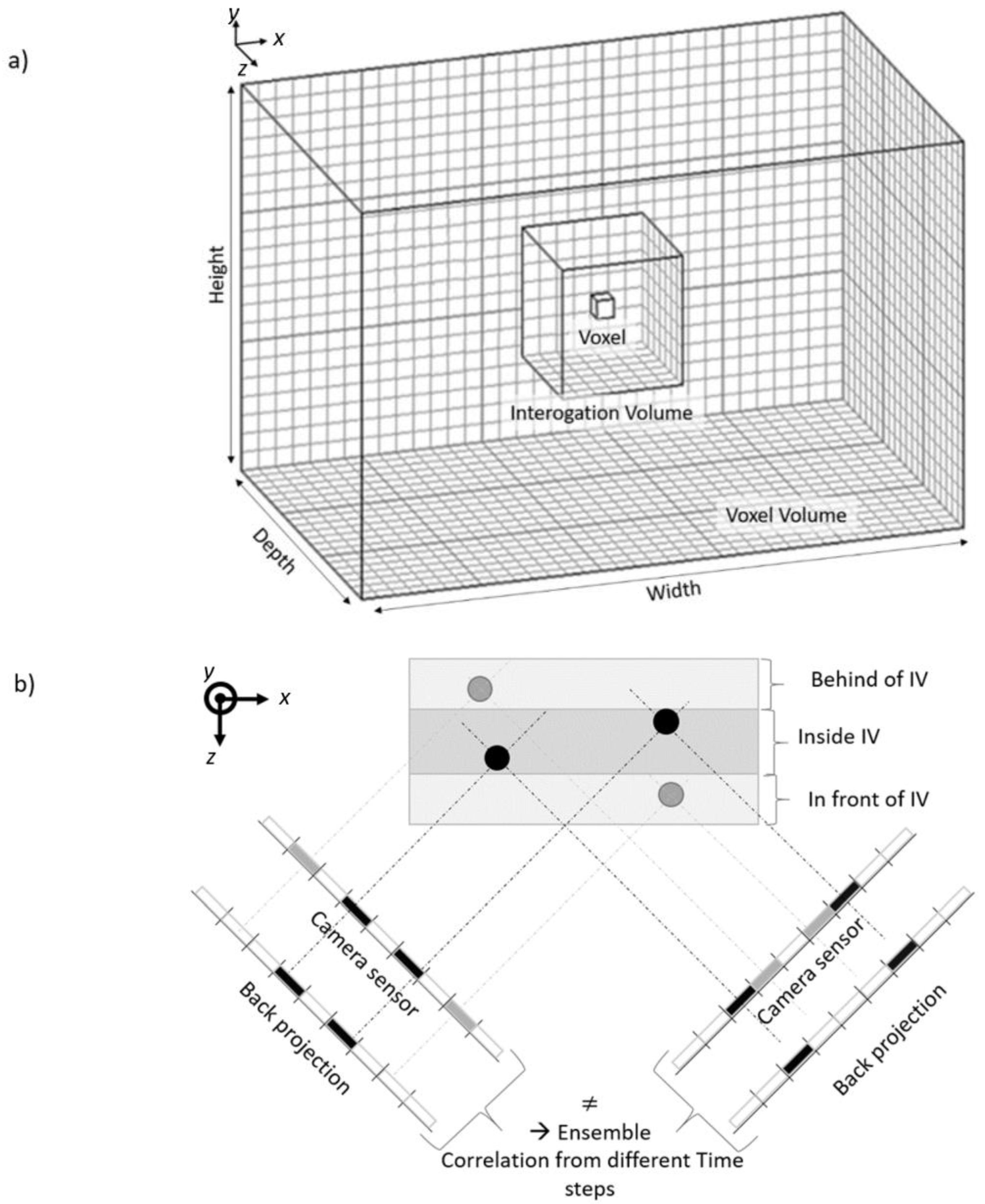
2.2. Cross-Correlation of Original Images with Back-Projected Images
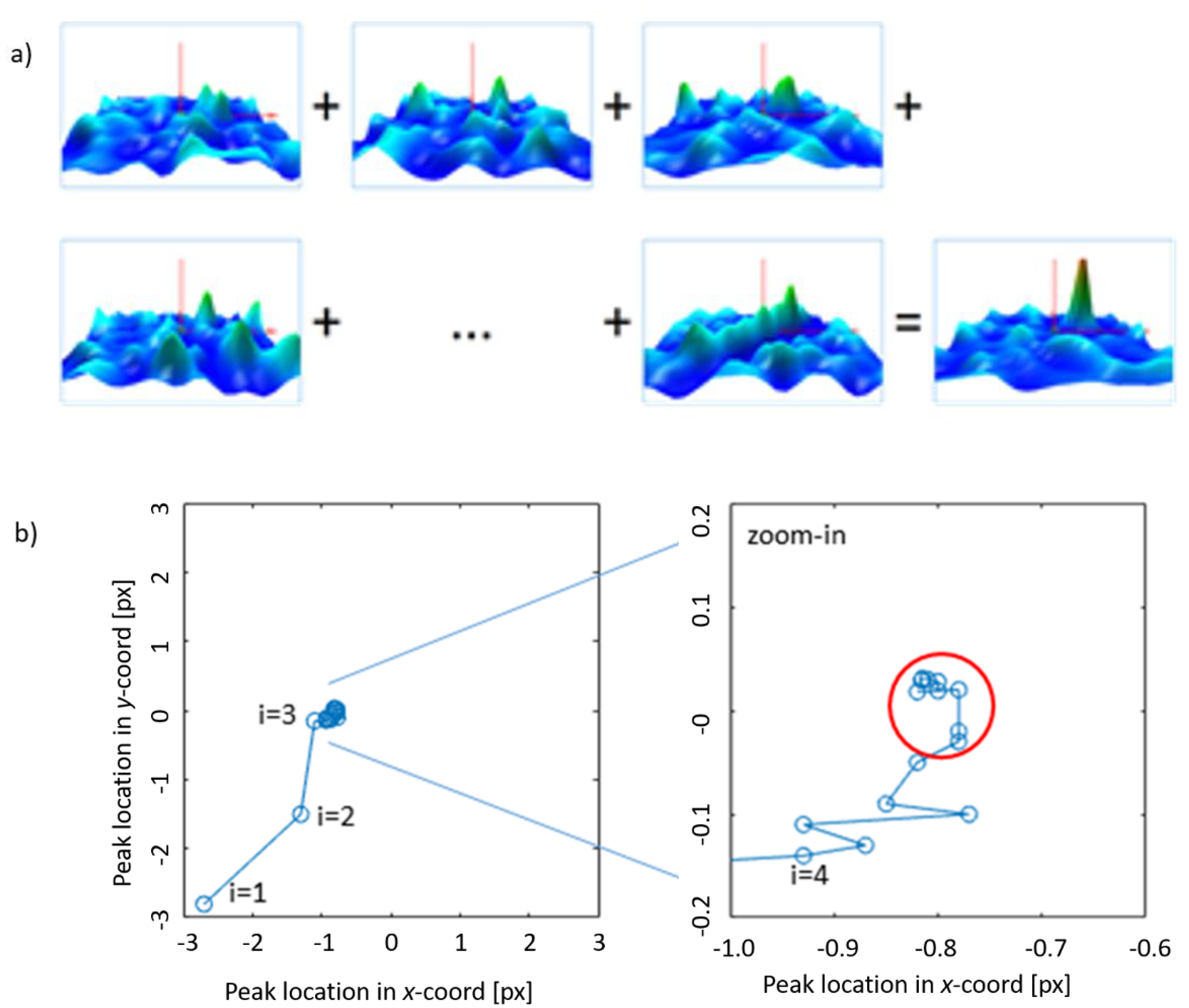
2.3. Ensemble Averaging of Correlation Maps from Snapshots
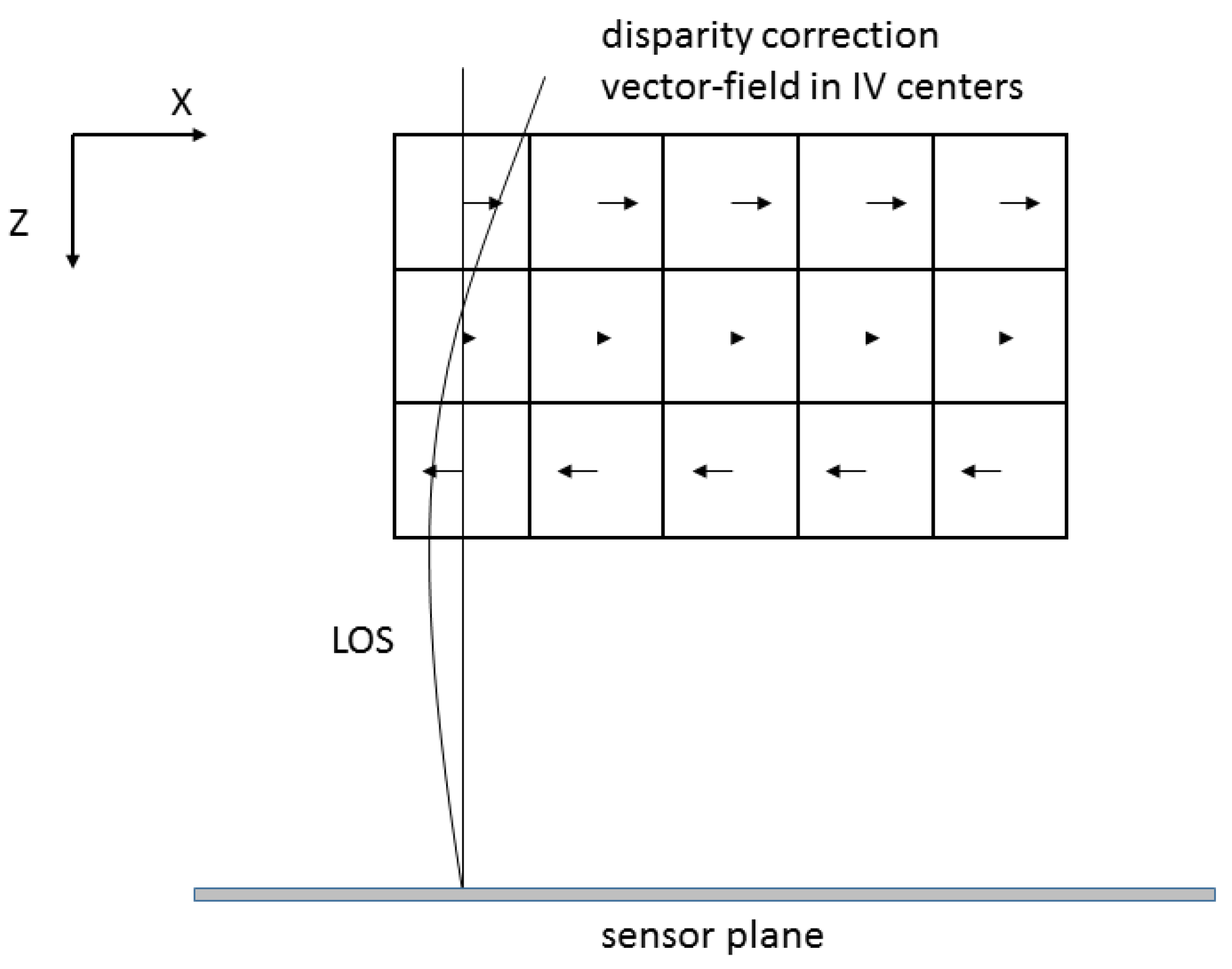
2.4. Correction Steps
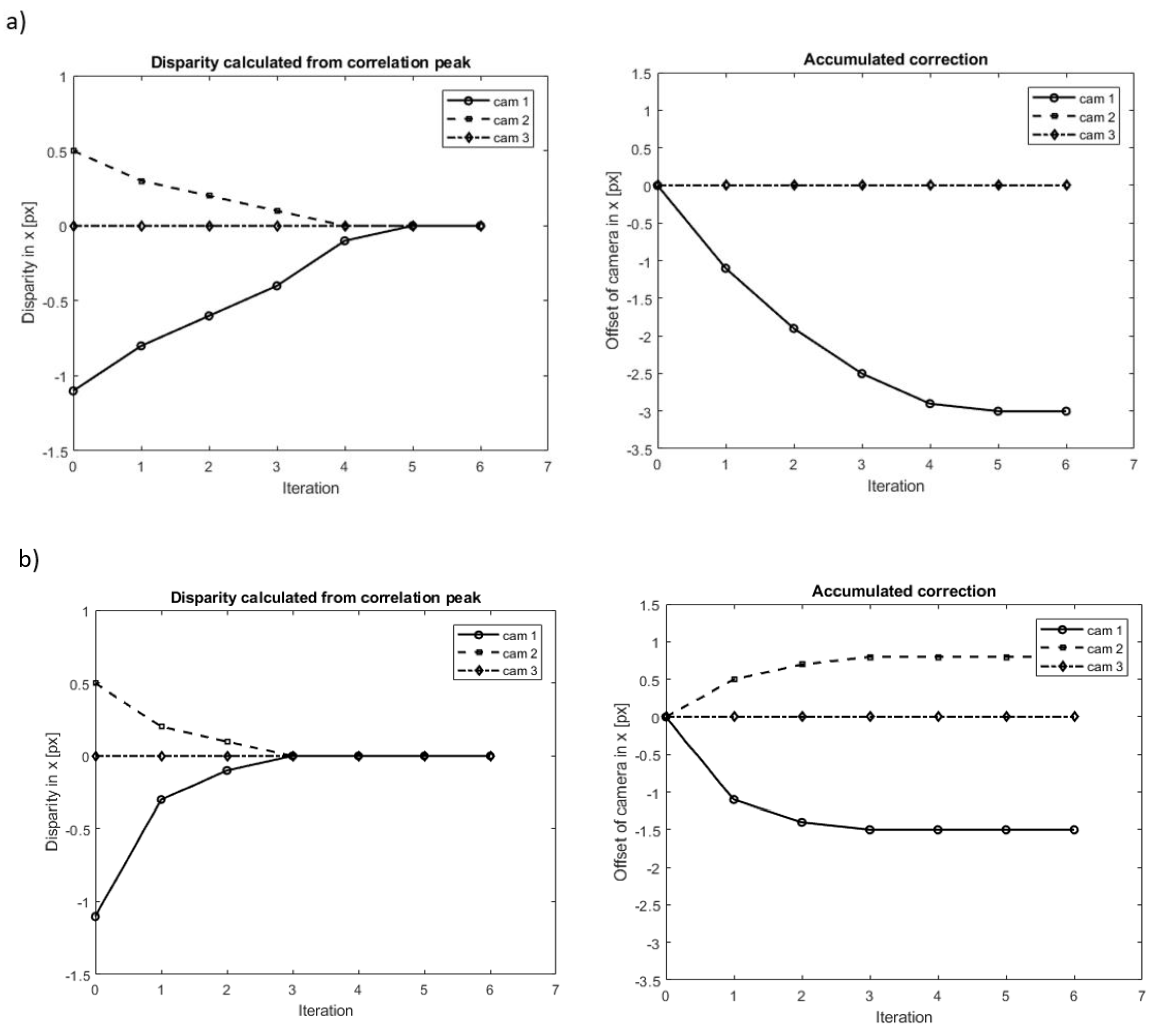
2.5. Typical Iterative Correction Performance
2.6. Treating Larger Mismatch with Image Pre-Processing Using Gaussian Blur
3. Numerical Assessment
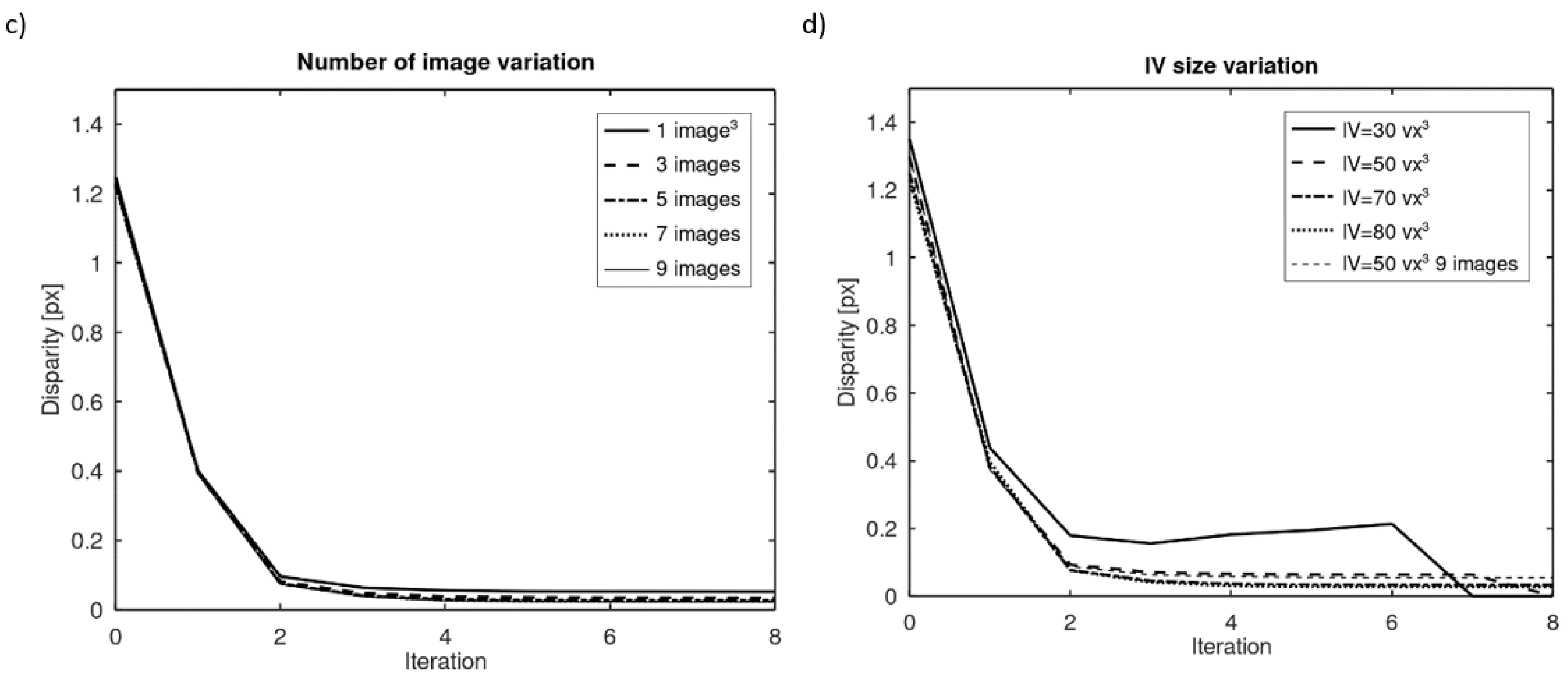
3.1. Influence of Particle Image Diameter and Seeding Density
3.2. Influence of Errors on All Cameras
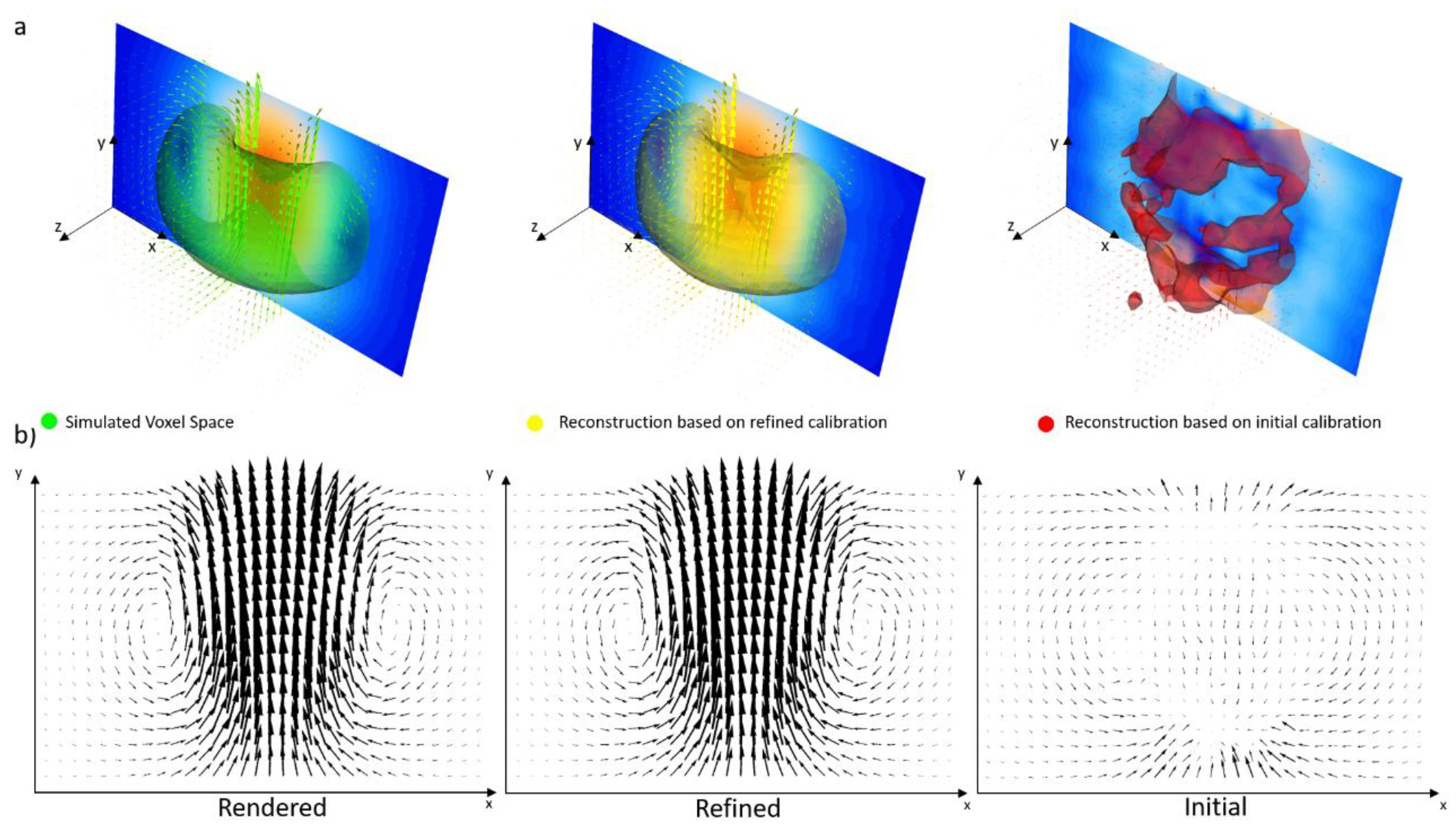
3.3. Performance Tests with Synthetic Velocity Data
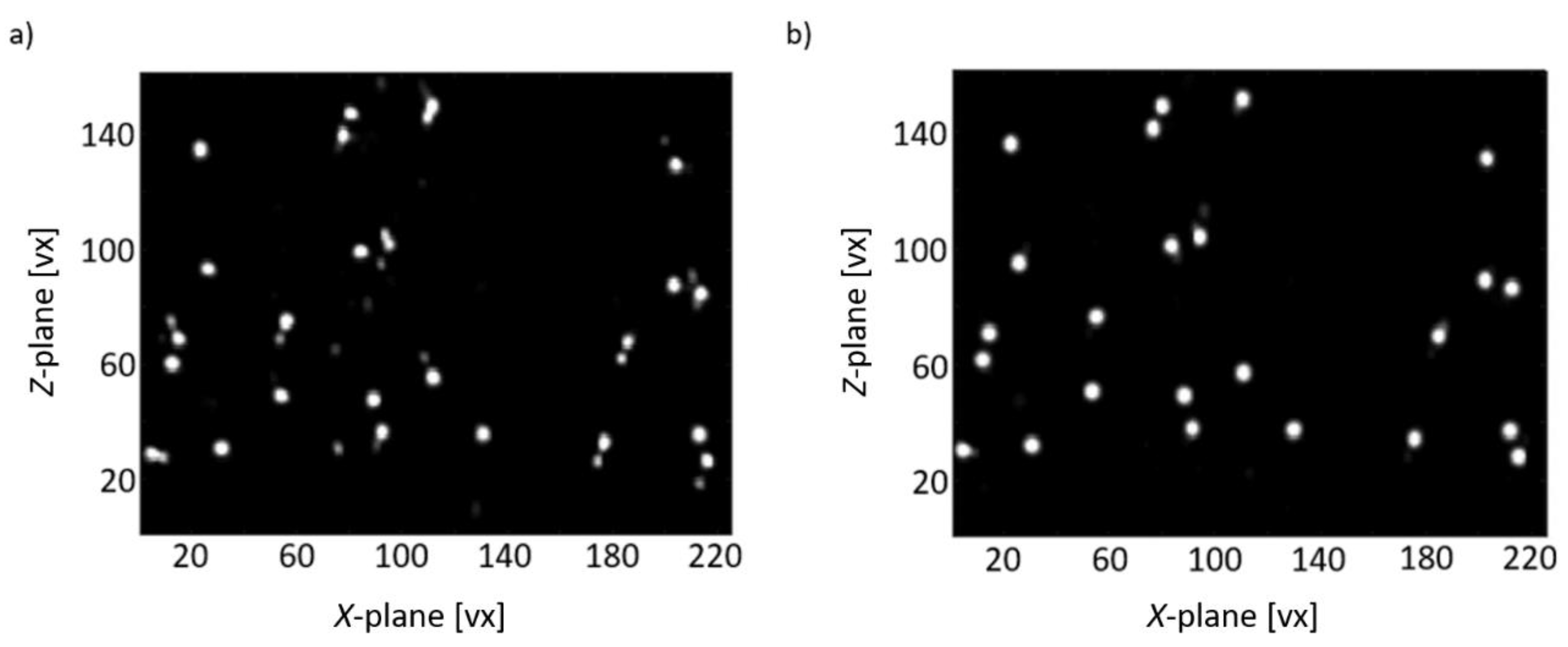
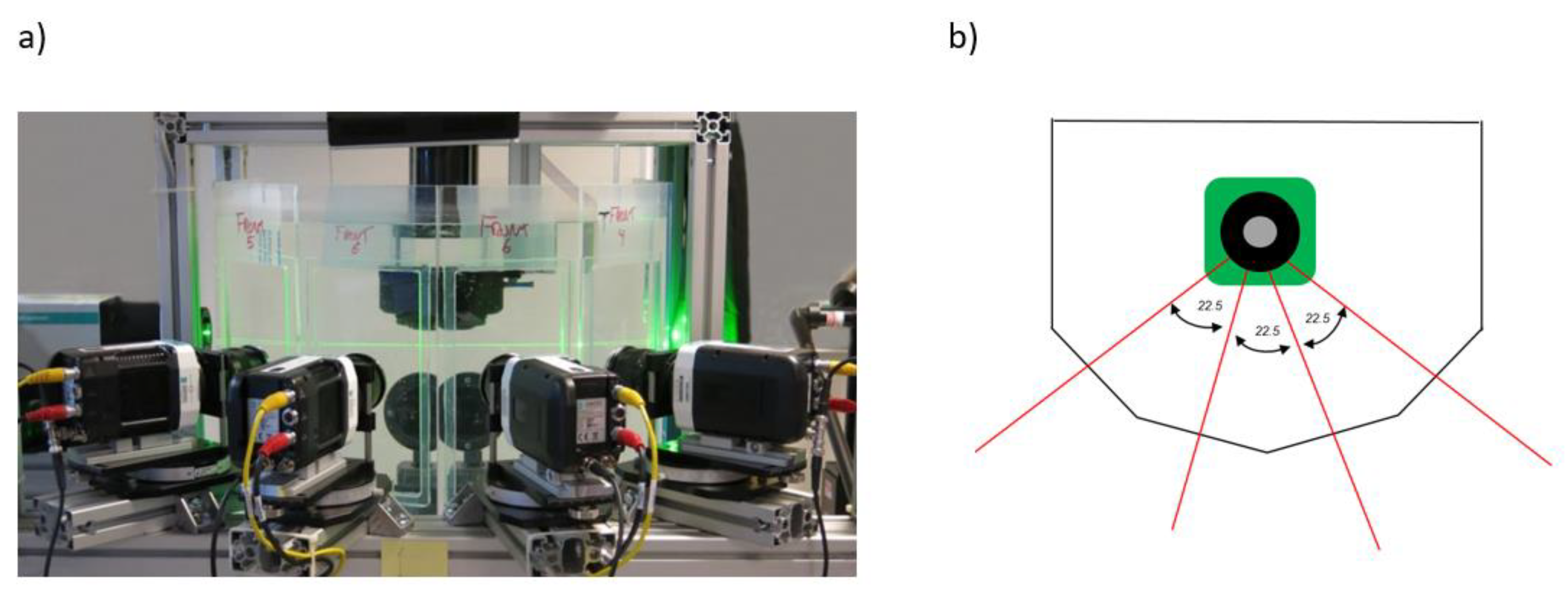
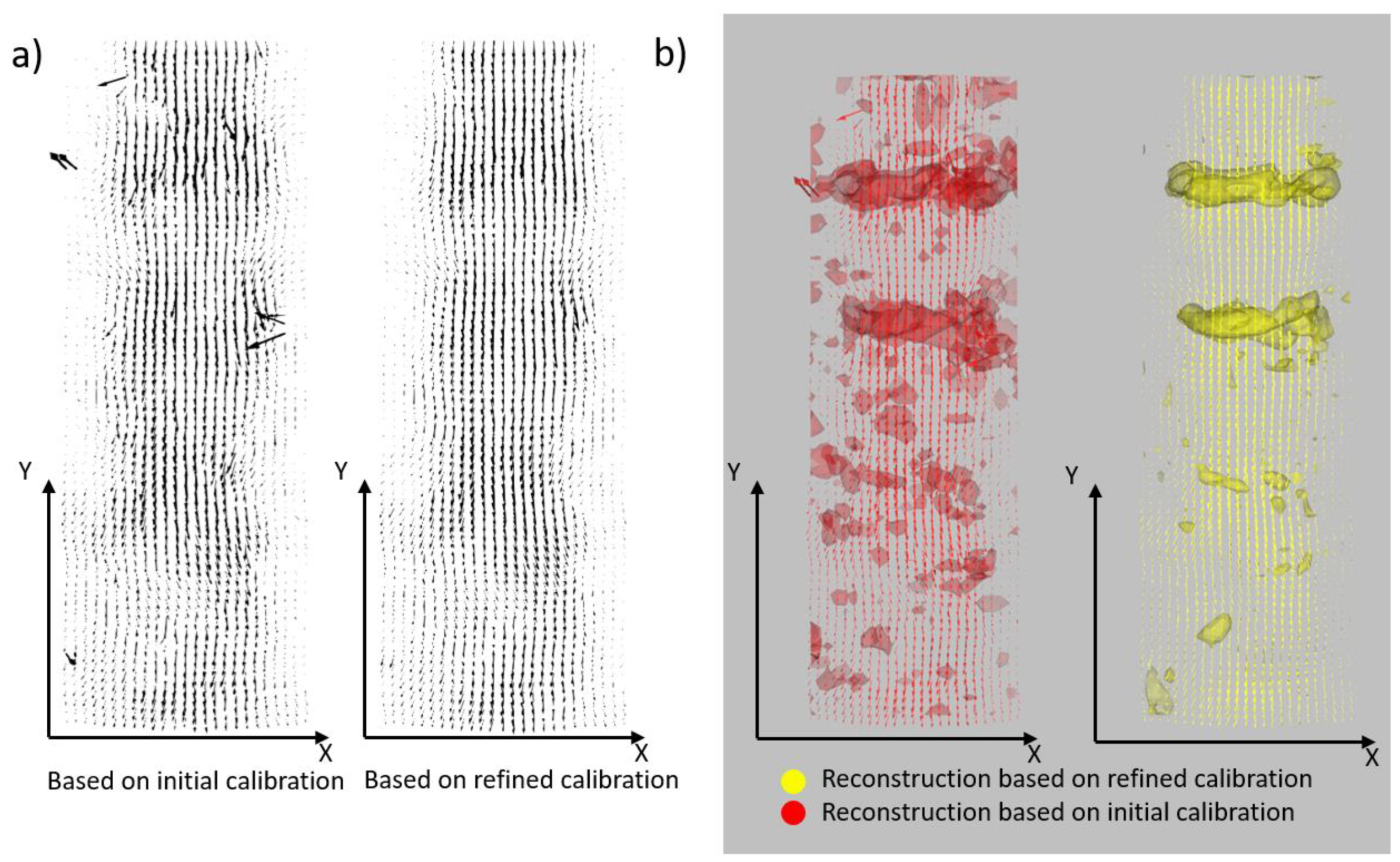
4. Performance Tests with Experimental Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Cam #1 | Cam #2 | Cam #3 | Cam #4 | |
|---|---|---|---|---|
| Camera size full width × height (px) | 250 × 250 | 250 × 250 | 250 × 250 | |
| Camera alpha α | α1 = −45° | α2 = 0° | α3 = +45° | |
| Camera beta β | β1 = 0° | β2 = 0° | β3 = 0° | |
| Camera pixel size (µm) | 10 | 10 | 10 | |
| Magnification (mm/vx) | 1/10 | 1/10 | 1/10 | |
| pixel to voxel ratio | 1 | 1 | 1 | |
| Lens configuration | Ideal telecentric | Ideal telecentric | Ideal telecentric | |
| Initial mapping function | Ideal rectilinear | Ideal rectilinear | Ideal rectilinear | |
| Initial camera error translational | Δpx = +3 | - | - | |
| Initial camera error rotational | Δγ1 = 0° | - | - | |
| Refined mapping and LOS equation | 3rd order X,Y 2nd order Z | 3rd order X,Y 2nd order Z | 3rd order X,Y 2nd order Z |
| Cam #1 | Cam #2 | Cam #3 | Cam #4 | |
|---|---|---|---|---|
| Camera size full width × height (px) | 800 × 500 | 800 × 500 | 800 × 500 | 800 × 500 |
| Camera alpha α | α1 = 0° | α2 = +45° | α3 = 0° | α4 = −45° |
| Camera beta β | β1 = −45° | β2 = 0° | β3 = +45° | Β4 = 0° |
| Camera pixel size (µm) | 10 | 10 | 10 | |
| Magnification (mm/vx) | 1/10 | 1/10 | 1/10 | 1/10 |
| pixel to voxel ratio | 1 | 1 | 1 | 1 |
| Lens configuration | Ideal pinhole | Ideal pinhole | Ideal pinhole | Ideal pinhole |
| Initial mapping function | Ideal rectilinear | Ideal rectilinear | Ideal rectilinear | Ideal rectilinear |
| Initial camera error translational (px) | Δpy = +5 | Δpy = +5 | Δpx = −3 | Δpx = −3 |
| Initial camera error rotational | Δγ1 = 0° | - | - | - |
| Refined mapping and LOS equation | 3rd order X,Y 2nd order Z | 3rd order X,Y 2nd order Z | 3rd order X,Y 2nd order Z | 3rd order X,Y 2nd order Z |
| Cam #1 | Cam #2 | Cam #3 | Cam #4 | |
|---|---|---|---|---|
| Camera size full width × height (px) | 1280 × 800 | 1280 × 800 | 1280 × 800 | 1280 × 800 |
| Camera alpha α | α1 = −33.75° | α2 = −11.25° | α3 = 11.25° | α4 = 33.75° |
| Camera beta β | β1 = 0° | β2 = 0° | β3 = 0° | β4 = 0° |
| Camera pixel size (µm) | 20 | 20 | 20 | 20 |
| Magnification (mm/vx) | 1/10 | 1/10 | 1/10 | 1/10 |
| pixel to voxel ratio | 1:1.1 | 1:1.1 | 1:1.1 | 1:1.1 |
| Lens configuration | Zeiss 100 mm | Zeiss 100 mm | Zeiss 100 mm | Zeiss 100mm |
| Initial mapping function | Soloff | Soloff | Soloff | Soloff |
| Initial camera error translational | unknown | unknown | unknown | unknown |
| Initial camera error rotational | unknown | unknown | unknown | unknown |
| Refined mapping and LOS equation | 3rd order X,Y 2nd order Z | 3rd order X,Y 2nd order Z | 3rd order X,Y 2nd order Z | 3rd order X,Y 2nd order Z |
Appendix B
Appendix C
References
- Soloff, S.M.; Adrian, R.J.; Liu, Z.C. Distortion compensation for generalized stereoscopic particle image velocimetry. Meas. Sci. Technol. 1997, 8, 1441–1454. [Google Scholar] [CrossRef]
- Arroyo, P.; Hinsch, K. Recent Developments of PIV towards 3D Measurements. In The PIV Book: Particle Image Velocimetry; Schroeder, A., Willert, C.E., Eds.; Topics Appl. Physics; Springer-Verlag: Berlin/Heidelberg, Germany, 2008; Volume 112, pp. 127–154. [Google Scholar]
- Scarano, F. Tomographic PIV: Principles and practice. Meas. Sci. Technol. 2012, 24, 12001. [Google Scholar] [CrossRef]
- Elsinga, G.E.; Scarano, F.; Wieneke, B.; van Oudheusden, B.W. Tomographic particle image velocimetry. Exp. Fluids 2006, 41, 933–947. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.E.; Scarano, F.; Kähler, C.; Wereley, S.T.; Kompenhans, J. Particle Imaging Velocimetry, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 978-3-319-68851-0. [Google Scholar]
- Weis, S.; Schröter, M. Analyzing X-ray tomographies of granular packings. Rev. Sci. Instrum. 2017, 88, 051809. [Google Scholar] [CrossRef] [PubMed]
- Sarno, L.; Papa, M.N.; Villani, P.; Tai, Y.C. An optical method for measuring the near-wall volume fraction in granular dispersions. Granul. Matter 2016, 18, 80. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, X.; Yao, L.; Gréhan, G.; Cen, K. Direct measurement of particle size and 3D velocity of a gas–solid pipe flow with digital holographic particle tracking velocimetry. Appl. Opt. 2015, 54, 2514–2523. [Google Scholar] [CrossRef] [PubMed]
- Spinewine, B.; Capart, H.; Larcher, M.; Zech, Y. Three-dimensional Voronoï imaging methods for the measurement of near-wall particulate flows. Exp. Fluids 2003, 34, 227. [Google Scholar] [CrossRef]
- Joshi, B.; Ohmi, K.; Nose, K. Novel Algorithms of 3D Particle Tracking Velocimetry Using a Tomographic Reconstruction Technique. J. Fluid Sci. Technol. 2012, 7, 242. [Google Scholar] [CrossRef][Green Version]
- Wieneke, B. Volume self-calibration for 3D particle image velocimetry. Exp. Fluids 2008, 45, 549–556. [Google Scholar] [CrossRef]
- Bruecker, C.H.; Hess, D.; Watz, B. Volumetric Calibration Refinement using masked back-projection and image correlation superposition. In Proceedings of the 19th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 16–19 July 2018. [Google Scholar]
- Atkinson, C.H.; Soria, J. Algebraic Reconstruction Techniques for Tomographic Particle Image Velocimetry. In Proceedings of the 16th Australasian Fluid Mechanics Conference, Brisbane, Australia, 2–7 December 2007. [Google Scholar]
- Kühn, M. Untersuchung Großskaliger Strömungsstrukturen in Erzwungener und Gemischter Konvektion Mit Der Tomografischen Particle Image Velocimetry. Ph.D. Thesis, Technische Universität Ilmenau, Ilmenau, Fakultät Für Maschinenbau, 2011. [Google Scholar]
- Santiago, J.G.; Wereley, S.T.; Meinhart, C.D.; Adrian, R.J. A particle image velocimetry system for microfluidics. Exp. Fluids 1998, 25, 316–319. [Google Scholar] [CrossRef]
- Cornic, P.; Illoul, C.; Le Ant, Y.; Cheminet, A.; Le Besnerais, G.; Champagnat, F. Calibration drift within a Tomo-PIV setup and Self-Calibration. In Proceedings of the 11th Symposium on Particle Image Velocimetry PIV’15, Santa Barbara, CA, USA, 14–16 September 2015. [Google Scholar]
- Novara, M.; Batenburg, K.J.; Scarano, F. Motion tracking-enhanced MART for tomographic PIV. Meas. Sci. Technol. 2010, 21, 35401. [Google Scholar] [CrossRef]
- de Silva, C.M.; Baidaya, R.; Marusic, I. Enhancing Tomo-PIV reconstructionquality by reducing ghost particles. Meas. Sci. Technol. 2013, 24, 024010. [Google Scholar] [CrossRef]
- Elsinga, G.E.; Westerweel, J.; Scarano, F.; Novara, M. On the velocity of ghost particles and the bias errors in Tomographic-PIV. Exp. Fluids 2011, 50, 825–838. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Westfeld, P.; Maas, H.G.; Pust, O.; Kitzhofer, J.; Brücker, C. 3D least square matching for volumetric velocity data processing. In Proceedings of the 15th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 5–8 July 2010. [Google Scholar]
- Maas, H.G.; Stefanidis, A.; Gruen, A. From Pixels to voxels: Tracking Volume Elements in Sequences of 3D Digital Images. In Proceedings of the ISPRS Commission III Symposium: Spatial Information from Digital Photogrammetry and Computer Vision, Munich, Germany, 5‒9 September 1994; Volume 30. Part 3/2. [Google Scholar]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, Stream, and Convergence Zones in Turbulent Flows; Center for Turbulence Research Report CTR-S88: Stanford, CA, USA, 1998. [Google Scholar]
- Mueller, K. Fast and Accurate Three-Dimensional Reconstruction from Cone-Beam Projection Data Using Algebraic Methods. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 1998. [Google Scholar]


| Particle Density ppp | Angular Displacement of Cam #1 and Cam #3 | Noise Level Variance | Initial Correction Step of Cam 1 (from +3 px Error-Shift) | Minimum Number of Ensemble Additions to Achieve Peak Position within 0.1 px Radius | Iterations to Correct Cam #1 Down to 0.1 px Offset |
|---|---|---|---|---|---|
| 0.001 | ±45° | 0 | −1.1 | 4 | 5 |
| 0.003 | ±45° | 0 | −1.0 | 6 | 7 |
| 0.005 | ±45° | 0 | −0.8 | 10 | 9 |
| 0.008 | ±45° | 0 | −0.4 | 20 | 13 |
| 0.010 | ±45° | 0 | −0.3 | 22 | - |
| 0.001 | ±22° | 0 | −0.6 | 4 | 10 |
| 0.001 | ±45° | 0.00 | −1.1 | 3 | 5 |
| 0.001 | ±45° | 0.01 | −0.6 | 6 | 7 |
| 0.001 | ±45° | 0.02 | −0.5 | 10 | 10 |
| 0.001 | ±45° | 0.03 | −0.6 | 20 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruecker, C.; Hess, D.; Watz, B. Volumetric Calibration Refinement of a Multi-Camera System Based on Tomographic Reconstruction of Particle Images. Optics 2020, 1, 114-135. https://doi.org/10.3390/opt1010009
Bruecker C, Hess D, Watz B. Volumetric Calibration Refinement of a Multi-Camera System Based on Tomographic Reconstruction of Particle Images. Optics. 2020; 1(1):114-135. https://doi.org/10.3390/opt1010009
Chicago/Turabian StyleBruecker, Christoph, David Hess, and Bo Watz. 2020. "Volumetric Calibration Refinement of a Multi-Camera System Based on Tomographic Reconstruction of Particle Images" Optics 1, no. 1: 114-135. https://doi.org/10.3390/opt1010009
APA StyleBruecker, C., Hess, D., & Watz, B. (2020). Volumetric Calibration Refinement of a Multi-Camera System Based on Tomographic Reconstruction of Particle Images. Optics, 1(1), 114-135. https://doi.org/10.3390/opt1010009





