A Triple Correlator of Radiation Intensities of a Multimode Semiconductor Laser
Abstract
:1. Introduction
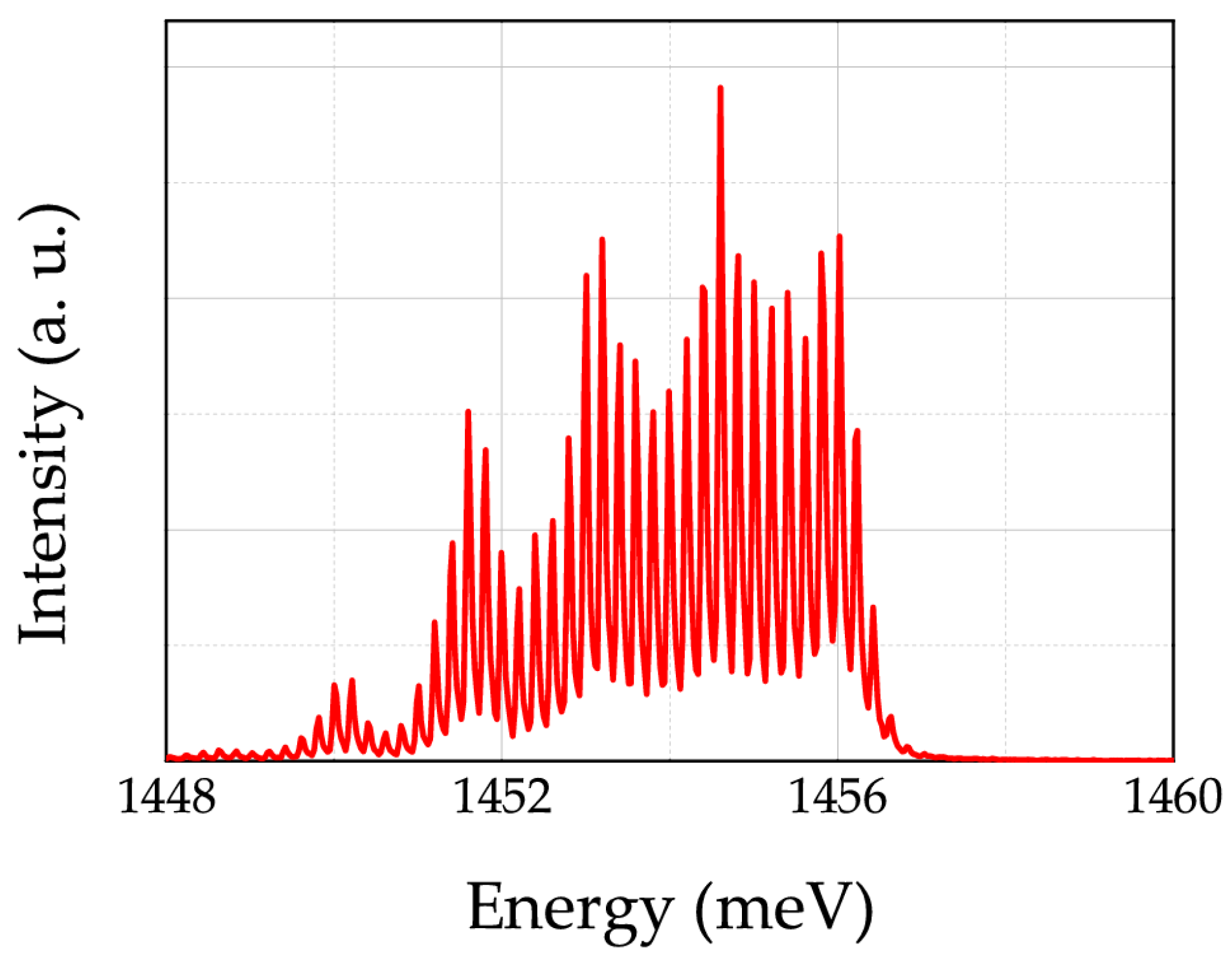
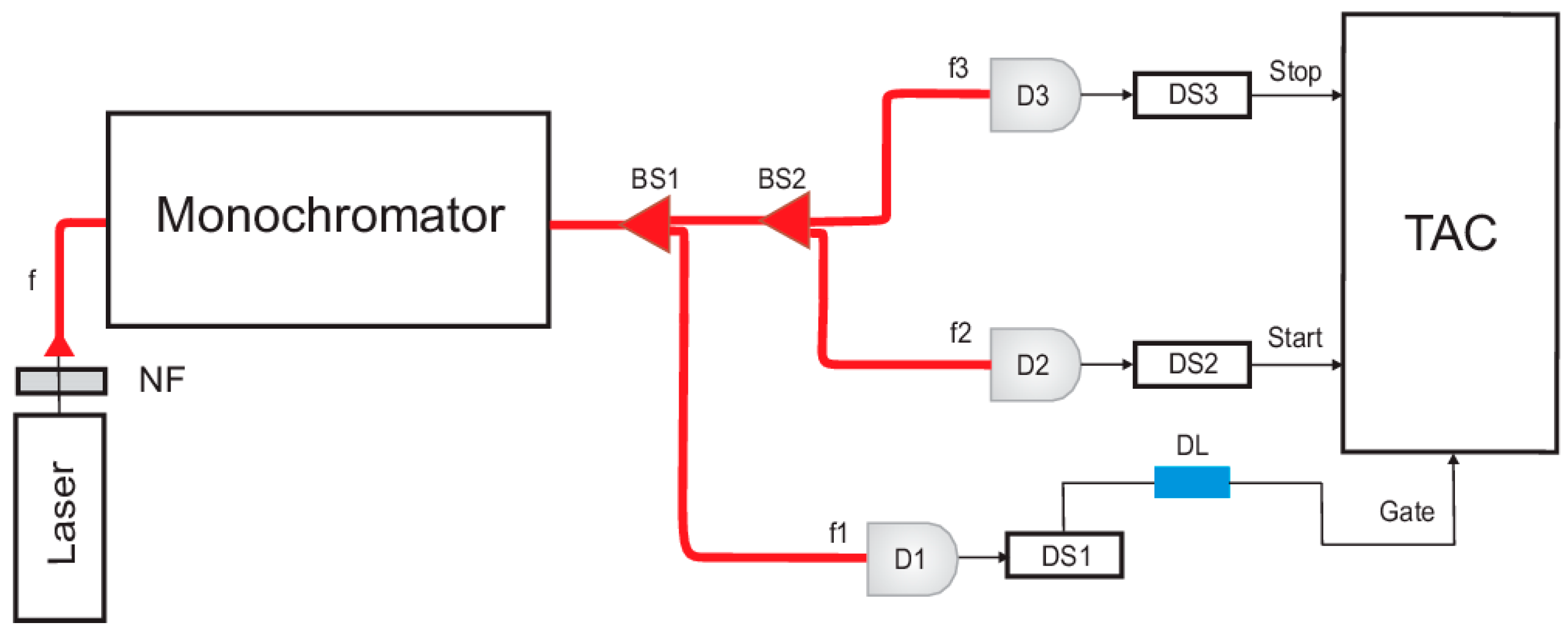
2. Experiments and Methods
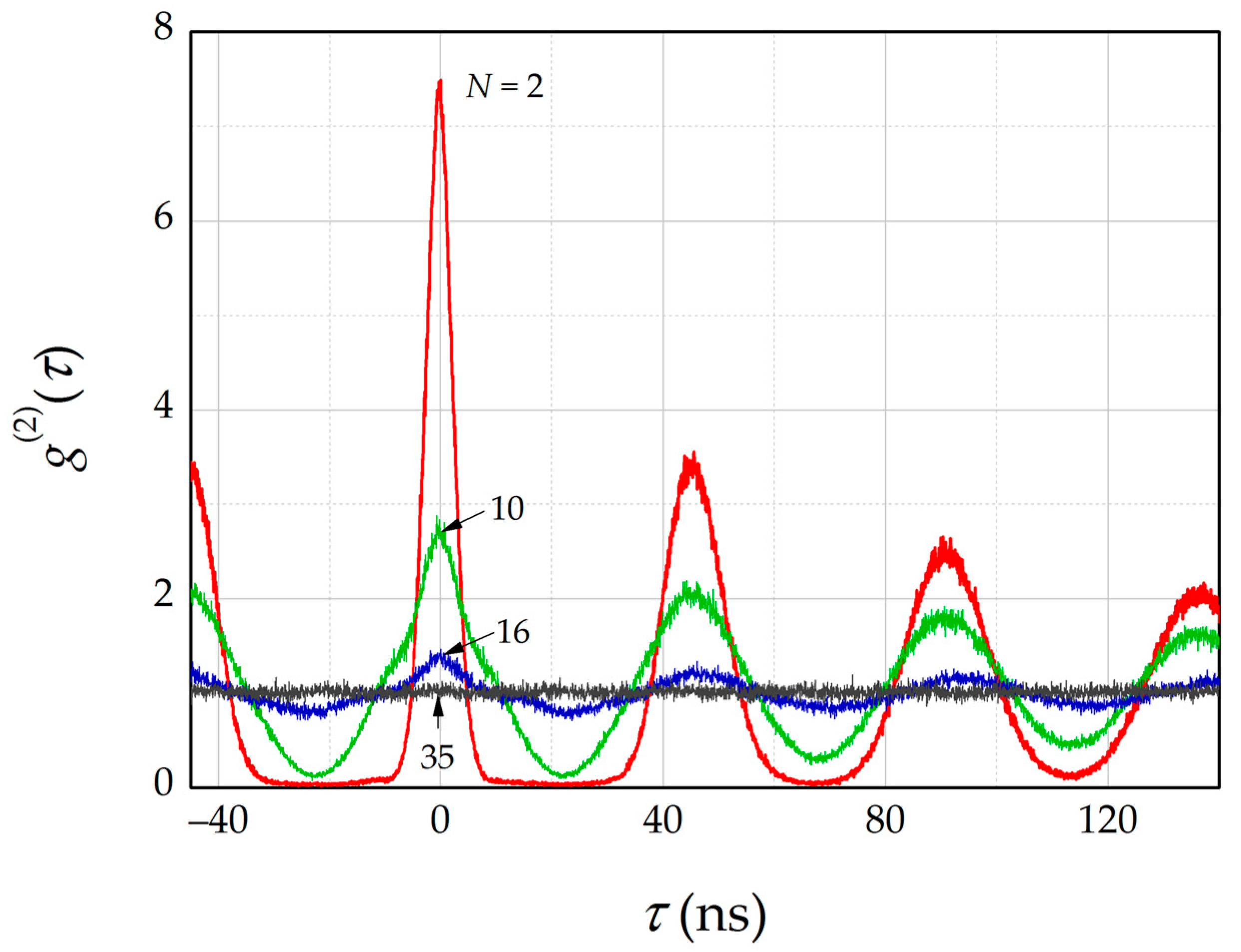
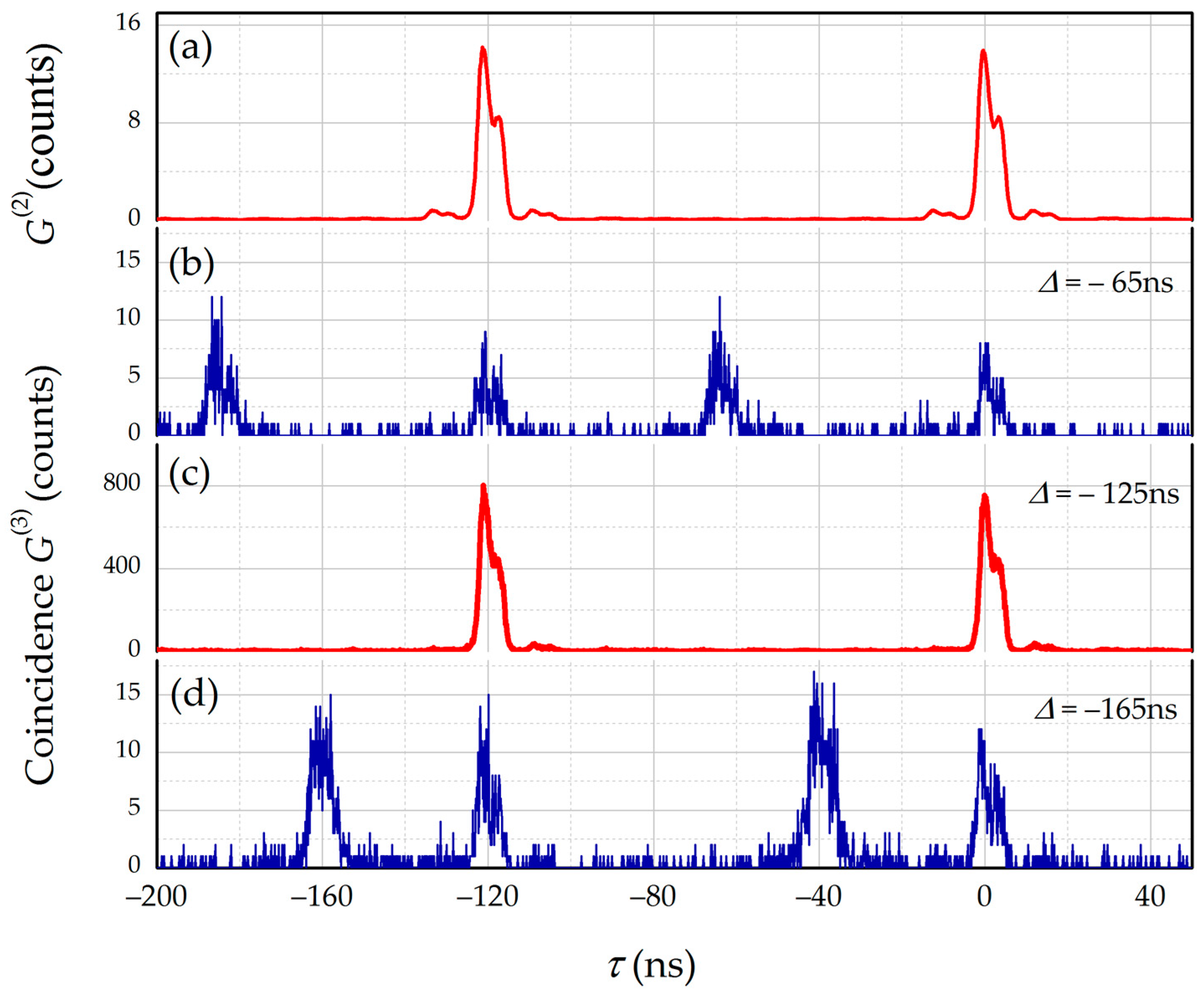
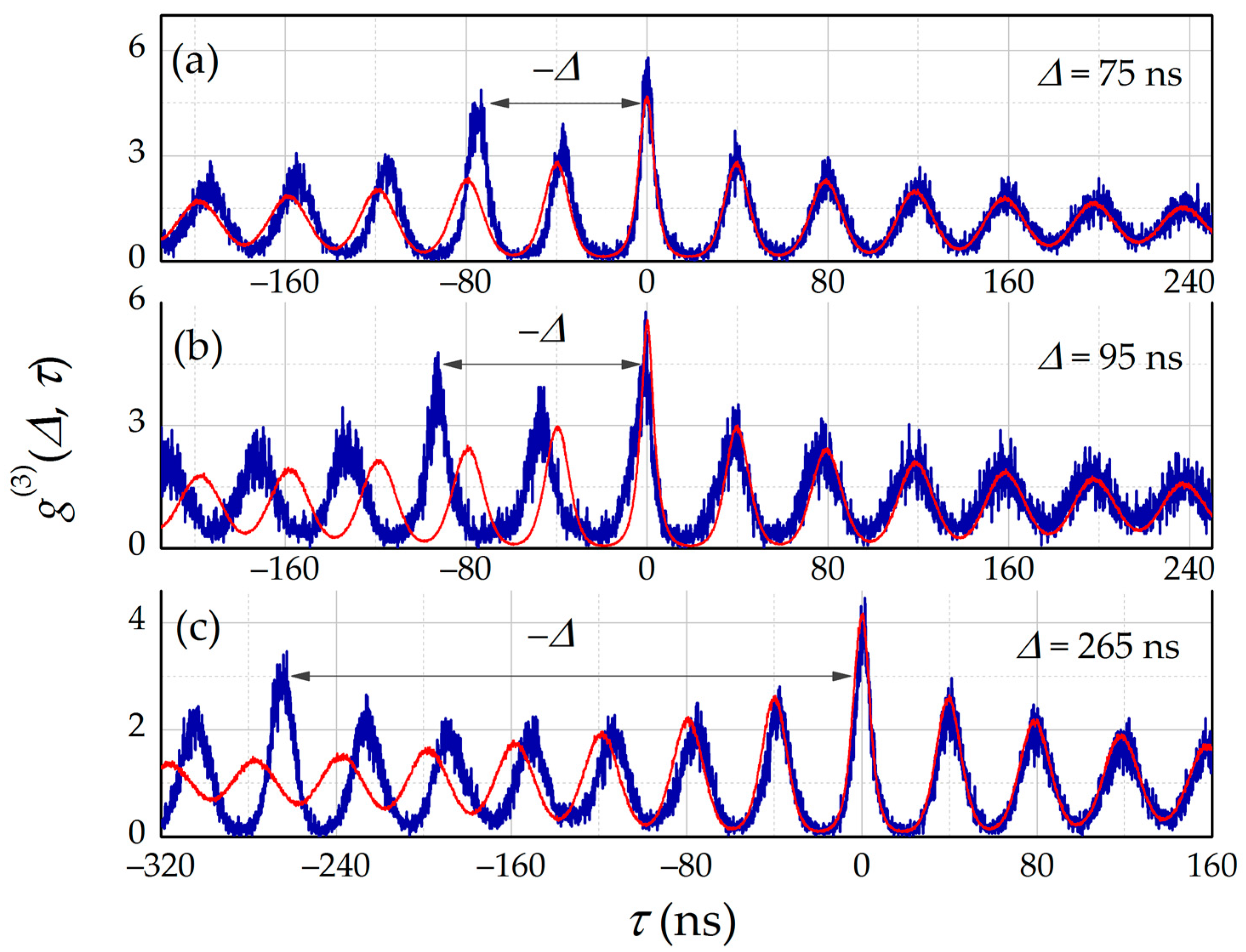
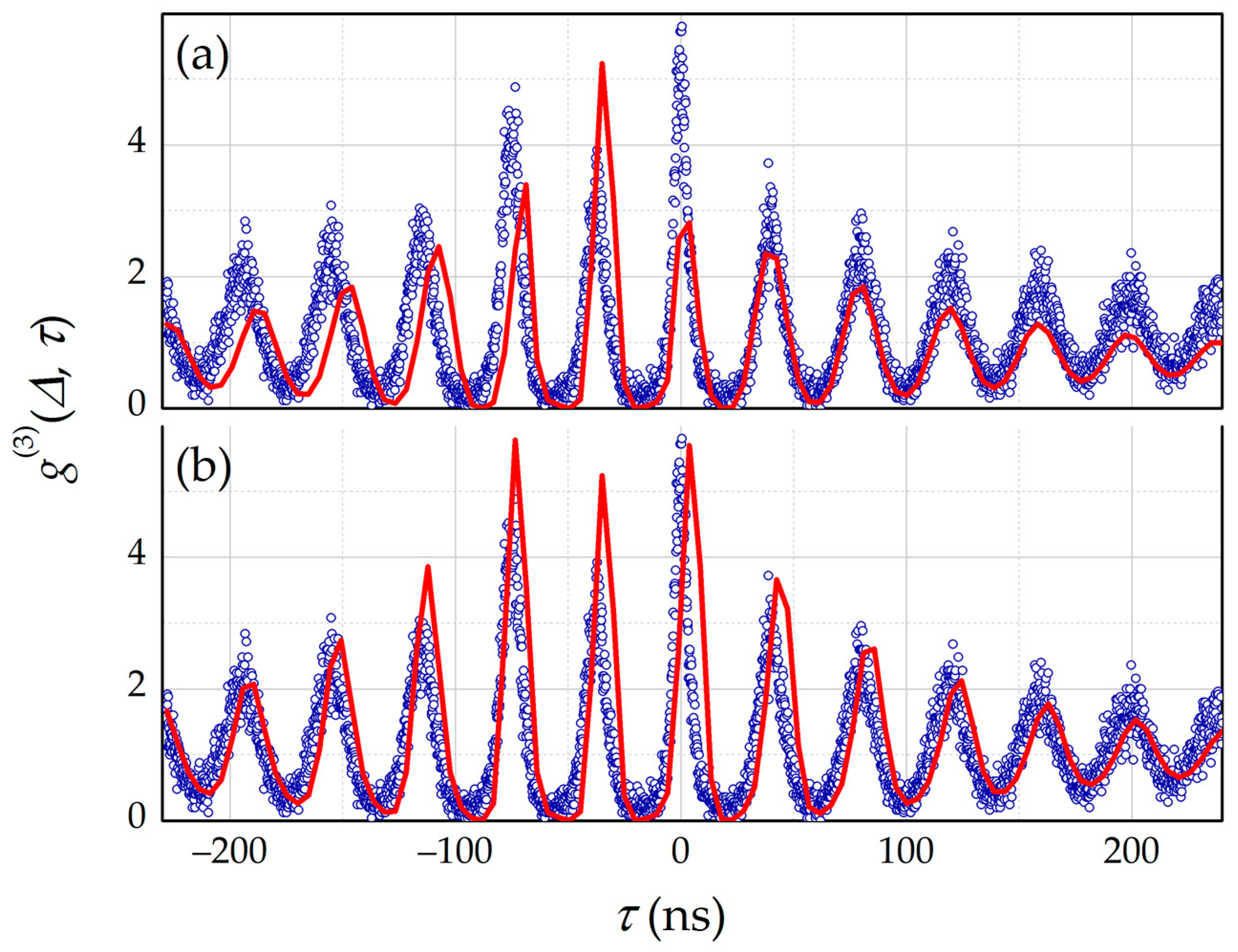
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hanbury Brown, R.; Twiss, R. Interferometry of the intensity fluctuations in light. I. Basic theory: The correlation between photons in coherent beams of radiation. Proc. R. Soc. A 1957, 242, 300–324. [Google Scholar]
- Glauber, R.J. Coherent and incoherent states of the radiation field. Phys. Rev. 1963, 151, 2766–2788. [Google Scholar] [CrossRef]
- Mandel, L. Fluctuations of photon beams and their correlations. Proc. R. Soc. 1958, 72, 1037–1048. [Google Scholar] [CrossRef]
- Mandel, L. Intensity fluctuations of partially polarized light. Proc. R. Soc. 1963, 81, 1104–1114. [Google Scholar] [CrossRef]
- Cao, D.-Z.; Xiong, J.; Zhang, S.-H.; Lin, L.-F.; Gao, L.; Wang, K. Enhancing visibility and resolution in nth-order intensity correlation of thermal light. Appl. Phys. Lett. 2008, 92, 201102. [Google Scholar] [CrossRef]
- Li, H.-G.; Zhang, Y.-T.; Cao, D.-Z.; Xiong, J.; Wang, K.-G. Third-order ghost interference with thermal light. Chin. Phys. 2008, B17, 4510–4515. [Google Scholar]
- Agafonov, I.N.; Iskhakov, T.S.; Penin, A.N.; Chekhova, M.V. Classical visibility limit for three-photon interference. JETP Lett. 2007, 85, 381–385. [Google Scholar] [CrossRef]
- Koryukin, I.V.; Povyshev, V.A. Antiphase dynamics of a multimode quantum well semiconductor laser. Laser Phys. 2007, 17, 680–683. [Google Scholar] [CrossRef]
- Ohtsubo, J. Semiconductor Lasers: Stability, Instability and Chaos, 3rd ed.; Springer-Verlag: Berlin, Germany, 2017; pp. 1–626. [Google Scholar]
- Kim, Y.-S.; Slattery, O.; Kuo, P.S.; Tang, X. Two-photon interference with continuous-wave multi-mode coherent light. Optics Express 2014, 22, 3611–3620. [Google Scholar] [CrossRef] [PubMed]
- Demenev, A.A.; Domaretskii, D.R.; Parakhonskii, A.L.; Lebedev, M.V. On the origin of nonclassical light generation upon resonant excitation of a GaAs semiconductor microcavity. JETP Lett. 2017, 106, 549–554. [Google Scholar] [CrossRef]
- Lebedev, M.V.; Demenev, A.A.; Parakhonsky, A.L.; Misochko, O.V. Multimode semiconductor laser: Quantum versus classical behavior. J. Russ. Laser Res. 2019, 40, 64–70. [Google Scholar] [CrossRef] [Green Version]
- Leggett, A.J.; Garg, A. Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks? Phys. Rev. Lett. 1985, 54, 857–860. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wiseman, H.M.; Milburn, G.J. Interpretation of quantum jump and diffusion processes illustrated on the bloch sphere. Phys. Rev. A 1993, 47, 1652–1665. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gammelmark, S.; Julsgaard, B.; Mølmer, K. Past quantum states of a monitored system. Phys. Rev. Lett. 2013, 111, 160401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Q.; Greplova, E.; Julsgaard, B.; Mølmer, K. Correlation functions and conditioned quantum dynamics in photodetection theory. Phys. Scr. 2015, 90, 128004. [Google Scholar] [CrossRef] [Green Version]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lebedev, M.; Demenev, A.; Parakhonsky, A.; Misochko, O. A Triple Correlator of Radiation Intensities of a Multimode Semiconductor Laser. Optics 2020, 1, 32-39. https://doi.org/10.3390/opt1010003
Lebedev M, Demenev A, Parakhonsky A, Misochko O. A Triple Correlator of Radiation Intensities of a Multimode Semiconductor Laser. Optics. 2020; 1(1):32-39. https://doi.org/10.3390/opt1010003
Chicago/Turabian StyleLebedev, Michael, Andrey Demenev, Andrey Parakhonsky, and Oleg Misochko. 2020. "A Triple Correlator of Radiation Intensities of a Multimode Semiconductor Laser" Optics 1, no. 1: 32-39. https://doi.org/10.3390/opt1010003
APA StyleLebedev, M., Demenev, A., Parakhonsky, A., & Misochko, O. (2020). A Triple Correlator of Radiation Intensities of a Multimode Semiconductor Laser. Optics, 1(1), 32-39. https://doi.org/10.3390/opt1010003




