Analysis on the Leakage and Rubbing Force of the Combined Finger Seal Based on Equivalent Dynamic Model Considering Thermal Effects
Abstract
1. Introduction
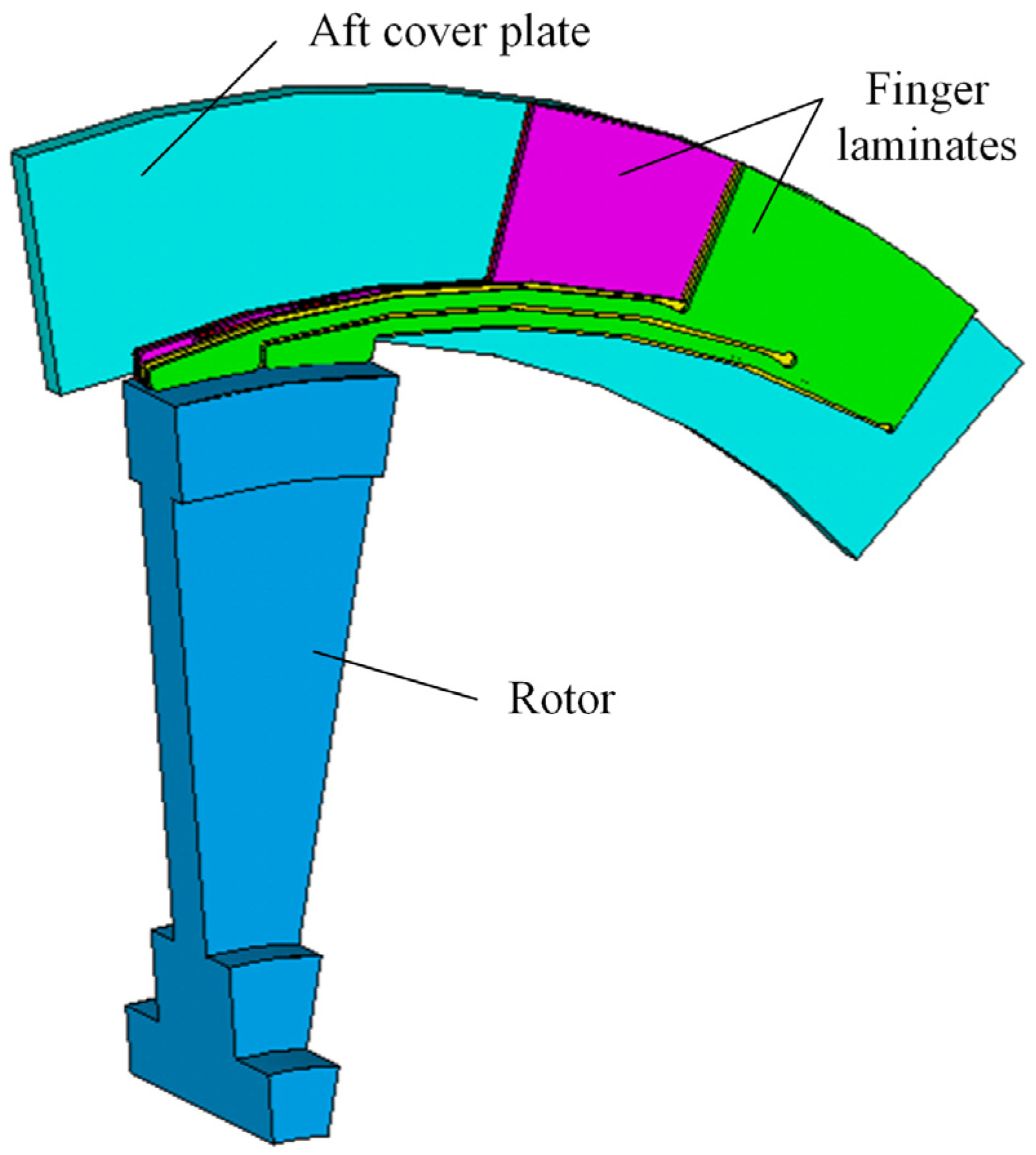
2. Structural Composition of the Combined Finger Seal
- (1)
- Three layers of Type Y finger laminates on the high-pressure side and two layers of Type X finger laminates on the low-pressure side, with adjacent finger laminates staggered. This configuration is denoted as the 3Y+2X type.
- (2)
- Four layers of Type Y finger laminates on the high-pressure side and one layer of Type X finger laminates on the low-pressure side, with adjacent finger laminates staggered. This configuration is denoted as the 4Y+1X type.
3. Equivalent Dynamic Model of Finger Seal Considering Thermal Effects
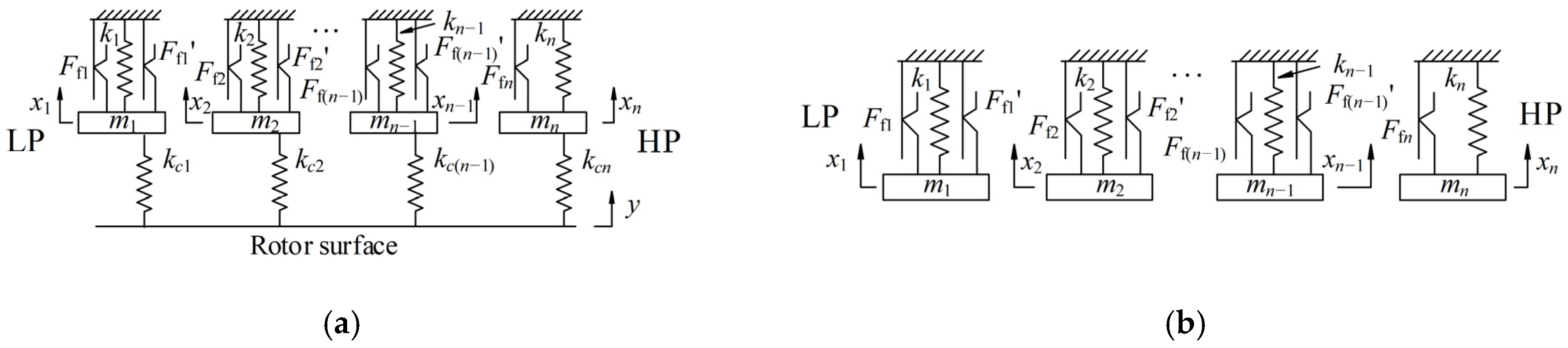
3.1. Equivalent Dynamic Model of Finger Seal
3.2. Equivalent Mass
3.3. Contact Stiffness Coefficient Between the Finger Foot and the Rotor
3.4. Frictional Resistance of Finger Seal System
3.5. Equivalent Structural Stiffness Coefficient
3.6. Displacement Excitation of the Rotot
4. Thermal Analysis Model and Boundary Conditions for Finger Seal
4.1. Structural Model and Thermal Boundary Conditions of Finger Seal System
4.2. Fitting Formula for Equivalent Structural Stiffness Considering Thermal Effects
5. Calculation Method for Dynamic Leakage Rate and Rubbing Force
5.1. Dynamic Leakage Rate
5.2. Rubbing Force
6. Results and Discussion
6.1. Leakage and Rubbing Force Under Different Configurations
6.2. Analysis of Operating Condition Effects
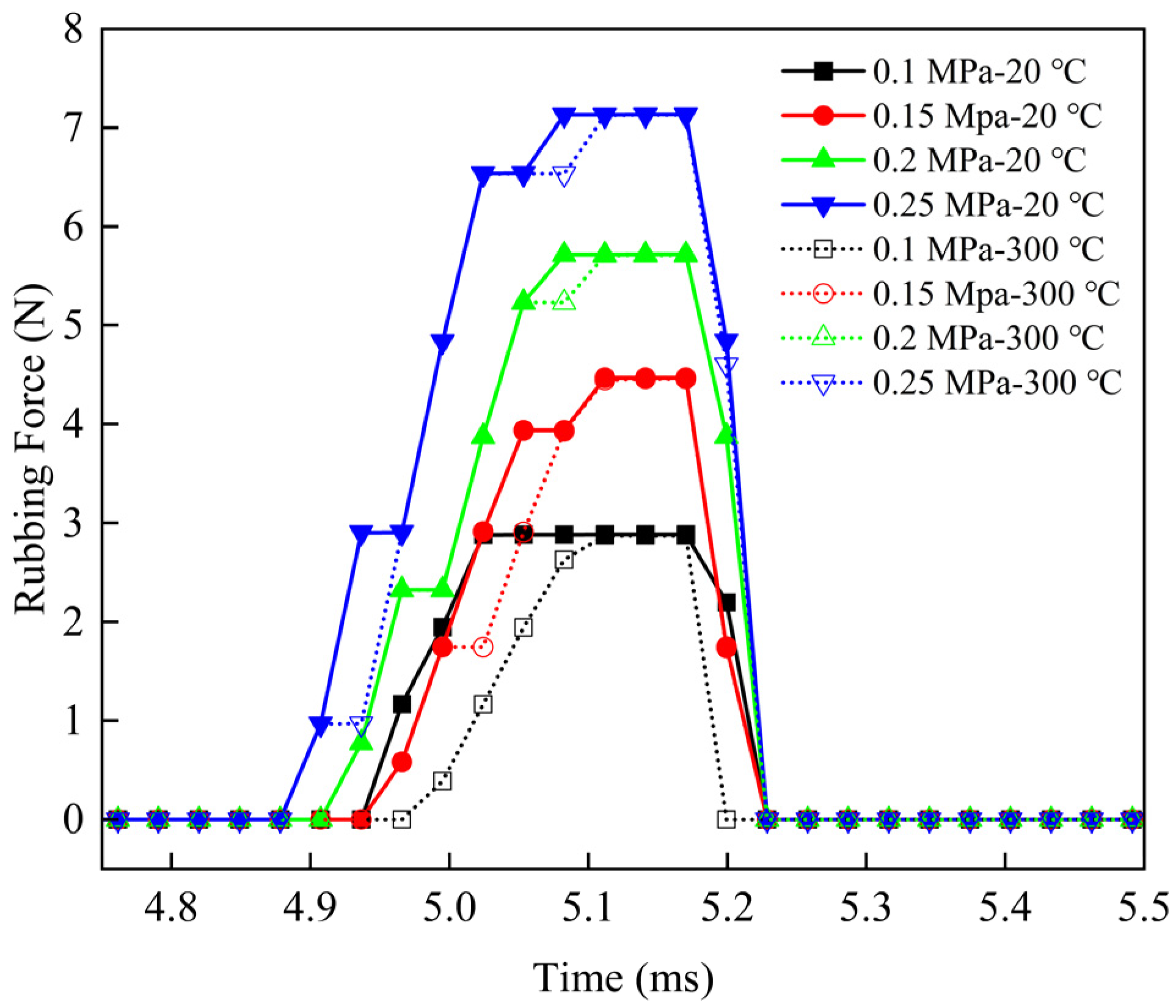
6.2.1. Different Pressure Differentials
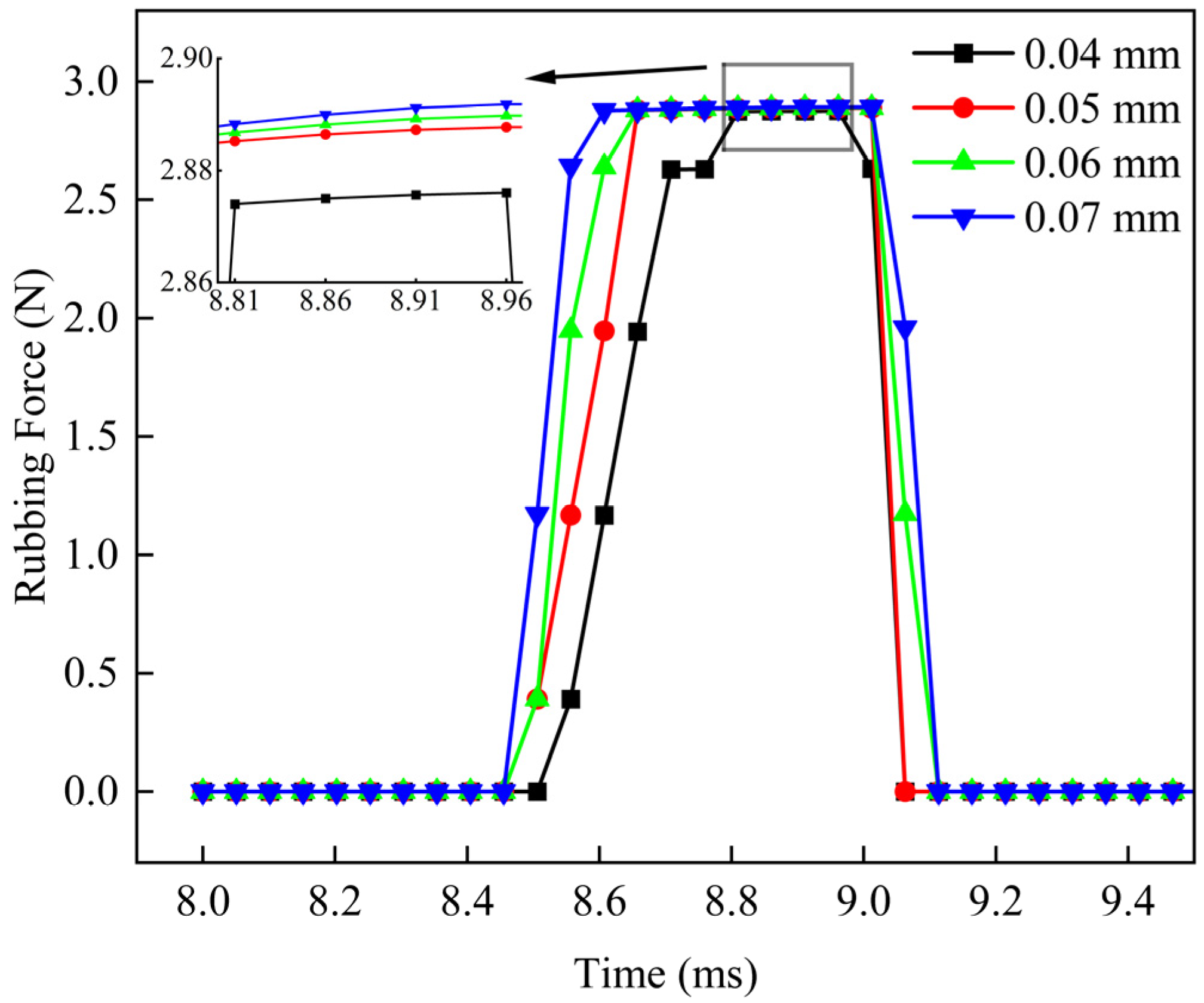
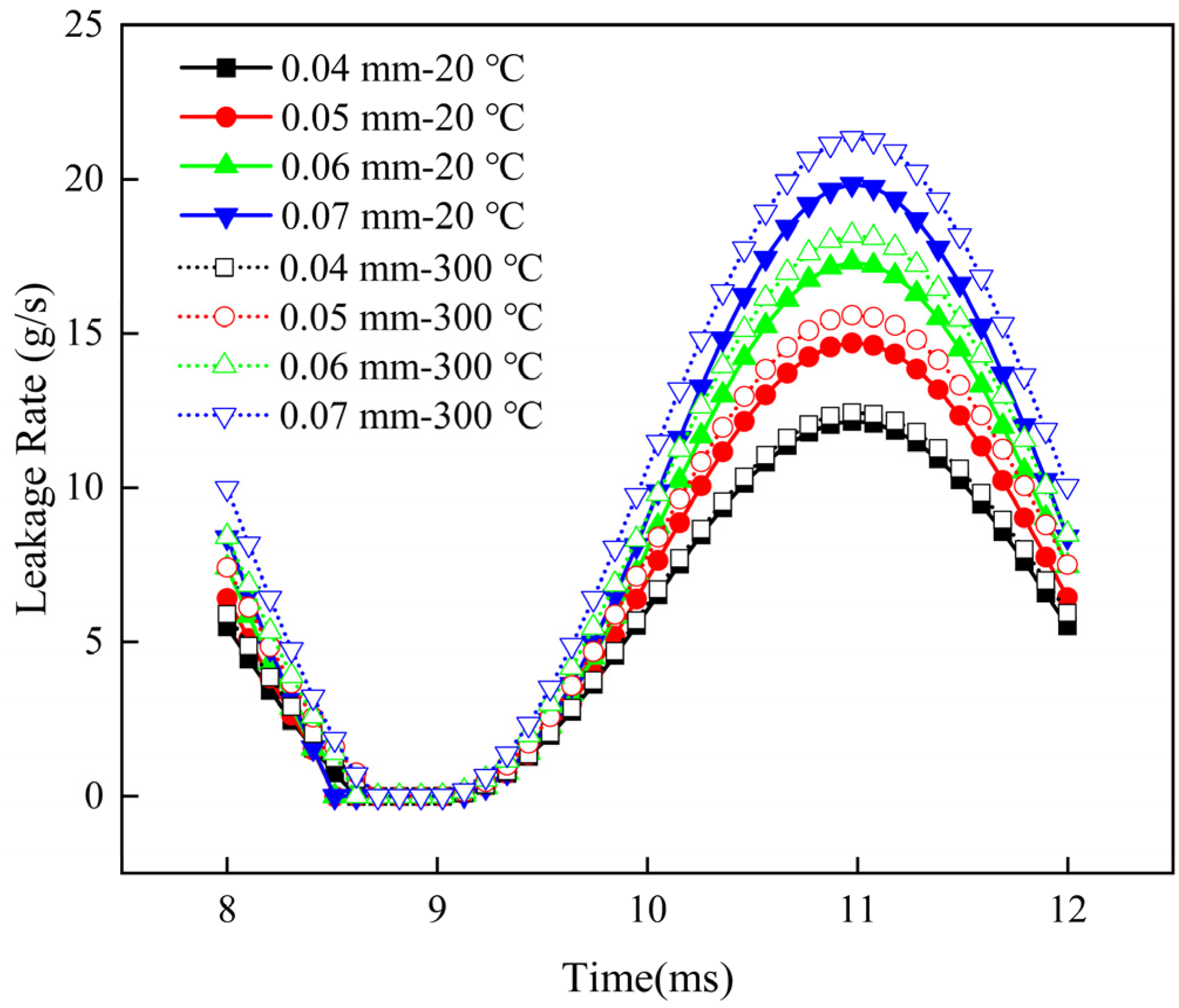
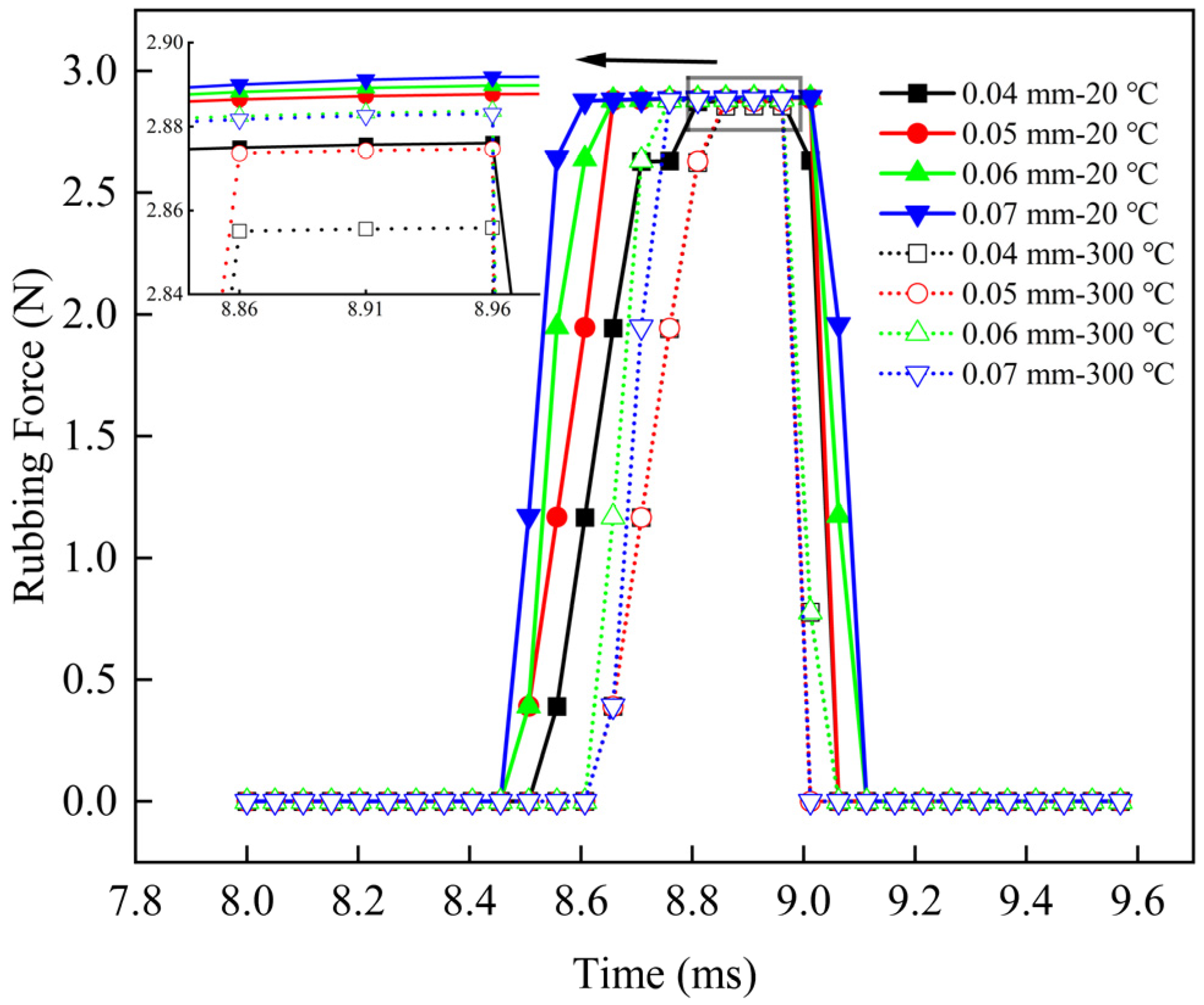
6.2.2. Different Displacement Excitations
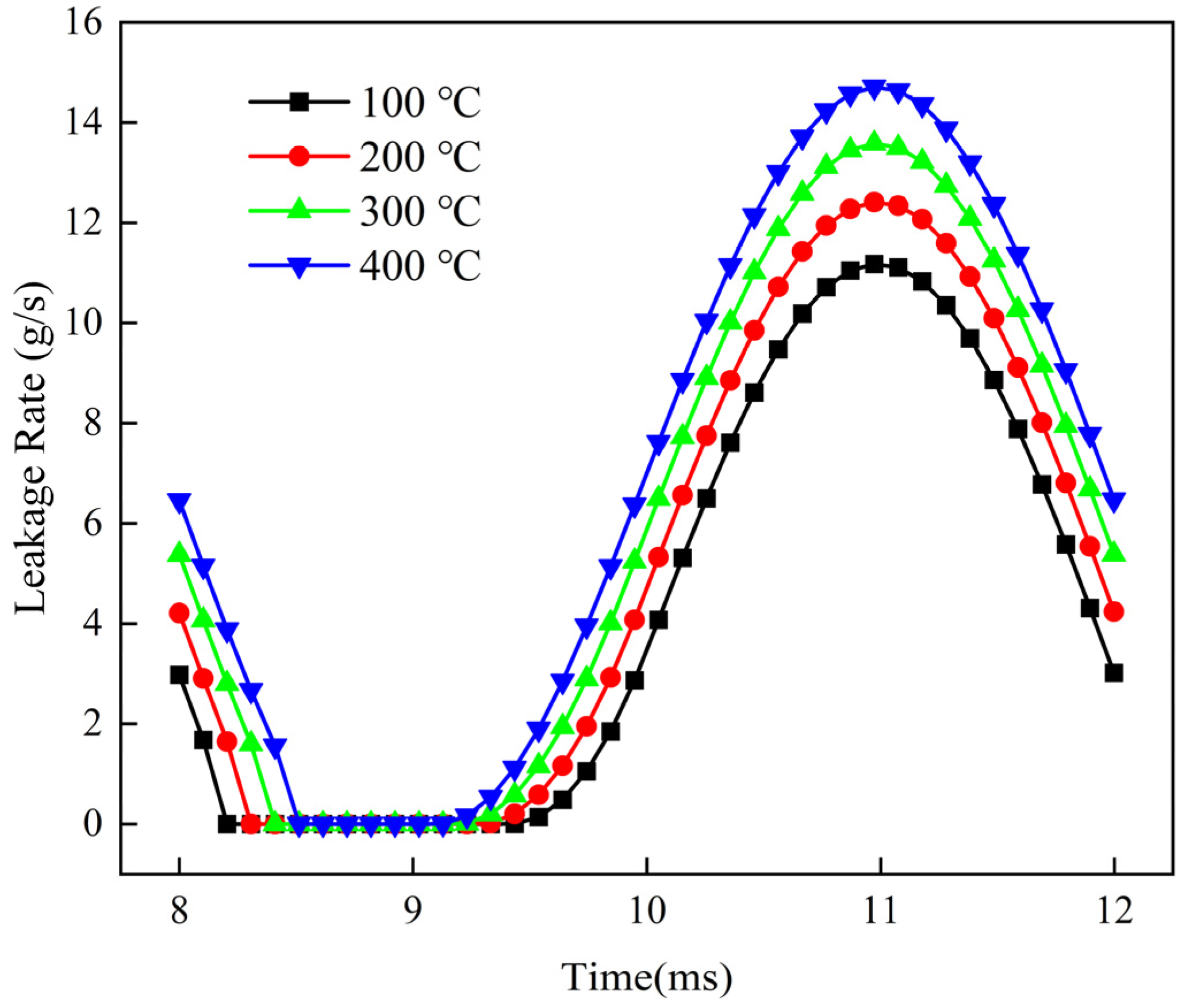
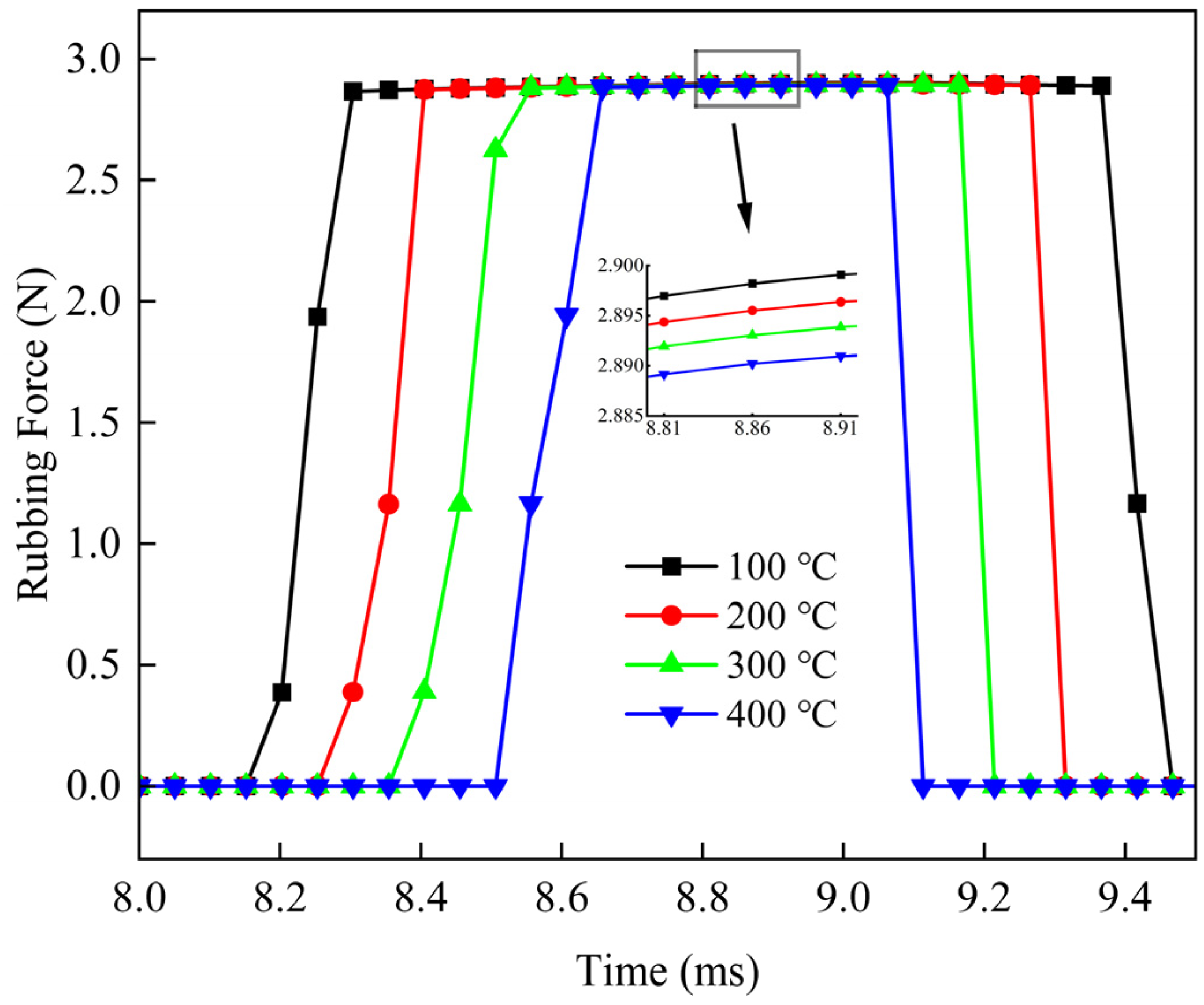
6.2.3. Different Temperatures
6.3. Comparison of Leakage Performance of Combined Finger Seals
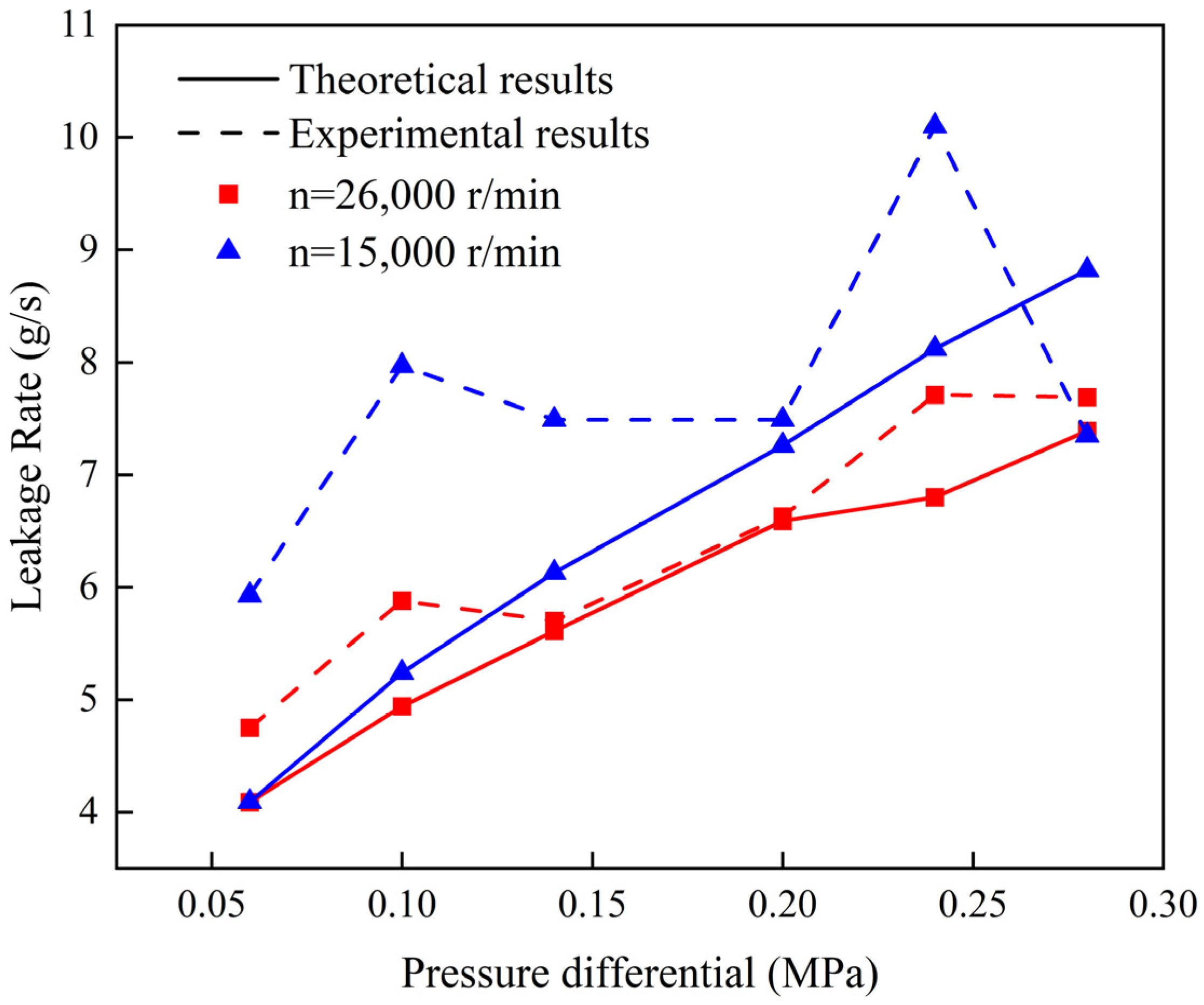
6.3.1. Comparison of Experimental and Computational Results
6.3.2. Comparison of Leakage Performance with Other Combined Finger Seals
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Proctor, M.P.; Kumar, A.; Delgado, I.R. High-Speed, High-Temperature Finger Seal Test Results. J. Propuls. Power 2004, 20, 312–318, NASA/TM—2002-211589. [Google Scholar] [CrossRef]
- MacKay, C.G.; Wright, E.S. Laminated Finger Seal. U.S. Patent 5071138, 10 December 1991. [Google Scholar]
- Arora, G.K.; Proctor, M.P.; Steinetz, B.M.; Delgado, I. Pressure Balanced, Low Hysteresis, Finger Seal Test Results. In Proceedings of the 35th Joint Propulsion Conference and Exhibit, Los Angeles, CA, USA, 20–24 June 1999. NASA/TM-1999-209191. [Google Scholar]
- Song, D.; Hua, K.; Cheng, Y.; Du, C.; Zhang, Y.; Jing, Y. Multi-scale modeling and mechanical performance analysis of finger seals with plain woven C/C composite. Sci. Rep. 2024, 14, 24382. [Google Scholar] [CrossRef]
- Rajesh, P.; Sharana, B.J. Optimization of finger seal pad design for reducing the leakage between the high-pressure and low-pressure region. J. Tribol. 2024, 41, 68–80. [Google Scholar]
- Du, C.; Zhang, Y.; Dong, S.; Cui, Y.; Ji, H. Mathematical calculation method for hysteresis characteristics of arc-shaped finger seal. J. Aerosp. Power 2022, 37, 1587–1596. [Google Scholar]
- Zhang, T.; Wang, J.; Liu, M. Effect of Rear Baffle Structure on Leakage Characteristics and Temperature Distribution of Finger Seals. Lubr. Eng. 2024, 49, 136–143. [Google Scholar]
- Wei, Y.; Ma, B.; Chen, X.; Xu, F.; Guo, J.; Liu, S.; Dou, W. Analysis of non-contact finger seal force based on deformation of the finger pad. J. Mech. Sci. Technol. 2024, 38, 4721–4732. [Google Scholar] [CrossRef]
- Wei, Y.; Ma, B.; Li, Y.; Schröder, K.-U. Numerical analysis of seal force in contacting finger seal. Bull. Pol. Acad. Sci. Tech. Sci. 2025, 73, e153840. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, Y.; Zhao, R.; Jiao, Y.; Chen, Z. Dynamic Analysis and Independent High-Order Nonlinear Dynamics of a Rotor-Bearing-Finger Seal System. Int. J. Appl. Mech. 2023, 15, 2350051. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, G.; Shen, X. Analysis of Dynamic Performance and Leakage for Finger Seal. ACTA Aeronaut. Astronaut Ica Sin. 2009, 30, 2193–2199. [Google Scholar]
- Braun, M.J.; Pierson, H.M.; Deng, D. Thermofluids Considerations and the Dynamic Behavior of a Finger Seal Assembly. Tribol. Trans. 2005, 48, 531–547. [Google Scholar] [CrossRef]
- Marie, H. Dynamic Simulation of Finger Seal-Rotor Interaction Using Variable Dynamic Coefficients. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006. AIAA 2006-4931. [Google Scholar]
- Lei, Y.; Chen, G. Finger Seal’s Hysteresis Characteristic Based on Dynamical Model. Chin. J. Mech. Eng. 2007, 43, 122–126. [Google Scholar] [CrossRef]
- Ma, X.; Chen, G.; Zhang, Y. Equivalent Dynamic Model of a Padded Finger Seal. Mech. Sci. Technol. Aerosp. Eng. 2008, 27, 1356–1360, 1364. [Google Scholar]
- Wang, J.; Xu, W.; Liu, M.; Zhu, S.; Kang, Y.; Song, X.; Gu, D.; Hu, X. Study on Interstage Pressure Equalization of Differential Multi-Stage Finger Seal with Structural Design, Flow and Heat Transfer Characteristics. Aerospace 2024, 11, 874. [Google Scholar] [CrossRef]
- Chen, G.; Wang, L.; Yu, Q.; Su, H. Dynamic Analysis of C/C Composite Finger Seal. Chin. J. Aeronaut. 2014, 27, 745–758. [Google Scholar] [CrossRef]
- Chen, G.-D.; Lu, F.; Yu, Q.-P.; Su, H. Dynamic analysis of finger seal using equivalent model based on distributed mass method. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2014, 228, 2992–3005. [Google Scholar] [CrossRef]
- Wang, L.-N.; Wang, Y.; Sun, H.-C.; Ren, G.-H.; Sun, L.-C.; Meng, D.-H. Dynamic analysis and experimental verification of the carbon-carbon composite finger seal under complex working states. Proc. Inst. Mech. Eng. Part G-J. Aerosp. Eng. 2019, 233, 2914–2922. [Google Scholar] [CrossRef]
- Chen, G.; Su, H.; Zhang, Y. Vaiable-Dimension Construction in the Axial Arrangement of Finger Seal Mechanism. J. Aerosp. Power 2003, 18, 488–491. [Google Scholar]
- Gibson, N.E.; Takeuchi, D.; Hynes, T. Second Generation Air-to-Air Mechanical Seal Design and Performance. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, 31 July–3 August 2011. AIAA 2011-5636. [Google Scholar]
- Wang, J.; Zhang, Y.; Cui, Y.; Hu, H.; Zhang, L.; Chen, L. High temperature wear behavior of NiCoCrAlY-Cr2O3-AgMo coating on GH4169 superalloy. Mater. Today Commun. 2023, 35, 105762. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Y.; Wang, W. New Equivalent Method for Normal Stiffness of Contact Interface. J. Mech. Eng. 2011, 47, 37–43. [Google Scholar] [CrossRef]
- Sun, S. Performance Analysis and Wear Rate Calculation of Finger Seal with Different Radial Stiffness Laminates. Master’s Thesis, Northwestern Polytechnical University, Xi’an, China, 2018. [Google Scholar]
- Sridhar, M.R.; Yovanovich, M.M. Thermal Contact Conductance of Tool Steel and Comparison with Model. Int. J. Heat Mass Transf. 1996, 39, 831–839. [Google Scholar] [CrossRef]
- Zagtodzki, P. Analysis of Thermomechanical Phenomena in Muti-Disc Clutches and Brakes. Wear 1990, 140, 291–308. [Google Scholar] [CrossRef]
- Chen, G.; Su, H.; Zhang, Y. Analysis and Design of Finger Seals; Northwestern Polytechnical University Press Co., Ltd.: Xi’an, China, 2012; 61p. [Google Scholar]
- Müller, C.; Müser, M.H.; Carbone, G.; Menga, N. Significance of Elastic Coupling for Stresses and Leakage in Frictional Contacts. Phys. Rev. Lett. 2023, 131, 156201. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C. Analysis of the Wear Characteristics and Service Life Prediction of Finger Seal. Master’s Thesis, Northwestern Polytechnical University, Xi’an, China, 2021. [Google Scholar]
- Li, N.; Peng, Z.; He, L.; Zhou, K.; Li, Q. Development of High-temperature and High-speed Seal Test Rig of Aeroengine. Lubr. Eng. 2014, 39, 121–123. [Google Scholar]
- Zhao, H.; Su, H.; Chen, G. Analysis of Total Leakage of Finger Seal with Side Leakage Flow. Tribol. Int. 2020, 150, 106371. [Google Scholar] [CrossRef]
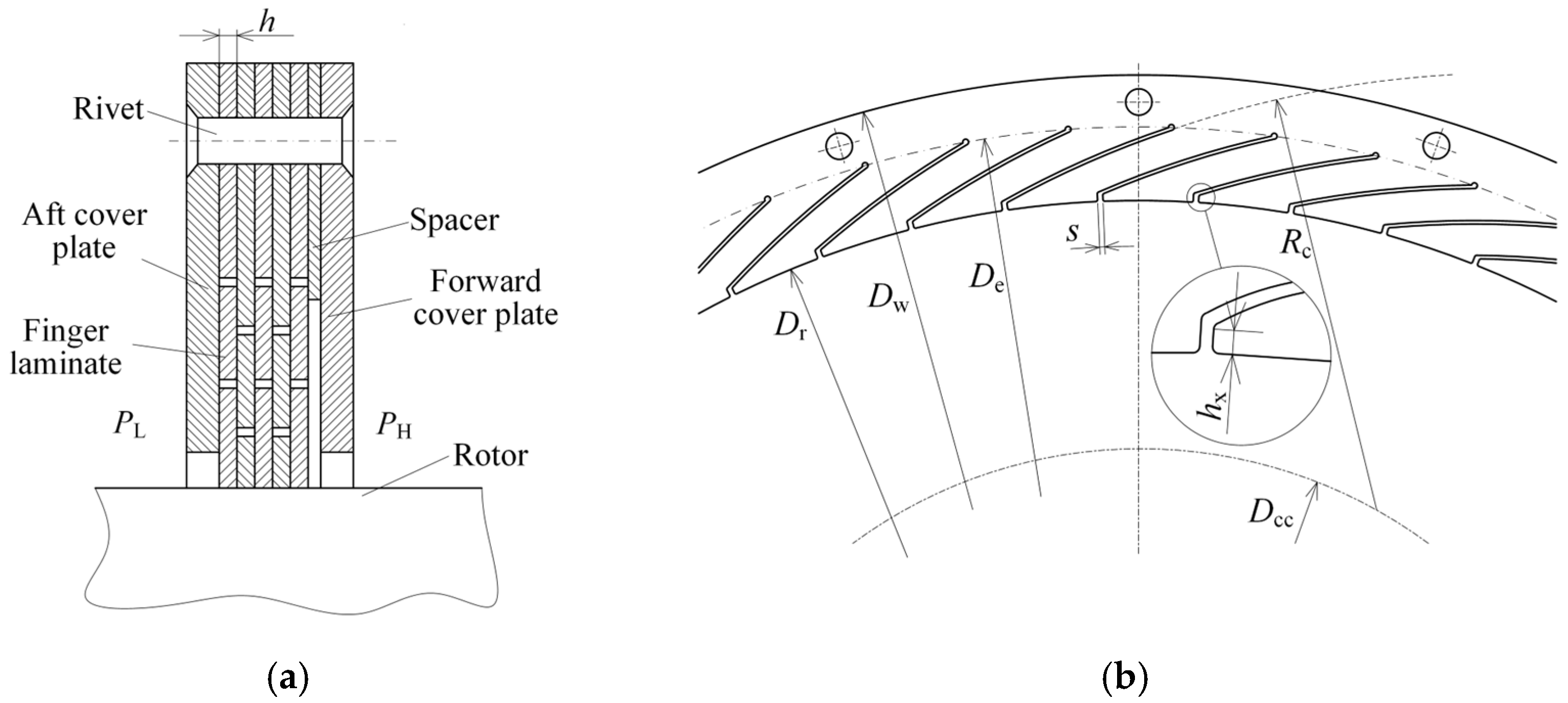
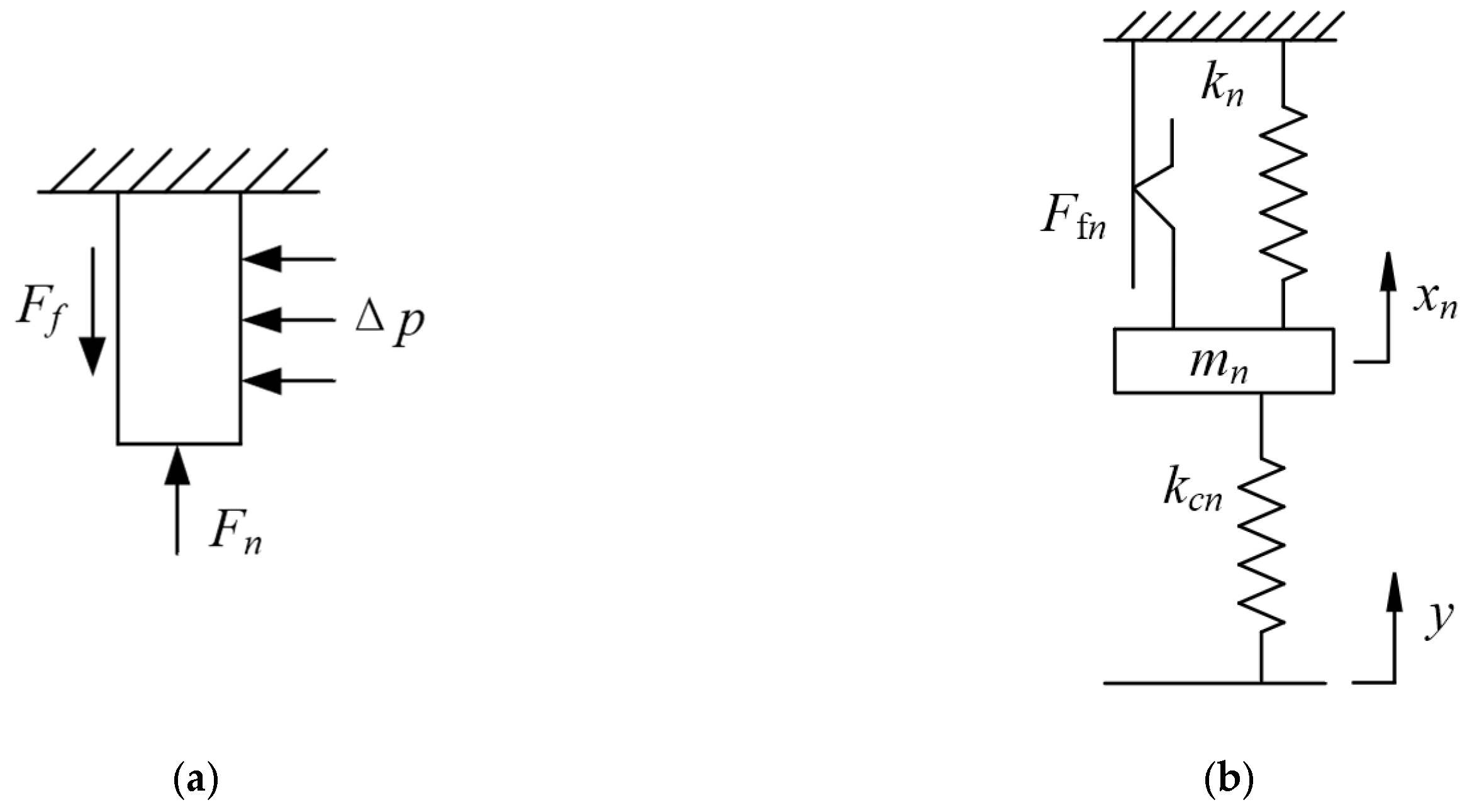



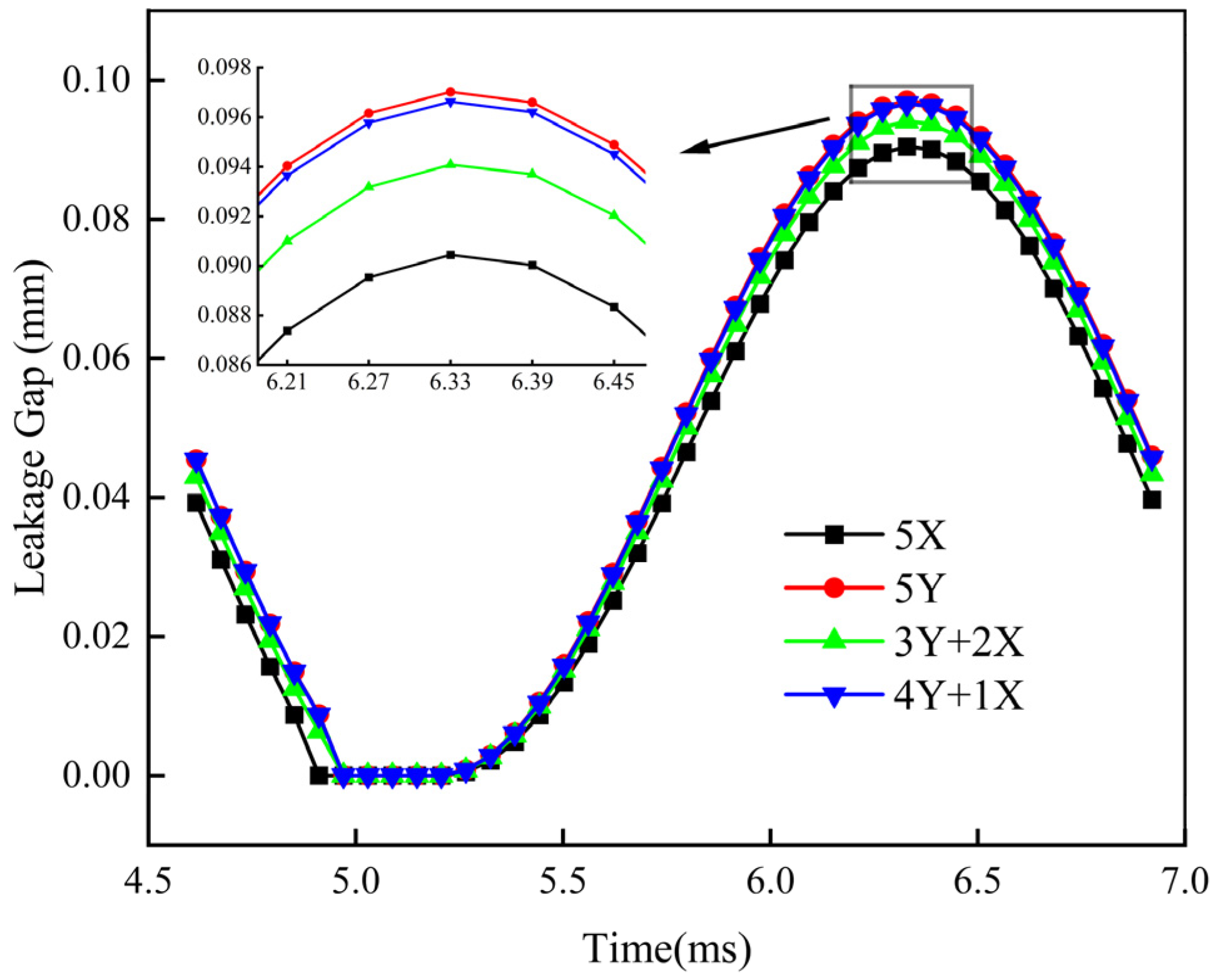
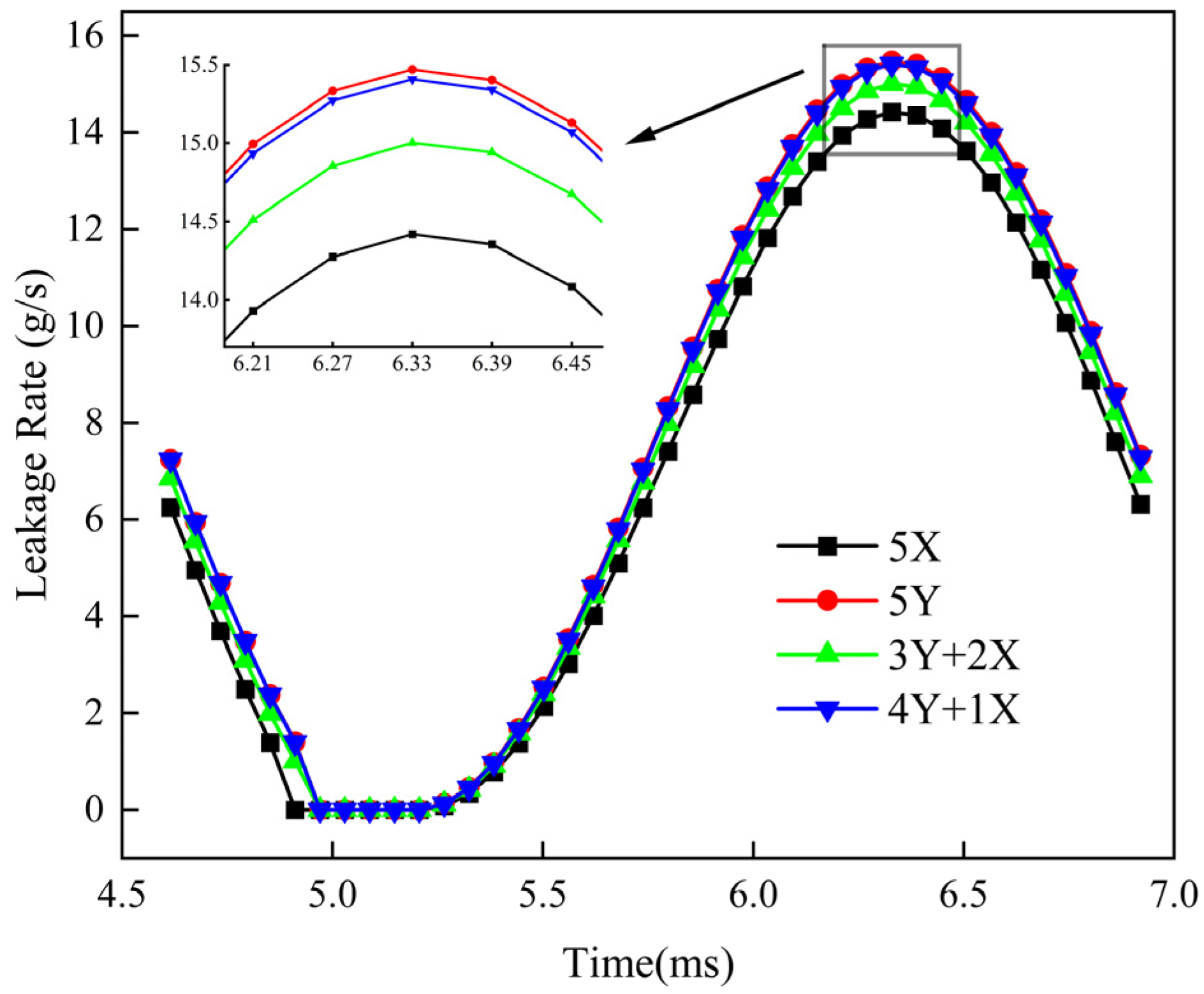


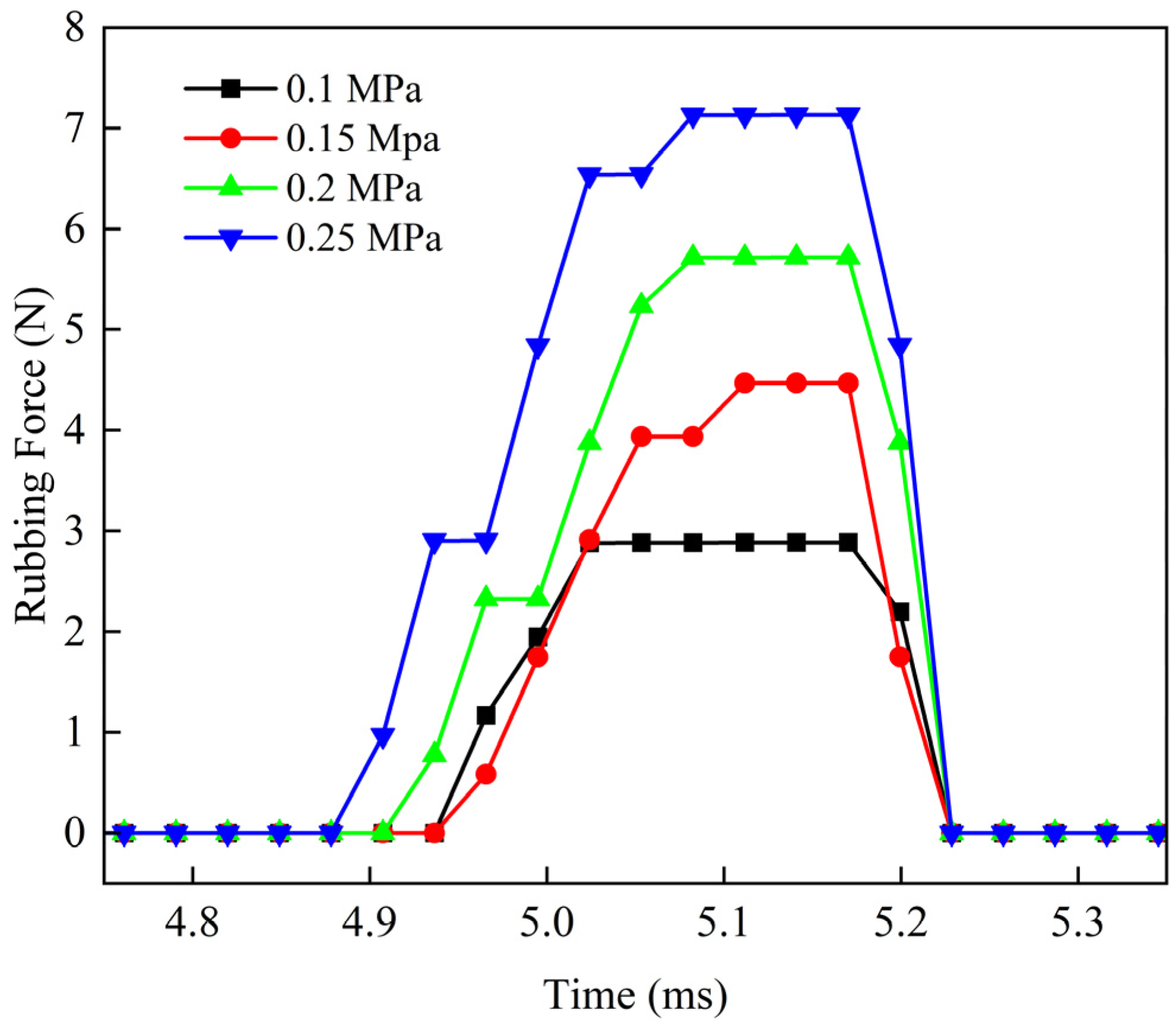
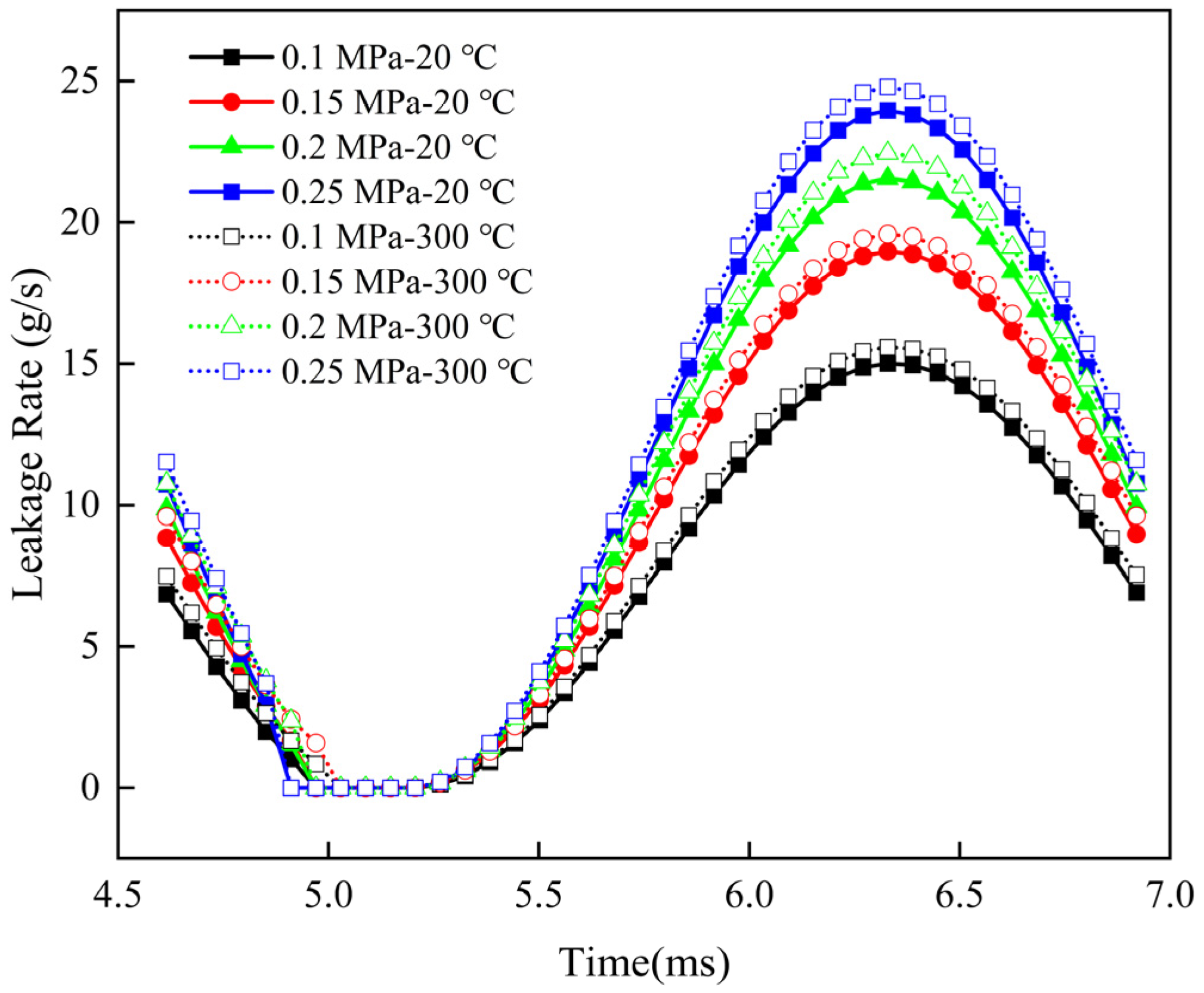

| Parameters | Symbol | Value | Units | |
|---|---|---|---|---|
| Type | Y | X | ||
| Arc profile radius | Rc | 89 | 90 | mm |
| Center circle diameter | Dcc | 27 | 23 | mm |
| Root diameter of finger beam | De | 185 | 180 | mm |
| Seal inner diameter | Dr | 165 | mm | |
| Seal outer diameter | Dw | 210 | mm | |
| Number of finger beams | nf | 48 | ||
| Gap between beams | s | 0.4 | mm | |
| Thickness of finger element | h | 0.5 | mm | |
| Number of finger elements | ns | 5 | ||
| Height of finger foot | hx | 2.2 | 3.2 | mm |
| Downstream protective clearance | gd | 1.2 | mm | |
| Type | Equivalent Structural Stiffness Coefficient (N/m) | Equivalent Mass (kg) | Contact Stiffness Coefficient Between Fingers and the Rotor (N/m) |
|---|---|---|---|
| X | 1587.70 | 1.70 × 10−4 | 34,427.09 |
| Y | 618.99 | 1.61 × 10−4 | 13,422.07 |
| Temperature (°C) | Kxt (N/m) | Kyt (N/m) | Kxj (N/m) | Kyj (N/m) |
|---|---|---|---|---|
| 100 | 1628.82 | 498.16 | 1826.91 | 529.1 |
| 200 | 1503.56 | 484.99 | 1727.92 | 516.42 |
| 300 | 1382.97 | 471.07 | 1624.88 | 506.63 |
| 400 | 1267.06 | 456.39 | 1517.77 | 499.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Su, H.; Su, Y.; Zhou, K. Analysis on the Leakage and Rubbing Force of the Combined Finger Seal Based on Equivalent Dynamic Model Considering Thermal Effects. Appl. Mech. 2025, 6, 80. https://doi.org/10.3390/applmech6040080
Zhang J, Su H, Su Y, Zhou K. Analysis on the Leakage and Rubbing Force of the Combined Finger Seal Based on Equivalent Dynamic Model Considering Thermal Effects. Applied Mechanics. 2025; 6(4):80. https://doi.org/10.3390/applmech6040080
Chicago/Turabian StyleZhang, Jifan, Hua Su, Yiting Su, and Kun Zhou. 2025. "Analysis on the Leakage and Rubbing Force of the Combined Finger Seal Based on Equivalent Dynamic Model Considering Thermal Effects" Applied Mechanics 6, no. 4: 80. https://doi.org/10.3390/applmech6040080
APA StyleZhang, J., Su, H., Su, Y., & Zhou, K. (2025). Analysis on the Leakage and Rubbing Force of the Combined Finger Seal Based on Equivalent Dynamic Model Considering Thermal Effects. Applied Mechanics, 6(4), 80. https://doi.org/10.3390/applmech6040080





