Impact Testing of AISI 1010 Low-Carbon Steel Spot-Welded Joints
Abstract
1. Introduction
2. Experimental Procedures
2.1. Material and Specimen Design
2.2. Welding Procedure
2.3. Impact Testing
3. Results and Discussion
3.1. Impact Test Results
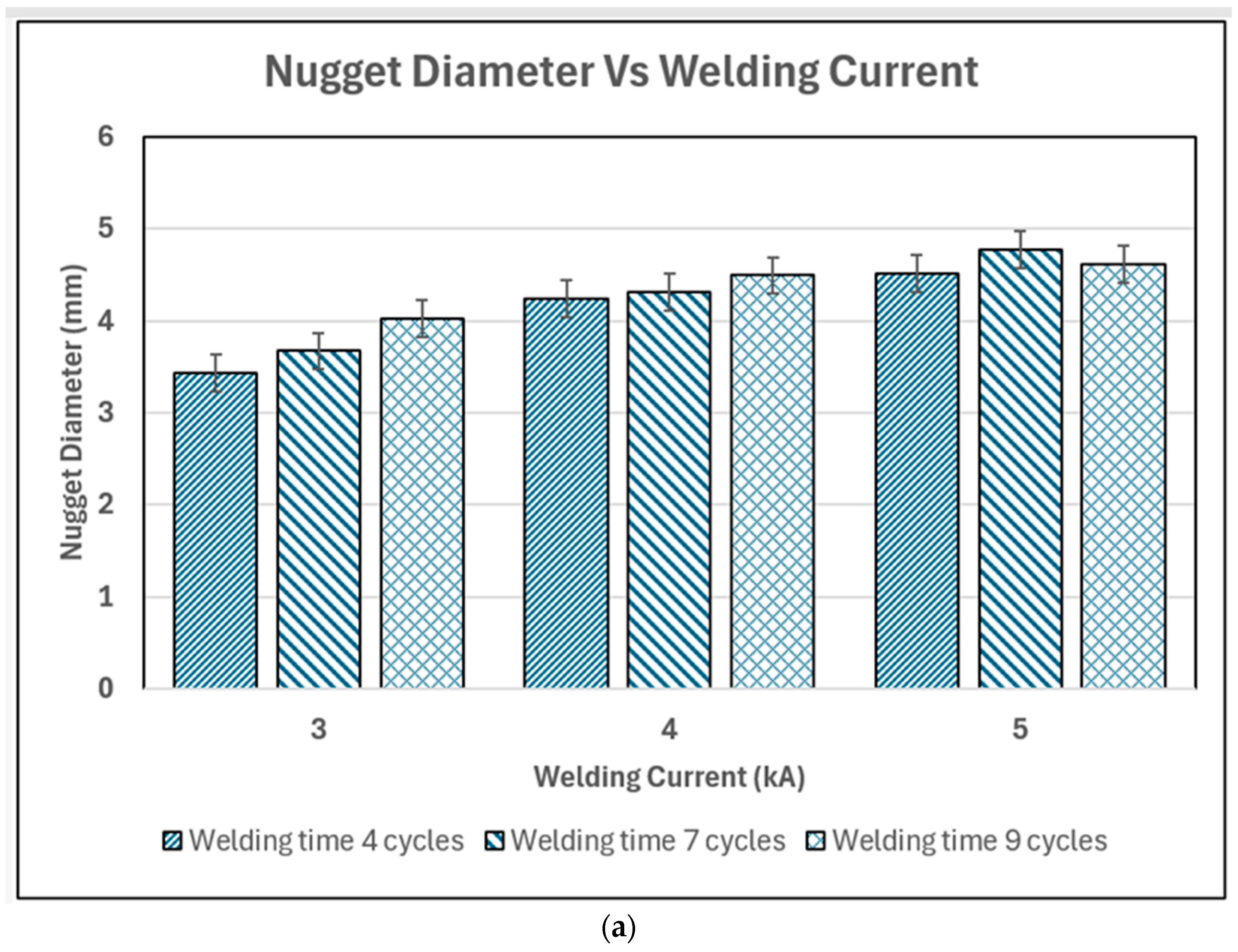
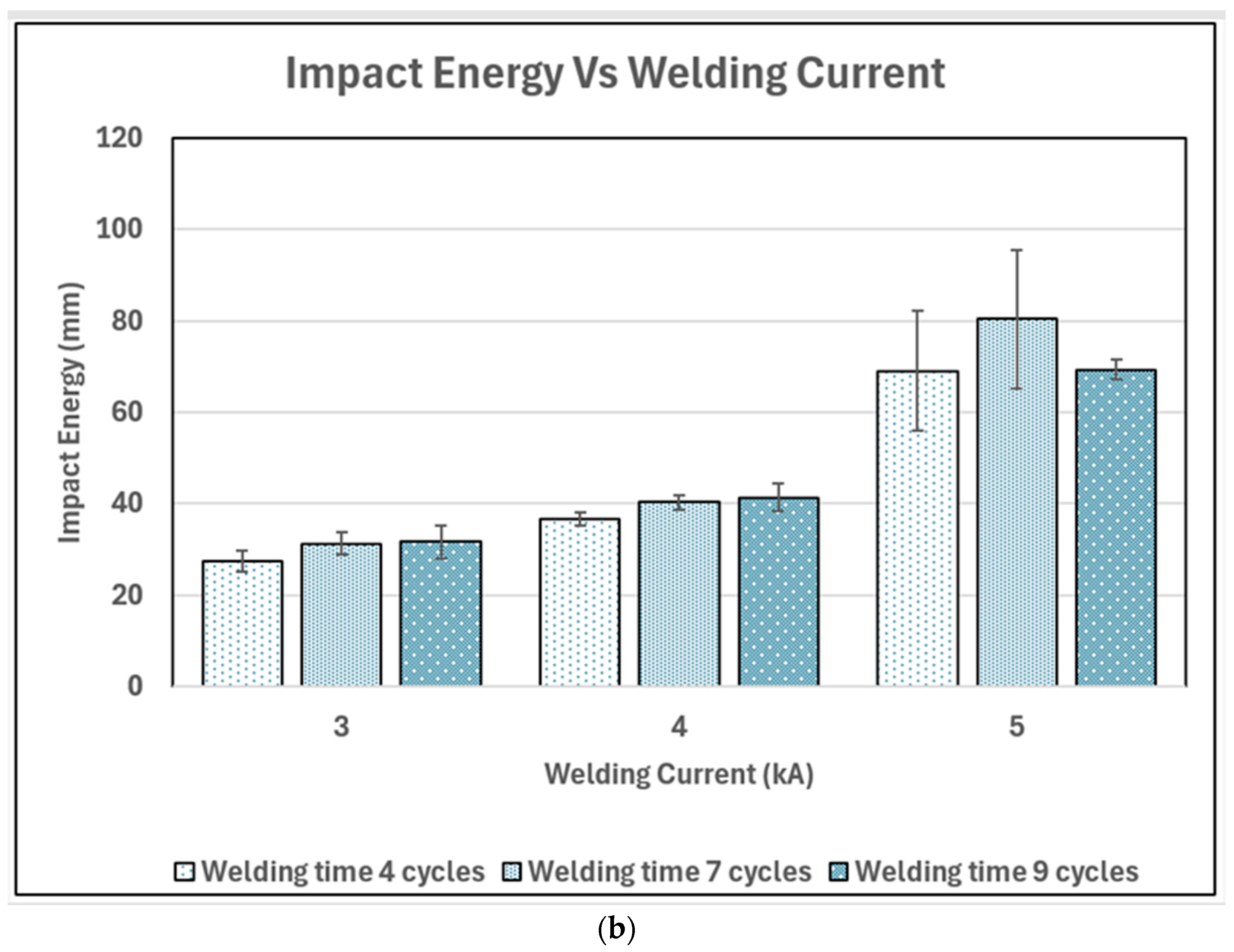
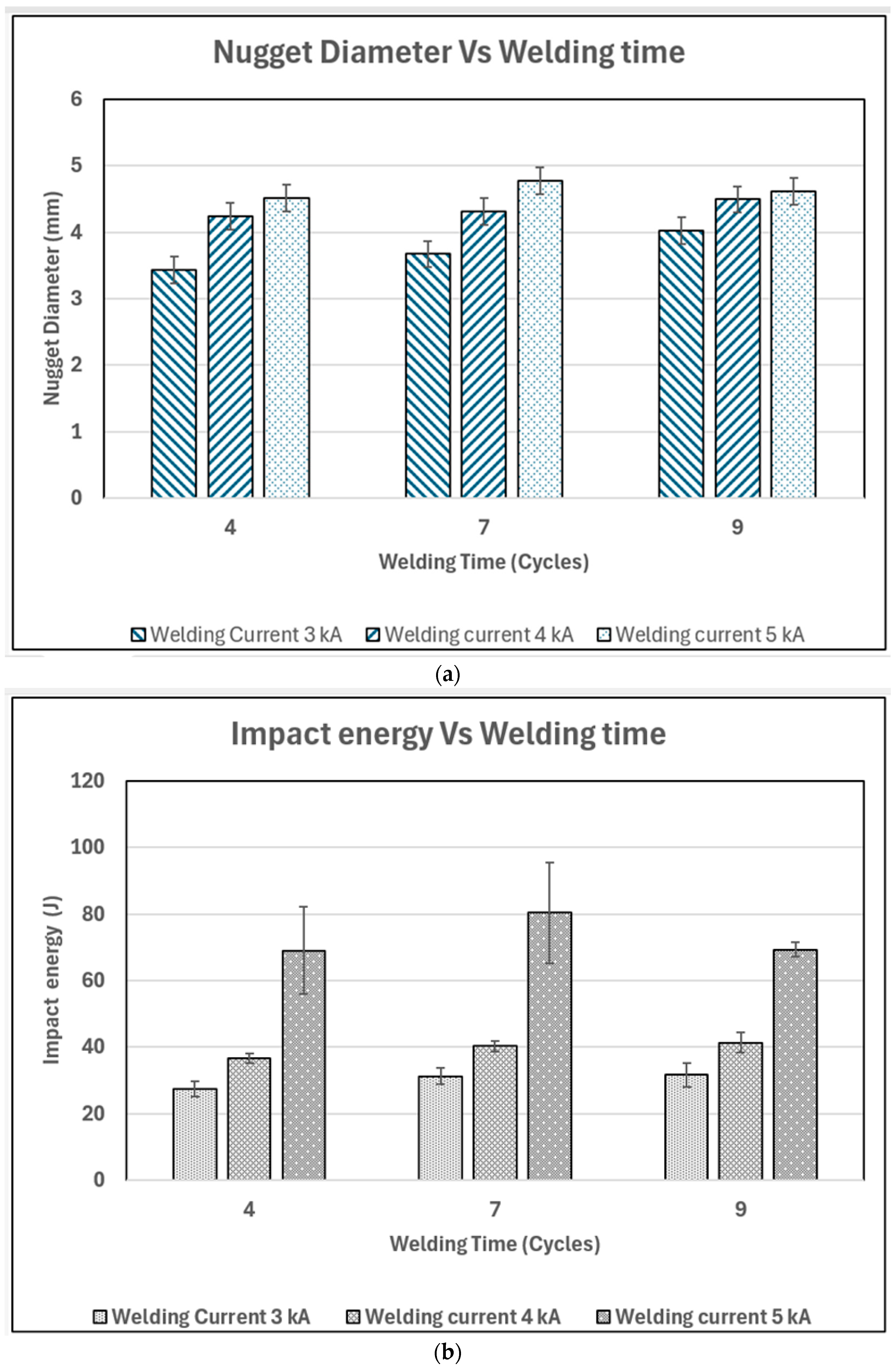
3.1.1. Effect of Welding Current
3.1.2. Effect of Welding Time
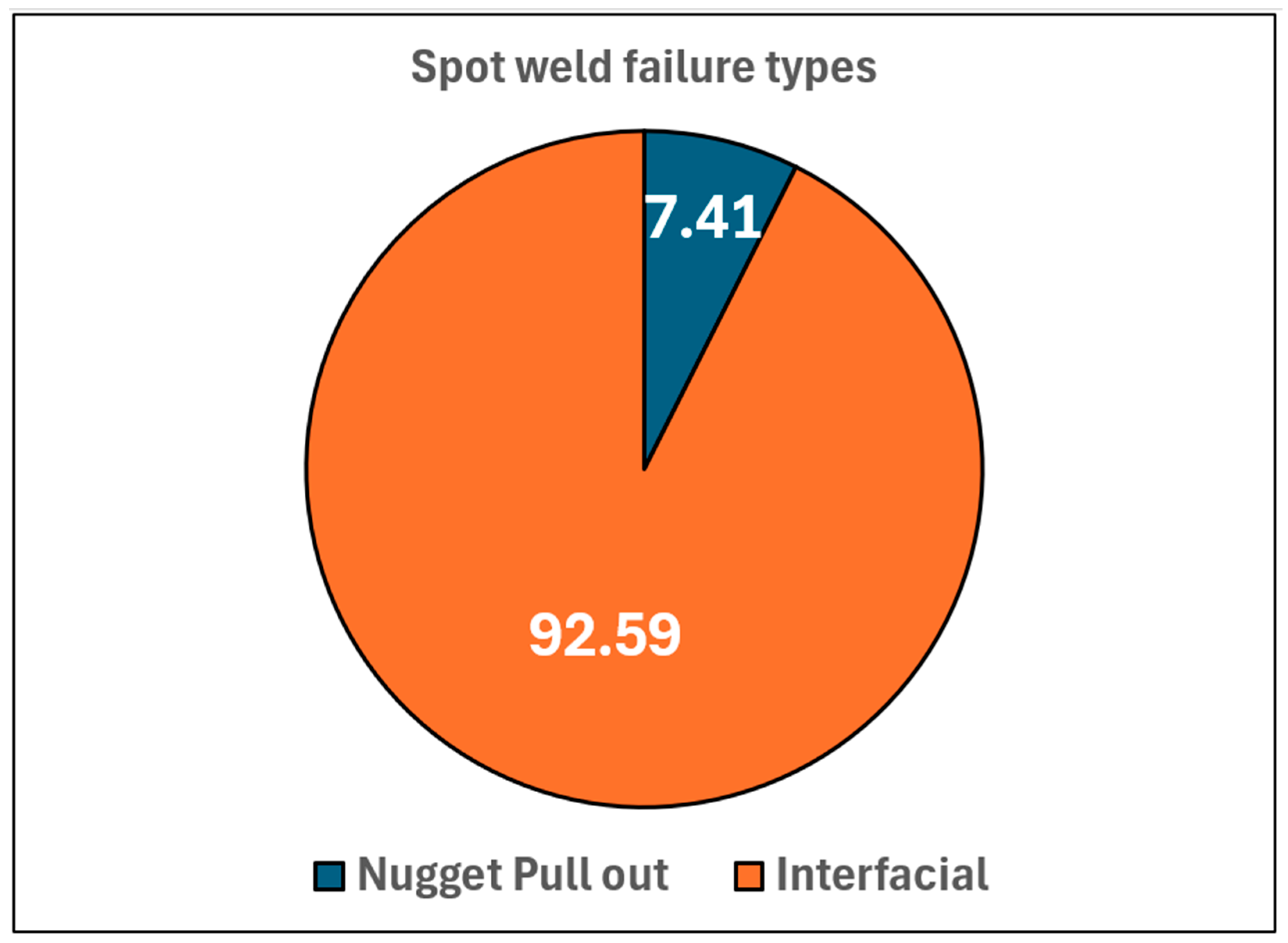
3.1.3. Failure Mode
3.2. Analysis Using Response Surface Methodology
3.2.1. Analysis of Variance
3.2.2. Model Graphs
3.3. Analysis Using RSM
4. Conclusions
- i.
- The highest impact energy obtained during impact testing was 98 J for the specimen that was welded using 5 kA of welding current and nine cycles welding time.
- ii.
- Both welding current and welding time affect the impact energy absorption capability of the spot weld. The increase in welding current allowed the temperature at the faying surface to rapidly increase to melting temperature, melting more metal, which resulted in a larger diameter. This caused the impact energy to increase. The increase in welding time had a similar effect and led to larger weld nuggets but only slightly higher impact energy.
- iii.
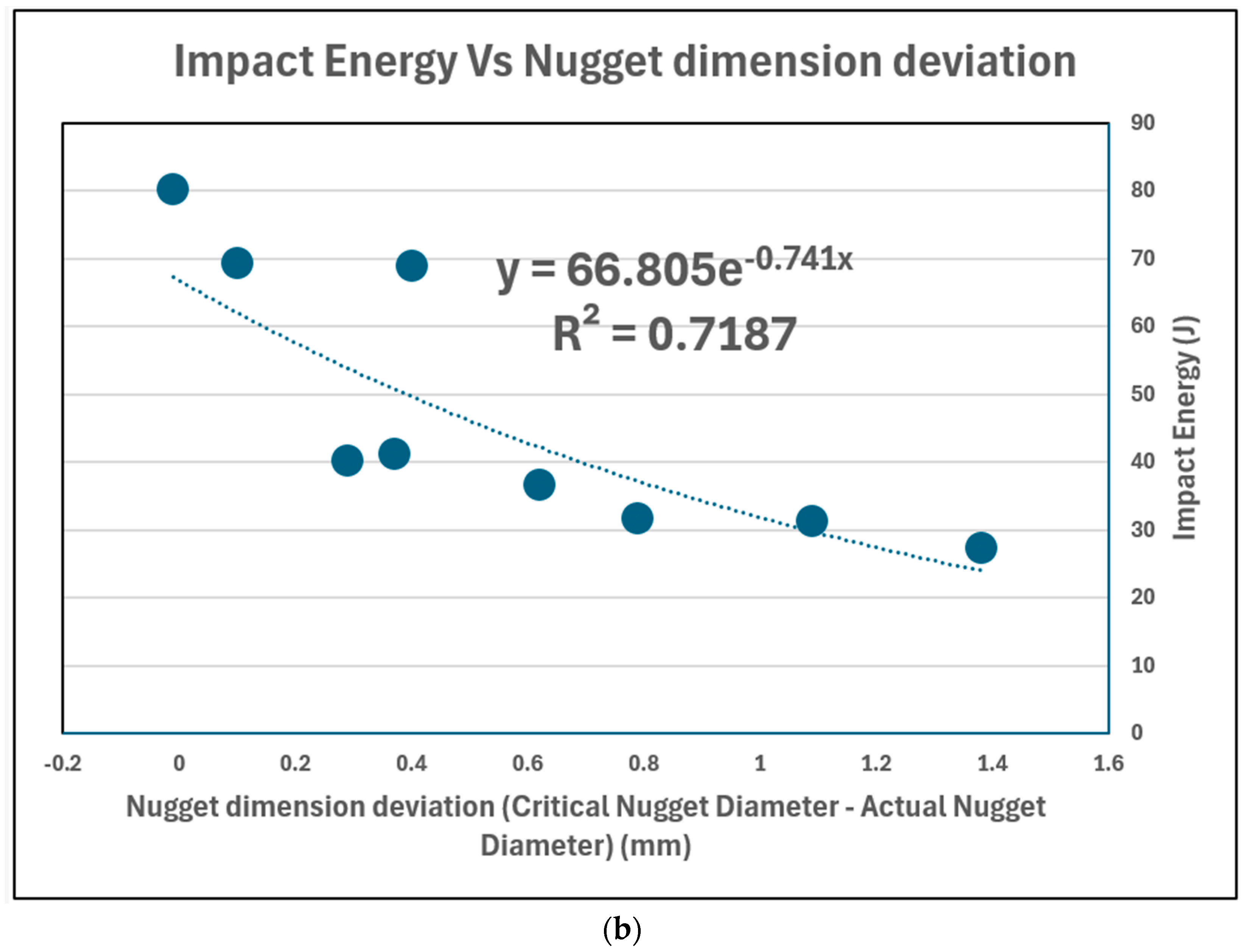
- The increase in both spot-welding process parameters caused the impact energy to increase and the nugget diameter to be larger. This occurred until a certain point, after which both the impact energy and nugget diameter values became lower.
- iv.
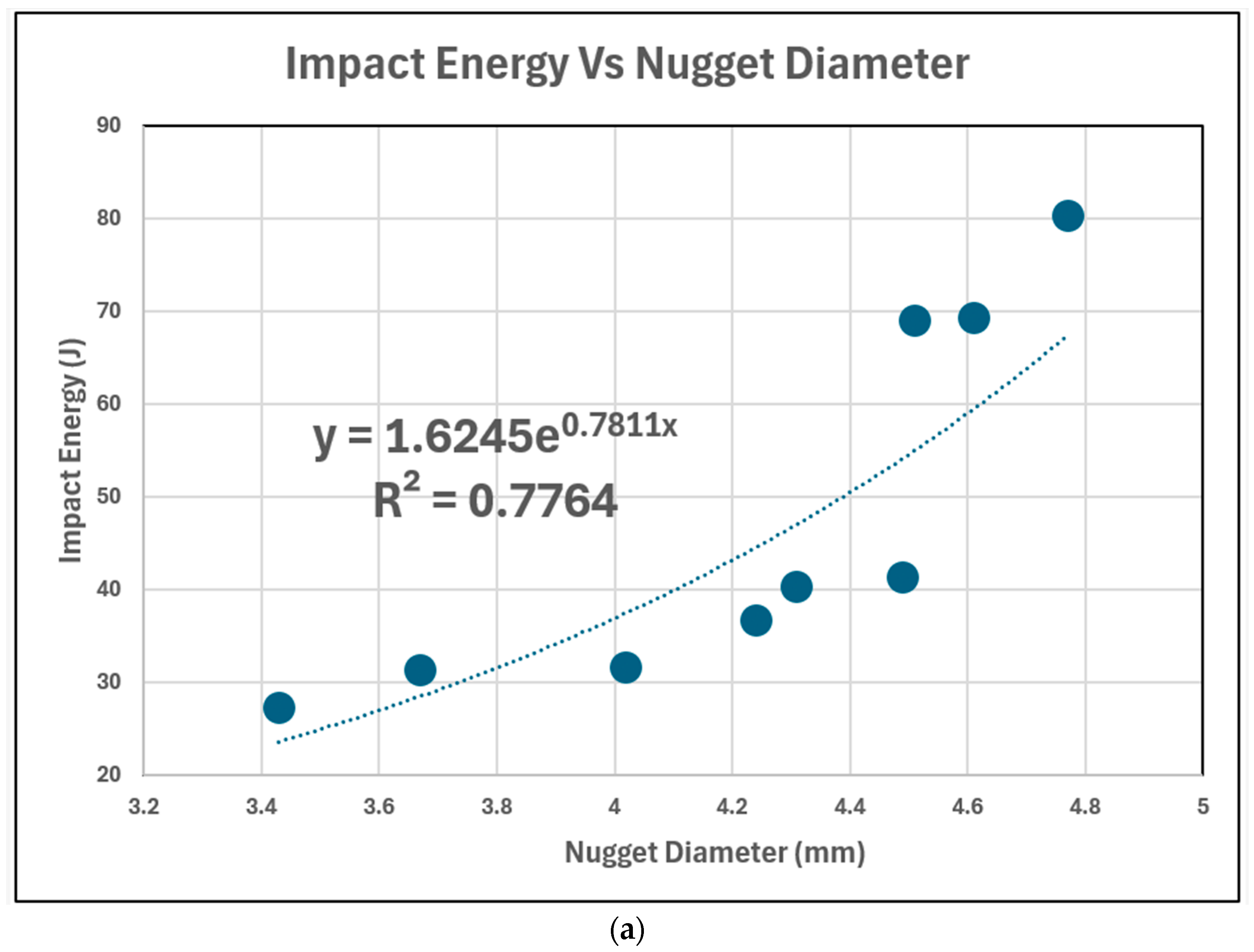
- There is a correlation between the nugget diameter and impact energy, in that the impact energy increases when the nugget diameter is larger.
- v.
- Results from ANOVA showed that the welding current has a greater effect on the impact energy and the welding performance of the spot weld.
- vi.
- Optimization of the model showed that a welding current of 5 kA and welding time of 6.728 cycles will produce an impact energy equal to 81.124 J with a desirability of 0.766.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chao, Y.J. Failure Mode of Spot Welds: Interfacial Versus Pullout. Sci. Technol. Weld. Join. 2003, 8, 133. [Google Scholar]
- Pouranvari, M.; Marashi, S.P.H.; Safanama, D.S. Failure Mode Transition in AHSS Resistance Spot Welds. Part II: Experimental Investigation and Model Validation. Mater. Sci. Eng. A 2011, 528, 8344–8352. [Google Scholar] [CrossRef]
- Darwisha, S.M.H.; Ghanya, A. Critical assessment of weld-bonded technologies. J. Mater. Process. Technol. 2000, 105, 221–229. [Google Scholar] [CrossRef]
- Shojaee, M.; Midawi, A.R.H.; Barber, B.; Ghassemi-Armaki, H.; Worswick, M.; Biro, E. Mechanical properties and failure behavior of resistance spot welded third-generation advanced high strength steels. J. Manuf. Process. 2021, 65, 364–372. [Google Scholar] [CrossRef]
- Soomro, I.A.; Pedapati, S.R.; Awang, M. A review of advances in resistance spot welding of automotive sheet steels: Emerging methods to improve joint mechanical performance. Int. J. Adv. Manuf. Technol. 2022, 118, 1335–1366. [Google Scholar] [CrossRef]
- Ramachandran, D.C.; Betiku, O.T.; Shojaee, M.; Salandari-Rabori, A.; Midawi, A.R.H.; Kim, J.-U.; Bakhtiari, R.; Macwan, A.; Biro, E. Effect of paint baking on the fusion boundary softening and fracture behavior of Q&P 980 steel resistance spot welds. Mater. Charact. 2023, 206, 113383. [Google Scholar] [CrossRef]
- Meilinger, Á.; Prém, L.; Al Al, S.A.A.; Gáspár, M. Comparison of RSW technologies on DP steels with modified instrumented Charpy impact test. Weld. World 2023, 67, 1911–1922. [Google Scholar] [CrossRef]
- Betiku, O.T.; Kim, J.-U.; Ikic, A.; Okoroafor, S.; Sherepenko, O.; Ghassemi-Armaki, H.; Biro, E. A novel method to evaluate the mechanical properties of resistance spot welds under dynamic loading. Manuf. Lett. 2024, 39, 11–15. [Google Scholar] [CrossRef]
- AZoM. Aisi 1010 Carbon Steel (Uns G10100). 2012. Available online: http://www.azom.com/article.aspx?ArticleID=6539 (accessed on 15 May 2016).
- Goodarzi, M.; Marashi, S.P.; Pouranvari, M. Dependence of Overload Performance on Weld Attributes for Resistance Spot Welded Galvanized Low Carbon Steel. J. Mater. Process. Technol. 2009, 209, 4379–4384. [Google Scholar] [CrossRef]
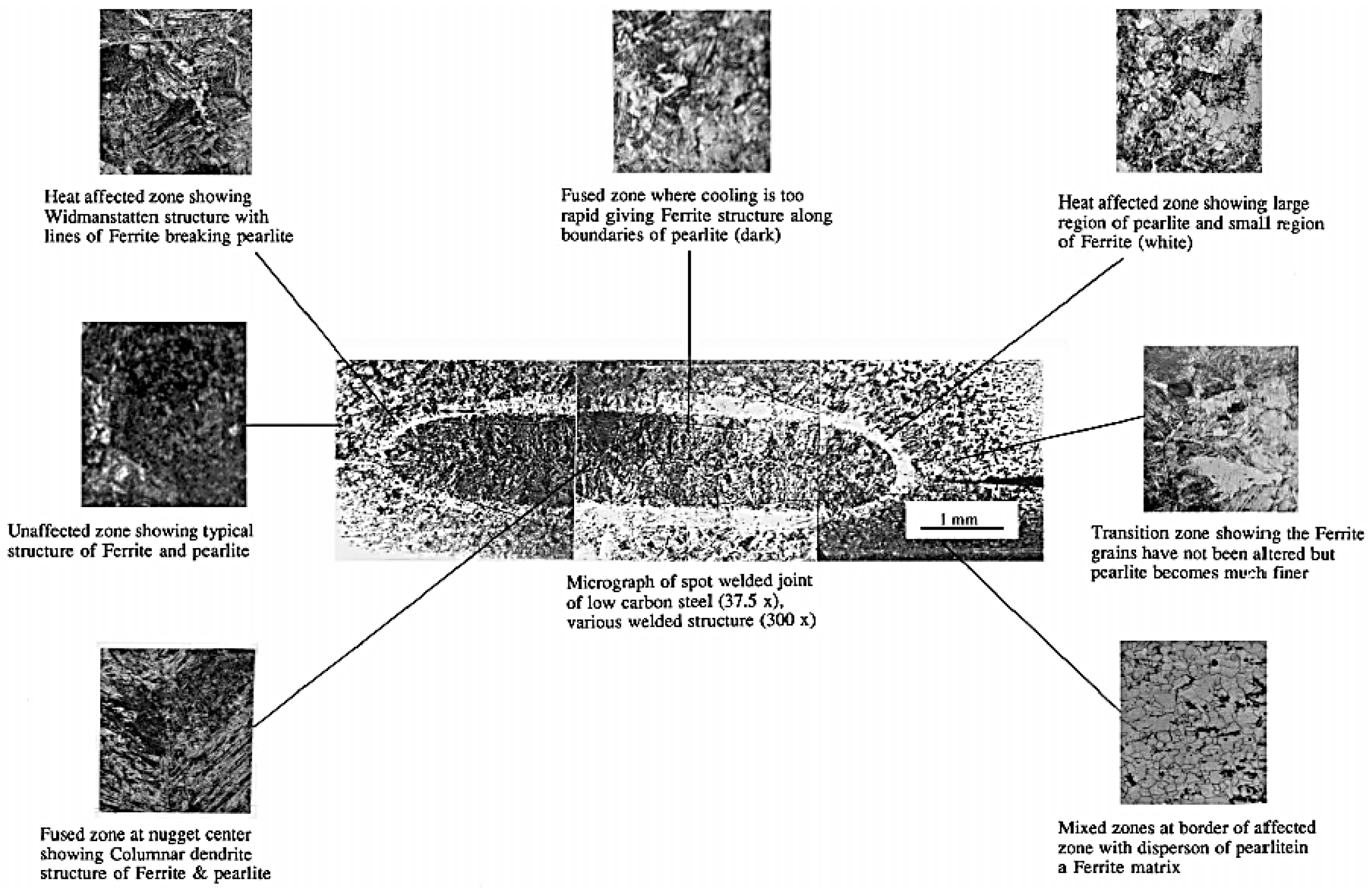

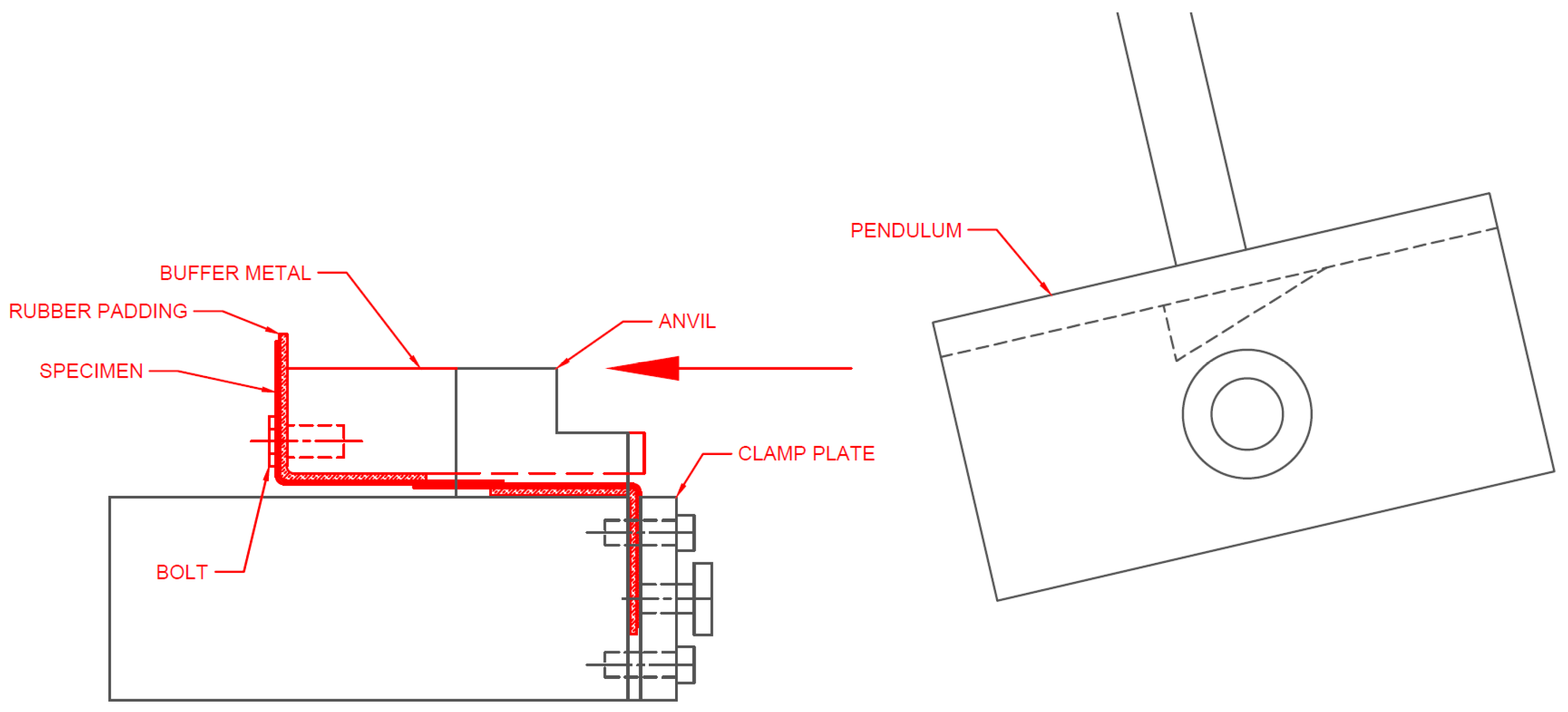

| Element | Content (%) |
|---|---|
| Iron (Fe) | |
| Carbon (C) | |
| Manganese (Mn) | |
| Sulfur (S) | |
| Phosphorous (P) |
| Property | Value |
|---|---|
| Density | |
| Tensile Strength (Ultimate) | |
| Tensile Strength (Yield) | |
| Elastic Modulus (Young’s Modulus) | |
| Shear Modulus | |
| Elongation at break (in 50 mm) | |
| Hardness, Vickers (after conversion from Brinell hardness) | 108 |
| Sample Number | Welding Current, I (kA) | Welding Time, t (Cycles) |
|---|---|---|
| 1–3 | 3 | 4 |
| 4–6 | 3 | 7 |
| 7–9 | 3 | 9 |
| 10–12 | 4 | 4 |
| 13–15 | 4 | 7 |
| 16–18 | 4 | 9 |
| 19–21 | 5 | 4 |
| 22–27 | 5 | 7 |
| 25–27 | 5 | 9 |
| Specimen | Welding Current (kA) | Welding Time (Cycles) | Impact Energy (J) | Failure Mode |
|---|---|---|---|---|
| 1.1 | 3 | 4 | 30 | Interfacial |
| 1.2 | 26 | Interfacial | ||
| 1.3 | 26 | Interfacial | ||
| 2.1 | 3 | 7 | 29 | Interfacial |
| 2.2 | 31 | Interfacial | ||
| 2.3 | 34 | Interfacial | ||
| 3.1 | 3 | 9 | 28 | Interfacial |
| 3.2 | 32 | Interfacial | ||
| 3.3 | 35 | Interfacial | ||
| 4.1 | 4 | 4 | 37 | Interfacial |
| 4.2 | 38 | Interfacial | ||
| 4.3 | 35 | Interfacial | ||
| 5.1 | 4 | 7 | 40 | Interfacial |
| 5.2 | 42 | Interfacial | ||
| 5.3 | 39 | Interfacial | ||
| 6.1 | 4 | 9 | 44 | Interfacial |
| 6.2 | 38 | Interfacial | ||
| 6.3 | 42 | Interfacial | ||
| 7.1 | 5 | 4 | 71 | Interfacial |
| 7.2 | 55 | Interfacial | ||
| 7.3 | 81 | Interfacial | ||
| 8.1 | 5 | 7 | 98 | Pullout |
| 8.2 | 68 | Interfacial | ||
| 8.3 | 85 | Pullout | ||
| 9.1 | 5 | 9 | 70 | Interfacial |
| 9.2 | 67 | Interfacial | ||
| 9.3 | 71 | Interfacial |
| Welding Current (kA) | Welding Time (Cycles) | Average Impact Energy (J) | Thickness (mm) | Nugget Diameter (mm) | Critical Nugget Diameter (mm) |
|---|---|---|---|---|---|
| 3 | 4 | 27.333 | 1.23 | 3.43 | 4.81 |
| 3 | 7 | 31.333 | 1.22 | 3.67 | 4.76 |
| 3 | 9 | 31.667 | 1.23 | 4.02 | 4.81 |
| 4 | 4 | 36.667 | 1.24 | 4.24 | 4.86 |
| 4 | 7 | 40.333 | 1.19 | 4.31 | 4.60 |
| 4 | 9 | 41.333 | 1.24 | 4.49 | 4.86 |
| 5 | 4 | 69.000 | 1.25 | 4.51 | 4.91 |
| 5 | 7 | 80.333 | 1.22 | 4.77 | 4.76 |
| 5 | 9 | 69.333 | 1.21 | 4.61 | 4.71 |
| Source | Sum of Squares | Degree of Freedom | Mean Square | F-Value | p-Value Prob > F |
|---|---|---|---|---|---|
| Model | 1.850 × 10−3 | 5 | 3.700 × 10−4 | 82.15 | <0.0001 |
| A—Welding Current | 1.777 × 10−3 | 1 | 1.777 × 10−3 | 394.54 | <0.0001 |
| B—Welding Time | 3.269 × 10−5 | 1 | 3.269 × 10−5 | 7.26 | 0.0136 |
| AB | 1.295 × 10−5 | 1 | 1.295 × 10−5 | 2.87 | 0.1047 |
| A2 | 1.787 × 10−5 | 1 | 1.787 × 10−5 | 3.97 | 0.0595 |
| B2 | 1.634 × 10−5 | 1 | 1.634 × 10−5 | 3.63 | 0.0706 |
| Residual | 9.459 × 10−5 | 21 | 4.504 × 10−6 | ||
| Lack of Fit | 3.169 × 10−5 | 3 | 1.056 × 10−6 | 0.21 | 0.8895 |
| Pure Error | 9.142 × 10−5 | 18 | 5.079 × 10−6 | ||
| Corrected Total | 1.945 × 10−5 | 26 |
| Term | Value | Term | Value |
|---|---|---|---|
| Standard Deviation | 2.122 × 10−3 | R-Squared | 0.9514 |
| Mean | 0.024 | Adjusted R-Squared | 0.9398 |
| Coefficient of Variation | 8.73 | Predicted R-Squared | 0.9157 |
| PRESS | 1.640 × 10−4 | Adequate Precision | 24.030 |
| Factor | Coefficient Estimate | Degree of Freedom | Standard Error | 95% CI Low | 95% CI High | VIF |
|---|---|---|---|---|---|---|
| Intercept | 0.024 | 1 | 9.423 × 10−4 | 0.022 | 0.027 | |
| A—Welding Current | −9.969 × 10−3 | 1 | 5.019 × 10−4 | −0.011 | −8.925 × 10−3 | 1.01 |
| B—Welding Time | −1.348 × 10−3 | 1 | 5.002 × 10−4 | −2.388 × 10−3 | −3.074 × 10−4 | 1.01 |
| AB | 1.032 × 10−3 | 1 | 6.086 × 10−4 | −2.337 × 10−4 | 2.298 × 10−3 | 1.01 |
| A2 | −1.726 × 10−3 | 1 | 8.664 × 10−4 | −3.528 × 10−3 | 7.590 × 10−5 | 1.00 |
| B2 | 1.730 × 10−3 | 1 | 9.085 × 10−4 | −1.591 × 10−4 | 3.620 × 10−3 | 1.01 |
| Number | Welding Current (kA) | Welding Time (Cycles) | Impact Energy (J) | Desirability |
|---|---|---|---|---|
| 1 | 5 | 6.728 | 81.124 | 0.766 |
| 2 | 5 | 6.751 | 81.123 | 0.766 |
| 3 | 5 | 6.705 | 81.123 | 0.766 |
| 4 | 5 | 6.600 | 81.093 | 0.765 |
| 5 | 5 | 6.563 | 81.074 | 0.765 |
| 6 | 5 | 6.989 | 80.997 | 0.764 |
| 7 | 5 | 6.215 | 80.635 | 0.759 |
| 8 | 5 | 7.277 | 80.564 | 0.758 |
| 9 | 5 | 7.518 | 79.975 | 0.750 |
| 10 | 5 | 5.754 | 79.391 | 0.742 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castillo, R.K.; Khandoker, N.; Islam, S.; Mazid, A.M. Impact Testing of AISI 1010 Low-Carbon Steel Spot-Welded Joints. Appl. Mech. 2025, 6, 79. https://doi.org/10.3390/applmech6040079
Castillo RK, Khandoker N, Islam S, Mazid AM. Impact Testing of AISI 1010 Low-Carbon Steel Spot-Welded Joints. Applied Mechanics. 2025; 6(4):79. https://doi.org/10.3390/applmech6040079
Chicago/Turabian StyleCastillo, Ralph Kenneth, Neamul Khandoker, Sumaiya Islam, and Abdul Md Mazid. 2025. "Impact Testing of AISI 1010 Low-Carbon Steel Spot-Welded Joints" Applied Mechanics 6, no. 4: 79. https://doi.org/10.3390/applmech6040079
APA StyleCastillo, R. K., Khandoker, N., Islam, S., & Mazid, A. M. (2025). Impact Testing of AISI 1010 Low-Carbon Steel Spot-Welded Joints. Applied Mechanics, 6(4), 79. https://doi.org/10.3390/applmech6040079





