Influence of Post-Curing Time and Print Orientation on the Mechanical Behavior of Photosensitive Resins in mSLA 3D Printing
Abstract
1. Introduction
2. Materials and Methods
- Exposure time: 2.2 s;
- Base exposure time: 20 s;
- Number of base layers: 5;
- Layer height: 0.05 mm.
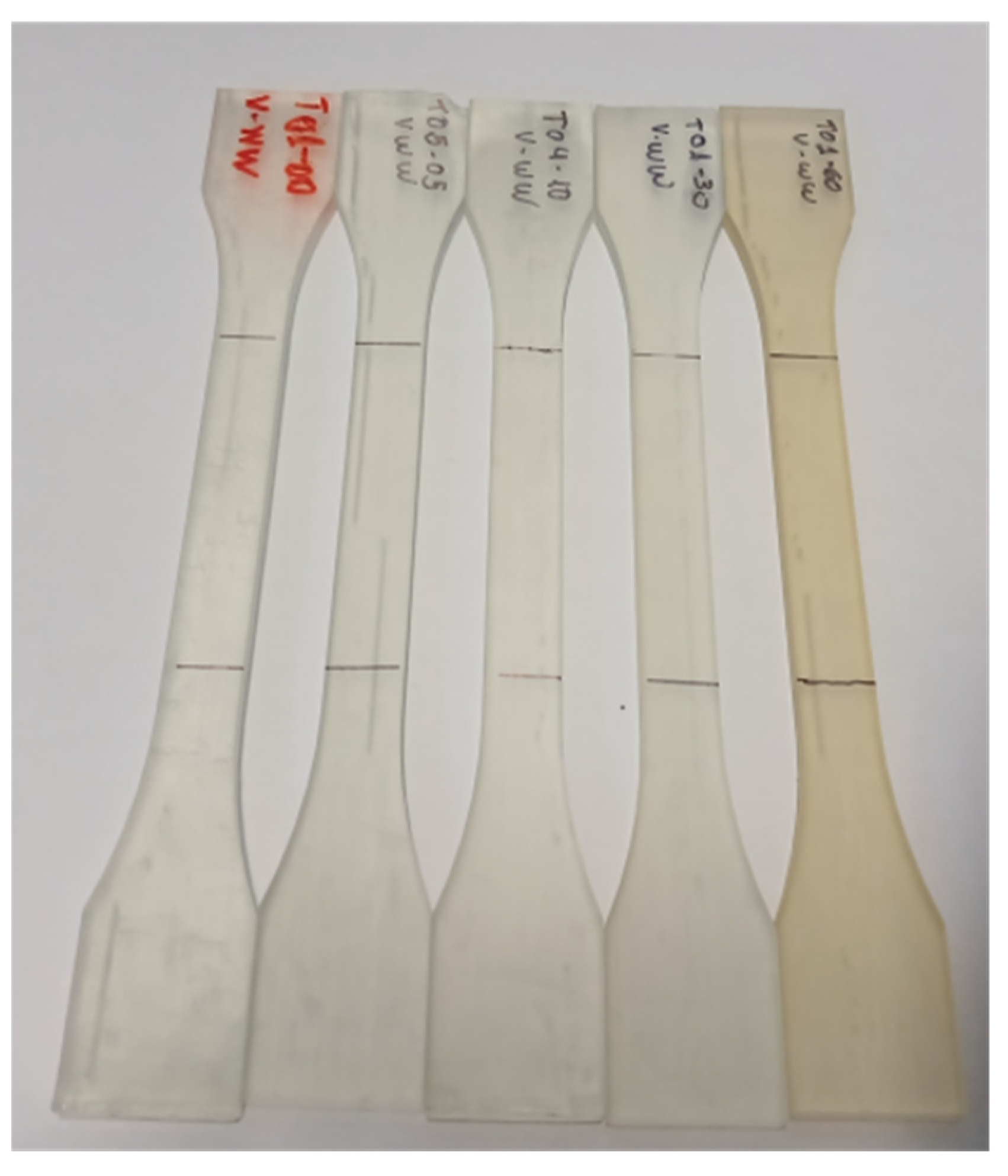
2.1. Specimen Preparation
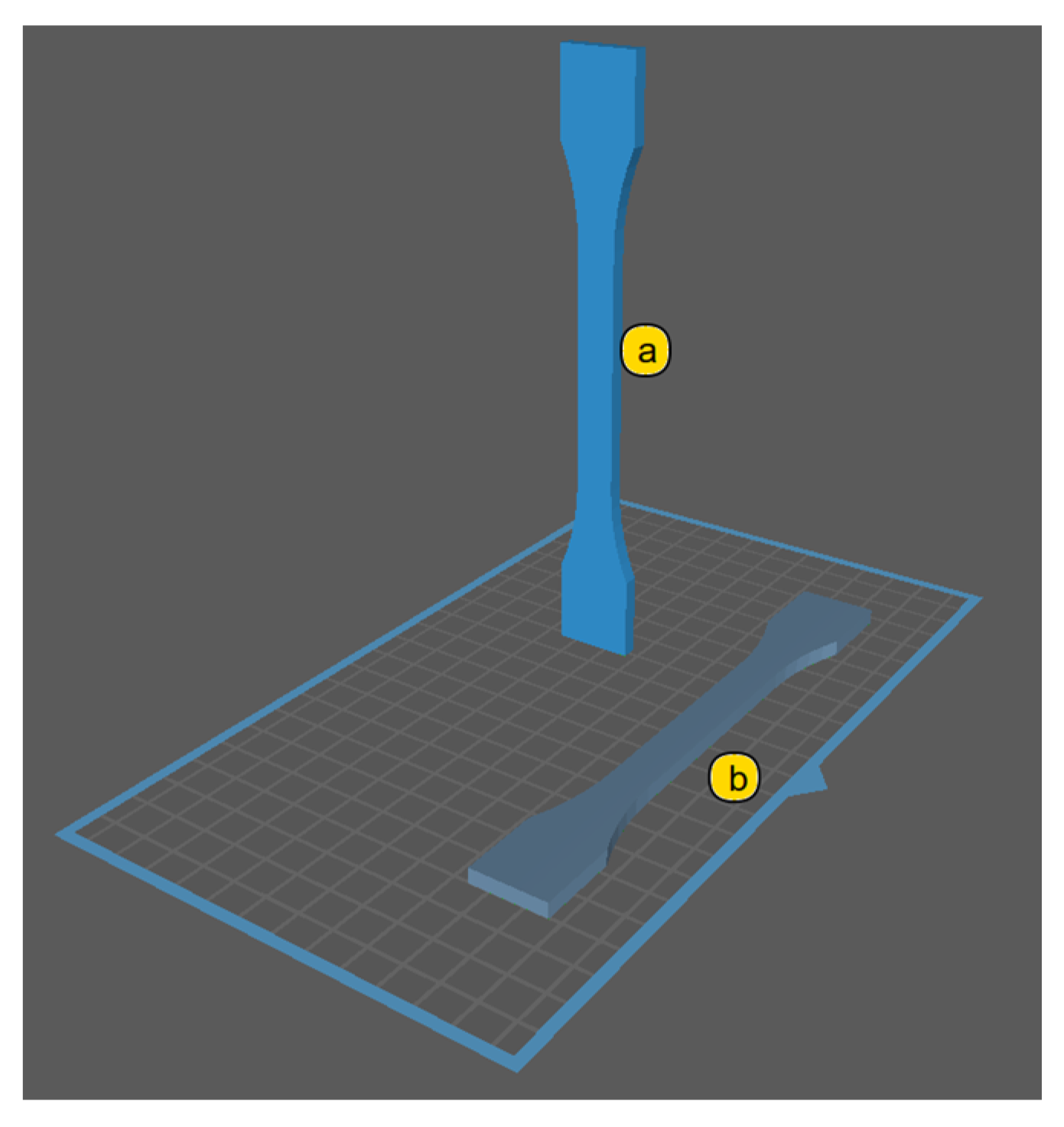
- Flat [XY] (a): specimen perpendicular to the printing platform.
- Vertical [Z] (b): specimen parallel to the platform, with its longitudinal axis perpendicular to the printing direction.
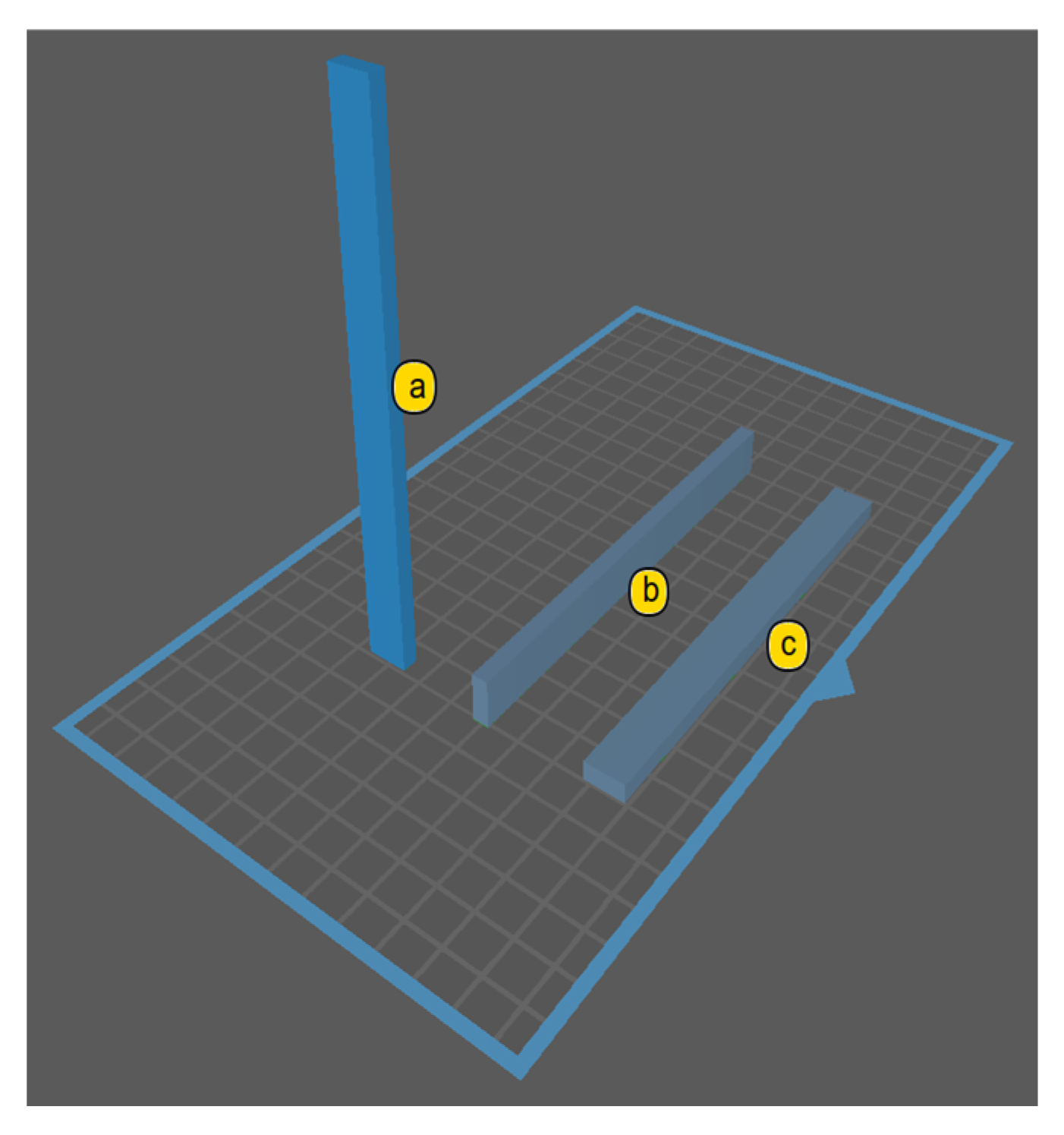
- Flat [XY]: specimen perpendicular to the printing platform;
- On-edge [XZ]: specimen parallel to the platform, with its longitudinal axis perpendicular to the printing direction;
- Vertical [Z]: specimen parallel to the platform, with its longitudinal axis parallel to the printing direction.
2.2. Post-Processing
2.3. Mechanical Testing
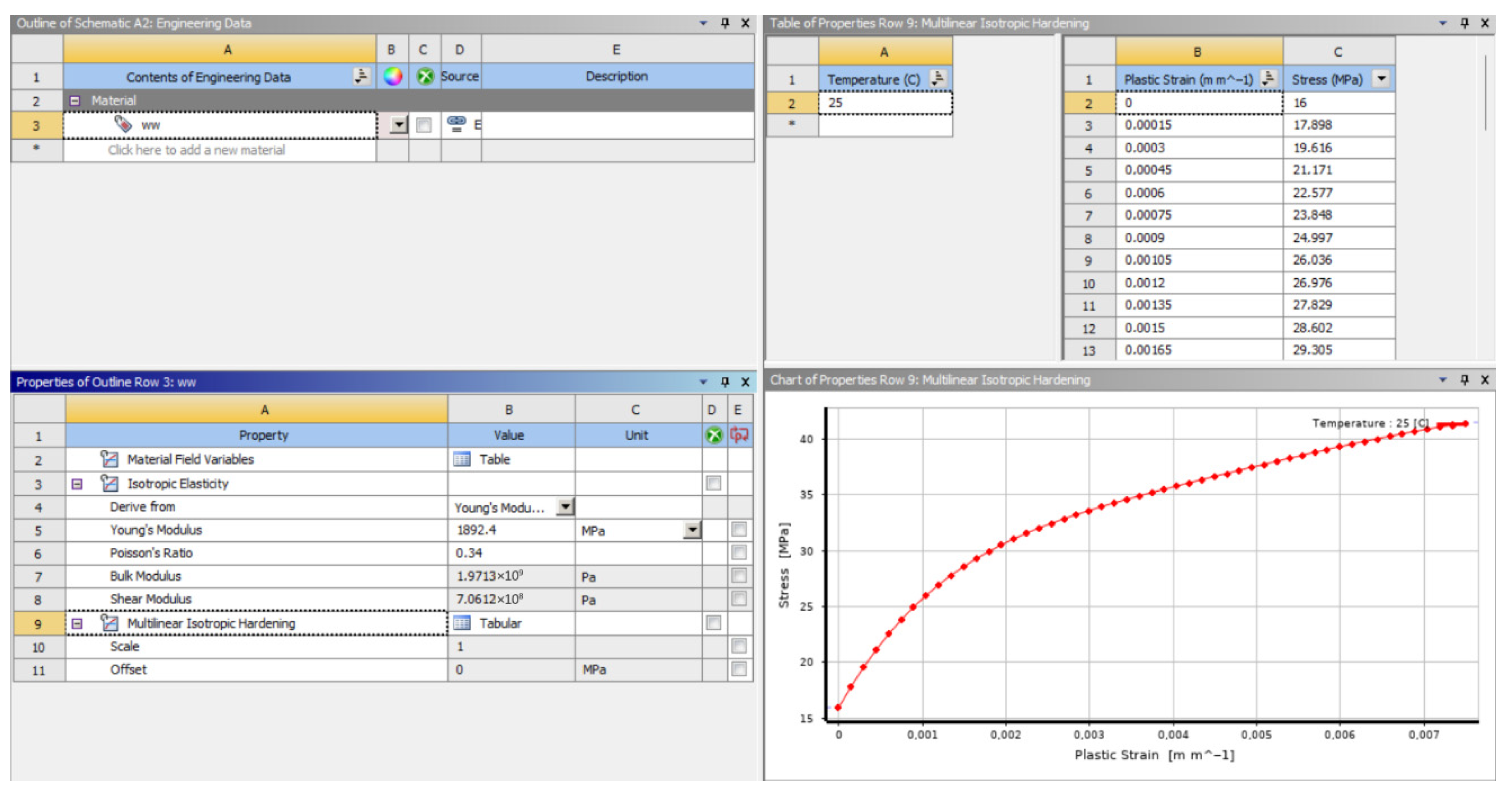
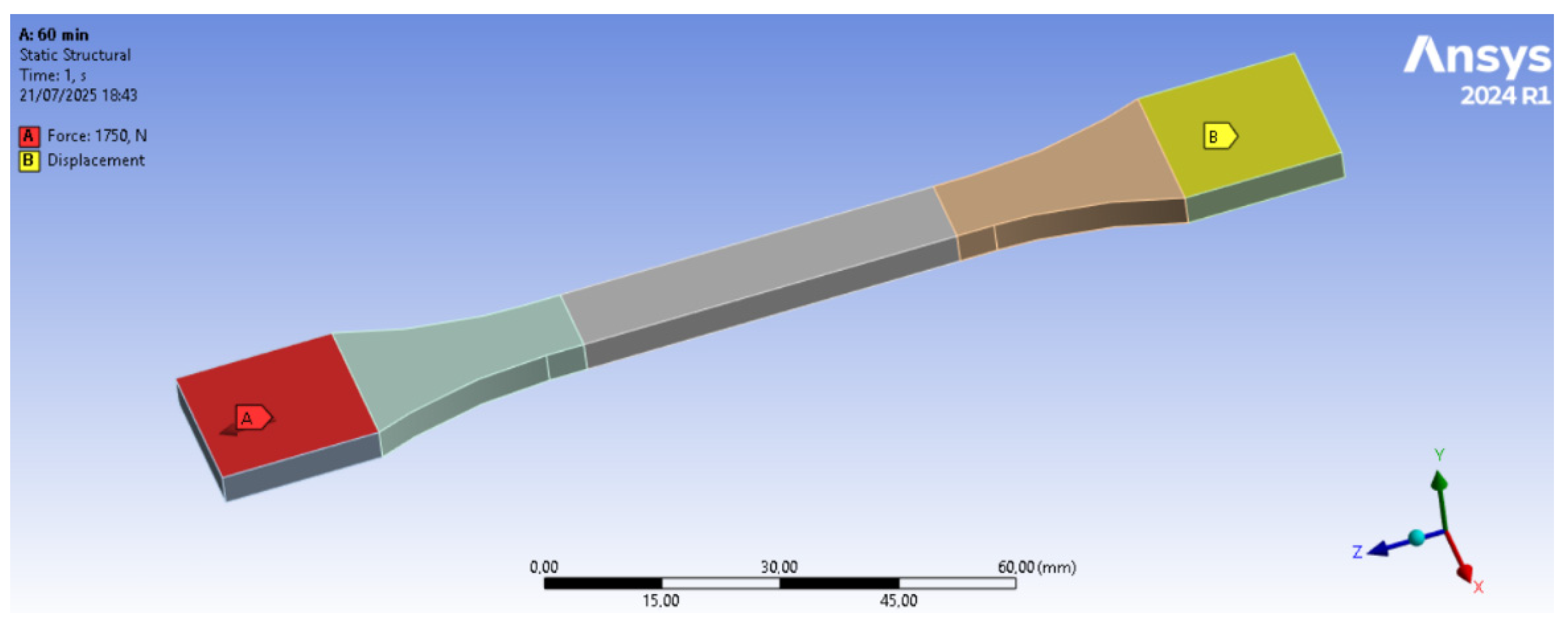
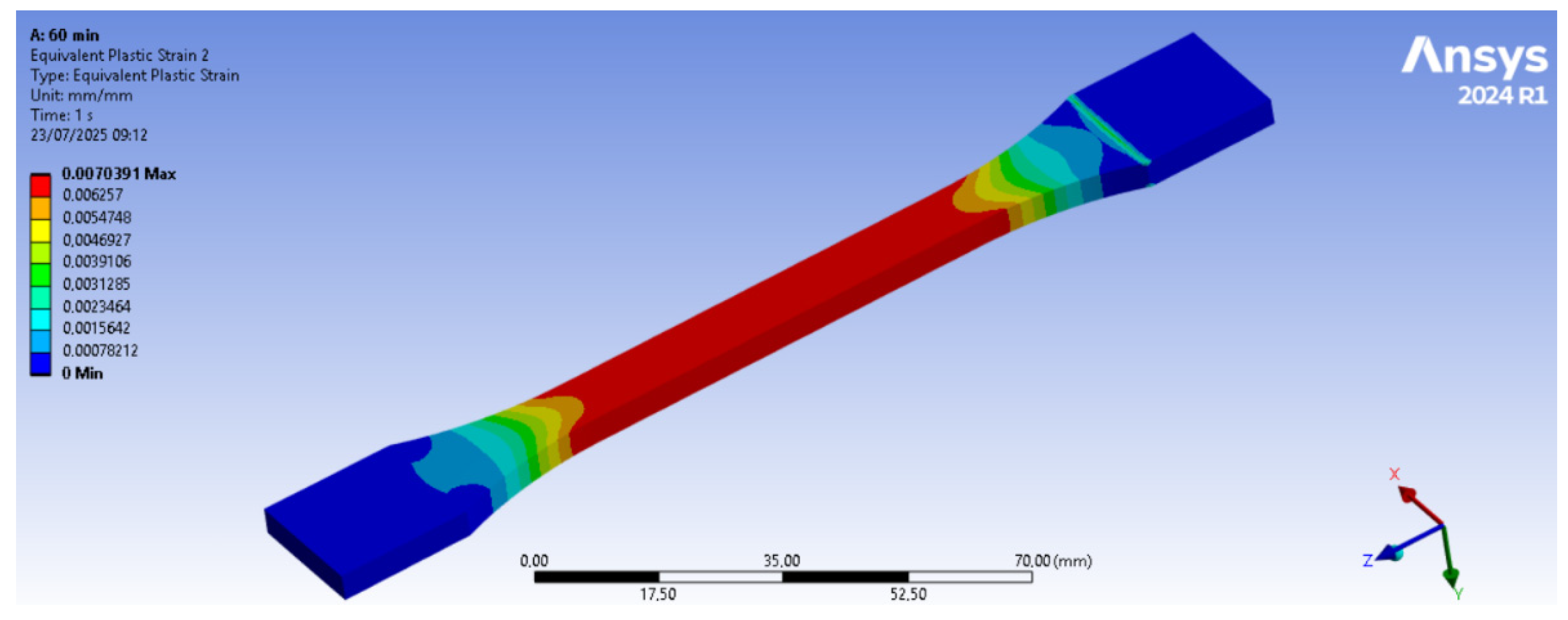
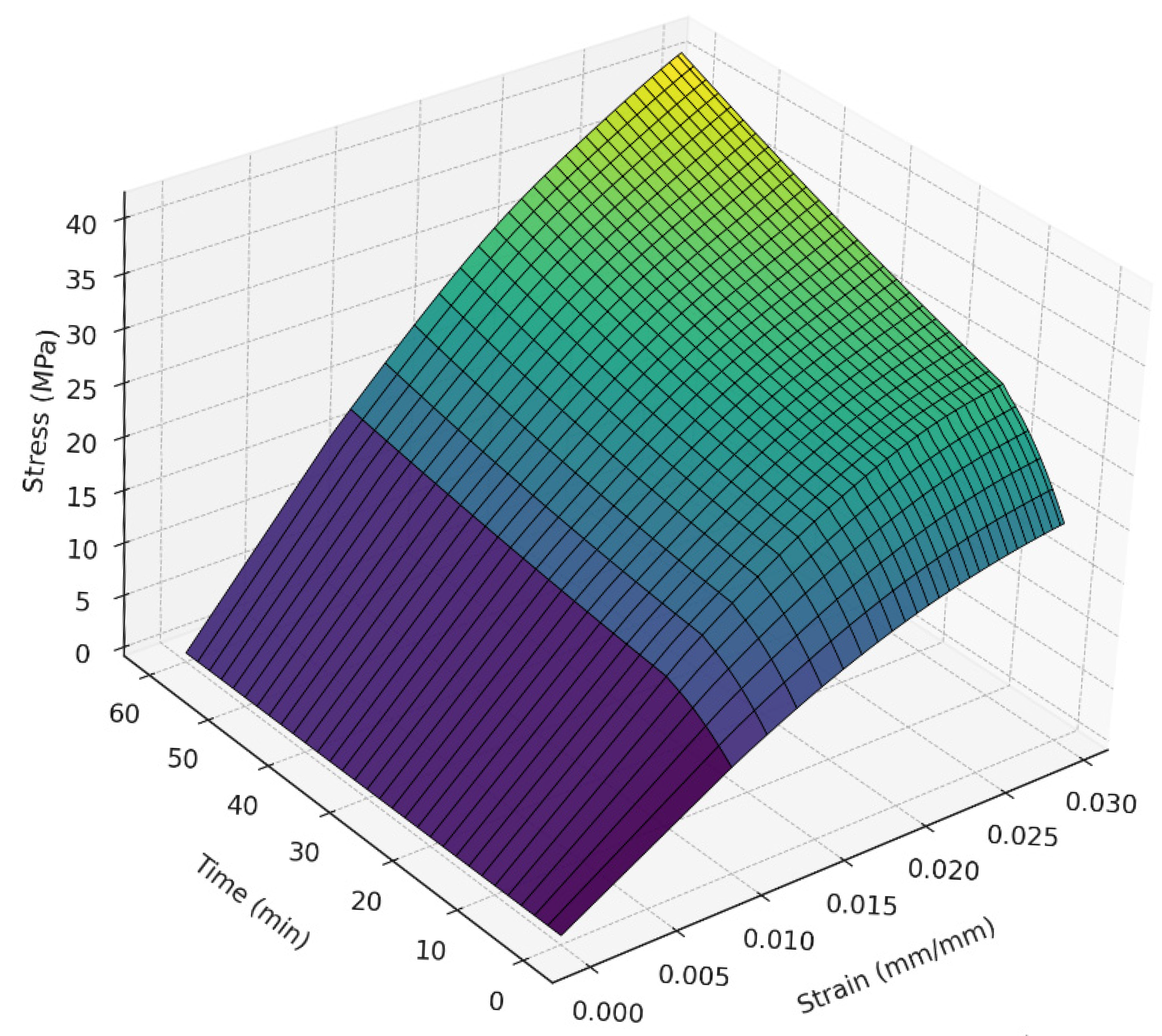
2.4. Data Processing and Numerical Simulation
- Data conversion: Automatic transformation of force–displacement into stress–strain.
- Linear region identification: Interactive interface for the user to define the start and end of the linear elastic region.
- Elastic modulus calculation: Least-squares linear fit to the identified elastic region.
- Secant modulus determination:
- 5.
- Interpolation and intersection: Automatic location of the intersection between the interpolated experimental curve and the offset line, defining the proportionality limit.
- 6.
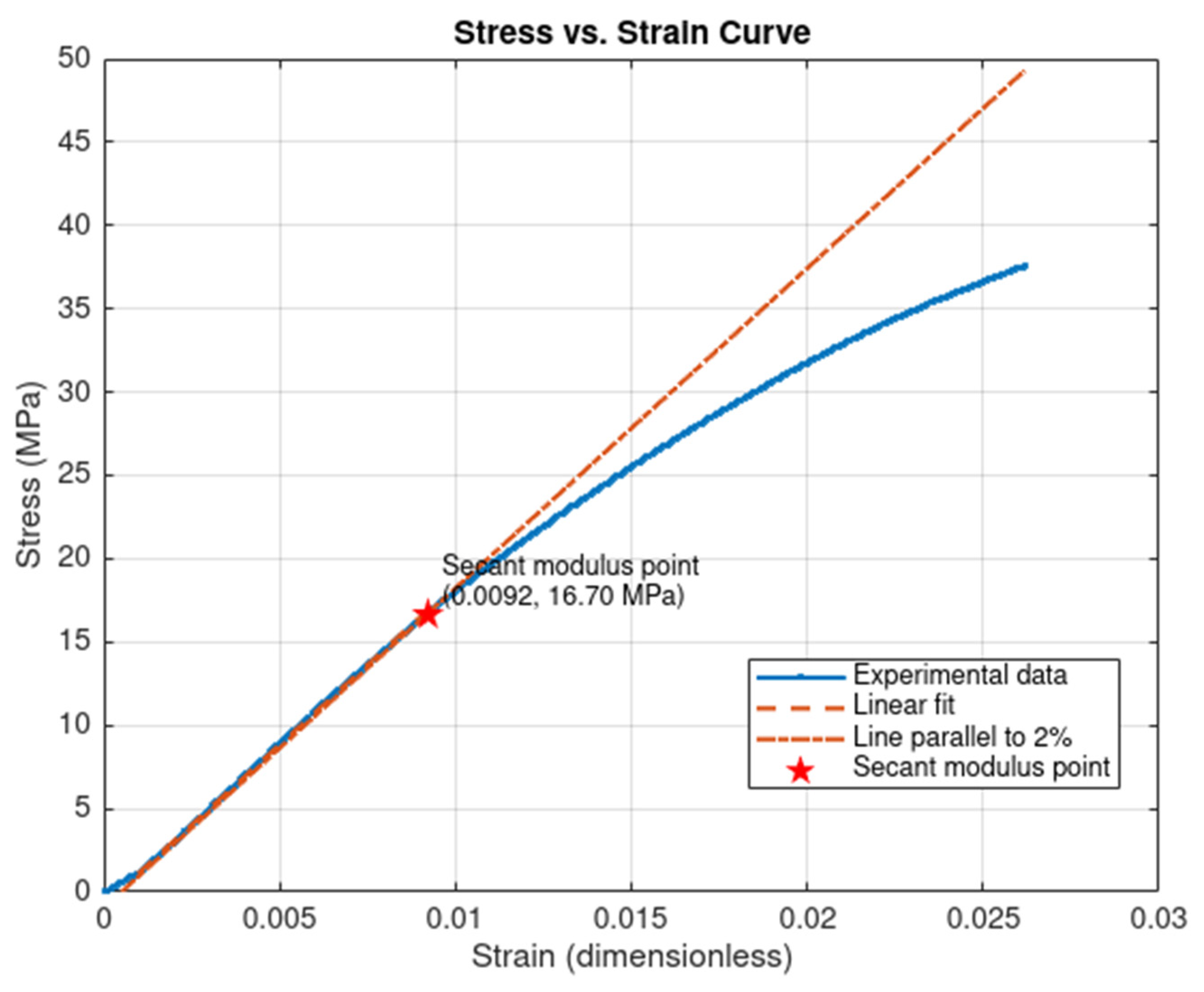
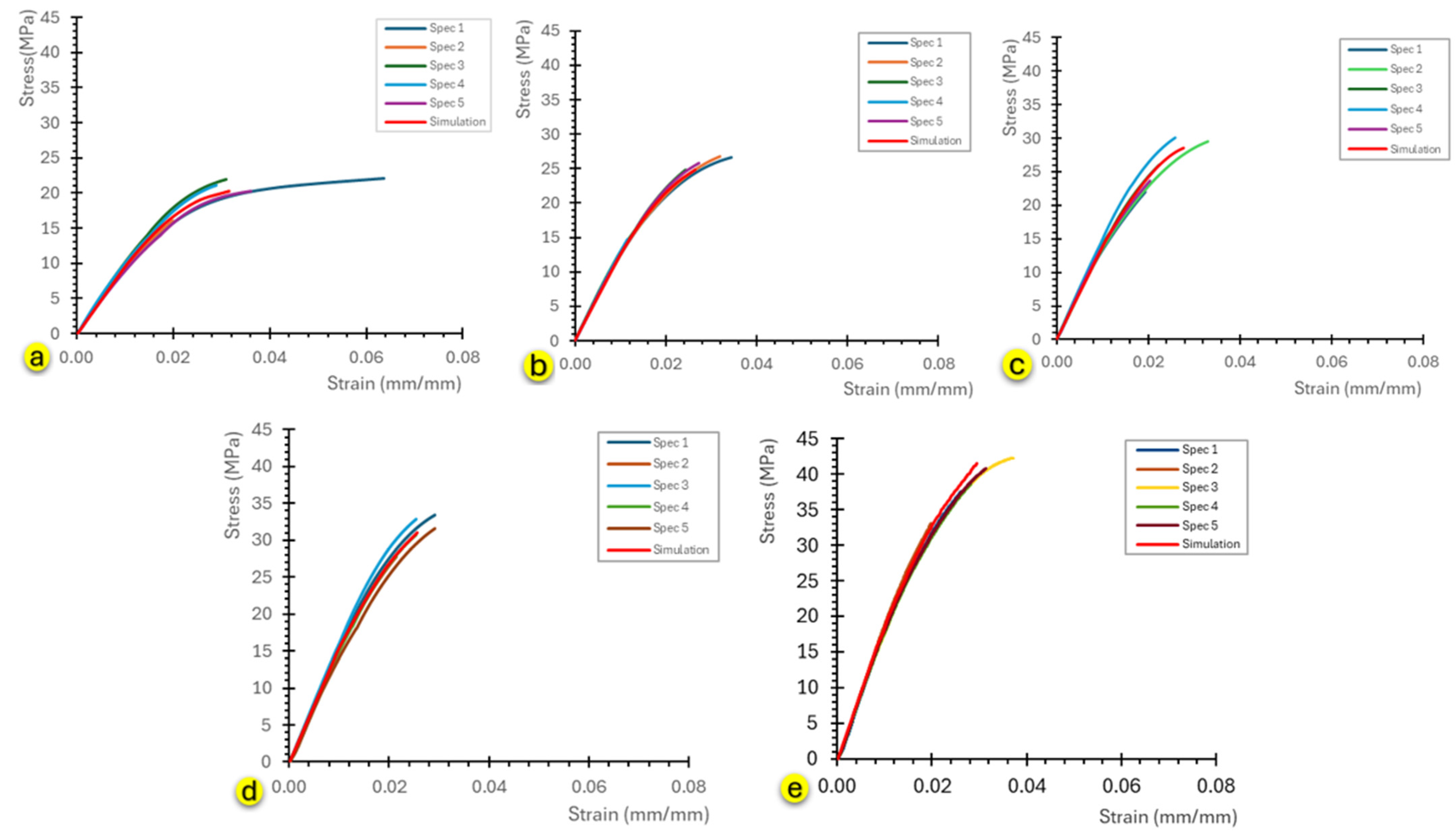
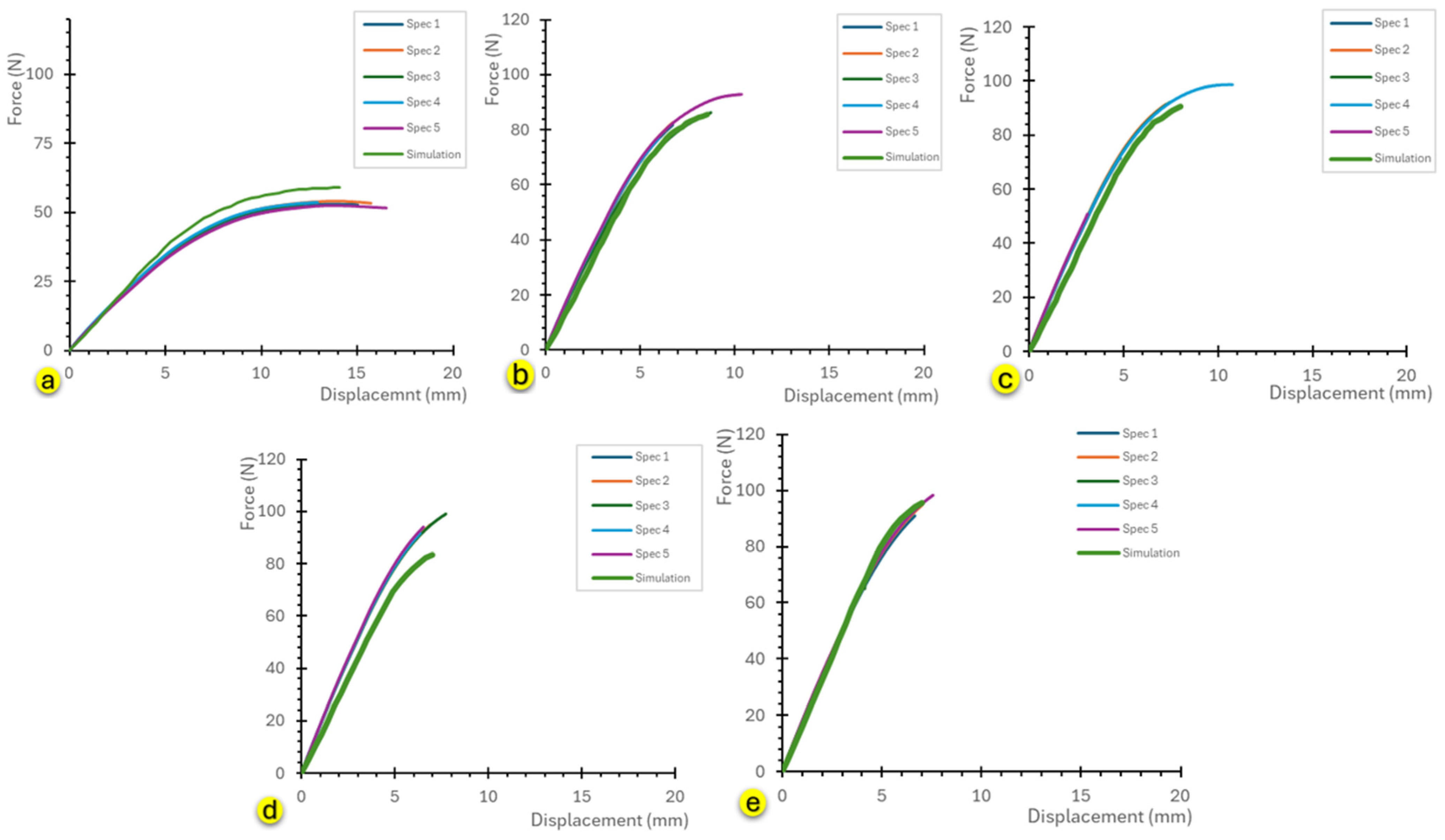
- Graphical visualization: Automatic generation of plots showing the experimental curve, linear fit, offset line, and clearly marked secant modulus point, as illustrated in Figure 10 for the 60 min curing time in the Flat [XY] orientation.
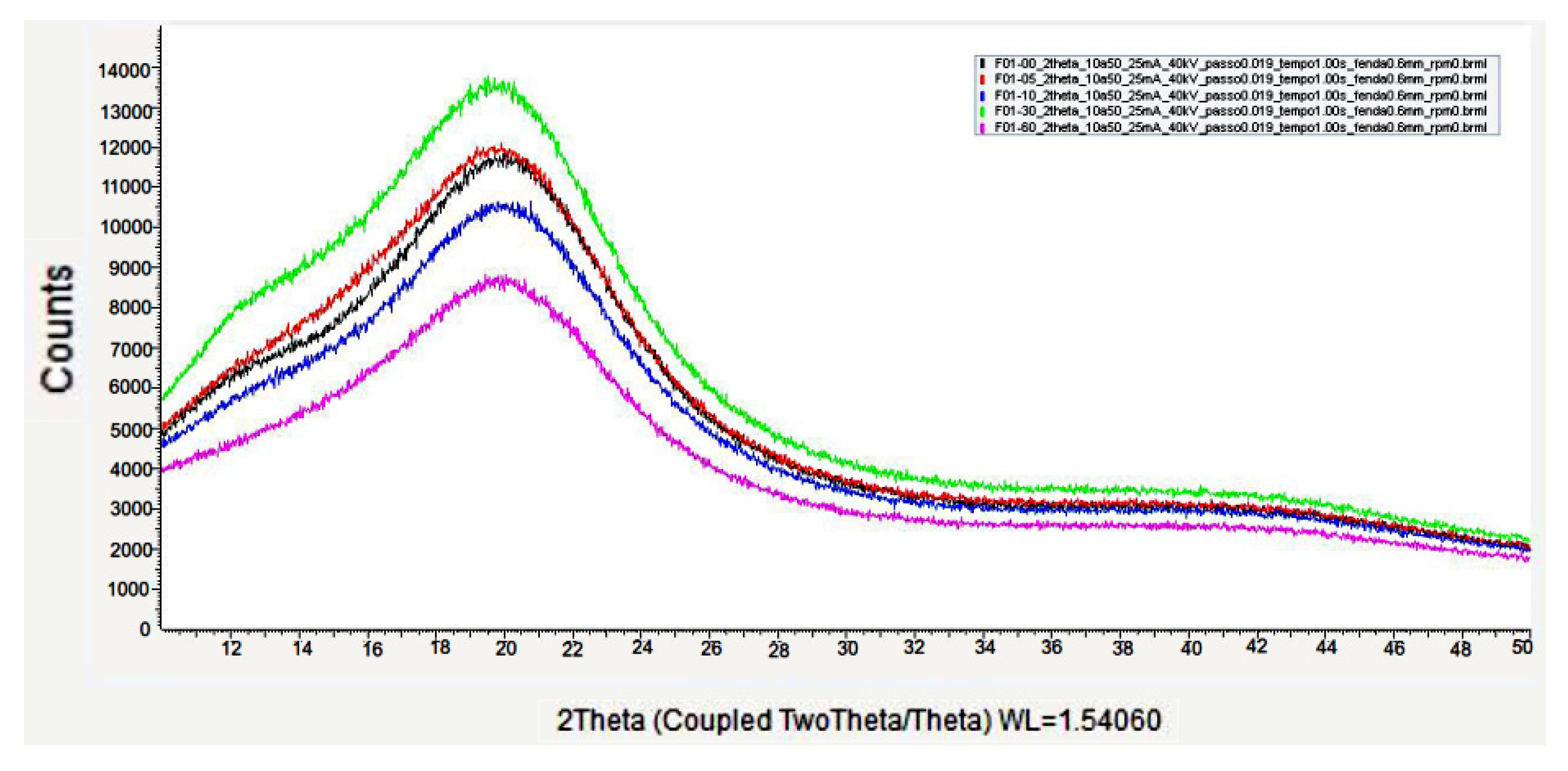
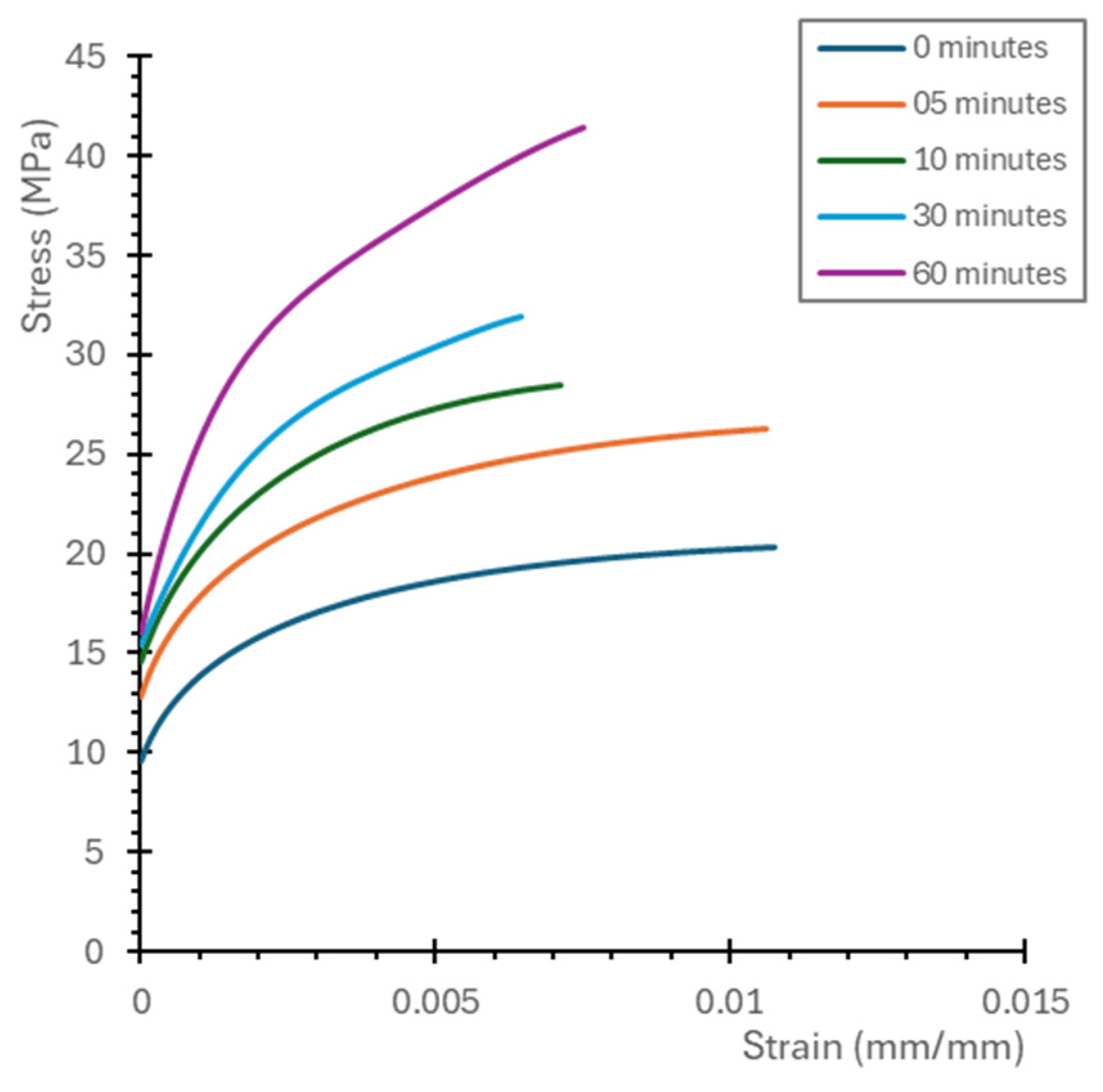
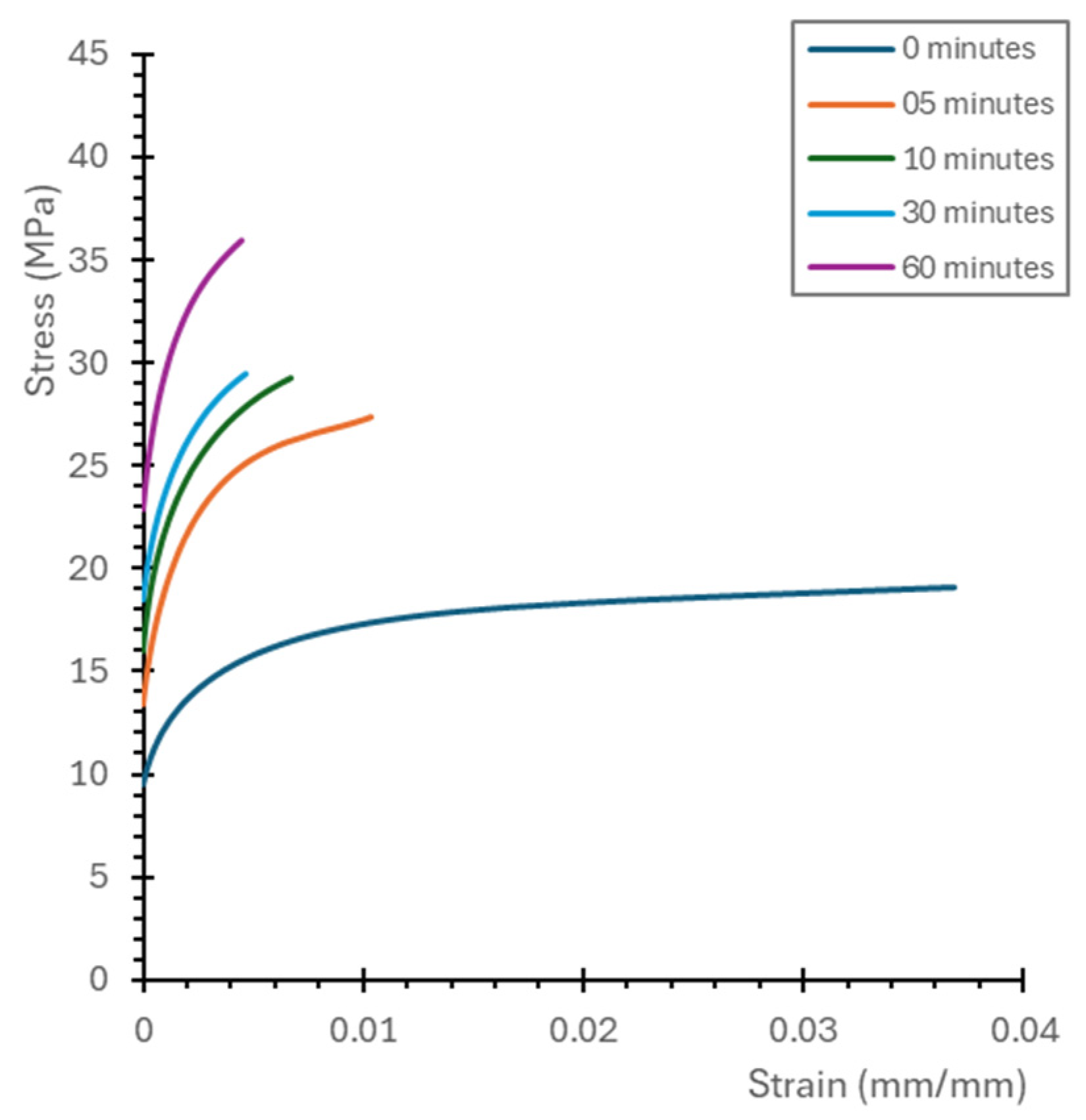
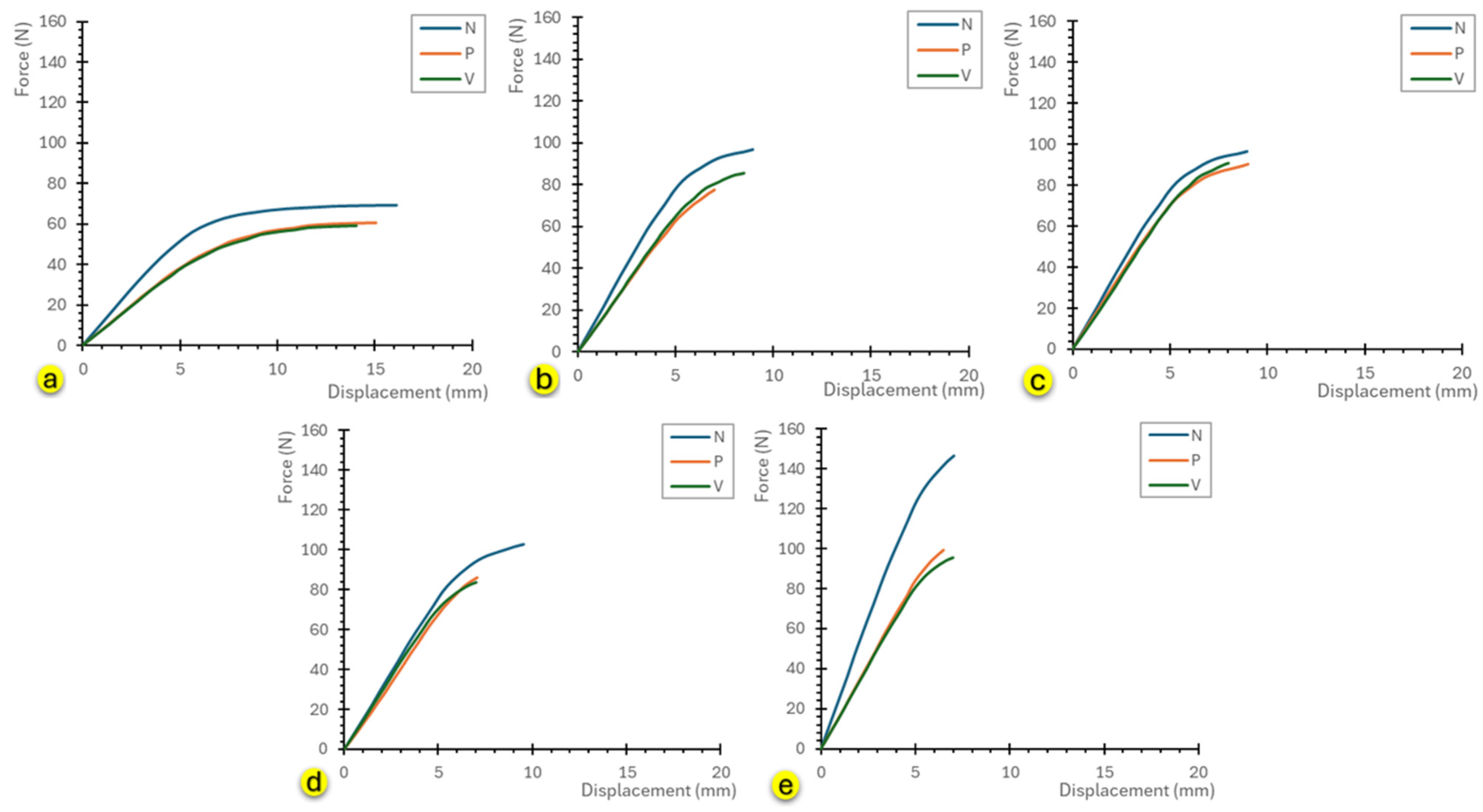
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| % 2 percent of the curve = (delta L)/L * 0.02 = (3.10/118)*0.02 = 0.0005 % variables x and y are vector already loaded in MATLAB % x: displacement in mm % y: force in N % Sample data area = 44; % Cross-sectional area in mm² initial_length = 118; % Initial length in mm % Stress and strain calculation stress = y ./ area; % Stress in MPa (N/mm²) strain = x ./ initial_length; % Dimensionless strain % Check if stress and strain have valid values if isempty(stress) || isempty(strain) || length(stress) ~= length(strain) |
| error(’Data error: stress and strain must be non-empty vectors of the same size.’); end % Ask user for initial and final index start_index = input(sprintf(’Enter the initial index of the linear region (1 to %d): ’, length(strain))); end_index = input(sprintf(’Enter the final index of the linear region (%d to %d): ’, start_index + 1, length(strain))); % Ensure indices are within valid range if start_index < 1 || end_index > length(strain) || start_index >= end_index |
| error(’Invalid indices. Make sure that 1 <= start index < end index <= %d.’, length(strain)); end % Linear fit in the identified region p = polyfit(strain(start_index:end_index), stress(start_index:end_index), 1); % The slope is the modulus of elasticity elastic_modulus = p(1); % Display results fprintf(’Linear region defined by user: Index %d to %d\n’, start_index, end_index); fprintf(’The modulus of elasticity is: %.2f MPa\n’, elastic_modulus); % Ensure a new figure is created figure; % Plot full graph plot(strain, stress, ’.-’, ’LineWidth’, 1.5); % Experimental data hold on; % Fitted data for linear fit plot strain_fit = strain(start_index:end_index); stress_fit = polyval(p, strain_fit); % Plot linear fit line plot(strain_fit, stress_fit, ’--’, ’LineWidth’, 1.5); % Linear fit line % ----------- Line parallel to 2% strain (offset) ------------ strain_offset = linspace(0.0005, max(strain), 100); % strains starting at 2% stress_offset = elastic_modulus * (strain_offset - 0.0005); % same slope, shifted % Plot the new offset line plot(strain_offset, stress_offset, ’-.’, ’LineWidth’, 1.5, ’Color’, [0.85 0.33 0.1]); % orange color % ----------- Calculation of the secant modulus point (intersection) ---------- % Interpolate experimental data with interp1 strain_interp = linspace(min(strain), max(strain), 1000); stress_interp = interp1(strain, stress, strain_interp, ’linear’); % Calculate the interpolated offset line stress_offset_interp = elastic_modulus * (strain_interp - 0.0005); % Difference between the curves difference = abs(stress_interp - stress_offset_interp); % Index of minimum difference (closest intersection point) [~, idx_intersec] = min(difference); strain_secant = strain_interp(idx_intersec); stress_secant = stress_interp(idx_intersec); % Plot secant modulus point plot(strain_secant, stress_secant, ’rp’, ’MarkerSize’, 10, ’MarkerFaceColor’, ’r’); text(strain_secant, stress_secant, sprintf(’ Secant modulus point\n (%.4f, %.2f MPa)’, strain_secant, stress_secant), ... |
| ’VerticalAlignment’, ’bottom’, ’FontSize’, 9); % Final plot adjustments xlabel(’Strain (dimensionless)’); ylabel(’Stress (MPa)’); title(’Stress vs. Strain Curve’); legend(’Experimental data’, ’Linear fit’, ’Line parallel to 2%’, ’Secant modulus point’, ’Location’, ’best’); grid on; hold off; |
Appendix B
| Equation: | IF($H$1<=9;B2+C2*$H$1+D2*$H$1^2;E2+F2*$H$1+G2*$H$1^2) | |||||||
| x | a0_0_9 | a1_0_9 | a2_0_9 | a0_10_60 | a1_10_60 | a2_10_60 | Time | Stress (y) |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 60 | 0 |
| 0.008455 | 8.225761 | 0.524709 | −0.01755 | 11.27145 | 0.044362 | 0.000574 | 16 | |
| 0.009608 | 9.347893 | 0.595396 | −0.01983 | 12.75166 | 0.05798 | 0.000463 | 17.89791 | |
| 0.010666 | 10.28529 | 0.672677 | −0.02282 | 14.26118 | 0.04909 | 0.000669 | 19.61621 | |
| 0.011637 | 11.09982 | 0.723295 | −0.02465 | 15.41168 | 0.047206 | 0.000813 | 21.17085 | |
| 0.01253 | 11.82321 | 0.768032 | −0.02622 | 16.42371 | 0.047194 | 0.000923 | 22.57672 | |
| 0.013352 | 12.4663 | 0.807783 | −0.02757 | 17.31665 | 0.048557 | 0.001005 | 23.84773 | |
| 0.014109 | 13.03959 | 0.843229 | −0.02874 | 18.10779 | 0.050803 | 0.001067 | 24.99682 | |
| 0.014808 | 13.55057 | 0.875133 | −0.02978 | 18.81237 | 0.053532 | 0.001114 | 26.03602 | |
| 0.015455 | 14.00817 | 0.903953 | −0.0307 | 19.44348 | 0.056444 | 0.001152 | 26.97648 | |
| 0.016055 | 14.4191 | 0.93012 | −0.03152 | 20.01142 | 0.059373 | 0.001182 | 27.82854 | |
| 0.016614 | 14.78946 | 0.953997 | −0.03227 | 20.52516 | 0.062201 | 0.001207 | 28.60173 | |
| 0.017136 | 15.12483 | 0.975893 | −0.03296 | 20.99251 | 0.064855 | 0.001228 | 29.30481 | |
| 0.017624 | 15.42925 | 0.996113 | −0.03359 | 21.41965 | 0.067316 | 0.001246 | 29.94585 | |
| 0.018084 | 15.70736 | 1.014832 | −0.03417 | 21.81213 | 0.069572 | 0.001263 | 30.53221 | |
| 0.018519 | 15.96262 | 1.032245 | −0.03471 | 22.1745 | 0.071635 | 0.001277 | 31.07063 | |
| 0.018931 | 16.19826 | 1.048506 | −0.03522 | 22.51083 | 0.073511 | 0.00129 | 31.5672 | |
| 0.019324 | 16.4162 | 1.063814 | −0.0357 | 22.8244 | 0.075223 | 0.001303 | 32.02746 | |
| 0.019701 | 16.61963 | 1.078202 | −0.03616 | 23.11809 | 0.076786 | 0.001314 | 32.4564 | |
| 0.020063 | 16.81032 | 1.09181 | −0.03659 | 23.39467 | 0.0782 | 0.001325 | 32.85848 | |
| 0.020414 | 16.98963 | 1.104748 | −0.037 | 23.65625 | 0.07948 | 0.001337 | 33.23769 | |
| 0.020754 | 17.15881 | 1.117091 | −0.03739 | 23.9043 | 0.080653 | 0.001348 | 33.59756 | |
| 0.021086 | 17.31945 | 1.128892 | −0.03777 | 24.14089 | 0.081694 | 0.001361 | 33.94121 | |
| 0.02141 | 17.47255 | 1.1402 | −0.03813 | 24.36716 | 0.082622 | 0.001374 | 34.27134 | |
| 0.021729 | 17.61894 | 1.151051 | −0.03848 | 24.584 | 0.083459 | 0.001389 | 34.5903 | |
| 0.022042 | 17.75931 | 1.161472 | −0.03881 | 24.79216 | 0.084222 | 0.001404 | 34.90011 | |
| 0.022352 | 17.89426 | 1.17148 | −0.03914 | 24.99213 | 0.084933 | 0.001421 | 35.20244 | |
| 0.022659 | 18.02426 | 1.181081 | −0.03944 | 25.18421 | 0.08562 | 0.001438 | 35.49871 | |
| 0.022963 | 18.14969 | 1.190287 | −0.03973 | 25.36867 | 0.086306 | 0.001456 | 35.79005 | |
| 0.023264 | 18.27086 | 1.199094 | −0.04001 | 25.54554 | 0.087024 | 0.001475 | 36.07735 | |
| 0.023564 | 18.38802 | 1.207489 | −0.04027 | 25.71466 | 0.087813 | 0.001494 | 36.3613 | |
| 0.023863 | 18.50138 | 1.215456 | −0.04051 | 25.87578 | 0.088718 | 0.001512 | 36.64238 | |
| 0.02416 | 18.61108 | 1.222972 | −0.04074 | 26.0285 | 0.089788 | 0.001529 | 36.92088 | |
| 0.024456 | 18.71724 | 1.230013 | −0.04093 | 26.17236 | 0.091079 | 0.001544 | 37.19696 | |
| 0.024751 | 18.81997 | 1.236547 | −0.04111 | 26.30678 | 0.092649 | 0.001557 | 37.47063 | |
| 0.025044 | 18.91934 | 1.242537 | −0.04126 | 26.43116 | 0.094553 | 0.001566 | 37.74179 | |
| 0.025336 | 19.01542 | 1.247948 | −0.04137 | 26.54468 | 0.09688 | 0.00157 | 38.01021 | |
| 0.025626 | 19.10826 | 1.252747 | −0.04146 | 26.64661 | 0.099704 | 0.001569 | 38.27562 | |
| 0.025914 | 19.19791 | 1.256898 | −0.0415 | 26.73621 | 0.103099 | 0.00156 | 38.53766 | |
| 0.026201 | 19.28442 | 1.260365 | −0.04151 | 26.81276 | 0.107139 | 0.001543 | 38.7959 | |
| 0.026485 | 19.36785 | 1.263117 | −0.04148 | 26.87554 | 0.111898 | 0.001517 | 39.04991 | |
| 0.026767 | 19.44826 | 1.265123 | −0.0414 | 26.9239 | 0.117446 | 0.00148 | 39.29919 | |
| 0.027046 | 19.5257 | 1.266358 | −0.04128 | 26.95726 | 0.123849 | 0.001432 | 39.54326 | |
| 0.027322 | 19.60021 | 1.266877 | −0.04112 | 26.97765 | 0.13087 | 0.001375 | 39.78162 | |
| 0.027594 | 19.67179 | 1.266677 | −0.04092 | 26.98516 | 0.138496 | 0.001311 | 40.01379 | |
| 0.027864 | 19.73948 | 1.26652 | −0.04072 | 26.98877 | 0.146274 | 0.001243 | 40.23931 | |
| 0.028129 | 19.80339 | 1.266622 | −0.04053 | 26.99154 | 0.15405 | 0.001173 | 40.45773 | |
| 0.028391 | 19.86365 | 1.266966 | −0.04034 | 26.99342 | 0.161823 | 0.001102 | 40.66865 | |
| 0.028648 | 19.92038 | 1.267532 | −0.04016 | 26.99438 | 0.169592 | 0.001028 | 40.87171 | |
| 0.028901 | 19.97373 | 1.268301 | −0.03999 | 26.99436 | 0.177358 | 0.000953 | 41.06661 | |
| 0.029149 | 20.02385 | 1.269254 | −0.03983 | 26.99334 | 0.185121 | 0.000876 | 41.25308 | |
| 0.029393 | 20.07084 | 1.27038 | −0.03968 | 26.9913 | 0.19288 | 0.000796 | 41.43094 | |
References
- Da Silva, T.M.; Immich, F.; De Araujo, T.S.; Lund, R.G.; Da Silva, A.F.; Piva, E.; Da Rosa, W.L.D.O. Photosensitive resins used in additive manufacturing for oral application in dentistry: A scoping review from lab to clinic. J. Mech. Behav. Biomed. Mater. 2023, 141, 105732. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Miller, J.; Vezza, J.; Mayster, M.; Raffay, M.; Justice, Q.; Al Tamimi, Z.; Hansotte, G.; Sunkara, L.D.; Bernat, J. Additive Manufacturing: A Comprehensive Review. Sensors 2024, 24, 2668. [Google Scholar] [CrossRef] [PubMed]
- Roes, F.; Boyer, R.; Dutta, B. 1—Introduction to aerospace materials requirements and the role of additive manufacturing. In Additive Manufacturing for the Aerospace Industry; Froes, F., Boyer, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–6. [Google Scholar]
- Alami, A.H.; Ghani Olabi, A.; Alashkar, A.; Alasad, S.; Aljaghoub, H.; Rezk, H.; Abdelkareem, M.A. Additive manufacturing in the aerospace and automotive industries: Recent trends and role in achieving sustainable development goals. Ain Shams Eng. J. 2023, 14, 102516. [Google Scholar] [CrossRef]
- Turkcan, H.; Imamoglu, S.Z.; Ince, H. To be more innovative and more competitive in dynamic environments: The role of additive manufacturing. Int. J. Prod. Econ. 2022, 246, 108418. [Google Scholar] [CrossRef]
- Quan, H.; Zhang, T.; Xu, H.; Luo, S.; Nie, J.; Zhu, X. Photo-curing 3D printing technique and its challenges. Bioact. Mater. 2020, 5, 110–115. [Google Scholar] [CrossRef]
- Pinto, C.C.; Silva, F.D.; Guidi, E.S. Analytical, Experimental, and Finite Element Study of Stress Concentration for Samples Printed on Masked Stereolithography Devices. Appl. Mechan. 2025, 6, 21. [Google Scholar] [CrossRef]
- Kumar, S.; Bhushan, P.; Pandey, M.; Bhattacharya, S. Additive manufacturing as an emerging technology for fabrication of microelectromechanical systems (MEMS). J. Micromanufacturing 2019, 2, 175–197. [Google Scholar] [CrossRef]
- Minin, A.; Blatov, I.; Rodionov, S.; Zubarev, I. Development of a cell co-cultivation system based on protein magnetic membranes, using a mSLA 3D printer. Bioprinting 2021, 23, e00150. [Google Scholar] [CrossRef]
- Taormina, G.; Sciancalepore, C.; Messori, M.; Bondioli, F. 3D printing processes for photocurable polymeric materials: Technologies, materials, and future trends. J. Appl. Biomater. Funct. Mater. 2018, 16, 151–160. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, P. 3D printing of photopolymers. Polym. Chem. 2018, 9, 1530–1540. [Google Scholar] [CrossRef]
- Wu, J.; Zhao, Z.; Hamel, C.M.; Mu, X.; Kuang, X.; Guo, Z.; Qi, H.J. Evolution of material properties during free radical photopolymerization. J. Mech. Phys. Solids 2018, 112, 25–49. [Google Scholar] [CrossRef]
- Brighenti, R.; Cosma, M.P. Mechanical behavior of photopolymerized materials. J. Mech. Phys. Solids 2021, 153, 104456. [Google Scholar] [CrossRef]
- Štaffová, M.; Ondreáš, F.; Svatík, J.; Zbončák, M.; Jančář, J.; Lepcio, P. 3D printing and post-curing optimization of photopolymerized structures: Basic concepts and effective tools for improved thermomechanical properties. Polym. Test. 2022, 108, 107499. [Google Scholar] [CrossRef]
- Nowacki, B.; Kowol, P.; Kozioł, M.; Olesik, P.; Wieczorek, J.; Wacławiak, K. Effect of Post-Process Curing and Washing Time on Mechanical Properties of mSLA Printouts. Materials 2021, 14, 4856. [Google Scholar] [CrossRef] [PubMed]
- Salmoria, G.V.; Ahrens, C.H.; Beal, V.E.; Pires, A.T.N.; Soldi, V. Evaluation of post-curing and laser manufacturing parameters on the properties of SOMOS 7110 photosensitive resin used in stereolithography. Mater. Des. 2009, 30, 758–763. [Google Scholar] [CrossRef]
- Uzcategui, A.C.; Muralidharan, A.; Ferguson, V.L.; Bryant, S.J.; McLeod, R.R. Understanding and Improving Mechanical Properties in 3D printed Parts Using a Dual-Cure Acrylate-Based Resin for Stereolithography. Adv. Eng. Mater. 2018, 20, 1800876. [Google Scholar] [CrossRef]
- Diniță, A.; Neacșa, A.; Portoacă, A.I.; Tănase, M.; Ilinca, C.N.; Ramadan, I.N. Additive Manufacturing Post-Processing Treatments, a Review with Emphasis on Mechanical Characteristics. Materials 2023, 16, 4610. [Google Scholar] [CrossRef]
- Bednarczyk, P.; Walkowiak, K.; Irska, I. Epoxy (Meth)acrylate-Based Thermally and UV Initiated Curable Coating Systems. Polymers 2023, 15, 4664. [Google Scholar] [CrossRef]
- ISO 527-2; Plastics—Determination of Tensile Properties—Part 2: Test Conditions for Moulding and Extrusion Plastics. ISO: Geneva, Switzerland, 2012.
- ISO 178; Plastics—Determination of Flexural Properties. ISO: Geneva, Switzerland, 2019.
- Chatani, S.; Kloxin, C.J.; Bowman, C.N. The Power of Light in Polymer Science: Photochemical Processes to Manipulate Polymer Formation, Structure, and Properties. Polym. Chem. 2014, 5, 2187–2201. [Google Scholar] [CrossRef]
- Rabek, J.F. Polymer Photodegradation: Mechanisms and Experimental Methods; Chapman & Hall: London, UK, 1995. [Google Scholar] [CrossRef]
- Andrady, A.L.; Hamid, S.H.; Hu, X.; Torikai, A. Effects of Increased Solar Ultraviolet Radiation on Materials. J. Photochem. Photobiol. B Biol. 1998, 46, 96–103. [Google Scholar] [CrossRef]
- Dietliker, K. A Compilation of Photoinitiators Commercially Available for UV Today; SITA Technology Ltd.: London, UK, 2002. [Google Scholar]
- Jakubiak, J.; Allonas, X.; Fouassier, J.P.; Sionkowska, A.; Andrzejewska, E.; Linden, L. Camphorquinone–Amines Photoinitiating Systems for the Initiation of Free Radical Polymerization. Polymer 2003, 44, 5219–5226. [Google Scholar] [CrossRef]
- Stansbury, J.W.; Idacavage, M.J. 3D Printing with Polymers: Challenges among Expanding Options and Opportunities. Dent. Mater. 2016, 32, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Decker, C.; Jenkins, A.D. Kinetic Approach of Oxygen Inhibition in Ultraviolet- and Electron Beam-Induced Polymerizations. Macromolecules. 1985, 18, 1241–1244. [Google Scholar] [CrossRef]
- O’Brien, A.K.; Bowman, C.N. Impact of Oxygen on Photopolymerization Kinetics and Polymer Structure. Macromolecules 2006, 39, 2501–2506. [Google Scholar] [CrossRef]
- Pospíšil, J. Mechanistic Action of Phenolic Antioxidants in Polymers—A Review. Polym. Degrad. Stab. 1988, 20, 181–202. [Google Scholar] [CrossRef]
- Scott, G. Atmospheric Oxidation and Antioxidants; Elsevier: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Dietliker, K. Photoinitiators for Free Radical and Cationic Polymerisation; SITA Technology Ltd.: London, UK, 1991. [Google Scholar]
- Gruber, H.F. Photoinitiators for Free Radical Polymerization. Prog. Polym. Sci. 1992, 17, 953–1044. [Google Scholar] [CrossRef]
- Singh, V. Literature Survey of Strain Rate Effects on Composites; TR18-001 (open), Swerea (now RISE) SICOMP: Mölndal, Sweden, 2018. [Google Scholar]
- Korolev, A.; Zadorin, A.; Mishnev, M. The Finite Element Method in Thermosetting Polymers’ and FRPs’ Supramolecular Structure and Thermomechanical Properties’ Modeling. Polymers 2024, 16, 3443. [Google Scholar] [CrossRef]
- Meißner, R.H.; Konrad, J.; Boll, B.; Fiedler, B.; Zahn, D. Molecular Simulation of Thermosetting Polymer Hardening: Reactive Events Enabled by Controlled Topology Transfer. Macromolecules 2020, 53, 9698–9705. [Google Scholar] [CrossRef]
- Gaikwad, P.S.; Krieg, A.S.; Deshpande, P.P.; Patil, S.U.; King, J.A.; Maiaru, M.; Odegard, G.M. Understanding the Origin of the Low Cure Shrinkage of Polybenzoxazine Resin by Computational Simulation. ACS Appl. Polym. Mater. 2021, 3, 6407–6415. [Google Scholar] [CrossRef]
- Zhang, J.-T.; Shang, Y.-D.; Zhang, M.; Liu, L.-S.; Zhai, P.-C.; Li, S.-X. Cure-Dependent Viscoelastic Analysis on the Residual Stresses and Distortion Created in Composite Corner during Curing. In Proceedings of the 2nd Annual International Conference on Advanced Material Engineering (AME 2016), Guangzhou, China, 24–25 July 2016; Atlantis Press: Paris, France, 2016; pp. 20–27. [Google Scholar] [CrossRef][Green Version]
- Bonhin, E.; David Müzel, S.; Cesar, G.; Oliveira, R.; Luiz, W.; Tupinambá, M.; Guidi, E.; Alexis, C.; Alvarado Silva, C.; De, F.; et al. Evaluation and Feasibility of Different Models and Methods for Composite Simulation Using Ansys. IAENG Int. J. Comput. Sci. 2024, 51, 918–924. [Google Scholar]
- Oliveira, G.C.R.d.; Rosario de Oliveira, V.A.; Alvarado Silva, C.A.; Guidi, E.S.; Silva, F.d.A. Modeling the Stress Field in MSLA-Fabricated Photosensitive Resin Components: A Combined Experimental and Numerical Approach. Modelling 2025, 6, 3. [Google Scholar] [CrossRef]











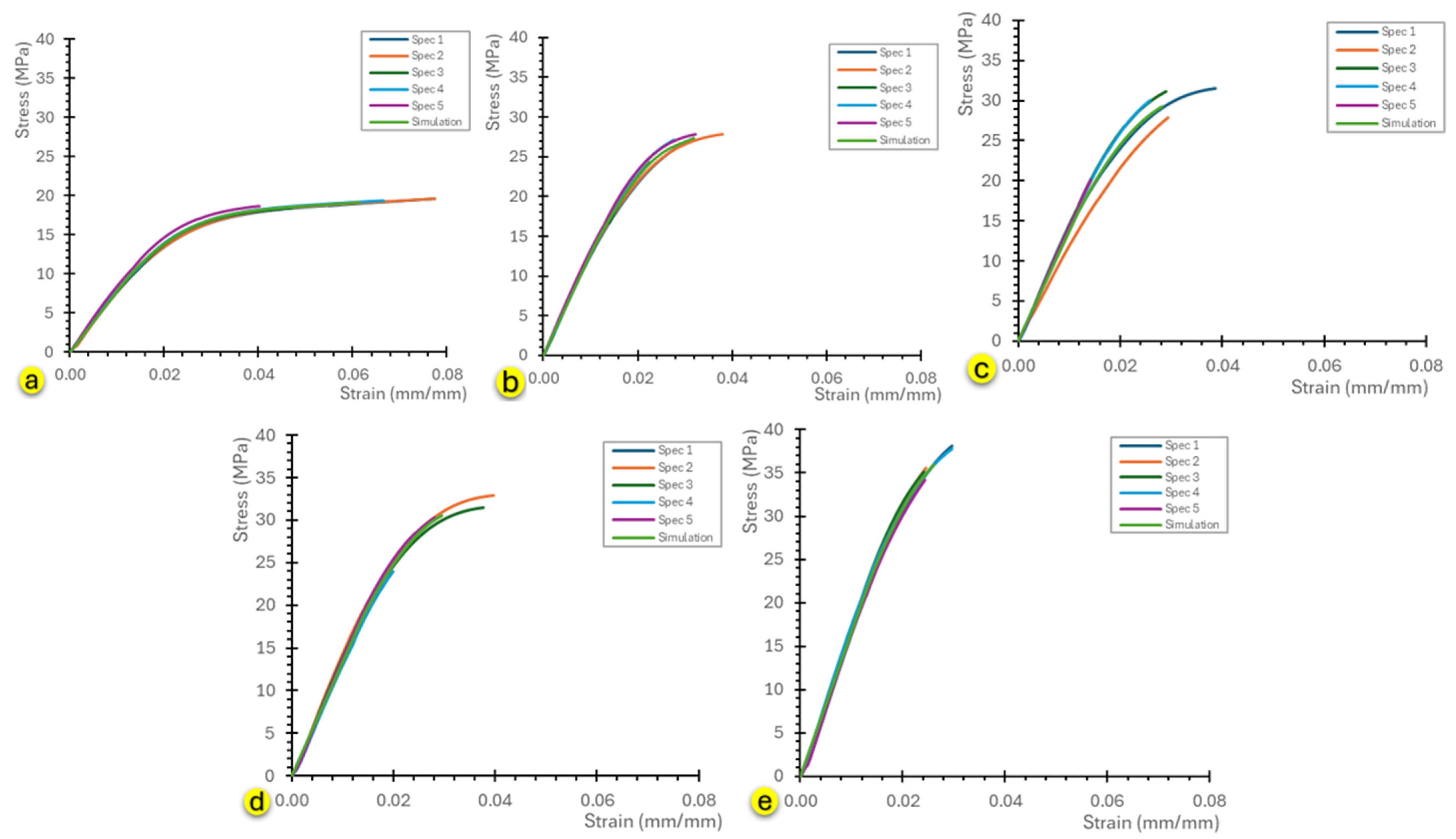
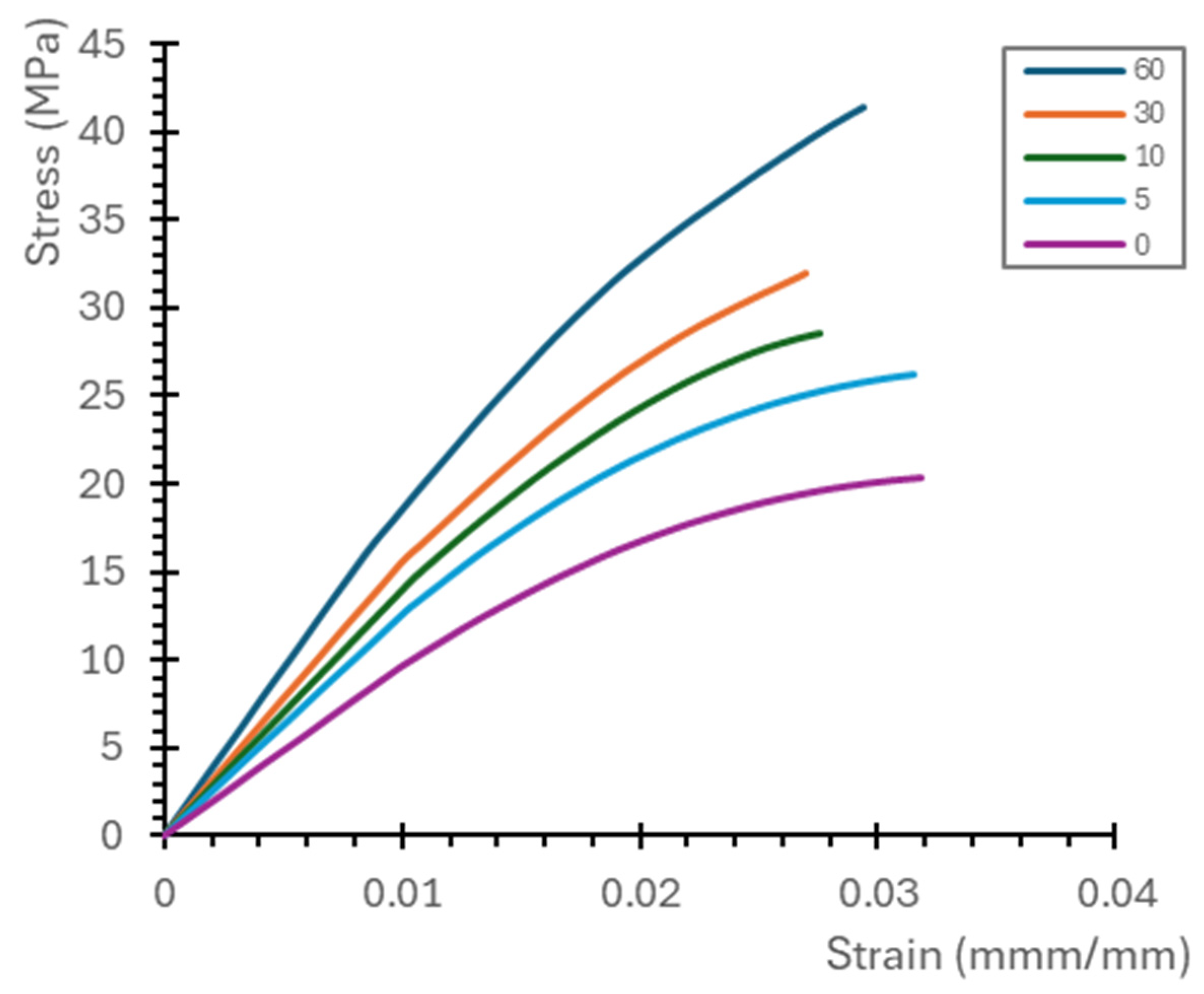
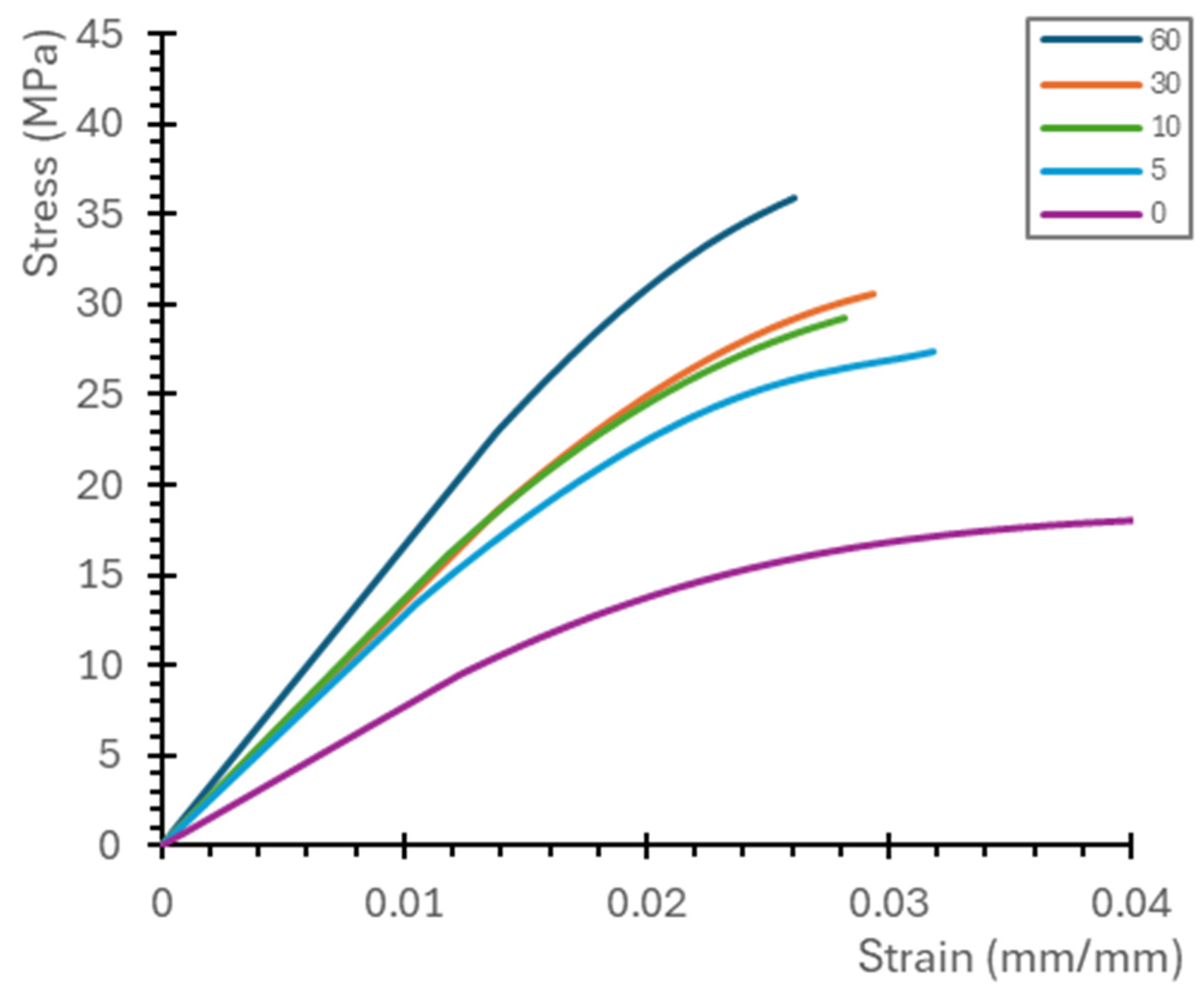

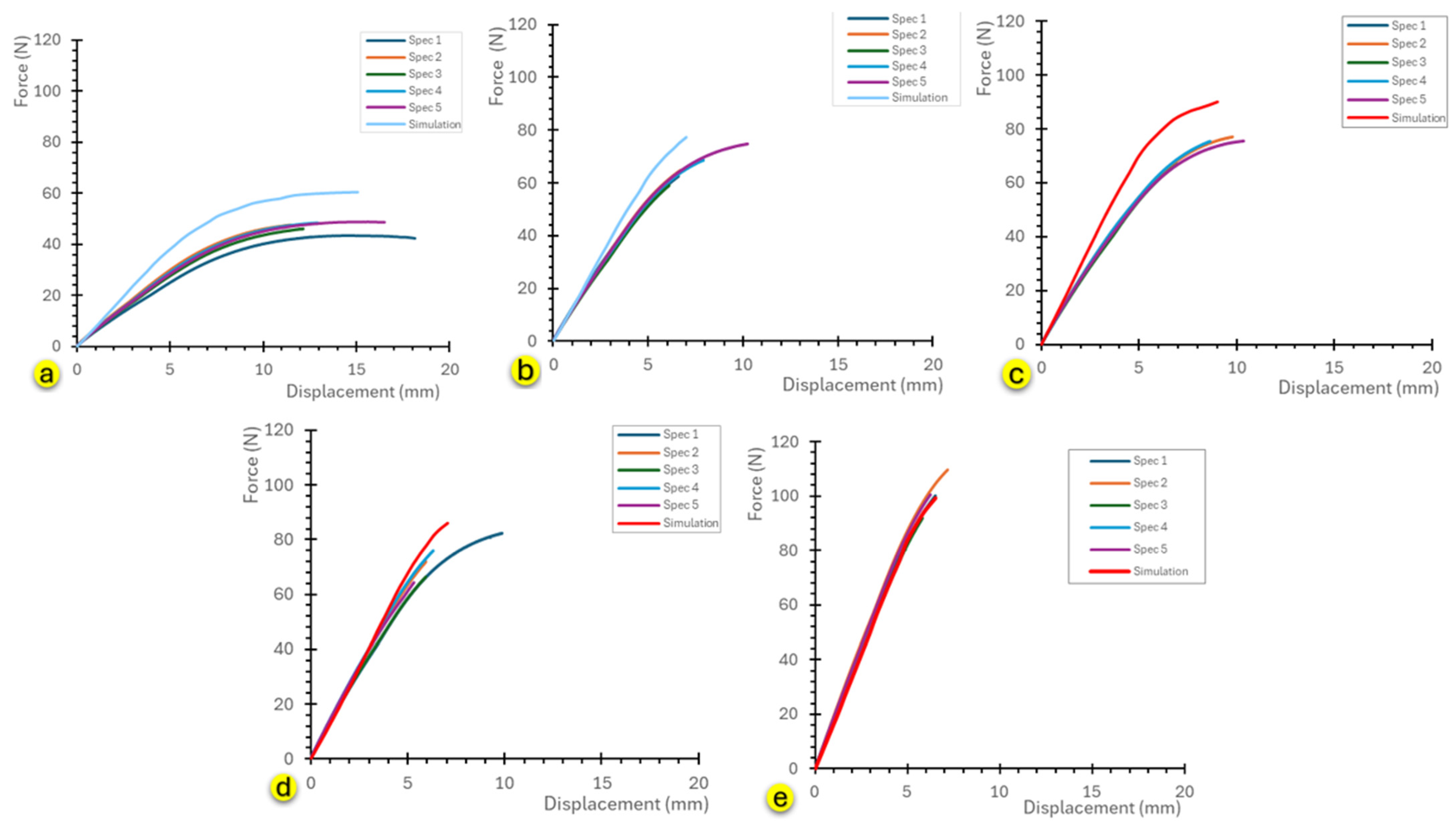
| Post-Curing Time (min) | 0 | 5 | 10 | 30 | 60 |
|---|---|---|---|---|---|
| Young’s Modulus (MPa) | 964.5 | 1255 | 1392.4 | 1551.5 | 1892.4 |
| Poisson’s Ratio | 0.34 | 0.34 | 0.34 | 0.34 | 0.34 |
| Shear Modulus (MPa) | 359.9 | 468.3 | 519.5 | 578.9 | 706.1 |
| Post-Curing Time (min) | 0 | 5 | 10 | 30 | 60 |
|---|---|---|---|---|---|
| Young’s Modulus (MPa) | 774 | 1278 | 1363 | 1339 | 1661.2 |
| Poisson’s Ratio | 0.34 | 0.34 | 0.34 | 0.34 | 0.34 |
| Shear Modulus (MPa) | 288.8 | 476.8 | 508.6 | 499.6 | 619.8 |
| Position | |||
|---|---|---|---|
| Exposure Time | Flat [XY] | On-Edge [XZ] | Vertical [Z] |
| 0 min | 16.0 mm | 15.0 mm | 14.0 mm |
| 05 min | 9.5 mm | 7.0 mm | 8.5 mm |
| 10 min | 9.0 mm | 9.0 mm | 8.0 mm |
| 30 min | 9.5 mm | 7.0 mm | 7.0 mm |
| 60 min | 7.0 mm | 6.5 mm | 7.0 mm |
| a0 | a1 | a2 | a3 | a4 | a5 | |
|---|---|---|---|---|---|---|
| 0 min | 4,533,820,000.00 | 646,962,000.00 | −26,541,900.00 | 193,738.00 | −8387.88 | 1048.53 |
| 5 min | 3934.12 | −153,492,000.00 | 22,219,200.00 | −1,115,860.00 | 2184.38 | 1327.71 |
| 10 min | 426,750,000,000.00 | −39,348,900,000.00 | 1,343,980,000.00 | −21,096,500.00 | 132,118.00 | 1186.95 |
| 30 min | 1.00 | 5,144,658,833.70 | −393,726,332.77 | 10,776,234.69 | −145,371.92 | 2267.45 |
| 60 min | 1.00 | 1,556,773,000.00 | −96,010,600.00 | 1,777,159.00 | −31,107.86 | 2067.92 |
| a0 | a1 | a2 | a3 | a4 | a5 | |
|---|---|---|---|---|---|---|
| 0 min | 1,085,050,000.00 | −293,125,000.00 | 29,652,300.00 | −1,280,220.00 | 11,677.20 | 775.27 |
| 05 min | 13,152,100,000.00 | −12,303,100,000.00 | 442,574,000.00 | −7,970,800.00 | 57,142.00 | 1176.92 |
| 10 min | 27,498,000,000.00 | −3,297,630,000.00 | 169,977,000.00 | −4,790,010.00 | 50,100.10 | 1215.67 |
| 30 min | 69,510,700,000.00 | −7,894,720,000.00 | 359,565,000.00 | −8,577,360.00 | 90,334.80 | 1031.80 |
| 60 min | 330,133,000,000.00 | −30,573,500,000.00 | 1,117,810,000.00 | −20,920,100.00 | 186,509.00 | 1074.73 |
| Post-Curing Time (min) | Young’s Modulus (MPa) | Shear Modulus (MPa) |
|---|---|---|
| 0 | 964.5 ± 45.2 | 359.9 ± 16.8 |
| 5 | 1255.0 ± 62.1 | 468.3 ± 23.2 |
| 10 | 1392.4 ± 58.9 | 519.6 ± 22.0 |
| 30 | 1551.5 ± 71.3 | 578.9 ± 26.6 |
| 60 | 1892.4 ± 89.7 | 706.1 ± 33.5 |
| Post-Curing Time (min) | Young’s Modulus (MPa) | Shear Modulus (MPa) |
|---|---|---|
| 0 | 774.0 ± 38.2 | 288.8 ± 14.3 |
| 5 | 1278.0 ± 59.4 | 476.9 ± 22.2 |
| 10 | 1363.0 ± 67.1 | 508.6 ± 25.0 |
| 30 | 1339.0 ± 61.8 | 499.6 ± 23.1 |
| 60 | 1661.2 ± 78.9 | 619.8 ± 29.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, G.C.R.d.; Oliveira, V.A.R.d.; Pinto, C.C.; Marques, L.F.B.; Santos, T.S.R.d.; Neto, A.d.R.d.F.; Silva, C.A.A.; Martins, M.S.; Silva, F.d.A.; Guidi, E.S. Influence of Post-Curing Time and Print Orientation on the Mechanical Behavior of Photosensitive Resins in mSLA 3D Printing. Appl. Mech. 2025, 6, 71. https://doi.org/10.3390/applmech6030071
Oliveira GCRd, Oliveira VARd, Pinto CC, Marques LFB, Santos TSRd, Neto AdRdF, Silva CAA, Martins MS, Silva FdA, Guidi ES. Influence of Post-Curing Time and Print Orientation on the Mechanical Behavior of Photosensitive Resins in mSLA 3D Printing. Applied Mechanics. 2025; 6(3):71. https://doi.org/10.3390/applmech6030071
Chicago/Turabian StyleOliveira, Geraldo Cesar Rosario de, Vania Aparecida Rosario de Oliveira, Carla Carvalho Pinto, Luis Felipe Barbosa Marques, Tuane Stefania Reis dos Santos, Antonio dos Reis de Faria Neto, Carlos Alexis Alvarado Silva, Marcelo Sampaio Martins, Fernando de Azevedo Silva, and Erick Siqueira Guidi. 2025. "Influence of Post-Curing Time and Print Orientation on the Mechanical Behavior of Photosensitive Resins in mSLA 3D Printing" Applied Mechanics 6, no. 3: 71. https://doi.org/10.3390/applmech6030071
APA StyleOliveira, G. C. R. d., Oliveira, V. A. R. d., Pinto, C. C., Marques, L. F. B., Santos, T. S. R. d., Neto, A. d. R. d. F., Silva, C. A. A., Martins, M. S., Silva, F. d. A., & Guidi, E. S. (2025). Influence of Post-Curing Time and Print Orientation on the Mechanical Behavior of Photosensitive Resins in mSLA 3D Printing. Applied Mechanics, 6(3), 71. https://doi.org/10.3390/applmech6030071





